Материал для проведения школьного этапа олимпиады по математике

Материал для проведения школьной математической олимпиады

(2010-1011 учебный год)

   7класс

1.Найдите значение выражения: 3-(1,6-1)·:1              3 балла.

2.Решите уравнение:   ·(1,5х+0,6)-0,8·(            3 балла.   

3. Докажите, что значение выражения не зависит от «у».

      -(12у-3(у-4))+9у.                                                              3 балла.   

4. Точки А (-3;1), В(1;1), С(1;-1)- вершины прямоугольника АВСD. Найдите координаты четвертой вершины прямоугольника и вычислите периметр и площадь, если единичный отрезок равен 0,5.                         4 балла.

5. Автомобиль ехал 3 часа по шоссе и 2 часа по проселочной дороге. По дороге его скорость была на 15 км/ч меньше, чем на шоссе. Всего за 5 часов автомобиль проехал 270 км. Найдите скорость автомобиля на шоссе и на проселочной дороге.                                                                                        5 баллов.

8 класс

1.Упростите выражение:  (               3 балла.

2. Зная, что   найдите значение выражения    3 балла.

3. Костюм стоил 800 рублей. Цену снизили на 15%, а потом увеличили на 15%. Сколько теперь стоит костюм?                                   4 балла.

4. В банке несколько вариантов использования денег:

а) вложить 800 рублей и получить 1000 рублей;

б) вложить 20 рублей и получить 30 рублей;

8) вложить 5000 рублей и получить 7000 рублей.

Какой вариант вы выберете и почему?                               4 балла.

5. Докажите, что биссектрисы внешних углов прямоугольника образуют квадрат.                                                                                   5 баллов.

9класс

1.При каком значении параметра m ровно один из корней уравнения равен нулю:

                                                                                                                      3 балла.

2.Цену некоторого товара снизили на 15 %, а потом еще на 20%. Найти         общий процент снижения цены.                                                       3 балла.

3. Упростите выражение:  (:             4 балла.

4. Определенную работу 15 рабочих выполняют за 300 дней. За сколько дней, работая с той же производительностью. Выполнят эту работу 20 человек?

5. Сравните значения выражений:  и           5 баллов.

                                                               10 класс

1.Какой цифрой оканчивается                           3 балла.

2.Укажите число целых значений, входящих в область определения функции:

                                     у =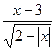                                      3 балла.

3.Общество с ограниченной ответственностью (ООО) пообещало начислить 1000% к вложенной сумме ежегодно. После успешной сдачи экзамена молодой человек внес в ООО вклад в 5 рублей. Какую сумму в рублях он получит после окончания вуза через 5 лет, если ООО выполнит свои обязательства.                                                                       4 балла.

4.Найти площадь круга, вписанного в равнобедренную трапецию АВСD (АВ‌‌‌ и CD основания)‌‌‌‌‌‌‌‌‌‌, если АВ=4,DC=14.                                5 баллов.

5.Докажите, что число (1+·2·3·…·2004  целое и делится на 2005. 

                                                                                    5 баллов.

11 класс

1. Решите уравнение: 2cosх+cos х=1.                            3 балла.

2.Вычислите:  - +             3 балла.

3. Решите неравенство: .                      4 балла.

4.Точка,  расположенная внутри равнобедренного треугольника с углом при основании , находится на одинаковом расстоянии 4 от боковых сторон и на расстоянии 10 от основания. Найдите длину боковой стороны. 

                                                                                            5 баллов.

5.В правильной шестиугольной призме  сторона

основания равна 6. Найдите расстояние от точки В до прямой  EF .                                                                      

                                                                                           5 баллов.