Материал для урока в 11 классе по теме Решение систем линейных уравнений. Метод Гаусса

Системы линейных уравнений

Определение 1. Системой линейных уравнений, содержащей               m уравнений и n неизвестных, называется система вида

 

 

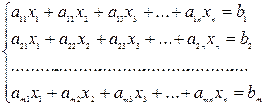
где  числа a_ij – называются коэффициентами системы, числа                    b_ij – свободными членами.

 

Определение 2. Система  уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

 

Определение 3. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

 

В последенем случае каждое решение  системы называется частным решением системы. Совокупность всех частных решений называется общим решением.

 

Решить систему – это значит выяснить, совместна она или несовместна. Если совместна, найти ее общее решение.

 

1.2   Решение систем линейных уравнений. Метод Гаусса.

 

Пусть дана система m линейных уравнений с n неизвестными:

 

 

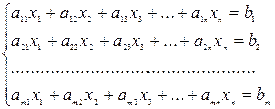
Матрица А = 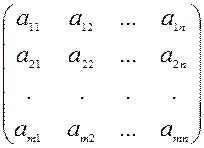, составленная из коэффициентов при неизвестных х_i (i = 1,2,…n), называется матрицей системы.

 

Матрица  B = 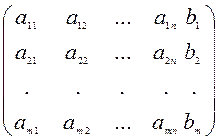, составленная из коэффициентов при неизвестных и свободных членов, называется расширенной матрицей.

 

Определение 4. Матрица А называется матрицей треугольного вида, если все ее элементы выше (ниже) главной диагонали равны нулю.

 

Например,   А = 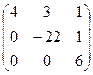    или   В =  - матрицы треугольного вида.

Метод Гаусса удобно использовать при решении систем с большим количеством уравнений. Этот метод  заключается в последоваетльном исключении неизвестных. Систему линейных уравнений приводят к системе с треугольной матрицей с помощью эквивалентных преобразований. Затем  из полученной системы переменные находят с помощью последовательных подстановок.

 

К эквивалентным преобразованиям относят следующие:

 

·        умножение и деление коэффициентов и свободных членов на одно и тоже число, отличное от нуля.

·        Сложение и вычитание уравнений.

·        Перестановка уравнений.

·        Исключение из системы уравнений, в которых все коэффициенты равны нулю.

 

 

 

Пример 1

 

Решить систему линейных уравнений методом Гаусса:

 

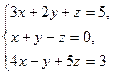
Выпишем расширенную матрицу системы:

 

 

 

Для упрощения вычислений поменяем первую и вторую строки местами:

 

 

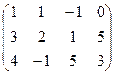
Умножим первую строку на –3 и сложим ее со второй строкой. Первую строку умножим на –4  и сложим с третьей сторокой, получим эквивалентную матрицу:

 

 

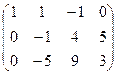
Умножим вторую строку на –1:

 

 

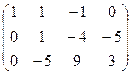
Умножим вторую строку на 5 и сложим с третьей строкой:

 

 

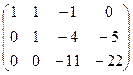
Разделим третью строку на –11:

 

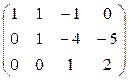
Получили матрицу треугольного вида (все элементы ниже главной диагонали равны нулю). Выпишем систему уравнений треугольного вида:

 

                           

 

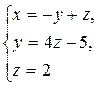
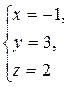
Ответ: х = -1, у = 3, z = 2

 

 

 

 

1.3  Решение систем линейных уравнений методом Крамера.

 

Для решения систем линейных уравнений с большим количеством уравнений применяют метод Гаусса. Если же уравнений в системе не так много, то удобнее использовать метод Крамера. Этот метод основан на вычислении определителей.

Пусть дана система n линейных уравнений с n неизвестными:

 

Составим определитель матрицы системы:

 

Заменим в определителе D первый столбик, соответствующий переменной х₁, на столбец свободных членов b₁, b₂, …,b_n, получим определитель D_х1:

 

 

 

Заменим в определителе D второй столбик, соответствующий переменной х₂, на столбец свободных членов b₁, b₂, …,b_n, получим определитель D_х2:

 

 

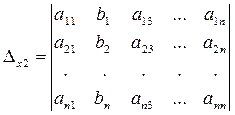
Аналогично поступаем с третьим, четвертым, …, n –ым столбцами определителя D. В итоге получим n+1 определитель. Для того, чтобы найти неизвестные х₁, х₂ , …, х_n используем формулы Крамера:

   ,      , …, 

 

При вычислении определителей могут возникнуть следующие случаи:

 

·        если определитель матрицы системы D отличен от 0, то система линейных уравнений имеет единственное решение;

·        если определитель матрицы системы D равен  0, а среди определителей              D_х1, D_х2, …, D_хn  есть хотя один отличный от 0, то система линейных уравнений не имеет  решений;

·        если определитель матрицы системы D равен  0 и все определители                     D_х1, D_х2, …, D_хn  равны 0, то система линейных уравнений  имеет бесконечно много решений.

 

 

Пример 3.

 

Решить систему линейных уравнений  методом Крамера:

 

Выпишем определитель матрицы системы D и вычислим его:

 

 

Так как  D0, то система имеет единственное решение.

Заменим в определителе D первый столбик на столбец свободных коэффициентов, получим D_х :

 

 

Заменим в определителе D второй столбик на столбец свободных коэффициентов, получим D_у :

 

 

Найдем значения переменных х и у по формулам Крамера:

 

   ,      

Ответ: (-3;1)

 

 

 

Пример 4.

 

Решить систему линейных уравнений методом Крамера:

 

 

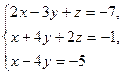
Выпишем определитель матрицы системы D и вычислим его:

 

 

Так как  D0, то система имеет единственное решение.

Заменим в определителе D первый столбик на столбец свободных коэффициентов, получим D_х :

 

 

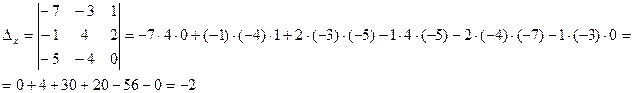
Заменим в определителе D первый столбик на столбец свободных коэффициентов, получим D_у :

 

 

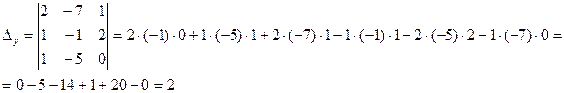
Заменим в определителе D первый столбик на столбец свободных коэффициентов, получим D_z :

 

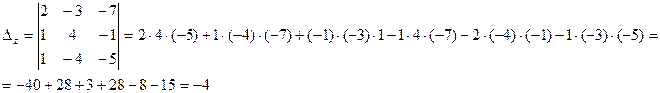
Найдем значения переменных х , у и z по формулам Крамера:

   ,       ,       

 

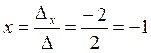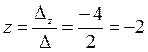
Ответ:  (-1; 1; -2)