МДК 02.01 Разработка, внедрение и адаптация ПО отраслевой направленности

Лекция 6.

Вероятностные модели систем

I. Вероятностные автоматы (дискретно-стохастические модели)

Основные соотношения. Рассмотрим особенности построения математических схем при дискретно-стохастическом подходе на вероятностных (стохастических) автоматах Р-схемах (англ. probabijistic automat).

Введем математическое понятие Р-автомата, используя понятия, введенные для F-автомата. Рассмотрим множество G, элементами которого являются всевозможные пары (x_i, z_s), где x_i и z_s – элементы входного подмножества Х и подмножества состояний Z соответственно. Если существуют две такие функции j и y, что с их помощью осуществляются отображения G®Z и G®Y, то говорят, что F = <Z, X, Y, j, y> определяет автомат детерминированного типа.

Рассмотрим более общую математическую схему. Пусть Ф – множество всевозможных пар вида (z_k, y_i), где у_i – элемент выходного подмножества Y. Потребуем, чтобы любой элемент множества G индуцировал на множестве Ф некоторый закон распределения следующего вида:

При этом b_kj = 1, где b_kj – вероятности перехода автомата в состояние z_k и появления на выходе сигнала y_j , если он был в состоянии z_s и на его вход в этот момент времени поступил сигнал x_i. Число таких распределений, представленных в виде таблиц, равно числу элементов множества G. Обозначим множество этих таблиц через В. Тогда четверка элементов P = <Z, X, Y, B> называется вероятностным автоматом (Р-автоматом).

Возможные приложения P-схемы. Пусть элементы множества G индуцируют некоторые законы распределения на подмножествах Y и Z, что можно представить соответственно в виде:

При этом z_k = 1 и q_j = 1, где z_k  и q_j  - вероятности  перехода Р-автомата в состояние z_k и появления выходного сигнала y_k при условии, что Р-автомат находился в состоянии z_s и на его вход поступил входной сигнал x_i.

Если для всех k и j имеет место соотношение q_j z_k = b_kj, то такой Р-автомат называется вероятностным автоматом Мили. Это требование означает выполнение условия независимости распределений для нового состояния Р-автомата и его выходного сигнала.

Пусть теперь определение выходного сигнала Р-автомата зависит лишь от того состояния, в котором находится автомат в данном такте работы. Другими словами, пусть каждый элемент выходного подмножества Y индуцирует распределение вероятностей выходов, имеющих следующий вид:

Здесь s_i = 1, где s_i – вероятность появления выходного сигнала y_i при условии, что Р-автомат находился в состоянии z_k.

Если для всех k и i  имеет  место  соотношение   z_k s_i = b_ki ,то такой Р-автомат называется вероятностным автоматом Мура. Понятие Р-автоматов Мили и Мура введено по аналогии с детерминированным F-автоматом. Частным случаем Р-автомата, задаваемого как P=<Z, X, Y, B>, являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминированно. Если выходной сигнал Р-автомата определяется детерминированно, то такой автомат называется Y-детерминированным вероятностным автоматом. Аналогично, Z-детерминированным вероятностным автоматом называется Р-автомат, у которого выбор нового состояния является детерминированным.

Пример 1. Пусть задан Y-детерминированный P-автомат

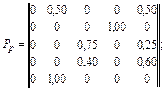
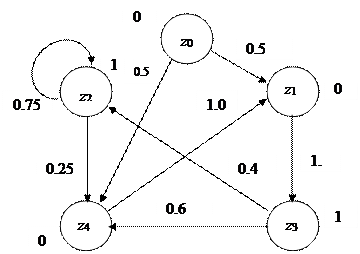На рис. 1 показан ориентированный граф переходов этого автомата. Вершины графа сопоставляются состояниям автомата, а дуги – возможными переходами из одного состояния в другое. Дуги имеют веса, соответствующие вероятностям перехода p_ij, а около вершин графа пишутся значения выходных сигналов, индуцируемых этими состояниями. Требуется оценить суммарные финальные вероятности пребывания этого P-автомата в состояниях z₂ и z₃.

Рис. 1. Граф вероятностного автомата.

При использовании аналитического подхода можно записать известные соотношения из теории марковских цепей и получить систему уравнений для определения финальных вероятностей:

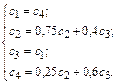
Таким образом, с₂ + с₃ = 13/23 = 0,5652. Другими словами, при бесконечной работе заданного в этом примере Y-детерминированного Р-автомата на его выходе формируется двоичная последовательность с вероятностью появления единицы, равной 0,5652.

Вероятностные автоматы используются в формальных моделях процессов обучения, в моделях сложного поведения, когда реакция автомата неоднозначна.

Пример 2.  Вероятностным автоматом может служить система автоматического управления движением транспорта на перекрёстке двух улиц с разной интенсивностью движения. Для простоты рассмотрим вероятностный автомат с двумя состояниями: «откр» — проезд по магистрали (улица с интенсивным движением) открыт и «закр» — магистраль перекрыта, разрешено поперечное движение. Входных сигналов тоже два: S₁ — «на поперечной улице ждет транспорт» и S₂ — «эта улица пуста». Переходные вероятности определены так:

Р (закр ® закр, S₂) = Р (откр ® закр, S₂) = 0;

Р (откр ® откр, S₂) = Р (закр ® откр, S₂) = 1;

Р (откр ® откр, S₁) = 0,7;

Р (откр ® закр, S₁) = 0,3;

Р (закр ® закр, S₁) = 0,5;

Р (закр ® откр, S₁) = 0,5.

Такой автомат по мере надобности пропускает поперечный транспорт, но не перекрывает магистраль при появлении на поперечном направлении каждой отдельной машины. Численные значения вероятностей переходов и время основного такта работы автомата необходимо выбирать исходя из конкретного транспортного режима.

Вероятностный автомат очень удобен как модель системы, поскольку адекватно отображает неполноту наших знаний о системе и позволяет без лишних усилий повышать точность модели по мере получения этих знаний. Функционирование вероятностного автомата без труда имитируется на компьютере.

II. Системы массового обслуживания (непрерывно-стохастические модели)

Основные соотношения. Особенности непрерывно-стохастического подхода рассмотрим на примере типовых математических Q-схем – систем массового обслуживания (англ. queueing system).

В качестве процесса обслуживания могут быть представлены различные по своей физической природе процессы функционирования экономических, производственных, технических и других систем, например: потоки поставок продукции некоторому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха, заявки на обработку информации ЭВМ от удаленных терминалов и т.д. При этом характерным для работы таких объектов является случайное появление заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени, т.е. стохастический характер процесса их функционирования.

Потоком событий называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени. Различают потоки однородных и неоднородных событий. Поток событий называется однородным, если он характеризуется только моментами поступления этих событий (вызывающими моментами) и задается последовательностью {t_n} = {0 £ t₁ £ t₂ ... £ t_n £ …}, где t_n – момент наступления п-го события – неотрицательное вещественное число. Однородный поток событий также может быть задан в виде последовательности промежутков времени между п-м и (n – 1)-м событиями {t_n}, которая однозначно связана с последовательностью вызывающих моментов {t_n}, где t_n = t_n – t_n-1, п ³ 1, t₀ = 0, т.е. t₁ = t₁.

Потоком неоднородных событий называется последовательность {t_n, f_n}, где t_n – вызывающие моменты; f_n – набор признаков события. Например, применительно к процессу обслуживания для неоднородного потока заявок может быть задана принадлежность к тому или иному источнику заявок, наличие приоритета, возможность обслуживания тем или иным типом канала.

В любом элементарном акте обслуживания можно выделить две основные составляющие: ожидание обслуживания заявкой и собственно обслуживание заявки. Это можно изобразить в виде некоторого i-го прибора обслуживания П_i (рис. 2), состоящего из накопителя заявок H_i, в котором может одновременно находиться j_i =  заявок, где L_i^H – емкость i-гo накопителя, и канала обслуживания заявок (или просто канала) K_i. На каждый элемент прибора обслуживания П_i поступают потоки событий: в накопитель H_i поток заявок w_i, на канал K_i — поток обслуживаний и_i .

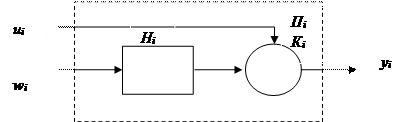Рис. 2. Прибор обслуживания заявок

Заявки, обслуженные каналом K_i, и заявки, покинувшие прибор П_i по различным причинам необслуженными (например, из-за переполнения накопителя H_i), образуют выходной поток y_i Î Y, т.е. интервалы времени между моментами выхода заявок образуют подмножество выходных переменных.

Обычно, поток заявок w_iÎW, т.е. интервалы времени между моментами появления заявок на входе K_i, образует подмножество неуправляемых переменных, а поток обслуживания u_iÎU, т.е. интервалы времени между началом и окончанием обслуживания заявки, образует подмножество управляемых переменных.

Пример. Прибор обслуживания – аэропорт, канал обслуживания – взлетная полоса, накопитель – воздушное пространство вокруг аэропорта, заявка – самолеты, требующие взлета или посадки.

Процесс функционирования прибора обслуживания П_i можно представить как процесс изменения состояний его элементов во времени z_i(t). Переход в новое состояние для П_i означает изменение количества заявок, которые в нем находятся (в канале K_i и в накопителе H_i). Таким образом, вектор состояний для П_i имеет вид: , где z_i^H – состояние накопителя H_i (z_i^H = 0 – накопитель пуст, z_i^H = 1 – в накопителе имеется одна заявка, ..., z_i^H = L_i^H – накопитель полностью заполнен); L_i^H – емкость накопителя Н_i, измеряемая числом заявок, которые в нем могут поместиться; z_i^k – состояние канала K_i (z_i^k = 0 – канал свободен, z_i^k = 1 – канал занят).

Возможные приложения Q-схем. В практике моделирования систем, имеющих более сложные структурные связи и алгоритмы поведения, для формализации используются не отдельные приборы обслуживания, а Q-схемы, образуемые композицией многих элементарных приборов обслуживания П_i. Если каналы К_i различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание (многоканальная Q-схема), а если приборы П_i и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание (многофазная Q-схема). Таким образом, для задания Q-схемы необходимо использовать оператор сопряжения R, отражающий взаимосвязь элементов структуры (каналов и накопителей) между собой.

Связи между элементами Q-схемы изображают в виде стрелок (линий потока, отражающих направление движения заявок). Различают разомкнутые и замкнутые Q-схемы. В разомкнутой Q-схеме выходной поток обслуженных заявок не может снова поступить на какой-либо элемент, т.е. обратная связь отсутствует, а в замкнутых Q-схемах имеются обратные связи, по которым заявки двигаются в направлении, обратном движению вход-выход.

Собственными (внутренними) параметрами Q-схемы будут являться количество фаз L_ф, количество каналов в каждой фазе L_kj, j = , количество накопителей каждой фазы L_Hk, k = , емкость i-го накопителя L_i^H. Следует отметить, что в теории массового обслуживания в зависимости от емкости накопителя применяют следующую терминологию для систем массового обслуживания: системы с потерями (L_i^H = 0, т.е. накопитель в приборе П_i отсутствует, а имеется только канал обслуживания К_i), системы с ожиданием (L_i^H®¥, т.е. накопитель Н_i имеет бесконечную емкость и очередь заявок не ограничивается) и системы смешанного типа (с ограниченной емкостью накопителя Н_i). Всю совокупность собственных параметров Q-схемы обозначим как подмножество Н.

Для задания Q-схемы также необходимо описать алгоритмы ее функционирования, которые определяют набор правил поведения заявок в системе в различных неоднозначных ситуациях. Неоднородность заявок, отражающая процесс в той или иной реальной системе, учитывается с помощью введения классов приоритетов.

В зависимости от динамики приоритетов в Q-схемах различают статические и динамические приоритеты. Статические приоритеты назначаются заранее и не зависят от состояний Q-схемы. Динамические приоритеты возникают при моделировании в зависимости от возникающих ситуаций. Исходя из правил выбора заявок из накопителя Н_i на обслуживание каналом К_i, можно выделить относительные и абсолютные приоритеты. Относительный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель Н_i, ожидает окончания обслуживания предшествующей заявки каналом K_i и только после этого занимает канал. Абсолютный приоритет означает, что заявка с более высоким приоритетом, поступившая в накопитель H_i, прерывает обслуживание каналом К_i заявки с более низким приоритетом и сама занимает канал (при этом вытесненная из К_i заявка может либо покинуть систему, либо может быть снова записана на какое-то место в H_i).

При рассмотрении алгоритмов функционирования приборов обслуживания П_i (каналов К_i и накопителей Н_i) необходимо также задать набор правил, по которым заявки покидают Н_i и К_i: для Н_i – либо правила переполнения, по которым заявки в зависимости от заполнения Н_i покидают систему, либо правила ухода, связанные с истечением времени ожидания заявки в Н_i, для К_i – правила выбора маршрутов или направлений ухода. Кроме того, для заявок необходимо задать правила, по которым они остаются в канале К_i или не допускаются до обслуживания каналом К_i, т.е. правила блокировок канала. При этом различают блокировки K_i по выходу и по входу. Такие блокировки отражают наличие управляющих связей в Q-схеме, регулирующих поток заявок в зависимости от состояний Q-схемы. Весь набор возможных алгоритмов поведения заявок в Q-схеме можно представить в виде некоторого оператора алгоритмов поведения заявок A.

Таким образом, Q-схема, описывающая процесс функционирования системы массового обслуживания любой сложности, однозначно задается в виде Q = <W, U, Н, Z, Y, R, A>.

Возможности оценки характеристик с использованием аналитических моделей теории массового обслуживания являются весьма ограниченными. Несравненно большими возможностями обладают имитационные модели, позволяющие исследовать Q-схему, задаваемую Q = <W, U, Н, Z, Y, R, A> без ограничений. На работу с Q-схемами при машинной реализации моделей ориентированы многие языки имитационного моделирования, например SIMULA, SIMSCRIPT, GPSS и др.

Скачано с www.znanio.ru