МДК 02.01 Разработка, внедрение и адаптация ПО отраслевой направленности

Лекция 7

Этапы машинного моделирования систем

 

1. Построение концептуальной модели системы и ее формализация

 

При машинном моделировании системы S характеристики процесса ее функционирования определяются на основе модели М, построенной исходя из имеющейся исходной информации об объекте моделирования. При получении новой информации об объекте его модель пересматривается и уточняется с учетом новой информации, т.е. процесс моделирования, включая разработку и машинную реализацию модели, является итерационным. Этот итерационный процесс продолжается до тех пор, пока не будет получена модель М, которую можно считать адекватной в рамках решения поставленной задачи исследования и проектирования системы S.

 

Моделирование систем с помощью ЭВМ можно использовать в следующих случаях:

а) для исследования системы S до того, как она спроектирована, с целью определения чувствительности характеристики к изменениям структуры, алгоритмов и параметров объекта моделирования и внешней среды;

б) на этапе проектирования системы S для анализа и синтеза различных вариантов системы и выбора среди конкурирующих такого варианта, который удовлетворял бы заданному критерию оценки эффективности системы при принятых ограничениях;

в) после завершения проектирования и внедрения системы, т.е. при ее эксплуатации, для получения информации, дополняющей результаты натурных испытаний (эксплуатации) реальной системы, и для получения прогнозов эволюции (развития) системы во времени.

 

Определение. Концептуа́льная моде́ль — это определённое множество понятий и связей между ними, являющихся смысловой структурой рассматриваемой предметной области.

 

Этапы моделирования систем. Основные этапы моделирования системы:

·         построение концептуальной модели системы и ее формализация;

·         алгоритмизация модели системы и ее машинная реализация;

·         получение и интерпретация результатов моделирования системы.

Взаимосвязь этапов моделирования систем и их составляющих (подэтапов) представлена на рис. 1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

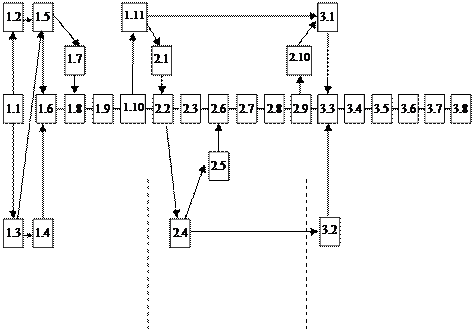
                Первый этап                       Второй этап                            Третий этап

 

 

Рис. 1. Взаимосвязь этапов моделирования систем.

 

Основные подэтапы:

1.1 – формулировка цели и постановка задачи машинного моделирования системы;

1.2 – анализ задачи моделирования системы;

1.3 – определение требований к исходной информации об объекте моделирования и организация ее сбора;

1.4 – выдвижение гипотез и принятие предположений;

1.5 – определение параметров и переменных модели;

1.6 –установление основного содержания модели;

1.7 – обоснование критериев оценки эффективности системы;

1.8 – определение процедур аппроксимации;

1.9 – описание концептуальной модели системы;

1.10 – проверка достоверности концептуальной модели;

1.11 – составление технической документации по первому этапу;

2.1 – построение логической схемы модели;

2.2 – получение математических соотношений;

2.3 – проверка достоверности модели системы;

2.4 – выбор инструментальных средств для моделирования;

2.5 – составление плана выполнения работ по программированию;

2.6 – спецификация и построение схемы программы;

2.7 – верификация и проверка достоверности схемы программы;

2.8 – проведение программирования модели;

2.9 – проверка достоверности программы;

2.10 – составление технической документации по второму этапу;

3.1 – планирование машинного эксперимента с моделью системы;

3.2 – определение требований к вычислительным средствам;

3.3 – проведение рабочих расчетов;

3.4 – анализ результатов моделирования системы;

3.5 – представление результатов моделирования;

3.6 – интерпретация результатов моделирования;

3.7 – подведение итогов моделирования и выдача рекомендаций;

3.8 – составление технической документации по третьему этапу.

 

Таким образом, на этапе построения концептуальной модели М_К и ее формализации проводится исследование моделируемого объекта с точки зрения выделения основных составляющих процесса его функционирования, определяются необходимые аппроксимации и получается обобщенная схема модели системы S, которая преобразуется в машинную модель М_М на втором этапе моделирования путем последовательной алгоритмизации и программирования модели. Последний, третий, этап моделирования системы сводится к проведению согласно полученному плану рабочих расчетов на ЭВМ с использованием выбранных программно-технических средств, получению и интерпретации результатов моделирования системы S с учетом воздействия внешней среды Е.

 

Построение и формализация концептуальных моделей систем

 

На первом этапе машинного моделирования – построения концептуальной модели М системы S и ее формализации – формулируется модель и строится ее формальная схема, т.е. основным назначением этого этапа является переход от содержательного описания объекта к его математической модели, другими словами, процесс формализации. Необходимо, во-первых, провести границы между системой S и внешней средой Е, далее упростить описание системы и построить сначала концептуальную, а затем формальную модели системы. Модель должна быть адекватной, т.е. с определенной степенью приближения на уровне понимания моделируемой системы S разработчиком. Модель должна отражать процесс ее функционирования во внешней среде Е.

Переход от описания к блочной модели. Наиболее рационально строить модель функционирования системы по блочному принципу. При этом могут быть выделены три автономные группы блоков такой модели. Блоки первой группы представляют собой имитатор воздействий внешней среды Е на систему S; блоки второй группы являются собственно моделью процесса функционирования исследуемой системы S; блоки третьей группы –вспомогательными и служат для машинной реализации блоков двух первых групп, а также для фиксации и обработки результатов моделирования.

Рассмотрим механизм перехода от описания процесса функционирования некоторой гипотетической системы к модели этого процесса. Описание свойств процесса функционирования системы S представим в виде концептуальной модели М_К как совокупности некоторых элементов, условно изображенных квадратами на рис. 2, а, и некоторой целевой функции.

а

		1	2
		3	4	5	6	7	8	9
10	11	12 I	13	14	15	16 II	17	18	19	20 III	21	22	23
24	25	26	27	28	29	30	31	32	33	34	35	36	37
	38	39	40	41	42	43	44	45
				46	47

 

б                                                                     Внешняя среда Е

ν₁                                          ν₂

 

                                              

                                        

x                                                                                             y

                              

 

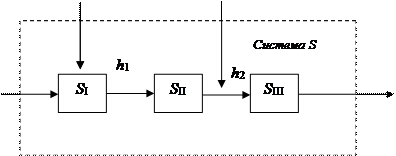
Рис. 2. Концептуальная модель системы:

а – описательная; б – блочная (структурная)

 

Эти квадраты представляют собой описание некоторых подпроцессов исследуемого процесса функционирования системы S, воздействия внешней среды Е и т.д. Переход от описания системы к ее модели согласно целевой функции сводится к исключению из рассмотрения некоторых второстепенных элементов описания (элементы 5-8, 39-41, 43-47). Предполагается, что они не оказывают существенного влияния на ход процессов, исследуемых с помощью модели. Часть элементов (14, 15, 28, 29, 42) заменяется пассивными связями h₁, отражающими внутренние свойства системы (рис. 3.2, б). Некоторая часть элементов (1-4, 10, 11, 24, 25) заменяется входными  факторами х и воздействиями внешней среды v₁. Возможны и комбинированные замены: элементы 9, 18, 19, 32, 33 заменены  пассивной связью h₂ и воздействием внешней среды Е v₂. Элементы 22, 23, 36, 37 отражают воздействие системы на внешнюю среду у.

Оставшиеся элементы системы S группируются в блоки S_I, S_II, S_III, отражающие процесс функционирования исследуемой системы. Поведение этих блоков должно быть хорошо изучено и для каждого из них построена математическая модель, которая в свою очередь может содержать ряд подблоков. Построенная блочная (структурная) модель процесса функционирования исследуемой системы S предназначена для анализа характеристик этого процесса, который может быть проведен при машинной реализации полученной модели согласно заданной целевой функции.

Математические модели процессов. После перехода от описания моделируемой системы S к ее модели М_к, построенной по блочному принципу, необходимо построить математические модели процессов, происходящих в различных блоках. Математическая модель представляет собой совокупность соотношений (например, уравнений, логических условий, операторов), определяющих характеристики процесса функционирования системы S в зависимости от структуры системы, алгоритмов поведения, параметров системы, воздействий внешней среды Е, начальных условий и времени. Математическая модель является результатом формализации процесса функционирования исследуемой системы.

Формально процесс функционирования некоторой гипотетической системы S можно представить в виде m подсистем с характеристиками  с параметрами  при наличии входных воздействий  и воздействий внешней среды .

Тогда математической моделью процесса может служить система соотношений вида

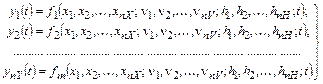    (1)

Если бы функции  были известны, то соотношения (1) оказались бы идеальной математической моделью процесса функционирования системы S. Обычно процесс функционирования системы S разбивают на ряд элементарных подпроцессов. Сущность формализации подпроцессов состоит в подборе типовых математических схем. Например, для стохастических процессов это могут быть схемы вероятностных автоматов (Р-схемы), схемы массового обслуживания (Q-схемы) и т.д.

 

Подэтапы первого этапа моделирования. Рассмотрим более подробно основные подэтапы построения концептуальной модели М_К системы и ее формализации (см. рис.1).

Реализацию каждого из подэтапов будем сопровождать примером. В качестве общего примера моделирования системы приведем следующую задачу:

В студенческом машинном зале расположены две ЭВМ и одно устройство подготовки данных (УПД). Студенты приходят с интервалом в 8 ± 2 мин, и треть из них хочет использовать УПД и ЭВМ, а остальные только ЭВМ. Допустимая очередь в машинный зал составляет четыре человека, включая работающего на УПД. Работа на УПД занимает 8 ± 1 мин, а на ЭВМ – 17 мин. Кроме того, 20 % работавших на ЭВМ возвращаются для повторного использования УПД и ЭВМ. Смоделировать работу машинного зала в течение 6 ч. Определить загрузку УПД, ЭВМ и вероятности отказа в обслуживании вследствие переполнения очереди. Определить соотношение желающих работать на ЭВМ и на УПД в очереди.

 

1.1. формулировка цели и постановка задачи машинного моделирования системы. Дается четкая формулировка цели и постановка задачи исследования конкретной системы S и основное внимание уделяется таким вопросам, как: а) признание существования цели и необходимости машинного моделирования; б) выбор методики решения задачи с учетом имеющихся ресурсов; в) определение масштаба задачи и возможности разбиения ее на подзадачи. В процессе моделирования возможен пересмотр начальной постановки задачи в зависимости от цели моделирования и цели функционирования системы.

 

Реализация подэтапа 1.1 для примера:

Необходимо исследовать работу студенческого машинного зала. В качестве цели моделирования выберем изучение функционирования системы, а именно оценивание ее характеристик с точки зрения эффективности работы системы, т.е. будет ли она простаивать, работать на износ или работать с запасом. В качестве цели эффективного функционирования системы целесообразно выбрать максимизацию загрузки УПД и ЭВМ и одновременно минимизацию вероятности отказа в обслуживании вследствие переполнения очереди к УПД и ЭВМ.

С учетом имеющихся ресурсов в качестве метода решения задачи выберем метод имитационного моделирования, позволяющий не только анализировать характеристики модели, но и проводить структурный, алгоритмический и параметрический синтез модели на ЭВМ при заданных критериях оценки эффективности и ограничениях.

Постановка задачи исследования функционирования студенческого машинного зала как системы, состоящей из УПД и двух ЭВМ и содержащей обратную связь, представлена в задании к курсовому проектированию, из которого следует, что необходимо определить:

·         загрузку УПД и каждой ЭВМ;

·         загрузку очереди к УПД и каждой ЭВМ;

·         вероятность отказа в обслуживании вследствие переполнения очереди к УПД или ЭВМ;

·         соотношение желающих работать на ЭВМ и на УПД в очереди.

Пересмотр начальной постановки задачи исследования не предусмотрен.

 

1.2. Анализ задачи моделирования системы. Анализ включает следующие вопросы: а) выбор критериев оценки эффективности процесса функционирования системы S; б) определение эндогенных и экзогенных переменных модели М; в) выбор возможных методов идентификации; г) выполнение предварительного анализа содержания второго этапа алгоритмизации модели системы и ее машинной реализации; д) выполнение предварительного анализа содержания третьего этапа получения и интерпретации результатов моделирования системы.

 

Реализация подэтапа 1.2 для примера:

В качестве критерия оценки эффективности процесса функционирования системы целесообразно выбрать вероятность отказа в обслуживании вследствие переполнения очереди к УПД или ЭВМ, которая должна быть минимальной, при этом загрузка УПД и каждой ЭВМ должна быть максимальной. Соотношение загрузки каждой ЭВМ и УПД должно быть в среднем одинаковым, чтобы каждое устройство было задействовано равноценно. В качестве еще одного традиционного критерия оценки эффективности процесса функционирования системы можно выбрать минимальное время обслуживания заявок в системе в целом при максимальном количестве обслуженных заявок.

Экзогенные (независимые) переменные модели:

·         интервал времени (интенсивность) прихода студентов в зал;

·         допустимая очередь в машинный зал;

·         время работы студентов на ЭВМ, УПД.

Эндогенные (зависимые) переменные модели:

·         загрузка УПД и каждой ЭВМ;

·         загрузка очереди к УПД и каждой ЭВМ;

·         количество студентов, работающих на каждой ЭВМ и УПД;

·         количество студентов, желающих повторно работать на УПД и ЭВМ;

·         количество студентов, которые получили отказ в обслуживании вследствие переполнения очереди к УПД или ЭВМ;

·         вероятность отказа в обслуживании вследствие переполнения очереди к УПД или ЭВМ;

·         соотношение желающих работать на ЭВМ и на УПД в очереди.

При построении математической имитационной модели процессов функционирования системы будем использовать непрерывно-стохастический подход на примере типовой Q-схемы, потому что исследуемая система – студенческий машинный зал – может быть представлена как система массового обслуживания с непрерывным временем обработки параметров при наличии случайных факторов.

Формализовав процесс функционирования исследуемой системы в абстракциях Q-схемы, на втором этапе алгоритмизации модели и ее машинной реализации выберем язык имитационного моделирования, потому что высокий уровень проблемной ориентации языка значительно упростит программирование, а специально предусмотренные в нем возможности сбора, обработки и вывода результатов моделирования позволят быстро и подробно проанализировать возможные исходы имитационного эксперимента с моделью. Для получения полной информации о характеристиках процесса функционирования системы необходимо будет провести полный факторный эксперимент, который позволит определить, насколько эффективно функционирует система, и выдать рекомендации по ее усовершенствованию.

 

1.3. Определение требований к исходной информации об объекте моделирования и организация ее сбора. После постановки задачи моделирования системы S определяются требования к информации, из которой получают качественные и количественные исходные данные, необходимые для решения этой задачи. На этом подэтапе проводится: а) выбор необходимой информации о системе S и внешней среде Е; б) подготовка априорных данных; в) анализ имеющихся экспериментальных данных; г) выбор методов и средств предварительной обработки информации о системе.

 

Реализация подэтапа 1.3 для примера:

Вся необходимая информация о системе и внешней среде представлена в задании к курсовому проектированию и не требует предварительной обработки.

 

1.4. Выдвижение гипотез и принятие предположений. Гипотезы при построении модели системы S служат для заполнения «пробелов» в понимании задачи исследователем. Выдвигаются также гипотезы относительно возможных результатов моделирования системы S, справедливость которых проверяется при проведении машинного эксперимента. Предположения предусматривают, что некоторые данные неизвестны или их нельзя получить. Предположения могут выдвигаться относительно известных данных, которые не отвечают требованиям решения поставленной задачи. Предположения дают возможность провести упрощения модели в соответствии с выбранным уровнем моделирования. При выдвижении гипотез и принятии предположений учитываются следующие факторы: а) объем имеющейся информации для решения задач; б) подзадачи, для которых информация недостаточна; в) ограничения на ресурсы времени для решения задач; г) ожидаемые результаты моделирования.

 

Реализация подэтапа 1.4 для примера:

Для заполнения пробелов в понимании задачи исследования, а также проверки возможных результатов моделирования при проведении машинного эксперимента выдвигаем следующие гипотезы:

·         загрузка УПД будет меньше загрузки ЭВМ, т.к. интервал времени работы студентов на УПД меньше, чем на ЭВМ;

·         вероятность отказа в обслуживании вследствие переполнения очереди к УПД или ЭВМ будет больше 0,6, т.к., несмотря на то, что время работы обоих ЭВМ (17 мин) соответствует интенсивности прихода студентов в зал (8 ± 2 мин), которые равномерно рассредоточиваются между двумя ЭВМ, часть студентов (30 %) дополнительно желает работать на УПД. При этом время работы на УПД (8 ± 1 мин) соответствует интенсивности поступления студентов и, кроме того, 20 % работавших на ЭВМ возвращаются для повторного использования УПД и ЭВМ;

·         соотношение желающих работать на ЭВМ и на УПД в очереди составит 2:1, поскольку после работы на УПД студент обязательно будет работать на одной из ЭВМ, но, несмотря на то, что время работы на УПД меньше, часть студентов желает повторно поработать именно на УПД.

Для упрощения модели можно выдвинуть следующие предположения:

·         время перехода студента с УПД на ЭВМ равно нулю;

·         студент, желающий повторно работать на УПД и ЭВМ, считается уже находящимся в зале и место в очереди в зал он не занимает;

·         если студент не желает работать на УПД, то он занимает любую свободную ЭВМ;

·         после работы на УПД студент занимает только вторую ЭВМ;

·         20 % студентов возвращаются для повторного использования УПД и ЭВМ независимо от того, пользовались ли они ранее УПД.

 

1.5. Определение параметров и переменных модели. Прежде чем перейти к описанию математической модели, необходимо определить параметры системы, входные и выходные переменные, воздействия внешней среды и оценить степени их влияния на процесс функционирования системы в целом. Описание каждого параметра и переменной должно даваться в следующей форме: а) определение и краткая характеристика; б) символ обозначения и единица измерения; в) диапазон изменений; г) место применения в модели.

 

Реализация подэтапа 1.5 для примера:

Входные переменные модели:

·         интервал времени (интенсивность) прихода студентов в зал, t_пр ± Dt_пр, где t_пр – средний интервал времени между приходом студентов в машинный зал, Dt_пр – половина интервала, в котором равномерно распределено значение, единица измерения – минута.

Если интенсивность прихода студентов в зал будет меньше времени работы студентов на УПД и ЭВМ, то загрузка системы в целом будет возрастать, и, как следствие, будет увеличиваться количество студентов, которые получат отказ в обслуживании.

Выходные переменные модели:

·         количество студентов, отработавших на ЭВМ или УПД и ЭВМ за заданный интервал времени работы машинного зала, N_ОБС, единица измерения – количество студентов;

·         количество студентов, которые получили отказ в обслуживании вследствие переполнения очереди к УПД или ЭВМ за заданный интервал времени работы машинного зала, N_ОТК, единица измерения – количество студентов.

 

Параметры модели:

·         допустимая очередь в машинный зал, l_зал, единица измерения – количество студентов;

·         время работы студентов на первой и второй ЭВМ, t_ЭВМ1, t_ЭВМ2, единица измерения – минута;

·         время работы студентов на УПД, t_УПД ± Dt_УПД, где t_УПД – среднее время работы студентов на УПД, Dt_УПД – половина времени, в котором равномерно распределено значение, единица измерения – минута;

·         среднее время обслуживания студентов в машинном зале, t_ОБС, единица измерения – минута;

·         загрузка УПД, Z_УПД, единица измерения – относительная единица;

·         загрузка первой и второй ЭВМ, Z_ЭВМ1, Z_ЭВМ2, единица измерения – относительная единица;

·         загрузка очереди к УПД, Z_ОЧ.УПД, единица измерения – относительная единица;

·         загрузка очереди к первой и второй ЭВМ, Z_ОЧ.ЭВМ1, Z_ОЧ.ЭВМ2, единица измерения – относительная единица;

·         количество студентов, желающих работать только на ЭВМ, N_ЭВМ, единица измерения – количество студентов;

·         количество студентов, желающих работать не только на ЭВМ, но и на УПД, N_УПД, единица измерения – количество студентов;

·         количество студентов, желающих повторно работать на УПД и ЭВМ, N_ПР, единица измерения – количество студентов;

·         вероятность отказа в обслуживании вследствие переполнения очереди к УПД или ЭВМ, Р_отк, единица измерения – относительная единица.

Уменьшение допустимой очереди в машинный зал, и (или) увеличение времени работы студентов на УПД и ЭВМ, и (или) увеличение количества студентов, желающих повторно работать на УПД и ЭВМ, будет приводить к увеличению загрузки системы в целом и, как следствие, к увеличению количества студентов, которые получат отказ в обслуживании.

Воздействия внешней среды отсутствуют.

 

1.6. Установление основного содержания модели. На этом подэтапе определяется основное содержание модели и выбирается метод построения модели системы, которые разрабатываются на основе принятых гипотез и предположений. При этом учитываются следующие особенности: а) формулировка цели и постановка задачи моделирования системы; б) структура системы S и алгоритмы ее поведения, воздействия внешней среды Е; в) возможные методы и средства решения задачи моделирования.

 

Реализация подэтапа 1.6 для примера:

На основе анализа исходных данных и выдвинутых гипотез можно сделать вывод о том, что процессы, происходящие в моделируемой системе, являются процессами массового обслуживания, поэтому эти процессы целесообразно описать на языке Q-схем.

 

1.7. Обоснование критериев оценки эффективности системы. Для оценки качества процесса функционирования моделируемой системы необходимо определить совокупность критериев оценки эффективности как функцию параметров и переменных системы. Эта функция представляет собой поверхность отклика в исследуемой области изменения параметров и переменных и позволяет определить реакцию системы.

 

Реализация подэтапа 1.7 для примера:

Для оценки качества процесса функционирования моделируемой системы сформируем на основании анализа задачи моделирования системы функцию поверхности отклика в исследуемой области изменения параметров и переменных как совокупность критериев оценки эффективности. Эта функция позволит определить экстремумы реакции системы.

 

1.8. Определение процедур аппроксимации. Для аппроксимации реальных процессов, протекающих в системе S, обычно используются три вида процедур: а) детерминированная; б) вероятностная; в) определение средних значений.

При детерминированной процедуре результаты моделирования однозначно определяются по данной совокупности входных воздействий, параметров и переменных системы S. В этом случае отсутствуют случайные элементы, влияющие на результаты моделирования. Вероятностная (рандомизированная) процедура применяется в том случае, когда случайные элементы, включая воздействия внешней среды Е, влияют на характеристики процесса функционирования системы S и когда необходимо получить информацию о законах распределения выходных переменных. Процедура определения средних значений используется тогда, когда при моделировании системы интерес представляют средние значения выходных переменных при наличии случайных элементов.

 

Реализация подэтапа 1.8 для примера:

Для аппроксимации реальных процессов, протекающих в системе, воспользуемся процедурой определения средних значений выходных переменных, поскольку в системе имеются случайные значения переменных и параметров.

 

1.9. Описание концептуальной модели системы. На этом подэтапе построения модели системы: а) описывается концептуальная модель М_К в абстрактных терминах и понятиях; б) задается целевая функция; в) дается описание модели с использованием типовых математических схем; г) принимаются окончательно гипотезы и предположения; д) обосновывается выбор процедуры аппроксимации реальных процессов при построении модели.

 

Реализация подэтапа 1.9 для примера:

Концептуальная модель исследуемой системы представлена в виде структурной схемы (рис. 3), состоящей из одного входного потока х – студенты, приходящие в машинный зал, трех выходных потоков у₁, у₂ – студенты, отработавшие в машинном зале на соответствующей ЭВМ, и у₃ – студенты, которым не хватило места в зале, трех блоков – устройств (УПД, ЭВМ1, ЭВМ2), связанных между собой согласно условию задачи.

Целевая функция модели системы:

 

 

 

 

 

 

 

 

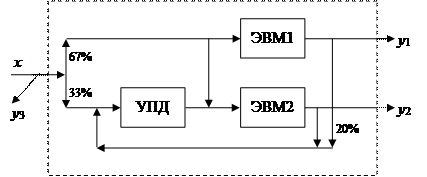 Концептуальная модель в виде структурной схемы

 

В качестве типовой математической схемы применяется Q-схема, состоящая из одного источника (И), накопителя (Н), трех каналов (К₁, К₂, К₃), шести клапанов (рис. 4). Заявки (студенты, приходящие в машинный зал) в систему поступают от источника И с интервалом 8 ± 2 мин в накопитель Н с емкостью L_Н, равной 3, поскольку по условию очередь в машинный зал может быть только из 4 человек, включая заявку в канале К₂ (УПД). Канал К₁ соответствует ЭВМ1, канал К₂ – УПД, канал К₃ – ЭВМ2. От источника заявки поступают в клапан 1, который управляется накопителем Н. В случае отсутствия места в накопителе заявки получают отказ N_ОТК. От накопителя Н заявки поступают в клапан 2, который условно управляется источником, распределяющим заявки между каналом К₁ (60 %) и каналами последовательной обработки К₂ и К₃ (30 %). Обработка (задержка) заявки в канале К₁ занимает 17 мин. Клапан 3 управляется каналом К₁, в случае его занятия заявка посылается на канал К₂. Обработка (задержка) заявки в
канале К₂ занимает 8 ± 1 мин. Клапан 4 принимает заявки от клапанов 2 и 6, управляется каналом К₂, в случае его занятия заявка встает в очередь. Обработка (задержка) заявки в канале К₃ занимает 17 мин. Клапан 5 принимает заявки от клапана 3 и канала К₂, управляется каналом К₃, в случае его занятия заявка встает в очередь. Клапан 6 принимает заявки от каналов К₁ и К₃, управляется соответствующим каналом, при этом 20 % заявок не уничтожается, а поступает на клапан 4 для повторного обслуживания в каналах К₂ и К₃. Остальные 80 % заявок считаются обслуженными N_ОБС и уничтожаются.

 

 

 

 

 

 

 

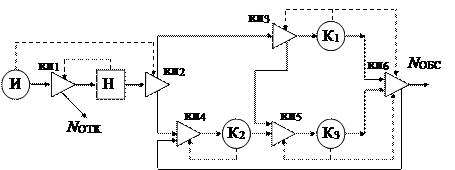
Рис. 4. Концептуальная модель в виде Q-схемы

Формальная модель системы:

Q = { И, Н, К₁, К₂, К₃, N_ОБС, N_ОТК, кл₁, кл₂, кл₃, кл₄, кл₅, кл₆, L_Н = 3 }.

Согласно разработанной концептуальной модели окончательные гипотезы и предположения совпадают с ранее принятыми. Выбранная процедура аппроксимации определения средних значений выходных переменных соответствует реальным случайным процессам, протекающим в системе массового обслуживания.

1.10. Проверка достоверности концептуальной модели. После того как концептуальная модель М_К описана, необходимо проверить достоверность некоторых концепций модели, перед тем как перейти к следующему этапу моделирования системы S. Один из методов проверки модели М_К: применение операций обратного перехода, позволяющих проанализировать модель, вернуться к принятым аппроксимациям и наконец, рассмотреть снова реальные процессы, протекающие в моделируемой системе. Проверка достоверности концептуальной модели М_К  должна включать: а) проверку замысла модели; б) оценку достоверности исходной информации; в) рассмотрение постановки задачи моделирования; г) анализ принятых аппроксимаций; д) исследование гипотез и предположений.

1.11. Составление технической документации по первому этапу. В конце этапа построения концептуальной модели М_К и ее формализации составляется технический отчет по этапу, который включает в себя: а) подробную постановку задачи моделирования системы S; б) анализ задачи моделирования системы; в) критерии оценки эффективности системы; г) параметры и переменные модели системы; д) гипотезы и предположения, принятые при построении модели; е) описание модели в абстрактных терминах и понятиях; ж) описание ожидаемых результатов моделирования системы S.

Скачано с www.znanio.ru