
Лекция 1
Основные понятия теории моделирования систем
Методологическая основа моделирования
Моделирование – это замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели путем проведения эксперимента с моделью.
Объект (лат. objectum – предмет) – все то, на что направлена человеческая деятельность. Технический объект – машина, механизм, технический комплекс, технологический процесс, а также любой их компонент, выделяемый в процессе моделирования путем деления структуры целостного объекта на отдельные блоки, части, элементы.
Гипотеза – определенные предсказания, предположения, основанные на небольшом количестве опытных данных, наблюдений, догадок. Быстрая и полная проверка выдвигаемых гипотез может быть проведена в ходе специально поставленного эксперимента. При формулировании и проверке правильности гипотез большое значение в качестве метода суждения имеет аналогия.
Аналогия – суждение о каком-либо частном сходстве двух объектов.
Эксперимент – процедура организации наблюдений каких-то явлений, которые осуществляют в условиях, близких к естественным, либо имитируют их. Различают пассивный эксперимент, когда исследователь наблюдает протекающий процесс, и активный, когда наблюдатель вмешивается и организует протекание процесса.
В общем процесс моделирования представлен следующим образом: используя априорные (ранее известные) данные об объекте, выдвигается гипотеза, по которой на основе аналогии строится наглядная упрощенная логическая схема (модель) и с ней проводится эксперимент для изучения свойств объекта.
Модель (лат. modulus – мера) – объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.
Пример 1. Рассмотрим физическую систему: тело массой m скатывающееся по наклонной плоскости с ускорением a, на которое воздействует сила F. Исследуя такие системы, Ньютон получил математическое соотношение: F=ma. Это физико-математическая модель системы или математическая модель физической системы. При описании этой системы (построении этой модели) приняты следующие гипотезы: 1) поверхность идеальна (т.е. коэффициент трения равен нулю); 2) тело находится в вакууме (т.е. сопротивление воздуха равно нулю); 3) масса тела неизменна; 4) тело движется с одинаковым постоянным ускорением в любой точке.
Пример 2. Совокупность предприятий функционирует на рынке, обмениваясь товарами, сырьем, услугами, информацией. Если описать экономические законы, правила их взаимодействия на рынке с помощью математических соотношений, например, системы алгебраических уравнений, где неизвестными будут величины прибыли, получаемые от взаимодействия предприятий, а коэффициентами уравнения будут значения интенсивностей таких взаимодействий, то получим математическую модель экономической системы, т.е. экономико-математическую модель системы предприятий на рынке.
При этом если результаты моделирования по каким-либо причинам не удовлетворяют исследователя, то процесс моделирования начинается с возврата на предыдущие стадии, то есть моделирование – процесс итерационный (рис. 1).
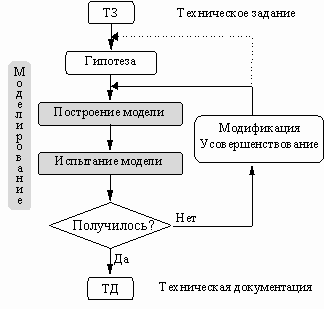
Рис. 1. Итерационный характер процесса моделирования.
Моделирование базируется на математической теории подобия, согласно которой абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же. При моделировании большинства систем (за исключением, возможно, моделирования одних математических структур другими) абсолютное подобие невозможно, и основная цель моделирования - модель достаточно хорошо должна отображать функционирование моделируемой системы.
Аксиомы теории моделирования
Любая дисциплина базируется на некотором наборе аксиом, которые принимаются "на веру" и не требуют доказательств. Есть такие аксиомы и в курсе моделирования. Познакомимся с основными из них.
Аксиома 1
Модель не существует сама по себе, а выступает в тандеме с некоторым материальным объектом, который она представляет (замещает) в процессе его изучения или проектирования.
Аксиома 2
Для естественных материальных объектов модель вторична, то есть появляется как следствие изучения и описания этого объекта (например, модель солнечной системы).
Для искусственных материальных объектов (создаваемых человеком или техникой) модель первична, так как предшествует появлению самого объекта (например, модель самолета, модель двигателя).
Аксиома 3
Модель всегда проще объекта. Она отражает только некоторые его свойства, а не представляет объект "во всем великолепии". Для одного объекта строится целый ряд моделей, отражающих его поведение или свойства с разных сторон или с разной степенью детальности. При бесконечном повышении качества модели она приближается к самому объекту.
Аксиома 4
Модель должна быть подобна тому объекту, который она замещает, то есть модель в определенном смысле является копией, аналогом объекта. Если в исследуемых ситуациях модель ведет себя так же, как и моделируемый объект, или это расхождение невелико и устраивает исследователя, то говорят, что модель адекватна оригиналу. Адекватность - это воспроизведение моделью с необходимой полнотой и точностью всех свойств объекта, существенных для целей данного исследования.
Аксиома 5
Построение модели не самоцель. Она строится для того, чтобы можно было экспериментировать не с самим объектом, а с более удобным для этих целей его представителем, называемым моделью.
Экспериментирование с моделью, "игра" позволяют добыть информацию о поведении и свойствах исследуемого объекта, не подвергая его опытам. Тут обнаруживается "великая сила моделирования": сложный, длительный, дорогой (а иногда и просто невозможный) физический эксперимент с реальным объектом заменяется более простым, быстрым и дешевым экспериментом с его моделью.
С моделью можно экспериментировать сколько угодно и как угодно, помещая ее в любые условия, не опасаясь катастрофических последствий опыта (пограничные и предельные испытания).
При проектировании новых технических объектов моделирование (то есть построение и последующее испытание модели) позволяет выявить работоспособность и качество работы проектируемого объекта до его физического воплощения.
Конечно, за все приобретения надо расплачиваться: платой за простоту, скорость и дешевизну модельного эксперимента является некоторая потеря точности и надежности получаемых результатов. Следует, правда, заметить, что эти потери поддаются контролю со стороны разработчика модели.
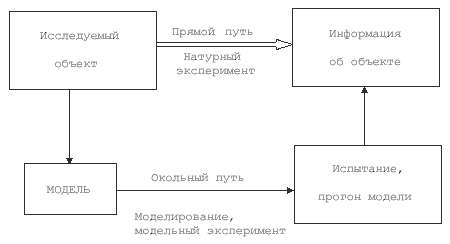
Рис. 2. Способы получения информации об объекте.
Системный подход к моделированию
Любой искусственный объект можно рассматривать с двух точек зрения - глазами пользователя и глазами разработчика.
Покупая телевизор, Вас интересует, прежде всего, его дизайн и технические характеристики, например размер экрана. Вы смотрите на объект как бы с внешней стороны - глазами пользователя. Телевизор в данном случае - это в буквальном смысле черный ящик и содержимое его для Вас не представляет никакого интереса.
Другое дело - разработчик. Чтобы спроектировать тот же телевизор, надо решить, из каких деталей он будет изготовлен и как их собрать воедино, чтобы все работало. Таким образом, разработчика теперь интересует внутреннее строение объекта - его структура.
Все сказанное подтверждается рисунком 1, правда, в качестве примера выбран другой объект - интегральная микросхема (ИМС).
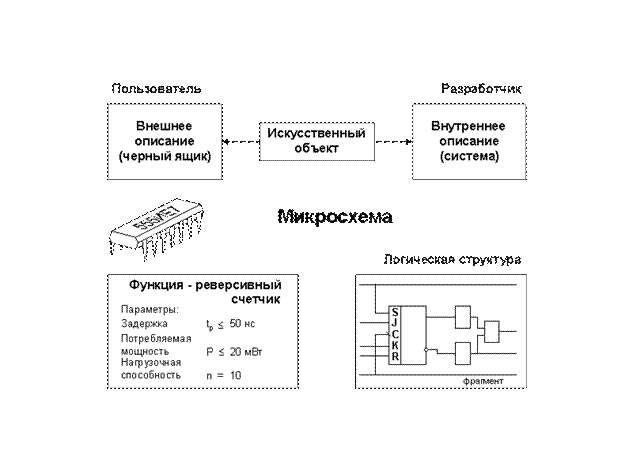 Рис. 1. Разные
точки зрения на один и тот же объект
Рис. 1. Разные
точки зрения на один и тот же объект
Рассмотренный пример демонстрирует два альтернативных подхода к моделированию - детерминистский (классический, Ньютоновский) и системный.
В первом случае (детерминистский подход), объект рассматривается как черный ящик. Его работа (поведение) описывается некоторой функцией и сопровождается определенным набором параметров. Предполагается, что внешняя среда ("окружение") не оказывает влияния на работу объекта.
Такой изолированный взгляд значительно упрощает изучение объектов, но приводит к необходимости делать массу (порой необоснованных) допущений. Например, в электронике приходится предполагать, что входные сопротивления неизмеримо выше выходных (Rвх->1, Rвых->0), а мощности любых источников питания и выходных сигналов бесконечно велики.
Главное достоинство этого подхода - простота исследования объекта - нередко вступает в противоречие с точностью и надежностью получаемых результатов.
Системный подход предлагает вам "забраться" внутрь черного ящика и посмотреть, что там есть. Вы увидите, что на самом деле объект представляет собой совокупность связанных между собой элементов (структуру), которые еще и влияют друг на друга.
Кроме того, системный подход предполагает, что "окружение" оказывает влияние на поведение объекта, и этим влиянием пренебрегать нельзя.
Итак, можно зафиксировать первую особенность системного подхода: он рассматривает объект не как черный ящик, а как сложно организованную систему, состоящую из множества взаимодействующих элементов. Поведение объекта должно рассматриваться "в окружении" (с учетом влияния внешней среды). То же самое можно сказать и об отдельном элементе системы.
Кстати, любой элемент можно в свою очередь раздробить на более мелкие части и повторно применить к ним системный подход. Таким образом, можно говорить о структурной декомпозиции объекта и его иерархической организации (рис. 4).
Для иерархического описания определены две операции противоположного действия:
· Push - понизить (детализировать) описание;
· Pop - повысить уровень описания (спрятать структуру в черный ящик).
Что же дает нам системный подход? Прежде всего, он позволяет представить одну сложную задачу совокупностью более простых, которые можно решать быстрее и легче. А главное, их можно решать параллельно.
Во-вторых, проектирование на любом иерархическом уровне ведется с учетом окружающей среды. Это исключает ситуации, когда готовый проект при реализации отказывается работать из-за не идеальности источников питания, внешних помех и наводок, изменения температуры, неучтенной нагрузки и т.п.
Благодаря системному подходу, реализованному в процедурах иерархического проектирования, удалось расширить класс принципиально решаемых задач (например, проектирование СБИС (сверх-больших интегральных схем)) и повысить качество проектирования.
Примечательной особенностью системного подхода является его универсальность: с неизменным успехом он применим как для сложных, так и для простых объектов, а при многоуровневом описании сложных систем он "работает" на любом иерархическом уровне, то есть применим не только к системе, но и к любой ее части.
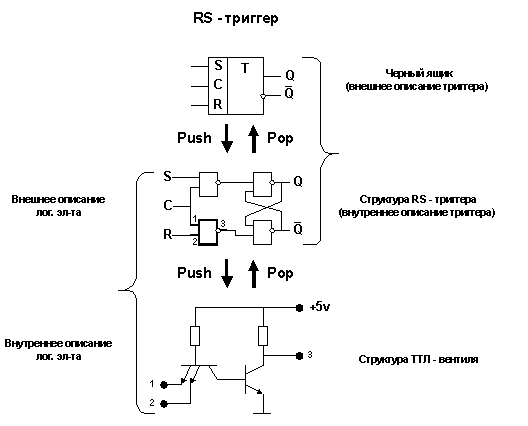
Рис. 4. Иерархическая организация объекта (на примере RS-триггера)
Системный подход к моделированию заимствует основные понятия, определения и методологию общей теории систем. Назовем некоторые из них.
Система - это совокупность связанных элементов, объединенных в одно целое для достижения определенной цели (например, логический элемент, триггер, счетчик, процессор). Другими словами, любой объект любой сложности можно рассматривать как систему.
Использование понятия «элемент», в принципе, вполне корректное, содержит, однако, некоторое неудобство, связанное с нашим представлением об элементарном как о неделимом. Составные же части системы сами, как известно, могут иметь сложную структуру, будучи ее подсистемами. С этой точки зрения представляется более удобным говорить не об элементах, а о компонентах системы, которые становятся элементами только на последнем, нижнем уровне ее декомпозиции.
Понятия компонентов и взаимодействия между ними являются необходимыми. Но их явно недостаточно при исследовании конкретных систем. Все в этом мире взаимосвязано. При таком определении, если бы ему следовали в реальном исследовании, понятие любой системы было бы применимым к чему угодно, а стало быть, пустым. Где, к примеру, границы политической системы? Можно, например, рассматривать и звезды на небе как часть политической системы. Ведь если политик верит звездочету (а такое в современной политике не исключение), то через него и звезды влияют на принятие политических решений, вне зависимости от того, верит ли звездам политолог.
Если ограничиться двумя названными критериями, то в силу всеобщей взаимосвязи, присущей нашему миру, принципиально неразрешимой становится проблема границы. На деле же (явно или неявно) мы всегда принимаем во внимание еще один критерий, называя системой лишь такую совокупность взаимосвязанных элементов, которой в той или иной степени присуща качественная определенность, целостность. Иными словами, совокупность элементов образует систему только в том случае, когда отношения между ними порождают некое качество, по которому данную совокупность отличают от окружающей среды. Качество это называют системным или интегративным.
Существенно, что качество это является таким свойством совокупности, которое «помечает» собой каждый из принадлежащих ей элементов, присваивается им. Так совокупность людей, соединенных родственными связями, образует систему, называемую семьей, а ее «элементы» - члены семьи - приобретают в ней качества быть отцом, братом, сыном и т.п. В производственном коллективе эти качества отходят на второй план, и его члены как элементы новой системы приобретают качества, связанные с реализацией общей производственной функции - быть рабочим, инженером, менеджером и т.д.
Никто, однако, не называет системой простую совокупность, результат сложения аддитивного, не порождающего нового качества. Именно целостную совокупность и называют системой. Целостность можно при этом рассматривать как степень консолидации системы, меру интегративного качества.
Чтобы разобраться в системе, изучить, исследовать ее (задача анализа), надо описать систему, зафиксировать ее свойства, поведение, структуру и параметры, то есть построить одну или несколько моделей.
Для этого надо ответить на три основные вопроса:
· Что она делает (узнать поведение, функцию системы);
· Как она устроена (выяснить структуру системы);
· Каково ее качество (насколько хорошо она выполняет свои функции).
Покажем это на рис. 5.
Структура системы - это фиксированная совокупность элементов, составляющих систему, и связей между ними.
Наиболее часто структура системы изображается в виде схемы. Это может быть блок-схема, структурная, функциональная или принципиальная схема. Наконец, это может быть монтажная схема или сборочный чертеж, печатная плата или топология. Такие схемы называют инженерной формой представления структуры схемы.
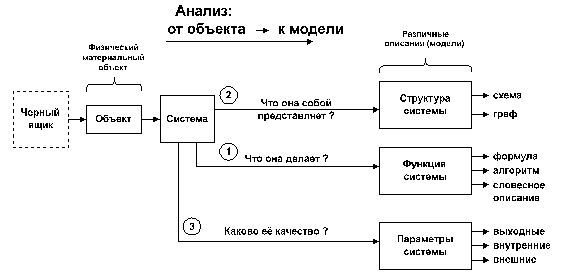
Рис. 5. Описание объекта как системы
Параметры системы - это величины характеризующие качество, свойства или режимы работы объекта. Различают выходные, внутренние и внешние параметры.
Выходные параметры - это показатели качества системы. По ним можно судить о правильности функционирования системы и ее качестве. Они позволяют сравнивать однотипные по назначению системы, сделать выбор подходящего варианта.
Выходных параметров обычно много и их принято представлять вектором: Y = (y1,y2,...,yn)
Например, если в качестве системы рассматривается операционный усилитель, то его выходными параметрами будут:
· y1 - коэффициент усиления;
· y2 - полоса пропускания;
· y3 - напряжение смещения нуля;
и т.п.
Внутренние параметры - это параметры структурных (внутренних) элементов системы: X = (x1,x2,...,xn)
Для рассмотренных примеров элементами системы являются транзисторы, резисторы, конденсаторы, диоды и т.п. Следовательно, в качестве Х-параметров могут выступать коэффициент усиления по току b транзистора, частота единичного усиления fт, тепловой ток Iк0, напряжение пробоя коллекторного перехода, температурный коэффициент сопротивления, технологический разброс и т.п.
Внешние параметры - это параметры внешней среды, оказывающие влияние (обычно отрицательное) на функционирование системы. Q = (q1,q2,...,qn)
Прежде всего, это параметры источников питания, температура, внешние наводки и помехи. Входные сигналы и нагрузка также являются внешними по отношению к системе параметрами ("окружением").
Параметры входных сигналов иногда выделяют в отдельную группу и называют входными параметрами: I = (i1,i2,...,in)
Конечно, в этом нет особой необходимости, однако графическое представление объекта становится более наглядным (рис. 6).
Функция системы - это формализованное или содержательное (словесное) описание принципа работы (функционирования) системы. Функцию системы желательно представить в аналитической форме, используя тот или иной математический аппарат, например функциональный анализ, теорию очередей, Марковские модели, исследование операций, математическую логику и т.п.
Для сложных систем не удается получить формализованное описание. В этом случае поведение системы представляется алгоритмом, записанным в той или иной форме (блок- или граф- схемы алгоритмов, операторные схемы).
В крайнем случае, можно довольствоваться словесным описанием работы системы, от которого, правда, мало толку, если говорить об автоматизации проектирования.
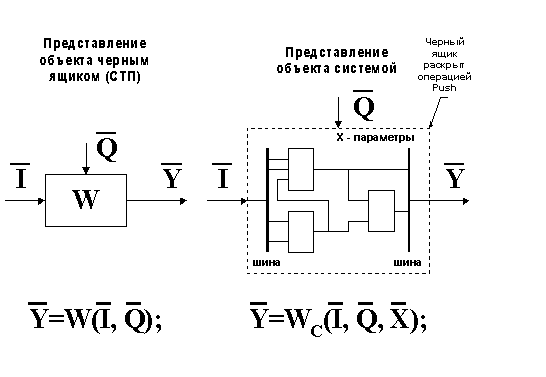
Рис. 6. Графическое представление объекта черным ящиком и системой
Как видно из рисунка 6 между различными видами параметров, существует некоторая зависимость. Правильнее говорить, что выходные параметры объекта (а, значит, и его качество), зависят от входных воздействий, параметров внешней среды и, конечно же, от качества составляющих объект элементов (Х-параметров).
Такая зависимость представляется в аналитической форме и называется глобальной функцией объекта W.
В первом случае мы ничего не знаем о составляющих объект элементах, то есть нам неизвестны его Х-параметры. Поэтому глобальная функция объекта записывается в упрощенном виде, как его реакция на внешние воздействия I и Q
Для динамических объектов в глобальную функцию добавляется еще одна координата - время t.
Y = Wc(I,Q,t) - черный ящик или Y = Wc(I,Q,X,t) - система
Надо сказать, что существование глобальной функции еще не означает, что она известна исследователю или проектировщику объекта. Задача как раз и заключается в том, чтобы отыскать эту функцию. Однако чаще всего ее не удается представить в аналитической форме, то есть так, как показано на рисунке 6 (в виде аналитической модели).
Для сложных объектов приходится довольствоваться алгоритмическим описанием объекта (в виде поведенческой имитационной модели).
До сих пор, говоря о системе, мы предполагали, что объект уже существует и задача сводится к изучению, исследованию его. Отыскав его функцию и структуру; "измерив" его параметры, мы тем самым решили эту задачу. Ее название всем известно - типичная задача анализа (от гр. analysis - разложение, расчленение). Объект - есть, и надо лишь побольше узнать о нем (системный анализ, спектральный анализ, анализ крови и т.п.).
Но чаще инженер встречается с противоположной задачей - объекта нет, и его предстоит создать, спроектировать. Это задача синтеза объекта.
Рассуждая с позиции системного подхода, мы можем сказать, что для ее решения надо сделать три шага: выявить функцию системы (абстрактный синтез), разработать структуру системы (структурный синтез) и определить параметры системы так, чтобы получить желаемое качество проекта.
Внешне процедура синтеза выглядит весьма убедительно и обнадеживающе.
Сначала надо выявить глобальную функцию системы, рассматривая саму систему на абстрактном уровне в виде черного ящика, о котором известно только то, что он будет делать (рис. 7).
Затем следует "транслировать" функциональное описание в структурное, например, разбивая глобальную функцию системы на подфункции и повторяя, при необходимости, это дробление до тех пор, пока не будут получены элементарные функции, структуры которых очевидны (или уже реализованы). Этот этап порождения структуры, реализующий необходимые функции, называют структурным синтезом.
На третьем этапе (параметрический синтез) остается лишь подобрать параметры системы так, чтобы достичь желаемого качества ее работы.
Несмотря на внешнюю привлекательность и стройность процедуры формального синтеза оказываются исключительно сложными.
Лишь для узкого класса технических систем разработаны и используются на практике методы формального синтеза. К ним можно отнести пассивные электрические цепи (в частности, фильтры), типовые системы автоматического управления, цифровые автоматы, комбинационные и некоторые несложные регистровые схемы.
В остальных случаях у инженера нет альтернативы веками проверенному методу проб и ошибок, реализованному в процедуре итерационного проектирования (она была рассмотрена в первой лекции). Напомним суть этого метода: сначала создается базовый вариант системы, а затем он улучшается, пока не будет достигнуто желаемое качество работы.
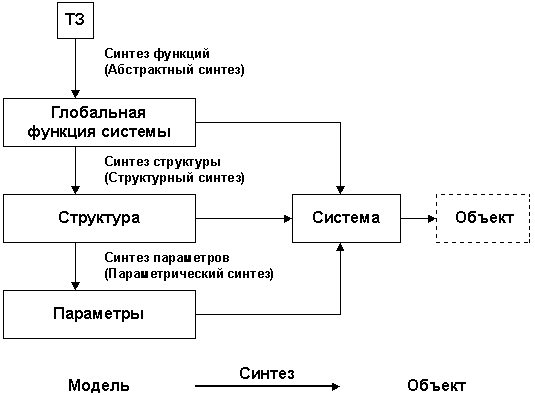
Рис. 7. Этапы синтеза объекта
Что же припасено в арсеналах инженера для улучшения проекта?
Из глобальной функции системы
|
Y = Wc(I,Q,X) |
(вектор ) Y |
видно, что улучшить ее качество можно тремя способами:
· воздействием на вектор Х - параметрический метод;
· изменением функции Wс ;
· воздействием на внешние параметры I и Q.
Параметрический метод - есть не что иное, как улучшение качества входящих в систему элементов. Например, если в разработке есть резисторы с большим технологическим разбросом и они ухудшают работу, то их можно заменить высокоточными (прецизионными) резисторами, низкочастотные транзисторы - высокочастотными и т.п.
Этот метод самый простой и потому рекомендуется начинать "борьбу за качество" именно с него. Он не требует никаких изменений модели. Достаточно лишь "прогнать" ее на новом наборе Х-параметров.
Для третьего метода не придумано подходящего названия. Мы назовем его методом уменьшения отрицательного влияния внешней среды. Например, при проектировании электрических схем - экранирование.
Заканчивая разговор, подведем итог.
Только системный подход может гарантировать хорошее качество проекта. Основные задачи, с которыми имеет дело инженер (анализ, синтез, улучшение проекта), оказываются непременными спутниками любого процесса проектирования. На рисунке 8 на них акцентировано особое внимание.
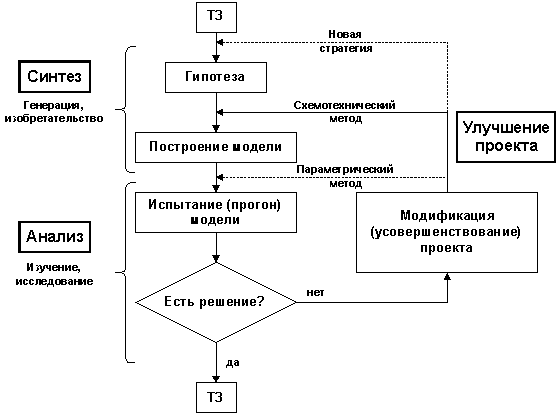
Рис. 8. Основные задачи инженера
Характеристики моделей систем
При моделировании рассматривают следующие характеристики моделей:
1. Цель функционирования определяется степенью целенаправленности поведения модели М. Модели могут быть разделены на одноцелевые, предназначенные для решения одной задачи, и многоцелевые, позволяющие разрешить или рассмотреть ряд сторон функционирования реального объекта.
2. Сложность оценивается по общему числу элементов в системе и связей между ними. В качестве элементов можно выделить уровни иерархии, отдельные функциональные подсистемы в модели М, входы и выходы и т.д.
3. Целостность указывает на то, что создаваемая модель М является одной целостной системой S(M), включает в себя большое количество составных частей (элементов), находящихся в сложной взаимосвязи друг с другом.
4. Неопределенность проявляется в системе: по состоянию системы, возможности достижения поставленной цели, методам решения задач, достоверности исходной информации и т.д. Основной характеристикой неопределенности служит мера информации – энтропия, позволяющая в ряде случаев оценить количество управляющей информации, необходимой для достижения заданного состояния системы. При моделировании основная цель – получение требуемого соответствия модели реальному объекту, и в этом смысле количество управляющей информации в модели можно также оценить с помощью энтропии и найти то предельное минимальное количество, которое необходимо для получения требуемого результата с заданной достоверностью.
5. Поведение системы позволяет оценить эффективность достижения системой поставленной цели. В зависимости от наличия случайных воздействий можно различать детерминированные и стохастические системы, по своему поведению – непрерывные, дискретные и т.д. Поведение системы S позволяет применительно к модели М оценить эффективность построенной модели, а также точность и достоверность полученных при этом результатов. Очевидно, что поведение модели М не обязательно совпадает с поведением реального объекта, причем часто моделирование может быть реализовано на базе иного материального носителя.
6. Адаптивность – способность приспособиться к различным внешним возмущающим факторам в широком диапазоне изменения воздействий внешней среды, а также изучение поведения модели в изменяющихся условиях, близких к реальным. Существенным может оказаться вопрос устойчивости модели к различным возмущающим воздействиям.
7. Организационная структура системы моделирования как комплекс технических средств, информационного, математического и программного обеспечения системы моделирования позволяет оптимизировать время моделирования и точность получаемых результатов.
8. Управляемость модели со стороны экспериментаторов для получения возможности рассмотрения протекания процесса в различных условиях, имитирующих реальные. Наличие многих управляемых параметров и переменных модели в реализованной системе моделирования дает возможность поставить широкий эксперимент и получить обширный спектр результатов.
9. Возможность развития модели позволяет создавать мощные системы моделирования для исследования многих сторон функционирования реального объекта.
Цели и проблемы моделирования систем
Любую модель строят в зависимости от цели, которую ставит перед ней исследователь, поэтому одна из основных проблем при моделировании – это проблема целевого назначения. Подобие процесса, протекающего в модели М, реальному процессу является не целью, а условием правильного функционирования модели, и поэтому в качестве цели должна быть поставлена задача изучения какой-либо стороны функционирования объекта (контроль параметров, оценка характеристик, управление объектом, прогнозирование поведения объекта).
Для упрощения модели М цели делят на подцели и создают более эффективные виды моделей в зависимости от полученных подцелей моделирования. Например, для отраслевых АСУ наиболее существенными целями являются задачи прогноза, потребления, сбыта продукции, размещение предприятий по отрасли с учетом всевозможных факторов (наличие сырья, людских ресурсов, энергии и т.д.). Для АСУ предприятием весьма существенно изучение процессов оперативного управления производством, оперативно-календарного планирования, перспективного планирования.
Далее определяются с целью функционирования системы, которая обеспечивала бы эффективную работу системы, например минимизация вероятности отказа в обслуживании приборов, максимизация загрузки устройств, устойчивость системы, чувствительность к изменению параметров.
Если цель моделирования и функционирования системы ясна, то возникает следующая проблема: построение модели М. Построение модели оказывается возможным, если имеется информация или выдвинуты гипотезы относительно структуры, алгоритмов и параметров исследуемого объекта. На основании их изучения осуществляется идентификация объекта.
Если модель М построена, то следующей проблемой можно считать проблему работы с ней, т.е. реализацию модели, основные задачи которой – минимизация времени получения конечных результатов и обеспечение их достоверности.
Для правильно построенной модели М характерным является то, что она выявляет лишь те закономерности, которые нужны исследователю, и не рассматривает не существенные для данного исследования свойства системы S.
Таким образом, характеризуя проблему моделирования в целом, необходимо учитывать, что от постановки задачи моделирования до интерпретации полученных результатов существует большая группа сложных научно-технических проблем:
· идентификация реальных объектов;
· выбор вида моделей;
· построение моделей и их машинная реализация;
· взаимодействие исследователя с моделью в ходе машинного эксперимента;
· проверка правильности полученных в ходе моделирования результатов;
· выявление основных закономерностей, исследованных в процессе моделирования.
Средства вычислительной техники, которые в настоящее время широко используются либо для вычислений при аналитическом моделировании, либо для реализации имитационной модели системы, могут лишь помочь с точки зрения эффективности реализации сложной модели, но не позволяют подтвердить правильность той или иной модели. Только на основе отработанных данных, опыта исследователя можно с достоверностью оценить адекватность модели по отношению к реальному процессу.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.