
Лекция 2
Классификация видов моделирования систем
Классификацию моделей проводят по различным критериям. Мы будем использовать наиболее простую и практически значимую (рис. 1).
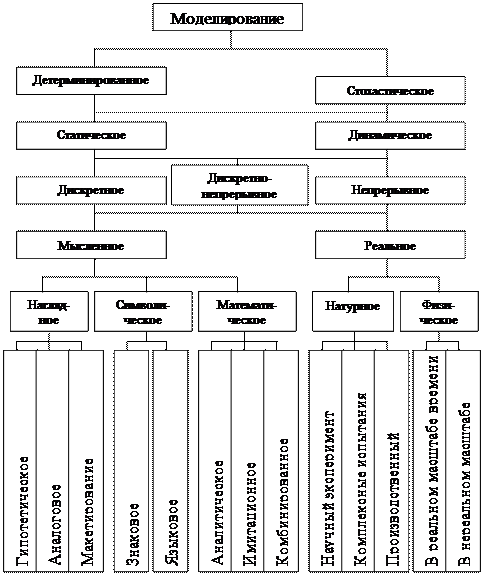
Рис. 1. Классификация видов моделирования систем
Модель называется статической, если среди параметров, участвующих в ее описании, нет временного параметра. Статическая модель в каждый момент времени дает лишь "фотографию" системы, ее срез.
Пример. Закон Ньютона F=am - это статическая модель движущейся с ускорением a материальной точки массой m. Эта модель не учитывает изменение ускорения от одной точки к другой.
Модель динамическая, если среди ее параметров есть временной параметр, т.е. она отображает систему (процессы в системе) во времени.
Пример. Модель S=gt2/2 - динамическая модель пути при свободном падении тела. Динамическая модель типа закона Ньютона: F(t)=a(t)m(t).
Модель дискретная, если она описывает поведение системы только в дискретные моменты времени.
Пример. Если рассматривать только t=0, 1, 2, :, 10 (сек), то модель St=gt2/2 или числовая последовательность S0=0, S1=g/2, S2=2g, S3=9g/2, :, S10=50g может служить дискретной моделью движения свободно падающего тела.
Модель непрерывная, если она описывает поведение системы для всех моментов времени из некоторого промежутка времени.
Пример. Модель S=gt2/2, 0<t<100 непрерывна на промежутке времени (0;100).
Модель детерминированная, если каждому входному набору параметров соответствует вполне определенный и однозначно определяемый набор выходных параметров; в противном случае - модель недетерминированная, стохастическая (вероятностная). То есть детерминированное моделирование отображает детерминированные процессы, т.е. процессы, в которых предполагается отсутствие всяких случайных воздействий; стохастическое моделирование отображает вероятностные процессы и события.
Пример. Приведенные выше физические модели - детерминированные. Если в модели S=gt2/2, 0<t<100 мы учли бы случайный параметр - порыв ветра с силой p при падении тела, например, так: S(p)=g(p)t2/2, 0<t<100, то мы получили бы стохастическую модель (уже не свободного!) падения.
В зависимости от формы представления объекта (системы) можно выделить мысленное и реальное моделирование.
Мысленное моделирование часто является единственным способом моделирования объектов, которые либо практически нереализуемы в заданном интервале времени, либо существуют вне условий, возможных для их физического создания. Например, на базе мысленного моделирования могут быть проанализированы многие ситуации микромира, которые не поддаются физическому эксперименту. Мысленное моделирование может быть реализовано с помощью наглядного, символического и математического моделирования.
При наглядном моделировании на базе представлений человека о реальных объектах создаются различные наглядные модели, отображающие явления и процессы, протекающие в объекте.
В основу гипотетического моделирования исследователем закладывается некоторая гипотеза о закономерностях протекания процесса в реальном объекте, которая отражает уровень знаний исследователя об объекте и базируется на причинно-следственных связях между входом и выходом изучаемого объекта. Гипотетическое моделирование используется, когда знаний об объекте недостаточно для построения формальных моделей.
Пример: представление объекта исследований в виде «черного ящика».
Аналоговое моделирование основывается на применении аналогий различных уровней. Наивысшим уровнем является полная аналогия, имеющая место только для достаточно простых объектов. С усложнением объекта используют аналогии последующих уровней, когда аналоговая модель отображает несколько либо только одну сторону функционирования объекта.
Примеры: чертеж, схема, график, план, описание какого-либо явления, процесса или предмета.
Мысленный макет или макетирование может применяться в случаях, когда протекающие в реальном объекте процессы не поддаются физическому моделированию, либо может предшествовать проведению других видов моделирования. В основе построения мысленных макетов также лежат аналогии, однако обычно базирующиеся на причинно-следственных связях между явлениями и процессами на объекте.
Пример: разработка печатной платы для радиоэлектронного устройства с помощью специальной компьютерной программы.
Символическое моделирование представляет собой искусственный процесс создания логического объекта, который замещает реальный и выражает основные свойства его отношений с помощью определенной системы знаков, отображающих набор понятий, (знаковое моделирование) и символов из специального словаря, очищенного от неоднозначности (языковое моделирование).
Пример 1. Дорожные знаки – знаковая модель.
Пример 2. Языковая модель словообразования. Пусть B - множество производящих основ существительных, C - множество суффиксов, P - прилагательных, "+" - операция конкатенации слов, ":=" - операция присваивания, "=>" - операция вывода (выводимости новых слов), Z - множество значений (смысловых) прилагательных. Языковая модель M словообразования: <zi><=<pi>:=<bi>+<si>. При bi - "рыб(а)", si - "н(ый)", получаем по этой модели pi - "рыбный", zi - "приготовленный из рыбы".
Математическое моделирование
Для исследования характеристик процесса функционирования любой системы S математическими методами, включая и машинные, должна быть проведена формализация этого процесса, т.е. построена математическая модель.
Математическое моделирование – процесс установления соответствия данному реальному объекту некоторой математической модели и исследование этой модели для получения характеристик объекта.
Любая математическая модель, как и всякая другая, описывает реальный объект лишь с некоторой степенью приближения к действительности.
Математическое моделирование делится на аналитическое, имитационное и комбинированное.
При аналитическом моделировании свойства, процессы объекта описываются в виде функциональных соотношений (алгебраических, интегродифференциальных, конечно-разностных и т.п.) или логических условий, которые решаются либо в общем виде, либо при конкретных начальных данных (численными методами на ЭВМ), либо качественно (например, оценка устойчивости решения).
Наиболее полное исследование процесса функционирования системы можно провести, если известны явные зависимости, связывающие искомые характеристики с начальными условиями, параметрами и переменными системы S. Однако, такие зависимости удается получить только для сравнительно простых систем. При усложнении систем исследование их аналитическим методом наталкивается на значительные трудности, которые часто бывают непреодолимыми. Поэтому, желая использовать аналитический метод, в этом случае идут на существенное упрощение первоначальной модели, чтобы иметь возможность изучить хотя бы общие свойства системы. Такое исследование на упрощенной модели аналитическим методом помогает получить ориентировочные результаты для определения более точных оценок другими методами.
Численный метод позволяет исследовать по сравнению с аналитическим методом более широкий класс систем, но при этом полученные решения носят частный характер. Численный метод особенно эффективен при использовании компьютеров.
В отдельных случаях исследования системы могут удовлетворить и те выводы, которые можно сделать при использовании качественного метода анализа математической модели. Такие качественные методы широко используются, например, в теории автоматического управления для оценки эффективности различных вариантов систем управления.
Модель имитационная, если она предназначена для испытания или изучения возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров модели.
Пример. Требуется смоделировать работу аэропорта с одной взлетно-посадочной полосой. Известен порядок пропуска к полосе взлетающих и прибывающих самолетов, время нахождения самолета на полосе, критическое время ожидания прибывающих самолетов. Вариируя величины среднего интервала прибытия и взлета самолетов, мы можем посмотреть, каким образом изменяется коэффициент загрузки полосы, среднее время ожидания самолетов. Задав определенные критерии эффективности работы аэропорта, сможем подобрать оптимальные параметры – средние времена прибытия и взлетасамолетов.
При имитационном моделировании реализующий модель алгоритм воспроизводит процесс функционирования системы S во времени, причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики системы S.
Основным преимуществом имитационного моделирования по сравнению с аналитическим является возможность решения более сложных задач. Имитационные модели позволяют достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия и др., которые часто создают трудности при аналитических исследованиях. В настоящее время имитационное моделирование – наиболее эффективный метод исследования больших систем, а часто и единственный практически доступный метод получения информации о поведении системы, особенно на этапе ее проектирования.
При имитационном моделировании с помощью компьютера осуществляется синтез структуры, алгоритмов и параметров модели, а также анализ и поиск оптимального варианта системы по некоторым критериям оценки эффективности. Когда результаты, полученные при воспроизведении на имитационной модели функционирования системы, являются реализациями случайных величин и функций, тогда для нахождения характеристик процесса требуется его многократное воспроизведение с последующей статистической обработкой информации.
Метод имитационного моделирования позволяет решать задачи анализа больших систем S, включая задачи оценки: вариантов структуры системы, эффективности различных алгоритмов управления системой, влияния изменения различных параметров системы. Имитационное моделирование может быть положено также в основу структурного, алгоритмического и параметрического синтеза больших систем, когда требуется создать систему, с заданными характеристиками при определенных ограничениях, которая является оптимальной по некоторым критериям оценки эффективности.
Комбинированное (аналитико-имитационное) моделирование при анализе и синтезе систем позволяет объединить достоинства аналитического и имитационного моделирования. При построении комбинированных моделей проводится предварительная декомпозиция процесса функционирования объекта на составляющие подпроцессы, и для тех из них, где это возможно, используются аналитические модели, а для остальных подпроцессов строятся имитационные модели.
Такой комбинированный подход позволяет охватить качественно новые классы систем, которые не могут быть исследованы с использованием только аналитического и имитационного моделирования в отдельности.
При реальном моделировании исследуются различные характеристики на реальном объекте целиком либо на его части. Такие исследования могут проводиться как на объектах, работающих в нормальных режимах, так и при организации специальных режимов для оценки интересующих исследователя характеристик (при других значениях переменных и параметров, в другом масштабе времени и т.д.). Реальное моделирование является наиболее адекватным, но при этом его возможности с учетом особенностей реальных объектов ограничены. Например, проведение реального моделирования АСУ предприятием потребует, во-первых, создания такой АСУ, а во-вторых, проведения экспериментов с управляемым объектом, т.е. предприятием, что в большинстве случаев невозможно.
Реальное моделирование делят на натурное и физическое.
При натурном моделировании исследования проводят на реальном объекте с последующей обработкой результатов эксперимента на основе теории подобия. Научный эксперимент характеризуется использованием средств автоматизации проведения активного эксперимента и обработки информации. При комплексных испытаниях вследствие повторения испытаний изделий выявляются общие закономерности о надежности этих изделий, о характеристиках качества и т.д., при этом в реально протекающий процесс вводятся критические ситуации и определяются границы устойчивости. Производственный эксперимент связан с обобщением опыта, накопленного в ходе производственного процесса.
Отличие эксперимента от реального протекания процесса заключается в том, что в нем могут появиться отдельные критические ситуации и определяться границы устойчивости процесса. В ходе эксперимента вводятся новые факторы и возмущающие воздействия в процессе функционирования объекта. Одна из разновидностей эксперимента – комплексные испытания, которые также можно отнести к натурному моделированию, когда вследствие повторения испытаний изделий выявляются общие закономерности о надежности этих изделий, о характеристиках качества и т.д. В этом случае моделирование осуществляется путем обработки и обобщения сведений, проходящих в группе однородных явлений. Наряду со специально организованными испытаниями возможна реализация натурного моделирования путем обобщения опыта, накопленного в ходе производственного процесса, т.е. можно говорить о производственном эксперименте. Здесь на базе теории подобия обрабатывают статистический материал по производственному процессу и получают его обобщенные характеристики.
Пример – испытание прочности подводной лодки путем опускания на большую глубину – этап комплексных испытаний.
При физическом моделировании исследования проводятся на установках, которые сохраняют природу явлений и обладают физическим подобием. Физическое моделирование может протекать в реальном и нереальном (псевдореальном) масштабах времени, а также может просматриваться без учета времени. Например, так называемые «замороженные» процессы, которые фиксируются в некоторый момент времени.
Пример 1. – изучение разрушительной силы волны не в море, а в бассейне.
Пример 2 - две системы, первая из которых имеющая механическую природу, состоит из оси, передающей вращение через пружину и маховик, погруженный частично в вязкую тормозящую жидкость, валу, жестко связанному с маховиком. Вторая система — электрическая — состоит из источника электродвижущей силы, соединённого через катушку индуктивности, конденсатор и активное сопротивление со счётчиком электрической энергии. Если подобрать значения индуктивности, ёмкости и сопротивления так, чтобы они определённым образом соответствовали упругости пружины, инерции маховика и трению жидкости, то эти системы обнаружат структурное и функциональное сходство (даже тождество), выражаемое, в частности, в том, что они будут описываться одним и тем же дифференциальным уравнением. Это уравнение может служить «теоретической моделью» обеих систем, любая же из них — «экспериментальной моделью» этого уравнения и «аналоговой моделью» друг друга. Эта аналогия лежит в основе электрического моделирования механических систем: электрические модели гораздо более удобны для экспериментального исследования, нежели моделируемые механические.
Особое место в моделировании занимает кибернетическое моделирование, в котором отсутствует непосредственное подобие физических процессов, происходящих в моделях, реальным процессам. Реальный объект рассматривают как «черный ящик», имеющий ряд входов и выходов, исследуемую функцию реального объекта формализуют в виде некоторых операторов связи между входом и выходом, причем на базе совершенно иных математических соотношений и, естественно, иной физической реализации процесса.
Тип модели зависит от информационной сущности моделируемой системы, от связей и отношений его подсистем и элементов, а не от его физической природы.
Пример. Математические описания (модели) динамики эпидемии инфекционной болезни, радиоактивного распада, усвоения второго иностранного языка, выпуска изделий производственного предприятия и т.д. являются одинаковыми с точки зрения их описания, хотя процессы различны.
Границы между моделями различного типа или же отнесение модели к тому или иному типу часто весьма условны. Можно говорить о различных режимах использования моделей - имитационном, стохастическом и т.д.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.