Метод перестановок (шифрование перестановками)
Исходный текст разбивается на ключевые группы с равными количествами букв в группах. В каждой группе по заданному правилу производится перестановка букв.
Табличный вариант
Записываем исходный текст по строкам в матрицу из N столбцов. Затем шифруем текст переставляя столбцы матрицы в заданном порядке перестановок. Этот порядок перестановок есть ключ (и операция) перестановок. Заданный порядок перестановок можно выразить осмысленным словом (ключом) с неповторяющимися буквами и
производить шифрование, т.е. перестановку колонок таблицы в той последовательности, в которой располагаются в алфавите буквы ключевого слова.
Пример. Зашифруем текст «ШИФРУЙТЕ ПЕРЕСТАНОВКАМИ» с помощью матрицы из
6 колонок и ключевого слова «ДЕЗАВИ».
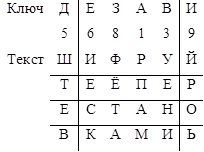— порядок букв ключа в алфавите
Пробелы между словами исходного текста и конец текста заполняем для полноты матрицы произвольными буквами.
Получаем, читая по столбцам в порядке перестановок следующую шифровку: РПАМУЕНИШТЕВИЕСКФЁТАЙРОЬ или группами по 6 букв:
РПАМУЕ НИШТЕВ ИЕСКФЁ ТАЙРОЬ
Расшифровка
— Определяем число колонок, деля количество знаков в шифрограмме на число букв в ключе 30 / 6 = 5 .
— Выписываем ключевое слово с обозначением последовательности букв ключа в алфавите и под ними в колонки с указанной последовательностью выписываем текст шифровки. Открытый текст читаем по строкам.
Усложнение табличного варианта.
Шифруемый текст вписываем в таблицу выбранной размерности по некоторому маршруту, например по спирали. Затем колонки выписываем либо подряд, либо переставляя по ключу. Расшифровываем в обратной последовательности.
Перестановка по маршрутам Гамильтона.
Такая сравнительно простая перестановка является по оценкам американских специалистов достаточно стойким шифром.
Исходный текст разбивается на группы по 8 букв. 1-ая операция — вписывание исходного текста в шаблон с 8-ю знакоместами с указанным на них порядком вписывания. Например текст «ШИФРУЙТЕ ПЕРЕСТАНОВКАМИ» вписываем без пробелов, а конец текст дополним до полноты шаблона буквами «А».
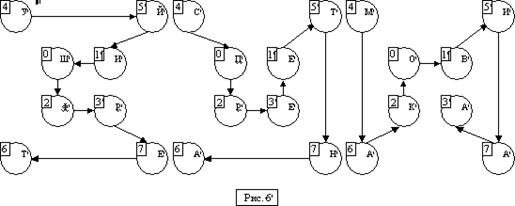
Рисунок 5.1
2-ая операция — последовательное повторение 5-ти разных маршрутов Гамильтона. На рисунках нам хватило 3-х маршрутов. Выписываем по этим маршрутам шифрограмму:
|
УЙИШФРЕТ |
СПРЕЕТНА |
МАКОВИАА |
|
1-я перестановка |
2-я перестановка |
3-я перестановка |
Для перестановки букв в группах по 8 количество разных перестановок
(маршрутов)
= 8(
) = 8!= 40320 . Количество возможных перестановок быстро
увеличивается с ростом длины группы перестановок.
Если злоумышленник угадает длину группы, то он может перебрать последовательно все возможные перестановки пока не найдёт осмысленную. Для малой длины группы это легко особенно с помощью ЭВМ. Посмотрим как усложняется этот пример с ростом длины группы.
|
Длина группы |
Количество перестановок |
Время просмотра их на ЭВМ со скоростью 1 перестановка/сек. |
|
8 |
40320 |
11.2 часа |
|
10 |
3628800 |
42 суток |
|
12 |
479 106 |
5544 суток » 15 лет |
Количество M перестановок для группы из N букв равно:
= N = N!
Перестановки удобно задавать числовыми ключами (гаммами)
Так перестановки Гамильтона будут иметь вид:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
исх. текст |
Ш |
И |
Ф |
Р |
У |
Й |
Т |
Е |
П |
Е |
Р |
Е |
С |
Т |
А |
Н |
О |
В |
К |
А |
М |
И |
А |
А |
|
ключи шифрования |
3 |
2 |
4 |
5 |
0 |
1 |
7 |
6 |
1 |
4 |
2 |
3 |
0 |
5 |
7 |
6 |
3 |
4 |
2 |
7 |
0 |
5 |
1 |
6 |
|
шифротекст |
У |
Й |
И |
Ш |
Ф |
Р |
Е |
Т |
С |
П |
Р |
Е |
Е |
Т |
Н |
А |
М |
А |
К |
О |
В |
И |
А |
А |
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Расшифрование производится в обратном порядке (двигаться в направлении обратном стрелке перестановки), т.е. ключи перестановки для расшифрования будут: Перепишем ключи шифрования в виде
|
Ключ шифрования: |
03 |
12 |
24 |
35 |
40 |
51 |
67 |
76 |
03 — 0-е место исх. текста переставляется на 3-е место шифрограммы - ключ шифрования, упорядоченный по 1-му знаку |
|
Ключ расшифр.: |
30 |
21 |
42 |
53 |
04 |
15 |
76 |
67 |
|
|
Ключ шифрования: |
04 |
15 |
23 |
30 |
42 |
53 |
67 |
76 |
|
|
Ключ расшифр.: |
4 |
5 |
3 |
0 |
2 |
3 |
7 |
6 |
или так:
|
3 |
2 |
4 |
5 |
0 |
1 |
7 |
6 |
— маршрут шифрования |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
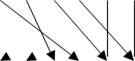
Номера по порядку знакомест
группы
4 5 1 0
2 3 7 6
— маршрут 4 5 1 0 2 3 7 6 расшифрования
Очевидно, что две (разные) перестановки подряд не увеличивают стойкость шифра, т.к. эквивалентны некоторой одной.
Статистика букв шифротекста перестановки такая же как и у исходного текста. Но знание её не помогает взломать шифр, т.к. буквы поменялись местами, однако в рассмотренных вариантах оказывается проявляются статистические закономерности букв ключа, что может позволить раскрыть его.
Метод перестановок (шифрование перестановками)
Пример. Зашифруем текст «ШИФРУЙТЕ
Рисунок 5.1 2-ая операция — последовательное повторение 5-ти разных маршрутов
Ключ шифрования: 03 12 24 35 40 51 67 76 03 — 0-е место исх
Очевидно, что две (разные) перестановки подряд не увеличивают стойкость шифра, т
© ООО «Знанио»
