«Метод площадей при решении геометрических задач второй части ОГЭ».

Тема: «Метод площадей при решении геометрических задач второй части ОГЭ».

Цель: Рассмотрение теоретических  основ;
Формирование представления о методе площадей;
Использование метода площадей при решении планиметрических (второй части ОГЭ и некоторых конкурсных) задач.

Актуальность

Предмету геометрия отведено по учебному плану меньше часов, чем алгебре. Учащиеся испытывают трудности при выполнении геометрических заданий. Это задачи повышенной трудности,  в модуле «Геометрия» на ОГЭ. Тема «Метод площадей»  - актуальна в связи с решением таких задач на экзамене (как №24, №25, №26)
и  на различных олимпиадах и конкурсах.

План

I.        Введение

II.     Основная часть.

1. Метод площадей.

2. Определение метода площадей. Характеристики метода.

3. Основные свойства площадей и ключевые задачи.

4. Практический диапазон применимости метода площадей к решению задач

III.  Выводы

IV.  Заключение

V.    Приложение. Причины ошибок. Классификация

I.       Введение

Определение проблемы: необходимость разбора решения геометрических задач из второй части экзаменационной работы по выбранному методу.

Задачи

1. Изучение научно-методической литературы по проблеме исследования.

Изучение метода площадей и после определения проблемы научиться применять свойства площадей для составления соотношений, связывающих ключевые задачи с неизвестными, используя различные приёмы.

2. Анализ различных учебных пособий с целью изучения и описания метода площадей.

3. Рассмотрение некоторого диапазона применимости метода площадей к решению задач.

4. Рассмотрение на примерах структуры процесса решения таких задач  и развитие умения самостоятельно анализировать и конструировать свои знания; классифицировать задачи.

5. Умение ориентироваться в планиметрическом пространстве и нахождение  путей решения.

Трудности решения геометрических задач обусловлены следующими факторами:
Неалгоритмичность задач.
Необходимость выбора метода решения задачи и теоремы для решения конкретной задачи из большого набора известных фактов.

Обсуждение методов исследования. Метод конкретных ситуаций (следование принципу «процесс обсуждения важнее самого решения»), самостоятельное изучение и подготовленное в письменном виде решение проблемы.

Результаты исследования.

Сбор, анализ полученных данных, систематизация решенных задач, корректировка их. Оформление результатов исследовательской работы в электронном виде.

II.    Основная часть

1. Метод площадей.

      В школьном курсе математики, самыми трудными считаются

геометрические задачи. Как научиться решать геометрические задачи,

особенно сложные, конкурсные? При решении геометрических задач, как

правило, алгоритмов нет, и выбирать наиболее подходящую к данному

случаю теорему не просто.

     В данной работе рассматривается один из самых распространенных

алгоритмов решения геометрических задач – метод площадей. Значимость метода площадей заключается в том, что он является предметом изучения и одновременно средством для изучения последующего материала.

Методы решения планиметрических задач. (Дополнительный материал).

Некоторые методы решения геометрических задач (№24, 25, 26)

·         Метод дополнительных построений

·         Метод вспомогательной окружности.

·         Метод подобия

·         Метод площадей

·         Также возможно использование векторного способа на плоскости, возможно использование координатного способа. Учащийся не ограничен в выборе метода решения этих задач.

Геометрические задачи повышенной сложности ОГЭ

В работах на примерах решения конкретных задач обычно используются такие методы:

1.      Удвоение медианы

2.      Использование введения буквенных обозначений величин

3.      Метод вспомогательных построений

4.      Построение вспомогательных отрезков в трапеции

5.     Использование осевой симметрии

6.      Переход к равновеликой вспомогательной фигуре

7.      Метод площадей.

8. Введение вспомогательной окружности.

(См. в презентации ключевые задачи)

4.      Построение вспомогательных отрезков в трапеции

5.     Использование осевой симметрии

6.      Переход к равновеликой вспомогательной фигуре

7.      Метод площадей.

8. Введение вспомогательной окружности.

(См. в презентации ключевые задачи)

Рассмотрим в нашем исследовании метод площадей. 

2. Определение метода площадей. Характеристики метода.

Из названия следует, что главным объектом данного метода является площадь.

 Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры.

1. Весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное.
 Здесь и проявляется основная особенность метода площадей:
из геометрической задачи он "делает" её алгебраической, сводя всё к решению уравнения (а иногда и системы уравнений).

2. Одна из разновидностей метода площадей сводится к использованию в задаче свойства аддитивности площади: если фигура разбита на части, то ее площадь равна сумме площадей этих частей. S=S1+S2+S3

2. Универсального метода для решения всех задач на площади

многоугольников нет, но существуют приемы, применимые ко многим

задачам. Понятие площади мы используем даже при решении тех задач,
в условии которых отсутствует упоминание площади. Поэтому можно

говорить о методе площадей в геометрии.

4. Метод площадей состоит в применении различных её свойств для нахождения соотношений, связывающих их с неизвестными.

Остановимся подробнее на характеристике и диапазоне применимости метода площадей.

3. Основные свойства площадей

Свойство 1. Если вершину треугольника передвигать по прямой, параллельной основанию, то площадь при этом не измениться.

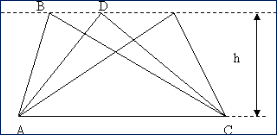Доказательство:

Рассмотрим ▲ABC и ▲ADC. Они

имеют общее основание и равные

высоты, т.к. прямые AC и BD

параллельные, то расстояние между

ними равно h - высоте ▲ABC и ▲ADC.

Свойство 2. Если два треугольника имеют одинаковые высоты, то отношение их

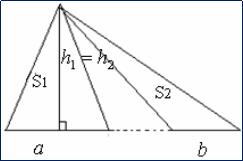площадей равно отношению длин оснований, т. е. сторон,
на которые опущены эти высоты.

Доказательство:

Пусть h1 = h2 в двух треугольниках

с основаниями a и b.

Рассмотрим отношение площадей

этих треугольников, получим:

 = .

Свойство 3

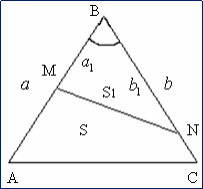Если два треугольника имеют общий угол, то их площади относятся

как произведение сторон, заключающих этот угол.

Доказательство:

Рассмотрим ▲ABC и ▲MBN.   

Пусть AB = k∙MB, BC = k∙NB и ABC=MBN .

Используя формулу площади треугольника, получим: отношение подобных площадей ▲ABC и ▲MBN.

Тогда получим:    = k² .

Свойство №4

Медиана треугольника делит его на две равновеликие части.

Доказательство:

Рассмотрим ▲ABC . Пусть

медиана  - BM , тогда

AM=MC=1/2AC. Медиана делит

треугольник на два равновеликих с одинаковой

высотой. Найдем площади

треугольников ▲ABM и ▲MBC. S_{ABM =} S_CBM.

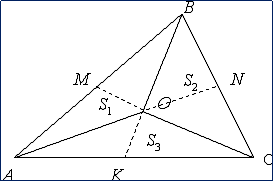
Свойство №5

Медианы треугольника делят

его на три равновеликие части.

Аналогично доказывается.

Медианы треугольника делят его
на 6 равновеликих частей.

Утверждение. Два треугольника
являются равновеликими,

если равны их высоты и основания.

Свойство №6

Средние линии треугольника площади S

отсекают от него

треугольники площади ¼ S.

Доказательство

Рассмотрим ▲ABC. NM - средняя линия

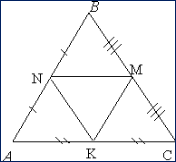в треугольнике и она равна половине

основания AC.

Если SABC = S, то  можно доказать, что

площади всех треугольников равны

одной четвертой части площади ▲ABC.

4. Применение свойств метода площадей к решению задач.

В данном пункте рассмотрим систему геометрических задач, решаемых методом площадей. Задачи построены по нарастающему уровню сложности.

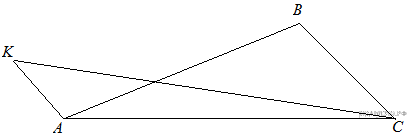
№1(Задания типа № 24).

 Сто­ро­ны AC, AB, BC тре­уголь­ни­ка ABC равны 2,   и 2 со­от­вет­ствен­но. Точка K рас­по­ло­же­на вне тре­уголь­ни­ка ABC , причём от­ре­зок KC пе­ре­се­ка­ет сто­ро­ну AB в точке, от­лич­ной от B. Из­вест­но, что тре­уголь­ник с вер­ши­на­ми K, A и C по­до­бен ис­ход­но­му. Най­ди­те ко­си­нус угла AKC, если ∠KAC > 90°. Найти площадь треугольника АВС.

Решение.

Рассмотрим по­доб­ные тре­уголь­ни­ки ABC и AKC и уста­но­вим со­от­вет­ствие между их углами. Про­тив боль­шей сто­ро­ны все­гда лежит боль­ший угол, в тре­уголь­ни­ке ABC это угол ABC в тре­уголь­ни­ке , в свою очередь, есть тупой угол  и он яв­ля­ет­ся наибольшим, зна­чит, ∠КАС = ∠АВС.  Угол АСК за­ве­до­мо не может быть равен углу  так как он со­став­ля­ет толь­ко его часть. Сле­до­ва­тель­но, угол АСВ равен углу АКС.

Найдём ко­си­нус угла , ис­поль­зуя тео­ре­му косинусов:

   1)        

2) S _ABC =   • СА• СВ•  ;

Найдём:   =  ;   )² =   =      =   . S _ABC =

 Ответ:     =   ; S _ABC = .

          Задания типа № 25.

 №2. В па­рал­ле­ло­грам­ме ABCD диа­го­на­ли AC и BD пе­ре­се­ка­ют­ся в точке O. До­ка­жи­те, что пло­щадь па­рал­ле­ло­грам­ма ABCD в че­ты­ре раза боль­ше пло­ща­ди тре­уголь­ни­ка BOC.

Решение.

Проведём вы­со­ту  так, чтобы она про­хо­ди­ла через точку О. Углы  и  равны друг другу как вертикальные. Вспом­ним также, что диа­го­на­ли де­лят­ся точ­кой пе­ре­се­че­ния пополам, следовательно,  Рас­смот­рим тре­уголь­ни­ки  и , они прямоугольные, имеют рав­ные углы и рав­ные гипотенузы, сле­до­ва­тель­но, эти тре­уголь­ни­ки равны, а зна­чит, равны от­рез­ки  и . Таким образом, 

Площадь па­рал­ле­ло­грамм равна  а пло­щадь тре­уголь­ни­ка 

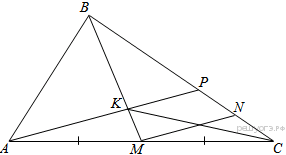
Типа №26.  №3.

 В тре­уголь­ни­ке ABC на его ме­ди­а­не BM от­ме­че­на точка K так, что BK : KM = 10 : 9. Прямая AK пе­ре­се­ка­ет сто­ро­ну BC в точке P. Найдите от­но­ше­ние пло­ща­ди четырёхугольника KPCM к пло­ща­ди тре­уголь­ни­ка ABС.

Решение.

Пусть площадь треугольника  равна 

Проведём прямую  параллельную  Точка  — середина  следовательно,  — средняя линия треугольника значит,

 По теореме Фалеса для угла  находим:

а так как  получаем, что 

Стороны треугольников  и  сонаправлены, их площади относятся как произведение отношений сонаправленных сторон,
поэтому

 откуда , в то время как   следовательно,  

Тем самым, для искомого отношения площадей имеем:.

 Ответ. .

Олимпиадные задачи:  9 класс.

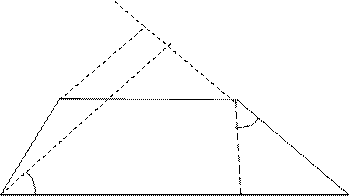
1. Сторона KP трапеции NMКP равна 3 см. Расстояние из вершин N и М до стороны КР равны 7см  и 5 см соответственно. Найдите площадь трапеции NMКP.

Решение.  Сделаем чертеж. Опустим перпендикуляры из точек N и М на сторону КР и построим перпендикуляр KH к стороне NP.

Обозначим ∠ANP через α. Заметим, что ∠BMK  = ∠ANP = α (стороны этих углов соответственно параллельны), а также∠HKP = ∠ANP = α (в прямоугольных треугольниках NAP и KHP угол с вершиной Р– общий).Тогда имеем три подобных прямоугольных треугольника: NAP, MВK  и КНР.

Значит:  МК=  , NP=  , КH= . Следовательно,

S_NMKP=  (MK + NP)KH= = 18 (кв.см). Ответ: 18 кв.см

№2. 10 класс

а) В треугольнике АВС на продолжении медианы ВМ выбрана точка К так, что МК:ВМ = 1:2. Известно, что АВ=5, ВС=3, СК=4. Найти АК.

б) Найти площадь треугольника АВС.

Решение. Сделаем чертёж:

Обозначим  ∠АМК через α. Тогда ∠АМВ = π-α, ∠ВМС = α, ∠СМК = π-α.

Применим теорему косинусов к треугольникам АВМ,  ВСМ, СКМ и АКМ.

КМ= х, тогда ВМ= 2х, АМ =СМ= у.

Имеем:

25= у²+4х²+4ху cosα,

9= у²+4х²- 4ху cosα,

16 = у²+ х²+2ху cosα.

Решив систему трёх уравнений с тремя неизвестными, получим:

,  ,  .

Из треугольника АКМ имеем: АК²= 12-2. Тогда АК=2 .

б)  Найти площадь треугольника АВС.

S_ABC =  • 2•MB • MC• ; ∠ВМС = α;  ; =

 =  ;  S_ABC =  • 2•2• •   = 2 =   •

Ответ: 2 . S_ABC =  .

Выводы.

1.  При решении геометрических задач внимательно анализировать условие задачи, находить взаимосвязь между элементами геометрических фигур, применять свойства и конкретные приёмы решения задач.

2. Использовать приравнивание  выражений, полученных  по различным формулам площади для одной и той же фигуры, что позволит получить зависимость между ее элементами. Полезно рассматривать отношение площадей фигур, одна из которых (или обе) содержит в себе искомые элементы.

3. Применять также метод «вспомогательного элемента», который заключается во включении в решение некоторого дополнительного объекта, прямо не фигурирующего в условии, если с его помощью можно получить новые умозаключения и результаты с последующим исключением объекта.

4. Для развития умений самостоятельно конструировать свои знания, рассматривая различные структуры процесса решения задач, ориентируясь в информационном и социальном пространстве.

Заключение.

     Подводя итог обзору методов решения и методов поиска решения геометрических задач, заметим, что не все этапы в равной степени обязательно присутствуют в решении любой задачи. Мы рассмотрели примеры, показывающие, что не всегда приходится выявлять характерные особенности конфигурации и, наоборот, некоторые решения одним этим этапом, по сути, и исчерпывались. Отдельно следует сказать об анализе полученного решения. Основная функция анализа - контроль правильности полученного решения,

Иногда в ходе анализа необходимо провести исследование, существует ли полученная конфигурация, не относится ли она к разряду невозможных, при каких условиях возможно ее существование.

Изучение методов решения геометрических задач будет более эффективным, если рассматривать на примере одной задачи возможности использования

различных геометрических приёмов.

Приложение

1. Причины ошибок в решении геометрических задач

·         Незнание и/или непонимание аксиом, определений, теорем

·         Неумение их применять

·         Невнимательное чтение условия и вопроса задания

·         Вычислительные ошибки

·         Нарушения логики в рассуждениях

·         Принятие ошибочных гипотез. Недостатки в работе с рисунком.

2.  Классификация задач, решаемых методом площадей

1. В условии задачи упоминается о площади
2. В условии задачи не упоминается о площади

3. Задачи на выражение площади несколькими способами

4. Задачи на использование свойства аддитивности.

5. Задачи на использование свойств отношения площадей.

6. Комбинированные задачи.