
"Решение алгебраических уравнений методом замены переменной"
1. Уравнения вида
![]()
|
1.
2.
3.
4.
|
5.
6.
7.
8.
|
Способ
решения: ![]() Обратим
внимание, что сумма свободных членов первой и четвертой скобки равна сумме
свободных членов второй и третьей скобки. Перемножив эти скобки, получим
Обратим
внимание, что сумма свободных членов первой и четвертой скобки равна сумме
свободных членов второй и третьей скобки. Перемножив эти скобки, получим ![]() . Сделаем
замену
. Сделаем
замену ![]() , получим
уравнение
, получим
уравнение ![]() , раскроем
скобки
, раскроем
скобки ![]() , найдем корни
по теореме обратной теореме Виета
, найдем корни
по теореме обратной теореме Виета ![]() или
или ![]() . Возвращаемся
к замене и решаем еще два уравнения:
. Возвращаемся
к замене и решаем еще два уравнения:
1)![]()
![]()
![]()
![]() , решений нет.
, решений нет.
2)![]()
![]()
![]() или
или ![]()
Ответ: ![]() ;
; ![]()
2. Уравнения вида ![]()
![]() .
.
|
1.
2.
3.
4.
|
5.
6.
7.
8.
|
Способ
решения: ![]() . Сначала
умножим обе части уравнения на
. Сначала
умножим обе части уравнения на ![]() , чтобы
поменять местами слагаемые во второй скобке. Получим уравнение
, чтобы
поменять местами слагаемые во второй скобке. Получим уравнение ![]() . Перемножим
те скобки, в которых произведение свободных членов одинаково, т. е. первую
скобку на четвертую, а вторую на третью. Получим
. Перемножим
те скобки, в которых произведение свободных членов одинаково, т. е. первую
скобку на четвертую, а вторую на третью. Получим ![]() . Так как
. Так как ![]() не является
корнем данного уравнения, то разделим обе части уравнения на
не является
корнем данного уравнения, то разделим обе части уравнения на ![]() ; получим
; получим 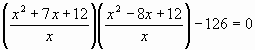 ; преобразуем
полученное выражение
; преобразуем
полученное выражение ![]() ; сделаем
замену переменной
; сделаем
замену переменной ![]() ; и решим
уравнение
; и решим
уравнение ![]() ;
; ![]()
![]()
![]() ;
; ![]() . Возвратимся
к замене и решим ещё два уравнения:
. Возвратимся
к замене и решим ещё два уравнения:
1) ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
2) ![]() ;
; ![]() ;
; ![]() ,
, ![]()
Ответ: ![]() ;
; ![]() ;
; ![]()
3. Симметрические уравнения и возвратные уравнения
|
1.
2.
3.
4.
5.
|
1.
2.
3.
4.
5.
|
Способ
решения: ![]() . Так как
. Так как ![]() не является
корнем уравнения, разделим обе части уравнения на
не является
корнем уравнения, разделим обе части уравнения на ![]() , получим
, получим ![]() ; группируем
; группируем![]() ; выносим за
скобки общий множитель
; выносим за
скобки общий множитель ![]() (*); делаем
замену переменной
(*); делаем
замену переменной ![]() ; возводим обе
части полученного равенства в квадрат
; возводим обе
части полученного равенства в квадрат ![]() ; выражаем
; выражаем ![]() ; подставляем
полученное выражение в уравнение (*) и решаем уравнение
; подставляем
полученное выражение в уравнение (*) и решаем уравнение ![]() ;
; ![]() ;
; ![]() ;
; ![]() или
или ![]() . Возвращаемся
к замене и решаем уравнения 1)
. Возвращаемся
к замене и решаем уравнения 1) ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
2) ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Ответ: ![]() ;
; ![]() ;
; ![]()
4. Дробно-рациональные уравнения
|
1. 2.
3.
4.
5.
|
6. 7.
8.
9.
10.
|
Способ
решения: ![]() ОДЗ:
ОДЗ: ![]()
Сделаем
замену ![]() ; возведем обе
части в квадрат, получим
; возведем обе
части в квадрат, получим ![]() , выразим
, выразим ![]() и подставим в
исходное уравнение, получим
и подставим в
исходное уравнение, получим ![]() . Решаем
полученное уравнение
. Решаем
полученное уравнение ![]() ;
; ![]() ;
; ![]() ;
; ![]() получаем два
уравнения:
получаем два
уравнения:
1) ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
2) ![]() ;
; ![]() ;
; ![]() ,
, ![]() .
.
Ответ: ![]() ;
; ![]() ;
; ![]()
5. Однородные уравнения
|
1.
2.
3.
4.
5.
|
1.
2.
3.
4.
5.
|
Способ
решения: ![]() Так как
Так как ![]() не является
корнем уравнения, разделим обе его части на
не является
корнем уравнения, разделим обе его части на ![]() , получим
, получим 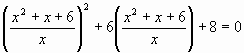 ; сделав
замену переменной
; сделав
замену переменной ![]() ; и, решив
полученное уравнение
; и, решив
полученное уравнение ![]() , находим
корни
, находим
корни ![]() ;
; ![]() ;
Возвратившись к замене, решим ещё два уравнения:
;
Возвратившись к замене, решим ещё два уравнения:
1) ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
2) ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]() , решений нет.
, решений нет.
Ответ: ![]() ;
;![]()
Уравнения, решаемые методом выделения квадрата двучлена
|
1) 2)
3)
4)
|
5) 6)
7)
|
8) 9)
10)
|
Способ
решения: ![]() ОДЗ:
ОДЗ: ![]() . Обратим
внимание на то, что знаменателем дроби является квадрат суммы двучлена, значит
выделять будем квадрат разности
. Обратим
внимание на то, что знаменателем дроби является квадрат суммы двучлена, значит
выделять будем квадрат разности ![]()
![]()
![]()
![]()
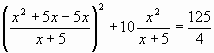
![]()
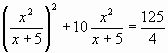 ; сделав
замену переменной
; сделав
замену переменной ![]() , получим
уравнение
, получим
уравнение ![]() ; преобразуем
его к виду
; преобразуем
его к виду ![]() и решим:
и решим:![]() ;
; ![]() ;
; ![]() ;
; ![]() . Возвратимся
к замене и решим уравнения:
. Возвратимся
к замене и решим уравнения:
1)![]() ;
; ![]() ;
; ![]() ;
;![]() ;
; ![]() ;
; ![]() .
.
2) ![]() ;
; ![]() ;
;![]()
![]() , решений нет.
, решений нет.
Ответ: ![]() ;
; ![]()
Примеры:
Основная трудность решения задач методом подстановки заключается в том, что иногда трудно угадать вид самой подстановки и вид уравнений, где подстановку можно использовать.
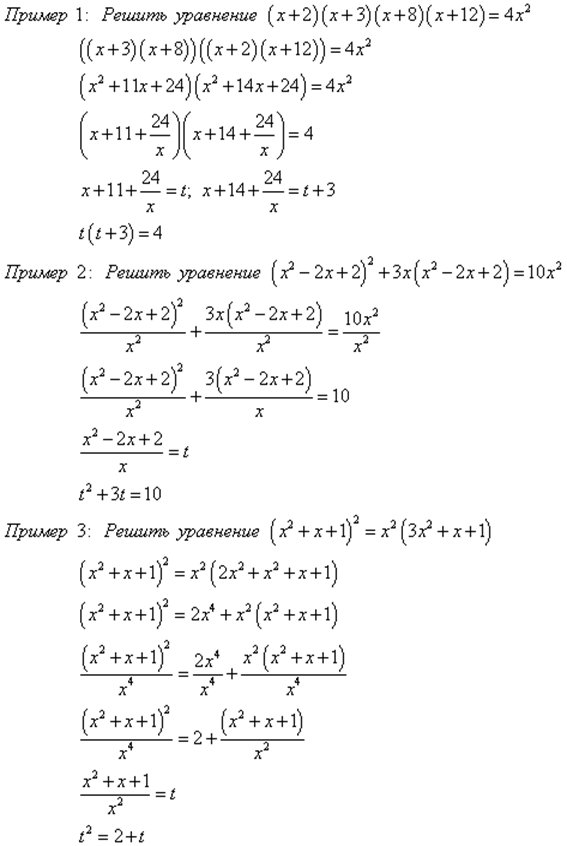
Рассмотрим ещё примеры:

ТРИГОНОМЕТРИЧЕСКОЙ ПОДСТАНОВКИ ПРИ РЕШЕНИИ ЗАДАЧ
1.1 Иррациональные уравнения
Иррациональные уравнения часто встречаются на вступительных экзаменах по математике, так как с их помощью легко диагностируется знание таких понятий, как равносильные преобразования, область определения и другие. Методы решения иррациональных уравнений, как правило, основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным, которое либо равносильно исходному иррациональному уравнению, либо является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. Эквивалентность не нарушается при возведении обеих частей в нечетную степень. В противном случае требуется проверка найденных решений или оценка знака обеих частей уравнения. Но существуют и другие приемы, которые могут оказаться более эффективными при решении иррациональных уравнений. Например, метод тригонометрической подстановки.
Пример 1. Решите уравнение
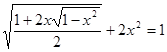 [12].
[12].
Решение с помощью тригонометрической подстановки
Так
как ![]() ,
то
,
то ![]() .
Поэтому можно положить
.
Поэтому можно положить ![]() .
Уравнение примет вид
.
Уравнение примет вид
![]() .
.
Положим
![]() ,
где
,
где ![]() ,
тогда
,
тогда
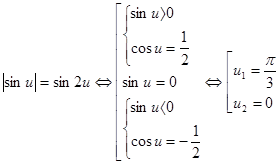 .
.
![]() .
.
![]() .
.
Ответ:
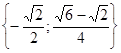 .
.
Пример 2. Решите уравнение
![]() [14].
[14].
Решение с помощью тригонометрической подстановки
Область
определения уравнения задается неравенством ![]() ,
что равносильно условию
,
что равносильно условию ![]() ,
тогда
,
тогда ![]() .
Поэтому можно положить
.
Поэтому можно положить ![]() . Уравнение примет вид
. Уравнение примет вид
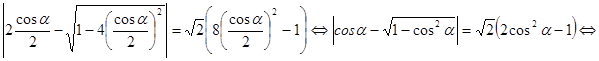
![]() .
.
Так как ![]() ,
то
,
то ![]() .
Раскроем внутренний модуль
.
Раскроем внутренний модуль
![]() .
.
Положим
![]() ,
тогда
,
тогда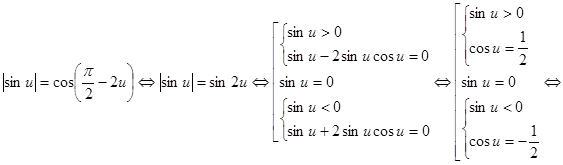
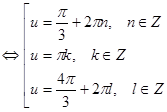 .
.
Условию
![]() удовлетворяют
два значения
удовлетворяют
два значения ![]() и
и
![]() .
.
![]() .
.
![]()
![]()
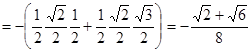 .
.
Ответ:
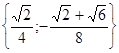 .
.
Пример
3.
Решите уравнение ![]() [31].
[31].
Решение с помощью тригонометрической подстановки
Так
как ![]() ,
то
,
то ![]() .
Заметим, что отрицательное значение неизвестного не может быть решением задачи.
Действительно, преобразуем исходное уравнение к виду
.
Заметим, что отрицательное значение неизвестного не может быть решением задачи.
Действительно, преобразуем исходное уравнение к виду
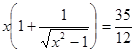 .
.
Множитель
в скобках в левой части уравнения положительный, правая часть уравнения тоже
положительная, поэтому множитель ![]() в
левой части уравнения не может быть отрицательным. Вот почему
в
левой части уравнения не может быть отрицательным. Вот почему ![]() ,
тогда
,
тогда ![]() ,
поэтому можно положить
,
поэтому можно положить ![]() Исходное
уравнение перепишется в виде
Исходное
уравнение перепишется в виде
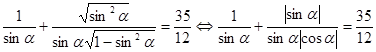 .
.
Так
как ![]() ,
то
,
то ![]() и
и
![]() .
Уравнение примет вид
.
Уравнение примет вид
![]() .
.
Пусть ![]() .
Перейдем
от уравнения к равносильной системе
.
Перейдем
от уравнения к равносильной системе
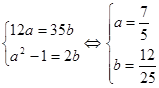 .
.
Числа
![]() и
и
![]() являются
корнями квадратного уравнения
являются
корнями квадратного уравнения
![]() .
.
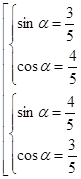 .
.
Ответ:
![]() .
.
Пример 4. Решить уравнение ![]() [4].
[4].
Решение с помощью тригонометрической подстановки
Так
как переменная ![]() может
принимать любые действительные значения, положим
может
принимать любые действительные значения, положим ![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,так
как
,так
как ![]() .
.
Исходное уравнение с учетом проведенных преобразований примет вид
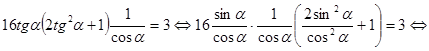
![]()
![]() .
.
Так
как ![]() ,
поделим обе части уравнения на
,
поделим обе части уравнения на ![]() ,
получим
,
получим
![]() .
.
Пусть
![]() ,
тогда
,
тогда ![]() .
Уравнение примет вид
.
Уравнение примет вид
![]() .
.
![]() .
.
Учитывая подстановку ![]() ,
получим
совокупность из двух уравнений
,
получим
совокупность из двух уравнений
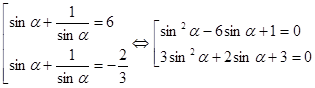 .
.
Решим каждое уравнение совокупности по отдельности.
1)
![]() .
.
![]() .
.
![]() не
может быть значением синуса, так как
не
может быть значением синуса, так как ![]() для
любых значений аргумента.
для
любых значений аргумента.
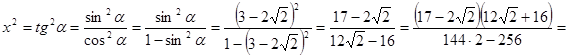
![]() .
.
Откуда
![]() .
.
Так
как ![]() и
правая часть исходного уравнения положительна, то
и
правая часть исходного уравнения положительна, то ![]() .
Из чего следует, что
.
Из чего следует, что ![]() .
.
2)
![]() .
.
![]() .
.
Это уравнение корней не имеет, так как ![]() .
.
![]() .
.
Ответ: ![]() .
.
Пример
5.
Решить уравнение ![]() [51].
[51].
Решение с помощью тригонометрической подстановки
Так
как переменная ![]() может
принимать любые действительные значения, можно положить
может
принимать любые действительные значения, можно положить ![]() .
Уравнение примет вид
.
Уравнение примет вид
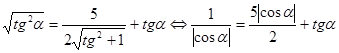 .
.
В
силу того, что ![]() ,
можно раскрыть модуль
,
можно раскрыть модуль
![]()
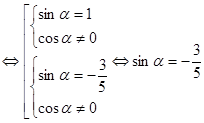 .
.
Так
как ![]() ,
то
,
то ![]() .
.
Ответ:
![]() .
.
1.2 Рациональные уравнения
Тригонометрическая подстановка применяется при решении рациональных уравнений, когда уравнение не имеет рациональных корней или найденные рациональные решения не исчерпывают всего множества решений уравнения.
При решении иррациональных уравнений возможность введения тригонометрической подстановки была видна по структуре уравнения. В нескольких следующих задачах применение метода тригонометрической подстановки не так очевидно. Вот почему прежде чем ввести подстановку, нужно доказать законность такого введения.
Пример 1. Сколько корней имеет уравнение
![]() [37].
[37].
Решение
этой задачи любым методом начинается одинаково. Докажем, что все корни данного
уравнения принадлежат промежутку ![]() .
Действительно, если
.
Действительно, если
![]() .
.
Но тогда в исходном уравнении слева стоит произведение больше восьми, а справа единица, что невозможно.
Решение с помощью тригонометрической подстановки
Положим
![]() .
Тогда каждому корню
.
Тогда каждому корню ![]() исходного
уравнения будет соответствовать ровно один корень
исходного
уравнения будет соответствовать ровно один корень ![]() ,
где
,
где ![]() .
Наоборот, каждому корню
.
Наоборот, каждому корню ![]() уравнения
соответствует ровно один корень исходного уравнения. Таким образом, задача
может быть переформулирована так: сколько корней на промежутке
уравнения
соответствует ровно один корень исходного уравнения. Таким образом, задача
может быть переформулирована так: сколько корней на промежутке ![]() имеет
уравнение
имеет
уравнение
![]() .
.
Так
как ![]() и
и
![]() ,
то можно взять
,
то можно взять ![]() .
Заметим, что если
.
Заметим, что если ![]() -
корень данного уравнения, то и
-
корень данного уравнения, то и ![]() тоже
корень. Вот почему достаточно рассмотреть
тоже
корень. Вот почему достаточно рассмотреть ![]() ,
то есть отыскать только положительные решения. С
учетом выше изложенного исходное уравнение перепишется в виде
,
то есть отыскать только положительные решения. С
учетом выше изложенного исходное уравнение перепишется в виде
![]()
![]()
![]()
![]() .
.
Так как ![]() ,
то можно обе части равенства умножить на
,
то можно обе части равенства умножить на ![]() ,
получим
,
получим
![]()
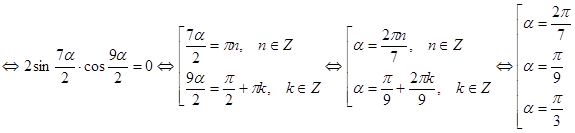 .
.
Ответ: шесть корней.
Пример
2.
Решить уравнение ![]() .
.
Если для выше приведенных задач не удается найти нетрадиционный путь решения, то все равно остается вероятность справиться с задачей с помощью стандартных школьных рассуждений, правда, затратив при этом гораздо больше времени. Эта задача лишает такого выбора, так как ее решение другим способом не представляется возможным.
Решение с помощью тригонометрической подстановки
Поделим все члены уравнения на 2. Уравнение примет вид
![]() .
.
Докажем,
что все корни данного уравнения по модулю не превосходят единицы. Пусть ![]() ,
тогда
,
тогда ![]() .
Получили, что при
.
Получили, что при ![]() левая
часть уравнения по модулю больше единицы, а правая – меньше единицы, что
невозможно.
левая
часть уравнения по модулю больше единицы, а правая – меньше единицы, что
невозможно.
Положим ![]() .
Уравнение примет вид
.
Уравнение примет вид
![]() .
.
Условию
![]() удовлетворяют
три значения
удовлетворяют
три значения
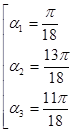 .
.
Поскольку кубическое уравнение не может иметь больше трех различных корней, то мы нашли все решения.
Ответ:
![]() .
.
1.3 Показательные уравнения
Приведем пример задания, решить которое без введения тригонометрической подстановки не представляется возможным.
Пример 1. Решить
уравнение ![]() .
.
Пусть ![]() ,
тогда уравнение перепишется в виде
,
тогда уравнение перепишется в виде
![]() .
.
Введем замену ![]() ,
получим
,
получим
![]() .
.
Это уравнение мы уже решали[1]. Его корни
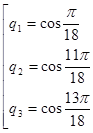 .
.
Два последних значения меньше нуля,
поэтому нам подходит только ![]() .
Перейдем к переменной
.
Перейдем к переменной ![]() ,
а затем к переменной
,
а затем к переменной ![]()
![]() .
.
§2. Решение систем
В данном параграфе предложены системы повышенной сложности, решить которые, не зная специальных методов решения, сложно.
Пример 1. Решить систему уравнений
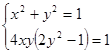 [3].
[3].
Решение с помощью тригонометрической подстановки
Так как квадрат суммы чисел ![]() и
и
![]() равен
единице, то каждое из этих чисел по модулю не превосходит единицы и их можно
рассматривать как синус и косинус некоторого угла. Поэтому можно положить
равен
единице, то каждое из этих чисел по модулю не превосходит единицы и их можно
рассматривать как синус и косинус некоторого угла. Поэтому можно положить
![]() Второе
уравнение системы примет вид
Второе
уравнение системы примет вид
![]() .
.
Условию ![]() удовлетворяют
четыре значения
удовлетворяют
четыре значения
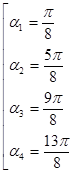 .
.
![]()
![]() .
.
![]()
![]() .
.
![]()
![]() .
.
![]()
![]() .
.
Ответ: 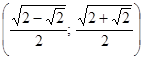 ;
;
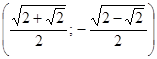 ;
;
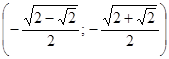 ;
;
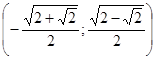 .
.
Ответ: ![]() .
.
Пример 2. Сколько решений имеет система уравнений
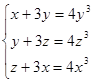 [18].
[18].
Здесь представлена так
называемая циклическая система уравнений. Подобные системы часто предлагаются
на вступительных экзаменах в вузы с повышенными требованиями по математике
[30]. Решить эти системы, не зная специальных методов решения, очень сложно. В
данном случае подбором устанавливается решение ![]() .
Попытки доказать, что система не имеет других решений, положительных
результатов не дают. Неоценимую помощь в решении такого класса задач оказывает
метод тригонометрической подстановки.
.
Попытки доказать, что система не имеет других решений, положительных
результатов не дают. Неоценимую помощь в решении такого класса задач оказывает
метод тригонометрической подстановки.
Перепишем систему в виде
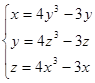 .
.
Докажем, что все числа ![]() по
абсолютной величине не превосходят единицы. Пусть
по
абсолютной величине не превосходят единицы. Пусть ![]() –
максимальное из чисел
–
максимальное из чисел ![]() и
и
![]() ,
то
,
то ![]() .
Пришли к противоречию. Если число
.
Пришли к противоречию. Если число ![]() –
минимальное и
–
минимальное и ![]() ,
то
,
то ![]() .
Опять пришли к противоречию. Итак
.
Опять пришли к противоречию. Итак ![]() .
.
Решение с помощью тригонометрической подстановки
Положим ![]() .
Тогда
.
Тогда ![]() ,
,
![]() ,
,
![]() .
Число решений исходной системы равно числу решений уравнения
.
Число решений исходной системы равно числу решений уравнения
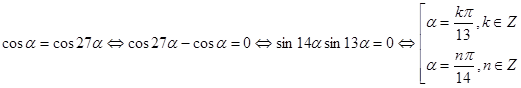 .
.
Условию ![]() удовлетворяет
27 решений
удовлетворяет
27 решений
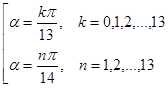 .
.
Ответ: 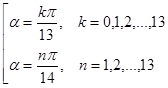 .
.
Пример 3. Известно, что ![]() . Доказать, что
. Доказать, что ![]() [9]. При этом замена переменных,
входящих в неравенство, с одной стороны, сокращает число переменных, а с
другой, позволяет привести неравенство к виду, более удобному для исследования
его свойств.
[9]. При этом замена переменных,
входящих в неравенство, с одной стороны, сокращает число переменных, а с
другой, позволяет привести неравенство к виду, более удобному для исследования
его свойств.
Пример
1. Доказать, что ![]() [43].
[43].
При
![]() неравенство
верное.
неравенство
верное.
Решение с помощью тригонометрической подстановки
Для
любых ![]() найдется
угол
найдется
угол ![]() ,
что
,
что ![]() .
Исходное неравенство примет вид
.
Исходное неравенство примет вид
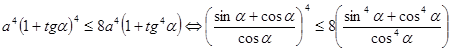 .
.
Так как ![]() ,
то
,
то ![]() .
Умножим обе части неравенства на
.
Умножим обе части неравенства на ![]() ,
получим
,
получим
![]()
![]()
![]()
![]() .
.
Второй множитель всегда положительный, а первый не превосходит 0, поэтому все произведение не положительно.
Пример:
Суть метода
состоит в замене переменной х тригонометрической функцией, например ![]() . Решение исходного уравнения
сводится к решению тригонометрического уравнения. Но тригонометрическое уравнение
обычно имеет бесконечное множество решений, а исходное - конечное.
. Решение исходного уравнения
сводится к решению тригонометрического уравнения. Но тригонометрическое уравнение
обычно имеет бесконечное множество решений, а исходное - конечное.
Решение с помощью тригонометрической подстановки
Так как сумма квадратов ![]() и
и ![]() равна единице, то каждое из чисел
равна единице, то каждое из чисел ![]() и
и ![]() по
абсолютной величине не превосходит единицы, и их можно рассматривать как синус
и косинус некоторого угла. Поэтому законна подстановка
по
абсолютной величине не превосходит единицы, и их можно рассматривать как синус
и косинус некоторого угла. Поэтому законна подстановка
![]() .
.
Аналогично ![]() . Доказываемое
неравенство запишется в виде
. Доказываемое
неравенство запишется в виде
![]() .
.
§3. Доказательство неравенств
Как правило, навыки решения и доказательства неравенств, за исключением квадратичных, формируются на более низком уровне, чем уравнений. Эта особенность имеет объективную природу: теория неравенств сложнее теории уравнений. Тем не менее, многие приемы и методы решения неравенств совпадают с приемами и методами решения уравнений. В том числе, к доказательству неравенств применим метод замены переменной.

Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.