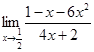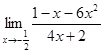Методическая разработка " Подготовка к сдаче ОГЭ по математике"

1

 Вектор задан координатами начала и конца:  . Найдите длину вектора

2

Коллинеарны  ли вектора  и ?

3

 Векторы  , .  Найдите координаты вектора

4

 Найдите координаты вектора , если ,

5

 Векторы , . Найдите скалярное произведение векторов

6

Найдите значения  m, при которых вектора  , коллинеарные

7

 Перпендикулярны ли векторы  и

8

 Координаты точек А (2; -3), В (4; 0), С (3; 1), Д (-4; 1). Сравните длины векторов ||  с  ||

9

 Координаты точек  К (5; -4);  М (1; 6). Найдите координаты середины отрезка КМ

10

 Найдите произведение векторов    если ,   и угол  между векторами   и   равен 30⁰

11

Найдите координаты вектора , если ,

12

Найдите угол между векторами  и  , если

13

  А(2;-4)  и В (0;6) – концы отрезка АВ  . М- середина отрезка АВ. Найдите длину отрезка АМ

14

При каких значениях векторы и будут коллинеарные?

15

При каких значениях векторы и будут  перпендикулярные?

16

Найдите  , если  - угол между векторами  = 2i – j   и    = -5j + 4j

1

Решите уравнение 

2

Решите уравнение  

3

 Решите уравнение

4

Решите уравнение

5

Решите уравнение

6

Решите уравнение

7

Решите уравнение

8

Решите уравнение     

9

Решите уравнение  

10

Решите уравнение  

11

Решите уравнение 

12

Решите уравнение

13

Решите уравнение     

14

Решите уравнение     

15

Решите уравнение     

16

Решите уравнение     

1

Вычислите значение выражения  

2

Вычислите значение выражения  

3

Найдите значение выражения 

4

Найдите область определения функции

5

Вычислите значение выражения

6

 Вычислите значение выражения

7

Найдите область определения

8

Найдите область определения функции

9

Найдите значение выражения  

10

Вычислите значение выражения   

11

Вычислите значение выражения    

12

Вычислите значение выражения  

13

Найдите область определения функции

14

Найдите значение выражения  

15

Вычислите значение выражения

1

Решите уравнение 

2

Решите уравнение  

3

 Решите уравнение

4

Решите уравнение

5

Решите уравнение

6

Решите уравнение

7

Решите уравнение

8

Решите уравнение     

9

Решите уравнение  

10

Решите уравнение  

11

Решите уравнение 

12

Решите уравнение

13

Решите уравнение     

14

Решите уравнение     

15

Решите уравнение     

16

Решите уравнение     

1

Запишите формулу общего члена последовательности: ; ; ; ;  …….Является ли число  членом этой последовательности? Если да, то почему?

2

Исследуйте последовательность  на монотонность, ограниченность, сходимость

3

Исследуйте последовательность   на монотонность, ограниченность, сходимость

4

Исследуйте последовательность  на монотонность, ограниченность, сходимость

5

Выпишите пять первых членов последовательности и выясните, является ли число членом последовательности

6

Исследуйте  последовательность на ограниченность, монотонность, сходимость

7

Исследуйте последовательность   на монотонность, ограниченность, сходимость. Является ли число 1 членом последовательности?

8

Запишите формулу общего члена последовательности: 2,9,28, 65, 126,  …  и определите каким  членом  последовательности является число 1001?

9

Исследуйте последовательность  на монотонность, ограниченность, сходимость

10

14 Содержится ли среди  членов последовательности с общим членом  число - 30 ?  Найдите пятый член этой последовательности

11

Исследуйте  последовательность на ограниченность и  монотонность

Запишите формулу общего члена последовательности: ; ; ; ;  …   Является ли число  членом этой последовательности? Если да, то почему?

1

Вычислите     

2

Вычислите  предел  

3

Вычислите предел 

4

Вычислите предел  

5

Вычислите предел 

6

Вычислите предел 

7

 Вычислите   предел                    

8

Вычислите предел   

9

 Вычислите предел

10

 Вычислите предел 

11

  Вычислите     

12

Вычислите предел 

13

Вычислите предел 

14

 Вычислите  предел  

15

 Вычислите  предел  

1

Найдите силу, действующую на материальную точку массой m = 0,5 кг, движущуюся прямолинейно по закону  в момент времени t₀ = 3с

2

 В какой момент времени тело, движущееся по закону  остановится?

3

Найдите ускорение и кинетическую энергию тела массой m = 1 кг, движущегося прямолинейно по закону  в момент времени t₀ = 3 c

4

 Ускорение прямолинейного движения материальной точки задается формулой   . Найдите закон изменения скорости, если V(0) =  1.

5

Алюминиевый провод диаметром 10 мм имеет массу 7,3 кг. Найдите длину провода, если  _ал.=2, 6 г/см³

6

Точка движется прямолинейно согласно закону , м. Найдите закон движения точки, если известно, что ее скорость выражается формулой , м/с и в момент времени t=1 c координата точки равнялась числу 7

7

Найдите силу, действующую на материальную точку массой

m =2 кг, движущуюся прямолинейно по закону , м, в момент времени t ₀ = 1c

8

 Найдите точки, в которых скорость изменения функции  больше скорости изменения функции у = 12х – 150

9

Скорость движущейся точки меняется по закону м/с. Найдите путь, пройденный точкой за промежутки времени от  до

10

При каких значениях  аргумента скорость изменения   функции больше скорости изменения функции , если

11

Найдите закон изменения скорости, если ускорение прямолинейного движения материальной точке задается  формулой м/с² и  м/с

12

По прямой движутся две материальные точки по законам  и . В каком промежутке времени скорость первой точки больше скорости второй точки?

13

Найдите ускорение и кинетическую энергию тела массой кг, двигающегося прямолинейно по закону  в момент времени

1

 В каких точках угловой коэффициент касательной к графику функции   равен

2

Составьте уравнение касательной к графику функции   в точке х₀ = 2

3

Найдите тангенс угла наклона касательной к графику функции  в точке с абсциссой   х₀ = 1

4

Составьте уравнение касательной к графику функции  в точке

5

Составьте уравнение  касательной к графику функции в точке  

6

Составьте уравнение касательной к графику функции в точке х₀ = 3

7

 Напишите уравнение касательной к графику функции   в точке  

8

Найдите уравнение кривой, проходящей через точку А (2, 3), если угловой коэффициент касательной в точке с абсциссой х равен

3 х²

9

Найдите точки, в которых тангенс угла наклона касательной к графику функции  равен

10

 Составьте уравнение касательной к графику функции   в точке х₀ = -1

11

Сравните углы , которые образуют с положительным направлением оси ОХ касательные  к графикам функций  в точке   и   в точке х₀ = 2

12

Составьте уравнение  касательной к графику функции в точке  

13

Определите под каким углом наклонена касательная к оси ОХ к графику функции в  точке  ?

14

Найдите тангенс угла наклона касательной к графику функции  в точке с абсциссой   

15

Составьте уравнение касательной к графику функции

в точке

1

Стороны треугольника равны 10см, 10см и 12см , касаются шара. Расстояние от  центра шара до плоскости треугольника равно 4см. Найдите объем шара

2

 Параметр осевого сечения конуса равен 24 см, а величина угла наклона образующей к плоскости основания 60⁰. Найдите площадь поверхности конуса

3

Основание пирамиды – равнобедренный треугольник со сторонами 6 см и 8 см. Все боковые ребра равны 9 см. Найдите объем пирамиды

4

Стороны основания треугольной пирамиды равны 16 см, 63 см и 65 см. Найдите объем пирамиды, если боковые грани наклонены к основанию под углом 45⁰

5

Периметр осевого сечения конуса равен 24 см, а величина угла наклона образующей  к плоскости основания 60⁰ . Найдите площадь полной поверхности конуса и его объем

6

 Угол при вершине осевого сечения конуса равен 120⁰. Площадь боковой поверхности равна  см². Найдите объем конуса

7

 Основание пирамиды – прямоугольный треугольник, катеты которого 6 см и 8 см. Все боковые ребра пирамиды равны 13 см. Найдите объем пирамиды

8

У правильной четырехугольной призмы площадь боковой поверхности равна 8 см^2,, а площадь полной поверхности – 40 см². Найдите объем призмы

9

 Точки А, В и С   ∆ АВС принадлежат поверхности шара. Найдите расстояние от центра шара до плоскости ∆ АВС, если R_ш =  см и стороны ∆ АВС равны 3 см, 5 см и 4 см

10

 Какого вида параллелепипед обладает свойствами: две смежные боковые грани перпендикулярны плоскости основания?

11

Боковые ребра треугольной пирамиды образуют с плоскостью основания углы по 60⁰; стороны основания равны 20см, 12см и 29см. Найдите объем пирамиды

12

Основание  прямоугольного параллелепипеда – квадрат. Найдите его объем, если диагональ его боковой грани, равна 8см и образует с плоскостью основания угол 30⁰

13

Боковые ребра пирамиды равны гипотенузе прямоугольного треугольника лежащего в её основании, и равны 12см. Найдите объем пирамиды

14

Периметр осевого сечения конуса равен 24 см, а величина угла наклона образующей к плоскости основания 60⁰. Найдите площадь поверхности конуса

1

Исследуйте функцию  на монотонность и экстремумы

2

Исследуйте функцию  на монотонность и экстремумы

3

 Найдите промежутки убывания функции

4

Исследуйте функцию  на монотонность и экстремумы

5

Решите неравенство , если   и  

6

Исследуйте функцию   на монотонность и экстремумы

7

Исследуйте функцию  на точки перегиба и выпуклость

8

Найдите значения х, при которых производная  функции  неотрицательная

9

 Найдите промежутки возрастания функции

10

Исследуйте функцию  на выпуклость и точки перегиба

11

 Найдите промежутки убывания  функции

12

Найдите , если

13

Найдите наибольшее и наименьшее значения функции  на отрезке  

14

Исследуйте функцию  на монотонность и экстремумы

15

Исследуйте функцию  на монотонность и экстремумы

16

При каких значениях х выполняется равенствоесли

17

Найдите критические точки функции . Определите, какие из них являются точками максимума, а какие точками минимума?

17

Исследуйте функцию  на точки перегиба и выпуклость

19

Найдите наименьшее и наибольшее значения  функции   на отрезке

20

Найдите наименьшее значение функции    на отрезке

1

Постройте график функции, зная что  и

2

Постройте график функции, производная которой равна и

3

Постройте график функции, если  и

Постройте график функции, зная что  и

4

Постройте график функции, зная что  и

5

Постройте график функции

6

Постройте график функции

    7

Постройте график функции