МЕТОДИЧЕСКАЯ РАЗРАБОТКА ДЛЯ ПРОВЕДЕНИЯ ЗАНЯТИЯ ПО ТЕМЕ «ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ДЛЯ ИССЛЕДОВАНИЯ ФУНКЦИЙ НА МОНОТОННОСТЬ И ЭКСТРЕМУМЫ»

Теоретическое занятие

 Дисциплина: Математика

Название работы:

МЕТОДИЧЕСКАЯ РАЗРАБОТКА ДЛЯ ПРОВЕДЕНИЯ ЗАНЯТИЯ ПО ТЕМЕ «ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ДЛЯ ИССЛЕДОВАНИЯ ФУНКЦИЙ НА МОНОТОННОСТЬ И ЭКСТРЕМУМЫ»

Автор работы:

Шкурина Надежда Анатольевна, преподаватель

Образовательная организация:

КГБПОУ «Техникум горных разработок имени В.П. Астафьева», п. Ирша

2020г.

Занятие с элементами исследования "Применение производной для исследования функций на монотонность и экстремумы"

Тип занятия: изучения нового материала с элементами исследования.

Форма занятия: исследование.

Цель: Организация деятельности обучающихся, направленная на овладение системой математических знаний и умений по теме «Применение производной для исследования функций на монотонность и экстремумы», необходимых для решения задач, применения в практической деятельности.

Задачи:

1.                 Дать представление о связи свойств функции с её производной, учить чтению и анализу графиков функций.

2.                 Развивать умение анализировать, сопоставлять, сравнивать, формулировать выводы по результатам собственной деятельности.

3.                 Развивать навыки использования компьютера и мультимедийных учебных программ для организации собственной познавательной и исследовательской  деятельности.

4.                 Развивать такие качества личности, как ясность и точность мысли, логическое мышление, алгоритмическая культура, интуиция, критичность.

5.                 Воспитывать средствами математики культуру личности: умения выслушать и принимать во внимание взгляды других людей, умение справляться с неопределённостью и сложностью.

Время реализации занятия: 45 мин.

Знания, умения, навыки, которые актуализируют,/приобретут,/закрепят/др. обучающиеся в ходе урока:

1.                 Систематизации знаний табличных производных.

2.                 Формирование умений применять табличные производные;

3.                 Умение извлекать необходимую информацию;

·                    навыки пользоваться правилами дифференцирования;

·                    умение работать в парах, в группах.

Необходимое оборудование и материалы: Доска, мультимедийная разработка занятия, бланки листов для проведения контроля, звуковое сопровождение, проектор, презентация. Электронная тестовая оболочка http://videouroki.net.

Дидактическое обеспечение мероприятия:

1.                   Планы работы.

2.                   Карточки с тестовыми заданиями.

Основные этапы урока

1.                 Организационный момент(2мин)

2.                 Объявление темы и цели урока(2 мин)

3.                 Проверка домашнего задания. Устная работа(6мин)

4.                 Изучение нового материала (исследовательская работа)(10мин)

5.                 Обсуждение результатов (защита исследований)(12мин)

6.                 Физкультминутка(1 мин)

7.                 Закрепление изученного материала(8мин)

8.                 Итоги занятия и выставление оценок. Рефлексия (2мин)

9.                 Домашнее задание(2мин)

Ход урока

 1. Организационный момент

Ребята, здравствуйте, садитесь!

- Сегодня у нас необычный урок, к нам пришли гости, посмотрите на них и улыбнитесь. Посмотрите друг на друга и тоже улыбнитесь, ведь веселому человеку легче добиться успеха. А успех нам необходим.

- И так начнем? Перед вами 3 карточки.

- Оцените, пожалуйста, своё психологическое и эмоциональное состояние в начале урока.  Для этого поднимите карточку с одним из цветов.

·                     Красная – испытываете напряжение, тревогу, дискомфорт

·                     Жёлтая – неуверенность, что-то смущает.

·                     Зелёная – испытываете спокойствие, уверенность, вам комфортно.

Зелёный цвет: Влияет на сердечно-сосудистую и вегетативную нервную системы, сердцебиение, аритмию, снижает артериальное давление. Устраняет возбуждение, беспокойство, снимает эмоциональное напряжение. При отсутствии зелёного цвета повышается возбудимость, нервозность, раздражительность, усиливается злость, гнев, подозрительность.

Восточные мудрецы определяли его как символ юности и гармонии Природы.

– Мне нравится, что сегодня у Вас хорошее психологическое и эмоциональное состояние. Соберёмся с силами. В четыре приёма глубоко вдохнём воздух через нос и в пять приёмов с силой выдохнем, задувая воображаемую свечу.

Я бы хотела познакомить вас с тем, что нам предстоит сегодня выполнить:

1.     Проверка  домашнего задания

2.     Устная работа

3.     Изучение нового материала (исследовательская работа)

4.     Обсуждение результатов (защита исследований)

5.     Закрепление изученного материала

6.     Итог занятия

7.     Домашнее задание

2. Объявление темы и цели урока

- Ребята ни для кого не секрет, что каждая наука оперирует своей лексикой. Увлекшись изучением с вами последней темы по алгебре, я в беседе с учителем истории сказала: «Неважно сколько ученик знает, но важно, чтобы у него была положительная производная». Коллега не поняла меня. А вы можете прояснить мою фразу? (Это означает важно, чтобы скорость  приращения знаний у ученика была положительна – это залог того, что его знания возрастут).

- Скажите на данный момент у вас положительная производная?

- Вот мы изучаем производную.  Вы не задумывались над тем, а так ли это важно в жизни?

- Зачем она нужна?

- Где мы встречаемся с производной и используем её?

- Можно ли без неё обойтись в математике и не только?

- Как вы думаете, какова тема нашего занятия? (изучить применение производной)

Откроем тетради, запишем число и тему сегодняшнего урока.

Тема занятия «Применение производной для исследования функций на монотонность и  экстремумы»

Выдающийся русский математик и кораблестроитель академик Алексей Николаевич Крылов (1863-1945г.) однажды заметил, человек обращается к математике « не затем, чтобы любоваться неисчислимыми сокровищами, ему прежде всего нужно ознакомиться со столетиями испытанными инструментами и научиться ими правильно и искусно владеть».

С одним из таких инструментов мы уже знакомы – это производная. Мы сегодня сформируем начальное представление о приложениях производной в математике и в жизни, «откроем» зависимость между свойствами монотонности функции, экстремумами и значениями её производной; и  рассмотрим применение производной для решения  задач.

3. Проверка домашнего задания(актуализация ЗУНов)

Прежде чем приступить к изучению новой темы, давайте проверим нашу готовность к вычислению производных.

Назовите устно производные следующих функций.

Устная работа. Учебник: Глава 9, стр.180, №5

1) Укажите количество промежутков монотонности функции

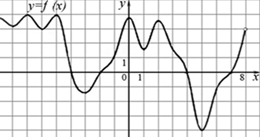   (10)

2)           На графике функции найдите промежутки убывания и в ответе укажите сумму длин этих промежутков (12)

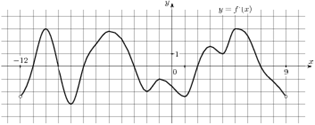
3) На графике найдите промежутки возрастания и в ответе укажите сумму длин этих промежутков (11)

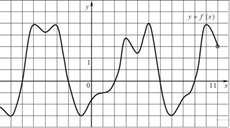
4)                Материальная точка движется прямолинейно по закону x(t)=3t²+2t+27, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=2c. (14)

(10, 12, 11, 14)

- Расположите  их в порядке возрастания: 10, 11, 12, 14

Меньшее из них 10 – является временем наибольшей работоспособности, а большее из них – 14- временем наибольшего утомления.

Факт: Работоспособность человека во время бодрствования изменяется волнообразно. Поэтому у человека в день два пика наибольшей трудоспособности 10-12 часов и 16-18 часов и один момент наибольшего утомления. Работоспособность начинает снижаться в 13 часов и к 14 часам её уже невозможно компенсировать волевым усилием. В течение недели так же отмечаются три этапа: понедельник – врабатывание; вторник, среда, четверг – устойчивая работоспособность; пятница, суббота – утомление (демонстрируется кривая работоспособности).

Так как у нас сейчас 11 часов, время наивысшей работоспособности, так  используем его с пользой,  получим знания, чтобы ваша производная была положительной всегда, и покажем  истинную вашу красоту, не только внешнюю, но и внутреннюю.

4. Изучение нового материала (исследовательская работа)

а) Постановка проблемы

(По результатам работы на данном этапе урока обучающиеся констатируют: задание  для них является невыполнимым).

б) Включение в деятельность

- Перед нами возникает проблема (задача). Мы не можем ответить на данные вопросы. -Что же делать, как нам выполнить это задание? (нам нужно разработать правило, с помощью которого мы сможем указать промежутки возрастания и убывания, а также узнать, что такое точки экстремума и как их определять, используя  график  производной функции).

в) Предварительная работа

Посмотрите на слайд, здесь представлен график некоторой возрастающей дифференцируемой функции. Проведем касательные к графику функции в точках х₁ и х₂.

- Что общего у построенных прямых? (острый угол образуется с осью х, то есть у прямых  положительный угловой коэффициент).

- Чему равен угловой коэффициент касательной? (значению производной в точке х₀ или в абсциссе точки касания)

- Таким образом, f ‘(x₁)>0 и , f ‘(x₂)>0.

- Как вы думаете,  чему равна производная в точке х₃? (=0)

(Слайд)  Получаем:  В любой точке х из области определения возрастающей дифференцируемой функции:

f ’ (x) ≥ 0

- Рассмотрим ещё один график, но убывающей дифференцируемой функции. Проведём касательные к графику в точках х₁ и х₂.

- Что общего у построенных прямых? (тупой угол образуется с осью х, то есть у прямых  отрицательный угловой коэффициент).

- Чему равен угловой коэффициент касательной? (значению производной в точке х₀ или в абсциссе точки касания)

- Таким образом, f ‘(x₁)<0 и , f ‘(x₂)<0.

- Как вы думаете,  чему равна производная в точке х₃? (=0)

Таким образом, получаем: В любой точке х из области определения убывающей дифференцируемой функции:

f ’ (x) ≤ 0.

- Эти рассуждения говорят о том, что между характером монотонности функции и знаком её производной есть какая-то определенная связь.

- Попробуем  установить или предсказать  связь между характером монотонности функции, точками экстремума и знаками её производной, как  например поэт Андрей Белый предсказал  вступление в атомный век!

«Мир – рвался в опытах Кюри
Атомной, лопнувшею бомбой
На электронные струи
Невоплощённой гекатобомбой ...»

- Знакомы ли вам эти строки? Эти строки в 1921 году написал Андрей Белый. Это всего за пятнадцать лет до того, как учёные начали работать над созданием бомбы!

- Для этого проведём исследование.

г) Исследовательская работа

«Начинать исследования можно по-разному... Все равно начало почти всегда оказывается весьма несовершенной, нередко безуспешной попыткой. Есть истины, как страны, наиболее удобный путь, к которым становится известным лишь после того, как мы испробуем все пути. Кому-то приходится, рискуя собой, сходить с проторенной дороги, чтобы указать другим правильный путь... На пути к истине мы почти всегда обречены, совершать ошибки»  так говорил  французский  философ-материалист, атеист Дени Дидро (1713 – 1784) – современник Декарта, Лейбница, личный  библиотекарь Екатерины Великой.

-Нам нужно создать 2 группы, которые составят  так называемые «математические портреты» функции и её производной, то есть «откроют» зависимость между свойствами монотонности функции, экстремумами и знаками  производной.

(рассадить обучающихся по парам за компьютеры)

Для каждой группы предложен план проведения практической работы и каждая группа по окончанию должна сделать выводы по своему вопросу и нам всем объяснить материал так, чтобы все его поняли.

1 группа(группа делится на пары, после окончания работы пары соединяются в группы и делают вывод).

Установите зависимость между свойствами монотонности функции и знаками производной (укажите промежутки  монотонности  (возрастание, убывание))

1.                 Откройте презентацию.

2.                 Изучите материал презентации или видеолекции.

3.                 Выполните тестовое задание в электронной тестовой оболочке http://videouroki.net. по теме «Применение производной для исследования функций на монотонность».

4.                 Сделайте вывод: попробуйте описать этот факт, используя математические термины:

Вывод: 1) Если во всех точках открытого промежутка Х выполняется неравенство f’(x)≥0, то функция y = f(x) возрастает на промежутке Х.

2) Если во всех точках открытого промежутка Х выполняется неравенство f’(x)≤0, то функция  y = f(x)  убывает  на промежутке Х.

2 группа(группа делится на пары, после окончания работы пары соединяются в группы и делают вывод).

На графике функции и графике производной функции установите связь между промежутками монотонности и  знаками производной, укажите точки экстремума(точки минимума и максимума)

1.                 Откройте презентацию.

2.                 Изучите материал презентации или видеолекции.

3.                 Выполните тестовое задание в электронной тестовой оболочке http://videouroki.net. по теме «Применение производной для отыскания точек экстремума»

4.                 Сделайте вывод: попробуйте описать этот факт, используя математические термины:

Вывод: Если в точке х_о производная меняет знак с плюса на минус, то х_о     является  точкой максимума.

Вывод: Если в точке х_о производная меняет знак с - на +, то х_о является  точкой минимума.

Если слева от точки  f’(x)<0, то эта точка является точкой минимума функции  или крайняя точка из промежутка убывания  является точкой минимума.

Если слева от точки  f ’(x)>0, то эта точка является точкой максимума  или крайняя точка из промежутка возрастания  является точкой максимума.

Был предложен алгоритм нахождения точек экстремума и промежутков возрастания, но расписан не по порядку, ваша задача была составить его в правильном порядке (напечатать на листах отдельно и по одному шагу по порядку крепить на доске):

1.                 Сделать выводы о монотонности функции и о её точках экстремума.

2.                 Найти точки, в которых производная равна 0 (стационарные).

3.                 Найти производную функции y=f(x).

4.                 Отметить эти точки на числовой прямой и определить знаки производной на получившихся промежутках.

5. Обсуждение результатов деятельности обучающихся (защита результатов исследований)

6. Физминутка

- Знаете ли вы, что такое «царственная осанка»?

- Попробуем принять царственную позу: спина прямая, мышцы головы без напряжения, выражение лица очень значительное: ведь вы знаете такое количество табличных производных, правила дифференцирования, умеете составлять уравнения касательных, которое не по силам  даже царственным особам. Очень быстро активизируем свой мозг. Для этого интенсивно промассажируем межбровную точку: указательным пальцем правой руки делаем 5 круговых движений в одну сторону и в другую. Повторим это 3 раза

- Каждая группа у доски защищает свой результат исследования – это(1, 2 группа защищают свои результаты)

Группа учащихся пришла к выводу, что промежутки монотонности и точки экстремума не всегда можно определить точно, используя графический метод. Разрешить проблему можно, применяя аналитический метод и используя производную. Найдем точки экстремума предложенной функции аналитическим методом, используя производную.

Для того, чтобы исследовать функцию на монотонность и экстремумы, необязательно строить график производной, достаточно определить знаки производной на промежутках, на которые стационарные точки разбивают область определения функции. Использование аналитического способа поможет вам быть точными.

7. Закрепление изученного материала

На доске запишите решение вашей задачи аналитическим методом.

Найдите промежутки монотонности и точки экстремума функции y=x³ – 5x.

1.                 Найти производную функции y=f(x).

2.                 Найти точки, в которых производная функции равна 0.

3.                 Отметить эти точки на числовой прямой и определить знаки производной на получившихся промежутках.

4.                 Сделать выводы о монотонности функции и о её точках экстремума.

Каждый сегодня на занятии занимался исследовательской деятельностью, создавая свой интеллектуальный продукт. Дома Света дополнительно занималась исследованием, выясняла, где можно ещё применять производную кроме уроков математики? Удалось ли Свете убедиться в том, что производную можно применить не только на уроках математики? Света, пожалуйста, убеди нас всех в этом (защита исследовательской работы).

Скажите, скорость приращения знаний у вас сегодня на занятии положительна? Чтобы приращение ваших знаний по теме было положительным, постарайтесь выполнять максимально посильную для себя работу.

8. Итоги занятия и выставление оценок. Рефлексия.

Итак: наше занятие подходит к концу Сегодня на занятии мы учились определять промежутки монотонности и точки экстремума функции  по графику функции и графику её производной. Сделали вывод о том, что не всегда удобно использовать графический метод для нахождения промежутков монотонности и точек экстремума. Вывели алгоритм, при помощи которого можно находить промежутки возрастания и убывания функции и точки максимума и минимума аналитически.

У каждого человека есть определенный кругозор. Когда этот кругозор сужается до бесконечности малого, то он обращается в точку. Тогда человек говорит, что это есть его точка зрения. Выскажите, пожалуйста, свою точку зрения по нашему сегодняшнему занятию:

- понравилось ли вам сегодняшнее занятие?

- какой момент был самым интересным?

- какой момент был самым трудным?

- все ли поняли тему занятия?

Каждый прикрепите к доске звезду такого цвета, которая соответствует вашим сегодняшним знаниям на занятии. (Отлично изучил тему. Были пробелы, но я их решил самостоятельно. Были пробелы, но я их решил с помощью группы. Проблемы не решены.)

- Однажды Морис Клайн американский математик сказал:

«Музыка может возвышать или умиротворять душу,

живопись – радовать глаз,

поэзия – пробуждать чувства,

философия – удовлетворять потребности разума,

инженерное дело – совершенствовать материальную сторону жизни людей,

а математика способна достичь всех этих целей!»

9. Домашнее задание

1)                Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники, и вы выбирая область деятельности будете знать, что можно применить производную для решения какого-то вопроса. Подготовить сообщение о применении производной в географии и химии. (2 человека)

2)                Учебник: Глава 9, стр.183-187, опорный конспект. Вопросы 1-2. Задачник: №9.40(1).

ПЕРЕЧЕНЬ ОСНОВНОЙ И ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ

Основная литература:

1.     Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учеб. для студ. учреждений сред. проф. образования. — М., 2017.

2.     Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студ. учреждений сред. проф. образования. — М., 2017.

Дополнительная литература:

3.     Широбокова Т.С. Организация и проведение исследовательской деятельности обучающихся в образовательных учреждениях системы СПО / Т.С. Широбокова // Научные исследования в образовании. – 2011. – № 7.

4.     Иванова Л.В., Аронов А.М. О необходимости и механизмах разработки системы современной методической деятельности// Молодые профессионалы Сибири: Сборник аналитических, информационных материалов по итогам Полуфинала Национального чемпионата «Молодые профессионалы» (WorldSkillsRussia) в Сибирском федеральном округе -2016. – Красноярск: ООО РПБ «Амальгама», 2016. – 248 с. – С.84- 88

5.     Баженова К.А., Аронов А.М. Организация учебно-исследовательской деятельности школьников: учебно-методическое пособие/ Под редакцией А.С. Обухова. – М.: Национальный книжный центр, 2016. – 128 с. (Библиотека журнала «Исследователь/Researcher»)

6.     Аронов А. М., Первышина Г.Г. Экспертиза исследовательских работ  школьника// информационно-методический журнал «Дополнительное образование в Красноярском крае» №1, 2010. – с.48 – 51.

7.     Гердт Н.А. НИРС как одно из условий формирования профессионально-творческого потенциала студентов СПО / Гердт Н.А. // Молодой ученый. – 2015. – №21. – С. 772-774.

8.     Аронов А.М., Конторин В. А.,  Харви Ланс О деятельностном определении понятий куратор и наставник// Современное образование в условиях реформирования: инновации и перспективы: сб. материалов IV Всероссийской науч.-практ. конф., 16 апреля 2013 г./ Под общ. ред. А.И. Таюрского.-Красноярск, 2013.- с. 446, с. 383-386

9.     Боровских А.В., Розов Н.Х. Деятельностные принципы в педагогике и педагогической логике. - М.: МАКС Пресс, 2010.- 80 с.

Самоанализ урока

         Исследовательская деятельность студентов(ИДС) – это новый метод обучения, которые позволят формировать творческих знающих специалистов, способных самостоятельно решать научные проблемы и быть инициативными в учебе и будущей жизнедеятельности.

ИДС формирует личностные качества студента, его мотивацию, рефлексию и самооценку.

            Для того, чтобы активизировать работу памяти и подготовить опорные знания студента для успешного восприятия и усвоения новых, структура урока основного типа требовала, чтобы новые знания давались на базе имеющихся, т.е. нужна была их актуализация. Более того, актуализация означала и психологическую подготовку учащегося: пробуждался его интерес к теме, создавался эмоциональный настрой, оценка готовности отдельных учащихся к восприятию нового материала.

            Основным видом деятельности обучающихся на этапе актуализации стала устная работа. А начальным моментом мыслительного процесса обучающихся явилась проблемная ситуация.

Дидактический материал, используемый на занятии позволил увлечь студентов, а так же побудил к самостоятельным действиям в практической деятельности, способствовал выработке навыков умственных операций и действий, навыков переноса знаний, развитию внимания, воли, творческого воображения, догадки, формированию способности открывать новые знания и находить новые способы действия.

         Мыслительная деятельность обучающихся стимулировалась постановкой вопросов. Путем задавания мною вопросов студент учился находить различие и сходства в предметах и явлениях, находить и обобщать факты, подтверждающие правило, находить причину явления и оценивать его значение, видеть проявление закономерности.

         На начальным этапе эвристического решения проблемы обучающиеся пытались найти ответ на возникший вопрос на основе известных ему знаний, личного опыта. Когда это им не удавалось, они начинали придумывать план решения.

         Умение студента находить в учебном материале нужные факты и приемы формировалось путем организации систематической самостоятельной деятельности обучающихся.

         В ходе занятия обучающимся в форме презентации были предоставлены необходимые факты для анализа и размышления. На этапе закрепления изученного материала обучающиеся анализировали, сравнивали и делали выводы, шли от неправильных догадок, предложений и прямых заблуждений к правильным предложениям.

Многие уже знакомые нам гаммы педагогической партитуры звучат иначе при переходе от соло к ансамблю. Речь идет о работе в группах. Работа в парах, группах учила студентов коллективному сотворчеству, решению задач сообща.

Скачано с www.znanio.ru