
Открытый урок по математике
Тема урока: « Формулы сложения»
Цели урока:
· образовательная: продолжить формирование знаний, умений и навыков учащихся по формулам сложения, закрепить знание учащихся формул сложения;
· развивающая: развитие алгоритмического мышления, памяти, внимания;
развивать у учащихся умение излагать мысли, делать выводы, обобщения;
развивать познавательный интерес, логическое мышление.
· воспитательная: развитие самоконтроля, формирование адекватной самооценки своей деятельности на уроке, адекватного отношения к оцениванию со стороны учителя и одноклассников, стимулирование трудолюбия, аккуратности, воспитание чувства ответственности перед товарищами при выполнении коллективной работы.
Методы обучения:
· практические;
· самостоятельная работа;
· закрепление материала;
· обобщающий.
Средства обучения: тренировка, контроль ЗУН.
Форма обучения: групповая форма обучения.
Оборудование: доска, раздаточный материал (карточки с заданиями, дешифраторами и кроссвордом); проектор.
Связь между предметами: русский язык, литература.
Предварительная подготовка: класс разбит на группы примерно по 4-5 чел.
Ход урока
1. Организационный этап включает в себя взаимное приветствие учителя и учащихся, раздачу учебников, тетрадей, ручек. Запись на доске и воспроизведение учителем даты, темы урока и домашнего задания (выполняют по желанию). Постановка целей урока. Отметка отсутствующих. Организация внимания, создание рабочей обстановки.
Итак, тема нашего урока « Формулы сложения».
Основная цель урока – вывести формулы сложения для косинуса суммы и разности углов, отработать их применение при вычислениях и выполнении преобразований тригонометрических выражений.
2. Актуализация знаний.
Урок мы начнём с выполнения небольшой устной работы, которая нацелена на повторение основных тригонометрических тождеств, проверку усвоения предыдущего материала.
Вычислить:
1.
![]() = -
= - ![]() = -
= -![]()
2.
![]() =
= ![]() =
= ![]()
3.
![]() =
= ![]() =
= ![]()
4.
(1
– sin(-β))(1- sinβ) = (1+![]() )(1- sinβ) = sin2β
)(1- sinβ) = sin2β
5. (1 – cos(-β))(1+ cos(-β)) = (1- cosβ)(1+ cosβ) = cos2β
6.
cos![]()
7. cosπ +sinπ =-1+0 =-1
8.
sin![]()
9.
cos75°=![]() -
-![]()
10.
![]() =
=![]() *
*![]() =0
=0![]()
Итак, при выполнении устной работы мы повторили табличные значения синуса, косинуса некоторых углов. И столкнулись с проблемой нахождения значений косинуса и синуса углов, которых нет в таблице. Сейчас мы займёмся выводом формул, которые помогут нам в разрешении создавшейся ситуации.
Сначала
выведем формулы сложения и разности косинусов. Начнем с ![]() , посмотримединичный окружность, точку с
координатами (1;0) назовем буквой Д.
, посмотримединичный окружность, точку с
координатами (1;0) назовем буквой Д.
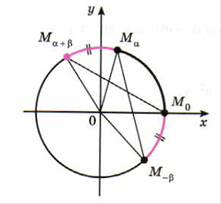
Д(1;0) Повернем
начальную точку на угол α получим точку А и ее координаты по определению
равны А(![]() ). Далее начальную точку повернем на угол
–β, получим точку В и ее координаты вычисляется как В(
). Далее начальную точку повернем на угол
–β, получим точку В и ее координаты вычисляется как В(![]() ). Мы знаем , что
). Мы знаем , что ![]() , а
, а ![]() мы координаты точки В можно записать так В(
мы координаты точки В можно записать так В(![]() ). Теперь от луча ОА отложим угол β,
при этом начальная точка пройдет дугу длиной α+β, назовем точку Сс
координатами(
). Теперь от луча ОА отложим угол β,
при этом начальная точка пройдет дугу длиной α+β, назовем точку Сс
координатами(![]() );
);![]()
С(![]() );
);![]() . Соединим
точку А с точкой В, и точку С с точкой Д, получим два равнобедренных
треугольника. Рассмотрим два треуг. АОВ и СОД. Эти два треугольника равны по
двум сторонам и углу между ними. Раз треугольники равны, значит и равны
соответствующие стороны АВ=СД, значит расстояние между точками АВ (АВ=СД) равно
расстоянию между точками СД. Если равны расстояние, значит равны их
квадратыт.е. АВ2=СД2. Вспомним формулы для нахождения
расстояния между двумя точками плоскости
. Соединим
точку А с точкой В, и точку С с точкой Д, получим два равнобедренных
треугольника. Рассмотрим два треуг. АОВ и СОД. Эти два треугольника равны по
двум сторонам и углу между ними. Раз треугольники равны, значит и равны
соответствующие стороны АВ=СД, значит расстояние между точками АВ (АВ=СД) равно
расстоянию между точками СД. Если равны расстояние, значит равны их
квадратыт.е. АВ2=СД2. Вспомним формулы для нахождения
расстояния между двумя точками плоскости
d2=![]()
Воспользуемся этой формулой для того, чтобы выразить АВ2 т.е. возведем в квадрат
АВ2=(![]() +(
+(![]() ) (1 )первое
слагаемое - квадрат разности (
) (1 )первое
слагаемое - квадрат разности (![]() , второе
слагаемое–квадрат суммы (
, второе
слагаемое–квадрат суммы (![]() (формулы сокращенного
умножения). Распишем первое слагаемое, второе слагаемое по формуле сокращенного
умножения, (основное тригонометрическое тождество равно 1), приведем подобное и
запишем результат. АВ2=2+2
(формулы сокращенного
умножения). Распишем первое слагаемое, второе слагаемое по формуле сокращенного
умножения, (основное тригонометрическое тождество равно 1), приведем подобное и
запишем результат. АВ2=2+2![]() Теперь выразим СД2
Теперь выразим СД2
При этом в скобочках от координаты точки С будем вычитывать
координаты точки Д. (Д(1;0)), а С(![]() )и у
нас получится
)и у
нас получится
СД2=(![]()
Первое слагаемое квадрат разности распишем по формуле
сокращенного умножения, а второе слагаемое просто запишем. Внимательно
посмотрим на данное выражение, здесь тоже есть основное тригонометрическое
тождество, затем запишем результат. =2-2![]() . Приравняем
СД2=АВ2
. Приравняем
СД2=АВ2
2-2![]() 2+2
2+2![]() Замечаем в левой части 2 и в
правой части, сокращаем на 2 и каждое слагаемое можно поделить на 2. Перепишем
полученное равенство, умножим только на -1, чтобы избавиться знака – перед
косинусом и в результате будет вот такая формула
Замечаем в левой части 2 и в
правой части, сокращаем на 2 и каждое слагаемое можно поделить на 2. Перепишем
полученное равенство, умножим только на -1, чтобы избавиться знака – перед
косинусом и в результате будет вот такая формула
![]() (1)
(1)
Косинус суммы мы получили. Теперь выведем формулу для косинуса разности
![]() мы запишем, как косинус
суммы, но к α мы будем прибавлять угол -βи для данного выражения
можно применить формулу косинуса суммы мы получим =
мы запишем, как косинус
суммы, но к α мы будем прибавлять угол -βи для данного выражения
можно применить формулу косинуса суммы мы получим =![]()
![]()
![]()
![]()
Запишем полученную формулу: ![]() (2)
(2)
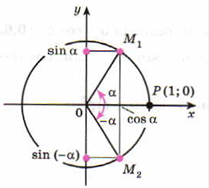
Чтобы вывести формулу ![]() , рассмотрим
прямоугольный треугольник с острым углом γ, тогда второй острый угол
равен
, рассмотрим
прямоугольный треугольник с острым углом γ, тогда второй острый угол
равен ![]() . Для угла γ
. Для угла γ ![]() это отношение прилежащего
катета к гипотенузе, но этот катет для угла
это отношение прилежащего
катета к гипотенузе, но этот катет для угла ![]() будет противолежащим, значит
это отношение будет равно
будет противолежащим, значит
это отношение будет равно ![]() т.е. мы получили
т.е. мы получили ![]() . (3)
. (3)
![]() это отношение
противолежащего катета к гипотенузе, это отношение будет равно
это отношение
противолежащего катета к гипотенузе, это отношение будет равно ![]() . (4)Выведем
формулу
. (4)Выведем
формулу![]() при этом
при этом ![]() γ и заменим
γ и заменим ![]()
![]() скобки раскроем и
перегруппируем слагаемые
скобки раскроем и
перегруппируем слагаемые
![]() =
=![]() (можно применить формулу
косинус разности)
(можно применить формулу
косинус разности)
![]() и
и![]() можно заменить (синус на
косинус на
можно заменить (синус на
косинус на ![]() , и
, и![]() и получим окончательный
результат
и получим окончательный
результат
![]() (5)
(5)
Для разности![]() место угла β берем отрицательный
угол –β и у нас получится.
место угла β берем отрицательный
угол –β и у нас получится.
![]() ) = (здесь
мы можем применять формулу синуса суммы)=
) = (здесь
мы можем применять формулу синуса суммы)=![]() Заменим
Заменим
![]()
![]() в результате имеем
в результате имеем
![]() =
=![]() (6) (эту
формулу запишем ко всем формулам).
(6) (эту
формулу запишем ко всем формулам).
Выведем формулы длясложение![]() Сначала нужно выписать все
формулы сложения синусов и косинусов. Тангенс суммы и разности = по определению
отношению синуса этого угла к косинусу этого угла, затем распишем и числитель и
знаменатель по формулам сложения.
Сначала нужно выписать все
формулы сложения синусов и косинусов. Тангенс суммы и разности = по определению
отношению синуса этого угла к косинусу этого угла, затем распишем и числитель и
знаменатель по формулам сложения.
![]() =
=![]() воспользуемся основными
свойствами дроби, дробь т.е и числитель и знаменательможно делить на одно и то
же выражение, при этом значение дроби не изменится, в данном случае я буду
делить и числитель и знаменатель на выражение
воспользуемся основными
свойствами дроби, дробь т.е и числитель и знаменательможно делить на одно и то
же выражение, при этом значение дроби не изменится, в данном случае я буду
делить и числитель и знаменатель на выражение ![]() , каждое
слагаемое делим на произведение косинуса, получим
, каждое
слагаемое делим на произведение косинуса, получим
![]() =
=![]() (7) точно
также находим разность тангенса, и числитель и знаменатель делим на
(7) точно
также находим разность тангенса, и числитель и знаменатель делим на![]() , получим
, получим
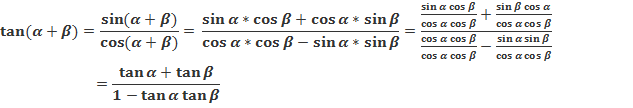
Аналогично выводятся тангенс разности
![]() =
=![]() (8)
(8)
Выведем формулы для котангенса, идея вывода формулы та же самая
сtg(α+β)=![]() =
=![]() =в
данном случае будем делить на произведение синусов
=в
данном случае будем делить на произведение синусов![]()
=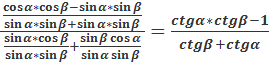
сtg(α+β)=![]() формулу сложения мы получили
формулу сложения мы получили
сtg(α-β)=![]() (10)
(10)
Мы получили формулы сложения:
![]()
![]()
![]()
![]() =
=![]()
![]() =
=![]()
![]() =
=![]()
7. сtg(α+β)=![]()
8.сtg(α-β)=![]()
Математическая разминка: «Что здесь зашифровано?»
Учащиеся выполняют задания в тетрадях по карточке. Затем сверяют свои ответы с помощью дешифратора №1 (Приложение 1), который представлен на проекторе и заносят соответствующую букву в тетрадь.
Задания, которые вызвали затруднение у учащихся, выполняются у доски.
Карточка
Вариант №1
1. ![]()
2.![]()
3. 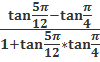
4. ![]()
5. ![]()
6. ![]()
7. 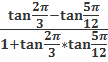
Вариант №2
1.![]()
2. ![]()
3. 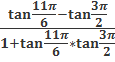
4. ![]() -
-![]()
5. ![]()
6. ![]()
7. 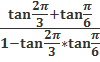
(Ответы: 1-й вариант – Пифагор; 2-й вариант – Архимед).
3. Самостоятельная работа.
Знаете ли вы, кто высказал следующие фразы?
1. Стараться оставить после себя больше знаний и счастья, чем их было раньше, улучшить и умножить полученное нами наследство – вот над чем мы должны трудиться. (Д.Дидро – французский философ).
2. Есть только одно благо - знание и только одно зло – невежество (Сократ – древнегреческий философ.).
3.
Любая книга — умный друг:
Чуть утомит, она смолкает;
Она безмолвно поучает,
С ней назидателен досуг
(Лопе де Вега – испанский поэт).
4. Ум заключается не только в знании, но и в умении применять знания на деле (Аристотель - древне греческий философ, ученый.)
5. Разум человеческий владеет тремя ключами, открывающими все: цифрой, буквой, нотой. Знать, думать, мечтать. Все в этом. (В.Гюго – французский писатель).
6. Свойство мудрого человека состоит в трех вещах: первое – делать самому то, что он советует другим, второе – никогда не поступать против справедливости и третье – терпеливо переносить слабости людей, окружающих его (Л.Н.Толстой – русский писатель).
Для того чтобы узнать авторов этих высказываний, необходимо заполнить кроссворд, используя результаты заданий в карточках 1-6 и сверив их с дешифратором №2 (Приложение 2), который представлен вниманию учащихся на экране проектора.
Кроссворд

Й 6.5 6.4 6.3 6.2 6.1 3.3 3.2 Т 2.4 2.3 2.2 5.1 ю 5.2 О 1.3. 1.2.
Задания к кроссворду
Задания к кроссворду
Карточка №1
1.1.![]() *
*![]() +
+ ![]()
1.2 ![]() *
*![]()
1.3 ![]()
1.4 ![]()
Карточка №2
2.1 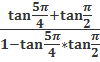
2.2 ![]()
2.3 ![]()
2.4 ![]()
2.5 ![]()
Карточка №3
3.1 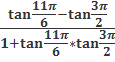
3.2 ![]()
3.3 2*(![]() )
)
Карточка №4
4.1![]()
4.2
![]()
4.3
![]()
4.4 ![]() +
+![]()
4.5 ![]()
4.6 2*![]()
Карточка №5
5.1 ![]()
5.2 ![]()
Карточка №6
6.1 ![]()
6.2 ![]()
6.3 2*(![]() )
)
6.4 ![]()
6.5 ![]()
6.6 ![]()
4. Итоги урока.
Ответы к кроссворду выводятся на экране проектора. Подводятся итоги работы каждой группы на протяжении всего урока, в группах оценивается деятельность каждого учащегося, результаты объявляются в конце урока.
5. Домашнее задание.
6. Рефлексия
Цветограмма: Каждый ученик оценивает свою работу с помощью цветных жетонов.
|
Цвет жетона |
Оценка своей деятельности |
|
Красный |
Был активен, смог проявить свои способности |
|
Зеленый |
Стремился быть активным, но не смог в полной мере себя проявить |
|
Желтый |
Проявил себя не в полной мере, так как не стремился к этому |
|
Синий |
Совсем не проявил себя |
Приложение 1
Дешифратор №1
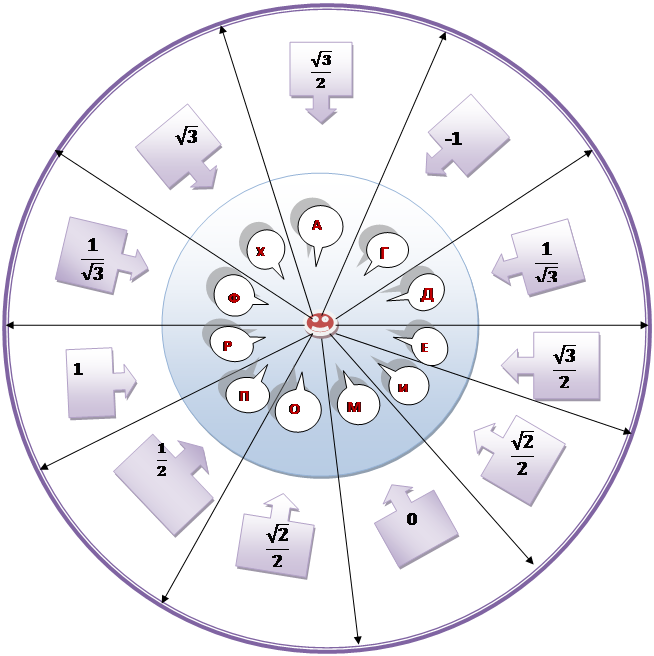
Приложение 1
Дешифратор №2
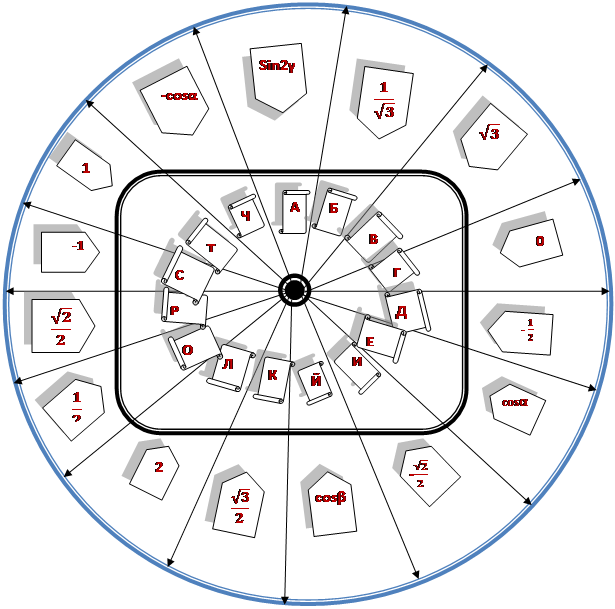
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.