Методическая разработка и использованием материалов библиотеки ЦОК к уроку математики в 11 классе на тему: "Производная и её геометрический смысл"

Конспект урока на тему: Производная и её геометрический смысл

УМК: Ш.А. Алимов, Ю.М.Колягин и др. «Алгебра и начала анализа» учебник для 10-11 классов общеобразовательных учреждений. М.: Просвещение, 2020 года.

Цели урока:

     Обучающие:

1.   повторить основные формулы и правила дифференцирования, физический и геометрический смысл производной;

2.   вывести уравнение касательной к графику дифференцируемой функции;

3.   сформировать умение комплексного применения знаний, умений, навыков и их перенос в новые условия; 

4.   проверить знания,  умения, навыки учащихся по данной теме.

         Развивающие:

1.     способствовать развитию мыслительных операций: анализ, синтез, обобщение;

2.     оказать помочь в формировании умений  самооценки и взаимооценки;

3.     развивать познавательную активность, вычислительные навыки.

         Воспитательные:

1.   воспитывать добросовестное отношение к труду, инициативность, организованность.

Тип урока:

комбинированный

Структура урока:

Организационный этап.

Этап проверки домашнего задания.

Этап всесторонней проверки знаний.

Этап подготовки учащихся  к активному  усвоению знаний.

Этап усвоения новых знаний.

Этап закрепления новых знаний.

Этап постановки домашнего задания и инструктаж по его выполнению.

Оборудование: программа презентаций Microsoft Office PowerPoint, презентация, компьютер, мультимедиа проектор.

План урока:

1.     Организационный момент (1 мин)

2.     Проверка домашнего задания (3 мин)

3.     Проверка знаний (17 мин)

4.     Подготовка обучающихся  к активному  усвоению знаний (1 мин)

5.     Усвоения новых знаний (5 мин)

6.     Закрепления новых знаний (10 мин)

7.     Подведение итогов урока (1 мин)

8.     Домашнее задание (2 мин)

Ход урока:

I. Организационный момент

Приветствие класса. Проверка готовности класса к уроку.

Учитель знакомит с темой, целями и ходом урока.

II. Проверка домашнего задания

№ 858, 859

III. Проверка знаний

1)    Устный опрос:

1.     Сформулируйте определение производной.

Определение: Пусть функция f (x) определена на некотором промежутке, х – точка этого промежутка и число h # 0 такое, что х + h также принадлежит данному промежутку. Тогда предел разностного отношения     

при h → 0 (если этот предел существует) называется производной функции

f (х) в точке х и обозначается f  '(х). Таким образом,  

2.     Как называется операция нахождения производной?

Операция нахождения производной называется дифференцированием.

3.     Какая функция называется дифференцируемой в точке?

Если функция f (х) имеет производную в точке х, то эта функция называется дифференцируемой в этой точке.

4.     Какая функция называется дифференцируемой на некотором промежутке?

Если функция f (х) имеет производную в каждой точке некоторого промежутка, то говорят, что эта функция дифференцируема на этом промежутке.

5.     В чем заключается физический (механический) смысл производной?

Тангенс угла наклона касательной есть величина, показывающая мгновенную скорость изменения функции в данной точке.

6.     В чем заключается геометрический смысл производной?

Значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке.

7.     Сформулируйте правило нахождения производной суммы, произведения, частного.

2)    «Верно-неверно»

Если ученик согласен с ответом – он ставит у себя в тетради «+», если – нет «-«. 

Цель данного задания –  понимание смысла теоретических знаний.

1.Если функция дифференцируема в точке, то она в этой точке непрерывна?

Да

2.Если функция непрерывна в точке, то она в этой точке дифференцируема?

Нет

3. Верно ли, что тангенс угла наклона касательной к графику функции – есть значение производной функции в точке касания?

Да

4.Верно ли, что производная суммы функций равна сумме производных    функций?

Да

5.Верно ли, что производная функции у = ln x имеет производную в точке  

х = - 5?

Нет

6.Верно ли, что первая производная пути от времени – это есть мгновенная скорость материальной точки?

Да

7.Верно ли, что функция у =cos x  дифференцируема на множестве действительных чисел?

Да

Ответы:  + - + + - + +

3)    Решение задач

1.     Решение задач на нахождение производной в точке, углового коэффициента касательной к графику функции.

Данные задачи учащиеся решают с использование интерактивной доски, каждая задача изображается на отдельном слайде. (1 – 11 слайд)

Учащиеся по мере движения слайдов обсуждают решения задач.

2.       Самостоятельная работа: 5 заданий из открытого банка заданий (1в., 2 в.)

ИЗ ОТКРЫТОГО БАНКА ЗАДАНИЙ 1в

1.      На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.

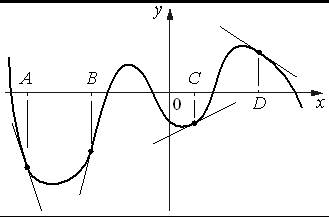
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

ТОЧКИ                     ЗНАЧЕНИЯ ПРОИЗВОДНОЙ

 A                                            1)  0,5

 B                                            2)  − 0,7

 C                                            3)  4    

 D                                            4)  −3

В таблице под каждой буквой укажите соответствующий номер.

2.      На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.

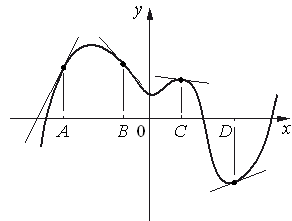
В правом столбце указаны значения производной функции в точках A, B, C

 и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

ТОЧКИ                     ЗНАЧЕНИЯ ПРОИЗВОДНОЙ

A                                            1)  − 

B                                             2)  2

C                                             3)  

D                                             4)  − 1

В таблице под каждой буквой укажите соответствующий номер.

3.      На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x₀. Найдите значение производной функции f(x)

в точке x₀.

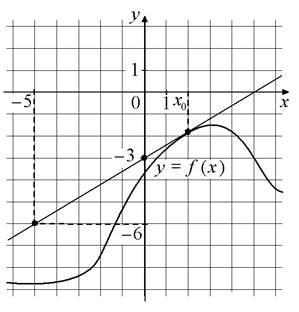
4.      На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x₀. Найдите значение производной функции f(x)

в точке x₀.

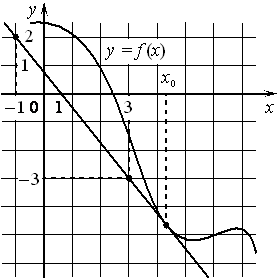
5.      На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x₀. Найдите значение производной функции f(x)

в точке x₀.

ИЗ ОТКРЫТОГО БАНКА ЗАДАНИЙ 2в

1.На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.

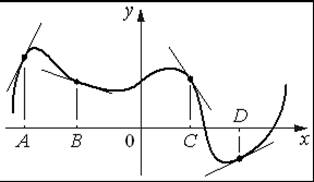
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

 ТОЧКИ                    ЗНАЧЕНИЯ ПРОИЗВОДНОЙ

A                                 1)  − 1,5

 B                                2)  0,5

 C                                3)  2    

 D                                4)  − 0,3

таблице под каждой буквой укажите соответствующий номер.

2. На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.

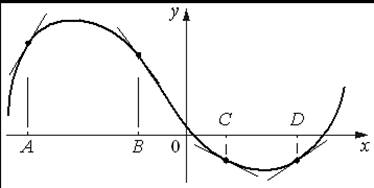
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

 ТОЧКИ                    ЗНАЧЕНИЯ ПРОИЗВОДНОЙ

A                                 1)  ⅔  

 B                                2)  - ½

 C                                3)  -1⅓

 D                                4)  1⅔

 В таблице под каждой буквой укажите соответствующий номер.

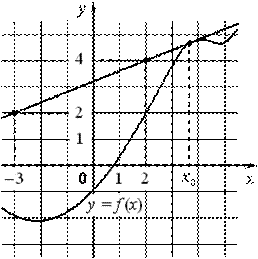
  3.На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой

x₀. Найдите значение производной функции f(x) в точке x₀.

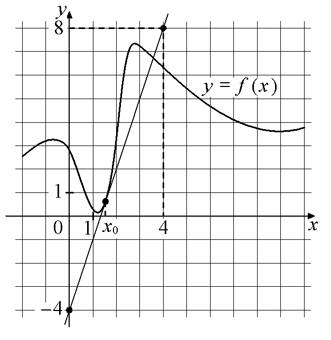
4. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой

x₀. Найдите значение производной функции f(x) в точке x₀.

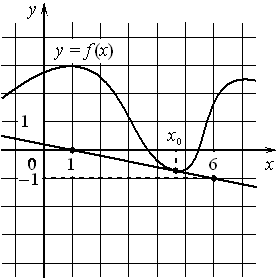
5. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой

x₀. Найдите значение производной функции f(x) в точке x₀.

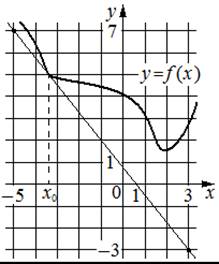
IV.  V. Подготовка обучающихся  к активному  усвоению знаний. Усвоение новых знаний.

Вывод уравнения касательной к графику дифференцированной функции y = f (x) в точке ( х₀; f (x₀) ).

VI.  Закрепления новых знаний.

Запишите алгоритм нахождения уравнения касательной к графику функции        y = f (x) в точке х₀.

Решаем №860 (1,3)

VII. Подведение итогов урока.

VIII. Домашнее задание.

№860(2,4,6), 866(2,4)

Скачано с www.znanio.ru