Методическая разработка на тему "Дифференциальное исчисление"":

ГАОУ СПО «Балашовское медицинское училище»

 

 

 

 

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

 

 

Практического занятия для преподавателей

математики

Тема:

«Дифференцирование функции»

 

 

Специальности: 060101 «Лечебное дело»

 

 

Количество часов: 2 учебных часа

преподаватель: Вересова Н. С.

 

Утверждена

На заседании ЦМК________

_________________________

Протокол №___ от_______ г.

Председатель ЦМК

_______________________

 

 

 

 

г. Балашов

Государственным стандартом Минздрава Российской Федерации в рамках изучения базового курса «Математики» по рабочей программе 2012 года на изучение темы «Дифференцирование функции» отводится 10 часов, из них 4 практических занятия.

Практическое занятие по теме «Дифференцирование функции» (2 часа) имеет цель научить учащихся находить производные функции,

использовать её геометрический и механический смысл. Использовать свойства производных. Находить частные производные.

Структура практического занятия: организационный момент; формулирование темы и ее обоснование; определение цели занятия и сообщение плана; обобщение и систематизация лекционного материала; выполнение практического задания; контроль за усвоением знаний по изучаемому материалу, подведение итогов занятия и домашнее задание.

По теме занятия приведен список литературы для самоподготовки, что не исключает возможность студентов самостоятельно расширять этот список с целью углубления знаний по теме. Работа по подбору рабочих источников полезна при подготовке студентами докладов, рефератов, проектов, презентаций, или при выполнении самостоятельных работ.

По форме организации практическое занятие – это закрепление и систематизация знаний.

 

ЦЕЛИ ЗАНЯТИЙ

Учебные:

§  научить учащихся находить производные функции;

§  научить использовать геометрический и механический смысл производной;

§  научить использовать свойства производных;

§  находить частные производные.

В ходе закрепления материала студенты должны:

Знать:

§  определение непрерывности и дифференцируемости функции;

§  определение производной функции, её геометрический и механический смысл;

§  основные свойства производных;

§  таблицу производных основных функций;

§  определение функции нескольких переменных.

Уметь:

§  находить производные элементарных и сложных функций;

Владеть навыками:

§  нахождения производных функции;

§  решения задач, предусмотренных данной темой.

 

ВОСПИТАТЕЛЬНЫЕ:

§  воспитать культуру общения, тактичность, коммуникабельность - при общении с преподавателем и своими однокурсниками в ходе занятия и при обсуждении спорных моментов при решении упражнений;

§  воспитывать организованность, собранность, целеустремлённость - при подготовке к занятию, при усвоении нового материала, при выполнении домашнего задания;

§  воспитывать вежливость, отзывчивость, взаимовыручку, необходимые для межличностного и профессионального общения;

§  формировать и поддерживать стремление к знаниям;

§  воспитывать творческое отношение к приобретению новых знаний;

§  формировать уважительное отношение к личности;

§  воспитывать дисциплинированность и самостоятельность - при выполнении индивидуальной и самостоятельной работы.

 

РАЗВИВАЮЩИЕ:

§  развивать такие психологические процессы, как логическое мышление, абстрагирование, анализ, синтез, обобщение, дифференцирование; гибкость ума.

§  развивать познавательную активность и умение применять приобретенные знания на практике;

§  развить аккуратность, точность - при записях в рабочих тетрадях, выполнении чертежей и рисунков;

§  развить память словесно-логическую, зрительную, образную - на протяжении всего занятия, при выполнении домашнего задания;

§  внимательность, исполнительность - при конспектировании определений, наиболее важных, узловых вопросов занятия, при решении задач и примеров.

 

Структура практического занятия. Этапы планирования занятия

№	Название этапа	Краткое описание деятельности		Цель	Время	Оснащенность
		преподавателя	студентов
1	Организация занятия	Отмечает отсутствующих. Уточняет готовность студентов к занятию.	Готовят тетради с лекционным материалом	Мобилизировать студентов на работу	1 мин	Журнал успеваемости и посещаемости группы.
2	Формулирование темы и ее обоснование	Сообщает тему, акцентирует внимание на ее значимости.	Записывают в тетрадь тему, слушают обоснование.	Раскрыть теоретическую значимость темы	2 мин	Тетрадь для практических занятий
3	Определение цели занятия	Сообщает цели занятия	Слушают преподавателя	Показать студентам конечный результат	2 мин	Тетрадь для практических  занятий
4	Сообщение плана занятия	Сообщает план занятия	Слушают преподавателя	Конкретизировать внимание студентов	3 мин	Тетрадь для практических занятий
5	Обобщение и систематизация лекционного материала по теме.	Проводит устный опрос в соответствии с планом	Отвечают на вопросы преподавателя	Обобщить и систематизаровать знания по теме	15-20 мин	Тетрадь, таблицы, слайды, мультимедиа установка
6	Практические задания	Комментирует предложенные задания	Решают предложенные задачи	Закрепление знаний	20 мин	ПК, карточки, слайды, мультимедиа установка
7	Физкультминутка. Гимнастика для глаз.	Комментирует упражнения	Выполняют упражнения	Снятие физического и зрительного напряжения	1-2  мин
8	Практические задания	Комментирует предложенные задания	Решают предложенные задачи	Закрепление знаний	20 мин	ПК, карточки, слайды, мультимедиа установка
9	Контроль изученного	Проводит письменный опрос по карточкам (тест)	Отвечают на вопросы  задания	Контроль уровня усвоения материала	10 мин	Карточки
10	Подведение итогов занятия	Подводит итоги занятия, отмечает достижение результатов	Слушают преподавателя		2 мин	Тетрадь, таблицы
11	Домашнее задание	Называет объем материала для подготовки домашнего задания	Записывают в тетрадь	Подготовка студентов к следующему практическому занятию	3 мин	Тетрадь

 

Тема: «Дифференцирование функции»

План:

1.       Организация занятия. Формулировка темы (ее обоснование) и целей занятия;

2.       Обобщение и систематизация лекционного материала по теме;

3.       Практические задания;

4.       Физкультминутка. Гимнастика для глаз;

5.       Практические задания;

6.       Контроль  изученного материала;

7.       Подведение итогов занятия;

8.       Домашнее задание.

Оснащение занятия:

§       карточки с заданиями для выполнения практического задания;

§       карточки контролирующего характера (тесты).

 

 

 

1.     Организация занятия. Формулировка темы и целей занятия.

Преподаватель приветствует студентов, отмечает отсутствующих. Формулирует тему и цели занятия.

Преподаватель:

« На сегодняшнем занятии мы с вами:

1. научимся находить производную функции, использовать её геометрический и механический смысл;

2. закрепим знание формул и свойств производных;

3.  научимся находить частные производные».

2.     Обобщение и систематизация лекционного материала по теме.

 

Вопросы:

1.     Какая функция называется непрерывной в точке х₀?

2.     Что называют окрестностью точки х₀?

3.     Выполнение каких двух условий  требуется для непрерывности функции в точке?

4.     Что называют приращением аргумента х в точке x₀?

5.     Что называют приращением функции в точке x₀?

6.     Как звучит свойство непрерывности функции?

7.     В чем заключается геометрический смысл производной?

8.     В чем заключается физический смысл производной?

9.     Что называют  мгновенной скоростью?

10. Каков механический смысл второй производной?

Проверка знания таблицы производных:

Учитель просит записать на отдельных листах формулы таблицы производных и основные правила дифференцирования, спрашивая их в произвольном порядке (см. таблица №1, ПРИЛОЖЕНИЕ)

 

3.     Практические задания.

Задание №1.  Устный счёт

Найдите производные функций:
а) f(x) = sin x;   б) f(x) = x2;    в) g(x) = 2x;    г) g(x) = 3 + 2x; д) y = (3+2х)2;  е) у = 9 +12х + 4х2. ж)f(х)=(4х-2)3	з) f(x) = cos 3x и) f(x) = 4x3 –x2  к) f(x) = e2x л) f(x) = 2x  м) f(x) = ln (5-x) н) f(x) = 12 sin 3 x о) f(x) = 78 π x

 

Задание №2.

Найти производную функции используя определение производной.

                                           

Решение:

Преподаватель демонстрирует на доске решение примера, опираясь на знания студентов.

Из определения производной вытекает следующая схема для её вычисления.

Шаг 1. Дадим аргументу приращение и найдём

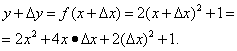
Шаг 2. Найдём приращение функции:

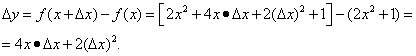
Шаг 3. Найдём отношение приращения функции к приращению аргумента:

Шаг 4. Вычислим предел этого отношения при , т.е. производную:

 

Задание №3.

Найти производную функции

В ходе выполнения задания преподаватель выявляет знание основных свойств вычисления производной функции.

Решение:

Преподаватель: «Перед нами функция, являющаяся алгебраической суммой степенных функций с поcтоянными множителями. Какие правила нам понадобятся для нахождения производной?»

Учащиеся перечисляют правила:

·       правила вычисления производной алгебраической суммы функций ,

·       правила вынесения постоянного множителя за знак производной

·       и формула дифференцирования степенной функции .

Последовательно применяя эти правила, отвечающий у доски студент добивается следующего результата:

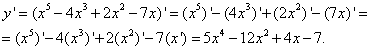
Задание № 4.

Найти производную функции

Преподаватель поясняет выполнение задания:

«Применим правило дифференцирования произведения ,

а затем найдём производные сомножителей так же, как в предыдущей задаче».

Отвечающий у доски студент добивается следующего результата:

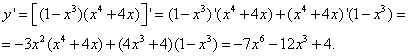
Задание №5. Найти производную функции у =

Применяя правило дифференцирования частного , учащийся переписывает исходный пример в виде:

Затем, так же как и выше, вычисляет производные в числителе. И находит искомую производную:

 

4.     Физкультминутка. Гимнастика для глаз.

(см. приложение)

 

5.     Практические задания

Задание №6. На использование механического смысла производной

Тело движется прямолинейно по закону (м). Определить скорость его движения в момент с.

Решение:

Для выполнения задание необходимо вспомнить с учащимися механический смысл производной:

Пусть задан путь  движения материальной точки. Скорость данной материальной точки в момент времени  есть производная от пути  по времени :     .

Значит, искомая скорость - это производная от пути, то есть:

В заданный момент времени    (м/с).

Ответ. (м/с).

Задание №7. На использование геометрического смысла производной

На рисунке №1 изображен график функции и касательная к нему в точке с абсциссой . Найти значение .
Решение:  Из геометрического смысла производной получаем, что  Найдем угол . Рассмотрим треугольник - прямоугольный, равнобедренный. Тогда , а значит А отсюда следует, что Ответ.

Задание №8:  Найти частные производные функции  

Решение: Найдем частную производную по x первого порядка:  

Найдем частную производную по x второго порядка:

 

Аналогично находим частную производную первого и второго порядка по y:   ,       

6.      Контроль изученного материала

Тест: «Дифференцирование функции»

Преподаватель: «В ответе укажите номер задания и букву, под которой расположен правильный ответ».

 1. Найдите производную функции в точке x₀=-1
а) 2;    б) -2;    в) -1;    г) 3.

2. Найдите производную функции
а) 4x-1;    б) 2x-1;    в) 2x²+1;    г) 4x+1.

3.  Найдите производную функции
а) xsinx-cosx;   б) xsinx+cosx;   в) sinx-xcosx;   г) xcosx+sinx.

4. Найдите производную функции
а) sinx-;    б) cosx+1;    в) –sinx+1;    г) –sinx-1.

5. Найдите производную функции
а) 3x²+2x-1;    б) 2x³+3x+1;    в) 3x²-2x+1;    г) 3x²+2x+1.

6.  По данной производной определите исходную функцию и запишите свой ответ: y΄=4x+cosx.

7.  Укажите пары: «функция – график производной этой функции»

1. ;      2. ;      3.

                                    

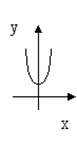
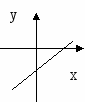
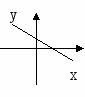
а)                              б)                                    в)

 

В ответе укажите номер формулы и букву, под которой расположен соответствующий график функции.

7.     Подведение итогов занятия

 

Сегодня мы с вами:

Научились находить производную функции, использовать её геометрический и механический смысл; закрепили знание формул и свойств производных;

научились находить частные производные.

Молодцы, Вы хорошо работали на занятии, оценки ……………….

 

8.     Задание домашнего задания.

Знать:

1.                определение непрерывности и дифференцируемости функции;

2.                основные свойства производных;

3.                таблицу производных основных функций.

Выполнить задание:
1. Дано . Найти .
2. Дано . Найти у˝.

 

 

Список использованной литературы

 

 

1.     Филимонова       Е.В. Математика: Учебное пособие для средних специальных учебных заведений. / Е.В. Филимонова. — 2-е изд., доп. и перераб. — Ростов-на- Дону.: Феникс, 2008. —  207 с.

2.     Михеев B.C., Стяжкина О.В., Шведова О.М. Математика: Учебное пособие для среднего профессионального образования. / В.С.Михеев. — Ростов-на-Дону.: Феникс, 2009. — 466 с.

3.     Киселева, JI.B. Пособие по математике для студентов медицинских училищ и колледжей — М.: ФГОУ «ВУНМЦ Росздрава», 2005. — 210 с.

4.     Привалова, Т.Б. Математика/ Т.Б. Привалова, Новгородова А.А., Антонюк М.В.. Пособие для студентов медицинских училищ и колледжей - М.: ВУНМЦ, 1999г. — 224 с.

5.     Кормилкина Е.В. «Прикладная математика в сестринском деле терапии, фармакологии и педиатрии» СПБАК ,2002. — 459 с.

6.     Интернет – ресурсы.

 

 

 

 

Приложение

 

Таблица №1

Сначала — отдых Пальминг

 Сядьте прямо, расслабьтесь. Прикройте глаза таким образом: середина ладони правой руки должна находиться напротив правого глаза, то же самое с левой рукой. Ладони должны лежать мягко, не нужно с силой прижимать их к лицу. Пальцы рук могут перекрещиваться на лбу, могут располагаться рядом — как вам удобнее. Главное, чтобы не было "щелочек", пропускающих свет. Когда вы в этом удостоверились, опустите веки. В результате получается, что ваши глаза закрыты и, кроме того, прикрыты ладонями рук.

Теперь опустите локти на стол. Главное, чтобы шея и позвоночник находились почти на одной прямой линии. Проверьте, чтобы ваше тело не было напряжено, и руки, и спина, и шея должны быть расслаблены. Дыхание должно быть спокойным.

Теперь попытайтесь вспомнить что-нибудь, доставляющее вам удовольствие: как вы отдыхали на море, как вас все поздравляли с днем рождения, звездное небо… Можно делать это упражнение под музыку. Сознательно расслабить глаза очень сложно (вспомните, что своим сердцем вы тоже не можете управлять). Поэтому не нужно пытаться контролировать свое состояние —  это только повредит цели занятия, вместо этого подумайте лучше о чем-нибудь приятном.

Выполнять упражнение несколько минут.

После выполнения упражнения постепенно приоткройте ладони, дайте закрытым глазам немного привыкнуть к свету, и лишь затем их открывайте.

 

 

"Письмо носом"

 Это упражнение направлено как на то, чтобы расслабить мышцы ваших глаз, так и на то, чтобы расслабить вашу шею. Напряжение в этой области нарушает правильное питание глаз (иначе говоря, замедляется процесс кровоснабжения).

Упражнение выполнять сидя. Расслабьтесь. Закройте глаза. Представьте, что кончик носа — это ручка, которой можно писать, главное, чтобы вы и ваши глаза не напрягались). Теперь пишите (или рисуйте) в воздухе своей ручкой. Что именно, не важно. Напишите разные буквы, названия городов и стран. Нарисуйте домик с дымом из трубы (такой, как рисовали в детстве), просто кружочек или квадратик.

"Сквозь пальцы"

 Расслабление глаз может быть достигнуто за счет того, что вы смотрите, не концентрируясь на чем-то одном. Чтобы снять с глаз напряжение, вам предлагается это упражнение. Его можно выполнять сидя, лежа, стоя.

Согните руки в локте так, чтобы ладони находились чуть ниже уровня глаз. Разомкните пальцы. Делайте плавные повороты головой вправо-влево, при этом смотрите сквозь пальцы, вдаль, а не на них. Пусть взгляд скользит, не задерживаясь на чем-то одном. Если вы делаете все правильно, руки будут "проплывать" мимо вас: вам должно казаться, что они движутся.

Делайте попеременно три поворота с открытыми глазами и три с закрытыми (при этом даже закрытые глаза должны ни на чем "не задерживаться" взглядом. Сделайте упражнение 20–30 раз, дышите при этом свободно, не напрягайтесь.

 

Скачано с www.znanio.ru