Методическая разработка на тему: Понятие производной функции

Министерство сельского хозяйства и продовольствия Самарской области

государственное бюджетное  профессиональное образовательное учреждение

Самарской области

 «Борский государственный техникум»

Методическая разработка урока

по дисциплине: ОУД. 03 «Математика: алгебра и на­чала математического анализа; геометрия» и ЕН.01 «Математика»

На тему: «Понятие производной»

Подготовила:

Ситникова Н. С. – преподаватель

математики

с. Борское, 2019г.

Пояснительная записка.

Трудно назвать научную область, в которой бы не применялись математические методы изучения реальных объектов и процессов. Одним из важнейших разделов математики, используемых для описания и решения прикладных задач, является математический анализ. Примеры практических задач, дают нам ясное представление о значимости производной в области физики, геометрии, механики, биологии и экономики. Решение прикладных задач имеет большое воспитательное значение, так как воспитывает умение распознать то или иное математическое понятие в различных ситуациях и позволяет знакомить учащихся с математическим моделированием как методом научного познания окружающего мира.

В структуре изучаемой дисциплины ОУД.03 «Математика: алгебра и на­чала математического анализа; геометрия», а также ЕН.01 «Математика» выделяется следующий раздел: «Математический анализ». Содержание раздела включает тему урока «Понятие производной».

В результате изучения данной темы студент должен

Знать:

-определение производной, формулы для отыскания производных;

-методы нахождения производных;

-формулы нахождения производных;

Уметь:

-находить производную по таблице формул отыскания производных;

-определять правило дифференцирования функции;

-применять методы дифференцирования при решении прикладных задач.

Тема урока: Понятие производной.

Образовательная цель: 

-закрепление навыков вычисления производных;

-сформировать навыков и умений вычисления производной;

- познакомить учащихся с применением производной к решению некоторых физических и технических задач;

Развивающая цель: 

- развивать внимание, память, речь, аналитическое и логическое мышление;

-развивать мотивацию познавательной деятельности.

-развитие умений логически мыслить и аргументировано отстаивать свои убеждения.

Воспитательная цель: 

-воспитывать информационную культуру и культуру общения, готовить обучающихся к жизни в современном информационном обществе.

Тип урока: урок обобщения и систематизации знаний

Вид урока: практическая работа

Методические приемы и методы.

-самостоятельная работа (тест);

-практический- решение прикладных задач;

- научности;

-наглядности;

-последовательности изложения материалов;

-преемственности;

-соревновательности.

Межпредметные  связи:

-         физика;

-         информатика;

-         русский язык и культура речи (правильность и содержательность изложения материала);

-         иностранный язык (перевод терминов);

-         история (обращение к историческому материалу).

Методическая цель: способы активизации мыслительной деятельности студентов

ВВЕДЕНИЕ

Методическая разработка предназначена для изучения математики алгоритмическими методами.

В данной методичке систематизируются понятия предела и непрерывности функций в точке. Повторяются и углубляются знания по данной теме.

Теоретический материал разработки изложен в доступной форме, приводится достаточное количество примеров, что способствует лучшему усвоению учебного материала.

Методическая разработка предназначена для студентов техникума I-II курсов.

1. Непрерывность основных элементарных функций

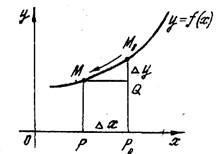Функция y = f(x) называется непрерывной при данном значении х, если бесконечно малому приращению х соответствует бесконечно малое приращение y, то есть если  (рис.1).

 Рис.1

2. Производная функции, её геометрический и механический смысл

Производной функции f(x) называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю.

                     (1)

1) Геометрический смысл производной

Пусть функция y = f(x), x Î [c; d] дифференцируема в точке x = a Î ]c; d[ (р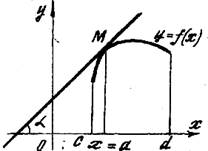ис.2)

Рис.2

Производная функции y = f(x) в точке x = a равна угловому коэффициенту касательной, проведенной к графику данной функции в его точке с абсциссой x = a.

                          (2)

2) Механический смысл производной

Пусть материальная точка движется прямолинейно по закону S = f (t).

Мгновенная скорость прямолинейного движения материальной точки в момент времени t есть производная пути по времени.

V(t) = S¢(t)                      (3)

3. Формулы дифференцирования основных элементарных функций

Заданы функции u=f(x), v=j(x), c = const.

Пример 1. Найти производную функции

Решение:   

Пример 2. Найти производную функции

Решение:

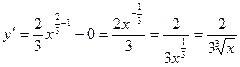
Пример 3. Найти производную функции y = x²(4x – 1)

Решение:

y = 4x³ – x²,

y¢ = 12x² – 2x

Пример 4. Найти производную функции

Решение:

Пример 5. Найти производную функции

Решение:

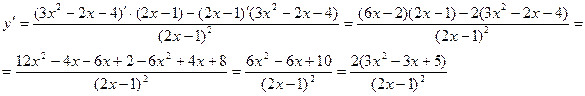
Пример 6. Написать уравнение касательной к кривой y = 1 – 2x² в точке ее А с абсциссой, равной 2.

Решение:

Найдем ординату точки А:

y = 1 - 2×2² = 1 – 8 = - 7

Искомая касательная находится среди прямых, определяемых уравнением y – y₁ = k(x – x₁).

Определим угловой коэффициент касательной по формуле k = y¢

k = (1 – 2x²)¢ = -4x

k = -4×2 = -8

Искомое уравнение примет вид:

y + 7 = -8(x-2)

y + 7 = -8x + 16

8x + y – 9 = 0

4. Сложная функция. Производная сложной функции

Сложной функцией называется функция вида  y = F(f(x)). Её можно записать: y = F(u), где u = f(x).

Пример 1. Функция y = sin5x есть сложная, составленная из функций y=sin u, где u = 5x.

Пример 2. Функция  – сложная; , где u = 1 – x³.

Пример 3. Функция  – сложная; y=ln u, где u = cos x

Производная сложной функции находится по формуле:

                             (2)

Производная сложной функции равна произведению производных функций, её составляющих.

Например:

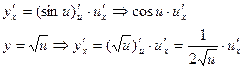
Пример 4. Найти производную функции y = sin 5x

Решение:

Обозначим u = 5x. Получим y = sin u

По формуле (2) имеем

Пример 5. Найти производную функции

Решение:

Обозначим . Получим y = sin u.

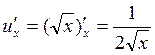
По формуле (2) находим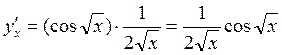

Пример 6. Найти производную функции .

Решение:

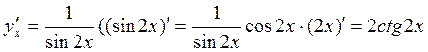
5. Производные высших порядков. Механический смысл второй производной

Производные высших порядков

Задана функция y = f(x), которая определена на интервале ]a;b[. Пусть в каждой точке этого интервала она имеет производную .

Производной второго порядка функции y = f(x) называется производная от её первой производной: .

Производной третьего порядка функции y= f(x) называется производная от её второй производной: .

Производной n-го порядка функции y = f(x) называется производная от её (n-1)-й производной: .

Пример 1. Найти производную третьего порядка функции y=4x³ – 3x² + 1.

Решение:

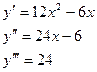
Механический смысл второй производной

Материальная точка движется прямолинейно по закону S=f(t), тогда скорость движения равна (формула (3)). Если движение неравномерное, то скорость v(t) также есть функция времени. Поэтому можно рассмотреть скорость изменения скорости движения, т.е. ускорение

Ускорение прямолинейно движущейся материальной точки равно производной скорости во времени или второй производной пути по времени.

Пример 2. Точка движется неравномерно прямолинейно по закону

S = 2t³ – 4t + 1. Найти величину ускорения в конце третьей секунды.

Решение:

Поставим в значение t = 3:

м/с².

6. Производные обратных тригонометрических функций

Функции y=f(x) и x=F(y) называются взаимно обратными, если:

1)    D(f) = E(F)

2)    E(f) = D(F)

3)    y₀ = f(x₀)      x₀ = F(y₀),

где     D – область определения;

          E – область значений функции.

Теорема.

Если производная  заданной монотонной функции существует и не равна нулю, то производная обратной функции x(y) определяется по формуле:

Доказательство.

Составим отношение 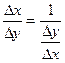. Так как функции y=f(x) и x=F(y) непрерывны, то при Dx®0; Dy®0. Поэтому ;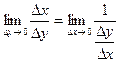

,                                             (1)

что и требовалось доказать.

Пример 1. Найти производную функции

Решение:

;          x = sin y – взаимно обратные функции

Итак,                      (2)

Пример 2. Найти производную функции y = arccos x.

Решение:

 и x=cos y – взаимно обратные функции.

                            (3)

Пример 3. Найти производную функции y = arctg x.

Решение:

;      

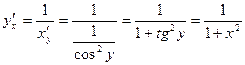
                                  (4)

Пример 4. Найти производную функции y = arcctg x.

Решение:

;     

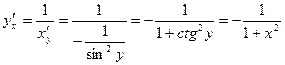
                              (5)

ЛИТЕРАТУРА

Основная

1.     Башмаков М.И. Математика. - М.: Издательский центр «Академия», 2014.

2.     Валуцэ И.И., Дилигул Г.Д. Математика для техникумов (на базе средней школы). - М.: Наука, 1980.

3.     Выгодский М.Я. Справочник по элементарной мате­матике. - М.: АСТ, 2006.

4.     Алгебра и начало анализа, I и П ч. /Под редакцией Г.Н.Яковлева. - М.: Наука, 1978.

5.     Геометрия, ч. I. /Под редакцией Г.Н.Яковлева. - М.: Наука, 1977.

6.     Яремчук Ф.П., Руденко П.А. Алгебра и элементарные функции (справочник). - Киев: Наукова думка, 1976.

Дополнительная

1.     Курс математики для техникумов, ч. I и П. /Под ред. Н.М.Матвеева. - М.: Наука, 1977.

2.     Зайцев И.Л. Элементы высшей математики для техникумов.- М.: Наука, 1972.

3.     Калкин Р.А. Алгебра и элементарные функции. - М.: Наука, 1969.

Скачано с www.znanio.ru