Самарский колледж строительства и предпринимательства (филиал) ФГБОУ ВО НИ

«Московский государственный строительный университет»

 

 

 

 

 

 

 

 

Методическая разработка

 

открытого занятия

по  дисциплине  «Математика»

на 1 курсе

Тема: Итоговое занятие по разделу «Основы тригонометрии»

 

 

 

 

 

 

 

 

 

Самара   2018

Оглавление

Пояснительная записка. 2

Описание занятия, цели и задачи. 3

Вступительное слово преподавателя. 4

Доклады по истории тригонометрии. 6

Краткий повтор свойств и графиков тригонометрических функций. 11

Решение задач на повторение. 12

Доклад «Доказательство тригонометрических тождеств». 12

Межпредметная связь с физикой. 14

Высказывания о математике. 15

Итоговая контрольная работа по разделу «Основы тригонометрии». 16

1 вариант. 16

2 вариант. 18

Ответы к контрольной работе. 20

Градация оценок: 20

Выставление оценок. 21

Заключительное слово преподавателя. 21

 

 

 

 

 

 

 

 

 

Пояснительная записка

 

Раздел «Тригонометрия», как известно, является одним из самых сложных. Поэтому для наибольшей доступности учебный курс построен в развивающем ключе, т.е. последующий материал строится на основе прошедшего.

После знакомства с основами тригонометрии: числовая окружность, определение тригонометрических функций, вывод основных тригонометрических тождеств, студентам предлагается перейти к детальному изучению формул тригонометрии: формулы сложения, формулы приведения и т.д. Причём параллельно с изучением новых формул студенты продолжают решать задачи на доказательство тригонометрических тождеств, на упрощение тригонометрических уравнений, но уже с участием этих новых формул.

Доказательство тождеств – это довольно трудный для студентов материал, а доказательство тригонометрических тождеств – вдвое трудней. Особенностью задач на доказательство тождеств является возможность их решения различными способами. Поэтому целесообразно было показать несколько вариантов (способов) доказательства тождеств, чтобы расширить возможности студентов при решении задач.

Много внимания уделено построению графиков тригонометрических функций, свойствам этих функций, а также формированию навыков работы с обратными тригонометрическими функциями.

Завершается раздел тригонометрии решением простейших тригонометрических уравнений и тригонометрических уравнений, сводящихся к квадратным.

Последнее занятие по разделу традиционно должно проходить в виде итоговой контрольной работы.

 

Данное занятие проводится как обобщающее, закрепляющее , расширяющее кругозор студентов итоговое занятие по курсу тригонометрии с последующей проверкой знаний и умений.

Для студентов подобные занятия обобщения являются уроками повторения не только предметных знаний и умений, но и способом актуализации средств мыслительной деятельности (анализ, сравнение, обобщение).

Т.к. данное занятие является обобщением не конкретной темы, а целого раздела, то совокупность задач подобрана таким образом, чтобы охватить все темы данного раздела.

Считаю, что такое итоговое занятие является более эффективным для студентов, чем проведение обычной контрольной работы по разделу, т.к. на занятии происходит обобщение, закрепление и повторение основных моментов с последующей контрольной проверкой знаний и умений, оценки за которую будут являться итоговыми по данному разделу.

 

 

Описание занятия, цели и задачи

 

Тема: Итоговое занятие по разделу «Основы тригонометрии».

Тип занятия: обобщающий, закрепляющий, контрольный.

Форма проведения занятия: беседа, решение задач, чтение докладов, чтение плакатов, итоговая проверочная работа по разделу тригонометрии.

Оборудование кабинета:

- плакаты с формулами, таблицами, графиками основных тригонометрических функций.

- высказывания о математике великих людей, крылатые выражения.

План занятия:

1. Вступительное слово учителя.

2. Чтение докладов по истории тригонометрии.

3. Решение 3-х основных задач по тригонометрии.

4. Краткий повтор свойств и графиков тригонометрических функций.

5. Доклад «Доказательство тригонометрических тождеств» с  приведением примеров.

6. Решение задачи для демонстрации межпредметной связи с  физикой.

7. Чтение учащимися высказываний о математике.

8. Контрольная проверка знаний и умений студентов по курсу тригонометрии.

9. Выставление оценок. Заключительное слово преподавателя.

Цели и задачи занятия:

Образовательные:

1. Повторить основные тригонометрические формулы, свойства и графики основных тригонометрических функций, формулы приведения и т.д.

2. Дать студентам дополнительные знания по истории тригонометрии, расширив таким образом познавательную сторону по данному разделу.

3. Обобщить способы доказательства тригонометрических тождеств, умение применять их на конкретных примерах.

4. Показать студентам межпредметную связь с другими дисциплинами на примере использования тригонометрии в колебательных процессах физики.

5. Закрепить навыки решения простейших тригонометрических уравнений и тригонометрических уравнений, сводящихся к квадратным.

6. Провести контроль студентов по курсу тригонометрии с последующей проверкой своих результатов.

Развивающие:

1. Развитие умения применять знания для решения задач различного рода, умения пользоваться формулами.

2. Развитие самоконтроля на уроке, когда студенты, выполнив контрольную работу, сами сравнивают свои результаты с готовыми ответами и выставляют себе оценки по соответствующей шкале.

Воспитательные:

1. Воспитание честности, умения реально оценивать свои знания

Вступительное слово преподавателя

 

Сегодняшнее занятие должно было бы проходить, как итоговая контрольная работа по разделу «Тригонометрия». Но вместо обычной контрольной работы проведём обобщающее, закрепляющее итоговое занятие по курсу тригонометрии с последующей проверкой ваших знаний и умений.

Тема: Итоговое занятие по разделу «Основы тригонометрии».

Цели и  задачи:

1. Повторить основные тригонометрические формулы, свойства и графики основных тригонометрических функций, формулы приведения и т.д.

2. Дать  дополнительные знания по истории тригонометрии, расширив таким образом познавательную сторону по данному разделу.

3. Обобщить способы доказательства тригонометрических тождеств, умение применять их на конкретных примерах.

4. Показать межпредметную связь с другими дисциплинами на примере использования тригонометрии в колебательных процессах физики.

5. Закрепить навыки решения простейших тригонометрических уравнений и тригонометрических уравнений, сводящихся к квадратным.

6. Провести контроль по курсу тригонометрии с последующей проверкой своих результатов.

План:  

1.  Вступительное слово учителя.

2.  Чтение докладов по истории тригонометрии.

3.  Решение 3-х основных задач по тригонометрии.

4.  Краткий повтор свойств и графиков тригонометрических функций.

5.  Доклад «Доказательство тригонометрических тождеств» с приведением примеров.

6.  Решение задачи для демонстрации межпредметной связи с физикой.

7.  Чтение учащимися высказываний о математике.

8.  Контрольная проверка знаний и умений учащихся по курсу тригонометрии.

9.  Выставление оценок. Заключительное слово преподавателя.

Мы прошли огромный раздел математики – тригонометрию, который включает в себя и преобразование тригонометрических выражений, и доказательство тригонометрических тождеств, и решение тригонометрических уравнений, и многое другое.

Мы записали основные тригонометрические формулы; узнали, что углы могут измеряться не только в градусной мере, но и в радианной; рассмотрели подробно каждую из 4-х основных тригонометрических функций, описали их свойства и построили графики; изучили формулы приведения; научились применять основные тригонометрические формулы для упрощения тригонометрических выражений и доказательства тригонометрических тождеств;а также научились решать различные тригонометрические уравнения.

Но мы упустили историю тригонометрии, которая начинается с 3 века до н.э.

Слово «тригонометрия»  искусственно составлено из двух греческих слов «тригонон» - треугольник и «метрезис» - измерение, то есть слово «тригонометрия» дословно означает измерение треугольников. Основная задача тригонометрии состоит в решении треугольников, то есть в вычислении неизвестных величин треугольника по данным значениям других его величин. Например, решение задачи о вычислении углов треугольника по данным его сторонам, или задачи вычисления сторон треугольника по его площади и углам и т.д. Так как любую вычислительную задачу геометрии можно свести к решению треугольников, то тригонометрия охватывает всю планиметрию и стереометрию, широко применяется во всех отделах естествознания и техники.

Стороны произвольного треугольника нельзя связать непосредственно с его углами с помощью алгебраических соотношений. Поэтому тригонометрия вводит в рассмотрение, кроме самих углов, ещё новые величины, тригонометрические величины, которые уже можно связать со сторонами треугольника простыми алгебраическими соотношениями.

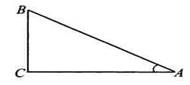sin A = BC/AB

cos A = AC/AB

tg A = BC/AC

ctg A = AC/BC

По данному углу можно вычислить соответствующее значение тригонометрической величины и обратно. Эти вычисления требуют долгих и утомительных расчетов, но эта работа уже проделана раз и навсегда и закреплена в таблицах.

Значения каждой тригонометрической величины меняется с изменением угла, а значит, тригонометрическая величина – есть функция от угла. Между различными тригонометрическими функциями существуют важные зависимости, их использование позволяет сокращать и облегчить вычисления.

Ознакомиться с историей тригонометрии, а также с некоторыми интересными фактами, связанными с тригонометрией, нам помогут доклады студентов, которые подготовили их заранее.

 

1.     «История развития тригонометрии»,

2.     «Названия тригонометрических функций»,

3.     «360 шагов за сутки»,

4.     «Современная тригонометрия и ее применение».

 

Хочу немного добавить, что потребность в решении треугольников раньше всего обнаружилась в астрономии, поэтому в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии. Значительных высот достигла тригонометрия у индийских средневековых астрономов, главным достижением которых стала замена хорд синусами, что позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.

Доклады по истории тригонометрии

 

«История развития тригонометрии»

 

Тригонометрия - слово греческое и в буквальном переводе означает измерение треугольников.

Слово «тригонометрия» впервые встречается в заглавии книги немецкого математика Питискуса в 1505 году, что обозначало науку об измерении треугольников. Хотя название возникло относительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны более двух тысяч лет назад.

Фактически различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в III веке до н.э. в работах великих математиков Древней Греции – Евклида, Архимеда, но тогда они не приобрели специального названия. 

Возникновение тригонометрии связано с землеизмерением, астрономией и строительным делом. Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом и Птолемеем во 2 веке н.э. Книга Птолемея "Альмагест", написанная в середине 2 в. и изданная в 16 веке на латинском и греческом языках, служила энциклопедией астрономических знаний свыше тысячи лет. Принципиальное значение имело составление Птолемеем первой таблицы синусов (долгое время она называлась таблицей хорд). Таким образом, появилось практическое средство решения ряда прикладных задач, и в первую очередь задач по астрономии.

Птолемей разработал так называемую геоцентрическую систему мира, согласно которой все наблюдаемые движения небесных светил объяснялись их движением (часто очень сложным) вокруг неподвижной Земли.
      Значительный вклад в развитие треугольников внес арабский ученый аль-Батани в 9-10 веках н.э. Он составил в конце IX - начале X в. первые таблицы синусов, он развил учение о тригонометрических функциях.

Теорему синусов уже в 13 веке знал азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Нассередин Туси в своей работе "Трактат о полном четырехугольнике" изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.
      Следующим ученым, чье имя связано с дальнейшим развитием тригонометрии, был немецкий математик XV века Региомонтан (настоящее имя его Иоганн Мюллер). В своем труде "Пять книг о различного рода треугольниках" он первым в Европе систематически изложил основы тригонометрии как самостоятельный раздел математики, первым дал формулу, выражающую сумму углов выпуклого многоугольника через число его сторон. В этой книге также впервые в Европе были рассмотрены задачи на максимум и минимум. Региомонтан доказал теорему тангенсов и составил также подробные тригонометрические таблицы. Благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе.

Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) - творца гелиоцентрической системы мира, Тихо Браге  (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета  (1540-1603), который полностью решил задачу об определении всех элементов плоского или сферического треугольника по трем данным.

Долгое время тригонометрия носила чисто геометрический характер. Факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. А наибольшие стимулы к развитию тригонометрии возникали в связи с решением задач астрономии, что представляло большой практический интерес (например, для решения задач определения местонахождения судна, предсказания затемнения и т. д.). Астрономов интересовали соотношения между сторонами и углами сферических треугольников. И надо заметить, что математики древности удачно справлялись с поставленными задачами. Постепенно тригонометрия органически вошла в математический анализ, механику, физику и технические дисциплины.

Начиная с XVII в., тригонометрические функции начали применять к решению уравнений задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т.д. Поэтому тригонометрические функции всесторонне и глубоко исследовались и приобрели важное значение для всей математики.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком  XVIII в. Леонардом Эйлером (1707-1783), членом Петербургской Академии наук. Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем применения формул тригонометрии, доказательства стали намного компактнее проще.

Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.

Позднее часть тригонометрии, которая изучая свойства тригонометрических функций и зависимости между ними, начали называть гониометрией (в переводе - наука об измерении углов). Термин гониометрия в последнее время мало употребляется. Изучение свойств тригонометрических функций и зависимостей между ними отнесено к курсу алгебры, а решение треугольников - к курсу геометрии.

 

«Названия тригонометрических функций»

Слово "синус" появилось в математике далеко не сразу. Этот термин имеет свою длительную (начиная с I-II вв.) и интересную историю.

Современный синус α, например, изучался как полухорда ( на индийском языке – джива), на которую опирается центральный угол величиной α, или как хорда удвоенной дуги. При переводе арабских математических текстов оно было заменено латинским синус (sinus – изгиб, кривизна).

Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XV веке немецким математиком, астрономом Регимонтаном (1467 г.). Он доказал теорему тангенсов.  Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе.

Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г.  Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности).

Термины "косинус" и "котангенс" были введены английским ученым Гюнтером в 1620 г. (Приставка "ко" означает "дополнение", от латинского complementum). «Косинус» означает «дополнительный синус».

«360 шагов за сутки»

 

Первые транспортиры возникли много тысяч лет назад. Предполагают, что это было связано с созданием первого календаря. Древние математики нарисовали круг и разделили его на столько частей, сколько дней в году. Но они думали, что в году не 365 или 366 дней, а 360 дней. Поэтому крег, обозначающий год, они разделили на 360 равных частей. Такое изображение было очень полезным, на нем можно было отмечать каждый прошедший день и видеть, сколько дней осталось до конца года.

Понятие градуса, как и появление первых инструментов для измерения углов, связывают с развитием цивилизации в древнем Вавилоне. Слово «градус» имеет латинское происхождение и означает в переводе «шаг», «ступень». Кроме градуса были введены такие единицы измерения как «минута» - 1/60 часть градуса и «секунда» - 1/60 часть минуты.
      По другой версии, вавилонские жрецы заметили, что солнечный диск укладывается по дневному пути Солнца 180 раз, т. е. "Солнце делает 180 шагов". Тогда путь за сутки равен "360 шагам". Круг стали делить на 360 частей, а 1/360 его часть называть градусом.

 

 

«Современная тригонометрия и ее применение»

 

Современный вид тригонометрии придал крупнейший математик 18 века Леонард Эйлер – швейцарец по происхождению, долгие годы работавший в России и являющийся членом Петербургской академии наук. Он ввел известные определения тригонометрических функций, сформулировал и доказал известные нам формулы приведения, выделил классы четных и нечетных функций. Эйлер ввел и само понятие функции и принятую в наши дни символику. Он придал всей тригонометрии ее современный вид. Функции sin x и cos x рассматривал как функции числа х – радианной меры соответствующего угла. Он ввел и обратные тригонометрические функции. Эйлер дал окончательное решение о знаках тригонометрических функций в разных четвертях, вывел все тригонометрические формулы из нескольких основных, ввел единообразное обозначения для тригонометрических функций.

Современные обозначения синуса и косинуса знаками sin и cos были впервые введены в 1739 г. швейцарским математиком И. Бернулли в письме к Л. Эйлеру, который и стал употреблять их в своих математических работах. Эйлер ввел также обозначения для функций угла х: tang x, cot x, sec x, cosec x.

До середины XIX в. большинство математиков, в том числе и великий Гаусс, квадрат синуса угла обозначали так: sinа². Французский математик Камбли издал ряд книг, где пользовался обозначением sin²а, которое прочно вошло в математическую литературу.

В 18-19 веках тригонометрия становится одной из глав математического анализа. Она находит большое применение в физике, технике, механике, особенно при изучении колебательных движений и других периодических процессов. Жан Фурье доказал, что всякое периодическое движение может быть представлено в виде суммы простых гармонических колебаний.

И. Бернулли применял символы тригонометрических функции. Из физики известно, что уравнение гармонического колебания (например, колебания маятника) имеет вид y=A*sin(wt+a). График гармонических колебаний называется синусоидой, поэтому в физике и технике гармонические колебания называю синусоидальными колебаниями.

Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца – это комплексно-алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.

Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалеких звезд в астрономии, между ориентирами в географии, контролировать системы навигации спутников.

Также тригонометрия применяется в музыке, акустике, оптике, анализе финансовых рынков, медицине, сейсмологии, метеорологии, картографии, топографии, архитектуре, машиностроении, экономике,компьютерной графике.

Краткий повтор свойств и графиков тригонометрических функций

 

Посмотрим на плакаты и вспомним свойства и графики тригонометрических функций.

По желанию вызываются учащиеся, чтобы прокомментировать плакаты со свойствами тригонометрических функций.

 

Решение задач на повторение

 

1.   Перевести величину угла из одной меры измерения в другую. Определить , какой координатной четверти принадлежит угол.

-60°;  150°;  3π/2;  -7π/4;  33π/5.

Вопросы:

- как перевести величину угла из градусной меры измерения в радианную;

- как перевести величину угла из радианной меры измерения в градусную;

- по какой мере измерения угла легче определить, какой координатной четверти принадлежит угол;

- как определить, в какой четверти лежит угол, если модуль его величины больше 360°.

 

2. Дано: sin α = - 8/17 ;  π<α<3π/2.

    Найти cos 2α;  tg α.

Вопросы:

- как определить знак тригонометрической функции;

- как найти значение ctg α по найденному значению tg α;

 

3.   Решить простейшее тригонометрическое уравнение:

2 sin α + √2 = 0.

Вопросы:

- к какому виду надо первоначально привести простейшее тригонометрическое уравнение;

- как определить, будет ли уравнение иметь решение, или нет;

- если выяснится, что уравнение имеет решение, какое будет количество решений;

- как найти множество решений для данного вида простейшего тригонометрического уравнения.

 

Доклад «Доказательство тригонометрических тождеств»

 

При доказательстве любых  тождеств,  и в частности  тригонометрических обычно  используют следующие способы:

1) выражение, стоящее в левой части равенства, с помощью тождественных преобразований приводят к выражению, стоящему в   правой   части равенства;

2) выражение, стоящее в правой части равенства, с помощью тождественных преобразований приводят к выражению, стоящему в   левой   части равенства;

3) выражения, стоящие в левой и  правой частях тождества, с помощью тождественных   преобразований   приводят  к одному и тому же виду;

4)  доказывают,  что разность между левой и правой частями данного тождества равна нулю;

5)   различные  специальные способы.

Поясним это на некоторых частных примерах.

Пример 1.   Доказать тождество

sin⁴α — cos⁴α  = sin² α  — cos² α .

Используя формулу для разности квадратов двух чисел, получаем:

sin⁴α — cos⁴α = (sin²α + cos²α) (sin²α — cos²α).

Ho sin²α  + cos²α  = 1.   

Поэтому  sin⁴α — cos⁴α = sin²α — cos²α, что и требовалось доказать.

 

Пример   2.   Доказать тождество

sin 2a = tg a (1+cos 2a)

Преобразуем правую часть тождества, используя основные тригонометрические тождества:

      tg a (1+cos 2a) =

                                                     =

      Тождество доказано.

 

Пример   3.   Доказать тождество

sin (+ α ) + cos ( π - α ) = cos ( 2π + α ) - 3sin (- α )

Преобразуем  левую  и правую части этого тождества, используя формулы приведения:

sin (+ α ) + cos ( π - α ) = — cos α — cos α  = — 2 cos α;

cos ( 2π + α ) - 3sin (- α ) = cos α — 3 cos α = — 2 cos α.

Итак, выражения, стоящие в обеих частях данного тождества, приведены к одному и тому же виду.

Тем самым тождество доказано.

 

Пример    4.    Доказать  тождество

sin⁴ α + cos⁴ α — 1 = — 2   sin²α cos²α.

Покажем, что разность между левой и правой частями. данного тождества  равна  нулю.   

Имеем:

 (sin⁴ α + cos⁴ α — 1) — (— 2   sin²α cos²α)  =

 (sin⁴ α + 2sin²α cos²α + cos⁴ α) — 1 = (sin²α  + cos²α)² — 1 = 1 — 1 = 0.

Тем самым тождество доказано.

 

Пример    5.   Доказать тождество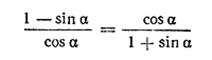

Это тождество   можно   рассматривать   как   пропорцию.   

Чтобы доказать справедливость    пропорции  , достаточно показать, что произведение ее крайних членов ad равно произведению ее средних членов bc.

Так мы поступим и в данном случае.

Покажем, что (1 — sin α) (1+ sin α) = cos α • cos α.

Действительно,   (1 — sin α)   (1 + sin α) = 1 —sin²α = cos²α.

Тем самым тождество доказано.

 

Межпредметная связь с физикой

 

В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Примерами простых колебательных систем могут служить груз на пружине или математический маятник.

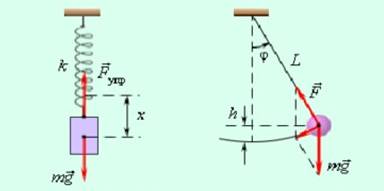
Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений, например: гармонические колебания, механические колебания.

Колебания, при которых изменения физических величин происходит по закону синуса или косинуса (гармоническому закону), называются гармоническими колебаниями.

Выражение, стоящее под знаком синуса или косинуса, называется фазой колебания.

В физике тригонометрия используется в темах: «Гармонические колебания и волны», «Переменный ток».

Задача:  Найти силу тока за время    t = 0,1 с , если частота  υ = 50 Гц , максимальное значение силы тока   I₀ = 0,5 А.

Общее уравнение гармонического колебания, т. е. любого колебательного движения или процесса, которое изменяется по синусоидальному закону, выглядит так:    x = x₀ ∙ sin (2πυt)

Это может быть и звук, и механическое движение, и ток, и напряжение.

 

 

Дано: t = 0,1 с. υ = 50 Гц I0 = 0,5 А	Решение: Сила тока подчиняется синусоидальному закону, т.е.  I = I 0 ∙ sin (2πυt) Подставляем исходные данные в эту формулу, получим: I = 0,5 ∙ sin (2π∙50∙0,1) = 0,5 ∙ sin (10π) =  = 0,5 ∙ sin (10π - 5∙2π) = 0,5 ∙ sin 0 = 0,5∙ 0 = 0. Вывод: через промежутки времени  t= 0,1 с. , начиная с начала отсчёта, сила тока будет равна нулю.
Найти:   I - ?

 

Высказывания о математике

 

·  В математических вопросах нельзя пренебрегать даже с самыми мелкими ошибками. (И. Ньютон)

·  Математика уступает свои крепости лишь сильным и смелым.

         (А.П. Конфорович)

·  Разве ты не заметил, что способный к математике изощрен во всех науках в природе? (Платон)

·  Вдохновение нужно в геометрии не меньше, чем в поэзии.

         (А.С. Пушкин)

·  В математике есть своя красота, как в живописи и поэзии.

         (Н.Е. Жуковский)

·  Математику уже затем учить надо, что она ум в порядок приводит.

(М.В. Ломоносов)

·  Математика - это язык, на котором говорят все точные науки.

(Н.И. Лобачевский)

·  Величие человека - в его способности мыслить. (Б. Паскаль)

·  Чтобы переварить знания, надо поглощать их с аппетитом. (А. Франц)

·  Известный польский математик Гуго Штейнгаус шутливо утверждает, что существует закон, который формулируется так: математик сделает это лучше. А именно, если поручить двум людям, один из которых математик, выполнение любой незнакомой им работы, то результат всегда будет следующим: математик сделает ее лучше.

·  Между духом и материей посредничает математика. (Хуго Штейнгаус)

·  Подобно тому как все искусства тяготеют к музыке, все науки стремятся к математике. (Джордж Сантаяна)

·  Математика может открыть определенную последовательность даже в хаосе. (Гертруда Стайн)

·  Закон 8/10/12 Восемь человек выполняют работу десяти человек лучше, чем двенадцать.

 

 

Итоговая контрольная работа по разделу «Основы тригонометрии»

1 вариант

 

1. Основное тригонометрическое тождество

    Выполняется при любых значениях a.

 

2. Упростить выражения:

    а) 1-cos²a = ___________________________________________________

 

    б) (1-sin a)(1+sin a) = __________________________________________

 

3. Следствием из основного тригонометрического тождества является формула, выражающая sin a через cos a:     sin a = _____________

 

4.                 Найти значение тригонометрической функции cos a, если известно,

что sin a =    и  0<a<

 

 

 

 

 

5. Тангенсом угла a называется отношение ______ угла a к _______ угла a      

                     tg a = __________

 

6. Из определения тангенса и котангенса следует:

                     tg a · ctg a = ___________

 

7. Формула  tg a =   не имеет смысла при  a = __________

 

8. Упростить выражения:

 

     а) tg a · cos a = ____________________________________________

   

     б)  = _________________________________________________

 

9. Доказать тождество:

     Sin² a - Sin² a · cos² a = Sin⁴ a

 

 

 

 

10. Упростить выражение:

 

        -  = __________________________________________

 

11.   Расставить знаки тригонометрических функций:

     знаки синуса                                    знаки тангенса

 

12.   Определить четность (нечётность) тригонометрических функций:

       sin (-x) = ____________

       cos (-x) = ____________

       tg (-x) = ____________

Вывод: чётной функцией является функция ___________

 

13.   Найти значение выражений:

             sin (-90˚) = ____________

             cos (-60˚) = ____________

             tg (-45˚) = ____________

 

14.   Упростить или вычислить, применяя формулы приведения:

            sin () = ___________

            cos 135⁰ = ______________________________________________

 

            ctg (2π – α) = ___________

 

            tg 240⁰ = _______________________________________________

 

15.   Вычислить:

             arcsin (-) = _________________________________________

            -6 arcctg (-) = _________________________________________

 

16. Решить уравнение:    2 sin x  -  1  =  0

 

 

 

Итоговая контрольная работа по разделу «Основы тригонометрии»

2 вариант

 

1. Основное тригонометрическое тождество

    Выполняется при любых значениях a.

 

2. Упростить выражения:

    а) sin²a -1 = _________________________________________________

 

    б) (1-cos a)(1+cos a) = _________________________________________

 

3. Следствием из основного тригонометрического тождества является формула, выражающая cos a через sin a     cos a = _____________

 

4.                 Найти значение тригонометрической функции sin a, если известно,

    что cos a =    и  0<a<

 

 

 

 

 

5. Котангенсом угла a называется отношение ________ угла a к ______ угла a      

                     сtg a = __________

 

6. Из определения тангенса и котангенса следует:

                     tg a · ______= 1

 

7. Формула  сtg a =   не имеет смысла при  a = __________

 

8. Упростить выражения:

   

     а) sin a · ctg a =______________________________________________

   

     б)  + 1 = ________________________________________________

 

9. Доказать тождество:

     cos² a - cos² a · sin² a = cos⁴ a

 

 

 

 

10. Упростить выражение:

 

        -  = ___________________________________________  

 

11. Расставить знаки тригонометрических функций:

     знаки косинуса                                    знаки котангенса

 

12. Определить четность (нечётность) тригонометрических функций:

      sin (-x) = ____________

      cos (-x) = ____________

      ctg (-x) = ____________

Вывод: чётной функцией является функция ___________

 

13. Найти значение выражений:

      sin (-45˚) = ____________

      cos (-90˚) = ____________

      ctg (-30˚) = ____________

 

14. Упростить или вычислить, применяя формулы приведения:

      cos () = ___________

      sin 330⁰ = ______________________________________________

     

      tg (2π – α) = ___________

     

      ctg 120⁰ = _______________________________________________

 

15. Вычислить:

         arccos (-) = _________________________________________

       - arctg (-1) = _________________________________________

 

16. Решить уравнение:    2 cos x  -    =  0

 

 

Ответы к контрольной работе

 

1 вариант 1. sin2a + cos2a = 1 2. a) sin2a     б) cos2a 3. 4.   cos a = 12/13 5.  tg a = 6.  tg a • ctg a = 1 7. при  а = π/2 + πn, nєZ 8. а) sin a     б) cos a 10.  -2 tg a 11.  Знаки синуса    +    +                                   -     -        Знаки тангенса    -     +                                      +    - 12. sin (-x) = - sin x       cos (-x) = cos x       tg (-x) = - tg x   13. sin (-90˚) = -1       cos (-60˚) = ½       tg (-45˚) = -1   14.  sin (π/2 + α) = cos α        cos 135˚ = -√2/2        ctg (2π – α) = - ctg α        tg 240˚ = √3   15.  a) –π/9       б) -5π     16.  х = (-1)ⁿ ∙ π/6 + πn, nєZ

2 вариант 1. sin2a + cos2a = 1 2. a) - cos2a     б) sin2a 3. cos a = ± √1 – sin2a   4.   sin a = 15/17 5.  ctg a = 6.  tg a • ctg a = 1 7. при  а = 0 + πn, nєZ 8. а) cos a     б) 10.  -2 сtg a 11.  Знаки косинуса   -      +                                      -      +        Знаки котангенса    -     +                                          +     - 12  cos (-x) = cos x       sin (-x) = - sin x       сtg (-x) = - сtg x   13. cos (-90˚) = 0       sin (-45˚) = -√2/2       ctg (-30˚) = -√3   14.  cos (π/2 + α) = - sin α        sin 330˚ = -½        tg (2π – α) = - tg α        ctg 120˚ = - 15.  a)  5π/14      б) π/10   16.  х = ± π/4 + 2πn, nєZ

 

Градация оценок:

 

15-16  заданий  – «5»

12-14  заданий  – «4»

8-11    заданий  – «3»

1-7      заданий  - «2»

 

Выставление оценок

 

После выполнения итоговой контрольной работы по курсу тригонометрии, студенты сравнивают свои ответы с правильными ответами и решениями, заранее записанными на обратной стороне доски. Если их решение правильное и совпадает с ответом на доске, студент ставит «+», если нет – знак « - ››. Далее студент считает количество «+» и по шкале оценок ставит сам себе оценку.

Во время проверки студентами своих работ преподаватель выставляет оценки в журнал за работу на уроке тем студентам, которые принимали непосредственное участие при проведении занятия, т.е. решали задачи, читали доклады, правильно комментировали плакаты со свойствами функций, а также тем, кто правильно отвечал на вопросы преподавателя, задаваемые по ходу занятия.

После проверки студентами своих работ преподаватель выставляет оценки за итоговую контрольную работу, которые являются итоговыми оценками по разделу тригонометрии.

Цели занятия достигнуты. Студенты не только решили итоговую контрольную работу по разделу тригонометрии, но и в полном объёме повторили основные задачи по данному разделу, а также ознакомились с историей тригонометрии и высказываниями великих людей о математике.

 

Заключительное слово преподавателя

 

Многие задаются вопросами: зачем нужна тригонометрия? Как она используется в нашем мире? И вот ответы на эти вопросы. Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов), когда требуется сферическая тригонометрия,  в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятности, в статистике, в биологии, в медицинской визуализации ,например, компьютерной томографии и ультразвук, в аптеках, в химии, в теории чисел, в сейсмологии, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях.

Уже в древности тригонометрия использовалась для:

· точного определения времени суток;

· вычисления будущего расположения небесных светил, моментов их восхода и заката, затмений Солнца и Луны;

· нахождения географических координат текущего места;

· вычисления расстояния между городами с известными географическими координатами.

Часто с синусами и косинусами приходится сталкиваться геодезистам. Они имеют специальные инструменты для точного измерения углов. При помощи синусов и косинусов углы можно превратить в длины или координаты расстояния между точками на земной поверхности.

Широко используется тригонометрия в строительстве, а особенно в архитектуре. Большинство композиционных решений и построений рисунков проходило именно с помощью геометрии. Но теоретические данные мало что значат. Хочу привести пример на построение одной скульптуры французского мастера Золотого века искусства. Пропорциональное соотношение в построении статуи было идеально. Однако при поднятии статуи на высокий пьедестал, она смотрелась уродливой. Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности. Поэтому велось множество расчетов, чтобы фигура на большой высоте смотрелась пропорционально.

Даже в медицине применяется тригонометрия. Медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии. Как утверждают медики,  формула сердца, о которой шла речь в докладе, в значительной степени облегчает процесс описания основных параметров деятельности сердца, ускоряя, тем самым, постановку диагноза и начало собственно лечения.

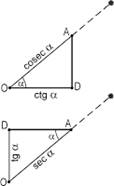
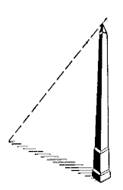           Гномон — древнейший астрономический инструмент, вертикальный предмет (стела, колонна, шест), позволяющий по наименьшей длине его тени (в полдень) определить угловую высоту солнца. Так, под котангенсом понималась длина тени от вертикального гномона; первоначально эти понятия использовались для расчёта солнечных часов. Тангенсом называлась тень от горизонтального гномона. Косекансом и секансом назывались гипотенузы соответствующих прямоугольных треугольников (отрезки AO).

Мы привели лишь малую часть того, где можно встретить тригонометрические функции.. Мы выяснили, что тригонометрия была вызвана к жизни необходимостью производить измерения углов, но со временем развилась и в науку о тригонометрических функциях.

Мы доказали, что тригонометрия тесно связана с физикой, встречается в природе, медицине. Можно приводить бесконечно много примеров периодических процессов живой и неживой природы. Все периодические процессы можно описать с помощью тригонометрических функций и изобразить на графиках.

Мы думаем, что тригонометрия нашла отражение в нашей жизни, и сферы, в которых она играет важную роль, будут расширяться.

Скачано с www.znanio.ru