Методическая разработка по теме: "Предел функции"

Урок по теме "Предел функции"

Цели урока:

• Образовательные:
• ввести понятие предела числа, предела функции;
• дать понятия о видах неопределенности;
• научиться вычислять пределы функции;
• систематизировать полученные знания, активизировать самоконтроль, взаимоконтроль.
• Развивающие:
• уметь применять полученные знания для вычисления пределов.
• развивать  математическое мышление.
• Воспитательная: воспитать интерес к математике и к дисциплинам умственного труда.

Формы работы учащихся:  фронтальная, индивидуальная

Необходимое оборудование:  интерактивная доска, мультимедиа проектор, карточки с устными и подготовительными упражнениями.

План урока

1. Организационный момент (3 мин.)
2. Ознакомление с теорией предела функции. Подготовительные упражнения. (12 мин.)
3. Вычисление пределов функции (10 мин.)
4. Самостоятельные упражнения (15 мин.)
5. Подведение итогов урока (2 мин.)
6. Домашнее задание (3 мин.)

ХОД УРОКА

1. Организационный момент

Приветствие учителя, отметить отсутствующих, проверить подготовку к уроку. Сообщить тему и цель урока. В дальнейшем все задания выводятся на интерактивную доску.

2. Ознакомление с теорией предела функции. Подготовительные упражнения.

Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Записывается предел следующим образом  .

Вычислим предел: 
Подставляем вместо х – 3.
Заметим, что предел числа равен самому числу.

Примеры: вычислите пределы 

Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной (в данной точке).

Вычислим значение функции в точке x₀ = 3 и значение его предела в этой точке.

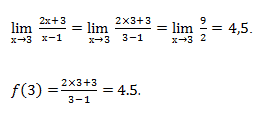
Значение предела и значение функции в этой точке совпадает, следовательно, функция непрерывна в точке x₀ = 3.

Но при вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.

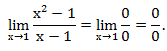
Основные виды неопределенностей: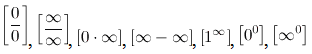  

Раскрытие неопределенностей

Для раскрытия неопределенностей используют следующее:

• упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;
• если предел при раскрытии неопределенностей существует, то говорят, что функция сходится к указанному значению, если такого предела не существует, то говорят, что функция расходится.

Пример: вычислим предел.
Разложим числитель на множители 

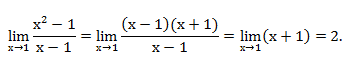
3. Вычисление пределов функции

 Пример 1. Вычислите предел функции: 

При прямой подстановке, получается неопределенность:

Разложим на множители числитель и знаменатель и вычислим предел.

Пример 2. Вычислите предел функции: 

При прямой подстановке, получается неопределенность.

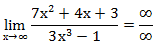
Помножим и числитель,  и знаменатель на .

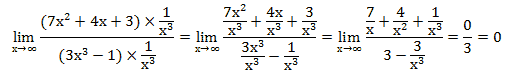
Учтем, что если число разделить на бесконечно большое число получится ноль. То есть предел Аналогично  

Пример 3. Вычислите предел функции: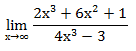 

При прямой подстановке, получается неопределенность.

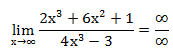
Помножим и числитель,  и знаменатель на .

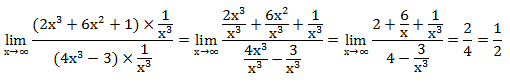
Мы учли, что 

4. Самостоятельные упражнения

Вычислите пределы:

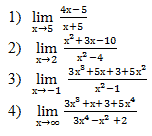
5. Подведение итогов урока

Данный урок первый  по теме: «Предел функции». На уроке рассмотрены способы нахождения пределов. Разобрано что такое неопределенность, как раскрывать неопределенности. Надо заметить, что есть пределы, для которых невозможно найти числовое значение.

6. Домашнее задание

Домашнее задание раздается на карточках каждому ученику.

Скачано с www.znanio.ru