МЕТОДИЧЕСКАЯ РАЗРАБОТКА ПРАКТИЧЕСКОГО ЗАНЯТИЯ НА ТЕМУ «РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ РАЗЛИЧНЫМИ МЕТОДАМИ»

 

 

 

 

 

 

 

 

 

 

 

МЕТОДИЧЕСКАЯ РАЗРАБОТКА ПРАКТИЧЕСКОГО ЗАНЯТИЯ

ПО ДИСЦИПЛИНЕ: ЕН.01 ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ

 

НА ТЕМУ «РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ РАЗЛИЧНЫМИ МЕТОДАМИ»

 

 

 

 

 

 

                                                                                     Разработчик:

преподаватель

Токарева О.П.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Методическая разработка практического занятия разработана на основе рабочей программы учебной дисциплины ЕН.01 Элементы высшей математики, в соответствии с ФГОС СПО специальности 09.02.07.

 

В разработке представлена методика проведения практического занятия с использованием мультимедийных технологий и компьютерной техники, направленной на активизацию мыслительной деятельности студентов и отработки навыков самостоятельной работы.

 

 

 

Разработчик:

 

Токарева О.П. – преподаватель первой категории ГБПОУ «Торезский индустриальный техникум им. А.Ф.Засядько»

 

 

 

Рассмотрено и одобрено на заседании цикловой комиссии общеобразовательных дисциплин (протокол № ____от  ________________)

 

 

 

 

 

ВВЕДЕНИЕ

 

Данная методическая разработка составлена в соответствии с рабочей программой по дисциплине ЕН.01 Элементы высшей математики.

Рабочая программа учебной дисциплины является обязательной частью образовательной программы среднего профессионального образования - программы подготовки специалистов среднего звена по специальности СПО 09.02.07 Информационные системы и программирование.

Рабочая программа разработана в соответствии с Федеральным государственным образовательным стандартом среднего профессионального образования по специальности 09.02.07 Информационные системы и программирование (утв. приказом Министерства образования и науки РФ от 9 декабря 2016 г. N 1547) с изменениями и дополнениями от 17 декабря 2020 г., 1 сентября 2022 г. и с учетом примерной основной образовательной программы по специальности СПО 09.02.07 «Информационные системы и программирование».

Данная тема занимает важное место в курсе высшей математики, так как тесно связана с темами «Матрицы и определители», «Решение систем линейных уравнений». Прежде, чем перейти непосредственно к решению систем линейных уравнений, обучающиеся знакомятся с такими понятиями как матрицы, определитель матрицы, обратная матрица, ранг матрицы. К моменту решения систем уравнений они уже знают матричный способ решения систем уравнений, метод Гаусса и знакомы с формулами Крамера.

 

Дисциплина: ЕН.01 Элементы высшей математики

 

Тема: «Решение систем линейных уравнений различными методами»

 

Вид занятия: практическое занятие.

 

Тип практического занятия: применение знаний и формирование умений.

 

Цели занятия

Методическая:

совершенствовать методику проведения практического занятия с использованием нестандартных форм и методов обучения, создать условия для формирования более полных и стойких знаний, умений и навыков обучающихся по дисциплине, для всестороннего развития их творческих способностей.

Образовательная:

повторить, обобщить и систематизировать теоретические знания, способы решения систем линейных уравнений различными методами; сформировать представление о структуре заданий по основным понятиям и методам линейной алгебры на экзамене, а также об уровне их сложности.

Развивающая:

способствовать формированию скорости мышления, развивать навыки самостоятельной работы, развивать умение правильно давать ответы на поставленные вопросы.

Воспитательная:

- воспитать познавательный интерес к дисциплине, творческие способности студентов; повышать общую культуру обучающихся.

 

Технические средства обучения: компьютеры, ноутбук, мультимедийный проектор, экран.

 

Методы и формы проведения занятия: работа в малых группах, метод презентации, работа с опорными конспектами, ролевая игра, работа за компьютерами.

 

Используемые технологии:

- ИКТ (мультимедийная презентация);

- элементы ролевой игры.

Междисциплинарные связи:

- обеспечивающие: Математика;

- обеспечиваемые: ЕН.02 Дискретная математика с элементами математической логики, ЕН.03 Теория вероятностей и математическая статистика, ОП.04 Основы алгоритмизации и программирования, ОП.10 Численные методы, МДК.02.03. Математическое моделирование.

 

Методическое обеспечение занятия:

-       рабочая программа дисциплины ЕН.01 Элементы высшей математики,

-       методическая разработка занятия,

-       карточки с заданиями;

-       мультимедийная презентация;

-       инструкция к практическому занятию.

 

Продолжительность занятия: 80 минут.

 

Основная литература:

1.     Шнарева, Г. В. Элементы высшей математики: учебник для СПО / Г. В. Шнарева. — Саратов, Москва: Профобразование, Ай Пи Ар Медиа, 2023. — 171 c. 

 

Дополнительная литература:

1.     Ельчанинова Г. Г. Элементы высшей математики. Типовые задания с примерами решений : учебное пособие / Г. Г. Ельчанинова, Р. А. Мельников. — Санкт-Петербург : Лань, 2020. — 92 с.

2.     Григорьев В.П. Элементы высшей математики: учебное издание / Григорьев В.П., Дубинский Ю.А, Сабурова Т.Н. - Москва : Академия, 2023. - 400 c. (Специальности среднего профессионального образования). - URL: https://academia-moscow.ru - Режим доступа: Электронная библиотека «Academia-moscow». - Текст : электронный.

 

Открытые электронные ресурсы:

1        Калькулятор матриц https://programforyou.ru/calculators/calculator-matric

2        Матричный калькулятор https://ru.onlinemschool.com/math/assistance/matrix/

3        Матричный калькулятор https://matrixcalc.org/ru/?ysclid=m1l3w3dfgs95398591

 

Ход занятия

 

1. Организационный момент

1.1 Взаимное приветствие студентов и преподавателя;

1.2 Проверка присутствия студентов;

1.3 Проверка готовности аудитории к занятию;

1.4 Организация внимания.

 

1.5.          Вступительное слово преподавателя.

Преподаватель озвучивает тему и цели занятия с демонстрацией их на слайдах № 1 и № 2 презентации.

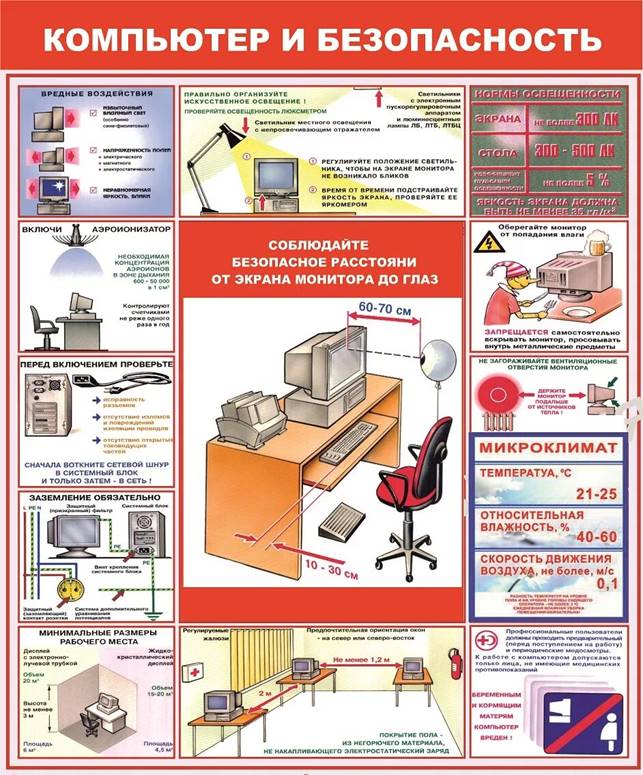
Поскольку, занятие проходит в лаборатории компьютерное техники, необходимо вспомнить правила Техники безопасности. (Приложение 1, слайд 3)

 

2.     Мотивация учебной деятельности студентов

Ребята, сегодня мы с вами погрузимся в мир линейной алгебры, а именно, в решение систем линейных уравнений. Зачем это нужно? Давайте разберемся!

Системы линейных уравнений встречаются в самых различных сферах: от экономики до инженерии, от физики до биологии. Например, при расчете оптимального бюджета на проект, при моделировании физических процессов. Системы линейных уравнений часто встречаются в задачах оптимизации, таких как линейное программирование, где необходимо найти оптимальные решения в условиях ограничений. В компьютерной графике системы линейных уравнений используются для трансформации объектов и решения задач интерполяции.

Понимание, как решать такие системы, поможет вам в будущей профессиональной деятельности.

На занятии мы будем использовать как компьютерные программы, такие как Excel, MathCAD, так и будем использовать открытые электронные ресурсы - Матричные калькуляторы. Это не только упростит процесс решения уравнений, но и позволит вам познакомиться с инструментами, которые широко используются в научных и профессиональных кругах. Умение работать с такими программами станет вашим конкурентным преимуществом на рынке труда.

 

3.     Актуализация опорных знаний студентов

3.1 Давайте вспомним основные понятия линейной алгебры и решим с вами кроссворд (слайд 4).

3.2  Блиц-опрос.

1. Какие способы решения систем линейных уравнений вам известны?

2. Какое равенство называют матричным уравнением?

3. По какой схеме нужно решать матричное уравнение?

4. Сформулируйте теорему Крамера.

5. Назовите формулы Крамера.

6. В чем заключается метод последовательного исключения неизвестных?

7. Какие преобразования используют при выполнении прямого хода?

 

4.     Выполнение практического задания

4.1. Работа с опорным конспектом (приложение 2).

4.2 Выполнение практического задания за компьютером

Студенты работают парами согласно выданного задания.

 

4.2.1 Примеры решения практического задания в MS Excel

 

Пример 1. Решить систему методом обратной матрицы: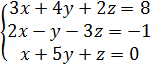

Идея решение СЛАУ методом обратной матрицы заключается в следующем.

Заданную систему записывают в матричной форме Ax=b, где A – матрица коэффициентов СЛАУ при неизвестных, b – вектор правых частей, x – вектор неизвестных, который вычисляют по формуле 

x=A^-1∙b, причем A^-1– это матрица обратная к A. Реализовать эту идею в MS Excel можно следующим образом. Введём матрицу A и вектор b в рабочий лист MS Excel (Рис. 1). Пусть матрицаА находится в ячейках B1:D3, а вектор b в диапазоне F1:F3. Выделим ячейки для хранения обратной матрицы, пусть это будут ячейки B5:D7.

 

 

 

 

 

 

 

 

 

 

 

 

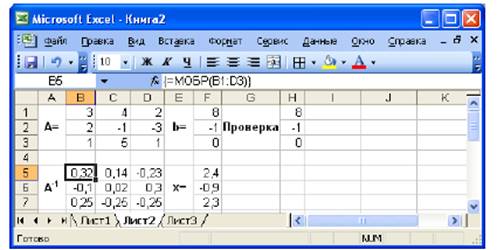
Рис. 1. Решение СЛАУ методом обратной матрицы

 

         Обратимся  к  Мастеру  функций,  и  в  категории  Математические  выберем функцию МОБР, предназначенную для вычисления обратной матрицы. В качестве аргумента этой функции укажем диапазон ячеек, в котором хранится матрица  A, т.е. МОБР(B1:D3).Теперь умножим полученную обратную матрицу на вектор b. Выделим ячейки для хранения результирующего вектора, например F5:F7.

         Обратимся к Мастеру функций, и в категории Математические выберем функцию МУМНОЖ, которая предназначена для умножения матриц. У этой функции два аргумента – диапазоны перемножаемых матриц. Введем в качестве первого аргумента диапазон ячеек, в котором содержится обратная матрица, а в качестве второго  –  ячейки,  содержащие  вектор  b,  т.е.  МУМНОЖ(B5:D7;F1:F3).Вектор неизвестных хранится в ячейках F5:F7. Для того чтобы проверить, правильно ли решена система уравнений, необходимо умножить матрицу A на вектор x и получить в результате вектор b. Умножение матрицы A на вектор x осуществляется при помощи функции МУМНОЖ(B1:D3; F5:F7).

 

Пример 2.Решить систему методом Крамера.

         В этом случае неизвестные x₁,x₂,…, x_n вычисляются по формуле:

где ∆– определитель матрицы A, ∆_i – определитель матрицы, получаемой из матрицы А путем замены i-го столбца вектором b.

 

 

 

 

 

 

 

 

 

 

 

 

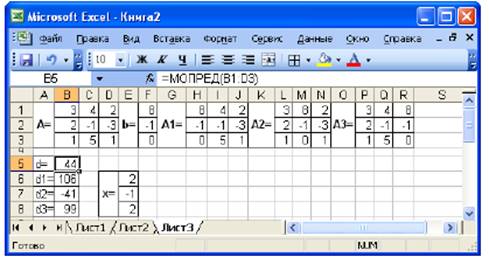
Рис. 2. Решение СЛАУ по формулам Крамера

        

Введём  матрицу  А  и  вектор  b  в  рабочий  лист.  Сформируем  три  вспомогательные матрицы, заменяя последовательно столбцы матрицы A на вектор b (Рис. 2). Вычислим определитель матрицы A. Установим курсор в ячейку B5 и обратимся  к  мастеру  функций.  В категории  Математические  выберем  функцию МОПРЕД, предназначенную для  вычисления определителя матрицы. В качестве аргумента зададим диапазон ячеек, в котором хранится матрица A:  МОПРЕД(B1:D5).

         Для вычисления вспомогательных определителей введем формулы:

B6=МОПРЕД(H1:J3), B7=МОПРЕД(L1:N3), B8=МОПРЕД(P1:R3).

         В результате в ячейке B5 хранится главный определитель, а в ячейках B6:B8 –  вспомогательные.  Проведем  вычисление  по  формулам  Крамера.  В  ячейку  Е6 введём формулу = Е6/$B$5. Затем скопируем её содержимое в ячейки Е7 и Е8. Система решена.

 

4.2.2 Примеры решения практического задания в Mathcad

Пример 1. Решить систему линейных уравнений методом обратной матрицы

 

 

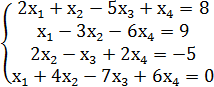
Решение показано на рис.2.

 

 

Рис. 3. Решение СЛАУ методом обратной матрицы

 

Пример 2. Решить систему линейных уравнений по формулам Крамера.

 

 

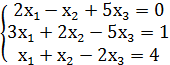
На рис. 4 приведен фрагмент рабочего документа, содержащий решение поставленной задачи.

Рис. 4. Решение СЛАУ по формулам Крамера

 

 

4.2.3 Примеры решения практического задания с помощью матричного онлайн-калькулятора https://ru.onlinemschool.com/math/assistance/equation/matr/

 

Пример 1. Решить систему линейных уравнений методом обратной матрицы

 

 

 

 

 

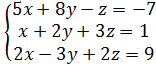
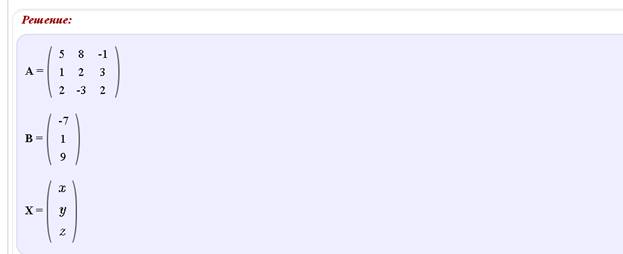
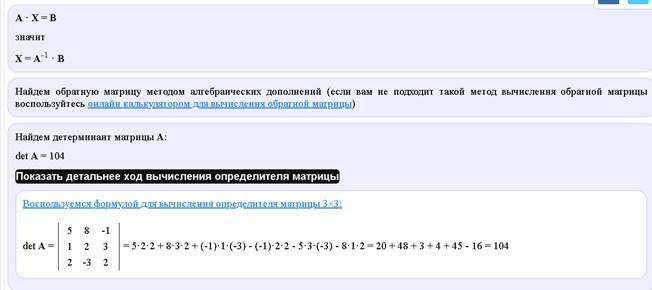
Пример 2. Решить систему линейных уравнений по формулам Крамера.

 

 

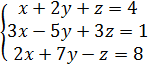
         Решения практического задания с помощью матричного онлайн-калькулятора https://ru.onlinemschool.com/math/assistance/equation/kramer/

 

 

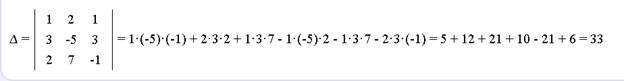
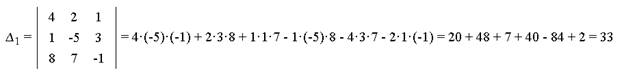
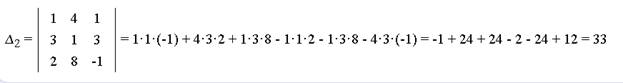
4.3        Проверка результатов практической работы студентов

Результаты выполненной работы представляет каждая группа отдельно. Студенты проговаривают озвучивают какой метод использовался, какие возникли трудности при решении заданий, называют преимущества и недостатки каждого метода и каждого программного средства, которое было применено в практической работе.

 

4.4 Подведение итогов занятия

Анализ работы студентов на занятии, их подготовки. Комментируются и выставляются отметки за устную заботу и по результатам выполнения работы за компьютером.

Преподаватель проводит рефлексию по принципу незаконченного предложения. Обучающимся предлагается устно закончить следующие предложения:

· На сегодняшнем занятии я понял, я узнал, я разобрался…

· Особенно мне понравилось…

· После занятия мне захотелось…

· Сегодня мне удалось…

· Было интересно…

· Было трудно…

· Я понял, что…

· Теперь я могу…

· Я научился…

· У меня получилось…

 

4.5 Домашнее задание

Преподаватель предлагает выполнить решение системы линейных уравнений методом Гаусса с помощью матричного онлайн-калькулятора.

 

 

ЛИТЕРАТУРА

1.     Элементы высшей математики: учеб. пособие [Электронный ресурс] / авт.-сост. М.Ф. Петянкин; под общ. ред. проф. М. И. Ломшина. – Саранск: Изд-во Мордов. ун-та, 2019. – 2.86 Мб.

2.     Лисичкин В.Т., Соловейчик И.Л. Математика в задачах с решениями: Учебное пособие. – 5-е изд. – СПб.: Издательство «Лань», 2014. – 464 с.

3.     Краткий курс высшей математики: Учебник / Под общ. Ред. К.В. Балдина. – 2-е изд. – М.: Издательско-торговая корпорация «Дашков и Кº», 2015. – 510 с.

4.     Баврин И.И. Теория вероятностей и математическая статистика: Учебник/И.И. Баврин. – М.: Высш.шк., 2005. – 160 с.

5.     Богомолов Н.В. Сборник задач по математике: учеб. пособие – М.: Дрофа, 2009. – 204 с.

6.     Богомолов, Н.В. Практические занятия по математике: Учеб. пособие / Н.В. Богомолов – М: «Высшая школа», 2003 - 495 с.

7.     Григорьев, В.П. Элементы высшей математики: учебник для студ. учреждений сред. проф. образования / В.П. Григорьев, Ю.А. Дубинский. – М: Издательский центр «Академия», 2014.- 320 с.

 

Приложение 1

 

Приложение 2

Задание 1.

 

 

 

 

 

 

Приложение 3

КРОССВОРД

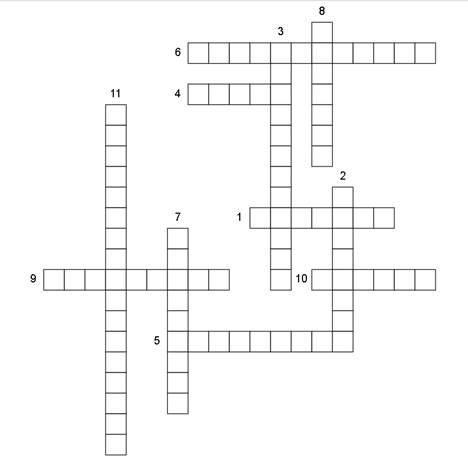
1.     Часть матрицы, находящаяся в вертикальном положении

2.     Если умножить матрицу на неё, то получится единичная матрица

3.     Одно из основных понятий линейной алгебры

4.     Определитель, который получается вычёркиванием строки и столбца.

5.     Матрица, при умножении на которую любая матрица остаётся неизменной

6.     Квадратная матрица, все элементы которой кроме диагональных-нулевые

7.     Операция вычисления матрицы, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго

8.     Математический объект, записываемый в виде прямоугольной таблицы элементов

9.     Что означает это действие c=a-b

10. Часть матрицы, находящаяся в горизонтальном положении

11. Матрица, полученная из исходной матрицы с заменой строк на столбцы

 

 

Скачано с www.znanio.ru