МЕТОДИЧЕСКАЯ РАЗРАБОТКА ПРАКТИЧЕСКОГО ЗАНЯТИЯ

 

По дисциплине: МАТЕМАТИКА

 

Раздел: Функции их свойства и графики Тема: «ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ ФУНКЦИИ»

Специальность: 35.02.16 Эксплуатация и ремонт сельскохозяйственной техники и оборудования Курс: 1 (базовой подготовки)

 

 

Автор – составитель: преподаватель математики высшей категории Утева Л.П.

 

Пояснительная записка

к методической разработке дисциплины «Математика» раздел: Функции их свойства и графики, тема «Показательные и логарифмические функции». Методическое пособие разработано для преподавателей и студентов с целью формирования знаний, умений по теме: «Показательные и логарифмические функции». В процессе практического занятия студенты закрепляют полученные знания:  определения функций, их свойства и графики, преобразования графиков, непрерывные и периодические функции, обратные функции и их графики, показательные, логарифмические функции.

В ходе занятия используются элементы групповой работы, личностно-ориентированной технологий, здоровья сберегающей технологии.

Методическая разработка составлена в соответствии с Федеральными государственными требованиями к минимуму содержания и уровню подготовки студента в рамках специальности 35.02.16 «Эксплуатация и ремонт сельскохозяйственной техники и оборудования. Освоение содержания учебной дисциплины «Математика», обеспечивает достижение студентами следующих результатов: личностных:

•                     развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования; 

•                     овладение    математическими    знаниями    и    умениями, необходимыми в повседневной жизни, для освоения смежных естественнонаучных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки; •  готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности; 

•                     готовность и способность к самостоятельной, творческой и ответственной деятельности;  метапредметных: 

•      умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;  

•      владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;  

•      готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;  предметных: 

•                     сформированность представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий; 

•                     владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач; 

Характернстика основных видов деятельности студентов (на уровне учебных действий):

-  Вычислять значения функции по значению аргумента.            

-  Определять положение точки на  графике  по  ее координатам и наоборот.

-  Использовать свойства      функций для сравнения значений степеней и логарифмов.

-  Строить графики логарифмических функций.

-  Выполнять преобразование графиков.

 

УЧЕБНО – МЕТОДИЧЕСКИЙ ПЛАН ЗАНЯТИЯ

Тема занятия: «Показательные и логарифмические функции»

Вид занятия: практическое занятие

Место проведения: кабинет математики

Продолжительность проведения занятия: 90 минут Цели занятия:

1.                  Образовательная: После изучения темы студент должен знать определения функций, их свойства и графики, преобразования графиков, непрерывные и периодические функции, обратные функции и их графики, показательные, логарифмические функции и  уметь вычислять значения функции по значению аргумента, определять положение точки на  графике  по  ее координатам и наоборот, использовать свойства функций для сравнения значений степеней и логарифмов, строить графики логарифмических функций, выполнять преобразование графиков.

2.                  Воспитательная: Формирование сознательного отношения к процессу обучения, стремления к самостоятельной работе и всестороннему овладению специальностью.

3.                  Развивающая:  Развитие интереса к учебному предмету, содействие активизации мышления обучающихся. Повышение интеллектуального уровня в процессе изучения математических понятий в ходе работы с различными источниками информации; Совершенствовать способности организовывать сотрудничество единомышленников, том числе с использованием современных информационно-коммуникационных технологий.

Требования ГОС к уровню подготовки студента студент должен: 

Студент  должен  уметь:

-  Вычислять значения функции по значению аргумента             

-  Определять положение точки на  графике  по  ее координатам и наоборот

-  Использовать свойства      функций для сравнения значений степеней и логарифмов

-  Строить графики логарифмических функций

-  Выполнять преобразование графиков;

Студент должен  использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

-  практических расчетов по формулам, включая формулы, содержащие степени, радикалы, используя при необходимости справочные материалы и простейшие вычислительные устройства.

Методы обучения: Информационно-развивающий, репродуктивный

Материально-техническое обеспечение занятия: Ноутбук, проектор, экран.

Методическое обеспечение занятий: учебники, электронная презентация, вопросы входного контроля, задачи и тесты.

 

 

 

Рекомендуемая литература:

1.    Алимов Ш. А., Колягин Ю. М., Сидоров Ю. В., Фёдорова Н. Е., Шабунин М. И. под научным руководством академика Тихонова А. Н. Алгебра и начала математического анализа 10 - 11кл. – М. Просвещение, 2011.

2.    Никольский С. М., Потапов М. К., Решетников Н. Н. и др. Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл. – М., 2006.

3.    Колягин Ю.М., Ткачева М.В, Федерова Н.Е. и др. под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл. – М., 2005. 4. Ю.А. Глазков, И.К. Варшавский Тематические тесты алгебра 10 класс Издательство: М.: Центр тестирования МО РФ ISBN: 5-94635-048-Х, 2001.

Интернет-ресурсы

1.                http://school-collection.edu.ru – Электронный учебник «Математика в            школе, XXI век».

2.                http://fcior.edu.ru - информационные, тренировочные и контрольные материалы.

3.                www.school-collection.edu.ru – Единая коллекции Цифровых образовательных ресурсов.

 

 

 

Хронологическая карта занятия

№	Основные этапы занятия.	Время	Содержание этапа. Методическое  обоснование
1.	Организационный момент. Цель: этап дисциплинирует и настраивает студентов на учебную деятельность. Приложение №1.	2 мин	Преподаватель отмечает отсутствующих на занятии, проверяет готовность аудиторий и студентов к занятию.
2.	Мотивация учебной деятельности. Целевая установка. Цель: активизировать познавательную деятельность студентов, показать значимость темы для будущей профессии специалиста.	3 мин.	Преподаватель подчеркивает значимость, актуальность темы. Определяет цели и план занятия.
3.	Актуализация опорных знаний: письменный опрос (тестирование). Цель: выявить уровень теоретических знаний, оценить степень подготовленности к занятию.	5 мин.	Индивидуальный тест- контроль.
4.	Методические указания к проведению самостоятельной работы. Цель: подготовка студентов к самостоятельной работе.	2 мин.	Преподаватель разъясняет цели, задачи и этапы выполнения Самостоятельной работы (письменная инструкция).
5.	Демонстрация презентации. Самостоятельная работа студентов. План: Самостоятельная работа с раздаточным материалом, Вопросы, тесты Приложение №2,5 -                     Решение упражнений учебника - Физ. Минутка. Цель: снятие напряжения с глаз. -                     Подготовка к индивидуальному	48 мин.	Визуальный метод: демонстрация презентаций. Индивидуально - групповая методика обучения. Преподаватель организует и контролирует выполнение студентами заданий направленных на формирование умений см. пояснительную записку.
	ответу по контрольным вопросам, выполнение заданий в тестовой форме. Приложение №3,4.		Преподаватель организует выполнение комплекса физических упражнений. Осмысление и систематизация полученных знаний. Цель: систематизировать и закрепить полученные знания и умения. Итоговый контроль по контрольным вопросам.
6.	Осмысление и систематизация полученных знаний. Цель: систематизировать и закрепить полученные знания и умения. Итоговый контроль по контрольным вопросам.	25 мин.	Индивидуальный устный и письменный контроль.
7.	Подведение итогов.	3 мин.	Обобщающее слово преподавателя. Выставление оценок с комментарием.
8.	Домашнее задание: Учебная литература. 1.Алимов Ш. А., Колягин Ю. М., Сидоров Ю. В., Фёдорова Н. Е., Шабунин М. И. под научным руководством академика Тихонова А. Н. Алгебра и начала математического анализа 10 - 11кл. – М. Просвещение, 2011. №201,№328	2 мин.	Вербальный контакт.
	Всего	90 мин.

 

 

 

 

Приложение №1 Методические рекомендаций для преподавателя

1. Проверить оснащенность кабинета необходимыми плакатами, учебниками, учебными пособиями, оборудованием, а также наличие у студентов справочников и лекций. 2. Осуществить контроль исходного уровня знаний студентов путем фронтального опроса, решения тестовых заданий, задач и т.д.

3. Продемонстрировать электронную презентацию Показательные и логарифмические функции.

5. Физ. Минутка рекомендуется на 25 минуте самостоятельной работы.

-  Рисуем горизонтальную восьмерку глазами (8 раз).

-  Рисуем Вертикальную восьмерку глазами (8 раз).

-  «Постреляем» глазами в разные стороны.

Смотрим на дерево за окном, на оконную раму (5 раз).

-  Сильно зажмурим глаза,

6. Дать задание для самостоятельной работы студентов  на самоконтроль (самопроверку). 7. Итоговый контроль по контрольным вопросам, тестовым заданиям, задачам, кроссвордам (по усмотрению преподавателя). 8. Подведение итогов занятия, оценка достижения поставленной цели и задание на дом.

 

 

Методическая разработка к практическому занятию для студента Тема: Показательные и логарифмические функции

Цель: Обобщить и закрепить знания по данной теме. Формировать умения:

-  Вычислять значения функции по значению аргумента.            

-  Определять положение точки на графике по  ее координатам и наоборот.

-  Использовать свойства функций для сравнения значений степеней и логарифмов.

-  Строить графики логарифмических функций.

-  Выполнять преобразование графиков.

Оснащение занятий: Вопросы для входного контроля, содержание учебного материала, карточки для закрепления материала, задания учебника.

Время занятия: 90 минут

Место проведения: кабинет математики

Задание	№ варианта, вопроса, задачи	Оценка
Контрольные  вопросы
Тест
Задачи
Домашнее задание
Общая оценка

 

 

 

Приложение №2

1.      Перечислите основные свойства степени

2.      Сформулируйте определение показательной функции

3.      Перечислите свойства показательной функции

4. 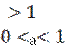     Изобразите схематически график показательной функции при а

5.      Изобразите схематически график показательной функции при 

6.      Сформулируйте определение логарифмической функции

7.      Перечислите свойства логарифмической функции

8.      Изобразите схематически график логарифмической функции при а

9.      Изобразите схематически график логарифмической функции при 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение №3

 

Тест по теме «Показательная функция» Вариант 1.

1. Из приведенных ниже функций укажите показательную:

³                     б) у 7^х                в) у  1₂           г) уе^х а)  у=х

х

1) а и в                            2) а и б                            3) в и г                            4) б и г

2. Из приведенных ниже утверждений верными являются:

а) функция у  а^х принимает в некоторой точке значение 0;

б) функция у  а^х является нечетной;

в) функция у  а^х пересекает ось Оу в точке (0; 1); 

г) функция у  а^х принимает только положительные значения.

1) а и в                            2) а и б                            3) в и г                            4) б и г

3. При каких значениях х выражении 4^х больше 1?

1) x>0                              2) x<0                              3) x>1                              4) x<1

4. Областью значений функции у3^х является множество

1) 0;                   2) ;0                    3) 0;                     4) ;0

5. Из приведенных ниже утверждений верными являются:

                                                            ^х                          1

а) графики функций у  7 и у _х симметричны относительно оси ординат;

7 ^х     1

б) графики функций у  7 и у _х пересекают ось Оу в точке (0; 1);

7 ^х     1

в) графики функций у  7 и у  _х симметричны относительно оси абсцисс;

7 ^х      1

г) графики функций у  7 и у _х пересекают ось Ох в точке (1; 0).

7

6. Из приведенных ниже функций укажите возрастающие:
х                                                                        3 х	х

1) а и в                            2) а и б                            3) в и г

4) б и г

 3                                   4		3
1) а и в                            2) а и б	3) в и г	4) б и г

а)  у_                     б) у^_ ^_                в) у_4 7^х           г) у^_^е_

 

         7. Корень уравнения     2^х          3^х 36равен

1) 1                                  2) 2                                  3) 3                                  4) 4

 

                                                                                                                          х1                     9

                                                                                                               49       4

         8. Выражение 2а, где а -  корень уравнения              , равно

                                                                                                              16        7

1) 9                                  2) 11                                3) -11                              4) -9

                                                                                                        х²21                          19х3

      9. Произведение корней уравнения ^ 9 ^   ^23^    равно

                                                                                            23           9 

1) 19                                2) -19                              3) -24                              4) -18

10.  Выражение 0,2+а, где а - корень уравнения 3^х2  9^2х1равно

1) 1                                  2) 0,2                               3) -1                                4) -0,2

2х3

11.  Решением неравенства 0,2х_2 5является множество

1) ;53U2; 2) 53;2      3) 53;2      4) ;53U2;

                                         

х²4х6

12.  Решением неравенства ^1^^{х24х3}  9является множество 

3

1) ;1U3;   2) 1;3                3) ;3U1;     4) 3;1

2х

13.  Наибольшее целое значение х, удовлетворяющее неравенству 10 ⁷  0,1, равно

1) -3                                 2) -4                                3) 0                                  4) не существует

14.  Наименьшее целое значение х, удовлетворяющее неравенству 2^х  2 , равно

1) 0                                  2) -1                                3) 1                                  4) не существует

х



15.  Наименьшее целое значение х, удовлетворяющее неравенству 4 ²  8, равно

1) -4                                 2) -3                                3) -2                                4) не существует

 

Тест по теме «Показательная функция» Вариант 2.

1. Из приведенных ниже функций укажите показательную:

⁷                     б) у 15^х                в) у 15           г) у _ ^е₃^х а)  у=х

_х

1) а и в                            2) а и б                            3) в и г                            4) б и г

2. Из приведенных ниже утверждений верными являются:

а) функция у  а^х не принимает значение 0;

б) функция у  а^х является четной;

в) функция у  а^х пересекает ось Оу в точке (0; 1); 

г) функция у  а^х принимает только неотрицательные значения.

1) а и в                            2) а и б                            3) в и г                            4) б и г

3. При каких значениях х выражении 5^х меньше 1?

1) x>0                              2) x<0                              3) x>1                              4) x<1

1 4. Областью значений функции у  _х является множество

5

1) 0;                   2) ;0                    3) 0;                     4) ;0

5. Из приведенных ниже утверждений верными являются: ^х                     1

а) графики функций у  7 и у  _х симметричны относительно оси ординат;

б) графики функций у  7^х и у _х не пересекают ось Ох;

7

                                                               ^х                          1

в) графики функций у 7 и у  _х симметричны относительно оси абсцисс;

7 ^х             1

г) графики функций у  7 и у  _х пересекают ось Оу в разных точках.

7

1) а и в                            2) а и б                            3) в и г

6. Из приведенных ниже функций укажите убывающие:
х                                                                        3 х	х

4) б и г

а)  у                     б) у                 в) у4 7^х           г) у ^_^е_

                3                                    4                                                                  3

1) а и в                            2) а и б                            3) в и г

         7. Корень уравнения     5^х        3^х  225равен

4) б и г 1) 1 2) 2      3) 3      4) 4

8. Произведение корней уравнения  36^х 46^х 12  0 равна

1) 4                                  2) -12                              3) 1                                  4) -2

9. Сумма корней уравнения 2129х28х  4 8х229х равно

                                                                            4              21

1) -37                               2) 37                                3) 1                                  4) -1

10.  Сумма корней уравнения 4^х 102^х 16  0 равна

1) -10                               2) 10                                3) -4                                4) 4

11.  Выражение 0,3+а, где а - корень уравнения   , равно

1) 0,7                               2) 1                                  3) 2,7                               4) 5 

12.  Наибольшее целое значение х, удовлетворяющее неравенству 2^3х2 2^х3 , равно

1) 2                                  2) 3                             3) 0                                      4) не существует

13.  Количество натуральных решений неравенства (0,2)^{2х23х3}  0,04 равно

1) 1                                  2) 2                                  3) 3                                 4) нет ответа

14.  Наименьшее целое значение х, удовлетворяющее неравенству 39^х1 123^х 1 0, равно

1) -2                                 2) 0                                  3) 2                                  4) -1

15.  Наибольшее целое значение х, удовлетворяющее неравенству 43^х 3^2х1  7, равно

1) 1                                  2) 0                                  3) -1                                4) не существует

 

Тест по теме «Логарифмическая функция»

Вариант 1	Вариант 2

 

 

 

 

 

Приложение № 4

 

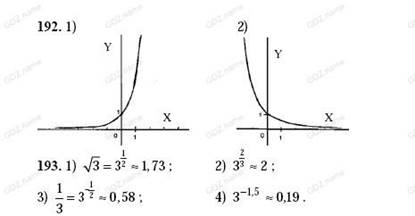
№192

№193

№194

№318

№322

№324

 

 

 

Приложение №5 Эталоны ответов тестов 

Ответы к тесту по теме «Показательная функция»

№ варианта	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	4	3	1	2	2	2	4	3	3	1	3	2	2	3	3
2	4	1	2	2	4	2	4	3	3	4	2	1	1	1	3

 

Ответы к тесту по теме «Логарифмическая функция»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение №6

Эталоны решения задач

 

 

 

 

 

Приложение №8

Критерии оценки решения задачи

5 - Задача решена, верно, с полным теоретическим обоснованием по ходу решения. 

4 - Задача решена, верно, с неполным теоретическим обоснованием.

3 - Задача решена посредством оказания помощи студентами из аудитории и/или преподавателем.

2 - Решение неверное, продвижения отсутствуют. Решение отсутствует.

 

Критерии оценивания тестовых заданий

15 вопросов                    5 (отлично)                        (14-15 ответов) 15 вопросов                    4 (хорошо)                         (11-13 ответов) 15 вопросов                    3 (удов)                              (10-8 ответа)

9 вопросов                      5 (отлично)                        (14-15 ответов)

9 вопросов                      4 (хорошо)                         (11-13 ответов) 9 вопросов                      3 (удов)                              (10-8 ответа)

 

Критерии оценивания вопросов Оценка устных ответов учащихся по математике Ответ оценивается отметкой «5», если студент:

-полно раскрыл и грамотно изложил материал в объеме, точно используя математическую терминологию и символику предусмотренном программой и учебником,

-                     отвечал самостоятельно без наводящих вопросов преподавателя.  Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков: - в изложении допущены небольшие пробелы, не исказившие ма- тематическое содержание ответа;

-допущены один – два недочета при освещении основного содержания

ответа, исправленные по замечанию преподавателя; Отметка «3» ставится в следующих случаях:

-неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала; - имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя; Отметка «2» ставится в следующих случаях:

-                     не раскрыто основное содержание учебного материала; - обнаружено незнание или непонимание студентом большей или наиболее важной части учебного материала;

-допущены ошибки в определении понятий, при использовании математической терминологии.