Методическая разработка урока по геометрии "Теорема Пифагора" (8 класс, геометрия)

Тема урока:  Применение теоремы Пифагора        

Тип урока: урок – практикум  по решению практических задач

Основные цели урока:  

-       обучение навыкам самостоятельного решения нестандартных задач на применение теоремы Пифагора.  Совершенствование навыков монологической речи, приобретение умения видеть и исправлять недочеты своего доклада.

-        развитие приёмов мышления: анализ, синтез, сравнение, обобщение; развитие умений индивидуальной и коллективной работы; развитие умений анализировать полученную информацию (увидеть главное, существенное в формулировке учебной задачи) и делать собственные выводы. Развитие критического мышления. Научить переносить имеющийся опыт решения задач в новые ситуации.

-        способствовать формированию навыков групповой работы (умение планировать учебное  сотрудничество с учителем и сверстниками), умения рассказывать свое решение товарищам, совместно устранять недочеты в решении.

Ход урока:

2. Организационный момент, деление класса на группы.
3. Актуализация опорных знаний.

Мы часто считаем, что есть науки фундаментальные, а есть прикладные, связанные с решением проблем нашей жизни. Математику подавляющее число учащихся, безусловно, относят к фундаментальным дисциплинам. Наверное, многие из вас задавали вопрос: «Вот мы учим корни, степени …. А зачем всё это нужно?». Но на самом деле нет чисто фундаментальных и чисто прикладных наук. Всякая наука содержит в себе фундаментальные и прикладные разделы. Есть фундаментальная и прикладная медицина, фундаментальная и прикладная физика, и значит, фундаментальная и прикладная математика. Другое дело, что в школьную программу многие научные разделы не входят ввиду их сложности. В частности, в школьных учебниках практически нет задач по прикладной математике, поскольку для их решения нужно знать такие разделы фундаментальной математики как производные, интегралы, дифференциальные уравнения и многое другое.

Сегодня мы с вами на достаточно простых для понимания примерах рассмотрим основные проблемы, решаемые в рамках прикладной математики. Я надеюсь, что, с одной стороны, вы увидите, что за внешне абстрактными числами и формулами скрываются подходы к решению практических задач, а, с другой стороны, вы поймете, почему задачи прикладной математики редко попадают в школьные учебники.

Начнем мы с известного стихотворения Михаила Юрьевича Лермонтова, написанного им в 1830 году.

УТРО НА КАВКАЗЕ

Светает — вьется дикой пеленой

Вокруг лесистых гор туман ночной;

Еще у ног Кавказа тишина;

Молчит табун, река журчит одна.

Вот на скале новорожденный луч

Зарделся вдруг, прорезавшись меж туч,

И розовый по речке и шатрам

Разлился блеск, и светит там и там…

а) Как вы думаете, почему мы начали урок именно с этого стихотворения?

б) По данным строкам стихотворения вы можете представить себе картинку, которую описывает автор?

в) Рассвет, луч солнца начинает постепенно освещать горы, горная речка, табун лошадей еще молчит.

Проблемы прикладной математики: увидеть в реальном объекте математическую составляющую.

Попробуйте сформулировать тему сегодняшнего урока: «Решение прикладных задач»

Давайте потренируемся.

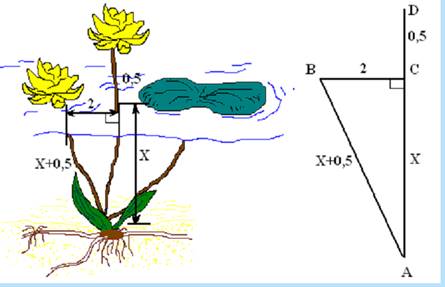
У древних индусов был обычай задачи предлагать в стихах:

Над озером тихим,

С полфута размером, высился лотоса цвет.

Он рос одиноко. И ветер порывом

Отнес его в сторону. Нет

Боле цветка над водой.

Нашел же рыбак его ранней весной

В двух футах от места, где рос.

Итак, предложу я вопрос:

Как озера вода здесь глубока.

Проблема вторая прикладной математики

Построить математическую модель реального объекта

CА – глубина озера, обозначим ее x. Тогда по теореме Пифагора имеем:

BА² – x²= АC², то есть

(x + 0,5)² – x²= 2²,

 x² + x + 0,25 – x²= 4,

х = 3,75.

Ответ: глубина озера равна 3,75 фута.

А сейчас вы можете более точно сформулировать, чем мы будем заниматься на уроке?

«Решение прикладных задач на применение теоремы Пифагора»

4. Осмысление и перенос полученных знаний по математике в ситуацию неопределенности (математический бой).

Каждая команда получает задания.

На решение задач отводится 10 минут, далее из одной команды приглашается докладчик, вторая команда выставляет оппонента.

В это время команды могут продолжать решение задач.

5. Выполнение самостоятельной работы в группах.
6. Выводы по результатам работы команд.

Каждая команда делает вывод о результатах своей работы:

4)      Какие трудности возникли с момента получения задания?

5)      Справились ли вы с решением всех задач? Как вы думаете, почему это произошло?

6)      Какие были допущены ошибки, в чем их причина и как избежать этого в дальнейшей работе?

7. Итог урока (рефлексия деятельности)

          Отвечают н вопросы учителя.

ü  Нужны ли знания полученные на уроке математике в повседневной жизни?

ü  Довольны ли вы своим выступлением на уроке? Чем именно?

ü  Что было самым сложным для вас?

«Учиться и, когда придет время, прикладывать усвоенное к делу — разве это не прекрасно!» (Конфуций)

Выставление оценок за урок.

8. Информация о домашнем задании. Решить задачу (раздать листы с домашним заданием).

Задачи  к уроку:

1.    На вершинах двух елок сидят две вороны. Высота елок равна 4 м и 6 м. Расстояние между ними равно 10 м. На каком расстоянии  нужно положить сыр для этих ворон, чтобы они находились в равных условиях, т.е. чтобы расстояния от них до сыра было одинаковым?

2. 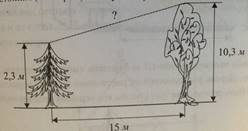   На расстоянии 15 м друг от друга стоят два дерева высотой 2,3 м и 10,3 м. Найдите расстояние (в метрах) между их вершинами.          

3.    Автомобиль выехал из гаража, после чего двигался 2 часа на север со скоростью 60 км/ч, затем повернул и поехал на запад, пробыв в пути еще пять часов и двигаясь со скоростью 70 км/ч. На каком расстоянии (в километрах) от гаража он оказался?

4.    Бамбуковый ствол в 9 футов высотой переломлен бурей так, что если верхнюю часть его пригнуть к земле, то верхушка коснется земли на расстоянии 3 футов от основания ствола. На какой высоте переломлен ствол?

5. 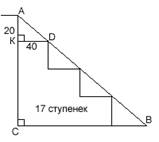   Эскалатор метрополитена имеет 17 ступенек от пола наземного вестибюля до пола подземной станции. Ширина ступенек 40 см, высота – 20 см. Определите:  а) длину лестницы; б) глубину станции по вертикали.

6. 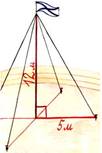   Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?

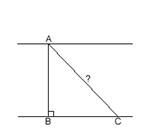
7.    Пловец поплыл от берега реки, всё время гребя в направлении по перпендикуляру к берегу (берега реки считаем параллельными). Плыл он, приближаясь к противоположному берегу со скоростью 3 км/ч. Через 5 мин. он был на противоположном берегу. Узнайте, на каком расстоянии от мести начала заплыва он вышел на противоположном берегу, считая скорость течения всюду равной 6 км/ч.