
Методические основы разработки обучения с применением активной оценки. Разработка занятия «Производная сложной функции»
Тип занятия изучение нового материала
Цель учебного занятия для учителя: планируется, что к окончанию занятия учащиеся будут знать вывод формулы производной сложной функции и уметь научится использовать ее для вычисления производной данной функции.
Задачи личностного развития учащихся: способствовать развитию мыслительных операций, развитию способностей к самооценке; исследовательских умений, культуры индивидуальной и парной работы
Нашобузу:
1. Знаю формулу производной сложной функции для вычисления.
2. Смогу использовать ее для вычисления производной данной функции.
3. Смогу организовать вычисление производной сложной функции по образцу и в измененной ситуации с целью формирования целостной системы дифференцирования.
Форма организации познавательной деятельности: индивидуальная, парная, групповая.
Оборудование и дидактический материал: компьютер, интерактивная доска, мультимедийный проектор, раздаточный материал, учебник «Алгебра и начала математического анализа 10-11 класс» под редакцией А.Н. Колмогорова
Ход учебного занятия.
|
Этапы занятия |
Деятельность учителя |
Деятельность учащихся |
|
|
Организационно-мотивационный этап Ожидаемый результат: психологическая готовность учащихся к уроку; актуализация субъектного опыта учащихся; познавательная мотивация; самоопределение учащихся на результат урока. Задача этапа: организовать актуализацию опорных знаний и умений учащихся; формирование познавательно интереса к уроку; создать условия для самоопределения учащихся на деятельность и ее результаты. |
|||
|
Организационный |
Приветствие, организует внимание учащихся, психологически настраивает к взаимодействию. |
Организуются, настраиваются на работу. |
|
|
Актуализация опорных знаний и учений учащихся. |
Обеспечивает мотивацию учения школьников, актуализацию субъективного опыта учащихся. На страницах интерактивной доски представлены слайды с устными упражнениями для актуализации опорных знаний и умений учащихся (Приложение 1) |
Слушают учителя и выполняют устные упражнения и проверяют их в режиме «самоконтроль». |
|
|
Мотивация. |
Предлагает учащимся, просмотрев две страницы на интерактивной доске, (Приложение 2) сформулировать тему учебного занятия. |
Просматривают страницы интерактивной доски, анализируют задания и участвуют в формулировке темы учебного занятия. |
|
|
Совместное целеполагание
|
Привлекает учащихся к постановке образовательных задач учебного занятия: что учащиеся должны знать и уметь. |
Участвуют в формулировке образовательных задач учебного занятия. |
|
|
Предлагает сформулировать задачи на языке учащихся. Задачи представлены на странице интерактивной доски. 1. На учебном занятии я знаю формулу производной сложной функции для вычисления. 2. Смогу использовать ее для вычисления производной данной функции. 3. Смогу организовать вычисление производной сложной функции по образцу и в измененной ситуации с целью формирования целостной системы дифференцирования. |
Учащиеся формулируют задачи для себя и сверяют с задачами, предложенными учителем.
|
||
|
Операционально – познавательный этап Ожидаемый результат: осознанное усвоение учащимися материала по теме учебного занятия; к окончанию урока смогут верно, выполнить выходной тест. Задача этапа: организовать целенаправленную деятельность учащихся. |
|||
|
Усвоение новых знаний и способов действий. Первичная проверка понимания изученного. |
Предлагает выполнить задания из учебника (работа в парах). №220, 223, 224, 227, 228 (см. стр.110-121) Организует самопроверку (техника «да – нет»). Организует коррекцию знаний и умений учащихся по теме учебного занятия. |
Выполняют предложенные задания. Самопроверкой проверяют правильность выполнения заданий. Слушают объяснение учителя и выполняют предложенные задания. |
|
|
Обобщение и систематизация знаний. |
Организует обобщение и систематизацию знаний по теме учебного занятия. Предлагает работу в парах (правило нахождения сложной функции). Предлагает оценить работу друг друга. |
Работая в парах, формулируют друг другу правило нахождения сложной функции. Оценивают работу друг друга
|
|
|
Контрольно – коррекционный и рефлексивный Ожидаемый результат: выяснение учащимися уровня учебных достижений, выявление ошибок и их коррекция; самооценка результатов деятельности учащихся на уроке; сознательный выбор домашнего задания. Задача этапа: организовать выполнение учащимися выходного теста, провести проверку выполнения и коррекцию знаний; организовать самооценку результатов учебной деятельности учащихся и осознанный выбор домашнего задания. |
|||
|
Контроль, самоконтроль, коррекция знаний. |
Предлагает выполнить выходной тест (Приложение 3). Контролирует и корректирует результаты выходного контроля, организует самоконтроль и самооценку деятельности учащихся, анализирует степень усвоения темы и выполнение когнитивных задач урока, корректирует выявленные пробелы в знаниях. |
Выполняют безотметочный тест на проверку уровня усвоения изучаемого материала. Осуществляют самоконтроль (сверяют с эталоном). Выявляют ошибки в выполнении задания, анализируют причины допущенных ошибок и возможные пути их устранения. |
|
|
Информация о домашнем задании |
Информирует о домашнем задании, проводит инструктаж о домашнем задании. № 221, 222, 225, 226, 229 (см. стр. 110-121) |
Записывают домашнее задание.
|
|
|
Рефлексия. Подведение итогов учебного занятия. |
Проводит рефлексивную беседу: Что мы делали удачно? Что вызвало у вас затруднение? Почему это случилось? Над чем, на ваш взгляд, следует поработать дома? |
Отвечают на вопросы учителя.
|
|
Приложение 1
Решение:
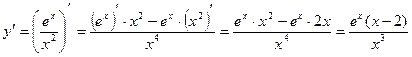
Приложение 2
1. Найдите общий синоним таким словам, как непростая, запутанная, затруднительная.
2. Вставьте пропущенное слово «Математическое понятие, отражающее однозначную парную связь элементов одного множества с элементами из другого множества, называется … »
Приложение 3
Вариант 1
Выберите правильный вариант ответа
1
Производная
функции ![]() равна: а)
равна: а)![]() ; б)
; б)![]() ;
в)
;
в)![]()
2
Производная
функции ![]() равна: а)
равна: а) ![]() ; б)
; б)![]() ; в)
; в)![]()
3
Вычислить
производную для функции ![]() :
а)
:
а)![]() ; б)
; б)![]() ;
;
в)![]()
Вариант 2
Выберите правильный вариант ответа
1
Производная
функции ![]() равна: а)
равна: а)![]() ; б)
; б)![]() ;
в)
;
в)![]()
2
Производная
функции ![]() равна: а)
равна: а) ![]() ; б)
; б)![]() ;
в)
;
в) ![]()
3
Вычислить
производную для функции ![]() :
а)
:
а)![]() ;
б)
;
б)![]() ;
;
в)![]()
Вариант 3
Выберите правильный вариант ответа
1
Производная
функции ![]() равна: а)
равна: а)![]() ; б)
; б) ![]() ;
в)
;
в) ![]()
2
Производная
функции ![]() равна: а)
равна: а)![]() ; б)
; б) ![]() ;
в)
;
в)![]()
3
Вычислить
производную для функции ![]() :
а)
:
а)![]() ;
б)
;
б)![]() ;
;
в)![]()
Вариант 4
Выберите правильный вариант ответа
1
Производная
функции ![]() равна: а)
равна: а)![]() ; б)
; б)![]() ;
в)
;
в)![]()
2
Производная
функции ![]() равна: а)
равна: а)![]() ; б)
; б)![]() ;
в)
;
в)![]()
3
Вычислить
производную для функции ![]() :
а)
:
а)![]() ;
б)
;
б) ![]() ;
;
в)![]() .
.
Ключи ответов
|
№ задания |
1 вариант |
2 вариант |
3вариант |
4 вариант |
|
ответ |
ответ |
ответ |
ответ |
|
|
1 |
в |
б |
в |
а |
|
2 |
б |
б |
б |
в |
|
3 |
а |
в |
в |
в |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.