УДК 372.8:512

ББК 74.262.21

П64

Серия «МГУ — школе» основана в 1999 году

Потапов М. К.

П64 Алгебра. Методические рекомендации. 7 класс : учеб. пособ ие для общеобразоват. организаций / М. К. Потапов, А. В. Шевкин. — М. : Просвещение, 2017. — 143 с. : ил. — (МГУ — школе.) — ISBN 978-5-09-042974-0.

Эта книга адресована учителям, работающим по учебнику серии «МГУ — школе» «Алгебра, 7» (авторы: С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин). В ней дана характеристика курса алгебры 7 класса, приведены примерное тематическое планирование, методические рекомендации по всем темам и решения наиболее трудных задач.

УДК 372.8:512

ББК 74.262.21

ISBN 978-5-09-042974-0	© Издательство «Просвещение», 2013
	© Художественное оформление.
	Издательство «Просвещение», 2017
	Все права защищены

Введение

О книге для учителя

Данная книга предназначена учителям, работающим по учебнику серии «МГУ — школе» «Алгебра, 7» (авторы: С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин). Этот учебник является частью учебного комплекта для 7—9 классов, рекомендованного Министерством образования и науки Российской Федерации, он продолжает серию учебников «МГУ — школе» тех же авторов для 5—6 классов.

В учебный комплект для 7 класса входят:

^●Алгебра. 7 класс: учебник для общеобразоват. организаций / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. — М.: Просвещение, 2013— 2016;

^●Алгебра. Дидактические материалы. 7 класс / М. К. Потапов, А. В. Шевкин. — М.: Просвещение, 2015;

^●Алгебра. Тематические тесты. 7 класс / П. В. Чулков. — М.: Просвещение, 2010—2016;

^●Алгебра. Методические рекомендации. 7 класс / М. К. Потапов, А. В. Шевкин. — М.: Просвещение, 2013—2016.

В данной книге рассмотрены концепция учебников алгебры серии «МГУ — школе» и структура учебника для 7 класса, приведено примерное тематическое планирование, даны методические рекомендации по изучению основных тем курса алгебры 7 класса и комментарии к решению некоторых трудных задач. Здесь же даны рекомендации по использованию дидактических материалов. Практически для всех пунктов учебника в книге имеются рубрики Решения и комментарии и Промежуточный контроль, к некоторым пунктам даётся рубрика Задания для повторения. В первой из них приведены условия многих задач из учебника и их решения или даны рекомендации, как найти решение, с пояснениями, помогающими обучению школьников. Во второй рубрике даны номера самостоятельных и контрольных работ по дидактическим материалам, а также тестов из сборника тематических тестов. В последней рубрике приводятся номера упражнений из раздела «Задания для повторения» учебника, которые можно использовать при изучении данного пункта.

Следует обратить внимание на то, что в пособии для учителей (как и в учебнике) рассмотрены вопросы обучения алгебре в 7 классе как в общеобразовательных классах, так и в классах с углублённым изучением математики. При этом сначала обсуждаются вопросы для общеобразовательных классов, затем для классов с углублённым изучением математики.

Авторы выражают благодарность учителям, сделавшим замечания и предложения, способствовавшие улучшению учебника: Т. Т. Бетоньян и Т. П. Зориной (Москва), В. И. Гридасову (Воронеж), О. А. Сухаревой (С.-Петерб ург),

Н. А. Филоненко (Дзержинский Московской области).

Об учебниках математики серии «МГУ — школе»

В серии «МГУ — школе» издательство «Просвещение» издаёт учебники «Математика» для 5 и 6 классов, «Алгебра» для 7, 8 и 9 классов, «Алгебра и начала математического анализа» для 10 и 11 классов (авторы: С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин). Эти учебники полностью отвечают требованиям Федерального государственного образовательного стандарта. Они рекомендованы министерством в качестве учебников для люб ых типов общеобразовательных организаций и входят в перечень учебников. Их издание является составной частью программы «МГУ — школе», разработанной по инициативе ректора Московского государственного университета академика В. А. Садовничего и нацеленной на сохранение и развитие лучших традиций отечественного математического образования.

Авторами учебников разработана концепция многоуровневых учебников математики. Приведём основные положения этой концепции.

^●Математика едина и может быть изложена в одном учебнике для работы по разным программам. Содержание учебника должно соответствовать научной точке зрения на изучаемые вопросы.

^●Учебник должен сочетать в себе научность, стройность, экономность и логичность изложения материала с доступностью для учащихся его учебных текстов.

^●Учебник не должен ограничиваться интересами среднего ученика, он должен удовлетворять интересам всех учащихся — от слабых до сильных для обеспечения их индивидуальной образовательной траектории.

^●Учебник должен быть пригоден для организации дифференцированного обучения и обеспечивать любой желаемый уровень глубины изучения материала с учётом устойчивых познавательных интересов.

^●Способ изложения материала в учебнике, организация учебных текстов и системы упражнений должны обеспечивать достижение разных целей обучения при работе по разным программам.

Структура учебников серии «МГУ — школе» и их методический аппарат отвечают положениям этой концепции.

Учебники серии «МГУ — школе» составляют три цикла — для 5—6, 7—9 и 10—11 классов. Обучение в каждом цикле можно начинать независимо от того, по каким учебникам учились школьники в предыдущие годы, так как в первом учебнике каждого цикла проводится повторение и систематизация изученного за предыдущие годы.

Учебники для 5—6 классов ориентированы на развитие интереса к математике в процессе обучения, в них много материала, нацеленного на повышенный уровень математической подготовки.

Учебники для 7—9 классов предназначены как для общеобразовательных классов, так и для классов с углублённым изучением математики.

Учебники для 10—11 классов охватывают содержание курса алгебры и начал математического анализа для всех профилей старшей школы.

Авторы учебников уверены, что не следует упрощать обучение за счёт сокращения числа изучаемых вопросов и необходимо сохранить фундаментальность изложения теории в учебниках, оставляя за учителем право более или менее глубокого изложения теоретического материала на уроке в зависимости от уровня подготовки класса и целей обучения. В учебниках коротко, ясно и доступно, без долгих введений излагается суть вопроса. Мотивировать появление тех или иных понятий, определений при необходимости должен учитель, так как в разных классах это надо делать по-разному.

Учебники серии «МГУ — школе» имеют высокий научный и методический потенциал. Они отличаются расположением учебного материала в естественной логической последовательности, позволяющей излагать материал более глубоко, экономно и строго. В соответствии с требованиями ФГОС учебники не только нацелены на формирование навыков, а учат действовать осознанно. Обычно обучение больше ориентировано на вопрос «как?», на действия по образцу, требует многократных повторений для поддержания навыков. В учебниках серии «МГУ — школе» уделяется достаточно внимания вопросу «почему?», имеющему большой развивающий потенциал для достижения личностных результатов освоения ООП основного общего образования. Учебники позволяют интенсифицировать процесс обучения, что в условиях уменьшения числа учебных часов особенно важно. Они полностью обеспечивают обучение тех школьников, которые хотят и могут обучаться основам наук.

Главный методический принцип, положенный в основу изложения теоретического материала, заключается в том, что ученик за один раз должен преодолевать не более одной трудности. Поэтому каждое новое понятие формируется, каждое новое умение отрабатывается сначала в чистом виде, затем трудности совмещаются, что позволяет учащимся контролировать процесс и результат учебной деятельности.

Аналогично выстроена и система упражнений. Это позволяет учащимся развивать умение ясно, точно, грамотно излагать свои мысли, понимать смысл поставленной задачи, выстраивать аргументацию. Сложность заданий в каждом пункте нарастает линейно: учитель определяет сам, на какой ступеньке лестницы сложности он может остановиться со своим классом или с конкретным учеником.

Одна из особенностей системы упражнений в учебниках заключается в том, что для каждого нового действия или приёма решения в учебниках имеется достаточное число упражнений, которые не перебиваются упражнениями на другие темы. Только тогда, когда новый материал освоен, можно подключать задания на соединение этого материала с ранее изученным, задания на повторение, не связанные с новым материалом, в итоге формируется умение контролировать процесс и результат учебной математической деятельности.

Важную роль в формировании первоначальных представлений о зарождении и развитии математики играют исторические сведения, завершающие каждую главу учебников. Этот материал способствует формированию представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации. Работа со старинными задачами — одна из сильных сторон учебников, она может много дать в воспитании уважения к традициям и истории, в развитии общеучебных умений.

Учебники серии «МГУ — школе» полностью обеспечивают обучение тех школьников, которые могут и хотят усвоить основы наук. Они нацелены на повышенный уровень математической подготовки учащихся. Учебники можно использовать и в классах с обычной программой по математике, если не изучать сверхпрограммный материал и пропускать сложные задачи, а также выбирать уровень полноты изложения теоретического материала на уроке и уровень предъявления требований к знаниям и умениям учащихся в соответствии с поставленными целями обучения и возможностями конкретного класса, оставаясь при этом на уровне не ниже обязательных требований к математической подготовке учащихся. При таком подходе у сильных учащихся будет возможность с помощью учебника более глубоко разобраться в любом вопросе, чего они часто лишены, если учебник написан в расчёте на среднего ученика.

Основные идеи курса алгебры 7—9 классов

Алгебра играет в математике большую роль, теперь существует даже тенденция «алгебраизации» математики. Наряду с фундаментальной ролью внутри математики алгебра имеет и прикладное значение. Достаточно отметить её выходы в физику, кибернетику, математическую экономику. Поэтому изучение алгебры в школе является важной частью фундамента естественно-научного образования.

Для учебников алгебры возможны два способа распределения учебного материала по годам обучения. Первый — в каждом классе дают понемножку буквенных выражений, уравнений, неравенств, функций и т. п., так как детям якобы скучно долго изучать одни и те же вопросы. При использовании такого способа распределения учебного материала страдают научная аккуратность и строгость изложения, появляются порочные логические круги, недомолвки и несуразности, что в первую очередь сказывается на обучении и воспитании сильных учащихся.

Так происходит, например, когда действительные числа рассматриваются после изучения тождеств, функций и их графиков. Реализация этого первого подхода к построению курса алгебры в процессе обучения чаще ориентирована на формирование навыков.

Но есть и второй способ распределения учебного материала по годам обучения, основанный на его внутренней логике. Он диктует последовательность появления в учебнике тех или иных вопросов, позволяет в каждом учебном году ставить главную задачу. Этот второй способ, принятый в учебниках серии «МГУ — школе», позволяет излагать материал в строгой логической последовательности, без ненужных повторов и недомолвок, что делает изложение даже сложных вопросов ясным и доступным. Учебники серии «МГУ — школе» обеспечивают системную подготовку по предмету, требуют меньше, чем обычно, времени, позволяют ориентировать процесс обучения на формирование результатов обучения и освоения содержания курса, требуемых ФГОС. Как показывает опыт работы по ним, интерес к предмету возникает у учащихся не от многообразия и частого чередования тем, а от того, что учащиеся имеют возможность «вжиться» в каждый элемент содержания, постепенно углубляя его понимание. Изложение материала в учебниках связное — подряд излагаются большие темы, нет чересполосицы мелких вопросов, нарушающих логику изложения крупных тем. Это позволяет каждый раз сосредоточиваться на одном вопросе и поэтому изучить его более глубоко и в то же время более экономно. Отдельные темы программы изучаются один раз и в полном объёме, чтобы потом к ним не возвращаться в теоретической части учебника. Дальнейшее закрепление и повторение, а иногда и развитие изученного ведётся через линию упражнений.

Содержание курса алгебры диктует порядок изложения основного учебного материала: сначала должны изучаться чисто алгебраические вопросы (алгебраические выражения), как более доступные в этом возрасте, а уж затем функциональные вопросы. Поэтому 7 класс посвящён алгебраическим выражениям, а изучение функций начинается лишь в 8 классе.

Школьный курс алгебры 7—9 классов на самом деле лишь наполовину является алгеброй, другая его половина приходится на вопросы математического анализа, изучаемые традиционно в курсе алгебры (длина отрезка, действительные числа, функции). Желательно различать эти составляющие и излагать алгебраические вопросы алгебраическими методами. Например, к буквенным выражениям часто подходят как к функциям многих переменных (функциональный подход), хотя естественнее говорить о них как о множестве объектов, подчинённых явно выписанным законам (алгебраический подход). Поэтому при изложении темы «Алгебраические выражения» авторы считают наобходимым оставаться на чисто алгебраической точке зрения. Одночлен определяется как произведение некоторых чисел и букв, многочлен — как сумма одночленов, алгебраическая дробь — как отношение многочлена к ненулевому многочлену. Приводятся правила, которым они подчинены. Например, в одночлене можно поменять местами множители, в многочлене можно привести подобные члены, алгебраическую дробь можно сократить на ненулевой многочлен и т. д. Эти свойства мотивируются по мере их введения, отмечается, что при замене букв числами в рассматриваемых буквенных равенствах последние превращаются в верные числовые равенства (за исключением случаев деления на нуль).

В учебниках для 7—9 классов достаточно внимания уделено решению уравнений, неравенств и их систем, построению графиков элементарных функций, решению текстовых задач, в том числе в общем виде, что необходимо для изучения курсов геометрии и физики.

Учебники алгебры серии «МГУ — школе» содержат весь материал программ как для классов с обычной программой по математике, так и для классов с углублённым изучением математики. Авторы считают принципиально важным иметь общий учебник для всех этих классов, что позволяет учащимся переходить без особых трудностей с одной программы обучения на другую, а учителям — проводить уровневую дифференциацию обучения как для разных классов, так и для отдельных учащихся. Такой учебник позволяет сильному учащемуся обычного класса разобраться в любом вопросе, изучить математику вплоть до уровня углублённого изучения. Учитель, работающий в классах с разной подготовкой, ведя обучение по одному учебнику в рамках одной авторской концепции, может лишь менять в зависимости от класса глубину погружения в теоретические и технические подробности.

В общеобразовательных классах дополнительные материалы и сложные задачи обычно не рассматриваются. Если же учитель имеет достаточно часов и его класс проявляет интерес к математике, то за счёт Дополнений к главам учебников, а также пунктов и отдельных задач со звёздочкой, необязательных в обычных общеобразовательных классах, можно расширить и углубить содержание изучаемого материала до объёма, предусмотренного программой для классов с углублённым изучением математики.

Об учебнике «Алгебра, 7» серии «МГУ — школе» Учебник «Алгебра, 7» содержит три главы:

1. Действительные числа.

2. Алгебраические выражения.

3. Линейные уравнения.

Курс алгебры в 7 классе начинается темой «Действительные числа», подводящей итог предшествующему изучению арифметики и в то же время закладывающей основы для дальнейшего изучения математики.

Материал первой главы должен сформировать у учащихся представление о действительном числе как о длине отрезка. Это даёт возможность легко объяснить, например, что график линейной функции есть прямая, и в дальнейшем значительно упростить рассуждения, связ анные с п остроением графиков квадратичной и других функций, с определением квадратного корня, так как каждой точке числовой оси соответствует действительное число. При таком построении курса изучение алгебраических выражений и функционального материала будет иметь полноценный научный фундамент.

Авторы учебника считают, что тема «Действительные числа» составляет теоретическую основу дальнейшего изложения. Весьма трудным с педагогической точки зрения является изложение в школе эволюции понятия числа. Каким образом и когда должно вводиться понятие действительного числа? Практически все согласны, что действительное число надо вводить как десятичную дробь, вообще говоря, бесконечную. Но на какой стадии обучения это надо сделать и как — здесь мнения специалистов расходятся. Авторы считают, что чем раньше сказать

школьнику о том, что действительное число есть бесконечная десят ичная дробь, тем лучше, потому что он оперирует с длиной отрезка, координатной осью и системой координат, графиками функций, квадратными корнями и т. д. Разговоры об иррациональности чисел, несоизмеримости с единицей, существовании корня значительно упрощаются, если у школьника есть представление, пусть даже самое элементарное, о числе как бесконечной десятичной дроби.

В начале 7 класса происходит обобщение и систематизация уже известных сведений о числе. Дополняя эти сведения, получаем, что рациональное число представимо в виде периодической десятичной дроби и, наоборот, любая периодическая дробь есть десятичное представление некоторого рационального числа. Отметим, что при этом нет необходимости вводить понятие сходящихся рядов. Достаточно привести примеры деления уголком числителя дроби на её знаменатель, чтобы прийти к выводу, что в итоге получается десятичная дробь, вообще говоря, бесконечная и периодическая. После этого приводятся примеры бесконечных непериодических десятичных дробей, которые и называют иррациональными числами.

Бесконечные десятичные дроби сравнивают так же, как конечные десятичные дроби. Что же касается действий над ними, то здесь уже приходится обращаться к приближённым методам.

Главное приложение десятичной дроби на этом этапе есть длина отрезка. Длиной отрезка AB при выбранном единичном отрезке называется число a, определяемое десятичной дробью

a = α₀,α₁α₂α₃... ,

где α₀ — приближённая длина отрезка AB с точностью до 1 с недостатком, α₀,α₁ — приближённая длина отрезка AB с точностью до 0,1 с недостатком, α₀,α₁α₂ — приближённая длина отрезка AB с точностью до 0,01 с недостатком и т. д.

Таким образом, длина любого отрезка есть записанное в десятичной системе число, которое конструируется на основе его последовательного приближения с недостатком.

Изучение главы 1 должно привести к следующему представлению о действительном числе: всякое действительное число можно записать в виде десятичной дроби (вообще говоря, бесконечной). Эти числа подчинены основным законам, изложенным в пункте 3.4. Длина любого отрезка — действительное число.

В результате изучения данной главы учащиеся должны повторить действия с обыкновенными и десятичными дробями, понять, что всем точкам координатной оси соответствуют числа и, наоборот, каждому числу соответствует точка координатной оси. Таким образом, координатная ось, которая ранее была «дырявой» — без иррациональных точек, теперь заполнена полностью, без пропусков.

Как уже отмечалось выше, при изложении материала главы 2 авторы стоят на чисто алгебраической точке зрения. А именно, одночлен определяется как произведение некоторых чисел и букв, многочлен — как сумма одночленов, алгебраическая дробь — как отношение одного многочлена к другому (ненулевому). Приводятся формальные правила, которым они подчинены. Нигде не фиксируется, что в этом исчислении буквы есть числа, которые только обозначены буквами.

Справедливость каждого из рассмотренных равенств следует из сформулированных правил. В дальнейшем выясняется, что каждое такое равенство является тождеств ом на некотором множестве чисел, т. е. равенством между числовыми выражениями, возникающими при замене букв числами (при условии, что эти выражения имеют смысл). В старые времена такие равенства называли «тожествами».

В 7 классе главное внимание уделяется технике преобразований на основе указанных правил, а трудности, связанные с функциональным представлением буквенных выражений (область определения рациональных функций, решение рациональных уравнений, т. е. потеря и приобретение корней, и т. д.), переносятся в старшие классы.

Во второй главе рассматривается также степень с целым показателем. Это позволяет, в частности, более компактно записывать рациональные выражения. Здесь же рассматривается стандартный вид числа.

В результате изучения данной главы учащиеся должны научиться правильно делать выкладки с одночленами, многочленами, алгебраическими дробями и уметь упрощать несложные буквенные выражения.

Глава 3 посвящена изучению линейных уравнений и их систем. При изучении линейного уравнения ax + b = 0 надо учесть, что ранее уже решалось много задач, сводящихся к уравнению первой степени, т. е. к случаю a ≠ 0. Теперь надо уделить внимание и случаю a = 0, когда линейное уравнение перестаёт быть уравнением первой степени. Это пригодится в дальнейшем при изучении систем линейных уравнений.

Способы решений систем двух уравнений первой степени с двумя неизвестными изучаются прежде всего в случаях, когда все коэффициенты при неизвестных отличны от нуля и непропорциональны. Затем на примерах рассматриваются остальные случаи.

В результате изучения этой главы учащиеся должны понять, что, применяя последовательно способ подстановки, они всегда решат систему линейных уравнений, т. е. придут либо к единственному решению, либо к бесконечному множеству решений, либо к противоречию, показывающему, что решений нет.

В учебнике достаточно внимания уделено решению текстовых задач при помощи линейных уравнений и их систем. Основной целью решения текстовых задач является развитие у учащихся умения делать логически правильные выводы на основе анализа имеющихся данных задачи и использовать эти данные для её решения. Авторы считают, что это пока наиболее действенный способ развития логического мышления и речи учащихся, повышающий эффективность обучения.

Работать по учебнику 7 класса можно после обучения в 6 классе по любому из учебников, рекомендованных Министерством образования и науки Российской Федерации, так как в начале учебника повторяются основные вопросы программы для 5—6 классов, что позволяет систематизировать изученное и подготовиться к изучению нового материала.

К данному курсу существует Электронная форма учебника (ЭФУ) — соответствующая по структуре, содержанию и художественному оформлению печатной форме учебника и включающая в себя интерактивные ссылки, расширяющие и дополняющие материал печатного учебника.

Функциональными особенностями ЭФУ является:

— удобный и понятный интерфейс и навигация по ЭФУ;

— работа в онлайн- и офлайн-режимах;

— тестовые задания к каждой теме, разделу учебника;

— возможность добавления материалов, созданных учителем;

— инструменты изменения размера шрифта, создания заметок и закладок.

Использование ЭФУ предоставляет учителю следующие возможности:

— организовать контроль и самоконтроль по результатам изучения темы;

— реализовать технологии мобильного, дистанционного или смешанного обучения;

— реализовать требования ФГОС по формированию информационно-образовательной среды системой электронных образовательных ресурсов и др.

Далее приведены методические рекомендации по изучению всех тем, включённых в учебник, и дидактические материалы для 7 класса с решениями наиболее трудных задач. Иногда комментарии к близким по содержанию пунктам объединены. При этом не обсуждается время, отводимое на изучение пункта, — при разных вариантах планирования могут быть различия. В комментариях для учителя не выделяется обязательный и необязательный материал, так как в учебнике есть соответствующие обозначения. Во многих пунктах книги для учителя методические комментарии даны в расчёте на возможно более глубокое изучение вопроса, поэтому при подготовке к уроку учитель должен отобрать главное, что будет изложено учащимся на уроке, решить, каким будет закрепление материала в классе и дома, каким и когда будет контроль изученного. При этом не надо стремиться донести до учащихся все подробности и тонкости изучаемого материала, если учащиеся существенно ограничены во времени изучения темы.

Учитывая, что Федеральный государственный стандарт по математике уделяет большее, чем прежде, внимание формированию не только предметных, но и личностных и метапредметных умений, учитель в организации учебной работы школьников должен использовать все возможности учебника для того, чтобы процесс изучения алгебраического материала доставлял учащимся возможности обог ащать свой опыт предметных, личностных и метапредметных действий, описанных в программе по алгебре для 7 класса.

При организации повторения курса алгебры за 7 класс необходимо обратить особое внимание на наиболее трудные темы курса для данного класса, постараться учесть индивидуальные пробелы учащихся. При повторении теории необходимо выделять основные теоретические факты, изученные за год, давая иллюстрации их применения на наиболее характерных примерах. При этом можно использовать задачи из раздела «Задания для повторения».

В рубрике Промежуточный контроль приведены номера самостоятельных (С—1) и контрольных (К—1) работ из дидактических материалов, относящиеся к изучаемой теме, а также тестов (Т—1).

Дидактические материалы используются для промежуточного контроля по теме (самостоятельные работы) и итогового контроля (контрольные работы). Следует учесть, что провести все самостоятельные работы с выставлением отметки со всем классом скорее всего не удастся, да это и не требуется. Некоторые из них можно использовать как домашние задания на отметку или как дополнительные задания на отметку заинтересованным учащимся. Самостоятельные работы отнесены к соответствующим темам, но могут использоваться и при изучении других тем (например, для организации повторения изученного через некоторый промежуток времени).

В обязательную часть самостоятельных работ на отметку можно включать не все задания, ориентируясь на уровень подготовки класса и на отводимое для работы время. Необязательные задания можно оценивать дополнительной отметкой. В обязательную часть контрольных работ в обычном классе можно не включать последнее задание.

О решении текстовых задач

Обратим внимание на важный вид учебной деятельности школьников — решение текстовых задач. В 7 классе продолжается работа с текстовыми задачами, начатая в 5—6 классах. С учащимися следует повторить основные арифметические способы решения текстовых задач и лишь после этого осваивать новые идеи, применяемые при решении текстовых задач.

В каждом классе работа с текстовыми задачами будет вестись в своём темпе, поэтому её нельзя заранее спланировать для всех классов и дать рекомендации по использованию задач по всем пунктам. Но такие рекомендации по работе с задачами разных видов даны в конце книги. Предполагается, что учитель сам будет планировать время включения работы с текстовыми задачами в учебный процесс с учётом имеющихся успехов его учащихся.

Здесь можно дать только один совет, которому полезно следовать. Работа с текстовыми задачами не должна вклиниваться в изучение нового материала до тех пор, пока основные умения по этому материалу не сформированы. Эта работа должна быть связана с повторением изученного, которое проводится под руководством учителя. Задачи должны разнообразить формы учебной деятельности, делать изучение математики более живым и интересным.

О работе в классах с углублённым изучением математики

Авторы учебников считают, что углублённое изучение математики можно начинать с 7 класса. В учебнике «Алгебра, 7» серии «МГУ — школе» материал, предназначенный только для классов с углублённым изучением математики, специально выделен. Это доказательства некоторых теорем, дополнительные вопросы, изложенные в пунктах, отмеченных звёздочками, и в Дополнениях к главам учебника, а также более сложные задачи. Весь этот материал не является обязательным в обычном классе, и его пропуск не нарушает цельности курса.

В классе с углублённым изучением математики используются и дидактические материалы. При этом большая часть заданий считается обязательной только для классов с углублённым изучением математики. Кроме того, в дидакт ических материалах имеются самостоятельные работы, отмеченные звёздочками. Они предназначены только для классов с углублённым изучением математики.

В классе с углублённым изучением математики надо больше внимания уделить решению задач различных олимпиад и конкурсов. Ниже к ряду пунктов сделаны специальные замечания о работе с такими задачами.

П римерное тематическое планирование работы

по учебнику «Алгебра, 7»

Примерное тематическое планирование приведено в двух вариантах:

вариант I — 3 ч в неделю, всего 102 ч, вариант II — 4 ч в неделю, всего 136 ч.

	I	II
Глава 1. Действительные числа	17	24
§ 1. Натуральные числа	4	4
1.1. Натуральные числа и действия с ними	1	1
1.2. Степень числа	1	1
1.3. Простые и составные числа 1.4. Разложение натурального числа на мно-	1	1
жители	1	1
§ 2. Рациональные числа 2.1. Обыкновенные дроби. Конечные десятич-	4	6
ные дроби 2.2. Разложение обыкновенной дроби в конеч-	1	1
ную десятичную дробь	1	1
2.3. Периодические десятичные дроби 2.4*. Периодичность десятичного разложения	1	1
обыкновенной дроби 2.5. Десятичное разложение рациональных	—	1
чисел	1	2
§ 3. Действительные числа	9	10
3.1. Иррациональные числа	1	1
3.2. Понятие действительного числа	1	1
3.3. Сравнение действительных чисел	1	1
3.4. Основные свойства действительных чисел	1	2
3.5. Приближения числа	2	2
3.6. Длина отрезка	1	1
3.7. Координатная ось	1	1
Контрольная работа № 1	1	1
Дополнения к главе 1	—	4

Продолжение

Глава 2. Алгебраические выражения	60	79
§ 4. Одночлены	8	9
4.1. Числовые выражения	1	1
4.2. Буквенные выражения	1	1
4.3. Понятие одночлена	1	1
4.4. Произведение одночленов	2	2
4.5. Стандартный вид одночлена	1	2
4.6. Подобные одночлены	2	2
§ 5. Многочлены	15	19
5.1. Понятие многочлена	1	1
5.2. Свойства многочленов	1	2
5.3. Многочлены стандартного вида	2	2
5.4. Сумма и разность многочленов	2	2
5.5. Произведение одночлена и многочлена	2	2
5.6. Произведение многочленов	2	3
5.7. Целые выражения	1	2
5.8. Числовое значение целого выражения	2	2
5.9. Тождественное равенство целых выражений	1	2
Контрольная работа № 2	1	1
§ 6. Формулы сокращённого умножения	14	23
6.1. Квадрат суммы	2	2
6.2. Квадрат разности	2	2
6.3. Выделение полного квадрата	1	2
6.4. Разность квадратов	2	2
6.5. Сумма кубов	1	2
6.6. Разность кубов	1	2
6.7*. Куб суммы	—	2
6.8*. Куб разности 6.9. Применение формул сокращённого умно-	—	2
жения	2	3
6.10. Разложение многочленов на множители	2	3
Контрольная работа № 3	1	1
§ 7. Алгебраические дроби	16	18
7.1. Алгебраические дроби и их свойства 7.2. Приведение алгебраических дробей к об-	3	3
щему знаменателю 7.3. Арифметические действия над алгебраи-	3	3
ческими дробями	4	4
7.4. Рациональные выражения 7.5. Числовое значение рационального выра-	2	3
жения 7.6. Тождественное равенство рациональных	2	3
выражений	1	1
Контрольная работа № 4	1	1

Продолжение

§ 8. Степень с целым показателем	7	8
8.1. Понятие степени с целым показателем	2	2
8.2. Свойства степени с целым показателем	2	2
8.3. Стандартный вид числа 8.4. Преобразование рациональных выраже-	2	2
ний	1	2
Дополнения к главе 2	—	2
Глава 3. Линейные уравнения § 9. Линейные уравнения с одним неизвест-	18	26
ным 9.1. Уравнения первой степени с одним неиз-	6	7
вестным 9.2. Линейные уравнения с одним неизвест-	1	1
ным 9.3. Решение линейных уравнений с одним	1	1
неизвестным 9.4. Решение задач с помощью линейных	2	2
уравнений	2	3
§ 10. Системы линейных уравнений 10.1. Уравнения первой степени с двумя неиз-	12	17
вестными 10.2. Системы двух уравнений первой степени	1	1
с двумя неизвестными	1	1
10.3. Способ подстановки	2	2
10.4. Способ уравнивания коэффициентов 10.5. Равносильность уравнений и систем	2	2
уравнений 10.6. Решение систем двух линейных уравне-	1	2
ний с двумя неизвестными 10.7*. О количестве решений системы двух уравнений первой степени с двумя неизвест-	2	2
ными 10.8*. Системы уравнений первой степени с	—	1
тремя неизвестными 10.9. Решение задач при помощи систем урав-	—	2
нений первой степени	2	3
Контрольная работа № 5	1	1
Дополнения к главе 3	—	2
Повторение	7	7
Повторение курса алгебры 7 класса	6	6
Итоговая контрольная работа № 6	1	1

Глава 1 Действительные числа

Изучение главы 1 должно привести к следующему представлению о действительном числе: всякое действительное число можно записать в виде десятичной дроби (вообще говоря, бесконечной) и к пониманию того, что длина любого отрезка — действительное число.

В результате изучения главы учащиеся должны повторить действия с натуральными, целыми и рациональными числами; понять, что всем точкам координатной оси соответствуют числа и, наоборот, каждому числу соответствует точка координатной оси.

Обобщение и систематизация изученных ранее сведений о числе формируют представление о математике как сфере человеческой деятельности, о её значимости для развития цивилизации, помогают формированию устойчивых познавательных интересов учащихся, способствуют развитию умения оценивать свои возможности. Многие задачи данной главы решаются разными способами, что позволяет развить критичность мышления, формировать коммуникативные компетенции в обучении, умения формулировать свои мысли, аргументировать их, отстаивать свою точку зрения.

§ 1. Натуральные числа

В § 1 систематизируются изученные ранее сведения о натуральных числах. При изучении первых пунктов желательно основательно проверить умение учащихся производить арифметические действия с натуральными числами, так как на них основано умение работать с рациональными числами. Начиная с пункта 1.1 можно использовать задачи, предназначенные сильным школьникам, учащимся классов с углублённым изучением математики.

В результате изучения параграфа каждый учащийся должен свободно производить арифметические действия с натуральными числами.

1.1. Натуральные числа и действия с ними

В данном пункте вводится понятие делимости нацело для натуральных чисел. При этом слово «нацело» обычно опускают. Полезно знать свойство делимости натуральных чисел, которое приведём с доказательством.

Если один из множителей делится на некоторое число, то и произведение делится на это число.

Доказательство. Пусть дано произведение натуральных чисел n ⋅ p и пусть число n делится на k. Это означает, что существует такое натуральное число r, что n = k ⋅ r. Тогда n ⋅ p = (k ⋅ r) ⋅ p = k ⋅ (r ⋅ p), а это означает, что произведение n ⋅ p делится на k.

Теперь докажем следующее свойство, приведённое в учебнике без доказательства.

Если m, n и k — натуральные числа и m делится на

n, а n делится на k, то m делится на k.

Доказательство. Натуральное число m делится на n, значит, существует такое натуральное число p, что m = n ⋅ p; натуральное число n делится на k, значит, существует т акое натуральное число r, что n = k ⋅ r. Тогда m = n ⋅ p = = (k ⋅ r) ⋅ p = k ⋅ (r ⋅ p), а это означает, что m делится на k.

Можно напомнить другие свойства натуральных чисел, которые изучались в 5 классе, их доказательства содержатся в Дополнении к главе 1.

Если каждое из двух чисел делится на некоторое число, то их сумма и разность делятся на это число.

Если одно из двух чисел делится на некоторое число, а другое на него не делится, то их сумма и разность не делятся на это число.

Все эти свойства используются при доказательстве признаков делимости натуральных чисел, а также при решении сложных задач на доказательство.

В классах с углублённым изучением математики здесь можно изучить признаки делимости, наибольший общий делитель и наименьшее общее кратное натуральных чисел, алгоритм Евклида (см. Дополнения к главе 1), решить задачи 173—177, 181.

Задания для повторения. При изучении данного пункта можно использовать задания 778—779.

Решения и комментарии

17. Натуральное число п делится на натуральное число р (р > 1). Докажите, что число п + 1 не делится на р.

Доказательство. По условию задачи натуральное число n делится на натуральное число p (p > 1), т. е. существует такое натуральное число k, что n = p ⋅ k. Предположим, что натуральное число n + 1 тоже делится на p, т. е. существует такое натуральное число r, что n + 1 = p ⋅ r. Тогда разность чисел n + 1 и n равна 1 и, кроме того, справедливо равенство 1 = p ⋅ r − p ⋅ k = p ⋅ (r − k).

Из этого равенства следует, что число 1 делится на число p, которое больше 1, что невозможно. Следовательно, предположение, что n + 1 делится на p, неверно, т. е. n + 1 не делится на p, что и требовалось доказать.

Здесь для доказательства использован метод рассуждения от противного. Учащиеся должны осознать, какое предположение сделано, какое противоречие получено из этого предположения, какой вывод следует из полученного противоречия. Этот метод рассуждения и дальше будет применяться, поэтому в классе с углублённым изучением математики его надо хорошо отработать.

18. Выписали первые 99 натуральных чисел: 1, 2, ..., 99. Запятые стёрли и получили натуральное число.

а) Сколько раз в записи этого числа встречается циф-

ра: 0, 1, 2, 3, ..., 9?

б) Делится ли это число на 9?

Решение. а) В записи 1, 2, 3, ..., 99 каждая цифра (кроме 0) встречается 20 раз: по 10 раз в разряде десятков и в разряде единиц, а цифра 0 встречается 9 раз в разряде единиц.

б) Сумма цифр полученного числа равна

0 ⋅ 9 + (1 + 2 + 3 + ... + 9) ⋅ 20 = 45 ⋅ 20,

она делится на 9, так как один из множителей делится на 9, следовательно, и число делится на 9.

19. Произведение первых п (п ≥ 2) натуральных чисел обозначают п! и читают «эн факториал»:

п! = 1 ⋅ 2 ⋅ 3 ⋅ ... ⋅ (n − 1) ⋅ п.

На сколько нулей оканчивается: а) 10!; б) 50!; в) 100!?

Решение. Так как каждый нуль в конце десятичной записи натурального числа получается при умножении числа, делящегося на 5, и чётного числа, то, чтобы выяснить, сколькими нулями оканчивается десятичная запись натурального числа m = n!, надо выяснить, сколько чисел в этом произведении имеют делитель 5 (точнее, сколько делителей 5 имеет число m).

а) Произведение 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 ⋅ 7 ⋅ 8 ⋅ 9 ⋅ 10 содержит два числа, имеющих множитель 5, — число 5 и число 10.

Следовательно, число 10! оканчивается двумя нулями.

б) Произведение 1 ⋅ 2 ⋅ 3 ⋅ ... ⋅ 48 ⋅ 49 ⋅ 50 содержит 10 чи-

сел, имеющих множитель 5 (5, 10, 15, 20, 25, 30, 35, 40, 45, 50), причём 25 и 50 имеют по два множителя 5, значит, число 50! оканчивается двенадцатью нулями.

в) Произведение 1 ⋅ 2 ⋅ 3 ⋅ ... ⋅ 98 ⋅ 99 ⋅ 100 содержит 20 чи-

сел, имеющих множитель 5 (5, 10, 15, 20, 25, ... , 95, 100), причём четыре из них — 25, 50, 75 и 100 — имеют по два множителя 5. Следовательно, число 100! оканчивается двадцатью четырьмя нулями.

1.2. Степень числа

В данном пункте вводится определение степени с натуральным показателем, приводятся свойства степеней, выражаемые равенствами

1) pⁿ⋅ qⁿ = (p ⋅ q)ⁿ; 2) pⁿ⋅ p^m = pⁿ⁺^m; 3) (p^m)ⁿ = p^m^⋅ⁿ.

Знание этих свойств обязательно для каждого учащегося, так как их применение будет встречаться очень часто. Задания для повторения. При изучении данного пункта можно использовать задания 782—783, 785—791.

Решения и комментарии

33. Используя свойство 3 степеней, запишите в виде степени: а) (2²)³; б) (3⁴)².

Решение. а) (2²)³ = 2²^⋅³ = 2⁶; б) (3⁴)² = 3⁴^⋅² = 3⁸.

788. Сравните значения числовых выражений: а) 4⁸и

8⁶; б) 14⁴и 2¹⁶.

Решение. а) 4⁸ = (2²)⁸ = 2²^⋅⁸ = 2¹⁶, 8⁶ = (2³)⁶ = 2³^⋅⁶ = 2¹⁸= = 2¹⁶⁺²= 2¹⁶ ⋅ 2²= 2¹⁶ ⋅ 4 > 2¹⁶, т. е. 4⁸ < 8⁶.

б) 14⁴ = (2 ⋅ 7)⁴ = 2⁴⋅ 7⁴; 2¹⁶ = 2⁴ ⋅ 2¹² = 2⁴ ⋅ (2³)⁴ = 2⁴ ⋅ 8⁴. Так

как 7⁴ < 8⁴, то 2⁴⋅ 7⁴ < 2⁴⋅ 8⁴, т. е. 14⁴ < 2¹⁶.

790. Между какими степенями числа 2 расположено число: а) 6; д) 1025?

Решение. а) 2¹ = 2, 2² = 4 < 6, а 2³ = 8 > 6. Следовательно, 2² < 6 < 2³.

д) 2⁴ = 16, 2⁵= 32, 2⁶= 64, 2⁷= 128, 2⁸= 256, 2⁹= 512, 2¹⁰= 1024 < 1025, 2¹¹= 2048 > 1025. Значит, 2¹⁰ < 1025 < 2¹¹.

1.3. Простые и составные числа

В данном пункте вводятся важные понятия: простые и составные числа. Отмечается, что число 1 не относят ни к простым, ни к составным числам. Это должны усвоить все учащиеся. Здесь же приведены две теоремы о свойствах простых чисел:

Теорема 1. Каждое отличное от единицы натуральное число имеет делитель — простое число.

Теорема 2. Простых чисел бесконечно много.

Доказательства этих теорем, основанные на рассуждении от противного, предназначены учащимся классов с углублённым изучением математики. В таком классе можно сформулировать ещё одно утверждение:

Если дано натуральное число p, то множество всех натуральных чисел разбивается на p непересекающихся классов чисел, имеющих при делении на p остатки:

0, 1, 2, ..., p − 1.

Это утверждение используется при решении многих задач. Например, множество всех натуральных чисел разбивается на три класса — тех, которые при делении на 3 дают: остаток 0 (числа вида 3n), остаток 1 (числа вида 3n + 1), остаток 2 (числа вида 3n + 2), где n — натуральное число. Любое натуральное число принадлежит только одному из этих классов. Отсюда, в частности, следует, что сумма любых трёх соседних натуральных чисел делится на 3. В самом деле, 3n + 3n + 1 + 3n + 2 = 3 (3n + 1) — делится на 3.

Задания для повторения. При изучении данного пункта можно использовать задания 784, 798—799.

Отметим, что в данном пункте под чётным числом понимается натуральное число, делящееся на 2, а под нечётным числом — натуральное число, делящееся на 2 с остатком 1.

Решения и комментарии

40. Докажите, что 2 — единственное чётное простое число.

Доказательство. Предположим противное: что существует простое чётное число p, большее 2. Тогда это число можно записать в виде p = 2n, где n — натуральное число, большее 1. Но тогда число p является составным, так как имеет больше двух делителей, оно делится на 1, на n и на p. Получилось противоречие с условием «число p — простое». Следовательно, не существует простое чётное число p, большее 2. Поэтому число 2 — единственное чётное простое число, что и требовалось доказать.

42. Можно ли простое число записать в виде суммы:

а) двух чётных чисел; б) двух нечётных чисел; в) чётного и нечётного чисел?

Решение. а) Нет, так как сумма двух чётных натуральных чисел чётная и больше 2, она не может быть простым числом (см. № 40).

б) Можно, но только для одного простого числа: 2 = 1 + 1, сумма двух других нечётных натуральных чисел чётная и больше 2, она не может быть простым числом (см. № 40).

в) Простое число 2 нельзя записать в виде суммы чётного и нечётного чисел, так как имеется только один способ записи числа 2 в виде суммы натуральных чисел: 2 = 1 + 1, т. е. в виде суммы двух нечётных чисел. Любое простое число n, большее 2, является нечётным, а любое нечётное число можно записать в виде суммы чётного и нечётного чисел, например, так: n = (n − 2) + 2.

43. Леонард Эйлер предложил такую формулу про-

стых чисел: p = п² − п + 41. Сколько простых чисел даёт эта формула при подстановке в неё последовательных натуральных чисел, начиная с 1? Выполните вычисления до получения первого составного числа.

Это хорошая вычислительная задача для группового решения. Следует распределить в классе задания всем учащимся: первый ученик вычисляет для п = 1, второй — для п = 2 и т. д. Многократно повторяющийся результат (p — простое число) приводит к гипотезе: p — простое число для любого натурального n. Но эта гипотеза неверна, в чём легко убедиться, взяв п = 41. Тогда p = 41² − 41 + 41 = 41².

Это число составное, так как делится на 1, 41 и 41².

Здесь учащиеся должны получить полезный опыт: чтобы доказать, что утверждение истинно, недостаточно одной лишь проверки верности утверждения даже для сорока чисел. Попутно мы получили и решение задачи 44.

45. а) Докажите, что одно из трёх соседних нечётных чисел делится на 3.

б) Известно, что р, р + 2, р + 4 — простые числа. Най-

дите р. Докажите, что других р не существует.

Доказательство. а) Пусть n, n + 2, n + 4 — соседние нечётные числа. Если n делится на 3, т. е. его можно записать в виде 3k, где k — некоторое натуральное число, то требуемое утверждение доказано. Если n не делится на 3, то его можно записать в виде 3k + 1 или 3k + 2, где k — некоторое натуральное число. В первом случае n + 2 = 3k + 3, т. е.

делится на 3, а во втором — n + 4 = 3k + 6, т. е. делится на 3.

Так как мы рассмотрели все возможные случаи, то среди любых трёх соседних нечётных чисел есть число, делящееся на 3, что и требовалось доказать.

б) Пусть p, p + 2, p + 4 — простые числа. Среди них нет числа 2, так как в противном случае не все они были бы простыми. Тогда эти числа нечётные. По доказанному выше среди них есть число, кратное 3. Единственное простое число, кратное 3, — это само число 3. Значит, p = 3 и других p не существует.

1.4. Разложение натуральных чисел на множители

В данном пункте вводятся понятия простого делителя и разложения натурального числа на простые множители, напоминается приём разложения натуральных чисел на простые множители, известный из 5 класса. Здесь же приводится (без доказательства) основная теорема арифметики:

Каждое отличное от 1 натуральное число можно разложить на простые множители, и такое разложение единственно.

Понимание этой теоремы необходимо каждому школьнику, так как она часто используется при решении задач. При этом считается, что любое простое число уже разложено на простые множители, например: 17 = 17¹, 29 = 29¹. Задания для повторения. При изучении данного пункта можно использовать задания 792—797.

Решения и комментарии

57. Сколько чисел от 1 до 100 не делится ни на 2, ни на 3?

Решение. В ряду натуральных чисел от 1 до 100:

а) есть числа, кратные числу 2. Это числа вида 2n: 2, 4, 6, ..., 100 — их 50;

б) есть числа, кратные 3. Это числа вида 3n: 3, 6, 9,

..., 99 — их 33;

в) есть числа, попавшие в оба списка. Это числа вида 6n: 6, 12, 18, ..., 96 — их 16.

Значит, всего чисел, которые делятся на 2, на 3 или на оба эти числа, 50 + 33 − 16 = 67. Тогда количество чисел, не делящихся ни на 2, ни на 3, равно 100 − 67 = 33.

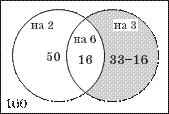Для иллюстрации решения задачи удобно применить круги Эйлера, называемые также диаграммами Эйлера — Венна

(рис. 1).

795. а) Какой цифрой не может оканчиваться квадрат натурального числа?

Решение. Из таблицы видно, что квадрат натурального числа не может оканчиваться цифрами

6 Рис. 1 2, 3, 7, 8.

Последняя цифра числа n	0	1	2	3	4	5	6	7	8	9
Последняя цифра числа n²	0	1	4	9	6	5	6	9	4	1

797. Найдите наименьшее натуральное число, дающее при делении на 2 остаток 1, на 3 остаток 2, на 4 остаток 3, на 5 остаток 4, на 6 остаток 5, на 7 остаток 6, на 8 остаток 7, на 9 остаток 8, на 10 остаток 9.

Решение. Для решения задачи найдём сначала число, на 1 большее искомого. Оно делится на 2, на 3, на 4, ..., на 10 без остатка. Наименьшее такое число равно

2 ⋅ 3 ⋅ 2 ⋅ 5 ⋅ 7 ⋅ 2 ⋅ 3 = 2520

(исключение любого из множителей приведёт к тому, что произведение не разделится на одно из чисел 7, 8, 9 или 10). Тогда искомое число есть 2519.

Дополнительные задания

1. Задание для исследования. Дано разложение составного числа A на простые множители:

а) A = p^m; б) A = p^m ⋅ qⁿ; в) A = p^m ⋅ qⁿ ⋅ r^k,

где p, q, r — простые числа.

Сколько различных делителей имеет число А?

Решение. а) Число А делится только на 1, p¹, p², ..., p^m, т. е. число всех различных делителей этого числа равно m + 1.

б) Выпишем все делители чисел p^m и qⁿ:

1, p¹, p², ..., p^m, 1, q¹, q², ..., qⁿ.

Полный список всех делителей числа А можно получить так: возьмём первое число в первой строке и умножим его на каждое число из второй строки, получим первые (n + 1) делителей. Затем возьмём второе число в первой строке и умножим его на каждое число из второй строки, получим второй набор из (n + 1) делителей и т. д. Наконец, возьмём (m + 1)-е число в первой строке и умножим его на каждое число из второй строки, получим (m + 1)-й набор из (n + 1) делителей. Отметим, что все полученные делители числа А различны и других делителей нет. Поэтому число всех делителей числа А равно

(m + 1) (n + 1).

в) Рассуждая так, как в предыдущем задании, по-

лучим, что число всех делителей числа А равно

(m + 1) (n + 1) (k + 1).

2. Задание 19 можно переформулировать так.

На какую наибольшую степень числа 5 делится число:

а) 10!; б) 50!; в) 100!?

Решение. в) Среди 100 чисел: 1, 2, 3, 4, ..., 99, 100 каждое 5-е делится на 5, т. е. имеет множитель 5. Таких чисел 100 : 5 = 20. Среди тех же 100 чисел каждое 25-е делится на 25 = 5², таких чисел 100 : 25 = 4. Так как 100 < 5³, то среди тех же 100 чисел нет чисел, делящихся на 125. Следовательно, в разложении числа 100! на простые множители число 5 будет сомножителем (20 + 4) раза.

Итак, число 100! делится на 5²⁴ (но не делится на 5²⁵),

т. е. 5²⁴ — наибольшая степень числа 5, на которую делится число 100!.

3. Сколькими нулями оканчивается: а) 250!; б) 1250!;

в) 62 500!?

Решение. а) Среди 250 чисел: 1, 2, 3, 4, ..., 249, 250 каждое 5-е делится на 5, т. е. имеет множитель 5. Таких чисел 250 : 5 = 50. Среди тех же 250 чисел каждое 25-е делится на 25 = 5², таких чисел 250 : 25 = 10. Среди тех же 250 чисел каждое 125-е делится на 125 = 5³, таких чисел 250 : 125 = 2. Так как 250 < 5⁴, то среди тех же 250 чисел нет чисел, делящихся на 625. Следовательно, в разложении числа 250! на простые множители число 5 будет сомножителем (50 + 10 + 2) = 62 раза.

Это решение можно записать кратко:

⁺₂⁺₃ = 50 + 10 + 2 = 62.

б) ⁺₂⁺₃⁺₄ = 250 + 50 + 10 + 2 = 312.

в) + 2 + 3 + 4 + 5 + 6 =

= 12 500 + 2500 + 500 + 100 + 20 + 4 = 15 624. Ответ. а) 62; б) 312; в) 15 624.

Промежуточный контроль. С—1, Т—1, С—2* (С—5*)^{^[1]}.

§ 2. Рациональные числа

В § 2 повторяется материал, изученный в 5—6 классах. Для учащихся, обучавшихся по учебникам серии «МГУ — школе», этот материал знаком, а для обучавшихся по другим учебникам материал о бесконечных десятичных дробях будет новым.

В результате изучения параграфа каждый учащийся должен свободно производить арифметические действия с рациональными числами и усвоить, что есть две формы записи рациональных чисел — в виде обыкновенной дроби p

, p ∈ Z, q ∈ N, и в виде бесконечной десятичной периодиq

ческой дроби.

2.1. Обыкновенные дроби. Конечные десятичные дроби 2.2. Разложение обыкновенной дроби в конечную десятичную дробь

В пунктах 2.1 и 2.2 вводятся понятия положительного рационального числа, обыкновенной положительной дроби, десятичного разложения обыкновенной дроби и др., рассматривается основное свойство дроби, выясняется возможность записи обыкновенной дроби, знаменатель которой не имеет других простых делителей, кроме 2 и 5, в виде конечной десятичной дроби, а также любой десятичной дроби в виде обыкновенной.

Задания для повторения. При изучении данного пункта можно использовать задания 805—814, 827—831. При этом не следует ставить задачу решить все задания, надо использовать те из них, в которых требуется прим енять ещё недостаточно сформированные у учащихся умения.

Решения и комментарии

67. Сократите дробь: г) ; д) ; е) .

Решение. г) ;

д) ;

е) .

Обратим внимание на подробную запись сокращения дробей, которая приведена выше. Она помогает учащимся лучше осознать смысл выполняемых действий (деление числителя и знаменателя дроби на общий множитель). На первых порах не стоит стремиться к использованию краткой записи с зачёркиванием числителя и знаменателя. Для некоторых учащихся сокращение дробей превращается именно в зачёркивание чисел, что зачастую приводит к ошибкам.

Например, они пишут неверные равенства:

= или = .

Промежуточный контроль. С—3 (С—2).

2.3. Периодические дроби

В данном пункте вводятся понятия бесконечной периодической десятичной дроби, периода дроби для положительных чисел, сформулированы два утверждения:

1) любое положительное рациональное число разлаq

гается в периодическую дробь;

2) любая периодическая дробь есть десятичное разложеp

ние некоторого положительн ого рационального числа .

Решения и комментарии

86. Подберите обыкновенную дробь, равную периоди-ческой дроби:

а) 0,(8); в) 0,(13); е) 0,(125).

Решение. При решении этого задания надо использовать наблюдения, полученные при рассмотрении примеров 1 и 2 из учебного текста, а также убедиться в верности результата с помощью деления числителя дроби на её знаменатель.

а) 0,(8) = ; в) 0,(13) = ; е) 0,(125) = .

87. Определите цифру сотого разряда после запятой в записи периодической дроби: б) 0,(25); в) 0,(123); д) 5,2(13).

Решение. б) 0,(25) = 0,252525... — во 2, 4, 6, ...,

100-м разрядах стоит цифра 5, т. е. сотая цифра 5;

в) 0,(123) = 0,123123123... — каждая тройка цифр после запятой оканчивается цифрой 3, а следующая начинается цифрой 1. Сотая цифра стоит после 33-й тройки, это цифра 1;

д) 5,2(13) = 5,2131313... — на чётных местах после за-

пятой стоит цифра 1. Сотая цифра 1.

Дополнительное задание

1. У данной дроби зачеркнули цифру сотого разряда после запятой. Увеличится или уменьшится при этом дробь: а) 0,(7); б) 0,(31); в) 0,(517)?

Решение. Для решения задачи надо сначала определить цифру сотого разряда после запятой (см. задание 87) и следующую за ней цифру.

а) Так как цифра сотого разряда после запятой не из-

менится, то новая дробь равна данной.

б) Так как цифра 1 сотого разряда после запятой за-

менится на цифру 3, то дробь увеличится.

в) Так как цифра 5 сотого разряда после запятой за-

менится на цифру 1, то дробь уменьшится.

2.4*. Периодичность десятичного разложения обыкновенной дроби

В данном пункте доказано утверждение 1, сформулированное в предыдущем пункте, показан способ перевода любой периодической дроби в обыкновенную. Материал этого пункта предназначен для классов с углублённым изуч ением математики, но желательно, чтобы и учащиеся обычных классов освоили способ перевода любой периодической дроби в обыкновенную.

Заметим, что в учебнике периодическая дробь определяется как результат деления уголком числителя дроби на её знаменатель. Так как не обоснованы правило умножения бесконечной десятичной дроби на 10^k и правило выч итания бесконечных десятичных дробей, то после перевода периодической дроби в обыкновенную нужно убедиться делением уголком числителя обыкновенной дроби на её знаменатель, что получена обыкновенная дробь, равная данной бесконечной десятичной дроби. В обычном классе на этой тонкости можно не останавливаться.

В классе с углублённым изучением математики можно сформулировать известное мнемоническое правило перевода любой периодической дроби в обыкновенную: для того чтобы записать периодическую десятичную дробь в виде обыкновенной дроби, надо в числителе записать разность числа до второго периода и числа до первого периода, в знаменателе записать столько девяток, сколько цифр в периоде, и приписать к ним столько нулей, сколько цифр между запятой и первым периодом.

Задания для повторения. При изучении данного пункта можно использовать задание 867. Это задание «на выносливость», на тренировку вычислений без сбоев. При выполнении задания 867б потребуется предварительно переводить бесконечные десятичные дроби в обыкновенные.

Решения и комментарии

89. Может ли период десятичного разложения обыкновенной дроби содержать 8 цифр?

Решение. При делении числителя дроби 6 на её знаменатель 7 может получиться не больше 6 остатков: 1, 2, 3,

4, 5, 6. Остаток 0 получиться не может, так как в разложении знаменателя несократимой дроби на простые множители содержится множитель 7, отличный от 2 и 5. Поэтому период десятичного разложения обыкновенной дроби не может содержать 8 цифр.

90. Покажите на примере, как периодическую дробь с периодом 9 можно превратить в конечную десятичную дробь.

Решение. Пусть дана дробь 0,(9). Выполнив рассуждения, как в примере 2 учебного текста, получим

x = 0,(9) = 0,999...,

10x = 9,999...,

10x − x = 9, 9x = 9, x = 1.

Одно и то же число x оказалось записанным двумя способами, причём сравнение чисел 0,999... и 1 по правилу сравнения десятичных дробей приводит к выводу, что эти числа не равны. Именно по этой причине бесконечные десятичные дроби с периодом 9 не рассматриваются. Заметим также, что такие дроби не могут получиться при делении уголком числителя обыкновенной дроби на её знаменатель.

2.5. Десятичное разложение рациональных чисел

В данном пункте необходимо повторить всё, что связано со знаком числа, на примере сначала целых чисел, затем рациональных чисел. Здесь можно повторить также правила сравнения рациональных чисел, операции с ними.

Только после этого следует поговорить о том, что каждое рациональное число можно записать как в виде обыкp новенной дроби , p ∈ Z, q ∈ N, так и в виде бесконечной q

десятичной периодической дроби.

Задания для повторения. При изучении этого материала можно использовать многие задания, например задания 816—826, 843—854. Решения и комментарии

104. Запишите рациональные числа в виде периодиче-ских дробей:

а) −; 0; –1,24; б) ; −; −2 .

Решение. а) − = –0,5 = –0,5(0); 0 = 0,(0); –1,24 = –1,24(0);

б) = 0,(3); − = –0,(571428); −2 = –2,(384615).

Периоды, отличные от нуля, получены делением числителя обыкновенной дроби на знаменатель уголком.

105. Запишите в виде рационального числа периоди-ческую дробь:

в) –2,(5); г) –0,(17); и) 4,37(0). Решение. в) –2,(5) = −2 ; г) –0,(17) = −;

и) 4,37(0) = 4,37 = 4 .

Промежуточный контроль. С—4 (С—3).

§ 3. Действительные числа

Материал § 3 следует изучать как новый, даже если в 5—6 классах учащиеся занимались по учебникам серии «МГУ — школе», так как он имеет исключительно важное значение для дальнейшего обучения.

В итоге изучения параграфа учащиеся должны понять, что существуют рациональные и иррациональные числа, образующие вместе множество действительных чисел, что при изображении действительных чисел на координатной оси она (ось) оказывается заполненной числами без просветов, что арифметические действия с действительными числами обладают обычными свойствами, т. е. для них справедливы те же законы (переместительный, сочетательный, распределительный), что и для натуральных чисел.

В обычных классах до окончания школы множество действительных чисел больше расширяться не будет, поэтому действия с действительными числами надо хорошо освоить, этих умений будет достаточно для дальнейшего изучения школьной математики и смежных дисциплин.

3.1. Иррациональные числа 3.2. Понятие действительного числа 3.3. Сравнение действительных чисел

В пунктах 3.1 и 3.2 вводятся понятия бесконечной непериодической десятичной дроби, иррационального числа и действительного числа, а также понятия целой части и модуля числа для действительных чисел, понятие противоположных чисел.

Надо, чтобы учащиеся поняли, что существуют не только рациональные, но и другие числа, не являющиеся рациональными (иррациональные числа). Здесь можно использовать не только материалы пунктов 3.1 и 3.2, но и «Исторические сведения», где показано геометрическое обоснование существования иррациональных чисел.

Важно, чтобы учащиеся поняли, что объединение множеств рациональных и иррациональных чисел даёт множество действительных чисел и что действительное число есть бесконечная десятичная дробь (если периодическая, то рациональное, если непериодическая, то иррациональное).

В пункте 3.3 вводятся правила сравнения действительных чисел.

На уроках, отведённых для изучения иррациональных и действительных чисел, будет не так много упражнений по новому материалу, поэтому на этих уроках можно выделить время для решения задач на повторение и решения текстовых задач.

Задания для повторения. При изучении данных пунктов можно использовать задания 862—865.

Решения и комментарии

133. Для чисел 2,(1) и 2,111 укажите хотя бы одно такое число, которое было бы больше одного из этих чисел и меньше другого.

Решение. Так как 2,(1) = 2,1111..., а 2,111 = 2,111000..., т. е. цифры в трёх разрядах после запятой одинаковые, то в четвёртом разряде надо оставить 0, а в пятом разряде можно поставить любую цифру, например 5, получится число, которое больше одного из этих чисел и меньше другого: 2,11105.

134. Числа а и b отрицательные, и | а | < | b |. Сравните числа:

а) а и 0; б) –b и 0; в) –b и а;

г) b и –а; д) –b и –а; е) а и | b |.

Решение. а) а < 0, так как отрицательное число меньше нуля;

б) –b > 0, так как положительное число больше нуля;

в) –b > а, так как положительное число больше отри-

цательного;

г) b < –а, так как отрицательное число меньше поло-

жительного;

д) –b > –а, так как из двух положительных чисел боль-

ше то, у которого модуль больше;

е) а < | b |, так как отрицательное число меньше поло-

жительного.

862. а) Каково наибольшее действительное число, меньш ее 0,9, в десятичную запись которого не входит цифра 9?

б) Существует ли наименьшее число, большее 1?

в) Каково наименьшее действительное число, большее 3,6, в бесконечную десятичную запись которого не входят цифры 0, 1 и 2?

Решение. а) Наибольшим действительным числом, меньш им 0,9, в десятичную запись которого не входит цифра 9, является число 0,(8) = 0,888... . Это число невозможно увеличить, не поставив хотя бы в одном из разрядов цифру 9.

б) Наименьшее число, большее 1, не существует, так как если бы оно существовало, то, обозначив его a (a > 1), можно получить число, меньшее a, но большее 1. Таким a + 1 числом, например, является число . В самом деле, так

как a > 1, то ^a⁺¹ > ¹⁺¹ = 1, но ^a⁺¹ < ^{a a}⁺ = a, т. е. 1 < ^a⁺¹ < a.

2 2 2 2 2

в) Наименьшим действительным числом, большим 3,6, в бесконечную десятичную запись которого не входят цифры 0, 1 и 2, является число 3,(3) = 3,333... , так как нельзя уменьшить это число, не поставив в каком-то разряде 0, 1 или 2.

3.4. Основные свойства действительных чисел

В данном пункте приведены 5 свойств, связанных со сравнениями действительных чисел, и 13 равенств, выражающих свойства действительных чисел. Запоминать все свойства и воспроизводить их не требуется, но учащиеся должны понимать, что существуют основные свойства действительных чисел, с помощью которых можно доказать другие свойства действительных чисел. Они должны уметь обосновывать свои действия, находя соответствующее свойство среди перечисленных в пункте 3.4. Вопрос: «Какими свойствами мы пользовались, выполняя вычисления?» — полезно задавать при выполнении заданий 146—147.

Важно, чтобы учащиеся научились сравнивать действительные числа, знали их свойства, которыми в дальнейшем будут пользоваться.

В классе с углублённым изучением математики надо подробнее обсудить свойства арифметических операций над действительными числами. Учащиеся должны понять, что на самом деле постулируется (принимается без доказательства), что сумма (разность, произведение, частное, кроме деления на нуль) двух действительных чисел является действительным числом и что это число единственное.

Решения и комментарии Вычислите (146—147):

146. а) 3,(27) ⋅ 5 − 3,(27) ⋅ 4.

Решение. 3,(27) ⋅ 5 − 3,(27) ⋅ 4 = 3,(27) ⋅ (5 − 4) = 3,(27) ⋅ 1 = = 3,(27).

Эта краткая запись иногда обосновывается с помощью «распределительного закона умножения относительно вычитания», которого нет среди свойств действительных чисел в пункте 3.4. Так в данном примере справедливость всех равенств следует из свойств 5) и 8) и правила умножения чисел с разными знаками:

3,(27) ⋅ 5 − 3,(27) ⋅ 4 = 3,(27) ⋅ 5 + (–3,(27) ⋅ 4) = = 3,(27) ⋅ 5 + 3,(27) ⋅ (–4) = 3,(27) ⋅ (5 + (–4)) = = 3,(27) ⋅ 1 = 3,(27). 147. а) (3,2 + (–1,7)) + 1,7.

Решение. (3,2 + (–1,7)) + 1,7 = 3,2 + (–1,7 + 1,7) = 3,2 + 0 = = 3,2.

Здесь применены свойства 2) и 7).

Надо предупредить учащихся, что при изучении следующей темы им понадобится калькулятор.

3.5. Приближения числа

В данном пункте вводятся понятия приближения числа, приближения с недостатком, приближения с избытком, приближения с округлением значащей цифры, приведены правила приближённых вычислений при сложении или вычитании и при умножении или делении, показаны примеры их применения. По первому из этих правил числа округляются с точностью до одного и того же десятичного разряда, результат операции получается с той же точностью. По второму правилу числа округляются с точностью до одного и того же количества значащих цифр, результат операции надо округлить с той же точностью (до того же количества значащих цифр).

В обычном классе можно ограничиться словами о том, что сумма (разность, произведение, частное, кроме деления на нуль) двух действительных чисел является действительным числом, что это число единственное и находится приближённо по правилам, описанным в пункте 3.4.

Надо, чтобы учащиеся поняли, что не существует алгоритмов вычислений с бесконечными непериодическими дробями, действия с ними выполняют приближённо.

Следует учесть, что слабые учащиеся с трудом усваивают данный материал, но его изучение необходимо, чтобы учащиеся осмысленно применяли калькулятор при приближённых вычислениях, а не выписывали в ответах «лишние» цифры. Материал этого пункта имеет важное значение для приближённых вычислений при изучении математики и смежных дисциплин, а также для практических расчётов.

Решения и комментарии 152. Найдите приближение с точностью до 0,01 числа: а) 127,(023); б) 0,1(27); в) –1,34(8);

г) –0,56789101112... .

Решение. а) 127,(023) = 127,023... ≈ 127,02; б) 0,1(27) = 0,127... ≈ 0,13;

в) –1,34(8) = –1,34888... ≈ –1,35;

г) –0,56789101112... ≈ –0,57. 153. Укажите значащие цифры числа:

а) 3,52; б) 0,352; в) 0,03520; д) 4,203;

е) 0,005; з) 7,0003; и) 10,0050; л) 0,00067. Решение. Значащие цифры числа можно подчеркнуть: а) 3,52; б) 0,352; в) 0,03520; д) 4,203;

е) 0,005; з) 7,0003; и) 10,0050; л) 0,00067.

154. Округлите число 1039,9301 до седьмой; шестой; пятой; четвёртой; третьей значащей цифры.

Решение. 1039,9301 ≈ 1039,930 (до седьмой значащей цифры);

1039,9301 ≈ 1039,93 (до шестой значащей цифры);

1039,9301 ≈ 1039,9 (до пятой значащей цифры);

1039,9301 ≈ 1040 (до четвёртой значащей цифры); 1039,9301 ≈ 1040 (до третьей значащей цифры).

Чтобы подчеркнуть, что в последнем случае выполнено округление до третьей значащей цифры, результат можно представить в виде двух множителей так, чтобы первый был округлён до третьей значащей цифры: 104 ⋅ 10. Так как стандартный вид числа ещё не изучен, то ответ можно записать и так: 10,4 ⋅ 100, 1,04 ⋅ 1000, 10,4 ⋅ 10², 1,04 ⋅ 10³. Это полезное упражнение, готовящее учащихся к введению стандартного вида числа.

155. Вычислите приближённо сумму, округлив данные числа с точностью до 0,1:

в) 0,100100010... + 0,238; г) 2,7(3) + 3,(42).

Решение. в) 0,100100010... + 0,238 ≈ 0,1 + 0,2 = 0,3;

г) 2,7(3) + 3,(42) = 2,7333... + 3,4242... ≈ 2,7 + 3,4 = 6,1. 158. Вычислите приближённо произведение, округлив данные числа с точностью до второй значащей цифры:

г) 0,56 ⋅ 0,(3); д) 0,(1) ⋅ 0,(2); е) 12,(45) ⋅ 10,(1). Решение. г) 0,56 ⋅ 0,(3) = 0,56 ⋅ 0,333... ≈ 0,56 ⋅ 0,33 =

= 0,1848 ≈ 0,18;

д) 0,(1) ⋅ 0,(2) = 0,111... ⋅ 0,222... ≈ 0,110 ⋅ 0,220 = 0,0242 ≈

≈ 0,024;

е) 12,(45) ⋅ 10,(1) = 12,4545... ⋅ 10,111... ≈ 12 ⋅ 10 = 120 = = 12 ⋅ 10 (или 1,2 ⋅ 10²).

159. Вычислите приближённо частное, округлив данные числа с точностью до второй значащей цифры:

г) 0,(2) : 2; д) 4,(2) : 1,(3); е) 45,6(12) : 10,(2). Решение. г) 0,(2) : 2 = 0,222... : 2 ≈ 0,22 : 2 = 0,11;

д) 4,(2) : 1,(3) = 4,222... : 1,333... ≈ 4,2 : 1,3 = 3,23... ≈ 3,2;

е) 45,6(12) : 10,(2) = 45,612... : 10,222... ≈ 46 : 10 = 4,6.

161. Даны числа а = 5,(1) и b = 2,123456... . Сумма а + b заключена между целыми числами 5 + 2 = 7 и 6 + 3 = 9: 7 < а + b < 9. Здесь числа 5 и 2 — приближения чисел а и b с точностью до 1 снизу, а числа 6 и 3 — приближения чисел а и b с точностью до 1 сверху.

Получите более точные границы для суммы а + b, найдя приближения а и b с точностью до: а) 0,1; б) 0,01; в) 0,001.

Решение. а) 5,1 < а < 5,2 и 2,1 < b < 2,2; 7,2 < а + b < 7,4 с точностью до 0,1;

б) 5,11 < а < 5,12, 2,12 < b < 2,13; 7,23 < а + b < 7,25 с

точностью до 0,01;

в) 5,111 < а < 5,112, 2,123 < b < 2,124; 7,234 < а + b < 7,236 с точностью до 0,001.

Замечание. На эту задачу полезно обратить внимание, так как неравенства и сложение верных числовых неравенств не являются предметом изучения в 7 классе, но складывать верные числовые неравенства требуется, например в геометрии. Здесь можно опираться на интуитивно ясные факты — свойства действительных чисел (пункт 3.4).

Выполняя задание а), мы фактически сложили верные числовые неравенства. Так как a = 5,1111..., b = 2,1234... и

5,1 < a < 5,2,

2,1 < b < 2,2, то

5,1 + 2,1 < a + b < 5,2 + 2,2.

Используемое здесь свойство верных числовых неравенств можно доказать с опорой на свойства действительных чисел.

Пусть известно, что m < a < n и x < b < y. Докажем, что m + x < a + b < n + y.

Доказательство. Так как m < a, то m + x < a + x. Так как x < b, то a + x < a + b. Тогда m + x < a + b. Аналогично показывается, что a + b < n + y.

Промежуточный контроль. С—5 (С—4).

3.6. Длина отрезка 3.7. Координатная ось

В пункте 3.6 на конкретных примерах описан процесс измерения отрезка с точностью до 1, до 0,1, до 0,01, ... . Важным для всех учащихся является понимание того, что длина любого отрезка есть бесконечная десятичная дробь и что каждая положительная бесконечная десятичная дробь есть длина некоторого отрезка.

В пункте 3.7 вводятся понятия направления на прямой, начальной точки, единичного отрезка, координатной оси, координаты точки, начала координат оси Ox, положительной координатной полуоси и отрицательной координатной полуоси.

Важно, чтобы учащиеся поняли, что каждой точке координатной оси соответствует единственное действительное число — координата этой точки, что двум разным точкам соответствуют разные координаты, а любому действительному числу соответствует единственная точка координатной оси и что координатная ось заполнена полностью, на ней нет просветов, как это было после изучения рациональных чисел.

В классе с углублённым изучением математики стоит подробнее остановиться на понятии взаимно однозначного соответствия, приведя примеры взаимно однозначного соответствия множеств натуральных чисел и чётных натуральных чисел, множеств натуральных чисел и целых чисел.

Задания для повторения. При изучении данного пункта можно использовать задания 868—879.

Решения и комментарии

164. Дан квадрат со стороной 1 см. Верно ли, что существует действительное число, выражающее длину диагонали этого квадрата?

Решение. Верно, так как каждый отрезок имеет длину, выражаемую бесконечной десятичной дробью.

В классе с углублённым изучением математики можно рассмотреть геометрическое обоснование того, что эта дробь не является периодической, т. е. что длина диагонали выражается иррациональным числом.

171. в) Начертите координатную ось и укажите на ней данные числа, выбрав удобный единичный отрезок и положение начала координатной оси: ; ; 0,75; ; .

Решение. Так как = ; = ; 0,75 = = ; = ,

то длину единичного отрезка удобно взять равной 6 см, или 12 клеткам тетради (рис. 2).

6 Рис. 2 172. Укажите на координатной оси числа:

в) 300; 400; 600; е) –0,24; –0,28; –0,22.

Решение. Здесь можно не изображать начало координат, указав лишь длину отрезка, соответствующего 100 (в задании в) и 0,02 (в задании е) единицам (рис. 3).

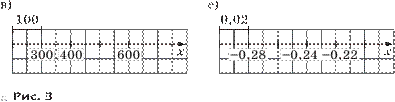
Промежуточный контроль. К—1.

Дополнения к главе 1

Материал, дополняющий программу обычных классов до программы классов с углублённым изучением математики, позволяет сильным учащимся обычных классов подготовиться к олимпиадам. В классе с углублённым изучением математики учащиеся должны освоить некоторые методы доказательства утверждений, что способствует достижению таких метапредметных результатов, как умение создавать обобщения, устанавливать аналогии, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение и делать выводы.

1. Делимость чисел

В данном пункте сначала доказана теорема о делимости суммы и разности двух чисел на число, на которое делится каждое из этих чисел. В отличие от доказательства этого факта в 5 классе на конкретном числовом примере, здесь приведено общее доказательство (на буквах). Далее приведено доказательство одного из известных ранее признаков делимости (на 9). Это доказательство проведено для шестизначных чисел в общем виде. Затем вводятся понятия наибольшего общего делителя и наименьшего общего кратного, доказано свойство НОД (a, b) ⋅ НОК (a, b) = a ⋅ b, введены алгоритм Евклида, понятие взаимно простых чисел, деление с остатком целых чисел.

Решения и комментарии

174. Докажите признак делимости: число а = a_{5 4 3 2 1 0}a a a a a делится на 11, если сумма а₀ − а₁ + а₂ − а₃ + а₄ − а₅ делится на 11.

Решение. Признак делимости на 11 можно сформулировать так: «Если разность между суммами цифр числа, стоящих на нечётных и на чётных местах, делится на 11, то и число делится на 11».

Здесь предлагается доказать признак делимости для шестизначного числа.

Доказательство. Так как

а = 10⁵ ⋅ а₅ + 10⁴ ⋅ а₄ + 10³ ⋅ а₃ + 10² ⋅ а₂ + 10 ⋅ а₁ + а₀ =

= (100 001 ⋅ а₅ + 9999 ⋅ а₄ + 1001 ⋅ а₃+ 99 ⋅ а₂ + 11 ⋅ а₁) +

+ (а₄ + а₂ + а₀) − (а₅ + а₃ + а₁)

и сумма в первых скобках делится на 11, то число а делится на 11, если

(а₄+ а₂ + а₀) − (а₅ + а₃ + а₁)

делится на 11.

175. а) Придумайте и докажите признак делимости на 125.

Решение. Если три последние цифры натурального числа образуют число, делящееся на 125, то и число делится на 125 (считайте запись 000 записью числа 0).

Например, так как числа 0, 125, 375 делятся на 125, то числа 7000, 7125, 7375 делятся на 125.

Доказательство. Любое многозначное число можно записать в виде 1000а + a_{2 1 0}a a . Так как 1000а делится на

125, то если число a_{2 1 0}a a делится на 125, то и данное многозначное число делится на 125.

177. Вычислите НОД и НОК чисел:

а) 231 и 217; б) 639 и 221; з) 1999 и 2000.

Решение. а) Так как 231 = 3 ⋅ 7 ⋅ 11, 217 = 7 ⋅ 31, то

НОД (231, 217) = 7, а НОК (231, 217) = 3 ⋅ 7 ⋅ 11 ⋅ 31 = 7161.

б) Так как 639 = 3² ⋅ 71, 221 = 13 ⋅ 17, то

НОД (639, 221) = 1, а НОК (639, 221) = 639 ⋅ 221 = 141 219.

з) Так как разность чисел 2000 и 1999 равна 1, то это

взаимно простые числа, НОД (2000, 1999) = 1, а НОК (2000, 1999) = 2000 ⋅ 1999 = 3 998 000.

178. Докажите, что произведение:

а) двух последовательных целых чисел делится на 2;

б) трёх последовательных целых чисел делится на 6;

в) четырёх последовательных целых чисел делится

на 24.

Решение. а) Из двух последовательных целых чисел одно чётное, другое нечётное, поэтому произведение этих чисел делится на 2.

б) Из трёх последовательных целых чисел одно делится на 3 и ещё хотя бы одно делится на 2, поэтому произведение этих чисел делится на 6.

в) Из четырёх последовательных целых чисел хотя бы одно делится на 3 и два делятся на 2. Причём одно из чётных чисел делится на 4, а их произведение делится на 8, поэтому произведение четырёх последовательных целых чисел делится на 3 ⋅ 8 = 24.

179. а) Найдите все целые числа, которые при делении на 4, на 3, на 2 дают остаток 1.

б) Найдите все целые числа, которые при делении на 4 дают остаток 3, при делении на 3 дают остаток 2, при делении на 2 дают остаток 1.

Решение. а) Так как число 12n делится на 4, на 3, на 2, то число 12n + 1 при любом целом n при делении и на 4, и на 3, и на 2 даёт остаток 1, т. е. все искомые целые числа задаются формулой 12n + 1, где n — любое целое число.

б) Если целое число при делении на 4 даёт остаток 3, при делении на 3 даёт остаток 2, при делении на 2 даёт остаток 1, то после увеличения этого числа на 1 новое число будет делиться без остатка на 4, на 3, на 2. Значит, новое число задаётся формулой 12n. Тогда все искомые целые числа задаются формулой 12n − 1, где n — любое целое число.

180. Определите число квадратов, на которые можно разрезать прямоугольник:

а) 18 × 5; б) 28 × 11; в) 157 × 44,

используя алгоритм Евклида.

Решение. а) Применив алгоритм Евклида для чисел 18 и 5, получим, что прямоугольник 18 × 5 можно разрезать на 3 квадрата со стороной 5, 1 квадрат со стороной 3, 1 квадрат со стороной 2, 2 квадрата со стороной 1. Значит, данный прямоугольник можно разрезать на 3 + 1 + 1 + 2 = 7 квадратов.

б) Применив алгоритм Евклида для чисел 28 и 11, по-

лучим, что прямоугольник 28 × 11 можно разрезать на 2 квадрата со стороной 11, 1 квадрат со стороной 6, 1 квадрат со стороной 5, 5 квадратов со стороной 1. Значит, данный прямоугольник можно разрезать на 2 + 1 + 1 + 5 = 9 квадр атов.

в) Применив алгоритм Евклида для чисел 157 и 44, получим, что прямоугольник 157 × 44 можно разрезать на 3 квадр ата со стороной 44, 1 квадрат со стороной 25, 1 квадрат со стороной 19, 3 квадрата со стороной 6, 6 квадратов со стороной 1. Значит, данный прямоугольник можно разрезать на 3 + 1 + 1 + 3 + 6 = 14 квадратов.

2. Исторические сведения

В данном пункте приведена информация о развитии знаний человечества о числе и вкладе российских учёных в науку о числе. Это способствует воспитанию российской гражданской идентичности: уважение к Отечеству, знание истории, культуры своего народа, основ культурного наследия народов России и человечества. Материал, представленный в данном пункте, помогает также формированию целостного мировоззрения, объясняет роль разных народов в истории математики, воспитывает уважительное отношение к разным народам мира.

Глава 2 Алгебраические выражения

Изучение главы 2 должно привести учащихся к пониманию того, что наряду с числами есть другие объекты — алгебраические выражения — и с этими объектами можно проводить преобразования по вполне определённым правилам, похожим на аналогичные правила для чисел.

В результате изучения главы учащиеся должны научиться правильно делать выкладки с одночленами, многочленами, алгебраическими дробями и уметь упрощать не очень сложные рациональные выражения.

Использование преобразований и упрощений выражений, приводящих сложную задачу к простой, обращение внимания учащихся на красоту и простоту того или иного теоретического факта способствуют эстетическому развитию учащихся. Использование арифметических способов решения, составление числового или буквенного выражения для решения задачи, способствует не только развитию мышления учащихся, но и обучению их планированию своей деятельности, осознанному выбору наиболее эффективных способов решения.

§ 4. Одночлены

В § 4 вводится понятие одночлена, формулируются правила преобразования одночленов, приведения их к стандартному виду и приведения подобных одночленов. Умения обращаться с одночленами будут использованы при изучении следующего параграфа «Многочлены». Основная цель изучения § 4 — научиться приводить одночлены к стандартному виду, приводить подобные одночлены.

4.1. Числовые выражения

В п. 4.1 рассматриваются понятия числового выражения и его значения, подчёркивается, что числовое выражение может не иметь смысла, так как именно этот факт будет нужен при рассмотрении алгебраических выражений.

Здесь также показан приём решения текстовых задач составлением числового выражения, ведётся работа, готовящая учащихся к введению буквенных выражений и использованию их для решения текстовых задач.

Решения и комментарии

188. а) Турист шёл 1 ч со скоростью 5 км/ч и 4 ч со скоростью 4 км/ч. Определите среднюю скорость туриста на пройденном участке пути.

Решение. Чтобы определить среднюю скорость туриста, надо пройденный путь разделить на время движения.

Задачу можно решить по действиям:

1) 1 ⋅ 5 + 4 ⋅ 4 = 21 (км) — путь, пройденный туристом;

2) 1 + 4 = 5 (ч) — время движения туриста;

3) 21 : 5 = 4,2 (км/ч) — средняя скорость туриста.

Можно также решить эту задачу составлением числового выражения:

21 : 5 = 4,2 (км/ч).

Ответ. 4,2 км/ч.

189. а) Первый кусок сплава массой 300 г содержит

40 % олова, а второй кусок сплава массой 200 г содержит 30 % олова. Определите процентное содержание олова в новом сплаве, полученном сплавлением этих кусков.

Решение. 1) 0,4 ⋅ 300 + 0,3 ⋅ 200 = 120 + 60 = 180 (г) — масса олова в новом сплаве;

2) 300 + 200 = 500 (г) — масса нового сплава;

3) 36 (%) — процентное содержание олова в

новом сплаве.

Задачу можно решить составлением числового выражения:

36 (%).

Ответ. 36%.

190. а) Зарплата сотрудника фирмы составляла 20 000 р. Сначала её повысили на 30 %. Через некоторое время эту зарплату увеличили ещё на 20 %. Определите новую зарплату сотрудника фирмы.

Решение. 1) 20 000 + 0,3 ⋅ 20 000 = (1 + 0,3) ⋅ 20 000 = = 26 000 (р.) — зарплата сотрудника после первого повышения;

2) 26 000 + 0,2 ⋅ 26 000 = (1 + 0,2) ⋅ 26 000 = 31 200 (р.) — зарплата сотрудника после второго повышения.

Замечание. Для обучения школьников решению задач на многократное увеличение (уменьшение) величины на несколько процентов, для понимания формулы сложных процентов важно научить их «свёрнутому» выполнению действий 1) и 2) с помощью вынесения общего множителя за скобки. Короче решение задачи можно записать составлением числового выражения:

(1 + 0,2) ⋅ (1 + 0,3) ⋅ 20 000 = 1,2 ⋅ 1,3 ⋅ 20 000 = 31 200 (р.).

Ответ. 31 200 р.

4.2. Буквенные выражения

В данном пункте вводится основное понятие главы 2 — алгебраическое выражение. Это понятие относится к основным понятиям алгебры и поэтому не определяется. В учебнике приводится лишь описание этого понятия: последовательно вводятся объекты, каждый из которых в дальнейшем будет называться алгебраическим выражением.

Сначала в числовом выражении заменяют числа буквами — получают буквенное выражение, которое называют также алгебраическим выражением. Затем добавляют к этим объектам числа и буквы, и их также называют алгебраическими выражениями. Наконец, вводят понятие суммы, разности, произведения и частного двух алгебраических выражений — как запись этих выражений с соответствующим знаком арифметической операции между ними — и каждый из полученных объектов также называют алгебраическим выражением.

Таким образом, описано, что понимают под термином «алгебраическое выражение». Стоит подчеркнуть, что учащиеся должны только понимать, что тот или иной объект есть алгебраическое выражение, но нельзя требовать от них давать определение алгебраического выражения.

Стоит обратить внимание на фразу на с. 64 учебника: «Впрочем, не для всяких двух выражений можно определить частное. Это связано с делением на 0». Здесь можно сказать, что если заданы два алгебраических выражения (a + c) и (2 − 2), то запись не называют алгебраическим выражением, так как делить на нуль нельзя. Говорят, что запись не имеет смысла, она не определяет

частное двух алгебраических выражений (a + c) и (2 − 2).

В этом пункте объясняется, что значит решить задачу в общем виде, на конкретных примерах приводятся формулы простых процентов (многократное увеличение суммы на одно и то же число процентов от её первоначальной величины — задача 3) и сложных процентов (многократное увеличение суммы на одно и то же число процентов от изменяющейся после каждого увеличения величины — задача 4). Так как при решении текстовых задач в общем виде буквы заменяют числа (точнее, величины), то решение задач на знакомые сюжеты в общем виде является хорошей подготовкой и мотивацией учащихся к освоению действий с буквенными выражениями.

Задания для повторения. При изучении данного пункта можно использовать задания 887—894.

Решения и комментарии

196. а) Два брата коллекционируют почтовые марки. У старшего брата в п раз больше марок, чем у младшего, а всего у них 150 марок. Сколько марок у каждого?

Решение. Если число марок младшего брата составляет 1 часть, то число марок старшего брата составляет n частей, т. е. на 150 марок приходится (n + 1) частей. Тогда

150 150n у младшего брата марок, у старшего — марок. n + 1 n + 1

150 150n

Ответ. и марок.

n + 1 n + 1

197. а) Турист шёл 2 ч со скоростью х км/ч и 3 ч со скоростью у км/ч. Определите среднюю скорость туриста на пройденном участке пути.

Решение. Эта задача аналогична задаче 188.

2 ⋅ x + 3 ⋅ y = 2x + 3y (км/ч).

Ответ. км/ч.

198. Скорость катера относительно воды равна и км/ч, а скорость течения реки равна v км/ч. Расстояние между пристанями А и В равно 60 км. Определите время движения катера от А до В и обратно.

Решение. 1) (ч) — время движения по течению;

2) (ч) — время движения против течения; 3) + (ч) — время движения туда и обратно.

Ответ. + ч.

199. а) Первый кусок сплава массой 400 г содержит р % олова, а второй кусок сплава массой 100 г содержит q % олова. Определите процентное содержание олова в новом сплаве, полученном сплавлением этих кусков.

Решение. 1) 4p (г) — масса олова в первом ку-

ске;

2) q (г) — масса олова во втором куске;

3) 4p + q (г) — масса олова в новом сплаве;

4) 100 + 400 = 500 (г) — масса нового сплава;

5) (%) — процентное содержание

олова в новом сплаве.

4p q+

Ответ. %.

200. а) Вкладчик положил в банк а р. Банк обязуется выплачивать ему ежемесячно р % дохода от первоначальной суммы вклада. Каков будет доход вкладчика через год?

б) Вкладчик положил в банк а р. Банк обязуется на-

числять на его счёт в конце каждого года р % дохода от суммы вклада, находившейся на счёте в течение этого года. Какая сумма будет на счёте у вкладчика в конце третьего года? Решение.

а) a ^⋅^p⋅ 12 = ^3ap (р.) — доход вкладчика за год.

100 25

б) 1) a ⋅ ⎛^⎜⎝1 ⁺₁₀₀^p⎞^⎟⎠ (р.) — сумма на счёте вкладчика в конце первого года;

2) a ⋅ ⎛^⎜⎝1 ⁺₁₀₀^p⎞^⎟⎠² (р.) — сумма на счёте вкладчика в конце второго года;

3) a ⋅ ⎛^⎜⎝1 ⁺₁₀₀^p⎞^⎟⎠³ (р.) — сумма на счёте вкладчика в конце третьего года.

325ap a ^⋅⎛^⎜⎝1 ⁺₁₀₀p ⎞^⎟⎠³ р.

Ответ. а) р.; б)

4.3. Понятие одночлена

В данном пункте вводится понятие одночлена. Оно, так же как и понятие алгебраического выражения, вводится последовательно. Сначала одночленом называют алгебраическое выражение, являющееся произведением букв и чисел. Так как и буквы, и числа — алгебраические выражения, а выше уже определили, что понимают под произведением алгебраических выражений, то такое определение корректно. Важно здесь подчеркнуть, что знак умножения в записи одночлена обычно опускается (но не между числовыми множителями). Затем добавляют к уже введённым объектам числа и буквы, и их также называют одночленами. Таким образом, описано, что понимают под термином «одночлен».

Для дальнейшего обучения важно, чтобы учащиеся знали, что есть и термин «нулевой одночлен», и понимали, что этот термин означает.

Далее сформулированы четыре свойства одночленов. Необходимо, чтобы учащиеся усвоили эти свойства.

Задания для повторения. При изучении данного пункта можно использовать задание 895.

Решения и комментарии

203. Является ли одночленом выражение: б) а + b; ж) ³ хy; л) ^p аху?

4 b

Решение. б) а + b не является одночленом, так как это не число, не буква и не произведение чисел и букв;

ж) хy — одночлен, так как это произведение числа

и букв х и y; p

л) аху не является одночленом, так как содержит b

деление на букву b.

205. а) Напишите все одночлены, получающиеся изменением порядка множителей одночлена 3аb.

Решение. 3аb, 3bа, а3b, аb3, bа3, b3а. 206. Упростите запись одночлена:

а) 0аb; в) 1kpх; д) а5b (–3) с (–8). Решение.

а) 0аb = 0; в) 1kpх = kpх; д) а5b (–3) с (–8) = 120аbс.

4.4. Произведение одночленов

В данном пункте вводятся понятия произведения одночленов, k-й степени буквы, приводятся три свойства степени буквы, которые должны освоить все учащиеся. Затем сформулированы ещё три свойства одночленов.

Следует отметить, что здесь принят алгебраический подход: вводятся новые объекты — одночлены — и, естественно, формулируются правила, которым они подчинены. Так как под буквой можно понимать не только число, то для новых объектов правила обращения с ними должны быть сформулированы, так как они не могут вытекать из каких-то других правил. Конечно, если под буквами понимать только числа, то все правила обращений с ними — свойства одночленов — будут следовать из свойств действительных чисел, об этом будет сказано в конце § 5.

Такой алгебраический подход — формулировка правил, а не попытка вывести их, например, из свойств действительных чисел — не только полезен для дальнейшего обучения, но и помогает слабым учащимся лучше усвоить изучаемое. Им надо только запомнить правила, а не вспоминать, как они могут быть выведены из свойств действительных чисел.

Задания 214—217 предназначены для тренировки учащихся в преобразованиях произведения одночленов и применении свойств степени. Их можно выполнить разными способами, что затрудняет сравнение полученных результатов, поэтому желательно придерживаться с учащимися единого порядка записи одночленов: сначала числовой множитель, затем буквенные множители в порядке алфавита, записанные в соответствующих степенях. Тем самым учащиеся будут подготовлены к введению понятия стандартного вида одночлена в следующем пункте учебника.

Задание 224 нацелено на развитие алгебраического языка, на усвоение терминов, часто используемых в алгебре.

Задания для повторения. При изучении данного пункта можно использовать задания 896—898.

Решения и комментарии

214. Найдите одночлен, равный произведению одночленов:

а) 3аb ⋅ 2а; г) 7е²k ⋅ 6е³k; ж) 3а²bс ⋅ 6аbс. Решение.

а) 3аb ⋅ 2а = 6а²b; г) 7е²k ⋅ 6е³k = 42е⁵k²;

ж) 3а²bс ⋅ 6аbс = 18а³b²с². 218. Представьте данную степень в виде произведения:

а) (xy)²; в) (2х)³; ж) (13ху)⁹.

Решение.

а) (xy)² = x²y²; в) (2х)³ = 8х³; ж) (13ху)⁹ = 13⁹х⁹у⁹. 219. Возведите в степень:

б) (b²)³; в) (2а)²; з) (9b²с)².

Решение.

б) (b²)³ = b⁶; в) (2а)² = 4а²; з) (9b²с)² = 81b⁴с².

4.5. Стандартный вид одночлена

В данном пункте вводятся понятия одночлена стандартного вида, коэффициента одночлена, приведения одночлена к стандартному виду и степени ненулевого одночлена.

Стоит подчеркнуть, что на самом деле есть три определения одночлена стандартного вида:

1) для ненулевого одночлена, содержащего буквы; 2) для ненулевого одночлена, не содержащего буквы; 3) для нулевого одночлена.

Обратим внимание, что степень одночлена определяется только по записи одночлена в стандартном виде. Степень одночлена стандартного вида есть сумма показателей всех его букв. Ненулевой одночлен, не содержащий букв (т. е. действительное число, не равное 0), имеет степень нуль. Важно, чтобы учащиеся усвоили, что единственный одночлен, для которого степень не определяется, — это нулевой одночлен (число 0).

Задание 229 нацелено на развитие алгебраического языка, на усвоение терминов, часто используемых в алгебре.

Решения и комментарии

228. Приведите одночлен к стандартному виду: а) (–2) b3; г) 3а²а³8; ж) (–3) b³с²b⁴ (–4). Решение.

а) (–2)b3 = –6b; г) 3а²а³8 = 24а⁵;

ж) (–3)b³с²b⁴ (–4) = 12b⁷с².

230. Приведите одночлен к стандартному виду, найдите его коэффициент и степень:

а) 3асb5; з) 0; и) ху (–1) уzх².

Решение. а) 3асb5 = 15аbс — коэффициент 15, степень 3; з) 0 — коэффициент 0, степень не определена;

и) ху (–1) уzх² = − х³у²z — коэффициент −,

степень 6.

4.6. Подобные одночлены

В данном пункте вводятся понятия подобных одночленов, суммы и разности подобных одночленов и приведения подобных членов. Этот материал будет в дальнейшем часто использоваться при изучении многочленов и алгебраических дробей.

Задания для повторения. При изучении данного пункта можно использовать задание 899.

Решения и комментарии 238. Найдите сумму подобных одночленов:

а) а²bс + 2аbса + (–3bса²); б) (–аbа²) + 7а²bа + а³b. Решение. а) а²bс + 2аbса + (–3bса²) = 1а²bс + 2а²bс +

+ (–3а²bс) = (1 + 2 + (–3)) а²bс = 0а²bс = 0;

б) (–аbа²) + 7а²bа + а³b = (–1а³b) + 7а³b + 1а³b = = (–1 + 7 + 1)а³b = 7а³b. 239. Найдите разность подобных одночленов: а) 3аbс − 7аbс; б) 9а³b² − 9а³b².

Решение. а) 3аbс − 7аbс = (3 − 7) аbс = –4аbс; б) 9а³b² − 9а³b²= (9 − 9) а³b²= 0а³b² = 0.

Промежуточный контроль. С—6.

§ 5. Многочлены

В § 5 вводится понятие многочлена, формулируются правила преобразования многочленов, приведения их к стандартному виду и определяются сумма, разность и произведение многочленов. Умение обращаться с многочленами будет использовано при изучении следующего параграфа «Формулы сокращённого умножения». Изучению материала данного параграфа надо уделить особое внимание, так как формируемые здесь умения будут в дальнейшем постоянно использоваться при выполнении преобразований алгебраических выражений.

Основная цель изучения параграфа — овладение тремя арифметическими действиями (сложение, вычитание, умножение) над многочленами.

5.1. Понятие многочлена

В данном пункте вводятся понятия многочлена и члена многочлена. Сначала многочленом называют сумму нескольких одночленов. Затем добавляют к этим объектам одночлены, а значит, и числа, их также называют многочленами. Число нуль называют нулевым многочленом.

Многочлен 3a + (–2b) принято записывать так: 3a − 2b. Это выражение также называют многочленом. Когда говорят, что алгебраическое выражение 3a − 2b является многочленом, то имеют в виду, что это сумма одночленов 3a и –2b.

Решения и комментарии

245. Запишите многочлен, членами которого являются одночлены:

в) 2а, b³ и (–2); г) х³, 0,5у², (–х) и (–5ху).

Решение. в) 2а + b³ + (–2) = 2а + b³ − 2;

г) х³ + 0,5у² + (–х) + (–5ху) = х³ + 0,5у² – х – 5ху.

246. Запишите многочлен в виде суммы одночленов: в) –ху − у²; г) –2x² − 0,5у.

Решение. в) –ху − у² = (–ху) + (–у²); г) –2x² − 0,5у = (–2x²) + (–0,5у).

247. Является ли многочленом выражение:

а) 2а − 7,2; б) х² − 3х + 4; г) ^3m; д) 0? 1 − n

Решение. а) 2а − 7,2 — да; б) х² − 3х + 4 — да;

г) — нет, так как алгебраическое выражение со1 − n держит деление на буквенное выражение;

д) 0 — да.

5.2. Свойства многочленов

В данном пункте сформулированы свойства многочленов:

1) члены многочлена можно менять местами;

2) прибавление к многочлену нуля (нулевого многочлена) не изменяет его;

3) в многочлене можно приводить подобные члены.

Здесь также показаны примеры упрощения многочленов. Отметим, что подобными членами многочлена являются его члены — одночлены, являющиеся подобными.

Решения и комментарии

250. а) Какими свойствами многочленов воспользовались при упрощении многочлена:

а + b − а = а − а + b = 0 + b = b?

Решение. а + b − а = а − а + b — свойство 1; а − а + b = а (1 − 1) + b = 0 + b — свойство 3; 0 + b = b — свойство 2. 252. Упростите многочлен:

а) 12а + 5b − 4а; в) 17x − 4у + 5х + 4у.

Решение. а) 12а + 5b − 4а = 12а − 4а + 5b = (12 − 4) а + 5b =

= 8а + 5b;

в) 17x − 4у + 5х + 4у = 17x + 5х + 4у − 4у = (17 + 5) х + + (4 − 4) у = 22х + 0у = 22х. 253. Упростите многочлен:

ж) хух − 2х²у + 2х − 3х; з) ba² − 3a³+ 7aba + 3a² − 8a²b.

Решение. ж) хух − 2х²у + 2х − 3х = х²у − 2х²у + (2 − 3) х = = (1 − 2) х²у − х = –х²у − х.

з) ba² − 3a³+ 7aba + 3a² − 8a²b = a²b + 7a²b − 8a²b − 3a³ + 3a² = = (1 + 7 − 8) a²b − 3a³ + 3a² = 0a²b − 3a³ + 3a² = –3a³ + 3a².

5.3. Многочлены стандартного вида

В данном пункте вводится понятие многочлена стандартного вида и специальные названия многочленов — двучлен и трёхчлен, утверждается, что любой многочлен можно привести к стандартному виду. Для ненулевого многочлена определяется понятие степени многочлена. Для нулевого многочлена понятие степени многочлена не определено. Подчеркнём, что стандартный вид нулевого многочлена — число 0.

Решения и комментарии

257. Приведите многочлен к стандартному виду, определите его степень:

а) 4а²b + 5b²а + bаа + 3аbа;

б) 5а³ − 7ах³ − 2ах³ − а³х − ах³.

Решение. а) 4а²b + 5b²а + bаа + 3аbа = 4a b² + 5аb² +

+ a b²+ 3a b² = 8а²b + 5аb²; степень многочлена равна 3;

б) 5а³ − 7ax³− 2ax³ − а³х − ax³ = 5а³ − 10ах³ − а³х; степень

многочлена равна 4. 258. Упростите выражение:

в) у² ⋅ 2х − 3х² ⋅ 2у + 2ху ⋅ 2у − ху ⋅ (–4х);

г) хх ⋅ (–2х) − у ⋅ 3ху + 7х² ⋅ (–2х) − 4у² ⋅ 2х.

Решение. в) у² ⋅ 2х − 3х² ⋅ 2у + 2ху ⋅ 2у − ху ⋅ (–4х) = 2xy² −

− 6x y² + 4xy² + 4x y² = 6ху² − 2х²у;

г) хх ⋅ (–2х) − у ⋅ 3ху + 7х² ⋅ (–2х) − 4у² ⋅ 2х = − 2x³ − 3xy² −

− 14x³ − 8xy²= –16х³ − 11ху².

259. Вместо букв С и D подберите одночлены так, чтобы выполнялось равенство:

а) 2а + С + а + 5b = 3а + 8b; б) 3х + С + у + D = 11х + 5y.

Решение. а) Так как 2а + С + а + 5b = 3а + 5b + С, то равенство 3а + 5b + С = 3а + 8b выполняется при С = 3b;

б) равенство 3х + С + у + D = 11х + 5y выполняется при С = 8х, D = 4y.

В задании б) возможен другой ответ: С = 4y, D = 8х. Промежуточный контроль. С—7.

5.4. Сумма и разность многочленов

В данном пункте определяется сумма и разность двух многочленов, формулируются правила раскрытия скобок (заключения в скобки), перед которыми стоит знак «+» («–»). Эти правила должны освоить все учащиеся, так как от этого зависит успешность дальнейшего изучения алгебры.

Начать объяснение правил работы со скобками можно с повторения правил раскрытия скобок (заключения в скобки) применительно к числовым выражениям. Для этого можно выполнить задания такого вида.

1. Раскрывая скобки, вычислите значение числового выражения:

а) 3,89 + (45,11 − 3,89); б) 7,99 − (5,87 + 7,99);

в) 5 − (575 − 7999) − (7999 − 575). Решение. а) 3,89 + (45,11 − 3,89) = 3,89 + 45,11 − 3,89 =

= 45,11;

б) 7,99 − (5,87 + 7,99) = 7,99 − 5,87 − 7,99 = –5,87;

в) 5 − (575 − 7999) − (7999 − 575) = 5 − 575 + 7999 − 7999 +

+ 575 = 5.

2. Перепишите данное числовое выражение, изменив знак перед скобками на противоп оложный:

а) 73,8 + (51,3 − 43,9); б) 1,75 − (45,7 + 79,9);

в) 5 − (–575 + 799) + (799 − 575).

Решение. а) 73,8 + (51,3 − 43,9) = 73,8 − (–51,3 + 43,9); б) 1,75 − (45,7 + 79,9) = 1,75 + (–45,7 − 79,9);

в) 5 − (–575 + 799) + (799 − 575) = 5 + (575 − 799) − − (–799 + 575).

Заметим, что использование рассмотренных примеров для чисел не ставит целью (да и не может!) дать обоснования действиям с многочленами. Но опора на имеющийся у учащихся опыт обращения с числовыми выражениями позволяет им быстрее и надёжнее освоить действия с новыми объектами. Тем самым реально осуществляются межпредметные связи между математическими предметами (математика 5—6, алгебра 7), повышающие эффективность обучения.

Задания для повторения. При изучении данного пункта можно использовать задания 903, 904, 908.

Решения и комментарии

273. Даны многочлены: А = а + b, В = 3а − 2b, С = а − 7b.

Найдите:

а) А + В + С; б) А + В − С;

в) А − В − С; г) –А − В − С.

Решение. а) А + В + С = (а + b) + (3а − 2b) + (а − 7b) = а + b +

+ 3а − 2b + а − 7b = 5а − 8b;

б) А + В − С = (а + b) + (3а − 2b) − (а − 7b) = а + b + 3а − 2b −

− а + 7b = 3а + 6b;

в) А − В − С = (а + b) − (3а − 2b) − (а − 7b) = а + b − 3а + 2b −

− а + 7b = –3а + 10b;

г) –А − В − С = –(а + b) − (3а − 2b) − (а − 7b) = –а − b − 3а + + 2b − а + 7b = –5а + 8b.

274. Заключите первые два члена многочлена в скоб-ки со знаком минус перед ними, а последние — в скобки со знаком плюс перед ними:

а) х² − у² + 2х − 1; б) 9у² − 1 − х² − 6у. Решение. а) х² − у² + 2х − 1 = –(у² − х²) + (2х − 1); б) 9у² − 1 − х² − 6у = –(1 − 9у²) + (–х² − 6у).

275. Дан многочлен а + b − с − р. Представьте его как:

а) сумму многочленов, чтобы одно из слагаемых было

(а + b);

б) разность многочленов, чтобы уменьшаемое было

(а + b);

в) разность многочленов, чтобы уменьшаемое было

(b − с).

Решение.

а) а + b − с − р = (а + b) + (–с − р);

б) а + b − с − р = (а + b) − (с + р);

в) а + b − с − р = (b − с) − (р − а).

Промежуточный контроль. С—8.

5.5. Произведение одночлена и многочлена

В данном пункте определяется произведение одночлена и многочлена и преобразование многочлена — вынесение за скобки общего множителя. Вводится понятие противоположных многочленов, объясняется, что при умножении многочлена на 1 получается тот же самый многочлен. Очень важно, чтобы учащиеся научились находить произведение одночлена и многочлена, а также выносить за скобки общий множитель многочлена.

Поскольку рассматриваемые в данном пункте преобразования напоминают применение распределительного закона для действительных чисел, то объяснение нового материала можно начать с выполнения заданий такого типа.

1. Вычислите, раскрывая скобки:

а) 3,54 ⋅ (100 − 9,91) + 3,54 ⋅ 9,91;

б) 15,3 ⋅ (9,1 + 10) − 15,3 ⋅ 9,1.

Решение. а) 3,54 ⋅ (100 − 9,91) + 3,54 ⋅ 9,91 = 3,54 ⋅ 100 −

− 3,54 ⋅ 9,91 + 3,54 ⋅ 9,91 = 354;

б) 15,3 ⋅ (9,1 + 10) − 15,3 ⋅ 9,1 = 15,3 ⋅ 9,1 + 15,3 ⋅ 10 − − 15,3 ⋅ 9,1 = 153.

2. Вычислите, вынося общий множитель за скобки:

а) 7,95 ⋅ 5,81 − 7,95 ⋅ 4,81;

б) 5,3 ⋅ 7,1 + 5,3 ⋅ 2,9;

в) 2,3 ⋅ 2,1 + 2,3 ⋅ 9,9 − 2,3 ⋅ 2.

Решение. а) 7,95 ⋅ 5,81 − 7,95 ⋅ 4,81 = 7,95 ⋅ (5,81 − 4,81) =

= 7,95 ⋅ 1 = 7,95;

б) 5,3 ⋅ 7,1 + 5,3 ⋅ 2,9 = 5,3 ⋅ (7,1 + 2,9) = 5,3 ⋅ 10 = 53;

в) 2,3 ⋅ 2,1 + 2,3 ⋅ 9,9 − 2,3 ⋅ 2 = 2,3 ⋅ (2,1 + 9,9 − 2) = = 2,3 ⋅ 10 = 23.

Обратим внимание на задание 282, предоставляющее редкую возможность наглядной иллюстрации алгебраических равенств. Такие задания надо использовать, так как наглядные иллюстрации помогают убедить учащихся в том, что получаемые ими новые знания согласуются с их прежним опытом. Это делает усвоение новых знаний более прочным.

Задания для повторения. При изучении данного пункта можно использовать задание 906.

Решения и комментарии

286. Вынесите за скобки общий множитель многочлена:

д) х³у⁴ − х²у² + ху³; ж) –2а²b + 4аb² − 4b³. Решение. д) х³у⁴ − х²у² + ху³ = ху² ⋅ (х²у² − х + у);

ж) –2а²b + 4аb² − 4b³ = –2b ⋅ (а² − 2аb + 2b²).

288. Подберите вместо букв М и N одночлены так, чтобы равенство было верным:

в) N ⋅ (2х − М) = 12х² − 18хy;

г) 3а ⋅ (N + М) = 15аbс − 3ас².

Решение. в) Так как 12х² − 18хy = 6х (2х − 3y), то N = 6х;

М = 3y;

г) так как 15аbс − 3ас² = 3а (5bс − с²), то N = 5bс; М = –с² (или М = 5bс; N = –с²).

289. а) Упростите выражение а − (b − (а + b) − а).

Решение. I способ. а − (b − (а + b) − а) = а − (b − а − b − а) = = а − (–2а) = а + 2а = 3а.

II способ. а − (b − (а + b) − а) = а − b + (а + b) + а = 2а − b + а + + b = 3а.

290. а) Докажите, что (п + 1)! − п ⋅ п! = п!.

б) Вычислите: 11! − (1 ⋅ 1! + 2 ⋅ 2! + 3 ⋅ 3! + ... + 10 ⋅ 10!).

Решение. а) (п + 1)! − п ⋅ п! = (п + 1) ⋅ п! − п ⋅ п! = (п + 1 − п) × × п! = 1 ⋅ п! = п!, что и требовалось доказать.

б) Из доказанного выше следует, что для любого на-

турального n верно равенство

п ⋅ п! = (п + 1)! − п!.

Применим это равенство для преобразования выражения в скобках:

11! − (1 ⋅ 1! + 2 ⋅ 2! + 3 ⋅ 3! + ... + 10 ⋅ 10!) = = 11! − (2! − 1! + 3! − 2! + 4! − 3! + ... + 11! − 10!) = = 11! − (–1! + 11!) = 11! + 1! − 11! = 1! = 1.

Дополнительное задание. Докажите, что сумма противоположных многочленов есть нулевой многочлен.

Доказательство. Пусть A — произвольный данный многочлен, –A — противоположный ему многочлен, тогда

A + (–A) = A ⋅ 1 + A ⋅ (–1) = A ⋅ (1 + (–1)) = A ⋅ 0 = 0.

Промежуточный контроль. С—9.

5.6. Произведение многочленов

В данном пункте определяется произведение двух многочленов. Рассматривается преобразование многочлена — разложение на множители. Умножение многочленов и разложение их на множители будут постоянно использоваться в дальнейшем, поэтому должны быть усвоены всеми учащимися.

Обратим внимание на задания 292—293 на чтение и запись алгебраических выражений и задание 304, предоставляющее наглядную иллюстрацию алгебраического равенства.

Подводя итог изученному в пунктах 5.1–5.6, отметим, что свойства многочленов в этих пунктах формулируются, но не доказываются. Так как и здесь используется алгебраический подход к введению новых объектов, то многочлены вводятся и для них формулируются правила, которым они подчинены.

Задания для повторения. При изучении данного пункта можно использовать задания 907—910.

Решения и комментарии

301. б) Докажите равенство

2x² − 11x + 15 = (x − 3) (2x − 5).

Доказательство. (x − 3) (2x − 5) = 2x² − 6x − 5x + 15 = 2x² − − 11x + 15, что и требовалось доказать. 308. Разложите многочлен на множители:

а) х (а + b) + у (а + b); б) (а + b) а − b (а + b). Решение. а) х (а + b) + у (а + b) = (а + b) (х + у); б) (а + b) а − b (а + b) = (а + b) (а − b).

309. При преобразованиях бывает необходимо изменять знаки членов многочлена на противоположные, например:

(а + b) = (–1) (–а − b) = –(–а − b)

или

(а − b) = (–1) (–а + b) = –(b − а).

Используя этот приём, разложите на множители:

а) а (х − у) + b (у − х); б) х (а − b) + у (b − а).

Решение.

а) а (х − у) + b (у − х) = а (х − у) − b (х − у) = (х − у) (а − b);

б) х (а − b) + у (b − а) = х (а − b) − у (а − b) = (а − b) (х − у).

311. ж) Упростите выражение (2т − п) (3п + 2т) (т − 5n). Решение.

(2т − п) (3п + 2т) (т − 5n) =

= (6тп − 3п² + 4т² − 2тп) (т − 5n) =

= (4тп − 3п² + 4т²) (т − 5n) = = 4m n² − 3mn² + 4т³ − 20mn² + 15п³ − 20m n² =

= 4т³ − 16т²п − 23тп² + 15п³.

Промежуточный контроль. С—10.

5.7. Целые выражения

В этом пункте вводится понятие целого выражения. Это алгебраическое выражение, в котором многочлены соединены знаками сложения, вычитания и умножения. Здесь имеется возможность повторить все действия с многочленами, изученные ранее, уделить внимание тренировке учащихся в упрощении целых выражений. Важно, чтобы у чащиеся поняли, что любое целое выражение можно преобразовать в многочлен стандартного вида.

Решения и комментарии

315. Преобразуйте выражение в многочлен стандартного вида и определите его степень:

в) (а + 2) (а − 1) − (а + 1) (а − 2);

г) (р + 2) (р − 1) + (р + 3) (р − 5).

Решение.

в) (а + 2) (а − 1) − (а + 1) (а − 2) = (а² + 2а − а − 2) −

− (а² + а − 2а − 2) = (а² + а − 2) − (а² − а − 2) = а² + а − 2 − а² +

+ а + 2 = 2а — степень 1;

г) (р + 2) (р − 1) + (р + 3) (р − 5) = (р² + 2р − p − 2) +

+ (р² + 3р − 5p − 15) = (р² + p − 2) + (р² − 2p − 15) =

= р² + p − 2 + р² − 2p − 15 = 2р² − p − 17 — степень 2. Упростите целое выражение (317—318): 317. д) 15х³y² − (5хy − 2) (3х²y + х); е) (а + b + с) (а + b − с) − аb;

ж) (а + 2b) (а + с) − (а − 2b) (а − с).

Решение. д) 15х³y² − (5хy − 2) (3х²y + х) =

= 15х³y² − (15х³y² − 6х²y + 5х²y − 2х) = 15х³y² −

− (15х³y² − x²y − 2x) = 15x³y² − 15x³y² + х²y + 2х = х²y + 2х;

е) (а + b + с) (а + b − с) − аb =

= (а² + аb + ас + аb + b² + bс − aс − bс − с²) − аb =

= (а² + 2ab + b² − с²) − ab = a² + ab + b² − c² − ab =

= a² + b² − c²;

ж) (а + 2b) (а + с) − (а − 2b) (а − с) = (а² + 2аb + ас + 2bc) − − (а² − 2аb − ас + 2bc) = а² + 2аb + ас + 2bc − а² + 2аb + ас − 2bc = = 4аb + 2ас.

318. а) (х² + у² + х + у) (х + у + ху).

Решение. (х² + у² + х + у) (х + у + ху) = х³ + ху² + х² + ху + + х²у + у³ + ху + у² + х³у + ху³ + х²у + ху² = х³ + 2ху² + х² + 2ху + + 2х²у + у³ + у² + х³у + ху³.

5.8. Числовое значение целого выражения

В данном пункте вводится понятие числового значения целого выражения при заданных значениях входящих в него букв. При решении задачи 1 объясняется, что значит доказать неравенство, а среди упражнений имеются простейшие задания на доказательство неравенств. Обратим внимание, что первоначально значения выражения находятся без упрощения буквенного выражения, а в дальнейшем ещё будет много примеров, когда необходимо сначала упростить буквенное выражение, а затем подставить в полученное выражение значения входящих в него букв.

Сильным учащимся такой пример можно привести уже на первом уроке по рассматриваемой теме.

Найдём значение выражения x³ − x² − x (x² − x + 5) при x = 3,2.

Если начать с подстановки значения 3,2 вместо x, вычисления будут долгими. Если же сначала упростить выражение:

x³ − x² − x (x² − x + 5) = x³ − x² − x³ + x² − 5x = –5x,

а потом подставить значение x = 3,2, то вычисления будут проще: при x = 3,2 имеем –5x = –5 ⋅ 3,2 = –16.

Такие примеры полезны с точки зрения мотивации изучения преобразований буквенн ых выражений.

Решения и комментарии

Вычислите значение выражения (328—329):

328. и) (m − п) (т + п) (п − т) (п + т) при т = –0,5, п = 0,3; к) (1 − х) (х − 2) (3 − х) (х − 4) при х = 2.

Решение. и) При т = –0,5, п = 0,3 имеем

(–0,5 − 0,3) (–0,5 + 0,3) (0,3 − (–0,5)) (0,3 + (–0,5)) =

= (–0,8) ⋅ (–0,2) ⋅ 0,8 ⋅ (–0,2) = –0,0256;

к) при х = 2 имеем (1 − 2) ⋅ (2 − 2) ⋅ (3 − 2) ⋅ (2 − 4) = 0.

329. а) а² + 5а − 13 при а = –3;

е) (а − b) (с − d) при а = 1, b = 2, с = –3; d = 4. Решение. а) При а = –3 имеем (–3)² + 5 ⋅ (–3) − 13 =

= 9 − 15 − 13 = –19;

е) при а = 1, b = 2, с = –3; d = 4 имеем (1 − 2) (–3 − 4) = 7.

332. а) Докажите, что для любого числа х верно неравенство х² − 5 ≥ –5.

Доказательство. Для любого числа х число х² — неотрицательное. Если к неотри цательному числу прибавить –5, то получится число, не меньшее –5, т. е. х² − 5 ≥ –5 для любого числа x, что и требовалось доказать.

Промежуточный контроль. С—11.

5.9. Тождественное равенство целых выражений

В учебнике на примерах разобраны некоторые приёмы доказательства тождеств. Эти приёмы должны освоить учащиеся, так как с их помощью далее будут доказываться тождества — формулы сокращённого умножения.

Напомним, что все нулевые многочлены считаются тождественно равными числу нуль.

Замечание. После обсуждения материала пункта 5.9 стоит сказать о том, что все рассмотренные ранее равенства были тождествами и поэтому все сформулированные выше свойства одночленов и многочленов следуют из свойств чисел, если под буквами понимают числа. Однако формулировка свойств одночленов и многочленов позволила всем учащимся преобразовывать их на основании этих правил, а не вспоминать каждый раз, на основании каких свойств чисел это можно делать. Тем более что под буквой можно понимать не только число.

Решения и комментарии

Докажите тождество (336—337):

336. з) (q − 1) (q − 1) (q − 1) = q³ − 3q² + 3q − 1.

Доказательство. Раскроем скобки в левой части доказываемого равенства:

(q − 1) (q − 1) (q − 1) = (q² − q − q + 1) (q − 1) = (q² − 2q + 1) (q − 1) =

= q³ − 2q² + q − q² + 2q − 1 = q³ − 3q² + 3q − 1, что и требовалось доказать.

337. з) (а − 2) (а + 2) (а² + 4) (а⁴ + 16) − а⁸ = –256.

Доказательство. Раскроем скобки в левой части доказываемого равенства:

(а − 2) (а + 2) (а² + 4) (а⁴ + 16) − а⁸ =

= (а² − 2а + 2а − 4) (а² + 4) (а⁴ + 16) − а⁸ =

= (а² − 4) (а² + 4) (а⁴ + 16) − а⁸ = (а⁴ − 4а² + 4а² − 16) (а⁴ + 16) − а⁸ =

= (а⁴ − 16) (а⁴ + 16) − а⁸ = а⁸ − 16а⁴ + 16а⁴ − 256 − а⁸ = –256, что и требовалось доказать.

Замечание. При выполнении заданий, аналогичных рассмотренным, учитель может показать, что он заранее знает результат, который пока что с некоторыми усилиями получают учащиеся. Можно раскрыть секрет учителя — он уже знает формулы сокращённого умножения. Когда учащиеся их изучат, они будут так же быстро определять результат умножения некоторых двучленов или результат возведения двучлена в квадрат. Это полезно с точки зрения повышения мотивации учащихся к учению. Они должны видеть, какие преимущества даёт в работе с многочленами знание некоторых фактов о них.

Промежуточный контроль. К—2.

§ 6. Формулы сокращённого умножения

В § 6 доказываются формулы сокращённого умножения многочленов и приводятся примеры их применения при упрощении выражений, а также при разложении многочленов на множители. Умение использовать формулы сокращённого умножения найдёт применение при решении большого круга задач, связанных с многочленами, при изучении алгебраических дробей, а также при изучении математики в следующих классах.

Основная цель изучения параграфа — освоить основные формулы сокращённого умножения и научиться применять их при решении различных задач. При этом надо научить учащихся не только, например, возводить двучлен в квадрат, но и видеть в простых случаях, что квадратный трёхчлен является квадратом суммы (разности). Особое внимание надо уделить разложению многочленов на множители, которое найдёт большое применение при изучении следующих разделов алгебры.

6.1. Квадрат суммы

В данном пункте доказывается формула квадрата суммы. Для положительных чисел a и b полезно дать наглядную иллюстрацию приведённому доказательству (задание 342), так как многие учащиеся нуждаются в опоре на наглядность, подтверждающую правильность результата, полученного алгебраическими средствами.

Для повышения мотивации учения полезно привести примеры применения изученной формулы для упрощения вычислений. Например:

Вычислим:

а) 49² + 2 ⋅ 49 ⋅ 51 + 51² = (49 + 51)² = 100² = 10 000;

б) 311² + 2 ⋅ 311 ⋅ 189 + 189² = (311 + 189)² = 500² = 250 000.

На первых порах полезно давать полную запись решения (см. решение задания 340) и не торопиться «сворачивать» вычисления там, где они легко выполняются устно. Так формула квадрата суммы будет усвоена быстрее и надёжнее, что поможет учащимся не путаться в вычислениях при изучении новых формул.

Начиная с первых уроков по теме следует уделить особое внимание правильному чтению формул. Для этого надо обратить внимание учащихся на операцию, которая выполняется последней.

Например, (49 + 51)² — квадрат суммы (последняя операция — возведение в квадрат, с неё и начинаем чтение выражения), а 49² + 51² — это сумма квадратов (последняя операция — сложение). На следующих уроках такого рода задания можно давать для устной работы.

Решения и комментарии

340. Используя формулу квадрата суммы, преобразуйте выражение в многочлен стандартного вида:

а) (а² + b)²; б) (х + у³)².

Решение. а) (а² + b)² = (а²)² + 2а²b + b² = а⁴ + 2а²b + b²; б) (х + у³)² = х² + 2ху³ + (у³)² = х² + 2ху³ + у⁶.

344. Любое натуральное число, оканчивающееся цифрой 5, можно записать в виде 10а + 5. Например, 25 = 10 ⋅ 2 + 5. Докажите, что для вычисления квадрата такого числа можно к произведению а (а + 1) приписать справа 25. Например, 25² = 625 (2 ⋅ 3 = 6). Доказательство.

(10а + 5)² = (10а)² + 2 ⋅ 10а ⋅ 5 + 5² = 100а² + 100а + 25 = = 100а (а + 1) + 25.

Полученный результат означает, что если число a (a = 2) умножить на число a + 1 (a + 1 = 3), произведение a (a + 1) (число 6) умножить на 100, а к результату прибавить 25, то получится искомое число (число 625). Это всё равно что к числу, равному произведению а (а + 1), приписать справа 25.

В качестве дополнения к этой задаче можно попросить учащихся вычислить 35², 75², 125² и т. п.

345. Представьте многочлен в виде квадрата суммы:ж) 16 + 8р + р²; з) 4т² + 9п² + 12тп.

Решение. ж) 16 + 8р + р² = 4² + 2 ⋅ 4 ⋅ р + р² = (4 + р)²;

з) 4т² + 9п² + 12тп = (2т)² + 2 ⋅ 2т ⋅ 3п + (3п)² = (2т + 3п)².

346. Вместо букв С и D подберите одночлены так, чтобы выполнялось равенство:

а) (а + С)² = D + 2аb + b²; г) (С + D)² = 9р² + 30рq + 25q². Решение. а) Так как (а + С)² = а² + 2аС + С², то С = b,

D = а²;

г) так как (С + D)² = С² + 2СD + D², то С = 3р, D = 5q или С = 5q, D = 3р.

В сильном классе можно показать решение задачи 918 на доказательство из раздела «Задания для повторения». Сложность задания заключается в том, чтобы заметить квадрат суммы до того, как раскрыты все скобки.

918. Докажите, что произведение четырёх последовательных натуральных чисел, увеличенное на 1, есть точный квадрат.

Решение. Пусть n — первое из четырёх натуральных чисел, тогда их произведение, увеличенное на 1, есть n (n + 1) (n + 2) (n + 3) + 1. Умножим первый множитель на четвёртый, а второй на третий:

n (n + 1) (n + 2) (n + 3) + 1 = (n² + 3n) (n² + 3n + 2) + 1 = = (n² + 3n)² + 2 (n² + 3n) + 1 = (n² + 3n + 1)².

6.2. Квадрат разности

В данном пункте доказывается формула квадрата разности. Для положительных чисел a и b (a > b) полезно дать наглядную иллюстрацию приведённому доказательству (задание 355). Доказательство предполагает, что при вычислении площади (a − b)² закрашенного квадрата из площади большого квадрата a² вычитается два раза площадь прямоугольника ab. При этом оказывается, что площадь маленького квадрата b² вычитается дважды. Поэтому, чтобы записать верное равенство, надо прибавить к разности b²:

(a − b)² = a² − ab − ab + b² = a² − 2ab + b².

Вычислим:

а) 129² − 2 ⋅ 129 ⋅ 109 + 109² = (129 – 109)² = 20² = 400;

б) 654² − 2 ⋅ 654 ⋅ 653 + 653² = (654 − 653)² = 1² = 1.

На первых порах полезно давать полную запись решения (см. решение задания 353) и не торопиться «сворачивать» вычисления там, где они легко выполняются устно. Так формула квадрата разности будет усвоена быстрее и надёжнее.

Решения и комментарии

353. Используя формулу квадрата суммы или разности, преобразуйте выражение в многочлен стандартного вида:

а) (а − b²)²; б) (х³ − у)².

Решение. а) (а − b²)² = а² − 2аb² + (b²)² = а² − 2аb² + b⁴; б) (х³ − у)² = (х³)² − 2х³у + у² = х⁶ − 2х³у + у².

357. Представьте многочлен в виде квадрата разности:в) 9т² − 6т + 1; д) 16р² − 56рq + 49q².

Решение. в) 9т² − 6т + 1 = (3т)² − 2 ⋅ 3т ⋅ 1 + 1² = (3т − 1)²;

д) 16р² − 56рq + 49q²= (4р)² − 2 ⋅ 4р ⋅ 7q + (7q)² = (4р − 7q)².

358. Докажите тождество:

а) (а − b)² = (b − а)²; б) (–а − b)² = (а + b)².

Доказательство. а) (а − b)² = ((–1) ⋅ (b − а))² = (–1)² ⋅ (b − а)² =

= 1 ⋅ (b − а)² = (b − а)²;

б) (–а − b)² = ((–1) (а + b))² = (–1)² ⋅ (а + b)² = 1 ⋅ (а + b)² = = (а + b)².

Замечание. Доказать оба тождества можно иначе: раскрыть скобки, применяя изученн ые формулы, и убедиться, что получаются одинаковые результаты. Важно, чтобы учащиеся понимали, что в правой и левой частях первого из этих равенств члены должны быть с противоположными знаками: (а − b)² = (b − а)², а в правой и левой частях второго из этих равенств члены должны быть с одинаковыми знаками: (–а − b)² = (а + b)². Это наблюдение полезно для самоконтроля.

359. Вместо букв С и D подберите одночлены так, чтобы выполнялось равенство:

б) (С − y)² = 4х² − D + y²; в) (С − D)² = 9m² − 12mn + 4n².

Решение. б) Так как (С − y)² = С² − 2Сy + y², то равенство выполняется при С = 2х, D = 4хy;

в) так как (С − D)² = С² − 2СD + D², то равенство выпол-

няется при С = 3m, D = 2n или С = 2n, D = 3m.

6.3. Выделение полного квадрата

В данном пункте на конкретных примерах показан приём выделения полного квадрата из многочлена второй степени и применение этого приёма для разложения многочлена на множители. Выделение полного квадрата из многочлена второй степени является важным умением, поэтому желательно, чтобы все учащиеся овладели им. Добиться этого поможет запоминание нескольких формул и запись их в обратном порядке. Например, ученик выучивает формулы

(а + 1)² = а² + 2а + 1, (а + 2)² = а² + 4а + 4, (а + 3)²= а² + 6а + 9,

затем учится «узнавать» среди многочленов полные квадраты и, наконец, учится дополнять многочлены до полных квадратов.

— Какого слагаемого не хватает в выражении а² + 2а, чтобы получить полный квадрат?

— Не хватает слагаемого 1.

— Добавим и вычтем 1: а² + 2а = а² + 2а + 1 − 1. Теперь можно выделить квадрат двучлена:

а² + 2а + 1 − 1 = (а + 1)² − 1.

В классе с углублённым изучением математики надо обратить внимание на примеры 5—7 учебного текста, показывающие применение выделения полного квадрата двучлена для доказательства неравенств.

Решения и комментарии 368. Выделите полный квадрат из многочлена: ж) т² − 6т + 9; з) 16 + 8р + р²; и) а² − 2а. Решение. ж) т² − 6т + 9 = т² − 2т ⋅ 3 + 3² = (т − 3)²; з) 16 + 8р + р² = 4² + 2 ⋅ 4 ⋅ р + р² = (4 + р)²;

и) а² − 2а = а² − 2а + 1 − 1 = (а − 1)² − 1.

369. Выделите полный квадрат из многочлена: а) –3а + 3 + а²; б) а² − 1 + 5а; в) т² − 2 + 11т.

Решение. а) –3а + 3 + а² = а² − 2 ⋅ а ⋅ 1,5 + 1,5² − 1,5² + 3 =

= (а − 1,5)² + 0,75;

б) а² − 1 + 5а = а² + 2 ⋅ а ⋅ 2,5 + 2,5² − 2,5² − 1 = (а + 2,5)² −

− 7,25;

в) т² − 2 + 11т = т² + 2 ⋅ 5,5 ⋅ т + 5,5² − 5,5² − 2 = (m + 5,5)² − − 32,25.

371. Докажите, что для любого числа х верно неравенство:

а) х² + 2х + 1 ≥ 0; б) х² + 4х + 4 ≥ 0; в) х² − 6х + 9 ≥ 0.

Доказательство. а) х² + 2х + 1 = (х + 1)² ≥ 0 для любого x; б) х² + 4х + 4 = (х + 2)² ≥ 0 для любого x;

в) х² − 6х + 9 = (х − 3)² ≥ 0 для любого x.

372. Докажите, что для любого числа х верно неравенство:

а) х² + 2х + 2 > 0; б) х² + 4х + 5 > 0; в) х² − 6х + 11 > 0. Доказательство.

а) х² + 2х + 2 = х² + 2х + 1 + 1 = (х + 1)² + 1 > 0 для любого x;

б) х² + 4х + 5 = х² + 4х + 4 + 1 = (х + 2)²+ 1 > 0 для любого x;

в) х² − 6х + 11 = х² − 6х + 9 + 2 = (х − 3)² + 2 > 0 для любо-

го x.

373. Докажите, что для любых чисел х и у верно неравенство:

а) х² + у² − 8х + 4у + 20 ≥ 0; б) х² + у² + 12х − 6у + 45 ≥ 0.

Доказательство. а) х² + у² − 8х + 4у + 20 = х² − 8х + 16 +

+ у² + 4у + 4 = (х − 4)² + (y + 2)² ≥ 0 для любых x и y;

б) х² + у² + 12х − 6у + 45 = х² + 12х + 36 + у² − 6у + 9 = = (х + 6)² + (y − 3)² ≥ 0 для любых x и y.

6.4. Разность квадратов

В данном пункте доказывается формула разности квадратов. Для положительных чисел a и b (a > b) полезно дать наглядную иллюстрацию приведённому доказательству (задание 383). Учащиеся должны заметить, что прямоугольник со сторонами a − b и a + b имеет такую же площадь, как и шестиугольник, площадь которого a² − b².

На первых порах полезно давать полную запись решения (см. решение задания 377 в учебнике) и не торопиться «сворачивать» вычисления там, где они легко выполняются устно.

Задания для повторения. При изучении данного пункта можно использовать задания 937—938.

Решения и комментарии

378. Вычислите, используя формулу разности квадратов:

д) 3,01 ⋅ 2,99; е) 10,2 ⋅ 9,8.

Решение. д) 3,01 ⋅ 2,99 = (3 + 0,01) (3 − 0,01) = 3² − (0,01)² =

= 9 − 0,0001 = 8,9999;

е) 10,2 ⋅ 9,8 = (10 + 0,2) (10 − 0,2) = 10² − (0,2)² = 100 − 0,04 = = 99,96.

380. Представьте выражение в виде разности квадратов:

а) х⁴ − 1; б) 4а² − 4; в) т⁶ − 25; г) 16у² − 49х². Решение. а) х⁴ − 1 = (х²)² − 1²; б) 4а² − 4 = (2a)² − 2²; в) т⁶ − 25 = (m³)² − 5²; г) 16у² − 49х² =(4y)² − (7х)². 381. Разложите многочлен на множители:

ж) т⁴ − п²; з) р⁸ − 49; и) 1 − х⁴; к) а⁴ − b⁴. Решение. ж) т⁴ − п² = (m²)² − n² = (m² − n) (m²+ n); з) р⁸ − 49 = (p⁴)² − 7² = (p⁴ − 7) (p⁴ + 7);

и) 1 − х⁴ = 1² − (x²)² = (1 − х²) (1 + х²) = (1 − х) (1 + х) (1 + х²);

к) a⁴ − b⁴ = (a²)² − (b²)² = (a² − b²) (a² + b²) = (a − b) (a + b) (a² + b²).

384. Вместо букв С и D подберите одночлены так, чтобы выполнялось равенство:

в) (3т − С) (D + 2п) = 9т² − 4п²;

г) (С + 5q) (5q + D) = 25q² − 16p⁴.

Решение. в) Так как 9т² − 4п² = (3т − 2п) (3т + 2п), то равенство выполняется при С = 2п, D = 3т;

г) так как 25q² − 16p⁴ = (5q + 4p²) (5q − 4p²), то равенство

выполняется при С = 4p², D = –4p² или С = –4p², D = 4p². 385. Упростите выражение:

б) (т − п) (п + т) − (т − п)² + 2п²;

в) (с − d)² − (с + d) (d − с) + 2сd.

Решение. б) I способ. (т − п) (п + т) − (т − п)² + 2п² = т² − − п² − (т² − 2тп + п²) + 2п² = т² − п² − т² + 2тп − п² + 2п² =

= 2тп;

II способ. (т − п) (п + т) − (т − п)² + 2п² =

= (т − п) (п + т − (т − п)) + 2п² = (т − п) (п + т − т + п) + 2п² =

= (т − п) ⋅ 2п + 2п² = 2п (т − п + п) = 2тп;

в) I способ. (с − d)² − (с + d) (d − с) + 2сd = с² − 2сd + d² −

− (d² − с²) + 2сd = с² − 2сd + d² − d² + с² + 2сd = 2с²;

II способ. (с − d)² − (с + d) (d − с) + 2сd = (с − d)² + (с + d) × × (с − d) + 2сd = (с − d) (с − d + с + d) + 2сd = (с − d) 2с + 2сd = = 2с (с − d + d) = 2с².

Замечание. Первый способ решения задания 385 основан на раскрытии скобок с помощью формул сокращённого умножения, а второй — на двукратном вынесении общего множителя за скобки.

387. Старинная задача. Я купил столько коробок с мылом, сколько было кусков в коробке. Сестра купила на 3 коробки меньше, чем я, но в каждой было на 3 куска больше, чем в купленных мной. У кого больше кусков и на сколько?

Решение. Пусть я купил n коробок с мылом по n кусков мыла в каждой коробке — всего n² кусков мыла. Сестра купила (n − 3) коробки, но в каждой было по (n+ 3) куска мыла — всего (n − 3) (n+ 3) = n² − 9 кусков мыла. У ме ня мыла больше на 9 кусков. 388. Разложите на множители выражение:

а) (3х + 2)² − х²; в) (4х + 3)² − (х + 1)².

Решение. а) (3х + 2)² − х² = (3х + 2 − х) (3х + 2 + х) =

= (2х + 2) (4х + 2);

в) (4х + 3)² − (х + 1)² = ((4х + 3) − (х + 1)) ((4х + 3) + (х + 1)) = = (4х + 3 − х − 1) (4х + 3 + х + 1) = (3х + 2) (5х + 4).

389. Разложите на множители выражение:

а) (3х + у)² − (2х − 3у)²; д) (2х² − у)² − х⁴.

Решение. а) (3х + у)² − (2х − 3у)² = ((3х + у) − (2х − 3у)) × × ((3х + у) + (2х − 3у)) = (3х + у − 2х + 3у) (3х + у + 2х − 3у) =

= (х + 4у) (5х − 2у);

д) (2х² − у)² − х⁴ = (2х² − у)² − (х²)² = (2х² − у − х²) × × (2х² − у + х²) = (х² − у) (3х² − у).

6.5. Сумма кубов 6.6. Разность кубов

В пунктах 6.5 и 6.6 доказываются формулы суммы и разности кубов, вводятся понятия неполного квадрата разности и суммы. Основное назначение этих формул заключается в их применении для разложения на множители многочленов. Желательно, чтобы каждый учащийся запомнил эти формулы и научился их применять.

Решения и комментарии

395. Упростите выражение:

а) (а³ + 1) (а⁶ − а³ + 1); б) (2 + n²) (n⁴ − 2n² + 4).

Решение. а) (а³ + 1) (а⁶ − а³ + 1) = (а³ + 1) ((а³)² − а³ ⋅ 1 + 1²) =

= (а³)³ + 1³ = а⁹ + 1;

б) (2 + n²) (n⁴ − 2n² + 4) = (n² + 2) ((n²)² − 2n² + 2²) = (n²)³ + + 2³ = n⁶ + 8.

398. Разложите двучлен на множители:

и) с⁶ + 125d³; к) 8р⁶ + q¹².

Решение. и) с⁶ + 125d³ = (с²)³ + (5d)³ =

= (с² + 5d) ((с²)² − с²5d + (5d)²) = (с² + 5d) (с⁴ − 5с²d + 25d²);

к) 8р⁶ + q¹² = (2р²)³ + (q⁴)³ = (2р²+ q⁴) ((2р²)² − 2р²q⁴ + (q⁴)²) = = (2р² + q⁴) (4р⁴ − 2р²q⁴ + q⁸).

400. Упростите выражение:

в) (3 + т) (т² − 3т + 9) − m (m − 2)²;

г) (р⁶ − q³) (р⁶ + q³) − (р⁸ − р⁴q² + q⁴) (р⁴ + q²).

Решение. в) (3 + т) (т² − 3т + 9) − m (m − 2)² = (т³+ 3³) −

− m (m² − 4m + 4) = т³+ 27 − m³+ 4m² − 4m = 4m² − 4m + 27;

г) (р⁶ − q³) (р⁶ + q³) − (р⁸ − р⁴q² + q⁴) (р⁴ + q²) = (р⁶)² − (q³)² − − ((р⁴)³ + (q²)³) = р¹² − q⁶ − р¹² − q⁶ = –2q⁶.

401. Докажите тождество:

в) (а + 2) (а² − 2а + 4) − а (а − 3) (3 + а) = 9а + 8;

г) т (т + п) (т − п) − (п + т) (т² − тп + п²) = –п² (т + п). Решение.

в) (а + 2) (а² − 2а + 4) − а (а − 3) (3 + а) = а³ + 2³ − а (а² − 3²) =

= а³ + 8 − а³ + 9а = 9а + 8, что и требовалось доказать;

г) т (т + п) (т − п) − (п + т) (т² − тп + п²) = т (т² – п²) − − (п³ + т³) = т³ − тп² − п³ − т³= –тп² − п³ = –п² (т + п), что и требовалось доказать.

408. Упростите выражение:

е) (1,21q² + 0,22pq + 0,04р²) (0,2р − 1,1q);

ж) ⎜⎝⎛ 91 m4 + m nk2 + 9n k2 2⎠⎟⎞ ⎝⎜⎛ 13 m2 − 3nk⎞⎟⎠.

Решение. е) (1,21q² + 0,22pq + 0,04р²) (0,2р − 1,1q) =

= (0,2р)³ − (1,1q)³ = 0,008р³ − 1,331q³;

ж) ⎜⎝⎛ 91 m4 + m nk2 + 9n k2 2⎞⎟⎠ ⎝⎜⎛ 13 m2 − 3nk⎠⎞⎟ = ⎝⎛⎜ 13 m2⎞⎠⎟ − (3nk)3 =

= m⁶− 27n k^{3 3}. 409. Разложите двучлен на множители:

е) т¹² − 64; ж) х⁹ − х⁶; з) с⁶d³ − k³.

Решение. е) т¹² − 64 = (т⁴)³ − 4³ = (т⁴ − 4) ((т⁴)² + 4т⁴ + 4²) =

= (т⁴ − 4) (т⁸ + 4т⁴ + 16) = (т² − 2) (т² + 2) (т⁸ + 4т⁴ + 16);

ж) х⁹ − х⁶ = х⁶ (х³ − 1) = х⁶ (х − 1) (х² + х + 1);

з) с⁶d³ − k³ = (с²d)³ − k³ = (с²d − k) ((с²d)² + с²dk + k²) = = (с²d − k) (с⁴d² + с²dk + k²).

411. Упростите выражение:

в) 2р² (2 − р) (р² + 2р + 4) − 4 (р − 5) (5 + р);

г) п⁵ (2 + п²) (п² − 2) − (т − п³) (т² + тп³ + п⁶).

Решение. в) 2р² (2 − р) (р² + 2р + 4) − 4 (р − 5) (5 + р) = = 2р² (8 − р³) − 4 (р² − 25) = 16р² − 2р⁵ − 4р² + 100 = –2р⁵ +

+ 12р² + 100;

г) п⁵ (2 + п²) (п² − 2) − (т − п³) (т² + тп³ + п⁶) =

= п⁵ ((п²)² − 2²) − (т³ − (п³)³) = п⁵ (п⁴ − 4) − (т³ − п⁹) = п⁹ − 4п⁵ − − т³ + п⁹ = 2п⁹ − 4п⁵ − т³. 412. Докажите тождество:

а) (а + b) (а − b) (а² − аb + b²) (а² + аb + b²) = а⁶ − b⁶;

б) (а − 1) (а − 2) (а² + а + 1) (а² + 2а + 4) = а⁶ − 9а³ + 8.

Решение. а) (а + b) (а − b) (а² − аb + b²) (а² + аb + b²) = (а³ + b³) ×

× (а³ − b³) = (а³)² − (b³)² = а⁶ − b⁶, что и требовалось доказать;

б) (а − 1) (а − 2) (а² + а + 1) (а² + 2а + 4) = (а³ − 1³) (а³ − 2³) =

= (а³ − 1) (а³ − 8) = а⁶ − а³ − 8а³ + 8 = а⁶ − 9а³ + 8, что и требовалось доказать.

6.7. Куб суммы 6.8. Куб разности

В пунктах 6.7 и 6.8 доказываются формулы куба суммы и куба разности. Эти формулы считаются необязательными, так как если знать, что (a + b)³ = (a + b) (a + b)², то и без формулы куба суммы это выражение можно преобразовать. Но всё же бывают ситуации, когда гораздо экономнее воспользоваться формулой сокращённого умножения именно для сокращения вычислений. Поэтому помнить эти формулы полезно. Есть ещё один аргумент: работа с большим числом формул лучше тренирует и память школьников, и технику преобразований буквенных выражений.

Для мотивации запоминания формул можно предложить следующие задания.

Пример 1. Вычислите:

а) A = 49³ + 3 ⋅ 49² ⋅ 51 + 3 ⋅ 49 ⋅ 51² + 51³;

б) B = 49³ − 3 ⋅ 49² ⋅ 48 + 3 ⋅ 49 ⋅ 48² − 48³.

Если не знать формулы, то вычисления будут громоздкими и долгими, а если применить формулы, то получим

а) A = (49 + 51)³ = 100³= 1 000 000;

б) B = (49 − 48)³ = 1³= 1.

Решения и комментарии

419. Выясните, является ли многочлен кубом какого-либо двучлена:

а) 8х³ + 12х²у + 6ху² + у³; в) 27 + 27b + 9b² + b³.

Решение. а) 8х³ + 12х²у + 6ху² + у³ = (2х)³ + 3 ⋅ (2х)² ⋅ у +

+ 3 ⋅ 2х ⋅ у² + у³ = (2х + у)³;

в) 27 + 27b + 9b² + b³ = 3³ + 3 ⋅ 3² ⋅ b + 3 ⋅ 3 ⋅ b² + b³ = (3 + b)³.

420. а) Упростите выражение двумя способами:

(х + 3)³ − (х + 2)³. Решение. I способ.

+ − + = + ⋅ ⋅ + ⋅ ⋅ + −

− (х + 3 х 2 + 3 х 2 + 2 ) =

= х³ + 9х² + 27х + 27 − х³ − 6х² − 12х − 8 = 3х² + 15х + 19; II способ.

(х + 3)³ − (х + 2)³ = (х + 3 − (х + 2)) ((х + 3)² + (х + 3) (х + 2) + (х + 2)²) = = (х + 3 − х − 2) (х² + 6х + 9 + х² + 5х + 6 + х² + 4х + 4) = = 3х² + 15х + 19.

426. Запишите выражение в виде степени двучлена:

е) а³ − 3а² + 3а − 1; з) а³ − 6а² + 12а − 8. Решение. е) а³ − 3а² + 3а − 1 = (a − 1)³; з) а³ − 6а² + 12а − 8 = (a − 2)³. 427. Выясните, является ли многочлен кубом какоголибо двучлена:

а) 1 − 3х + 3х² − х³; в) 8а³ − 36а²b + 54аb² − 27b³. Решение. а) 1 − 3х + 3х² − х³ = (1 − х)³;

в) 8а³ − 36а²b + 54аb² − 27b³ = (2a − 3b)³. 428. Упростите выражение двумя способами:

а) (х − 1)³ − (х + 1)³; б) (х + 2)³ + (х − 2)³. Решение. а) I способ. (х − 1)³ − (х + 1)³ =

= (х³ – 3х² + 3х − 1) − (х³+ 3х² + 3х + 1) = х³– 3х² + 3х − 1 − х³ −

− 3х² − 3х − 1 = –6х² − 2;

II способ. (х − 1)³ − (х + 1)³ = ((х − 1) − (х + 1)) ×

× ((х − 1)² + (х − 1) (х + 1) + (х + 1)²) = (х − 1 − х − 1) ×

× (х² − 2х + 1 + х² − 1 + х² + 2х + 1) = (–2) (3х² + 1) = –6х² − 2;

б) I способ. (х + 2)³ + (х − 2)³ = (х³ + 6x² + 12х + 8) +

+ (х³ − 6x² + 12х − 8) = х³ + 6x² + 12х + 8 + х³ − 6x² + 12х − 8 =

= 2х³ + 24x;

II способ. (х + 2)³ + (х − 2)³ =

= (х + 2 + х − 2) ((х + 2)² − (х + 2) (х − 2) + (х − 2)²) =

= 2х (х² + 4х + 4 − (х² − 4) + х² − 4х + 4) = 2х (х² + 12) = 2х³ + 24x.

429. Как получить формулу куба разности из формулы куба суммы?

Решение. Надо разность (a − b) представить как сумму (a + (–b)) и применить формулу куба суммы:

(a − b)³ = (a + (–b))³ = a³ + 3a² (–b) + 3a(–b)² + (–b)³ = = a³ − 3a²b + 3ab² − b³.

Промежуточный контроль. С—12.

6.9. Применение формул сокращённого умножения

В данном пункте приводятся все изученные формулы сокращённого умножения и напоминается, что все они являются тождествами. Далее рассматриваются примеры применения этих формул для упрощения выражений. Количество упражнений в данном пункте избыточно, не надо стремиться все их решить при изучении данного пункта — оставшиеся задания можно использовать для повторения, но главные идеи продемонстрировать и отработать надо. Учащиеся должны научиться видеть квадрат суммы двучлена a + 1 и одночлена 1 в задании 433а, находить произведение суммы и разности одних и тех же выражений в произведениях многочленов в задании 435, находить пары множителей, к которым применимы формулы сокращённого умножения, в заданиях 436—437, видеть возможности многократного применения формул сокращённого умножения в задании 437 и т. п.

Вспомнить формулы (a + b)ⁿ для n = 2, n = 3, а также получать новые формулы для n = 4, n = 5 совсем не трудно с помощью треугольника Паскаля, дающего коэффициенты разложения n-й степени двучлена в многочлен. Этот материал приводится в Дополнениях к главе 2, и его можно дать в классах с углублённым изучением математики.

Изучить формулы куба суммы и куба разности полезно ещё потому, что в старших классах учащиеся будут в обязательном порядке изучать бином Ньютона.

Решения и комментарии

433. б) Упростите выражение (т − п)² + 2п (т − п) + п². Решение. (т − п)² + 2п (т − п) + п² = (т − п + п)² = m². Преобразуйте выражение в многочлен (434—437):

434. а) (х + у + z) (х + у − z). Решение.

(х + у + z) (х + у − z) = (х + у)² − z² = х² + 2ху + у² − z². 435. а) (а + b + с + d) (а + b − с − d).

^{Решение.}(а + b + с + d) (а + b − с − d) =

= ((а + b) + (с + d)) ((а + b) − (с + d)) = (а + b)² − (с + d)² = = а² + 2аb + b² − (с² + 2сd + d²) = а² + 2аb + b² − с² − 2сd − d².

436. г) (3 − р) (р² + 9) (р + 3);

з) (5 + т) (т − 5) (т − 5) (m + 5).

Решение. г) (3 − р) (р² + 9) (р + 3) = (3² − р²) (р² + 9) =

= (9 − р²) (9 + р²) = 9² − (р²)² = 81 − р⁴;

з) (5 + т) (т − 5) (т − 5) (m + 5) = (т² − 5²) (т² − 5²) = = (т² − 25)² = (т²)² − 2т² ⋅ 25 + 25² = т⁴ − 50т² + 625.

437. а) (а + 1) (а + 2) (а² + 4) (а² + 1) (а − 2) (а − 1).

Решение. (а + 1) (а + 2) (а² + 4) (а² + 1) (а − 2) (а − 1) =

= (а + 1) (а − 1) (а² + 1) (а + 2) (а − 2) (а² + 4) = (а² − 1) (а² + 1) × × (а² − 4) (а² + 4) = ((а²)² − 1) ((а²)² − 16) = (а⁴ − 1) (а⁴ − 16) = = а⁸ − а⁴ − 16а⁴ + 16 = а⁸ –17а⁴ + 16. 446. а) Вычислите:

(2 + 1) (2² + 1) (2⁴ + 1) (2⁸ + 1) (2¹⁶ + 1) (2³² + 1).

Решение. Здесь нужно догадаться умножить данное произведение на число 1 = 2 − 1:

(2 + 1) (2² + 1) (2⁴ + 1) (2⁸ + 1) (2¹⁶ + 1) (2³² + 1) = = (2 − 1) (2 + 1) (2² + 1) (2⁴ + 1) (2⁸ + 1) (2¹⁶ + 1) (2³² + 1).

Далее, применив 6 раз формулу разности квадратов, получим 2⁶⁴ − 1.

447. Задача Ибн Сины. Если число, будучи разделено на 9, даёт остаток 1 или 8, то квадрат этого числа, делённый на 9, даёт остаток 1. Докажите.

Доказательство. Числа, о которых идёт речь в условии задачи, можно записать в виде 9n + 1 или 9k + 8 = 9 (k + 1) − 1, где n, k — некоторые натуральные числа. Квадраты этих чисел имеют вид

(9n)²+ 2 ⋅ 9n + 1 и (9 (k + 1))² − 2 ⋅ 9 (k + 1) + 1.

При делении на 9 эти числа дают остаток 1, что и требовалось доказать.

448. Задача Пифагора. Докажите, что всякое нечётное натуральное число, кроме 1, есть разность квадратов двух последовательных натуральных чисел.

Доказательство. Всякое нечётное натуральное число, кроме 1, можно записать в виде 2n + 1, где n — некоторое натуральное число. Запишем это число в виде 2n + 1 = n² + + 2n + 1 − n² = (n + 1)² − n² — это разность квадратов двух последовательных натуральных чисел, что и требовалось доказать.

6.10. Разложение многочленов на множители

В данном пункте приводится несколько способов разложения многочлена на множители:

1) вынесение за скобки общего множителя многочленов;

2) применение формул сокращённого умножения;

3) выделение полного квадрата;4) группировки членов многочлена;

5) применение нескольких способов.

Желательно добиться того, чтобы все учащиеся умели разложить многочлен на множители хотя бы в простых ситуациях, так как это умение потребуется им в дальнейшем обучении.

Задания для повторения. При изучении данного пункта можно использовать задания 919—923, 927—931.

Решения и комментарии

453. Вынесите общий множитель многочлена за скобки: ж) 2тп³ − 4т²п − 6т²п³; з) 6р⁴q³ + 8р²q³ − 10р³q². Решение. ж) 2тп³ − 4т²п − 6т²п³ = 2тп (п² – 2т − 3тп²); з) 6р⁴q³ + 8р²q³ − 10р³q² = 2р²q² (3р²q + 4q − 5р). 455. а) Разложите многочлен на множители:

16а²bс³ − 12ас³ + 28b²с² − 8аbс⁵.

Решение. 16а²bс³ − 12ас³ + 28b²с² − 8аbс⁵ = = 4с² (4а²bс − 3ас + 7b² − 2аbс³).

468. а) Преобразуйте данное целое выражение в произведение многочленов: (2т + п) (6т + 2п) − (т − 3п) (8п + 16т).

Решение. (2т + п) (6т + 2п) − (т − 3п) (8п + 16т) =

= (2т + п) (6т + 2п) − 8 (т − 3п) (п + 2т) = (2т + п) × × (6т + 2п − 8 (т − 3п)) = (2т + п) (6т + 2п − 8т + 24п) = = (2т + п) (26п − 2т) = 2 (2т + п) (13п − т).

469. Разложите выражение на множители, используя формулы сокращённого умножения:

д) (2х − у)² − (3х − 2у)²; з) (х − 2у)² + 4 (х − 2у) + 4.

Решение. д) (2х − у)² − (3х − 2у)² = (2х − у − (3х − 2у)) ×

× (2х − у + 3х − 2у) = (2х − у − 3х + 2у) (5х − 3у) = (у − х) (5х − 3у);

з) (х − 2у)² + 4 (х − 2у) + 4 = (х − 2у + 2)².

472. Разложите многочлен на множители, предварительно представив один из его членов в виде суммы:

а) х² − 3х + 2; г) х² − 3х − 4.

Решение. а) х² − 3х + 2 = х² − х − 2х + 2 = х (х − 1) − 2 (х − 1) =

= (х − 1) (х − 2);

г) х² − 3х − 4 = х² + х − 4х − 4 = х (х + 1) − 4 (х + 1) = (х + 1) × × (х − 4).

Замечание. Разложение квадратного трёхчлена на множители развивает способность ученика комбинировать алгебраические объекты, заменять одночлен суммой подходящих одночленов. Но учащимся можно раскрыть «секрет»: если они найдут значение неизвестного x₀, обращающее многочлен в нуль, то надо стараться получить множитель (x − x₀) в разложении этого многочлена на множители. Этот приём будет обоснован в 8 классе.

Так, в задании 472а число 1 обращает многочлен в нуль, и в разложении этого многочлена на множители имеется двучлен (х − 1), а в задании 472г число –1 обращает многочлен в нуль, и в разложении этого многочлена на множители имеется двучлен (х − (–1)) = х + 1.

473. Разложите многочлен на множители, предварительно выделив полный квадрат:

а) а² + 8а + 15; б) х⁴ + 4b⁴.

Решение. а) а² + 8а + 15 = а² + 8а + 16 − 1 = (а + 4)² − 1² =

= (а + 4 − 1) (а + 4 + 1) = (а + 3) (а + 5);

б) х⁴ + 4b⁴ = х⁴ + 4х²b² + 4b⁴ − 4х²b² = (х² + 2b²)² – 4х²b² = = (х² + 2b²)² − (2хb)² = (х² + 2b² − 2хb) (х² + 2b² + 2хb).

476. Задача Софии Жермен. Докажите, что при любых натуральных а ≠ 1 каждое число вида а⁴ + 4 является составным числом.

Доказательство. а⁴ + 4 = а⁴ + 4а² + 4 − 4а² = (а² + 2)² − − (2а)² = (а² + 2 − 2а) (а² + 2 + 2а) = (а² − 2а + 2) (а² + 2а + 2).

При a = 1 имеем а⁴ + 4 = 5, т. е. число а⁴ + 4 простое, т. е. не составное, а для натурального a > 1 число а⁴ + 4 делится на различные числа а² − 2а + 2 = (а − 1)² + 1 и а² − 2а + 2 = = (а + 1)² + 1, бо льшие 1, т. е. число а⁴ + 4 составное, что и треб овалось доказать.

477. Разложите многочлен на множители:

а) х⁴ − 3х² + 2; д) х¹⁶ − y¹⁶.

Решение. а) х⁴ − 3х² + 2 = х⁴ − х² − 2х² + 2 = х² (х² − 1) −

− 2 (х² − 1) = (х² − 1) (х² − 2) = (х − 1) (х + 1) (х² − 2);

д) х¹⁶ − y¹⁶ = (х⁸ + y⁸) (х⁸ − y⁸) = (х⁸ + y⁸) (х⁴ + y⁴) (х⁴ − y⁴) = = (х⁸ + y⁸) (х⁴ + y⁴) (х² + y²) (х² − y²) = (х⁸ + y⁸) (х⁴ + y⁴) (х² + y²) × × (х + y) (х − y).

479. Разложите многочлен на множители:

и) х⁸ + х⁴ + 1; л) х³ + 3х² + 3х − 26.

Решение. и) х⁸ + х⁴ + 1 = х⁸ + 2х⁴ + 1 − х⁴ = (х⁴ + 1)² − (х²)² =

= (х⁴ + 1 − х²) (х⁴ + 1 + х²) = (х⁴ − х² + 1) (х⁴ + х²+ 1);

л) х³ + 3х² + 3х − 26 = х³ + 3х² + 3х + 1 − 27 = (х + 1)³ − 3³ =

= (х + 1 − 3) ((х + 1)² + 3 (х + 1) + 9) = (х − 2) × × (х² + 2х + 1 + 3х + 3 + 9) = (х − 2) (х² + 5х + 13).

919. Верно ли, что если х — целое число и 5х + 9 делится на 17, то 10х + 1 также делится на 17?

Решение. 10х + 1 = 10х + 18 − 17 = 2 (5х + 9) − 17. Так как 5х + 9 делится на 17 по условию, то по свойствам делимости произведение 2 (5х + 9) и разность 2(5х + 9) − 17 делятся на 17. Тогда и 10х + 1 делится на 17.

922. Докажите, что если при некоторых целых х и у выр ажение х² + 9ху + y² делится на 11, то и х² − у² делится на 11.

Решение. Так как х² + 9ху + у² = (х − y)² + 11ху делится на 11 и 11ху делится на 11, то (х − y)² делится на 11. Тогда и х − y делится на 11.

В самом деле, предположим противное, что остаток от деления х − y на 11 равен p (p ≠ 0). Тогда х − y = 11k + p, где k — целое число, и (х − y)² = 121k² + 22kp + p² = 11 (11k² + 2kp) + + p² — не делится на 11, что противоречит доказанному. Следовательно, х − y делится на 11, поэтому и х² − у² = = (х − y) (х + y) делится на 11, что и требовалось доказать. 930. Разложите на множители:

а) bс (b + с) + ас (с − а) − аb (а + b); в) х³ + 5х² + 3х − 9.

Решение. а) bс (b + с) + ас (с − а) − аb (а + b) = b²с + bс² + + ас² − а²c − а²b − аb² = b²с − аb² + bс² − а²b + ас² − а²c = b² (с − а) +

+ b (с − а) (с + а) + ас (с − а) = (с − а) (b² + b (с + а) + ас) = (с − а) × × (b² + bс + bа + ас) = (с − а) (b (b + с) + a (b + с)) = (с − а) (b + с) ×

× (b + a);

в) х³ + 5х² + 3х − 9 = х³ − х² + 6х² − 6х + 9х − 9 = х² (х − 1) + + 6х (х − 1) + 9 (х − 1) = (х − 1) (х² + 6х + 9) = (х − 1) (х + 3)².

931. Разложите на множители:

д) k⁴ + k² − 20; е) т³ − 3т + 2;

ж) у⁴ − у² (z² + 1) + z²; з) с² + cd + с − 2d² + 2d.

Решение. д) k⁴ + k² − 20 = k⁴ + 5k² − 4k² − 20 = k² (k² + 5) − − 4 (k² + 5) = (k² + 5) (k² – 4) = (k² + 5) (k − 2) (k + 2);

е) т³ − 3т + 2 = т³ − т − 2т + 2 = т (т² − 1) − 2 (т − 1) = = т (т − 1) (т + 1) − 2 (т − 1) = (т − 1) (т (т + 1) − 2) = (т − 1) × × (т² − т + 2т − 2) = (т − 1) (т(т − 1) + 2 (т − 1)) = (т − 1) ×

× (т − 1) (т + 2) = (т − 1)² (т + 2);

ж) у⁴ − у² (z² + 1) + z² = у⁴ − у²z² − у² + z² = у² (у² − z²) −

− (у² − z²) = (у² − z²) (у² − 1) = (у − z) (у + z) (у − 1) (у + 1);

з) с² + cd + с − 2d² + 2d = с² − 4d² + cd + с + 2d² + 2d = = (с − 2d) (с + 2d) + c (d + 1) + 2d (d + 1) = (с − 2d) (с + 2d) + (d + 1) × × (с + 2d) = (с + 2d) (с − 2d + d + 1) = (с + 2d) (с − d + 1).

933. Французский математик Андриен Мари Лежандр предложил такую формулу простых чисел: р = 2х² + 29. Сколько простых чисел даёт эта формула при подстановке в неё последовательных целых значений х начиная с (–28)? Выполните вычисления до получения первого составного числа.

Решение. Выполнить это задание лучше группой, поручив вычисления с разными значениями x разным учащимся. При этом можно воспользоваться таблицей квадратов.

При х = –28 имеем р = 2 ⋅ (–28)² + 29 = 1597 — простое число; при х = –27 имеем р = 2 ⋅ (–27)² + 29 = 1487 — простое

число; при х = –26 имеем р = 2 ⋅ (–26)² + 29 = 1381 — простое

число;

...

при х = –1 имеем р = 2 ⋅ (–1)² + 29 = 31 — простое число; при х = 0 имеем р = 29 — простое число.

Далее, очевидно, что при x, равном 1, 2, ..., 28, получим те же ответы, что и при x, равном –1, –2, ..., –28. Таким образом, при 57 различных целых значениях x от –28 до 28 число р простое.

Очевидно, что при х = 29 или при х = –29 число р делится на 1, на 29 и на р = 29 ⋅ 59, т. е. является составным числом.

934. Докажите, что для любых натуральных чисел а и b найдётся такое целое значение х, что значение многочлена ах² + bх + 29 будет составным числом.

Доказательство. Если х = 29, то ах² + bх + 29 = а ⋅ 29² + + b ⋅ 29 + 29 = 29 ⋅ (29а + b + 1). Для любых натуральных а и b число 29 ⋅ (29а + b + 1) делится на 1, на 29 и на число 29а + b + 1, большее 29. Таким образом, при любых натуральных а и b нашлось число х = 29, такое, что ах² + bх + 29 — составное число.

Промежуточный контроль. C—13, К—3.

§ 7. Алгебраические дроби

В § 7 вводится понятие алгебраической дроби, формулируются свойства алгебраических дробей, правила действий с ними. Умения обращаться с алгебраическими дробями будут использоваться при изучении следующих тем, связанных с решением уравнений.

Основная цель изучения параграфа — научиться приводить алгебраические дроби к общему знаменателю, выполнять действия с алгебраическими дробями.

7.1. Алгебраические дроби и их свойства

В данном пункте рассматривается понятие алгебраической дроби — это частное двух многочленов, второй из которых не является нулевым многочленом. При введении понятия алгебраической дроби можно наглядно показать взаимосвязь понятий «число», «одночлен», «многочлен», «алгебраическая дробь» (рис. 4).

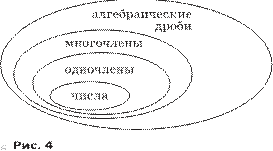
Здесь же вводятся свойства алгебраических дробей:

A = A , A = A C⋅ , − A = −A = A _,

1 B B C⋅ B B −B

позволяющие записывать многочлен в виде алгебраической дроби, приводить дроби к новому знаменателю или сокращать на общий множитель, менять знак перед дробью, меняя знак числителя или знаменателя. В учебнике приведены соответствующие примеры.

Задания для повторения. При изучении данного пункта можно использовать задание 942.

Решения и комментарии

486. Подберите одночлен или многочлен A так, чтобы равенство было верным:

12x y²x 3a x y2 ( + ) = A .

б) = ; в)

48xy A 12ab x y( + ) 4b

Решение. б) 12x y2 12xy x⋅ = x, следовательно, A = 4; =

48xy 12xy ⋅ 4 4

в) 3a x y2 ( + ) = 3a x y a( + ) ⋅ = a , следовательно, A = a. 12ab x y( + ) 3a x y( + ) ⋅ 4b 4b

Замечание. На первых порах не следует стремиться к краткой записи сокращения дробей с зачёркиванием множителей в числителе и знаменателе, чтобы учащиеся лучше осознавали то свойство алгебраических дробей, которое они применяют. Зачёркивание одинаковых чисел и букв может привести к грубым ошибкам — учащиеся будут сокращать дроби и в тех случаях, когда числитель и знаменатель не имеют общих множителей.

Сократите дробь (487—492):

24a b c^{5 6}48x y z^{3 4 3}

487. и) 36a b c7 4 ; к) 56xy z5 4 .

24a b c5 6 12 2⋅ a b b5 4 2 = 32ab22 ; Решение. и) 36a b c7 4 = 12 3⋅ a a b5 2 4 к) 48x y z^{3 4 3} = 6 8⋅ xx y z^{2 4 3} = 6x².

56xy z^{5 4}7 8⋅ xy yz z^{4 3}7yz

4mn m n( − ) 6a b^{2 3}(3 − a)

489. в) ; г) ₃₍₋₃₎.

2m n m( − ) 14ab a

4mn m n( − )

_в)= − 2 2⋅ mn m n( − )

= − ²ⁿ= −2n;

Решение.

2m n m( − ) 2m m n( − ) 1

6a b^{2 3}(3 − a)

_г)_{= −}2 3⋅ aab a³( − 3) _{= −}3a.

14ab a³( − 3) 2 7⋅ ab a³( − 3)

2mn − 6m ) 12m n − )

= − ¹;

е) 1612p qp q^{3 3}2 3−−248p qp q3 2^{2 4}₌84p qp q q^{2 3}_{2 2}((23p−−23qp)) _=
−2q p2(2p −−3qq) = −2q.

7.2. Приведение алгебраических дробей к общему знаменателю

В данном пункте показан приём приведения дробей к общему знаменателю, который должны освоить все учащиеся, так как на его основе они будут в дальнейшем складывать и вычитать дроби с разными знаменателями. Решения и комментарии

Приведите к общему знаменателю дроби (497—502):

497. к) ; л) .

Решение. к) 4/5 5 4⋅ = 20 и 3/1 = 1 3⋅ = 3 ;

12 12 4⋅ 48 16 16 3⋅ 48

л) ^3/8 8 3⋅ 24 ⁻^{^[2]}^/5 5 ⋅ − −10_.

1 13 3

498. з) и ; и) и .

5x −10x x 3

3 ⋅ x

2 + x 2 + x

7.3. Арифметические действия с алгебраическими дробями

В данном пункте вводятся определения суммы и разности алгебраических дробей с общим знаменателем. Здесь же отмечается, что сумму и разность дробей можно вычислять по формулам

A + C = A D B C⋅ + ⋅ и A − C = A D B C⋅ − ⋅ . (1)

B D B D⋅ B D B D⋅

Надо отметить, что применение формул (1) всегда приводит к верному результату, но в том случае, когда знаменатели данных дробей имеют общие множители, может оказаться неэкономным.

Далее вводятся определения произведения и частного двух алгебраических дробей, доказываются свойства алгебраических дробей.

0 1. Если B — ненулевой многочлен, то = 0. B

1 1 1 A ¹

2. = ⋅ . 3. = A ⋅ .

A B⋅ A B B B

4. AB − DC = AB + ⎛⎜⎝− DC ⎠⎟⎞. 5. AB − AB = 0.

Задания для повторения. При изучении данного пункта можно использовать задания 943—945.

Решения и комментарии

Преобразуйте в алгебраическую дробь (519—528):

3a 3b m n⁷3mn²

519. д) 7 5 − xy z4 5 ; е) a b c4 3 9 + a b c3 6 4 .

x y z

Решение.

д) x y zz4/3a − x y6 /3b = 37 5azz45 − x37 5by zx y6 5 = 3azx47−y z53b5x y6 ;

7 5 xy z4 5 x y

ba b c3/m n7 + aca b c5/^{3 6 4}3mn2 = a b cb m n3 7^{4 6 9}+ 3ac mna b c4 6 95 2 b m3 7na b c+ 3ac mn5 2

е) ^{4 3 9}= 4 6 9 .

Замечание. Важно обратить внимание учащихся на то, что, приводя дроби к общему знаменателю, можно не только умножать числитель и знаменатель дроби на один и тот же множитель, но и сокращать дробь на общий множитель числителя и знаменателя (задания 520—521).

520. и) 10p q3 15− 15p q2 2 − 9pq3 6−q6p q2 2 ;

3b 5a

к) 2a b3 − 8a b2 2 − 12a b3 − 3a4 .

Решение. и) 10 3 15− 15p q2 2 − 9pq3 6−q6p q2 2 = 5p q p2 (152 − 3q) − p q

− 3pq q2(63q − 2p) = p q p2 (23 − 3q) − pq q(32− 2p) = p q p2 (23 − 3q) +

+ pq p(2p/2− 3q) = p q p2 (23 − 3q) + p q p2 (22p− 3q) = p q p2 3(2+ 2−p3q);

к) 2a b3 3−b8a b2 2 − 12a b35a− 3a4 = 2a b a2 (3b− 4b) − 3a b a3 (54a − ) =

= 2 3 2 = 2 3/3 + 2 2/5 =

521. ж) (xx²−−22yxy)3 + 2y x1− _.

Решение. (xx²−−22yxy) ⁺1 ⁼x (x − 2y3) − x −¹2y =

3 2y x− (x − 2y)

= (x −x2y)²− _xx−−2y2/y1 ₌₍x ₋x2y₎²− _(xx−−22yy)²= x x(−x(− 2−y2)²y) = = x x(x−− 2+y2)2y = (x −2y2y)2 .

x yx y+− ⋅ 2x xyx²2−− 2y2 ; е) m162−− m3m²: mm²2+−49m .

526. д)

Решение. д) x yx y+− ⋅ 2x xyx22−− 2y2 = x yx y+− ⋅ 2 (x y x yx x y−( ) (− )+ ) =

= x y+ ⋅ x = (x y x+ ) = x _;x y− 2 (x y+ ) 2 (x y x y− ) ( + ) 2 (x y− )

е) 16 − m²: m²+ 4m ⁼(4 − m) (4 + m) ^:(m + 4) m = m2 − 3m m2 − 9 m m( − 3) (m − 3) (m + 3)

= (4 − mm m) ((4 +−m m3) () (m +− 43)) (mm + 3) = (4 − mm) (2m + 3) = 12 +mm m2− ²_.

p²− 4q²p³− 8q³

528. д) (p + 2q)2 : 4q2 + 2pq p+ 2 ;

128aa b²+ 6ab ⋅ 4a²+22−ab6ab+ b2 .

е) 3 − 3 3a

Решение. д) (pp²+−24qq)²2 : 4q2p+³2−pq p8q+³2 = (p −(2pq p+) (2q)+2 2q) ×

× (p q p−24q)(2 +²2+pq p2_{pq q}+ +24 ²₎= _{p q}p q+−22 ⋅ _{p q}₋12 = ₍p q₊(p q2−)(2 p q)−⋅12 ₎= _{p q}₊^;

е) 128aa b²⁺6ab ^⋅4a²⁺₂2−ab b6ab+ ²⁼(2a b a− 6) (a a b4(2₂+⁺2ab b) + ₂×

₃− ₃3a

_×4a3²a a+(2ab b− 2+b) ²₌(2a b a−6a a b a) ((24 ₂⁺+) (2ab b4 +²⁺₂2)ab b3a a⁺( ²)− 2b) =

₌(2a b a2 2−( ) (a b+ −)2b) = 2a2 4−a5ab+ 2+b 2b2 .

Промежуточный контроль. С—15, С—16.

7.4. Рациональные выражения

В данном пункте вводится понятие рационального выражения. Отметим, что алгебраическая дробь также является рациональным выражением. Здесь впервые появляются рациональные выражения — дроби, числители и знаменатели которых являются алгебраическими дробями. Разбираются примеры на выполнение нескольких действий с рациональными выражениями.

Главная цель данного пункта заключается в закреплении навыков действий с алгебраическими дробями.

Задания для повторения. При изучении данного пункта можно использовать задания 946—951.

Решения и комментарии

Преобразуйте в алгебраическую дробь (534—539):

534. в) ⎜⎝⎛ ab + bc + ac⎞⎟⎠ ⋅ abc ; г) 3x3⎛⎝⎜ x22 + 1y + x4⎞⎟⎠.

⎛ a + b + c⎞⎟⎠ ⋅ abc = ab ⋅ abc + bc ⋅ abc + ac ⋅ abc =

Решение. в) ⎜⎝ b c a

3 y

Замечание. При выполнении задания 534 можно сначала сложить дроби, затем выполнить умножение, а можно применить распределительный закон, как показано выше. Выполнение преобразований рационального выражения можно производить по действиям (задание 535). Спешить с переходом к выполнению преобразования «цепочкой» не следует. По мере формирования умения преобразовывать рациональные выражения переход к использованию «цепочки» в простых случаях произойдёт сам собой. 535. в) ⎜⎝⎛m − 1 +1m⎞⎟⎠ ⋅ 1 −mm m+−1 2 ; г) ⎛⎝⎜a + ac2⎞⎟⎠ : ⎛⎜⎝b + bca ⎞⎟⎠;

ж) ⎜⎝⎛ n xn+ − n xn− ⎟⎠⎞ : ⎛⎜⎝ n xn− + n xn+ ⎠⎞⎟.

Решение. в) 1) m ₋¹₌¹⁺^m^/^m− 1 = m (1 + m) −

1 + m 1 1 + m 1 + m

− 1 = m m+ ²− 1_;

1 + m 1 + m

2 ) m m+ ²−1 _⋅m+1 ⁼(m m²+ −1)(m+1) ⁼m m²+ −1 =

1+m 1−m m− 2 (1+m)(1−m m− 2) −(m2+ −1)

= −1 ;

^г)⎛⎜⎝a ⁺a_c2⎞⎟⎠ ^:⎛⎜⎝b + bc_a⎞⎠⎟ = ac a+_c2 : ab bc_a+ = a c a( _c+ ) : b a c( _a+ ) =

= a c a a( + ) = a²_;cb a c( + ) bc

ж) 1) ^{n x}⁻^/n − ^{n x}⁺^/n = n n x( − ) − n n x( + ) = n x+ n x− (n x n x+ ) ( − ) (n x n x+ ) ( − )

= n nx n nx²− − ( ²+ ⁾= n nx n nx²− − ²⁻= −2^nx_;

(n x n x+ ) ( − ) (n x n x+ ) ( − ) (n x n+ ) ( x) 2) ^{n x}⁺^/n + ^{n x}⁻^/n n n x( + ) + n n x( − ) =

= n x− n x+ (n x n x− ) ( + ) (n x n x− ) ( + )

= n nx n nx²+ + ²⁻= 2n²_;

(n x n x+ ) ( − ) (n x n x+ ) ( − )

3) :

(n x n x+ −2) (nx− ) (n x n x+ 2) (n²− ) = −(n x n x n2nx n x n x+ () (+ −) () 2− ₂) = −n .

539. а) a b3 −− 3 ⋅ a ab b2 + a + 2 − (a − b);

ab a b+ + a .

б) a b2 − 2 : a b2 − 2 a b+

a ba b³−− ³⋅ a ab b2 + a + 2 = (a b a ab b− () (a b a³−2 +³) + 2) = Решение. а) 1)

= (a b aa b33−− 33) = a;

2) a − (a − b) = a − a + b = b.

б) 1) a b2 − 2 : a b2 − 2 = (a b a bab a b2 −( 22) (− +2) ) = a bab+ ; ab a b+

2) ab a²ab a+ ²= a b a( + ) = _a_.

+ =

a b+ a b+ a b+ a b+

Промежуточный контроль. С—17.

7.5. Числовое значение рационального выражения В данном пункте вводится понятие числового значения рационального выражения при заданных значениях букв, здесь же рассматривается вопрос о значениях букв, при которых рациональное выражение определено (имеет смысл).

Для классов с углублённым изучением математики приводятся примеры доказательства числовых неравенств (задачи 1 и 2).

Решения и комментарии

549. а) Упростив рациональное выражение, найдите его значение при a = –3:

⎛^⎜⎝ aa+21 − a2 +a23a + 1⎞⎟⎠ : ⎛⎜⎝ aa+ 1 − a2a−2 1⎞⎟⎠.

a2 a3 a+1 2/a a3

Решение. 1) a + 1 − a2 + 2a + 1 = a + 1 − (a + 1)2 =

;

a 2 −1/ 2 2 − − 2 =

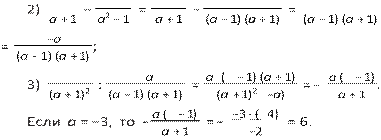a2 − 2

3m²+ 6mn + 3n²557. а) Упростите выражение 6n₂₋_6m2 и вычислите его значение при m = 0,5, n = .

Решение. 3m²+ 6mn + 3n²= 3 (m2 + 2mn n+ 2) =

6n − 6m 6 (n m−

= m n+

2 (n m m n− ) ( + ) 2 (n m− )

Если m = 0,5, n = , то

0 5, + 2 1 + 2 3 + 4

m n+ = 3 = 2 3 = 6 6 =

2 (n m− ) 2 ⎛⎜ 2₃− 0 5, ⎞⎠⎟ 2 ⎛⎜⎝ ₃2− 1₂⎠⎟⎞ 2 ⎝⎛⎜ 4₆− 3⎞⎟⎠

⎝

= : = 3 5, .

559. Найдите, если это возможно, числовые значения x, для которых значение алгебраической дроби — натуральное число:

12 x + 2

а) ; б) . x + 5 x

Решение. а) Так как число 12 имеет делителями целые числа 1, –1, 2, –2, 3, –3, 4, –4, 6, –6, 12, –12, то искомые значения x найдём, решив уравнения x + 5 = 1, x + 5 = –1, ..., x + 5 = 12, x + 5 = –12. Искомые значения x есть –4, –6, –3, –7, –2, –8, –1, –9, 1, –11, 7, –17.

x + 2 = 1 + ², а число 2 имеет делителями

б) Так как

x x

целые числа 1, –1, 2, –2, то искомые значения x равны 1, –1, 2, –2.

560. а) Докажите, что для любого числа x верно не2

равенство x₂+ _6x+ ₁₁≤ 1. Определите, при каком значении x левая часть неравенства равна правой.

Решение. Так как ₂2 ⁼²₂ и (x + 3)² + 2 ≥ 2 x + 6x + 11 (x + 3) + 2

при любом значении x, то неравенство ₂²≤ 1 верно x + 6x + 11

при любом значении x.

Левая часть неравенства равна правой при x = –3.

561. а) Докажите, что для любых чисел x и y верно 3

неравенство x2 + y2 − 6x + 2y + 13 ≤ 1. Определите, при каких значениях x и y левая часть неравенства равна правой.

Решение. Так как

и (x − 3)² + (y + 1)² + 3 ≥ 3 при любых значениях x и y, то

неравенство верно при любых значе-

ниях x и y.

Левая часть неравенства равна правой при x = 3 и y = –1.

Промежуточный контроль. С—18.

7.6. Тождественное равенство рациональных выражений

В данном пункте вводится понятие тождества, или тождественного равенства, для рациональных выражений, решаются задачи на доказательство тождеств.

Отметим три способа доказательства тождества A = B, где A и B — рациональные выражения. Можно выражение A преобразовать так, чтобы получить выражение B; можно выражение B преобразовать так, чтобы получить A (примеры 1 и 2 из учебника); можно каждое из выражений A и B преобразовать так, чтобы получить одно и то же выражение C (пример 3).

Замечание. Доказываемые тождества часто справедливы не для всех значений входящих в них букв, но в этом пункте мы не обращаем на это внимания, считая, что тождества рассматриваются только для тех значений букв, для которых имеют смысл обе части тождеств.

Задания для повторения. При изучении данного пункта можно использовать задания 957—958.

Решения и комментарии

568. Докажите тождество:

а) 1 + ¹+ ¹= 0;

(a b b c− ) ( − ) (b c c a− ) ( − ) (a c b a− ) ( − )

в) 2 a b4 −2 4 2 = 2 1 2 .

((a b+ ) − 4ab a b) (( − ) + 4ab a b) (( + ) − 2ab) a b−

Решение. Преобразуем левую часть предполагаемого тождества:

1 1 1 1

а) + + = −

(a b b c− ) ( − ) (b c c a− ) ( − ) (a c b a− ) ( − ) (a b b c− ) ( − )

− 1 − 1 = a c− /1 − a b− /1 −

(b c a c− ) ( − ) (a c a b− ) ( − ) (a b b c− ) ( − ) (b c a c− ) ( − ) b c− /1 a c a b− − ( − ) − (b c− ) = a c a b b− − + − + =

− =

(a c a b− ) ( − ) (a b b c a c− ) ( − ) ( − ) (a b b c a c− ) ( − ) ( − )

= ⁰= 0, что и требовалось доказать.

(a b b c a c− ) ( − ) ( − )

^б)((a b+ )²− 4ab a b) (( −a b4)−²+44ab a b) (( + )²− 2ab) =

= (a b a b a b− ) (²a b4+− ) (²4 ²₊²₎= ₍a b a b a b₋(a b a b2) (²+ 2+) () (²2 − ²2+) ²₎= ₍₍a b a b₋a b2) (− +2 ))²=⁼(a b^{a b}₂²−⁻_{2 2}²₎⁼_{a b}2 ¹₋2 , что и требовалось доказать.

569. а) Докажите тождество:

a b2 + 2 ⋅ ⎛⎜⎝ a b62a b−+ 2 : 6a b a b3 +2ab32+− 22a b2+ 6ab2 + a ba b2 ++ 2⎞⎟⎠ = ab a ba b2(+ +2 ). ab

Решение. Преобразуем левую часть предполагаемого тождества:

а) ⋅ ⎛⎜⎝ a b62a b−+ 2 : 6a b a b3 +2ab32+− 22a b2+ 6ab2 + a ba b2 ++ 2⎞⎟⎠ = a b2 + 2

= a b2 + 2 ⋅ ⎛⎜⎝ (a b2 − 2() (6a b6a a b+( )2⋅+2ab b a2)(+−b a b()2 + 2)) + aa b2 ++ 2⎞⎟⎠ = ab

= a b2 + 2 _⋅^⎜⎛ (a b a b a b a b₋−) ((6a b++ ) () ⋅62ab a b+ ( ) (− ²)+ ²₎+ _{a b}a b²₊+ ²⎞^⎟_⎠= ab

= a b2ab+ 2 _⋅⎛^⎜_⎝(a b a b₊−) (2ab²₊²)

+ 2 ₊a b+2 ^⎞⎟⎠ = a b+ /

a b

= a b²+ ²⋅ ⎛ −2ab

+ a²+ 2ab b+ ²^⎞=

⎜

ab ⎝ (a b a b+ ) ( 2 + 2) (a b a b+ ) ( 2 + 2)⎟⎠

= a b2ab+ 2 ⋅ (a b a b+a b2) (+ 22+ 2) = a b2ab+ 2 ⋅ a b1+ = ab a ba b2(+ +2 ), что и требовалось доказать.

Промежуточный контроль. С—19.

§ 8. Степень с целым показателем

В § 8 рассматриваются понятие степени с целым показателем, свойства степени с целым показателем, стандартный вид числа. Умение обращаться со степенью с целым показателем будет использоваться при изучении преобразований рациональных выражений и другого материала.

Основная цель изучения параграфа — научиться вычислять степени с целыми показателями и применять свойства степеней.

8.1. Понятие степени с целым показателем

В данном пункте напоминается определение степени с натуральным показателем для показателя n > 1 и показателем n = 1 и некоторые свойства степени, мотивируется введение определений степени с отрицательным показателем и степени с нулевым показателем, даются эти определения.

В результате изучения нового материала учащиеся должны осознать расширение понятия степени — теперь они умеют вычислять степень не только с натуральным, но и с любым целым показателем. Они должны понимать также, что у степени с неположительным целым показателем основание должно быть отлично от нуля. Успешность овладения учащимися умением вычислять степени чисел зависит от того, умеют ли они находить основание степени, т. е. различать ситуации –3² и (–3)². На формирование этого умения направлены задания 576, 580 и др.

Решения и комментарии

573. Определите, имеет ли смысл выражение. Если да, то вычислите его значение:

а) ⎛^⎜⎝⎞^⎟⎠⁰; б) (0,48 ⋅ 5,2 − 4,8 ⋅ 0,52)⁰.

Решение. а) Так как 0,25 ⋅ 79 > 0,25 ⋅ 60 = 15, а

15, то основание степени отлично от

нуля, поэтому ⎛⎜⎝0 25 79, ⋅ − 3 21 2, ⋅ 11¹⎞^⎟⎠⁰ = 1.

б) Так как 0,48 ⋅ 5,2 − 4,8 ⋅ 0,52 = 4,8 ⋅ 0,52 − 4,8 ⋅ 0,52 = 0,

то выражение (0,48 ⋅ 5,2 − 4,8 ⋅ 0,52)⁰ не имеет смысла. 576. в) Вычислите: 2^–2; –2²; (–2)²; (–2)^–2; –2^–2.

Решение. –(2 ⋅ 2) = –4; (–2)² = (−2) ⋅ (−2) =

= 4; (–2)^–2 ; –2^–2 .

579. Докажите, что для чисел a ≠ 0, b ≠ 0, k — целого

⎛ a⎞−k верно равенство ⎜⎝ b⎟⎠ = ⎛⎜⎝ ab⎞⎟⎠k.

⎛ a⎞⁻^k= 1 k = a1k = ab^kk = ⎜⎝⎛ ab⎟⎠⎞^k, что и

Доказательство. ⎜⎝ b⎠⎟ ⎛ a⎞

⎜⎝ b⎟⎠ bk

требовалось доказать.

582. Сравните с нулём:

а) 2^–3; б) (–2)³; в) (–2)^–3; г) –2³.

Решение. а) 2^–3 = > 0, аналогично показывается, что

целая степень любого положительного числа — положительное число;

б) (–2)³ = (–2) ⋅ (–2) ⋅ (–2) < 0;

в) (–2)^–3 0;

г) –2³ = –(2³) = –8 < 0. 583. Запишите в виде степени с целым показателем, если a ≠ 0:

а) a³ ⋅ a⁴; в) a¹³ : a⁶; д) (a⁴)⁶. Решение. а) a³ ⋅ a⁴ = a³⁺⁴ = a⁷; в) a13 : a6 = a13 − 6 = a7;

д) (a4)6 = a4 ⋅ 6 = a24.

8.2. Свойства степени с целым показателем

В данном пункте сформулированы пять свойств степени с целым показателем. Это те же свойства, которые ранее имели место для степеней с натуральным показателем, но теперь они справедливы и для целых показателей. Поэтому усвоить новый материал учащимся будет несложно. Важно объяснить учащимся, что каждое «новое» свойство можно доказать с опорой на соответствующее «старое» свойство, и рассмотреть примеры 1)—11) таких «доказательств» для заданных степеней.

Решения и комментарии

594. Сравните:

а) 3⁴ и 4³; г) 100²⁰⁰ и 200¹⁰⁰; д) 1999²⁰⁰⁰ и 1998¹⁹⁹⁹.

Решение. а) 3⁴ = 3 ⋅ 3 ⋅ 3 ⋅ 3 = 9 ⋅ 9 = 81, 4³ = 4 ⋅ 4 ⋅ 4 = 64; так как 81 > 64, то 3⁴ > 4³;

г) 100200 = 100100 + 100 = 100100 ⋅ 100100, 200100 = (2 ⋅ 100)100 = = 2¹⁰⁰ ⋅ 2¹⁰⁰; так как 100¹⁰⁰ > 2¹⁰⁰, то 100¹⁰⁰ ⋅ 100¹⁰⁰ > 2¹⁰⁰ ⋅ 100¹⁰⁰ и 100²⁰⁰ > 200¹⁰⁰;

д) 1999²⁰⁰⁰ > 1998²⁰⁰⁰ > 1998¹⁹⁹⁹, следовательно, 19992000 > 19981999.

596. Представьте а⁵⁰ в виде степени с основанием: а) а⁵; б) а²; в) а¹⁰.

Решение. а) а⁵⁰ = a⁵^⋅¹⁰ = (a⁵)¹⁰; б) а50 = a2 ⋅ 25 = (a2)25;

в) а50 = a10 ⋅ 5 = (a10)5.

597. Представьте в виде квадрата:а) а⁴; б) а²⁰; в) а⁵⁰.

Решение. а) а⁴ = a²^⋅² = (a²)²; б) а20 = a10 ⋅ 2 = (a10)2;

в) а50 = a25 ⋅ 2 = (a25)2.

8.3. Стандартный вид числа

В данном пункте вводятся понятия стандартного вида числа, порядка числа, приведены примеры выполнения арифметических действий с числами, записанными в стандартном виде. Здесь полезно разъяснить смысл выражения «число a больше числа b на порядок», например, число 2000 больше числа 200 на порядок, так как 2000 = 2 ⋅ 10³, 200 = 2 ⋅ 10². При изучении данного пункта нужно познакомить учащихся с использованием стандартного вида числа для записи «больших» и «маленьких» чисел (задание 610). В учебнике приведены примеры использования стандартного вида числа при вычислениях.

Можно попросить учащихся привести примеры использования стандартного вида числа для записи величин при изучении других школьных предметов и в справочной литературе, объяснить смысл часто употребляемой в последнее время приставки «нано» (от др.-греч. nanos — гном, карлик) — одной из приставок в системе СИ (10 ^–9 — одна миллиардная). Например, 1 нм (нанометр) = 10 ^–9 м. Можно попросить выяснить, какие ещё используются приставки в системе СИ (задание 611).

Задания для повторения. При изучении данного пункта можно использовать задания 824—825.

Решения и комментарии

603. Запишите число в стандартном виде, укажите порядок числа:

а) 27,4; б) 3821; в) 0,0011.

Решение. а) 27,4 = 2,74 ⋅ 10, порядок числа: 10; б) 3821 = 3,821 ⋅ 10³, порядок числа: 10³;

в) 0,0011 = 1,1 ⋅ 10⁻³, порядок числа: 10^–3.

608. Дано: а = 0,000002546, b = 648 400 000. Вычислите, округлив числа с точностью до третьей значащей цифры:

а) а ⋅ b; б) а : b; в) b : а.

Решение. а ≈ 2,55 ⋅ 10^–6, b ≈ 6,48 ⋅ 10⁸.

а) а ⋅ b ≈ (2,55 ⋅ 10^–6) ⋅ (6,48 ⋅ 10⁸) = 16,524 ⋅ 10² ≈ 1,65 ⋅ 10³;

б) а : b ≈ (2,55 ⋅ 10^–6) : (6,48 ⋅ 10⁸) = 0,3935... ⋅ 10^–14 ≈

≈ 3,94 ⋅ 10^–15;

в) b : а ≈ (6,48 ⋅ 10⁸) : (2,55 ⋅ 10^–6) = 2,541... ⋅ 10¹⁴ ≈ 2,54 ⋅ 10¹⁴.

610. а) Скорость движения Земли вокруг Солнца равна 3 ⋅ 10⁴ м/с. За какое время Земля пройдёт вокруг Солнца путь 1,8 ⋅ 10¹² м?

б) Скорость звука в воздухе (при 0 °С) равна 332 м/с. Через сколько минут звук достигнет объекта, находящегося на расстоянии 18,592 км от источника звука?

Решение. а) Искомое время равно (1,8 ⋅ 10¹²) : (3 ⋅ 10⁴) = = 0,6 ⋅ 10⁸ = 6 ⋅ 10⁷ (с).

В году содержится примерно 3 ⋅ 10⁷ с. Искомое время составляет примерно 2 года.

б) 332 м/с = 3,32 ⋅ 10² м/с, 18,592 км = 18 592 м ≈ 1,86 × × 10⁴ м. Искомое время равно (1,86 ⋅ 10⁴) : (3,32 ⋅ 10²) = = 0,5602... ⋅ 10² ≈ 56 (с).

8.4. Преобразование рациональных выражений

В данном пункте приведены примеры использования степени с отрицательным показателем для преобразования рациональных выражений. Изучаемый материал позволяет повторить формулы сокращённого умножения многочленов в усложнённой ситуации. В примере 3 впервые применяется идея замены числа буквой для преобразования выражений, которые с буквами записываются проще. Решения и комментарии

612. Запишите без отрицательных показателей степе-ней:

а) a^–1 + b^–1; в) (a^–2 − b^–2)^–1.

Решение. а) a–1 + b–1 = 1 + 1 = a b+ ;

a b ab

в) (a–2 − b–2)–1 = ⎛⎝⎜ a12 − b12⎟⎠⎞−1 = ⎝⎛⎜ b aa b22 2− 2⎞⎟⎠−1 = b aa b22 2− 2 .

613. Вычислите:

а) 5^–1 + 10^–1; б) (0,5 + 1)^–2; в) (2^–4 + 4^–2)^–1.

Решение. а) 5^–1 + 10^–1 = + = = ;

−2 −2 2

б) (0,5 + 1)–2 = ⎛⎜⎝ 12 + 1⎞⎟⎠ = ⎜⎝⎛ 32⎞⎟⎠ = ⎛⎜⎝ 23⎞⎟⎠ = 94;

−1 −1 −1

в) (2–4 + 4–2)–1 = ⎛⎜⎝ 214 + 412⎟⎠⎞ = ⎛⎜⎝ 161 + 161 ⎞⎟⎠ = ⎜⎝⎛ 18⎞⎟⎠ = 8.

614. а) Докажите, что верно равенство

(a–1 + b–1)2 = a–2 + 2a–1b–1 + b–2.

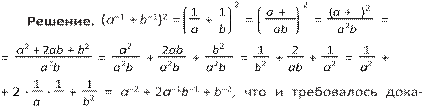
зать.

Замечание. Это задание можно выполнить с помощью замены букв.

Пусть a^–1 = x, b^–1 = y, тогда (a^–1 + b^–1)² = (x + y)² = = x² + 2xy + y² = (a^–1)² + 2a^–1b^–1 + (b^–1)² = a^–2 + 2a^–1b^–1 + b^–2, что и требовалось доказать.

a−2 − b−2

615. а) Упростите выражение a₋₁₊_b−₁.

Решение. aa−2 − b−2 = (a−1 − b−−11)(+ab−−11+ b−1) = a−1 − b−1 = 1a − 1b =

−1 + b−1 a

= b a− _.ab

616. При каких значениях а и b равно 0 выражение:

(a + 3)2

а) (a − 3)−2 − ((aa+−33))−22 ; б) ⎛⎜⎝ a ba b+− ⎞⎟⎠7 − ⎜⎝⎛ a ba b+− ⎞⎟⎠−7?

Решение. а) ((aa−+33))−²2 − ((aa+−33))−22 = (a + 3) (2 a − 3)2 −

− (a − 3) (²a + 3)²= 0 при любых значе ниях a, кроме тех, при которых данное выражение не существует, т. е. кроме a = 3 и a = –3.

⎛ a b+ ⎞7

б) ⎜⎝ a b− ⎟⎠ − ⎛⎜⎝ a ba b+− ⎞⎟⎠−7 = ⎜⎝⎛ a ba b+− ⎟⎠⎞7 − ⎛⎜⎝ a ba b+− ⎞⎟⎠7 = 0 при любых

значениях a и b, кроме тех, при которых данное выражение не существует, т. е. кроме a = b и a = –b.

617. Упростите выражение:a−2 + 2a b− −1 1 + b−2 a−3 + b−3

а) a−2 − b−2 ; б) a−2 − a b− −1 1 + b−2 .

a−2 +a2a b− −1 1 + b−2 = −1 −(ab−−11+) (ba−−1 21)+ b−1) =

Решение. а) −2 − b−2 (a

= aa−−11 +− bb−−11 = ((aa−−11 +− b abb ab−−11)) = b ab a+− ;

б) a−2 −aa b−3− −1 1+ b−3+ b−2 = (a−2(−aa b−3− −1 1+ b−3+) (ba−2−) (1 +ab−1−1+)b−1) =

= (a−3 + ab−−33) (+ ab−−13 + b−1) = a−1 + b−1 = 1a + 1b = a bab+ .

Замечание. Каждое из заданий а) и б) можно выполнить с помощью замены букв. Пусть a^–1 = x, b^–1 = y, тогда в задании а) имеем a−2 +a2−a b2− −−1 1b−2+ b−2 = x2 +x22xy y− y+2 2 = = (x y x y−(x y+) ( )2+ ) = x yx y+− = aa−−11 +− bb−−11 = ((aa−−11 +− bb ab−−1)) ab = b ab a+− .

618. б) Вычислите .

Решение. Пусть 1222 = a, 777 = b, тогда, пользуясь результатом задания 617б, имеем

1222⁻²1222− 1222−3⁻+¹777777⁻−¹3+ 777⁻² = a−2 −aa b−3− −1 1+ b−3+ b−2 = a bab+ =

619. Упростите выражение:

а) −1 ; в) ⎜⎝ x − x 1+ 3⎞⎟⎠−1 + ⎝⎜⎛ x 3+ 3 − x3⎞⎟⎠−1. ⎛ 1

⎛ 1

б) ⎜ − 1 ⎞⎟⎠−1+ ⎛⎜⎝ x 3+ 3 − x3⎟⎠⎞−1= ⎝⎜⎛ xx x+( 3+−3x) ⎞⎟⎠−1+ ⎛⎜⎝ 3xx x−(3 (+x3) 3)⎞⎟⎠−1=

⎝ x x + 3

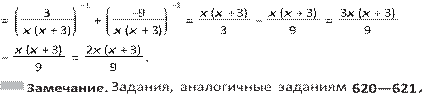
разобраны в тексте учебника (примеры 4 и 5).

Промежуточный контроль. С—21, К—5.

Дополнения к главе 2

1. Делимость многочленов

В классах с углублённым изучением математики можно завершить тему «Многочлены» изучением материала пункта 1 Дополнений к главе 2 (заметим, что это можно сделать и после изучения § 6). Здесь по аналогии с целыми числами рассматривается деление многочлена на многочлен — нацело и с остатком. Здесь можно привести формулы для аⁿ − bⁿ и а²ⁿ⁺¹ + b²ⁿ⁺¹, где n — натуральное число, проведя доказательство для нескольких значений n и оставив общее доказательство (методом математической индукции) для старших классов.

Материал, дополняющий программу обычных классов до программы классов с углублённым изучением математики, позволяет сильным учащимся обычных классов освоить деление многочлена на многочлен. Это умение поможет учащимся решать некоторые задачи с целочисленными данными. В классе с углублённым изучением математики учащиеся должны освоить ещё деление многочленов с остатком, понятие наибольшего общего делителя двух многочленов и алгоритм Евклида для многочленов.

Решения и комментарии

622. Докажите формулу разложения на множители:

а) a⁵ − b⁵; в) a⁵ + b⁵.

Доказательство. а) Для доказательства равенства

a⁵ − b⁵= (a − b) (a⁴ + a³b + a²b²+ ab³ + b⁴)

раскроем скобки в правой части равенства:

(a − b) (a⁴ + a³b + a²b²+ ab³ + b⁴) =

= a⁵ − a⁴b + a⁴b − a³b² + a³b² − a²b³ + a²b³ − ab⁴ + ab⁴ − b⁵ = a⁵ − b⁵.

в) Воспользуемся только что доказанным равенством:

a⁵ + b⁵ = a⁵ − (–b)⁵ =

= (a − (–b)) (a⁴ + a³ (–b) + a² (–b)² + a (–b)³ + (–b)⁴) = = (a + b) (a⁴ − a³b + a²b² − ab³ + b⁴).

a1999 + b1999

624. а) Сократима ли дробь a₁₉₉₇₊_b1997 ?

Решение. Так как показатели степеней нечётны, то числитель и знаменатель дроби можно разложить на множители:

a1999 + b1999 = (a + b) (a1998 − a1997b + ... − ab1997 + b1998), a1997 + b1997 = (a + b) (a1996 − a1995b + ... − ab1995 + b1996).

Дробь сократима на множитель (a + b).

Замечание. В задаче, естественно, речь идёт о дроби, имеющей смысл, для которой a ≠ 0, b ≠ 0, a ≠ –b.

625. Разделите с остатком многочлен:

а) х³ − 4х² + х + 6 на х + 1; на х − 2; на х − 3;

б) х⁴ + 2х³ + х² + 6 на х² + х + 1; на х² + х − 1; на х + 2.

Решение. Разделив уголком по образцам, показанным в учебнике, получим:

а) х³ − 4х² + х + 6 = (х + 1) (х² − 5х + 6); х³ − 4х² + х + 6 = (х − 2) (х² − 2х − 3); х³ − 4х² + х + 6 = (х − 3) (х² − х − 2);

б) х⁴ + 2х³ + х² + 6 = (х² + х + 1) (х² + х − 1) + 7; х⁴ + 2х³ + х² + 6 = (х² + х − 1) (х² + х + 1) + 7; х⁴ + 2х³ + х² + 6 = (х + 2) (х³ + х − 2) + 10.

Правильность вычисления полезно проверить, раскрыв скобки.

629. Найдите многочлен А, для которого верно равенство:

а) х¹² − 1 = (х⁴ − 1) ⋅ А; б) х¹² − 1 = (х² + 1) ⋅ А;

в) х¹² − 1 = (х² − 1) ⋅ А; г) х¹² − 1 = (х + 1) ⋅ А.

Решение. Здесь можно воспользоваться формулами сокращённого умножения, но проще применить деление уголком.

а) Так как х¹² − 1 = (х⁴ − 1) (х⁸ + х⁴ + 1), то А = х⁸ + х⁴ + 1;

б) так как х¹² − 1 = (х² + 1) (х¹⁰ − х⁸ + х⁶ − х⁴ + х² − 1), то

А = х¹⁰ − х⁸ + х⁶ − х⁴ + х² − 1;

в) так как х¹² − 1 = (х² − 1) (х¹⁰ + х⁸ + х⁶ + х⁴ + х² + 1), то

А = х¹⁰ + х⁸ + х⁶ + х⁴ + х² + 1;

г) так как х¹² − 1 =

= (х + 1) (х¹¹ − х¹⁰ + х⁹ − х⁸ + х⁷ − х⁶ + х⁵ − х⁴ + х³ − х² + х − 1), то А = х¹¹ − х¹⁰ + х⁹ − х⁸ + х⁷ − х⁶ + х⁵ − х⁴ + х³ − х² + х − 1.

630. Определите, при каких целых n значение алгебраической дроби:

5n + 7 3n²− 6n + 1

а) ; в)

n n − 2 является целым числом. 5n + 7 = ⁵ⁿ₊⁷= 5 ₊⁷, то данРешение. а) Так как

n n n n

ная дробь является целым числом, если n равно 1, –1, 7 или –7;

в) так как 3n²− 6n + 1 = 3n n( − 2) + 1 = 3n n( − 2) + 1 = n − 2 n − 2 n − 2 n − 2

= 3n + ¹, то данная дробь является целым числом, если n − 2 n равно 1 или 3.

2. Исторические сведения

В данном пункте приведена информация об использовании буквенных обозначений и зарождении алгебры. Разговор о вкладе в науку Ф. Виета, И. Ньютона, Б. Паскаля и Л. Ф. Магницкого — учёных и учителя математики и создателя первого популярного в России учебника «Арифметика» — поможет показать школьникам, что использование буквенной символики сделало алгебру наукой. При подготовке к этой беседе можно использовать не только текст исторических сведений, но и задания 631 и 632. Для небольших показателей степени учащиеся должны научиться находить коэффициенты бинома Ньютона с помощью треугольника Паскаля.

Глава 3 Линейные уравнения

Изучение главы 3 должно привести учащихся к пониманию того, как решать уравнения первой степени с одним неизвестным, линейные уравнения, системы линейных уравнений, как применять эти умения к решению текстовых задач.

В результате изучения главы учащиеся должны научиться решать линейные уравнения и их системы, решать текстовые задачи с помощью линейных уравнений и их систем.

Составление уравнений или систем уравнений для решения задач способствует не только развитию мышления и речи учащихся, но и обучению их планированию своей деятельности. Так, при решении задач учащиеся должны уметь выделять известные и неизвестные данные, намечать план действий, ставить вопросы, находить ответы на них, проверять, отвечает ли полученный результат условиям задачи. Это важнейшие метапредметные умения, необходимые при изучении математики и других школьных предметов.

§ 9. Линейные уравнения с одним неизвестным

В § 9 вводятся понятия уравнения первой степени с одним неизвестным, линейного уравнения с одним неизвестным, корня уравнения, показывается применение уравнений к решению текстовых задач.

9.1. Уравнения первой степени с одним неизвестным 9.2. Линейные уравнения с одним неизвестным

В пункте 9.1 даётся определение уравнения первой степени с неизвестным x и корня уравнения, объясняется, что значит решить уравнение, показывается, что каждое уравнение вида

kx + b = 0, (*)

где k и b — данные числа, k ≠ 0, имеет корень x₀ = ⁻^b, k

описывается алгоритм решения любого уравнения первой степени с одним неизвестным.

Здесь впервые применяется метод рассуждений с числовыми значениями. Из этого рассуждения следует, что в уравнении первой степени с одним неизвестным слагаемое можно переносить из одной части уравнения в другую с противоположным знаком, что обе части уравнения можно делить на одно и то же число, отличное от нуля.

В пункте 9.2 вводится понятие линейного уравнения с одним неизвестным x. Это — уравнение, правая и левая части которого являются многочленами степени не выше первой или числами. Таким образом, уравнение первой степени с одним неизвестным является линейным, но не всякое линейное уравнение является уравнением первой степени с одним неизвестным. Например, линейное уравнение 0 ⋅ x + b = 0 не является уравнением первой степени с неизвестным x, так как коэффициент k при неизвестном x равен нулю, следовательно, многочлен 0 ⋅ x + b не является многочленом первой степени.

Далее объясняется, что уравнение kx + b = 0 имеет единственный корень x₀ = − _k^b, если k ≠ 0; не имеет корней, если

k = 0, а b ≠ 0; имеет бесконечно много корней, если k = 0 и b = 0. Затем вводится понятие равносильных уравнений и формулируются три утверждения о равносильных преобразованиях уравнения, которые будут часто использоваться в дальнейшем. Решения и комментарии

636. Является ли данное уравнение уравнением первой степени с одним неизвестным:

ж) (4,7 − 4 − 0,7) x − 1 = 0; и) 0 = 7x − 2?

Решение. Чтобы ответить на поставленный вопрос, надо записать каждое уравнение в виде (*) и определить k и b.

ж) Уравнение можно переписать в виде 0 ⋅ x − 1 = 0;

здесь k = 0, b = –1; уравнение не является уравнением первой степени с одним неизвестным;

и) уравнение можно переписать в виде 7x − 2 = 0; здесь

k = 7, b = –2; уравнение является уравнением первой степени с одним неизвестным.

Замечание. Надо иметь в виду, что при выполнении задания и) не показано, на каком основании уравнение

0 = 7x − 2 (1)

можно переписать в виде

7x − 2 = 0. (2)

Обосновать это утверждение можно с помощью рассуждений с числовыми значениями.

Если число ^x₀ — корень уравнения (1), то верно числовое равенство 0 = 7x₀ − 2, которое не изменится, если к обеим его частям прибавить число –7x₀ + 2. Таким образом, получим верное числовое равенство –7x₀ + 2 = 0.

Теперь умножив на –1 обе части этого числового равенства, получим верное числовое равенство 7x₀ − 2 = 0, из которого следует, что число x₀ — корень уравнения (2).

Если число x₀ — корень уравнения (2), то верно числовое равенство 7x₀ − 2 = 0. Прибавив к обеим частям этого равенства число –7x₀ + 2, получим верное числовое равенство 0 = –7x₀ + 2. Умножив на –1 обе части этого числового равенства, получим верное числовое равенство 0 = 7x₀ − 2, из которого следует, что число x₀ — корень уравнения (1).

Следовательно, уравнения (1) и (2) равносильны. Поэтому уравнение (1) можно переписать в виде уравнения (2).

640. г) Решите уравнение 4x + 15 = 0.

Решение. Перенесём свободный член 15 в правую часть уравнения с противополож ным знаком: 4x = –15.

Затем разделим обе части нового уравнения на коэффициент 4 (4 ≠ 0): x = –3,75. Ответ. –3,75.

641. г) Число k ≠ 0. Решите уравнение kx − b = 0.

Решение. Перенесём свободный член –b в правую часть уравнения с противополож ным знаком: kx = b.

Затем разделим обе части нового уравнения на коэф-

фициент k (k ≠ 0): x =^b.

Ответ. .

644. Является ли данное уравнение линейным уравнением с одним неизвестным x:

д) –10 = 5x − 4; е) x² + 3x − 5 = 0?

Решение. д) Это линейное уравнение с одним неизвестным x, так как в его левой части стоит число (–10), а в правой — многочлен (5x − 4) первой степени с неизвестным x;

е) это уравнение не является линейным с одним неиз-

вестным x, так как в его левой части стоит многочлен x² + 3x − 5 второй степени с неизвестным x.

9.3. Решение линейных уравнений с одним неизвестным

В данном пункте разобраны пять примеров решения линейных уравнений. Три первых из них содержат три случая, встречающиеся при решении линейных уравнений (единственный корень, нет корней и бесконечно много корней — любое число является корнем уравнения). В примере 4 дважды применяются правила раскрытия скобок, в примере 5 обе части уравнения умножаются на число 6, чтобы освободиться от знаменателей 2, 3, 6.

На данном этапе главная цель заключается в том, чтобы обуч ить школьников решать линейное уравнение в любом из трёх упомянутых случаев. Решения и комментарии

653. Решите уравнение: л) –x + 3 + x = x − (x − 3); н) 6 (x − 3) = 12; п) 2 (x − 1) − 4 = 6 (x + 2).

Решение. Приведём краткую запись решения, которая должна быть в тетрадях учащихся. Решение у доски должно сопровождаться пояснениями выполняемых действий. Образцы таких пояснений есть в учебнике (примеры 1—5).

л) –x + 3 + x = x − (x − 3), н) 6 (x − 3) = 12,

3 = x − x + 3, 6x − 18 = 12, 3 − 3 = 0x, 6x = 12 + 18,

0 = 0x, 6x = 30, 0x = 0; x = 30 : 6, x — любое число; x = 5;

п) 2 (x − 1) − 4 = 6 (x + 2),

2x − 2 − 4 = 6x + 12,

2x − 6x = 6 + 12,

–4x = 18,

x = 18 : (−4), x = –4,5.

657. Решите уравнение:

е) 5x − 4 (x − 3 (x − 2 (x − 1))) = 2;

ж) x − (x − (x − (x − 1))) = 1 − (2 − (3 − (4 − x))).

Решение.

е) 5x − 4 (x − 3 (x − 2 (x − 1))) = 2,

5x − 4 (x − 3 (x − 2x + 2)) = 2,

5x − 4 (x − 3 (–x + 2)) = 2,

5x − 4 (x + 3x − 6) = 2,

5x − 4 (4x − 6) = 2,

5x − 16x + 24 = 2,

–11x = 2 − 24,

–11x = –22, x = 2;

ж) x − (x − (x − (x − 1))) = 1 − (2 − (3 − (4 − x))), x − (x − (x − x + 1)) = 1 − (2 − (3 − 4 + x)), x − (x − 1) = 1 − (2 − (–1 + x)), x − x + 1 = 1 − (2 + 1 − x),

1 = 1 − 2 − 1 + x,

1 = –2 + x, − x = –2 − 1, x = 3.

Замечание. Отметим, что в процессе решения уравнения неизвестные переносят обычно влево, а числа — вправо. Это необходимо лишь для единообразия оформления решения уравнения всеми учащимися класса и управления процессом обучения. На первых порах так и надо поступать. По мере освоения процедуры решения уравн ения ученик может переносить неизвестные вправо, чтобы получить положительный коэффициент перед x. Кроме того, иногда бывает полезно не раскрывать скобки, а делить обе части уравнения на число — задания

653 н, п.

н) 6 (x − 3) = 12, п) 2 (x − 1) − 4 = 6 (x + 2), x − 3 = 2, x − 1 − 2 = 3 (x + 2), x = 3 + 2, x − 3 = 3x + 6, x = 5; –3 − 6 = 3x − x,

–9 = 2x, x = –4,5.

Промежуточный контроль. С—22.

9.4. Решение задач с помощью линейных уравнен ий

В данном пункте приведены решения двух задач с помощью линейных уравнений. Следует отметить, что применение уравнений при решении текстовых задач для учащихся не является новой идеей. Но учащиеся могут предлагать решать некоторые задачи без уравнения — арифметически, особенно если они в 5—6 классах обучались по учебникам серии «МГУ — школе».

Начать работу с задачами хорошо с задачи 658, которую можно решать как арифметическую задачу на нахождение двух чисел по их сумме и разности. Например, так.

658. Найдите два числа, сумма которых равна 86 и одно число на 12 больше другого. Решение. I способ.

1) 86 − 12 = 74 — удвоенное меньшее число;

2) 74 : 2 = 37 — меньшее число; 3) 37 + 12 = 49 — большее число.

Ответ. 37 и 49.

Учитель всегда должен использовать инициативу учащихся для лучшего раскрытия темы урока. Поэтому если учащиеся предложат такое решение, пониманию которого поможет приведённый рисунок 5, то его запись надо оставить на доске и показать второй способ решения — с помощью уравнения. (Если учащиеся не предложат такого решения, то можно сказать, что 6 Рис. 5 в старые времена, когда ещё не умели применять уравнения для решения задач, эту задачу решали так.) Разумеется, следует убедиться, что задача решена верно: 37 + 49 = 86, 49 − 37 = 12.

Разбирая решение задачи с помощью уравнения, для краткой записи условия можно использовать рисунок 5 (под первым и вторым отрезками следует написать по букве x так, чтобы было понятно, что меньшее число — это x, а большее — это x + 12).

II способ. Пусть меньшее число x, тогда большее число есть x + 12. Так как их сумма равна 86, то верно равенство x + x + 12 = 86.

Решение полученного уравнения надо записать подробно:

2x + 12 = 86,

2x = 86 − 12,

2x = 74,

x = 74 : 2, x = 37.

Теперь найдём значение выражения x + 12 = 37 + 12 = 49.

Далее следует показать, что оба способа решения содержат одинаковые действия, и найти их в приведённых записях решений. Можно спросить: какое решение учащимся кажется более простым? Здесь не исключён ответ — первое. Но при любом ответе учащихся их надо подвести к мнению, что некоторые задачи можно решать разными способами. Иногда оказывается более простым один способ, иногда — другой.

Задачи 1 и 2 из учебника являются хорошими примерами того, что применение уравнений даёт инструмент для достаточно простого решения текстовых задач. Однако не надо подводить учащихся к неверному выводу о том, что применение уравнения всегда упрощает решение задачи.

Решения и комментарии

661. Надо разменять 100 р. монетами по 2 р. и 5 р. так, чтобы всех монет было 26. Сколько должно быть монет по 2 р.?

Решение. Пусть надо взять x монет по 2 р. и 26 − x монет по 5 р. Тогда всех монет будет на сумму 2x + 5 (26 − x) р., что по условию задачи равно 100 р. Составим уравнение:

2x + 5 (26 − x) = 100.

Решив это уравнение, получим его единственный корень 10. Следовательно, надо взять 10 монет по 2 р.

Проверим: монет по 5 р. было 26 − 10 = 16, а денег было на сумму 5 ⋅ 16 + 2 ⋅ 10 = 100 р. Ответ. 10 монет.

Промежуточный контроль. С—23.

§ 10. Системы линейных уравнений

В § 10 вводятся понятия линейного уравнения с двумя неизвестными, системы уравнений первой степени с двумя неизвестными, изучаются способы решения систем и их применение к решению текстовых задач.

10.1. Уравнения первой степени с двумя неизвестными

В данном пункте вводятся понятия уравнения первой степени с двумя неизвестными и его решения, объясняется, что значит выразить одно неизвестное через другое, разбирается пример, в котором решено уравнение первой степени с двумя неизвестными, т. е. получена запись всех пар чисел (x; y), в которых y — любое действительное число, а x выражен через y. Решения и комментарии

675. Найдите три решения уравнения:

а) x + y − 5 = 0; б) y − 5 = 0.

Решение. а) Уравнение имеет бесконечно много решений (5 − y; y), где y — любое число. Здесь достаточно выбрать три такие пары x и y. Например, (1; 4), (2; 3), (6; –1); б) чтобы понять, что и это уравнение имеет бесконеч-

но много решений (x; 5), где x — любое число, его полезно записать в виде 0x + y − 5 = 0. Здесь достаточно выбрать три такие пары x и y. Например, (0; 5), (2; 5), (–6; 5).

676. Выразите у через х из уравнения:

а) х + у = 5; б) 2х − у = 3; в) –3х + 2у = 7. Решение.

а) х + у = 5, | − x б) 2х − у = 3, | − 2х у = 5 − х; –у = 3 − 2х, | ⋅ (–1) у = –3 + 2х;

в) –3х + 2у = 7, | + 3х

2у = 7 + 3х, | ⋅ 0,5 у = 3,5 + 1,5х.

Замечание. Здесь и далее удобно за вертикальной чертой справа от уравнения писать слагаемое, прибавляемое к обеим частям уравнения, или множитель, на который умножается уравнение. При этом полезно писать знак операции, которая будет выполнена при переходе к следующему уравнению. Вместо «⋅ 0,5» можно писать «: 2».

678. Выразите х через у из уравнения: а) х − 3у + 2 = 0; б) 3х + 2у − 5 = 0.

Решение.

а) х = 3у − 2; б) 3х = 5 − 2y, | : 3 х = − у.

679. а) Запишите какое-либо решение уравнения

4х − у − 2 = 0.

Решение. Выразим у через х:

–у = –4х + 2, | ⋅ (–1) у = 4х − 2.

Теперь выберем любое значение x, например, x = 3, тогда у = 4 ⋅ 3 − 2 = 10.

Итак, (3; 10) — одно из решений данного уравнения.

680. Составьте уравнение первой степени с двумя не-известными из условия:

а) сумма двух чисел равна 10;

б) 2 л молока и 3 батона хлеба стоят 99 р.;

в) ручка дороже карандаша на 7 р.

Решение. Это задание готовит учащихся к решению текстовых задач с помощью систем уравнений с двумя неизвестными.

а) Пусть данные числа х и у, тогда составим уравне-

ние: х + у = 10;

б) пусть 1 л молока стоит х р., а 1 батон хлеба стоит у р., тогда 2 л молока и 3 батона хлеба вместе стоят

2х + 3у (р.), или 99 р. Составим уравнение: 2х + 3у = 99;

в) пусть ручка стоит х р., а карандаш — у р. Так как ручка дороже карандаша на 7 р., то составим уравнение: х − у = 7.

681. а) При каком a пара чисел (3; –2) является решением уравнения 2х − aу − 4 = 0?

Решение. Пусть при некотором a пара чисел (3; –2) является решением уравнения, тогда верно числовое равенство

2 ⋅ 3 − a ⋅ (–2) − 4 = 0,

из которого найдём a:

6 + 2a − 4 = 0, 2a + 2 = 0, | : 2

a + 1 = 0, | − 1 a = –1.

Итак, при a = –1 пара чисел (3; –2) является решением уравнения 2х − aу − 4 = 0.

10.2. Системы двух уравнений первой степени с двумя неизвестными 10.3. Способ подстановки

В пункте 10.2 вводятся понятия системы двух уравнений первой степени с двумя неизвестными, решения системы, объясняется, какие коэффициенты при неизвестных называют пропорциональными.

В пункте 10.3 показывается первый способ решения систем двух уравнений первой степени с двумя неизвестными с отличными от нуля и непропорциональными коэффициентами при неизвестных. Этот способ называют способом подстановки. Обоснование этого метода решения систем даётся с помощью рассуждений с числовыми значениями. В конце пункта приводится алгоритм решения систем двух уравнений первой степени с двумя неизвестными с отличными от нуля и непропорциональными коэффициентами при неизвестных.

Решения и комментарии

693. а) При каких a и b пара чисел (1; 0) является решением системы уравнений

{

2x + y = a, (1) bx − y = 2?

Решение. Пусть при некоторых a и b (которые требуется найти) пара чисел (1; 0) является решением системы уравнений (1), тогда верны числовые равенства:

2 ⋅ 1 + 0 = a, b ⋅ 1 − 0 = 2.

Первое равенство возможно лишь при a = 2, а второе — при b = 2. Следовательно, условию задачи удовлетворяют a = 2, b = 2.

694. а) Составьте систему двух уравнений первой степени с двумя неизвестными из условия: сумма двух чисел равна 7, а их разность равна 2.

Решение. Пусть большее число x, меньшее y, тогда верны два равенства: х + у = 7, х − у = 2.

Составим систему уравнений: x + y = 7, x − y = 2.

696. а) Решите способом подстановки систему уравне-

ний xx−−23yy=−07, = 0.

Решение. Из первого уравнения выразим x через y: х = 2у. Подставим 2у вместо х во второе уравнение: 2 ⋅ 2у − − 3у − 7 = 0. Решив полученное уравнение, найдём у:

4у − 3у − 7 = 0, у − 7 = 0, у = 7.

Теперь найдём x из равенства х = 2у: x = 2 ⋅ 7, x = 14 .

Пара чисел (14, 7) является решением системы.

Замечание. Здесь и далее полезно приучать учащихся к самоконтролю, с помощью которого можно обнаружить допущенные ошибки. Для этого надо задать вопрос: «Как проверить, что найденная пара чисел действительно является решением системы?» Учащиеся должны ответить: «Подставим найденные значения x = 14 и y = 7 в уравнения системы и проверим, получатся ли верные числовые равенства:

14 − 2 ⋅ 7 = 0 (верно),

2 ⋅ 14 − 3 ⋅ 7 − 7 = 28 − 21 − 7 = 0 (верно), следовательно, эта пара является решением системы».

2x − 3y + 7 = 0, 3x + 4y − 1 = 0.

699. а) Решите систему уравнений {

Решение. Из первого уравнения выразим x через y:

2х = 3у − 7, х = 1,5у − 3,5.

Подставим 1,5у − 3,5 вместо х во второе уравнение:

3 ⋅ (1,5у − 3,5) + 4у − 1 = 0.

Решив полученное уравнение, найдём у:

4,5у − 10,5 + 4у − 1 = 0,

8,5у − 11,5 = 0,

8,5у = 11,5, | ⋅ 2

17у = 23, у = .

Теперь найдём x из равенства х = 1,5у − 3,5:

x 3,5, x .

Пара чисел ⎛⎜⎝− 1725 , 1723⎞⎟⎠ является решением системы.

10.4. Способ уравнивания коэффициентов

В данном пункте подробно с помощью рассуждений с числовыми значениями обосновывается способ решения систем, называемый способом уравнивания коэффициентов. Приводится алгоритм решения систем двух уравнений первой степени этим способом для случая непропорциональных коэффициентов при неизвестных и разбираются ещё два примера решения систем.

Решения и комментарии

700. а) Решите систему уравнений { x + 2y − 3 = 0, x + y + 1 = 0.

Решение. Из первого уравнения системы вычтем второе, получим уравнение у − 4 = 0, откуда получим y = 4. Подставим 4 вместо у во второе уравнение: х + 4 + 1 = 0, откуда получим x = –5. Единственным решением системы является пара чисел (–5, 4).

701. а) Решите систему уравнений { x + 3y − 1 = 0, −x + 4y + 8 = 0.

Решение. Сложим уравнения системы, получим уравнение 7у + 7 = 0, откуда получим y = –1. Подставим –1 вместо у в первое уравнение: х − 3 − 1 = 0, откуда получим x = 4. Единственным решением системы является пара чисел (4, –1).

702. Решите систему уравнений:

{

x + 2y − 3 = 0, 2x + 5y − 15 = 0, 2x − 3y + 8 = 0; 3x + 2y − 6 = 0.

а) д) {

Решение. а) Умножим первое уравнение на 2, перепи-

2x + 4y − 6 = 0,

шем систему в виде {

2x − 3y + 8 = 0.

Из первого уравнения новой системы вычтем второе, получим уравнение 7у − 14 = 0, откуда получим y = 2. Подставим 2 вместо у в первое уравнение исходной системы: х + 4 − 3 = 0, откуда получим x = –1. Единственным решением системы является пара чисел (–1, 2).

д) Умножим первое уравнение на 3, а второе на 2,

перепишем систему в виде

{

6x + 15y − 45 = 0, 6x + 4y − 12 = 0.

Из первого уравнения новой системы вычтем второе, получим уравнение 11у − 33 = 0, откуда получим y = 3. Подставим 3 вместо у в первое уравнение исходной системы: 2х + 15 − 15 = 0, откуда получим x = 0. Единственным решением системы является пара чисел (0, 3).

10.5. Равносильность уравнений и систем урав нений

В данном пункте вводятся понятия линейного уравнения с двумя неизвестными, равносильных уравнений, рассматриваются три преобразования, приводящие данное уравнение к уравнению, ему равносильному.

1) Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное исходному.

2) Если перенести с противоположным знаком член уравнения из одной части в другую, то получим уравнение, равносильное исходному.

3) Если в левой и правой частях линейного уравнения привести подобные члены, то получится уравнение, равносильное исходному.

Затем вводится понятие равносильности систем уравнений.

Решения и комментарии 709. Равносильны ли уравнения:

а) 2x − 2y = x и x − y = 0; б) 3x − 5y = 0 и 3x = 5y?

Решение. а) Уравнения 2x − 2y = x и x − y = 0 не являются равносильными, так как пара чисел (1; 1) является решением второго уравнения, но не является решением первого.

б) Уравнения 3x − 5y = 0 и 3x = 5y равносильны, так как если пара чисел (x₀; y₀) — решение первого уравнения, то справедливо числовое равенство 3x₀ − 5y₀ = 0, но тогда справедливо и числовое равенство 3x₀ = 5y₀, т. е. пара чисел (x₀; y₀) является решением второго уравнения. Аналогично рассуждая, можно показать, что решение второго уравнения является решением первого. Так как эти утверждения справедливы для любого решения этих уравнений, то уравнения равносильны.

715. При каком a равносильны системы уравнений: ax − y = 5,_и{x − 2 = −y, x + y = 2 4x − 2y = 0.

Решение. Решив вторую систему, найдём её единственное решение ⎛^⎜⎝ 2₃; 4₃⎞^⎟⎠. Подставив найденные значения x и y

в первую систему, убедимся, что второе уравнение обращается в верное равенство, а из первого уравнения найдём a = 9,5. Следовательно, системы равносильны при a = 9,5.

10.6. Решение систем двух линейных уравнений с двумя неизвестными

В данном пункте на характерных примерах рассматривается решение систем, приводящихся после равносильных преобразований уравнений к системам, в которых некоторые из коэффициентов при неизвестных равны 0. В классах, работающих по обычной программе, можно сообщить без доказательства в общем виде (см. п. 10.7), как с помощью коэффициентов двух уравнений с двумя неизвестными можно определить, имеет ли данная система решение, единственное ли это решение, имеет ли система бесконечное множество решений (см. теорему из п. 10.7). Достаточно, если обоснование будет дано на конкретных примерах, как это сделано ниже при решении систем из задания 721.

Решения и комментарии

721. Решите систему уравнений:

а) б) { в) { 4x + 4y = 2, 2x + y = 1, x + y = 3,

2x + 2y = 1; 2x − y = 1; 3x + 3y = 6.

Решение. а) Выразим x через y из второго уравнения: x = 0,5 − y, подставим 0,5 − y вместо x в первое уравнение: 4(0,5 − y) + 4y = 2. Перепишем это уравнение в виде 0y = 0. Очевидно, что любое число y является решением этого уравнения. Для каждого такого y значение x определяется по формуле x = 0,5 − y.

Таким образом, пара чисел (0,5 − y; y), где y — любое действительное число, является решением системы.

б) Сложив два уравнения системы, получим уравнение 4x = 2. Это уравнение имеет единственный корень x = 0,5. Число y найдём из первого уравнения системы: y = 0. Пара (0,5; 0) — единственное решение системы уравнений.

в) Выразим y через x из первого уравнения: y = 3 − x, подставим 3 − x вместо y во второе уравнение: 3x + 3 (3 − x) = = 6. Перепишем это уравнение в виде 0x = –3. Очевидно, что это уравнение не имеет корней, следовательно, система не имеет решений.

Ответ. а) (0,5 − y; y), где y — любое действительное число; б) (0,5; 0); в) нет решений.

Замечание. а) Заметим, что коэффициенты при неизвестных и свободные члены этой системы пропорциональ-

ны: 4 ⁼⁴⁼². В этом случае система имеет бесконечно

2 2 1

много решений, так как одни и те же пары чисел x = 0,5 − y и y, где y — любое действительное число, являются решениями каждого из этих уравнений.

б) Заметим, что коэффициенты при неизвестных не пропорциональны: . В этом случае система имеет

единственное решение.

в) Заметим, что коэффициенты при неизвестных пропорциональны, но их отношение не равно отношению свободных членов: . В этом случае система не имеет решений, так как, разделив второе уравнение системы на 3, получим уравнение x + y = 2. Очевидно, что система уравнений

{x + y = 3, x + y = 2

не имеет решений, так как нет таких чисел x и y, что их сумма одновременно равна и 3, и 2.

Промежуточный контроль. С—24.

10.7*. О количестве решений системы двух уравнений первой степени с двумя неизвестными

В данном пункте в общем виде приводится доказательство теоремы о числе решений системы двух линейных уравнений с двумя неизвестными, на характерных примерах показывается её применение для решения систем. Задачи с параметром встречались нам ранее (задания 681, 693, 715). В данном пункте разбираются два задания с параметром a, при решении которых используется изученная теорема.

Решения и комментарии

727. а) При каком значении a система {^5x⁺^ay⁺⁶⁼^0, x + 2y − 5 = 0

не имеет решений?

Решение. Система не имеет решений, если .

Эти условия выполняются лишь при a = 10. Следовательно, при a = 10 система не имеет решений.

728. а) Существует ли значение a, при котором систе-

ма 6x + ay − 2a = 0, не имеет решений?

3x − 2y + 4 = 0

Решение. Система не имеет решений, если

^≠⁻^2a. Равенство ⁶⁼^a выполняется лишь при a = –4. Но

4 3 −2

a −2a при этом значении a не выполняется условие .

Следовательно, не существует значений a, при которых система не имеет решений.

729. а) При каком значении a система { −2x + ay + 6a = 0, x − y − 6 = 0

имеет бесконечно много решений?

Решение. Система имеет бесконечно много решений,

−2 = ^a= ^6a. Эти условия выполняются лишь при

если

1 −1 −6

a = 2. Следовательно, при a = 2 система имеет бесконечно много решений.

3ax + y − a = 0, 45x − y − 2 = 0

731. а) При каких значениях a система {

имеет единственное решение?

Решение. Система имеет единственное решение, если

3a 1 3a 1

≠ . Так как = лишь при a = –15, то система

45 −1 45 −1

имеет единственное решение при каждом a ≠ –15.

10.8*. Системы уравнений первой степени с тремя неизвестными

В данном пункте вводятся понятия уравнения первой степени с тремя неизвестными и его решения, системы трёх уравнений первой степени с тремя неизвестными и её решения, приводится пример решения такой системы. При этом подчёркивается, что с помощью подстановки решение системы трёх уравнений первой степени с тремя неизвестными можно свести к решению системы двух уравнений первой степени с двумя неизвестными.

Решения и комментарии

733. д) Решите систему уравнений ⎨⎪⎧2xx+−yy++zz==3,2,

⎪⎩3x − 2y + z = 2.

Решение. Выразим x через y и z из первого уравнения:

x = 3 − y − z, подставим 3 − y − z вместо x во второе и третье уравнения:

{2 3( − y − z) − y + z = 2, 3 3( − y − z) − 2y + z = 2.

Решив полученную систему, найдём её единственное решение: y = 1, z = 1. Теперь найдём x = 3 − 1 − 1 = 1. Следовательно, система имеет единственное решение (1; 1; 1).

10.9. Решение задач при помощи систем уравнений первой степени

В данном пункте разобраны решения трёх задач при помощи систем уравнений первой степени. Отметим, что начать работу нужно с более простых задач, аналогичные которым уже решались ранее, но другими методами — арифметически или с помощью линейного уравнения. Если учащиеся приведут различные способы решения одной и той же задачи, то эти способы решения полезно сопоставить. На первых порах использование системы даёт малозаметное преимущество: составляются более простые уравнения, но зато уравнений становится больше. Однако разбор решений задач из учебного текста должен убедить учащихся в том, что встречаются задачи, решение которых существенно упрощается, если применять системы уравнений.

Решения и комментарии

735. а) Одно число больше другого на 6. Сумма этих чисел равна 40. Найдите числа.

Решение. Пусть x — большее число, а y — меньшее. Составим два уравнения: x − y = 6, x + y = 40. Решив систему уравнений

{x − y = 6,

x + y = 40,

найдём её единственное решение: x = 23, y = 17. Следовательно, 23 и 17 — искомые числа.

736. а) Одно число в 2 раза больше другого. Если меньшее из этих чисел увеличить в 4 раза, а большее увеличить в 2 раза, то их сумма будет равна 44. Найдите числа.

б) Одно число в 3 раза меньше другого. Если одно из

чисел увеличить в 2 раза, то сумма станет равной 42. Найдите числа. Сколько решений имеет задача? Как следует изменить формулировку задачи, чтобы решение было единственным?

Решение. а) Пусть x — большее число, а y — меньшее. Составим два уравнения: x = 2y, 2x + 4y = 44. Решив систему уравнений

{x = 2y, 2x + 4y = 44,

найдём её единственное решение: x = 11, y = 5,5. Следовательно, 11 и 5,5 — искомые числа.

б) Пусть x — большее число, а y — меньшее. Составим первое уравнение: x = 3y.

Если в 2 раза увеличили большее число, то второе уравнение имеет вид 2x + y = 42. Решив систему уравнений

{

x = 3y,

2x + y = 42,

найдём её единственное решение: x = 18, y = 6. Следовательно, 18 и 6 — искомые числа.

Если же в 2 раза увеличили меньшее число, то второе уравнение имеет вид x + 2y = 42. Решив систему уравнений

{x = 3y, x + 2y = 42,

найдём её единственное решение: x = 25,2, y = 8,4.

Следовательно, задача имеет два решения: 25,2, 8,4 и 18, 6.

Чтобы задача имела единственное решение, надо в её условии слова «одно из чисел» заменить на «большее число» или «меньшее число».

746. Рассчитываясь за покупку, мальчик получил сдачу 70 р. монетами достоинством 5 р. и 10 р. Всего он получил 10 монет. Сколько монет достоинством 5 р. он получил?

Решение. Пусть мальчик получил x монет достоинством 5 р. и y монет достоинством 10 р. Всего монет было 10, составим первое уравнение: x + y = 10. Монет было на сумму 70 р., составим второе уравнение: 5x + 10y = 70. Решив систему уравнений

{

x + y = 10,

5x + 10y = 70,

найдём её единственное решение: x = 6, y = 4. Следовательно, монет достоинством 5 р. было 6.

749. Два куска одинаковой ткани стоят вместе 9100 р. Когда из первого куска продали столько, сколько было первоначально во втором, а из второго — половину того, что было первоначально в первом, то остаток первого куска оказался на 10 м больше остатка второго куска. Сколько метров ткани было в каждом куске, если 1 м ткани стоит 140 р.?

Решение. Сначала определим количество метров ткани в двух кусках вместе: 9100 : 140 = 65 (м). Пусть в первом куске было x м ткани, а во втором — y м ткани. Составим первое уравнение: x + y = 65. Остаток первого куска составил (x − y) м, а остаток второго — (y − 0,5x) м. Остаток первого куска был на 10 м больше, чем остаток второго.

Составим второе уравнение: (x − y) − (y − 0,5x) = 10.

Решив систему уравнений

{

x + y = 65,

1 5, x − 2y = 10,

найдём её единственное решение: x = 40, y = 25. Следовательно, в первом куске было 40 м ткани, а во втором — 25 м ткани.

750. Две бригады школьников во время производ-ственной практики заработали 11 700 р. Первая работала 15 дней, вторая — 14 дней. Сколько зарабатывала каждая бригада в день, если первая за 4 дня заработала на 1100 р. больше, чем вторая за 3 дня? Какое допущение необходимо сделать для решения задачи?

Решение. Для решения задачи необходимо сделать допущение, что бригады работали всё время с постоянной производительностью и в каждый день зарабатывали одну и ту же сумму денег.

Пусть первая бригада зарабатывала в день x р., а вторая — y р. Составим первое уравнение: 15x + 14y = 11 700. Первая бригада за 4 дня заработала на 1100 р. больше, чем вторая за 3 дня. Составим второе уравнение: 4x − 3y = 1100.

Решив систему уравнений

{

15x + 14y = 11700,

4x − 3y = 1100,

найдём её единственное решение: x = 500, y = 300. Следовательно, первая бригада зарабатывала в день 500 р., а вторая — 300 р.

751. В школьный буфет завезли 300 пирожных и бу-лочек, общая масса которых 20 кг. Масса всех пирожных такая же, как и всех булочек. Определите количество пирожных и булочек в отдельности, если масса пирожного 100 г, а булочки 50 г.

Решение. Пусть завезли x пирожных и y булочек. Составим первое уравнение: x + y = 300. Масса пирожных 100x г, а масса булочек 50y г, а всего 20 000 г. Составим второе уравнение: 100x + 50y = 20 000. Решив систему уравнений

{x + y = 300, 100x + 50y = 20 000,

найдём её единственное решение: x = 100, y = 200. Следовательно, в школьный буфет завезли 100 пирожных и 200 булочек.

752. а) 5 % одного числа и 4 % другого вместе состав-ляют 46, а 4 % первого числа и 5 % второго вместе составляют 44. Найдите эти числа.

Решение. Пусть x — первое число, а y — второе. Составим два уравнения: 0,05x + 0,04y = 46, 0,04x + 0,05y = 44.

Решив систему уравнений

{

0 05, x + 0 04, y = 46,

0 04, x + 0 05, y = 44,

найдём её единственное решение: x = 600, y = 400. Следовательно, первое число 600, а второе 400.

755. Сумма цифр двузначного числа равна 6. Если цифр ы этого числа переставить, то получится число, составляющее первоначального. Найдите это двузначное

число.

Решение. Пусть x — цифра десятков, а y — цифра единиц данного числа 10x + y. Составим два уравнения: x + y = 6,

(10x + y) = 10y + x. Решив систему уравнений

^⎨⎪⎪⎩⎧x7₄+(10yx=+6y,) = 10y + x,

найдём её единственное решение: x = 4, y = 2. Следовательно, данное двузначное число есть 42.

756. В трёх сосудах 54 л воды. Если из первого пе-релить во второй 4 л, то в обоих сосудах будет воды поровну, а если из третьего сосуда перелить во второй 17 л, то во втором окажется в четыре раза больше воды, чем в третьем. Сколько воды в каждом сосуде?

Решение. Пусть x, y и z — количество воды в первом, втором и третьем сосудах соответственно (в литрах). Составим три уравнения: x + y + z = 54, x − 4 = y + 4, y + 17 = = 4 (z − 17). Решив систему уравнений

⎧⎨⎪x_x+− ₄y += z_y=+ 54_4,,

⎪⎩y + 17 = 4 (z − 17),

найдём её единственное решение: x = 19, y = 11, z = 24. Следовательно, в первом, втором и третьем сосудах было соответственно 19, 11 и 24 л.

757. Задача Бхаскары (Индия, XII в.). Некто сказал другу: «Дай мне 100 рупий, и я буду вдвое богаче тебя». Друг ответил: «Дай мне только 10, и я стану в 6 раз богаче тебя». Сколько было у каждого?

Решение. Пусть у первого друга было x рупий, а у второго — y рупий. Составим два уравнения: x + 100 = 2 (y − 100) и y + 10 = 6 (x − 10). Решив систему уравнений

{

x + 100 = 2 (y − 100), y + 10 = 6 (x − 10),

найдём её единственное решение: x = 40, y = 170. Следовательно, у первого друга было 40 рупий, а у второго — 170 рупий.

759. в) Старинная задача. Отец имеет семь сыновей. Сумма лет первого и четвёртого сына равна 9 годам, первого и шестого — 8 годам, второго и пятого — 8 годам, второго и третьего — 9 годам, третьего и шестого — 6 годам, четвёртого и седьмого — 4 годам, а седьмого и пятого — также 4 годам. Сколько лет каждому?

Решение. При решении этой задачи можно ввести семь неизвестных. Но можно уменьшить их число до трёх. Пусть первому, второму и седьмому сыну было x, у и z лет соответственно. Так как сумма лет первого и четвёртого равна 9 годам, то четвёртому сыну было 9 − x лет. Сумма лет первого и шестого равна 8 годам, значит, шестому сыну 8 − x лет. Аналогично определим, что пятому сыну 8 − у лет, а третьему 9 − у лет. Используя оставшиеся три условия, составим три уравнения:

(9 − у) + (8 − x) = 6, 9 − x + z = 4, z + 8 − y = 4.

Решив систему уравнений

⎧⎨⎪179 −−xx+−zy==₄6_,,

⎪⎩z + 8 − y = 4,

найдём её единственное решение: x = 6, y = 5, z = 1. Следовательно, сыновьям было 6 лет, 5 лет, 4 года, 3 года, 3 года, 2 года и 1 год.

761. а) Если пути турист пройдёт пешком, а пути проедет на велосипеде, то затратит на весь путь 1,5 ч. Если же пути он проедет на велосипеде, а пути прой-

дёт пешком, то затратит на весь путь 2 ч 15 мин. За какое время он пройдёт весь путь пешком?

Решение. Пусть на весь путь пешком турист тратит x ч, а на тот же путь на велосипеде y ч. Тогда на пути пешком пути на велосипеде турист затратит x + y ч, или ч. Составим первое уравнение: x + y = . На пути на велосипеде и пути пешком он затратит y + x ч, или ч. Составим второе уравнение: y + x = .

Решив систему уравнений

^⎧⎪¹3 x + y = ,

⎨₁

⎪y +x =,

⎩3

найдём её единственное решение: x = 3, y = . Следовательно, пешком турист пройдёт весь путь за 3 ч.

Замечание. Отметим, что эту задачу можно решить арифметически. Второй раз турист увеличил время движения пешком на времени движения пешком, при этом

общее время движения увеличилось на 9 − ³ = ³ (ч). Если

4 2 4

бы он ещё раз увеличил время движения пешком на времени движения пешком, то общее время движения увеличилось бы ещё на ч. Но тогда весь путь пешком

он прошёл бы за 3 + ³ + = 3 (ч).

2 4 4

Не будем утверждать, что арифметическое решение оказалось проще, чем решение с помощью системы, оно требует большей изобретательности. Тем не менее мы рекомендуем рассмотреть с классом и это решение.

762. В трёх сосудах 36 л воды. Из первого сосуда перелили половину имевшейся в нём воды во второй сосуд, потом треть воды, оказавшейся во втором сосуде, — в третий и, наконец, четверть воды, оказавшейся в третьем сосуде, перелили в первый. После этих переливаний во всех сосудах оказалось воды поровну. Сколько воды было первоначально в каждом сосуде?

Решение. Пусть x, y и z — количество воды в первом, втором и третьем сосудах соответственно (в литрах). Составим первое уравнение: x + y + z = 36. После первого пеx x

реливания в первом сосуде стало л, а во втором + y л.

2 2

После второго переливания во втором сосуде стало 23 ⎛⎜⎝ x2 + y⎞⎟⎠ = x3 + 23y л, а в третьем 13 ⎛⎜⎝ x2 + y⎟⎠⎞ + z = x6 + 3y + z л. После третьего переливания в третьем сосуде стало

³4 ^⎛⎜⎝ ^x6 + 3^y+ z^⎞⎟⎠ = ^x₈+ ₄^y+ ³₄^z л, а в первом сосуде стало

14 ⎛⎜⎝ x6 + 3y + z⎞⎟⎠ + x2 = 1324x + 12y + 4z л. Так как после этих переливаний в трёх сосудах оказалось воды поровну, то верны равенства 13x + y + z = x + 2y и x + 2y = x + y + 3z.

24 12 4 3 3 3 3 8 4 4

Решив систему уравнений

⎧x + y + z = 36,

^⎪⎪13x + y + z = x + 2y ,

⎨ 24 12 4 3 3

⎪x 2y x y 3z

⎪⎩3 + 3 = 8 + 4 + 4 ,

найдём её единственное решение: x = 16, y = 10, z = 10. Следовательно, в первом, втором и третьем сосудах было 16, 10 и 10 л воды соответственно.

Замечание. Приведённое выше решение, разумеется, является технически сложным для семиклассников. Интересно отметить, что эту задачу можно решить арифметически. Это решение стоит показать, чтобы у учащихся не складывалось впечатление, что с помощью систем задачи всегда решаются проще, чем с помощью уравнения или применения арифметических способов решения. Приведём решение задачи 762 «обратным ходом».

Так как после третьего переливания в каждом сосуде оказалось по 36 : 3 = 12 (л) воды, а в третьем сосуде осталось имевшейся там после второго переливания воды, то после второго переливания в третьем сосуде было 12 : = = 16 (л) воды. В первый сосуд было перелито 16 − 12 = 4 (л). Тогда после первого переливания в первом сосуде стало 12 − 4 = 8 (л) воды, а так как из первого сосуда отлили половину имевшейся там воды, то первоначально в первом сосуде было 16 л. После второго переливания во втором сосуде осталось имевшейся в нём воды, т. е. после первого переливания во втором сосуде стало 12 : = 18 (л).

Так как из первого сосуда во второй перелито 8 л, то первоначально во втором сосуде было 18 − 8 = 10 (л). Тогда в третьем сосуде было 36 − 10 − 16 = 10 (л). Итак, в первом, втором и третьем сосудах было 16, 10 и 10 л воды соответственно.

Промежуточный контроль. К—7.

Дополнения к главе 3

1. Линейные диофантовы уравнения

В данном пункте вводится понятие линейного диофантового уравнения, приводятся примеры решения таких уравнений. Здесь же показывается применение линейных диофантовых уравнений для решения текстовых задач, предлагавшихся изучающим математику со времён монаха Алькуина^{^[3]} — одного из первых известных нам европейских составителей текстовых задач. В учебном тексте разобраны решения задач Леонардо Пизанского (Фибоначчи), Леонарда Эйлера.

Решения и комментарии

763. а) Решите линейное диофантово уравнение 3х + 5у = 10.

Решение. Выразим y через x: y = 2 − ^3x. Очевидно, что

y — целое число, только если x делится на 5, т. е. если x = 5n, где n — целое число. Тогда y = 2 − 3n, где n — целое число. Итак, все решения уравнения есть пары целых чисел: (5n; 2 − 3n), где n — целое число.

764. а) Объясните, почему уравнение 2х + 6y = 11 не имеет решений в целых числах.

Решение. При любых целых x и y число 2х + 6y делится на 2, а число 11 на 2 не делится.

765. Старинная задача. У покупателя и продавца есть купюры по 5 р. и 50 р. Сможет ли покупатель заплатить за покупку стоимостью: а) 112 р.; б) 30 р.?

Решение. а) Пусть покупатель дал x купюр по 5 р. и y купюр по 50 р. Здесь x и y — целые числа. Если, например, x = –2, то это означает, что покупатель получил две купюры по 5 р. в качестве сдачи. Составим уравнение: 5х + 50у = 112. Оно не имеет решений в целых числах (при любых целых x и y число 5х + 50у делится на 5, а число 112 на 5 не делится). Значит, покупатель не сможет заплатить за покупку стоимостью 112 р.

б) Пусть x — количество купюр по 5 р., y — количество купюр по 50 р. Решим уравнение 5х + 50у = 30 в целых числах. Разделив уравнение на 5, получим равносильное ему уравнение:

х + 10у = 6. (*)

Выразим y через x: y = ⁶⁻^x. Очевидно, что y — целое 10

неотрицательное число, если 6 − x делится на 10, т. е. если 6 − x = 10n, где n — целое число. Тогда x = 6 − 10n, y = n, где n — любое целое число. Таким образом, уравнение (*) имеет бесконечно много решений (6 − 10n; n), где n — любое целое число. Отметим только два из них.

При n = 0 имеем 6 купюр по 5 р. и 0 купюр по 50 р.

При n = 1 имеем (–4) купюры по 5 р. и 1 купюру по 50 р. (т. е. покупатель даст 1 купюру по 50 р. и получит сдачи 4 купюры по 5 р.).

Следовательно, покупатель сможет заплатить за покупку стоимостью 30 р.

769. Задача Джан Цюцзяня (Китай, V в.). 1 петух стоит 5 цяней (денежных единиц), 1 курица стоит 3 цяня, 3 цыплёнка стоят 1 цянь. Всего на 100 цяней купили 100 птиц. Спрашивается, сколько было в отдельности петухов, кур, цыплят.

Решение. Пусть x — количество петухов, y — количество кур, тогда цыплят было (100 − х − у). Составим уравнение:

5х + 3у + (100 − х − у) = 100.

Выразим y через x: y = 25 − x − ^3x. Очевидно, что

y — целое число, только если число x делится на 4.

Число x не может быть отрицательным и нулём, так как это количество петухов.

При x = 4 имеем y = 18, 100 − х − у = 78, т. е. купили

4 петуха, 18 куриц, 78 цыплят.

При x = 8 имеем y = 11, 100 − х − у = 81, т. е. купили

8 петухов, 11 куриц, 81 цыплёнка.

При x = 12 имеем y = 4, 100 − х − у = 84, т. е. купили 12 петухов, 4 курицы, 84 цыплёнка.

При x ≥ 16 число y отрицательное. Так как количество куриц не может быть числом отрицательным, то других решений, кроме перечисленных выше, нет.

771. Из «Арифметики» Л. Ф. Магницкого. Купил некто на 80 алтын гусей, уток и чирков. Гуся покупал по 2 алтына, утку — по 1 алтыну, чирка же — по 3 деньги, а всех куплено 80 птиц. Спрашивается, сколько каких птиц он купил. (1 алтын = 3 к., 1 деньга = 0,5 к.)

Решение. Пусть x — количество гусей, y — количество уток, тогда чирков было (80 − х − у). Гусь стоил 6 к., утка 3 к., чирок 1,5 к., а всего заплатили 240 к. Составим уравнение:

6х + 3у + 1,5 (80 − х − у) = 240.

Выразим y через x: y = 80 − 3x. Очевидно, что y — натуральное число, если натуральное число x меньше 27, т. е. 0 < x < 27. Тогда задача имеет 26 решений: гусей купили x, уток 80 − 3x, чирков 2x, где x — любое натуральное число, меньшее 27.

Промежуточный контроль. С—25.

2. Метод Гаусса

В данном пункте разбирается способ решения систем методом Гаусса, суть которого заключается в приведении системы к «треугольному» виду. Сначала учащиеся должны научиться решать такие системы (примеры 1—3 в учебном тексте и задание 774). Затем на примере 4 надо показать способ приведения системы к «треугольному» виду.

Решения и комментарии

775. Решите методом Гаусса систему уравнений:

г) ⎨^⎪⎧2xx++23yy+−34zz==47,, д)⎧⎨^⎪32xx +− 3yy−+z2= −z ₌12,,

⎪⎩3x − 4y + 5z = 2; ⎪⎩−x + 5y − 3z = −3;

ж) ⎧⎨⎪xx +− yy −+ zz == ₁1_,,

⎪⎩−x + y + z = −1.

Решение. г) С помощью первого уравнения исключим x во втором и третьем уравнениях, затем с помощью второго уравнения исключим y в третьем уравнении:

⎨⎪⎧2xx++23yy +−34zz == 47,, 2−1 3 ⎨⎪⎧x + 2yy++103zz == 41,,5

⎪⎩3x − 4y + 5z = 2;−1 ⎪⎩ 10y + 4z = 10;−0 5,

⎨⎪⎧x + 2yy++103zz == 41,, ⎧⎨⎪xy == 12,,

⎪⎩ 48z = 0; ⎪⎩z = 0.

д) С помощью третьего уравнения исключим x в первом и втором уравнениях, затем с помощью второго уравнения исключим y в первом уравнении:

⎨⎪⎧ 23xx−+3yy −+ z2z= −= 12,, 1 1⎧_⎨⎪ 167yy−−410z z= −= −4,10, :2

⎪⎩−x + 5y − 3z = −3; 3 2 ⎪⎩−x + 5y − 3z = −3;

⎧⎨⎪ 78yy−−45zz = −= −45,, 8−7 ⎧⎨⎪ 7y − 4z3z= −= 43,, :3

⎪⎩−x + 5y − 3z = −3;⎪⎩−x + 5y − 3z = −3;

⎧⎨⎪7zy=−1,4 = −4, ⎧⎨⎪7zy==1,0, ⎧⎨⎪zy == 10,,

⎪⎩−x + 5y − 3 = −3; ⎪⎩−x + 5y = 0; ⎪⎩x = 0.

ж) С помощью первого уравнения исключим z во вто-

ром и в третьем уравнениях:

⎧⎨⎪ x_x+− y_y+− _zz == 1₁,_,1₁1 _⎨⎪⎧₂x_x+ y + z == 1₂,_,⎧_⎨⎪_xy + z == ₁0,_,

⎪⎩−x + y + z = −1;− 1 ⎪⎩2x = 2; ⎪⎩x = 1.

Из второго и третьего уравнений найдём x = 1, а из первого уравнения получим z = –y. Таким образом, решением системы является любая тройка чисел (1; y; –y), где y — любое действительное число.

Промежуточный контроль. С—26.

3. Исторические сведения

В данном пункте приведена информация о зарождении алгебры как науки. Этот материал способствует формированию ответственного отношения к учению, готовности и способности учащихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов.

Обучение решению текстовых задач

Затруднительно «разложить» по пунктам учебника рекомендации по использованию текстовых задач при изучении алгебры в 7 классе. Причин тому несколько, а главная из них заключается в том, что разные учителя в разных классах могут делать это по-разному, так как классы имеют различные стартовые возможности в начале учебного года — одних обучали применению арифметических способов решения, других нет.

Текстовые задачи в учебнике решаются различными способами, что позволяет учащимся самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения этих задач. Работа с текстовыми задачами развивает умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации.

Выделим несколько типов текстовых задач (кроме задач на применение уравнений и их систем) и несколько идей их решения, которые полезно освоить всем учащимся.

1. Необходимо показать арифметические способы решения задач:

^●на части;

^●на нахождение двух чисел по их сумме и разности;

^●на дроби;

^●на совместную работу;

^●на движение по реке;

^●на движение;

^●на деление числа на части, пропорциональные данным числам;

^●на пропорции и проценты.

2. Необходимо показать несколько способов решения задач, которые обычно не изучают специально по школьным учебникам, поэтому их можно назвать нестандартными. Они оказываются эффективными при решении олимпиадных, конкурсных задач, задач из ГИА-9 и ЕГЭ-11:

^●обратный ход;

^●переформулировка задачи;

^●использование вспомогательных букв (неизвестных).

Приведём примеры задач каждого типа и приёмы их решения. Подробнее об арифметических способах решения задач можно прочитать в книге для учителя 5—6 классов. Во всех случаях, где это помогает решению, надо использовать схематические рисунки для графического представления условий задачи.

1.1. Задачи на части

988. В бидоне 6 л кваса. Из него отлили в 5 раз больше, чем осталось. Сколько литров кваса осталось в бидоне?

Решение. Пусть в бидоне осталась 1 часть кваса, тогда отлили кваса в 5 раз больше, т. е. 5 частей. Значит, всего частей было 1 + 5 = 6 и на каждую часть приходилось

6 : 6 = 1 (л) кваса.

Ответ. Остался 1 л кваса.

991. Брат и сестра коллекционируют открытки. У брата в 2 раза больше открыток, чем у сестры, а всего у них 60 открыток. Сколько открыток у каждого?

Решение. Пусть число открыток сестры составляет 1 часть, тогда число открыток брата — 2 части.

1) 1 + 2 = 3 (части) — приходится на 60 открыток;

2) 60 : 3 = 20 (открыток) — приходится на 1 часть (число открыток у сестры);

3) 20 ⋅ 2 = 40 (открыток) — число открыток у брата. Ответ. У брата было 40 открыток, у сестры — 20.

996. а) На первой полке в 2 раза больше книг, чем на второй, но на 23 книги меньше, чем на двух полках вместе. Сколько книг на каждой полке?

Решение. Пусть на второй полке стояла 1 часть всех книг, тогда на первой полке стояли 2 части всех книг.

1) 2 − 1 = 1 (часть) — всех книг приходится на 23 книги;

2) 23 ⋅ 2 = 46 (книг) — стояло на первой полке; 3) 23 ⋅ 1 = 23 (книги) — стояло на второй полке. Ответ. 46 и 23 книги.

Замечание. Если учащиеся уже приучены решать такие задачи при помощи уравнений, то мотивация рассмотрения решений арифметическим способом заключается в том, что арифметическое решение может оказаться полезным, так как оно часто позволяет решить задачу устно. Вторым моментом мотивации служит уверенность в том, что арифметические способы решения задач способствуют развитию мышления, умения рассуждать, а это необходимо каждому обучающемуся математике.

1.2. Задачи на нахождение двух чисел по их сумме и разности

993. За две книги заплатили 150 р. Определите стоимость каждой, если известно, что одна из них на 40 р. дешевле.

Решение. 1) 150 − 40 = 110 (р.) — удвоенная стоимость более дешёвой книги;

2) 110 : 2 = 55 (р.) — стоимость более дешёвой книги;

3) 55 + 40 = 95 (р.) — стоимость более дорогой книги. Ответ. 55 и 95 р.

994. а) Сумма двух чисел равна 106, а их разность равна 42. Найдите числа.

Решение. 1) 106 − 42 = 64 — удвоенное меньшее число; 2) 64 : 2 = 32 — меньшее число; 3) 32 + 42 = 74 — большее число.

Ответ. 32 и 74.

Представляют интерес сложные задачи, включающие в себя простые типовые задачи или предполагающие неочевидные рассуждения при арифметическом решении. Примеры таких задач находим у С. А. Рачинского. Эти задачи были предназначены для устного решения сельскими школьниками.

998. 3адачи С. А. Рачинского. а) Два мальчика играли в шашки. Через несколько минут на доске осталось пустых чёрных клеток втрое больше, чем занятых шашками, а у одного мальчика на 2 шашки больше, чем у другого. Сколько шашек осталось у каждого?

б) Дочь ткала одна 4 дня по 3 аршина в день, но потом стала ткать и мать — по 5 аршин в день. Когда их тканья стало поровну, они прекратили работу. Сколько аршин они соткали вдвоём?

в) Я всем своим ученикам дал орехов поровну. Четве-

ро из них съели по 12 орехов, и тогда у этих четверых осталось столько орехов, сколько получил от меня каждый из них. По скольку орехов я раздавал?

г) Некто имел 5 детей и дал им пряников поровну. Трое из них съели по 5 пряников, и тогда у всех троих осталось столько пряников, сколько у двух остальных. Сколько всех пряников роздано?

д) Если к моим деньгам прибавить 4 р., у меня будет столько же, сколько у моего брата. Если к моим деньгам прибавить 55 р., у меня будет в 4 раза больше, чем у моего брата. Сколько денег у каждого?

Решение. а) Чёрных клеток на доске 32. Пустых чёрных клеток втрое больше, чем занятых. Найдём количество занятых клеток, решив задачу «на части».

1) 1 + 3 = 4 (части) — приходится на все чёрные клетки; 2) 32 : 4 = 8 (клеток) — занято шашками.

Известно, что у одного мальчика шашек на 2 больше, чем у другого, а всего их 8, найдём число шашек каждого, решив задачу на нахождение двух чисел по их сумме и разности;

3) (8 − 2) : 2 = 3 (шашки) — у первого мальчика; 4) 3 + 2 = 5 (шашек) — у второго мальчика.

Рассмотрим и второй способ решения задачи.

Пусть x шашек осталось у первого мальчика, тогда у второго мальчика осталось x + 2 шашек, а всего 2x + 2 шашек. Они занимают 2x + 2 чёрных клеток, но пустых чёрных клеток втрое больше: 3 (2x + 2). Всех же чёрных клеток 32. Составим уравнение:

2x + 2 + 3 (2x + 2) = 32,

откуда x = 3, x + 2 = 5.

Ответ. 3 и 5 шашек.

б) I способ. 1) 3 ⋅ 4 = 12 (аршин) — соткала дочь одна;

2) 5 − 3 = 2 (аршина) — на столько аршин в день мать ткала больше, чем дочь;

3) 12 : 2 = 6 (дней) — работала мать, чтобы тканья стало поровну;

4) 5 ⋅ 6 = 30 (аршин) — соткала мать;

5) 30 + 30 = 60 (аршин) — они соткали вдвоём.

II способ. Пусть x дней работала дочь, тогда x − 4 дня работала мать, они соткали 3x и 5 (x − 4) аршин. Составим уравнение:

3x = 5 (x − 4),

откуда x = 10.

Всего соткали 10 ⋅ 3 ⋅ 2 = 60 (аршин).

Ответ. 60 аршин.

в) I способ. 1) 4 ⋅ 12 = 48 (орехов) — съели четверо уче-

ников.

Осталось столько, сколько дали одному, т. е. съели они ровно столько, сколько дано трём из них.

2) 48 : 3 = 16 (орехов) — дано каждому.

II способ. Пусть дали по x орехов каждому из четырёх учеников, всего 4x орехов. Составим уравнение:

4x = 4 ⋅ 12 + x,

откуда x = 16.

Ответ. 16 орехов.

г) I способ. Так как у троих осталось столько пряников, сколько у двух остальных, то трое съели столько пряников, сколько дали одному. Тогда роздано 5 ⋅ 15 = 75 (пряников).

Трудно рассчитывать, что учащиеся дадут такое решение, будет неплохо, если они решат задачу с помощью уравнения.

II способ. Пусть дали по x пряников, тогда согласно условию задачи имеем

2x = 3 (x − 5),

откуда x = 15, 5x = 75.

Ответ. 75 пряников.

д) I способ. Если к моим деньгам прибавить 4 р., то у меня будет столько же денег, сколько у моего брата.

6 Рис. 6

Если к полученной сумме добавить ещё 55 − 4 = 51 (р.), то у меня будет в 4 раза больше, чем у моего брата (рис. 6).

Следовательно, 51 р. в 3 раза больше, чем сумма брата.

1) 51 : 3 = 17 (р.) — у брата; 2) 17 − 4 = 13 (р.) — у меня.

II способ. Пусть у меня x р., тогда у брата (x + 4) р. Составим уравнение: x + 55 = 4 (x + 4),

откуда x = 13, x + 4 = 17.

Ответ. 13 и 17 р.

Замечание. Если эти задачи предлагаются после изучения применения уравнений для решения задач, то учащимся полезно предложить найти приведённое выше арифметическое решение задачи (попробуйте решить задачу тем методом, которым её решали дети, изображённые на картине (с. 254 учебника) Н. П. Богданова-Бельского). Такое заочное соревнование со сверстниками, жившими больше ста лет назад, обычно вызывает интерес у школьников, и эта работа будет хорошей тренировкой умения школьников рассуждать, будет способствовать развитию их мышления и речи. Кроме того, она будет вносить разнообразие в решение задач с помощью уравнения, которым тоже надо заниматься.

1.3. Задачи на дроби

1008. а) Найдите от числа 324.

б) Найдите число, которого равны 324.

в) Какую часть числа 450 составляет число 180?

Решение. а) 324 = 243. б) 324 : = 432.

в) Число 180 составляет = части числа 450.

1009. а) Найдите число, которого равны от 600. б) Найдите число, 0,6 которого равны 0,1 от 120.

Решение. а) от 600 равны 600 = 360. Искомое число равно 360 : = 900.

б) 0,1 от 120 равны 0,1 ⋅ 120 = 12. Искомое число равно 12 : 0,6 = 20.

1.4. Задачи на совместную работу

1016. б) Первая бригада может выполнить задание за 36 дней, а вторая — за 45 дней. За сколько дней две бригады выполнят задание, работая вместе?

Решение. 1) 1 : 36 = (задания) — может выполнить первая бригада за 1 день;

2) 1 : 45 = (задания) — может выполнить вторая бригада за 1 день;

3) + = (задания) — могут выполнить две бригады за 1 день;

4) 1 : = 20 (дней) — за столько дней две бригады выполнят задание.

Ответ. За 20 дней.

1019. Имеющихся на складе материалов хватит для работы первого цеха на 30 дней или второго цеха на 42 дня. Хватит ли имеющихся на складе материалов для работы двух цехов в течение 18 дней?

Решение. 1) 1 : 30 = (материалов) — расходует первый цех за 1 день;

2) 1 : 42 = (материалов) — расходует второй цех за 1 день;

3) + = (материалов) — расходуют два цеха за

1 день;

4) 1 : = 17,5 (дня) — на столько дней хватит матери-

алов двум цехам.

Так как 17,5 < 18, то имеющихся материалов не хватит для работы двух цехов в течение 18 дней.

Ответ. Не хватит.

1.5. Задачи на движение по реке

1000. Скорость течения реки 2,5 км/ч. За сколько часов катер, имеющий собственную скорость 20 км/ч, проплывёт расстояние между пристанями 12,6 км туда и обратно?

Решение. 1) 20 + 2,5 = 22,5 (км/ч) — скорость катера по течению реки;

2) 12,6 : 22,5 = 0,56 (ч) — время движения катера по течению реки;

3) 20 − 2,5 = 17,5 (км/ч) — скорость катера против течения реки;

4) 12,6 : 17,5 = 0,72 (ч) — время движения катера против течения реки;

5) 0,56 + 0,72 = 1,28 (ч) — время движения катера. Ответ. За 1,28 ч.

1001. Скорость лодки по течению 12 км/ч, а против течения 9 км/ч. Какова скорость течения реки и собственная скорость лодки?

Решение. 1) 12 − 9 = 3 (км/ч) — удвоенная скорость течения реки;

2) 3 : 2 = 1,5 (км/ч) — скорость течения реки; 3) 9 + 1,5 = 10,5 (км/ч) — собственная скорость лодки. Ответ. 1,5 км/ч и 10,5 км/ч.

1.6. Задачи на движение

1004. Дачник пришёл от дачи на станцию за 13 мин до отхода поезда. Если бы он на каждый километр тратил на 3 мин больше, то пришёл бы за 1 мин до отправления поезда. Далеко ли от станции живёт дачник?

Решение. 1) 13 − 1 = 12 (мин) — на столько больше времени потратил бы дачник, если бы шёл медленнее; 2) 12 : 3 = 4 (км) — расстояние от дачи до станции.

Ответ. 4 км.

1005. Старинная задача. Если предположить, что лошадь бежит втрое медленнее поезда железной дороги, то она будет от него отставать на одну версту каждые 3 мин.

Определите скорость поезда. Выразите ответ в километрах в час с точностью до десятых. (1 верста ≈ 1,067 км.)

Решение. Пусть путь лошади за 1 ч составляет 1 часть, тогда путь поезда за 1 ч составляет 3 части (рис. 7).

6 Рис. 7

1) 60 : 3 = 20 (вёрст) — на 20 вёрст лошадь отстаёт от поезда за 1 ч;

2) 3 − 1 = 2 (части) — приходится на 20 вёрст;

3) 20 : 2 = 10 (вёрст) — пробегает лошадь за 1 ч; 4) 10 ⋅ 3 = 30 (вёрст в час) — скорость поезда. Выразим эту скорость в километрах в час: 30 ⋅ 1,067 = 32,01 ≈ 32,0 (км/ч).

Ответ. 32,0 км/ч.

1006. От Москвы до Курска 537 км. Из Москвы в Курск вышел поезд со скоростью 60 км/ч. Через 6 ч, в 20 ч 55 мин, на промежуточной станции первый поезд встретился с поездом, вышедшим из Курска в Москву в 17 ч 55 мин. Определите, с какой скоростью двигался до встречи второй поезд.

Решение. 1) 60 ⋅ 6 = 360 (км) — путь, пройденный первым поездом до встречи;

2) 537 − 360 = 177 (км) — путь, пройденный вторым поездом до встречи;

3) 20 ч 55 мин − 17 ч 55 мин = 3 ч — время движения второго поезда;

4) 177 : 3 = 59 (км/ч) — скорость второго поезда. Ответ. 59 км/ч.

1007. К приезду начальника на станцию обычно присылают машину. Приехал он однажды на час раньше, пошёл пешком и, встретив посланную за ним машину, прибыл с ней на место на 10 мин раньше обычного срока. Во сколько раз скорость машины больше скорости начальника?

Решение. Машина была в пути на 10 мин меньше, чем обычно. Следовательно, она встретила начальника на 10 : 2 = 5 (мин) позже обычного. Значит, тот путь, который начальник прошёл пешком, машина проезжает за 5 мин. Но начальник был в пути до встречи с машиной 60 − 5 = 55 (мин). Поэтому скорость машины в 55 : 5 = = 11 (раз) больше скорости начальника. Ответ. В 11 раз.

1126. Две старушки вышли одновременно навстречу друг другу из двух городов. Они встретились в полдень и достигли каждая чужого города: первая — в 4 ч пополудни, а вторая — в 9 ч. Узнайте, когда они вышли из своих городов.

Решение. Пусть скорость первой старушки в п раз больше скорости второй старушки. Тогда на одном и том же участке пути первая тратит в п раз меньше времени, чем вторая, а вторая — в п раз больше, чем первая (рис. 8).

6 Рис. 8

До встречи они шли одинаковое время, поэтому числа

9 9

и 4n равны. Уравнение = 4n имеет единственный поn n

ложительный корень n₁ = 1,5, тогда до встречи они шли 4 ⋅ 1,5 = 6 (ч), т. е. вышли из своих городов в 6 ч утра. Ответ. В 6 ч утра.

1.7. Деление числа в данном отношении

1022. а) Разделите число a в отношении 2 : 3, если a = 200.

Решение. 1) 80 — первое число;

2) 120 — второе число.

Второе число можно было найти и вычитанием. Ответ. 80 и 120.

992. Старинная задача. Три швеи заработали в одном доме 21 р. 15 к., причём первая работала 4 дня по 10 ч ежедневно, вторая — 5 дней по 9 ч и третья — 7 дней по 8 ч. Сколько получит каждая из заработанной суммы сообразно времени, употреблённому на работу?

Решение. 1) 4 ⋅ 10 = 40 (ч) — работала первая швея; 2) 5 ⋅ 9 = 45 (ч) — работала вторая швея; 3) 7 ⋅ 8 = 56 (ч) — работала третья швея.

Сумму 2115 к. надо разделить на части, пропорциональные числам 40, 45, 56 (в отношении 40 : 45 : 56);

4) 40 + 45 + 56 = 141 (часть) — приходится на 2115 к.;

5) 2115 : 141 = 15 (к.) — приходится на 1 часть;

6) 40 ⋅ 15 = 600 (к.) — заработала первая швея; 7) 45 ⋅ 15 = 675 (к.) — заработала вторая швея; 8) 56 ⋅ 15 = 840 (к.) — заработала третья швея. Ответ. 6 р., 6 р. 75 к. и 8 р. 40 к.

1.8. Задачи на пропорции и проценты

Приведём пример задачи, в которой используется и прямая, и обратная пропорциональность величин.

1. Бригада трактористов за 3 дня, работая по 8 ч в день, вспахала 6 га пашни. Сколько гектаров пашни бригада трактористов вспашет (при той же производительности труда) за 2 дня, работая по 10 ч в день?

Решение. Так как бригада за 3 дня, работая по 8 ч в день, вспахала 6 га пашни, то если изменить значение только одной величины — число дней работы с 3 дней на 2 дня, то площадь уменьшится в раза. Если изменить ещё и значение второй величины — число часов работы в день с 8 ч на 10 ч, то площадь увеличится в раза.

Итак, бригада трактористов вспашет 6 : 5 га пашни.

Ответ. 5 га.

1011. а) Найдите 13 % числа 40.

б) Найдите число, 12 % которого равны 24.

в) Сколько процентов числа 480 составляет число 360?

Решение. а) 40 ⋅ 0,13 = 5,2 — искомое число. б) 24 : 0,12 = 200 — искомое число.

в) 75 %.

1014. Сумма 12 000 р. увеличилась на вкладе в банке на 5 %. Какая сумма получилась?

Решение. I способ. 1) 12 000 ⋅ 0,05 = 600 (р.) — 5 % от

12 000 р.;

2) 12 000 + 600 = 12 600 (р.) — получившаяся сумма.

II способ. 1) 100 + 5 = 105 (%) — составляет новая сумма от 12 000 р.;

2) 12 000 ⋅ 1,05 = 12 600 (р.) — получившаяся сумма. Ответ. 12 600 р.

1059. Торговец получил товар по оптовой цене а р., увеличил цену на 20 %. Для проверки он уменьшил новую цену на 20 % и удивился, так как не получил прежнего результата. Должен ли получиться прежний результат?

Решение. Если увеличить число a на 20 %, то получится число a + 0,20a = 1,2a. Заметим, что увеличить число на 20 % можно, умножив это число на 1 + 0,20 = 1,20. Аналогично уменьшить число на 20 % можно, умножив это число на 1 − 0,20 = 0,80. Поэтому после уменьшения суммы 1,2a на 20 % торговец получил 1,2a ⋅ 0,80 = 0,96a, что на 4 % меньше a.

1072. Рядовой Степанов почистил бак картошки за 4 ч, и у него 20 % всей картошки ушло в очистки.

За сколько часов он начистит такой же (по массе) бак картошки?

Решение. За 4 ч рядовой Степанов начистил 100 − 20 = = 80 (%), или , ведра картошки. Тогда ведро он начи-

стит за 4 : = 5 (ч).

Ответ. За 5 ч.

1073. Рядовой Кузнецов начистил бак картошки за 4 ч, и у него 20 % всей картошки ушло в очистки. За сколько часов он почистит такой же (по массе) бак картошки?

Решение. За 4 ч работы рядовой Кузнецов начистил бак картошки. Когда он почистит бак картошки, то начистит 100 − 20 = 80 (%) бака. На эту работу потребуется

4 ⋅ 0,8 = 3,2 (ч).

Ответ. За 3,2 ч.

1074. Рядовой Смирнов может почистить бак картошки за 3 ч, а начистит такой же (по массе) бак картошки за 4 ч. Сколько процентов картошки идёт у него в очистки?

Решение. За 4 ч работы рядовой начистил бак картошки, тогда за 3 ч он начистил бака картошки. Так как за

3 ч он почистил бак картошки, то 1 − ³ = ¹, или 25 %, кар-

4 4

тошки у него ушло в отходы. Ответ. 25 %.

1075. Рядовой Иванов может почистить котёл картошки за 4 ч, а рядовой Петров — за 6 ч. У рядового Иванова 10 % картошки идёт в очистки, а у рядового Петрова — 15 %. Однажды они сели вместе чистить котёл картошки. Сколько процентов картошки уйдёт в очистки при совместной работе?

Решение. При совместной работе рядовые Иванов и ⎛ 1 ⁺1⎞^⎟⎠ = 2,4 (ч). Иванов по-

Петров почистят котёл за 1 : ^⎜⎝ _{4 6}

чистит 0,6 котла картошки. Тогда Петров почи-

стит 1 − 0,6 = 0,4 котла картошки. В очистки у них уйдёт 0,1 ⋅ 0,6 + 0,15 ⋅ 0,4 = 0,12, или 12 %, всей картошки. Ответ. 12 %.

1077. Трава при сушке теряет p % своей массы. Сколько сена получится из m т свежей травы, если: а) р = 80, т = 3; б) р = 75, т = 8?

Решение. Из m т свежей травы получится т ⋅ ^⎛⎜⎝1 ⁻₁₀₀^p^⎞⎟⎠ т сена.

а) Если р = 80, т = 3, то т ⋅ ⎛⎜⎝1 − 100p ⎞⎟⎠ = 3 ⋅ ⎛⎜⎝1 − 10080 ⎞⎠⎟ = = 0,6 (т).

б) Если р = 75, т = 8, то т ⋅ ⎛⎜⎝1 − 100p ⎞⎟⎠ = 8 ⋅ ⎛⎜⎝1 − 10075 ⎞⎠⎟ =

= 2 (т).

Ответ. а) 0,6 т; б) 2 т.

Приведём теперь примеры текстовых задач, решаемых нестандартными способами.

2.1. Обратный ход

1. В автобусе было несколько пассажиров. На первой остановке вышло 7 и вошло 4, а на второй вышло 6 и вошло 13 пассажиров. Сколько пассажиров было в автобусе до первой остановки, если после второй остановки автобуса их стало 38?

Решение. Неизвестное число пассажиров до первой остановки можно вычислить обратным ходом, т. е. выполняя все действия в обратном порядке (можно представить, что описанные события сняли на плёнку и просматривают в обратном порядке):

38 − 13 + 6 − 4 + 7 = 34. Ответ. 34 пассажира.

2.2. Переформулировка задачи

1. Расстояние между пунктами А и В равно 34 км. Из пункта А в пункт В вышел пешеход со скоростью 5 км/ч. Одновременно с ним из А в В выехал велосипедист со скоростью 12 км/ч. Велосипедист доехал до пункта B, развернулся и с той же скоростью поехал навстречу пешеходу. На каком расстоянии от пункта В велосипедист встретит пешехода?

Решение. Чтобы найти время движения пешехода и велосипедиста до встречи, решим другую задачу: будем считать, что пешеход и велосипедист одновременно отправились навстречу друг другу с удвоенного расстояния (рис. 9).

1) 34 ⋅ 2 = 68 (км) — удвоен-

ное расстояние; ₆ Рис. 9

2) 12 + 5 = 17 (км/ч) — скорость сближения пешехода и велосипедиста;

3) 68 : 17 = 4 (ч) — время движения пешехода и велосипедиста до встречи;

4) 4 ⋅ 5 = 20 (км) — путь пешехода до встречи;

5) 34 − 20 = 14 (км) — расстояние от пункта В до места встречи.

Ответ. 14 км.

2. Две мухи ползут по стене от пола до потолка и об-ратно. Первая с одной и той же постоянной скоростью, а вторая вверх ползёт со скоростью, в 2 раза большей, а вниз со скоростью, в 2 раза меньшей, чем скорость первой мухи. Какая из них первой вернётся обратно, если от пола они стартовали одновременно?

Решение. Представим, что вторая муха вверх ползла со скоростью, в 2 раза меньшей, а вниз — со скоростью, в 2 раза большей. От этого время движения второй мухи вверх и вниз не изменится. Тогда, пока она приползёт вверх, первая муха, скорость которой в 2 раза больше, уже будет внизу. Следовательно, первая муха приползёт вниз первой.

Ответ. Первая муха.

2.3. Использование вспомогательных букв

(неизвестных)

1098. Мальчики составляют 45 % всех учащихся в школе. Известно, что 30 % всех мальчиков и 40 % всех девочек учатся без троек. Сколько процентов всех учащихся школы учатся без троек?

Решение. Пусть в школе было a учащихся. Тогда в ней было 0,45a мальчиков и a − 0,45a = 0,55a девочек. Без троек учатся 0,3 ⋅ 0,45a = 0,135a мальчиков и 0,4 ⋅ 0,55a = = 0,22a девочек, а всего 0,135a + 0,22a = 0,355a учащихся.

0,355a ⋅100% = 35,5 % учащихся.

Это составляет

a Ответ. 35,5 %.

Замечание. Вспомогательным неизвестным здесь является a. Найти его нам не удалось, что и не требовалось, но с помощью этого неизвестного мы получили ответ к задаче. В решении следующих задач уже будет два вспомогательных неизвестных.

1099. В некотором царстве, в некотором государстве правительство приняло постановление о запрете рекламы спиртных напитков. Это постановление поддержало 69 % всего взрослого населения, причём среди женщин 94 %, а среди мужчин 41 %. Определите, кого в этом царствегосударстве больше: мужчин или женщин, и на сколько процентов.

Решение. Пусть в голосовании приняли участие g женщин и m мужчин. Постановление поддержали 0,94g женщин и 0,41m мужчин, а всего 0,69 (g + m) человек. Составим уравнение:

0,94g + 0,41m = 0,69 (g + m),

из которого получим g = 1,12m. Это означает, что среди голосовавших женщин было на 12 % больше, чем мужчин.

Ответ. Женщин больше на 12 %.

1127. На дороге, соединяющей два горных селения, нет ровных участков. Автобус едет в гору всегда со скоростью 30 км/ч, а под гору со скоростью 60 км/ч. Найдите расстояние между горными селениями, если путь туда и обратно без остановок занимает ровно 2 ч.

Решение. Пусть на пути от первого селения ко второму сумма длин участков дороги, ведущих вверх, равна x км, а сумма длин участков дороги, ведущих вниз, равна y км. Количество таких участков не имеет значения, поэтому можно считать, что путь от первого селения ко второму сначала идёт в гору (x км), а потом с горы (y км). Тогда в обратном направлении путь тоже сначала идёт в гору (y км), а потом с горы (x км). На всю дорогу в двух направлениях потрачено x + ^y+ ^y+ ^x= ^{x y}⁺ ч, что по

30 60 30 60 20

условию равно 2 ч. Тогда из равенства = 2 получим,

что x + y = 40, т. е. расстояние между селениями равно 40 км.

Ответ. 40 км.

Задания на исследование

Ниже приведены условия задач, связанные с арифметикой целых чисел. Разбор решений этих задач позволит подготовить учащихся к решению олимпиадных задач, а также будет способствовать формированию компетентности в проведении учебно-исследовательской деятельности. Обсуждение решений этих задач способствует обобщению знаний и сотрудничеству со сверстниками и учителем. В ыполнение заданий данной рубрики поможет учащимся в развитии таких метапредметных умений, как: умение самостоятельно планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных задач; умение осуществлять контроль своей деятельности, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией; умение оценивать правильность выполнения учебной задачи, собственные возможности её решения; умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач.

1. Из бочки, содержащей 100 л сока, отливают 10 л сока и вливают в неё 10 л воды. Перемешав полученную смесь, из бочки отливают 10 л смеси и опять вливают в неё 10 л воды, и так делают неоднократно. Можно ли в результате таких операций получить смесь, содержащую 72,9 л сока?

Решение. После того как из бочки отлили 10 л сока и влили в неё 10 л воды, в бочке осталось 100 − 10 = 90 л сока.

При этом верно равенство 90 = 100 100 ⋅ ⎛^⎜⎝1 ⁻₁₀₀¹⁰⎞^⎟⎠.

Во время второй операции отлили 10 л смеси, содержащей 10 л сока. После чего осталось 90 81 л

сока. При этом верно равенство

100

= 100 ⋅ ⎛⎜⎝1 − 10010 ⎞⎟⎠ ⋅ ⎛⎜⎝1 − 10010 ⎟⎠⎞ = 100 ⋅ ⎜⎝⎛1 − 10010 ⎞⎠⎟2.

Во время третьей операции отлили 10 л смеси, содер-

жащей 10 ⋅ ⁸¹ л сока. После чего осталось 81 100 = 72,9 л сока.

Итак, в результате трёх операций можно получить смесь, содержащую 72,9 л сока. Ответ. Да.

Замечание. После третьей операции количество сока, оставшегося в бочке, можно вычислить так:

100

= 100 ⋅ ⎛⎜⎝1 − 10010 ⎞⎟⎠2 ⋅ ⎝⎛⎜1 − 10010 ⎞⎟⎠ = 100 ⋅ ⎜⎝⎛1 − 10010 ⎞⎠⎟3.

Полученный результат можно обобщить (пока без доказательства). После n-й операции в бочке останется

100 ⋅ ⎛⎜⎝1 − 10010 ⎞⎟⎠n л сока.

2. Из бочки, содержащей 100 л сока, отливают 1 л сока и вливают в неё 1 л воды. Перемешав полученную смесь, из бочки отливают 1 л смеси и опять вливают в неё 1 л воды, и так делают неоднократно. Можно ли в результате таких операций получить смесь, содержащую 50 л сока?

Решение. По аналогии с замечаниями к предыдущей задаче, после n-й операции в бочке останется

100 ⋅^⎛⎜_⎝1 ⁻₁₀₀¹^⎞⎟_⎠ л сока. Предположим, что задача имеет решение, т. е. найдётс я такое натуральное n, что верно равенство 100 ⋅^⎛⎜_⎝1 ⁻₁₀₀¹^⎞⎟_⎠ⁿ = 50, которое можно переписать

в виде 99ⁿ = 50 ⋅ 100ⁿ⁻¹. Но это равенство не выполняется ни для какого натурального n, так как для любого натурального n в левой части равенства стоит нечётное число, а в правой — чётное.

Итак, осуществить требуемое невозможно. Ответ. Нет.

3. а) При каком наибольшем натуральном числе n число 10! делится на nⁿ?

б) При каком наименьшем натуральном числе n число 10! не делится на nⁿ?

Решение. а) Так как 10! = 2⁸⋅ 3⁴⋅ 5²⋅ 7, то 10! делится на 1¹, 2², 3⁴, 4⁴ и не делится на 5⁵, 6⁶ и т. д. Поэтому:

а) наибольшее n, при котором число 10! делится на nⁿ, равно 4;

б) наименьшее n, при котором число 10! не делится

на nⁿ, равно 5.

Ответ. а) При n = 4; б) при n = 5.

4. Обыкновенную дробь с числителем 1 называют аликвотной дробью. Например, дроби — аликвот-

ные дроби.

а) Сколькими различными способами, не учитывая порядка слагаемых, можно представить дробь в виде

суммы двух аликвотных дробей, знаменатели которых — различные числа?

б) Придумайте способ записи аликвотной дроби в виде

суммы двух аликвотных дробей. Рассмотрите случаи: знаменатель дроби — простое число; знаменатель дроби — составное число.

Решение. а) У знаменателя дроби имеются четыре

пары различных взаимно простых делителей: 1 и 2; 1 и 3; 1 и 6; 2 и 3. Следовательно, данная дробь может быть представлена суммой двух аликвотных дробей с разными знаменателями (без учёта порядка слагаемых) четырьмя способами:

Замечание. Так как у знаменателя дроби имеется

четыре пары различных взаимно простых делителей: 1 и 2; 1 и 3; 1 и 6; 2 и 3 (без учёта порядка делителей) — и для каждой из них получено одно представление дроби в виде суммы аликвотных дробей, то получены все возможные представления дроби в виде суммы аликвотных

дробей (без учёта порядка слагаемых).

б) Результат, полученный выше, можно обобщить в

виде правил.

1. Если умножить числитель и знаменатель аликвотной дроби на сумму двух взаимно простых делителей знаменателя, полученную дробь заменить суммой двух дробей, знаменатели которых равны знаменателю полученной дроби, а числители — слагаемым вышеупомянутой суммы, наконец, сократить одну или обе из полученных дробей, то в результате получится сумма аликвотных дробей, равная данной дроби.

2. Если знаменатель исходной дроби — составное число, то количество возможных вариантов замены исходной дроби суммой двух аликвотных дробей равно числу пар взаимно простых делителей знаменателя исходной дроби.

Правомерность этого вывода подтверждается следующими преобразованиями:

1 = a + 1 = a + 1 = 1 + 1 _;a a a( + 1) a a( + 1) a a( + 1) a + 1 a a( + 1)

1 a b+ = a + b = 1 + 1 _.

ab ab a b( + ) ab a b( + ) ab a b( + ) b a b( + ) a a b( + )

Например, у числа 2 имеется только одна пара взаимно простых делителей: 1 и 2, поэтому имеется только один вариант представления дроби в виде суммы аликвотных дробей (без учёта порядка слагаемых):

У числа 4 имеется только две пары взаимно простых делителей: 1 и 2, 1 и 4, поэтому имеется только два варианта представления дроби в виде суммы аликвотных дробей (без учёта порядка слагаемых):

Заметим, что если взять пару не взаимно простых делителей 2 и 4, то мы получим повторение уже имеющегося варианта решения задачи:

5. Из ЕГЭ. Сколькими различными способами, не учитывая порядка слагаемых, можно представить дробь в виде суммы двух аликвотных дробей?

Решение. У знаменателя дроби имеются две пары

различных взаимно простых делителей: 1 и 5; 1 и 25. Следовательно, данная дробь может быть представлена суммой двух аликвотных дробей с разными знаменателями (без учёта порядка слагаемых) двумя способами:

;

Ответ. Двумя способами.

6. Сколькими различными способами, не учитывая п орядка слагаемых, можно представить дробь в виде суммы двух аликвотных дробей с разными знаменате лями?

Решение. У знаменателя дроби имеются семь пар

различных взаимно простых делителей: 1 и 2; 1 и 3; 1 и 4; 1 и 6; 1 и 12; 2 и 3; 3 и 4. Следовательно, данная дробь может быть представлена суммой двух аликвотных дробей с разными знаменателями (без учёта порядка слагаемых) семью способами:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) .

Ответ. Семью способами.

7. Найдите все пары натуральных чисел m и n, удов-

летворяющие уравнению 1 + ¹ = ¹, если одно из чисел

m n 12

чётное, а другое нечётное.

Решение. В предыдущем задании дробь представле-

на в виде суммы аликвотных дробей (без учёта порядка слагаемых) семью способами. Из них только в трёх случаях знаменатели дробей имеют разную чётность (один из них чётный, другой нечётный). При отыскании всех пар чисел (m; n) число пар удвоится, так как перестановка чисел в паре даёт новую пару.

Итак, условию задачи удовлетворяет шесть пар чисел (m; n): (15; 60), (60; 15), (13; 156), (156; 13), (21; 28), (28; 21).

8. Учитель хочет составить несколько вариантов задачи на совместную работу: «Первая бригада может выполнить задание за a дней, а вторая — за b дней. За сколько дней они выполнят это задание при совместной работе?» При этом он хочет, чтобы в каждом варианте был один и тот же ответ «За 24 дня». Сколько различных вариантов задачи он может составить, если a > b?

Решение. Для чисел a и b должно выполняться равенство 1 + ¹= ¹. a b 24

Выпишем все делители числа 24:

1, 2, 3, 4, 6, 8, 12, 24.

Образуем все пары взаимно простых делителей m и n так, чтобы выполнялось неравенство m < n:

1 и 2; 1 и 3; 1 и 4; 1 и 6; 1 и 8;

1 и 12; 1 и 24; 2 и 3; 3 и 4; 3 и 8.

Всего получилось 10 пар делителей. Для каждой из них числа a и b можно найти так же, как и для пары m = 2, n = 3:

Паре делителей m = 2, n = 3 соответствует пара чисел a = 60, b = 40.

Итак, можно составить 10 вариантов задачи с ответом «За 24 дня» при условии a > b.

Замечание. Без ограничения a > b задача имеет 21 решение: десять уже полученных, десять, удовлетворяющих условию a < b, и одно, удовлетворяющее условию a = b

(a = b = 48).

9. Из ЕГЭ. Найдутся ли хотя бы три десятизначных натуральных числа, делящиеся на 11, в записи каждого из которых использованы все цифры от 0 до 9?

Решение. Число делится на 11 тогда и только тогда, когда разность между суммами его цифр, стоящих на нечётных и на чётных местах, делится на 11 (признак делимости на 11 доказан при решении задания 174).

Запишем все цифры подряд, получим число 9 876 543 210. В этом числе указанная разность сумм равна 5, т. е. это число не делится на 11. Меняя местами, например, 5 и 8, мы одну сумму увеличиваем на 3, а другую уменьшаем на 3. Значит, разность между суммами его цифр, стоящих на нечётных и на чётных местах, становится равной 11, следовательно, число 9 576 843 210 удовлетворяет условию задачи. Меняя местами в числе 9 876 543 210, например, 4 и 1 или 3 и 6, получаем новые числа: 9 876 513 240 и 9 873 546 210, делящиеся на 11.

Примечание. В задаче не требуется нахождения всех чисел, обладающих указанным свойством. Ответ. Да.

10. Натуральное число, записанное несколькими еди-ницами, умножили на другое натуральное число, записанное нескольк ими единицами. Сколько цифр будет в записи результата, если в записи первого числа m единиц, а в записи второго числа n единиц (m ≥ n, 2 ≤ n ≤ 9). Какая цифра будет повторяться в середине записи произведения? Сколько раз?

Решение. Решение этой задачи нужно рассмотреть на нескольких конкретных примерах, которые подведут к следующему выводу:

6Рис. 10 количество цифр в записи произведения равно (m + n − 1) цифр. Цифра n будет повторяться в сер едине записи произведения m − (n − 1) = m − n + 1 раз.

11. Найдите несократимую дробь , такую, что q

100

p 123444...4321

= . q 1234555...54321

Решение. Воспользовавшись результатами предыдущей задачи, представим числитель и знаменатель дроби в виде произведения двух натуральных чисел, записанных одними единицами:

p 1111

Тогда = . Докажем теперь, что эта дробь несокраq 11111 тимая.

Предположим, что НОД (p, q) = d ≠ 1. Тогда число

11111 − 1111 = 10⁴

делится на d, т. е. d не имеет простых делителей, кроме 2 и 5. Но числа p и q не имеют таких делителей, следовательно, d = 1, т. е. дробь несократимая.

p 1111

Ответ. = .

q 11111

12. Из ЕГЭ. а) Найдите все тройки натуральных чисел m, n и k, удовлетворяющие уравнению 5 ⋅ k! = m! − n!.

Решение. Из равенства 5 ⋅ k! + n! = m! видно, что m > n и m > k. Рассмотрим три случая: 1) k > n; 2) k < n; 3) k = n.

1) Пусть k > n. Разделим обе части равенства 5 · k! + n! =

= m! на k!. В полученном равенстве 5 + ⁿ^! = ^m^! левая k! k!

часть дробная, правая целая, следовательно, в этом случае нет тройки чисел, удовлетворяющей данному равенству.

2) Пусть k < n. Разделим обе части равенства 5 · k! + n! =

= m! на n!. В полученном равенстве ⁵^⋅^k^! + 1 = ^m^! справа n! n!

целое число, а слева целое число только при условии k = 4 и n = 5. Но тогда m! должно быть равно 2 · 5!, что неверно, следовательно, в этом случае нет тройки чисел, удовлетворяющей данному равенству.

3) Пусть k = n. Получаем 6 ⋅ k! = m!. Это равенство возможно лишь в случаях m = 6, k = 5 (в этом случае n = 5) или m = 3, k = 1 (в этом случае n = 1).

Ответ. m = 6, k = n = 5; m = 3, k = n = 1.

13. Отличное от нуля число увеличили на p %, полученный результат уменьшили на q %. В результате снова получили первое число. Найдите все пары натуральных чисел (p; q), удовлетворяющие условию задачи.

Решение. Пусть данное число равно a. Тогда верно равенство

a ⋅ ⎛⎜⎝1 + 100p ⎞⎟⎠ ⎛⎜⎝1 − 100q ⎟⎠⎞ = a. (1)

Разделив равенство (1) на a, умножив полученное равенство на 10 000, имеем

(100 + p) (100 − q) = 10 000. (2)

Так как p > 0 и q > 0, то 100 + p > 100 − q и из равенства (2) следует, что 100 − q > 0.

Представим число 10 000 в виде произведения двух множителей всеми возможными способами так, чтобы множитель (100 − q) был меньше множителя (100 + p): 10 000 = 10 000 ⋅ 1 = 5000 ⋅ 2 = 2500 ⋅ 4 = 2000 ⋅ 5 = = 1250 ⋅ 8 = 1000 ⋅ 10 = 625 ⋅ 16 = 500 ⋅ 20 = 400 ⋅ 25 = = 250 ⋅ 40 = 200 ⋅ 50 = 125 ⋅ 80.

Теперь найдём все 12 пар чисел p и q, для каждой из которых верны пары равенств:

1) 100 + p = 10 000, 100 − q = 1;

2) 100 + p = 5000, 100 − q = 2;

3) 100 + p = 2500, 100 − q = 4;

4) 100 + p = 2000, 100 − q = 5;

5) 100 + p = 1250, 100 − q = 8;

6) 100 + p = 1000, 100 − q = 10;

7) 100 + p = 625, 100 − q = 16;

8) 100 + p = 500, 100 − q = 20;

9) 100 + p = 400, 100 − q = 25;

10) 100 + p = 250, 100 − q = 40;

11) 100 + p = 200, 100 − q = 50;

12) 100 + p = 125, 100 − q = 80.

В результате получим лишь 12 пар значений (p; q), удовлетворяющих условиям задачи: (9900; 99), (4900; 98), (2400; 96), (1900; 95), (1150; 92), (900; 90), (525; 84), (400; 80), (300; 75), (150; 60), (100; 50), (25; 20).

Оглавление

Введение. . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Примерное тематическое планирование работы

по учебнику «Алгебра, 7» . . . . . . . . . . . . . . . . . 15

Глава 1. Действительные числа . . . . . . . . . . . . . 18 Глава 2. Алгебраические выражения . . . . . . . . . . 41

Глава 3. Линейные уравнения . . . . . . . . . . . . . . 94 Обучение решению текстовых задач . . . . . . . . . . . 120 Задания на исследование . . . . . . . . . . . . . . . . . 134

Учебное издание

Серия «МГУ — школе» Потапов Михаил Константинович

Шевкин Александр Владимирович

АЛГЕБРА

Методические рекомендации

7 класс

Учебное пособие для общеобразовательных организаций

Центр естественно-математического образования Редакция математики и информатики

Зав. редакцией Т. А. Бурмистрова

Редактор Т. Г. Войлокова

Младший редактор Е. А. Андреенкова

Художник О. П. Богомолова

Художественный редактор О. П. Богомолова

Компьютерная графика С. А. Крутикова

Технический редактор и верстальщик Е. В. Саватеева

Корректоры Т. А. Дич, И. П. Ткаченко

Налоговая льгота — Общероссийский классификатор продукции ОК 0 05-93—

953000. Изд. лиц. Серия ИД № 05824 от 12.09.01. Подписано в печать

17.02.16. Формат 60 × 90¹/₁₆. Бумага газетная. Гарнитура Школь ная. Уч.-изд. л. 7,67. Тираж 50 экз. Заказ № . .

Акционерное общество «Издательство «Просвещение». 127521, Москва, 3-й проезд Марьиной рощи, 41.

Отпечатано в типографии «Onebook» ООО «Сам Полиграфист».

129090, Москва, Протопоповский пер., 6. Тел.: +7(495) 545-37-10.

E-mail: [email protected]

Сайт: www.onebook.ru

[1] Здесь и далее в скобках указан номер работы по старым изданиям дидактических материалов. Звёздочкой отмечены номера работ, рекомендуемых только для классов с углублённым изучением математики.

[2] (3 − x)²(x − 3)².

(x − 3)

Промежуточный контроль. С—14.

[3] Алькуин (Alcuin, ок. 730—19 мая 804), англ. учёный, богослов и писатель, друг и советник Карла Великого, положил начало органи зации учебного дела у франков.

Методические рекомендации. Алгебра 7 класс

УДК 372.8:512 ББК 74.262.21

Издательство «Просвещение», 2017

Следует обратить внимание на то, что в пособии для учителей (как и в учебнике) рассмотрены вопросы обучения алгебре в 7 классе как в общеобразовательных классах,…

Учебник должен быть пригоден для организации дифференцированного обучения и обеспечивать любой желаемый уровень глубины изучения материала с учётом устойчивых познавательных интересов

В учебниках серии «МГУ — школе» уделяется достаточно внимания вопросу «почему?», имеющему большой развивающий потенциал для достижения личностных результатов освоения

Учебники серии «МГУ — школе» полностью обеспечивают обучение тех школьников, которые могут и хотят усвоить основы наук

Учебники серии «МГУ — школе» обеспечивают системную подготовку по предмету, требуют меньше, чем обычно, времени, позволяют ориентировать процесс обучения на формирование результатов обучения и освоения…

Эти свойства мотивируются по мере их введения, отмечается, что при замене букв числами в рассматриваемых буквенных равенствах последние превращаются в верные числовые равенства (за исключением…

Материал первой главы должен сформировать у учащихся представление о действительном числе как о длине отрезка

Разговоры об иррациональности чисел, несоизмеримости с единицей, существовании корня значительно упрощаются, если у школьника есть представление, пусть даже самое элементарное, о числе как бесконечной десятичной…

Таким образом, координатная ось, которая ранее была «дырявой» — без иррациональных точек, теперь заполнена полностью, без пропусков

В результате изучения этой главы учащиеся должны понять, что, применяя последовательно способ подстановки, они всегда решат систему линейных уравнений, т

Далее приведены методические рекомендации по изучению всех тем, включённых в учебник, и дидактические материалы для 7 класса с решениями наиболее трудных задач

В обязательную часть самостоятельных работ на отметку можно включать не все задания, ориентируясь на уровень подготовки класса и на отводимое для работы время

Кроме того, в дидакт ических материалах имеются самостоятельные работы, отмеченные звёздочками

Понятие действительного числа 1 1 3

Куб разности 6.9. Применение формул сокращённого умно- — 2 жения 2 3 6

Системы линейных уравнений 10

Многие задачи данной главы решаются разными способами, что позволяет развить критичность мышления, формировать коммуникативные компетенции в обучении, умения формулировать свои мысли, аргументировать их, отстаивать свою…

Можно напомнить другие свойства натуральных чисел, которые изучались в 5 классе, их доказательства содержатся в

Делится ли это число на 9? Решение

Решения и комментарии 33.

В самом деле, 3 n + 3 n + 1 + 3 n + 2 = 3 (3 n + 1) — делится на 3

Но эта гипотеза неверна, в чём легко убедиться, взяв п = 41

Решения и комментарии 57. Сколько чисел от 1 до 100 не делится ни на 2, ни на 3?

Дополнительные задания 1. Задание для исследования

Решение. а) Среди 250 чисел: 1, 2, 3, 4,

Обыкновенные дроби. Конечные десятичные дроби 2

Периодические дроби В данном пункте вводятся понятия бесконечной периодической десятичной дроби, периода дроби для положительных чисел, сформулированы два утверждения: p 1) любое положительное рациональное число…

Так как цифра 1 сотого разряда после запятой за- менится на цифру 3, то дробь увеличится

Решение. При делении числителя дроби 6 на её знаменатель 7 может получиться не больше 6 остатков: 1, 2, 3, 4, 5, 6

Решение. а) − = –0,5 = –0,5(0); 0 = 0,(0); –1,24 = –1,24(0); б) = 0,(3); − = –0,(571428); − 2 = –2,(384615)

Надо, чтобы учащиеся поняли, что существуют не только рациональные, но и другие числа, не являющиеся рациональными (иррациональные числа)

Каково наибольшее действительное число, меньш ее 0,9, в десятичную запись которого не входит цифра 9? б)

Решения и комментарии Вычислите (146—147) : 146

Следует учесть, что слабые учащиеся с трудом усваивают данный материал, но его изучение необходимо, чтобы учащиеся осмысленно применяли калькулятор при приближённых вычислениях, а не выписывали…

Вычислите приближённо произведение, округлив данные числа с точностью до второй значащей цифры: г) 0,56 ⋅ 0,(3); д) 0,(1) ⋅ 0,(2); е) 12,(45) ⋅ 10,(1)

Используемое здесь свойство верных числовых неравенств можно доказать с опорой на свойства действительных чисел

В классе с углублённым изучением математики можно рассмотреть геометрическое обоснование того, что эта дробь не является периодической, т

Делимость чисел В данном пункте сначала доказана теорема о делимости суммы и разности двух чисел на число, на которое делится каждое из этих чисел

Доказательство. Любое многозначное число можно записать в виде 1000 а + a 2 1 0 a a

Если целое число при делении на 4 даёт остаток 3, при делении на 3 даёт остаток 2, при делении на 2 даёт остаток 1, то…

Глава 2 Алгебраические выражения

Решение. Чтобы определить среднюю скорость туриста, надо пройденный путь разделить на время движения

Короче решение задачи можно записать составлением числового выражения: (1 + 0,2) ⋅ (1 + 0,3) ⋅ 20 000 = 1,2 ⋅ 1,3 ⋅ 20 000…

Задания для повторения. При изучении данного пункта можно использовать задания 887—894

Первый кусок сплава массой 400 г содержит р % олова, а второй кусок сплава массой 100 г содержит q % олова

Ответ. а) р

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

02.04.2020

Методические рекомендации. Алгебра 7 класс

Введение

по учебнику «Алгебра, 7»

Глава 1 Действительные числа

1.1. Натуральные числа и действия с ними

1.2. Степень числа

1.3. Простые и составные числа

2.1. Обыкновенные дроби. Конечные десятичные дроби 2.2. Разложение обыкновенной дроби в конечную десятичную дробь

2.3. Периодические дроби

2.4*. Периодичность десятичного разложения обыкновенной дроби

2.5. Десятичное разложение рациональных чисел

3.1. Иррациональные числа 3.2. Понятие действительного числа 3.3. Сравнение действительных чисел

3.4. Основные свойства действительных чисел

3.5. Приближения числа

3.6. Длина отрезка 3.7. Координатная ось

1. Делимость чисел

2. Исторические сведения

Глава 2 Алгебраические выражения

4.1. Числовые выражения

4.2. Буквенные выражения

4.3. Понятие одночлена

4.4. Произведение одночленов

4.5. Стандартный вид одночлена

4.6. Подобные одночлены

5.1. Понятие многочлена

5.2. Свойства многочленов

5.3. Многочлены стандартного вида

5.4. Сумма и разность многочленов

5.5. Произведение одночлена и многочлена

5.6. Произведение многочленов

5.7. Целые выражения

5.8. Числовое значение целого выражения

5.9. Тождественное равенство целых выражений

6.1. Квадрат суммы

6.2. Квадрат разности

6.3. Выделение полного квадрата

6.4. Разность квадратов

6.5. Сумма кубов 6.6. Разность кубов

6.7*. Куб суммы 6.8*. Куб разности

6.9. Применение формул сокращённого умножения

6.10. Разложение многочленов на множители

7.1. Алгебраические дроби и их свойства

7.2. Приведение алгебраических дробей к общему знаменателю

7.3. Арифметические действия с алгебраическими дробями

7.4. Рациональные выражения

7.6. Тождественное равенство рациональных выражений

8.1. Понятие степени с целым показателем

8.2. Свойства степени с целым показателем

8.3. Стандартный вид числа

8.4. Преобразование рациональных выражений

1. Делимость многочленов

2. Исторические сведения

Глава 3 Линейные уравнения

9.1. Уравнения первой степени с одним неизвестным 9.2. Линейные уравнения с одним неизвестным

9.3. Решение линейных уравнений с одним неизвестным

9.4. Решение задач с помощью линейных уравнен ий

10.1. Уравнения первой степени с двумя неизвестными

10.2. Системы двух уравнений первой степени с двумя неизвестными 10.3. Способ подстановки

10.4. Способ уравнивания коэффициентов

10.5. Равносильность уравнений и систем урав нений

10.6. Решение систем двух линейных уравнений с двумя неизвестными

10.7*. О количестве решений системы двух уравнений первой степени с двумя неизвестными

10.8*. Системы уравнений первой степени с тремя неизвестными

10.9. Решение задач при помощи систем уравнений первой степени

1. Линейные диофантовы уравнения

2. Метод Гаусса

3. Исторические сведения

Обучение решению текстовых задач

1.1. Задачи на части

1.2. Задачи на нахождение двух чисел по их сумме и разности

1.3. Задачи на дроби

1.4. Задачи на совместную работу

1.5. Задачи на движение по реке

1.6. Задачи на движение

1.7. Деление числа в данном отношении

1.8. Задачи на пропорции и проценты

2.1. Обратный ход

2.2. Переформулировка задачи

(неизвестных)

Задания на исследование

6.7. Куб суммы 6.8. Куб разности