

УДК 372.8:512 16+
ББК 74.262.21
П64

Серия «МГУ — школе» основана в 1999 году
Потапов М. К.
П64 Алгебра. Методические рекомендации. 8 класс : учеб. пособие для общеобразоват. организаций / М. К. Потапов, А. В. Шевкин. — М. : Просвещение, 2017. — 160 с. : ил. — (МГУ — школе.) — ISBN 978-5-09-042973-3.
Эта книга адресована учителям, работающим по учебнику серии «МГУ — школе» «Алгебра, 8» (авторы С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин). В ней дана характеристика курса алгебры 8 класса, приведены примерное тематическое планирование, методические рекомендации по всем темам и решения наиболее трудных задач.
|
|
УДК 372.8:512 |
|
|
ББК 74.262.21 |
|
ISBN 978-5-09-042973-3 |
© Издательство «Просвещение», 2014 |
|
|
© Художественное оформление. |
|
|
Издательство «Просвещение», 2014 |
|
|
Все права защищены |
О книге для учителя
Данная книга предназначена для учителей, работающих по учебнику «Алгебра, 8» серии «МГУ — школе» (авторы С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин). Этот учебник является частью учебного комплекта для 7—9 классов, рекомендованного Министерством образования и науки Российской Федерации, он продолжает учебник «Алгебра, 7» серии «МГУ — школе» тех же авторов.
В учебный комплект для 8 класса входят:
• Алгебра. 8 класс: учебник для общеобразоват. организаций / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. — М.: Просвещение, 2014— 2016;
• Алгебра. Дидактические материалы. 8 класс / М. К. Потапов, А. В. Шевкин. — М.: Просвещение, 2010—2016;
• Алгебра. Тематические тесты. 8 класс / П. В. Чулков, Т. С. Струков. — М.: Просвещение, 2010—2016;
• Алгебра. Методические рекомендации. 8 класс / М. К. Потапов, А. В. Шевкин. — М.: Просвещение, 2014—2016.
В данной книге рассмотрены концепция учебников алгебры серии «МГУ — школе» и структура учебника для 8 класса, приведено примерное тематическое планирование, даны методические рекомендации по изучению основных тем курса алгебры 8 класса и комментарии к решению некоторых трудных задач. Здесь же даны рекомендации по использованию дидактических материалов. Практически для всех пунктов учебника в книге имеются рубрики Решения и комментарии и Промежуточный контроль, к некоторым пунктам даётся рубрика Задания для повторения. В первой из них приведены условия многих задач из учебника и их решения или даны рекомендации, как найти решение с пояснениями, помогающими обучению школьников. Во второй рубрике даны номера самостоятельных и контрольных работ по дидактическим материалам, а также номера тестов из сборника тематических тестов. В последней рубрике приводятся номера упражнений из раздела «Задания для повторения» учебника, которые можно использовать при изучении данного пункта.
Следует обратить внимание на то, что в пособии для учителей (как и в учебнике) рассмотрены вопросы обучения алгебре в 8 классе как в общеобразовательных классах, так и в классах с углублённым изучением математики. При этом сначала обсуждаются вопросы для общеобразовательных классов, затем — для классов с углублённым изучением математики.
В комментариях для учителя не выделяются необязательные задания, так как в учебнике есть соответствующие обозначения. При этом не обсуждается время, отводимое на изучение пункта, — при разных вариантах планирования могут быть различия. Во многих пунктах книги для учителя методические комментарии даны в расчёте на возможно более глубокое изучение вопроса, поэтому при подготовке к уроку учитель должен отобрать главное, что будет изложено учащимся на уроке, решить, каким будет закрепление материала в классе и дома, когда и каким будет контроль изученного. При этом не надо стремиться донести до учащихся все подробности и тонкости изучаемого материала, если учащиеся существенно ограничены во времени изучения темы.
В серии «МГУ — школе» издательство «Просвещение» издаёт учебники «Математика» для 5 и 6 классов, «Алгебра» для 7, 8 и 9 классов, «Алгебра и начала математического анализа» для 10 и 11 классов (авторы С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин). Эти учебники полностью отвечают требованиям Федерального государственного образовательного стандарта. Они рекомендованы министерством в качестве учебников для любых типов общеобразовательных организаций. Их издание является составной частью программы «МГУ — школе», разработанной по инициативе ректора Московского государственного университета академика В. А. Садовничего и нацеленной на сохранение и развитие лучших традиций отечественного математического образования.
Авторами учебников разработана концепция многоуровневых учебников математики. Приведём основные положения этой концепции.
• Математика едина и может быть изложена в одном учебнике для работы по разным программам. Содержание учебника должно соответствовать научной точке зрения на изучаемые вопросы.
• Учебник должен сочетать в себе научность, стройность, экономность и логичность изложения материала с доступностью для учащихся его учебных текстов.
• Учебник не должен ограничиваться интересами среднего ученика, он должен удовлетворять интересам всех учащихся — от слабых до сильных для обеспечения их индивидуальной образовательной траектории.
• Учебник должен быть пригоден для организации дифференцированного обучения и обеспечивать любой желаемый уровень глубины изучения материала с учётом устойчивых познавательных интересов.
• Способ изложения материала в учебнике, организация учебных текстов и системы упражнений должны обеспечивать достижение разных целей обучения при работе по разным программам.
Структура учебников серии «МГУ — школе» и их методический аппарат отвечают положениям этой концепции.
Учебники серии «МГУ — школе» составляют три независимых цикла — для 5—6, 7—9 и 10—11 классов. Обучение в каждом цикле можно начинать независимо от того, по каким учебникам учились школьники в предыдущие годы, так как в первом учебнике каждого цикла проводится повторение и систематизация изученного за предыдущие годы.
Учебники для 5—6 классов ориентированы на развитие интереса к математике в процессе обучения, в них много материала, нацеленного на повышенный уровень математической подготовки.
Учебники для 7—9 классов предназначены как для общеобразовательных классов, так и для классов с углублённым изучением математики.
Учебники для 10—11 классов охватывают содержание курса алгебры и начал математического анализа для всех профилей старшей школы.
Авторы учебников уверены, что не следует упрощать обучение за счёт сокращения числа изучаемых вопросов и необходимо сохранить фундаментальность изложения теории в учебниках, оставляя за учителем право более или менее глубокого изложения теоретического материала на уроке в зависимости от уровня подготовки класса и целей обучения. В учебниках коротко, ясно и доступно, без долгих введений излагается суть вопроса. Мотивировать появление тех или иных понятий, определений при необходимости должен учитель, так как в разных классах это надо делать по-разному.
Учебники серии «МГУ — школе» имеют высокий научный и методический потенциал. Они отличаются расположением учебного материала в естественной логической последовательности, позволяющей излагать материал более глубоко, экономно и строго. В соответствии с требованиями ФГОС учебники не только нацелены на формирование навыков, но и учат действовать осознанно. Обычно обучение больше ориентировано на вопрос «как?», на действия по образцу, требует многократных повторений для поддержания навыков. В учебниках серии «МГУ — школе» уделяется достаточно внимания вопросу «почему?», имеющему большой развивающий потенциал для достижения личностных результатов освоения ООП основного общего образования. Учебники позволяют интенсифицировать процесс обучения, что в условиях уменьшения числа учебных часов особенно важно. Они полностью обеспечивают обучение тех школьников, которые хотят и могут обучаться основам наук.
Главный методический принцип, положенный в основу изложения теоретического материала, заключается в том, что ученик за один раз должен преодолевать не более одной трудности. Поэтому каждое новое понятие формируется, каждое новое умение отрабатывается сначала в чистом виде, затем трудности совмещаются, что позволяет учащимся контролировать процесс и результат учебной деятельности.
Аналогично выстроена и система упражнений. Сложность заданий в каждом пункте нарастает линейно: учитель определяет сам, на какой ступеньке лестницы сложности он может остановиться со своим классом или с конкретным учеником.
Одна из особенностей системы упражнений в учебниках заключается в том, что для каждого нового действия или приёма решения в учебниках имеется достаточное число упражнений, которые не перебиваются упражнениями на другие темы. Только тогда, когда новый материал освоен, можно подключать задания на соединение этого материала с ранее изученным, задания на повторение, не связанные с новым материалом, в итоге формируется умение контролировать процесс и результат учебной математической деятельности.
Важную роль в формировании первоначальных представлений о зарождении и развитии математики играют исторические сведения, завершающие каждую главу учебников. Этот материал способствует формированию представления о математической науке как сфере человеческой деятельности, об этапах её становления, о её значимости для развития цивилизации. Работа со старинными задачами — одна из сильных сторон учебников, она может много дать в воспитании уважения к традициям и истории, в развитии общеучебных умений.
Учебники серии «МГУ — школе» полностью обеспечивают обучение тех школьников, которые могут и хотят учиться основам наук. Они нацелены на повышенный уровень математической подготовки учащихся. Учебники можно использовать и в классах с обычной программой по математике, если не изучать сверхпрограммный материал и пропускать сложные задачи, а также выбирать уровень полноты изложения теоретического материала на уроке и уровень предъявления требований к знаниям и умениям учащихся в соответствии с поставленными целями обучения и возможностями конкретного класса, оставаясь при этом на уровне не ниже обязательных требований к математической подготовке учащихся. При таком подходе у сильных учащихся будет возможность с помощью учебника более глубоко разобраться в любом вопросе, чего они часто лишены, если учебник написан в расчёте на среднего ученика.
Основные идеи курса алгебры 7—9 классов
Алгебра играет в математике большую роль, теперь существует даже тенденция «алгебраизации» математики. Наряду с фундаментальной ролью внутри математики алгебра имеет и прикладное значение. Достаточно отметить её выходы в физику, кибернетику, математическую экономику. Поэтому изучение алгебры в школе является важной частью фундамента естественно-научного образования.
Для учебников алгебры возможны два способа распределения учебного материала по годам обучения. Первый — в каждом классе дают понемножку буквенных выражений, уравнений, неравенств, функций и т. п., так как детям якобы скучно долго изучать одни и те же вопросы. При использовании такого способа распределения учебного материала страдают научная аккуратность и строгость изложения, появляются порочные логические круги, недомолвки и несуразности, что в первую очередь сказывается на обучении и воспитании сильных учащихся.
Так происходит, например, когда действительные числа рассматриваются после изучения тождеств, функций и их графиков. Реализация этого первого подхода к построению курса алгебры в процессе обучения чаще ориентирована на формирование навыков.
Но есть и второй способ распределения учебного материала по годам обучения, основанный на его внутренней логике. Он диктует последовательность появления в учебнике тех или иных вопросов, позволяет в каждом учебном году ставить главную задачу. Этот второй способ, принятый в учебниках серии «МГУ — школе», позволяет излагать материал в строгой логической последовательности, без ненужных повторов и недомолвок, что делает изложение даже сложных вопросов ясным и доступным. Учебники серии «МГУ — школе» обеспечивают системную подготовку по предмету, требуют меньше, чем обычно, времени, позволяют ориентировать процесс обучения на формирование результатов обучения и освоения содержания курса, требуемых ФГОС. Как показывает опыт работы по ним, интерес к предмету возникает у учащихся не от многообразия и частого чередования тем, а от того, что учащиеся имеют возможность «вжиться» в каждый элемент содержания, постепенно углубляя его понимание. Изложение материала в учебниках связное — подряд излагаются большие темы, нет чересполосицы мелких вопросов, нарушающих логику изложения крупных тем. Это позволяет каждый раз сосредоточиваться на одном вопросе и поэтому изучить его более глубоко и в то же время более экономно. Отдельные темы программы изучаются один раз и в полном объёме, чтобы потом к ним не возвращаться в теоретической части учебника. Дальнейшее закрепление и повторение, а иногда и развитие изученного ведутся через линию упражнений.
Содержание курса алгебры диктует порядок изложения основного учебного материала: сначала должны изучаться чисто алгебраические вопросы (алгебраические выражения) как более доступные в этом возрасте, а уж затем функциональные вопросы. Поэтому материал 7 класса посвящён алгебраическим выражениям, а изучение функций начинается лишь в 8 классе.
Школьный курс алгебры 7—9 классов на самом деле лишь наполовину является алгеброй, другая его половина приходится на вопросы математического анализа, изучаемые традиционно в курсе алгебры (длина отрезка, действительные числа, функции). Желательно различать эти составляющие и излагать алгебраические вопросы алгебраическими методами. Например, к буквенным выражениям часто подходят как к функциям многих переменных (функциональный подход), хотя естественнее говорить о них как о множестве объектов, подчинённых явно выписанным законам (алгебраический подход). Поэтому при изложении темы «Алгебраические выражения» авторы считают необходимым оставаться на чисто алгебраической точке зрения. Одночлен определяется как произведение некоторых чисел и букв, многочлен — как сумма одночленов, алгебраическая дробь — как отношение многочлена к ненулевому многочлену. Приводятся правила, которым они подчинены. Например, в одночлене можно поменять местами множители, в многочлене можно привести подобные члены, алгебраическую дробь можно сократить на ненулевой многочлен и т. д. Эти свойства мотивируются по мере их введения, отмечается, что при замене букв числами в рассматриваемых буквенных равенствах последние превращаются в верные числовые равенства (за исключением случаев деления на нуль).
В учебниках для 7—9 классов достаточно внимания уделено решению уравнений, неравенств и их систем, построению графиков элементарных функций, решению текстовых задач, в том числе в общем виде, что необходимо для изучения курсов геометрии и физики.
Учебники алгебры серии «МГУ — школе» содержат весь материал программ как для классов с обычной программой по математике, так и для классов с углублённым изучением математики. Авторы считают принципиально важным иметь общий учебник для всех этих классов, что позволяет учащимся переходить без особых трудностей с одной программы обучения на другую, а учителям — проводить уровневую дифференциацию обучения как для разных классов, так и для отдельных учащихся. Такой учебник позволяет сильному учащемуся обычного класса разобраться в любом вопросе, изучить математику вплоть до уровня углублённого изучения. Учитель, работающий в классах с разной подготовкой, ведя обучение по одному учебнику в рамках одной авторской концепции, может лишь менять в зависимости от класса глубину погружения в теоретические и технические подробности.
В общеобразовательных классах дополнительные материалы и сложные задачи обычно не рассматриваются. Если же учитель имеет достаточно часов и его класс проявляет интерес к математике, то за счёт Дополнений к главам учебников, а также пунктов и отдельных задач со звёздочкой, необязательных в обычных общеобразовательных классах, можно расширить и углубить содержание изучаемого материала до объёма, предусмотренного программой для классов с углублённым изучением математики.
Об учебнике «Алгебра, 8» серии «МГУ — школе» Учебник «Алгебра, 8» содержит четыре главы:
1. Простейшие функции. Квадратные корни.
2. Квадратные и рациональные уравнения.
3. Линейная, квадратичная и дробно-линейная функции.
4. Системы рациональных уравнений.
К каждой главе имеются дополнения, содержащие исторические сведения и необязательный материал, не входящий в программу, в конце учебника имеются задания для повторения.
В главе 1 вводится определение функции по Лобачевскому и Дирихле, обсуждаются разные способы задания функций. В частности, обсуждается вопрос о задании функции графиком и о том, что каждая функция имеет в декартовой системе координат свой график. Знание графика функции позволяет ввести важное понятие непрерывности функции на промежутке следующим образом: функцию y = f(x) называют непрерывной на промежутке I, если её график на промежутке I — непрерывная линия, т. е. линия, полученная непрерывным движением пера без отрыва его острия от бумаги.
Конечно, для искушённых в математике читателей понятно, что на самом деле одно понятие — непрерывность функции заменено на другое — непрерывность линии, которое, в свою очередь, требует достаточно хорошей математической подготовки для точного определения. Но на уровне учащихся 8 класса не надо вдаваться в такие тонкости. Ведь учащемуся вполне очевидно, какая линия является непрерывной.
Авторам представляется, что такое интуитивное понятие непрерывности функции вполне посильно любому учащемуся и его вполне достаточно для дальнейших исследований функций.
Затем делается вывод о том, что функция y = f(x) непрерывна на промежутке, если она определена в каждой точке этого промежутка и малому изменению аргумента х соответствует малое изменение функции у.
При этом очень важно остаться на интуитивном представлении о том, что такое малое изменение. Не стоит пытаться оформить «малое изменение» в какие-то количественные отношения. Авторы считают, что такое определение непрерывности функции на промежутке вполне достаточно вплоть до 11 класса, так как не противоречит жизненному опыту учащихся.
Далее в этой главе изучаются простейшие функции: y = x, y = x2, y = 1 . x
Поскольку после введения иррациональных чисел координатная плоскость заполнена полностью, то это позволяет доказывать, что график функции y = x есть прямая — биссектриса первого и третьего координатных углов. Подчеркнём, что этот график — вся прямая, т. е. непрерывная линия. Изучение функций y = x2 и y = 1 проходит стандартx
ным образом — сначала выясняются свойства функции, потом строится её график. При этом обсуждается вопрос непрерывности функции на соответствующем промежутке.
Затем в этой главе вводятся квадратные корни из чисел. По определению, квадратным корнем из данного числа называют такое число, квадрат которого равен данному числу.
Отсюда следует, что: а) есть и притом только два квадратных корня из любого положительного числа; б) квадратный корень из нуля единственный, он равен нулю; в) нет квадратного корня из отрицательного числа, т. е. нет действительного числа, квадрат которого равен отрицательному числу.
Все эти выводы подкрепляются графически: в системе координат изображают график функции y = x2 и прямую у = b, и тогда очевидно, что при b 0 прямая пересекает параболу в двух точках, при b = 0 — в одной точке, а при b 0 не пересекает.
![]() Вводится понятие
арифметического корня: арифметическим квадратным корнем из данного
неотрицательного числа b называют такое неотрицательное число, квадрат
которого равен b; это число обозначают b .
Вводится понятие
арифметического корня: арифметическим квадратным корнем из данного
неотрицательного числа b называют такое неотрицательное число, квадрат
которого равен b; это число обозначают b .
Таким образом, арифметический квадратный корень из положительного числа b единственный, его обозначают
![]() b
. В то же время есть два корня из положительного чис-
b
. В то же время есть два корня из положительного чис-
![]()
![]()
![]() ла
b — один b , а другой (– b ). Следует подчеркнуть, что в этом месте часто
происходит путаница. Путают определение корня и его обозначение: ещё раз
отметим, что есть два корня из любого положительного числа, в то же время
обозначение b принято только для одного
корня из положительного числа b, а именно для положительного корня.
ла
b — один b , а другой (– b ). Следует подчеркнуть, что в этом месте часто
происходит путаница. Путают определение корня и его обозначение: ещё раз
отметим, что есть два корня из любого положительного числа, в то же время
обозначение b принято только для одного
корня из положительного числа b, а именно для положительного корня.
Так как в этой главе вводятся множества чисел, которые применяются при исследовании свойств функций, то в Дополнениях к главе содержится общее понятие множества и ряд общих свойств множеств.
В результате изучения главы 1 учащиеся должны усвоить понятия функции и её графика, хорошо представлять себе графики простейших функций y = x, y = x2, y = 1 , усвоить понятие квадратного корня и знать его x
свойства.
Первый параграф главы 2 посвящён решению квадратных уравнений. Здесь же рассматривается теорема и формулы Виета. Второй параграф посвящён решению рациональных уравнений. Здесь рассматриваются в основном рациональные уравнения, решение которых сводится к решению одного или нескольких линейных или квадратных уравнений. Особое внимание уделяется рациональным уравнениям, в которых неизвестное входит в знаменатель. Даётся правило решения рациональных уравнений и подчёркивается, что отклонение от этого правила может привести к потере корней исходного уравнения и к приобретению лишних корней. Рассматривается также метод решения рациональных уравнений при помощи замены неизвестных.
Много внимания уделяется решению текстовых задач при помощи квадратных и рациональных уравнений.
В Дополнениях к главе приводится способ нахождения целых корней многочлена с целыми коэффициентами, позволяющий решать некоторые алгебраические уравнения высоких степеней. Также здесь рассматриваются первоначальные понятия о комплексных числах, поскольку возникает вопрос о корнях квадратного уравнения, имеющего отрицательный дискриминант.
В результате изучения главы 2 учащиеся должны научиться решать квадратные и рациональные уравнения и применять их к решению текстовых задач.
В главе 3 изучаются линейная, квадратичная и дробно-линейная функции. В первом параграфе этой главы показывается, что график линейной функции у = kх + b есть прямая и он может быть получен из графика функции у = kх сдвигами вдоль осей Ох и Оу.
Обратим внимание на функцию у = |х| и её график. Эта функция позволяет ещё раз вернуться к сдвигам графика функции у = |х| вдоль осей Ох и Oy при построении графика функции у = |х – a| + b, что помогает подготовить учащихся к рассмотрению сдвигов параболы вдоль осей Ох и Оу.
Во втором параграфе рассматривается квадратичная функция у = ах2 + bх + с (a 0) и показывается, что её график может быть получен из графика функции у = ах2 переносами вдоль осей Ох и Оу.
В третьей
главе рассматривается дробно-линейная функция, показывается,
что график функции y = ![]() k +y0, k
0, может быть получен из графика функx x − 0 ции y = k
параллельными переносами вдоль осей Ох и Оу. x
k +y0, k
0, может быть получен из графика функx x − 0 ции y = k
параллельными переносами вдоль осей Ох и Оу. x
Таким образом, в этой главе сложный вопрос о построении графиков функций путём переноса вдоль осей Ох и Оу рассмотрен для четырёх различных видов функций. Это способствует хорошему усвоению данного метода.
В главе 3 изучаются не только графики линейной, квадратичной и дробно-линейной функций, но и их свойства. В качестве необязательного материала рассматриваются функции у = {x} и y = [x], графики функций, содержащих модули, и уравнения прямой и окружности.
В результате изучения главы 3 учащиеся должны знать свойства линейной, квадратичной и дробно-линейной функций и уметь строить их графики.
В главе 4 рассматриваются системы рациональных уравнений. В первом параграфе показывается, что основной способ решения систем рациональных уравнений — это способ подстановки. Продолжается решение текстовых задач при помощи систем рациональных уравнений.
Второй параграф посвящён графическому способу решения систем уравнений. Следует иметь в виду, что на самом деле графическим способом системы уравнений решаются очень редко. Обычно графический способ используется для того, чтобы выяснить, имеет ли система решения и сколько. Однако в этом параграфе примеры подобраны так, чтобы решения системы были почти очевидны из графиков. Хотя для того чтобы убедиться, что решения найдены точно, их надо подставить в каждое уравнение системы и проверить, получатся ли верные равенства. В этом параграфе рассмотрен графический метод исследования системы двух уравнений с двумя неизвестными.
В Дополнениях к главе рассматривается решение уравнений с несколькими неизвестными в целых числах.
В результате изучения главы 4 учащиеся должны научиться решать системы рациональных уравнений хотя бы методом подстановки и применять системы к решению текстовых задач.
При организации повторения в 8 классе необходимо обратить особое внимание на наиболее трудные для данного класса темы курса, постараться учесть индивидуальные пробелы учащихся.
При повторении теории необходимо выделять основные теоретические факты, изученные за год, давая иллюстрации их применения на наиболее характерных примерах. При этом можно использовать задачи из раздела «Задания для повторения».
Система упражнений в учебнике построена в соответствии с принципом «от простого к сложному». После каждого учебного текста идут вопросы по изученной теории, затем упражнения по новому материалу, которые не перебиваются заданиями на повторение. Упражнения нацелены на освоение изученного материала, формирование умений, предусмотренных стандартом. В курсе алгебры много заданий, выполняемых по образцу, показанному в учебнике или учителем, но есть и более сложные упражнения, связанные с доказательством и исследованием. Они выделены в особые рубрики —«Доказываем» и «Исследуем».
Многие задания из рубрики «Исследуем» связаны с поиском значений параметра, при которых выполнено некоторое условие. Тем самым у учащихся формируются важные умения исследовать ситуацию, описанную в задаче, в зависимости от значения этой величины. Термин «параметр» в учебнике сознательно не используется, но подразумевается, а учащиеся фактически решают задачи, которые выносятся на итоговый контроль ОГЭ и ГВЭ, встречаются в различных конкурсах и олимпиадах, в дополнительных испытаниях при поступлении в вузы.
Развитию способностей учащихся искать и использовать информацию, связанную с изучаемым материалом, будут способствовать задания рубрики «Ищем информацию». Часть этих заданий можно выполнить в виде небольших сообщений (докладов) для одноклассников, математических газет.
К данному курсу существует Электронная форма учебника (ЭФУ) — соответствующая по структуре, содержанию и художественному оформлению печатной форме учебника и включающая в себя интерактивные ссылки, расширяющие и дополняющие материал печатного учебника.
Функциональными особенностями ЭФУ являются:
— удобный и понятный интерфейс и навигация по
ЭФУ;
— работа в онлайн- и офлайн-режимах;
— тестовые задания к каждой теме, разделу учебника;
— возможность добавления материалов, созданных учителем;
— инструменты изменения размера шрифта, создания заметок и закладок.
Использование ЭФУ предоставляет учителю следующие возможности:
— организовать контроль и самоконтроль по результатам изучения темы;
— реализовать технологии мобильного, дистанционного или смешанного обучения;
— реализовать требования ФГОС по формированию информационно-образовательной среды системой электронных образовательных ресурсов и др.
Об использовании дидактических материалов и сборника тестов
Дидактические материалы содержат три раздела:
I. Материалы для подготовки к самостоятельным ра-ботам.
II. Самостоятельные работы.
III. Контрольные работы.
В разделе I разобраны решения заданий, похожих на задания из самостоятельной работы и готовящих учащихся к выполнению соответствующей работы. Практика показывает, что учащиеся не любят читать учебник, полагаясь на то, что поняли всё, что требуется, из рассказа учителя, а подготовка к самостоятельной работе по первой части дидактических материалов, разбор решений задач, похожих на задания из самостоятельной работы, дают шанс овладеть умением читать математическую литературу и повышают результативность своей работы. Кроме того, такая работа хотя бы для части учащихся уменьшит вредную тягу к поиску готовых домашних заданий.
Дидактические материалы используются для промежуточного контроля по теме и итоговой контрольной работы. Следует учесть, что провести все самостоятельные работы с выставлением отметки со всем классом, скорее всего, не удастся, да это и не требуется. Некоторые из работ можно использовать как домашние задания на отметку или как дополнительные задания для наиболее заинтересованных учащихся. Самостоятельные работы отнесены к соответствующим темам, но могут использоваться и при изучении других тем (например, для организации повторения).
В обязательную часть самостоятельных работ на отметку можно включать не все задания, ориентируясь на уровень подготовки класса и на отводимое для работы время. Необязательные задания можно оценивать дополнительной отметкой.
В обычном классе в обязательную часть контрольных работ можно не включать последнее задание.
Виды контроля полезно разнообразить. Для этого можно использовать сборник «Алгебра. Тематические тесты. 8 класс» авторов П. В. Чулкова, Т. С. Струкова. Тестовый контроль интересен небольшой затратой времени на его проведение и оперативностью получения информации о качестве знаний и умений школьников. Тесты удобно использовать для организации текущего повторения, для дополнительного опроса учащихся, желающих исправить отметки по изученной теме или в четверти.
О решении текстовых задач
В учебнике «Алгебра, 8» достаточно внимания уделено решению текстовых задач при помощи рациональных уравнений и их систем. Основной целью решения текстовых задач является развитие у учащихся умения моделировать с помощью уравнения или системы уравнений ситуацию, описанную в задаче, делать логически правильные выводы на основе анализа имеющихся данных задачи и использовать эти данные для её решения. Решая текстовые задачи, учащиеся учатся планировать свою работу, выполнять её согласно намеченному плану, проверять полученный ответ на соответствие условиям задачи. Эти умения являются надпредметными, действия, их формирующие, называют универсальными учебными действиями. Этим действиям уделяется особое внимание в новых стандартах по математике.
Авторы считают, что решение текстовых задач является наиболее эффективным способом развития логического мышления и речи учащихся, повышает результативность обучения математике и другим предметам.
Обратим внимание на то, что решение текстовых задач является важным видом учебной деятельности школьников. В 8 классе продолжается работа с текстовыми задачами, начатая в 5—7 классах. Учащиеся должны освоить новые для себя идеи, применяемые при решении текстовых задач. В каждом классе работа с текстовыми задачами, не связанными с квадратными и рациональными уравнениями, будет вестись в своём темпе, поэтому её нельзя заранее спланировать для всех классов и дать рекомендации по использованию задач по всем пунктам. Но такие рекомендации по работе с задачами разных видов даны в конце данной книги. Предполагается, что учитель сам будет планировать момент включения работы с текстовыми задачами в учебный процесс по мере освоения учащимися текущего материала и с учётом их успехов.
Здесь можно дать только один совет, которому полезно следовать. Работа с текстовыми задачами на повторение не должна вклиниваться в изучение нового материала до тех пор, пока основные умения по этому материалу не сформированы. Задачи должны разнообразить формы учебной деятельности, делать обучение математике для учащихся более живым и интересным.
О работе в классах с углублённым изучением математики
В учебнике «Алгебра, 8» серии «МГУ — школе» материал, предназначенный только для классов с углублённым изучением математики, специально выделен. Это доказательства некоторых теорем, дополнительные вопросы, изложенные в пунктах, отмеченных звёздочками, и в Дополнениях к главам учебника, а также более сложные задачи. Весь этот материал не является обязательным в обычном классе, и его пропуск не нарушает цельности курса.
В классе с углублённым изучением математики используются и дидактические материалы. При этом все задания считаются обязательными только для классов с углублённым изучением математики. Кроме того, в дидактических материалах имеются самостоятельные работы, отмеченные звёздочками. Они предназначены только для классов с углублённым изучением математики. В них, в отличие от учебника, используется термин «параметр».
В классе с углублённым изучением математики надо больше внимания уделить решению задач различных олимпиад, конкурсов и турниров. В данной книге к ряду пунктов сделаны специальные замечания о работе с такими задачами.
Примерное тематическое планирование работы
Из двух вариантов тематического планирования вариант I (3 ч в неделю, всего 102 ч) предназначен для классов, работающих по обычной программе, а вариант II (4 ч в неделю, всего 136 ч) — для классов с углублённым изучением математики. Справа от параграфа или пункта указано число часов, отведённых на его изучение для каждого варианта планирования.
|
Глава 1. Простейшие функции. |
I |
II |
|
Квадратные корни |
26 |
32 |
|
§ 1. Функции и графики |
10 |
10 |
|
1.1. Числовые неравенства |
2 |
2 |
|
1.2. Координатная ось. Модуль числа |
2 |
2 |
|
1.3. Множества чисел |
2 |
2 |
|
1.4. Декартова система координат на плоскости |
1 |
1 |
|
1.5. Понятие функции |
2 |
2 |
|
1.6. Понятие графика функции |
1 |
1 |
|
§ 2. Функции y
= x, y = x2,
y = |
7 |
9 |
|
2.1. Функция y = x и её график 2.2. Функция y = x2 2.3. График функции y = x2 |
2 1 1 |
2 1 2 |
|
2.4. Функция y = 1 x |
1 |
1 |
|
2.5. График функции y = 1 x |
1 |
2 |
|
Контрольная работа № 1 |
1 |
1 |
|
§ 3. Квадратные корни |
9 |
11 |
|
3.1. Понятие квадратного корня |
2 |
2 |
|
3.2. Арифметический квадратный корень 3.3. Свойства арифметических квадратных |
2 |
2 |
|
корней |
3 |
3 |
|
3.4. Квадратный корень из натурального числа 3.5. Приближённое вычисление квадратных |
1 |
1 |
|
корней |
— |
2 |
|
Контрольная работа № 2 |
1 |
1 |
|
Дополнения к главе 1 |
— |
2 |
|
1. Множества |
— |
2 |
|
2. Исторические сведения Глава 2. Квадратные и рациональные |
— |
— |
|
уравнения |
29 |
38 |
|
§ 4. Квадратные уравнения |
16 |
16 |
|
4.1. Квадратный трёхчлен |
2 |
2 |
|
4.2. Понятие квадратного уравнения |
2 |
2 |
|
4.3. Неполное квадратное уравнение 4.4. Решение квадратного уравнения |
2 |
2 |
|
общего вида |
3 |
3 |
|
4.5. Приведённое квадратное уравнение |
2 |
2 |
|
4.6. Теорема Виета 4.7. Применение квадратных уравнений |
2 |
2 |
|
к решению задач |
2 |
2 |
|
Контрольная работа № 3 |
1 |
1 |
|
§ 5. Рациональные уравнения |
13 |
18 |
|
5.1. Понятие рационального уравнения |
1 |
1 |
|
5.2. Биквадратное уравнение |
2 |
2 |
|
5.3. Распадающееся уравнение 5.4. Уравнение, одна часть которого |
2 |
2 |
|
алгебраическая дробь, а другая — нуль |
3 |
3 |
|
5.5. Решение рациональных уравнений 5.6. Решение задач при помощи |
2 |
2 |
|
рациональных уравнений 5.7. Решение рациональных уравнений |
2 |
3 |
|
при помощи замены неизвестного |
— |
2 |
|
5.8. Уравнение-следствие |
— |
2 |
|
Контрольная работа № 4 |
1 |
1 |
|
Дополнения к главе 2 1. Разложение многочленов на множители |
— |
4 |
|
и решение уравнений |
— |
2 |
|
2. Комплексные числа |
— |
2 |
|
3. Исторические сведения Глава 3. Линейная, квадратичная |
— |
— |
|
и дробно-линейная функции |
22 |
31 |
|
§ 6. Линейная функция |
9 |
11 |
|
6.1. Прямая пропорциональность |
2 |
2 |
|
6.2. График функции y = kx |
2 |
3 |
|
6.3. Линейная функция и её график |
3 |
3 |
|
6.4. Равномерное движение |
1 |
1 |
|
6.5. Функция y = ЅxЅи её график |
1 |
1 |
|
6.6. Функции y = [x] и y = {x} |
— |
1 |
|
§ 7. Квадратичная функция |
8 |
9 |
|
7.1. Функция y = ax2 (a 0) 7.2. Функция y = ax2 (a 0) 7.3. График функции y = a(x – x0)2 + y0 |
2 2 2 |
2 2 2 |
|
7.4. Квадратичная функция и её график |
2 |
3 |
|
§ 8. Дробно-линейная функция |
5 |
7 |
|
8.1. Обратная пропорциональность |
1 |
1 |
8.2. Функция y = k (k 0) 1 1
x
8.3. Функция y = k (k 0) 1 2
x
8.4. Дробно-линейная функция и её график 1 2
Контрольная работа № 5 1 1
Дополнения к главе 3 — 4
1. Построение графиков функций,
содержащих модули — 2
2. Уравнение прямой, уравнение
окружности — 2
3. Исторические сведения — —
Глава 4. Системы рациональных уравнений 19 28
§ 9. Системы рациональных уравнений 10 12
9.1. Понятие системы рациональных уравнений 2 2
9.2. Решение систем рациональных уравнений
способом подстановки 2 3
9.3. Решение систем рациональных уравнений
другими способами 2 2
9.4. Решение задач при помощи систем
рациональных уравнений 4 5
§ 10. Графический способ решения
систем уравнений 9 13
10.1. Графический способ решения систем
двух уравнений первой степени с двумя
неизвестными 2 3
10.2. Графический способ исследования
системы двух уравнений первой степени
с двумя неизвестными 2 3
10.3. Решение систем уравнений первой
и второй степени графическим способом 2 3
10.4. Примеры решения уравнений
графическим способом 2 3
Контрольная работа № 6 1 1
Дополнения к главе 4 — 3
1. Решение уравнений в целых числах — 3
2. Исторические сведения — —
Повторение 6 7
Повторение курса алгебры 8 класса 5 6
Итоговая контрольная работа № 7 1 1
Первая глава начинается с повторения и расширения сведений о числовых неравенствах, числовых множествах, координатной оси и системе координат на плоскости. Далее вводятся понятия функции и её графика, рассматриваются свойства простейших функций y = x, y = x2,
y = 1 . Затем вводится понятие квадратного корня и изуx
чаются его свойства.
Цель изучения главы 1 — усвоить понятие функции и её графика, научиться строить графики простейших функций y = x, y = x2, y = 1 , усвоить понятие квадратноx
го корня, уметь использовать свойства квадратных корней.
Основная цель первого параграфа — повторить свойства числовых неравенств, ввести обозначения для числовых промежутков, напомнить о том, что между точками координатной оси и всеми действительными числами, а также между точками координатной плоскости и упорядоченными парами чисел имеется взаимно однозначное соответствие. Иными словами, надо, чтобы учащиеся осознали, что координатная ось полностью заполнена числами, что она не «дырявая». Это вскоре будет использовано при построении графиков функций, ведь необходимо, чтобы их можно было строить по всем точкам, а не только по «рациональным» точкам (т. е. имеющим рациональные координаты).
Затем вводится понятие функции по Лобачевскому и Дирихле, говорится, что функция может быть задана или формулой, или таблицей, или графиком. Вводятся понятия графика функции и непрерывности функции на промежутке.
В данном пункте формулируются пять правил, которым подчинены действительные числа. По сути, это аксиомы действительного числа, но такая терминология в учебнике не используется. Далее доказываются семь свойств — следствий этих пяти правил. Сообщается, что для нестрогих неравенств справедливы правила 3—5 и свойства 1—7.
Желательно, чтобы все учащиеся усвоили правила и свойства действительных чисел, поняли различие между правилами и свойствами — свойства выводятся из правил. Сильным учащимся и всем учащимся класса с углублённым изучением математики полезно освоить приёмы доказательства свойств, так как они часто используются при решении задач на доказательство.
Задания для повторения. При изучении данного пункта можно использовать задания 626, 627.
14. а) Докажите, что если а b и с d, то а – d b – с.
Доказательство. К обеим частям неравенства с d прибавим число (–c – d) и по правилу 4 получим верное числовое неравенство – d – c.
Сложив неравенства а b и – d – c, на основании свойства 1 получим верное числовое неравенство: а – d b – с,
что и требовалось доказать.
15. а) Докажите для положительных чисел а, b, с и
![]() d,
что если а b и с d, то a b . d c
d,
что если а b и с d, то a b . d c
Доказательство. Для положительных чисел с и d, таких, что с d, получим на основании свойства 5 верное
![]() неравенство
1 1 .
неравенство
1 1 .
d c
![]() Для
положительных чисел а, b, 1 и 1 , таких,
что d c
Для
положительных чисел а, b, 1 и 1 , таких,
что d c
![]() а
b и 1 1 , на основании свойства 2 получим верное d c
а
b и 1 1 , на основании свойства 2 получим верное d c
неравенство a b , что и требовалось доказать.
d c
16. а) Докажите, что если а b 0, то а2 b2.
Решение. Для отрицательных чисел а и b из неравенства а b на основании свойства 4 следует неравенство для положительных чисел – а и – b: – а – b. А для положительных чисел – а и – b из неравенства –а – b следует на основании свойства 6, что (–а)2 (–b)2, или, что то же самое, а2 b2, что и требовалось доказать.
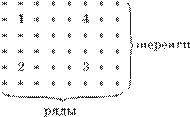 18. Солдат
построили не по росту, но с чётким разделением на ряды и шеренги. В каждом ряду
выбрали самого высокого, а из всех высоких — самого низкого. В каждой шеренге
выбрали самого низкого, а из всех низких — самого высокого. Кто же выше ростом:
самый низкий из высоких или самый высокий из низких?
18. Солдат
построили не по росту, но с чётким разделением на ряды и шеренги. В каждом ряду
выбрали самого высокого, а из всех высоких — самого низкого. В каждой шеренге
выбрали самого низкого, а из всех низких — самого высокого. Кто же выше ростом:
самый низкий из высоких или самый высокий из низких?
Указание. Рассмотрите случаи, когда два выбранных 6 Рис. 1 солдата стоят: 1) в одном ря-
ду; 2) в одной шеренге; 3) в разных рядах и шеренгах.
Решение. 1) Пусть два выбранных в соответствии с условиями задачи солдата стоят в одном ряду: солдат 1 — самый низкий из высоких, солдат 2 — самый высокий из низких (рис. 1). Так как в каждом ряду выбирали самого высокого (он оказался самым низким из высоких), то в этом ряду солдат 1 выше всех, значит, выше солдата 2. Итак, в этом случае самый низкий из высоких выше самого высокого из низких.
2) Пусть два выбранных солдата стоят в одной шеренге: солдат 2 — самый низкий из высоких, солдат 3 — самый высокий из низких (рис. 1). Так как в каждой шеренге выбирали самого низкого (он оказался самым высоким из низких), то в этой шеренге солдат 3 ниже всех, значит, ниже солдата 2. И в этом случае самый низкий из высоких выше самого высокого из низких.
3) Пусть теперь два выбранных солдата стоят в разных рядах и разных шеренгах: солдат 1 — самый низкий из высоких, а солдат 3 — самый высокий из низких. Так как в шеренге выбирали самого низкого, то солдат 3 ниже солдата 2. Но в каждом ряду выбирали самого высокого, следовательно, солдат 2 ниже солдата 1. Итак, солдат 3 ниже солдата 2, а солдат 2 ниже солдата 1, следовательно, солдат 3 ниже солдата 1. И в этом случае самый низкий из высоких выше самого высокого из низких.
Случай, когда солдат 3 оказался самым низким из высоких, а солдат 1 — самым высоким из низких, рассматривается аналогично, только сравнивать рост солдат 1 и 3 надо с ростом солдата 4.
![]() Здесь полезно
проверить, смогут ли учащиеся определить, какое свойство неравенств
использовано в решении задачи для случая 3 (свойство транзитивности
неравенств). 19. Даны две дроби 95 и 99 . Найдите:
Здесь полезно
проверить, смогут ли учащиеся определить, какое свойство неравенств
использовано в решении задачи для случая 3 (свойство транзитивности
неравенств). 19. Даны две дроби 95 и 99 . Найдите:
111 112
а) все несократимые дроби со знаменателем 50, заключённые между ними;
б) все несократимые дроби с числителем 50, заключён-
ные между ними;
в) все несократимые дроби с наименьшим натураль-
ным знаменателем, заключённые между ними.
Решение. а) Записав данные дроби в виде
десятичных, убедимся, что имеется только две десятичные дроби (0,86 и 0,88) с
двумя цифрами после запятой, заключённые между данными дробями и имеющие чётную
цифру в разряде сотых. Эти дроби запишем в виде обыкновенных и, сократив их на
2, получим ![]() и
и ![]() . Из полученных дро-
. Из полученных дро-
бей только одна несократимая: ![]() ;
;
б) рассмотрим несколько последовательных дробей с числителем 50, близких к данным дробям, и сравним их с данными дробями. Так как
![]()
![]()
![]()
![]()
![]()
![]() ,
,
то имеется две дроби с числителем 50,
заключённые между данными дробями. Это ![]() и
и ![]() , из них
только одна несократимая:
, из них
только одна несократимая: ![]() ;
;
в) искомые дроби больше ![]() и меньше 1, их надо
искать, начиная с дробей со знаменателем 3. Но самые большие из несократимых
дробей из этого промежутка со знаменателями 3, 4, 5, 6, т. е. дроби
и меньше 1, их надо
искать, начиная с дробей со знаменателем 3. Но самые большие из несократимых
дробей из этого промежутка со знаменателями 3, 4, 5, 6, т. е. дроби
2
![]() 3 4
3 4
![]() ,
, и ,
,
, и ,
3 4 5
меньше, чем ![]() . Так как
. Так как
![]()
![]()
![]() 99
99 ![]() ,
,
то дробь ![]() заключена
между
заключена
между ![]() и
и ![]() . Других дробей со
знаменателем 7 (и с меньшими знаменателями) между дробями
. Других дробей со
знаменателем 7 (и с меньшими знаменателями) между дробями ![]() и
и ![]() нет.
Следовательно, искомая дробь одна, это
нет.
Следовательно, искомая дробь одна, это ![]() .
.
В данном пункте вводятся понятия координатной оси, координаты точки, модуля действительного числа, рассматриваются примеры решения уравнений с модулями, сводящиеся к линейным уравнениям, разбираются свойства модуля числа. Здесь важно подчеркнуть, что между множеством точек координатной оси и множеством действительных чисел установлено взаимно однозначное соответствие и с введением иррациональных чисел координатная ось перестала быть «дырявой».
Умение определять координату точки, строить точку по её координате является обязательным для всех учащихся.
Задания для повторения. При изучении данного пункта можно использовать задания 623, 624, 629, 631.
24. а) Найдите значение a, при котором уравнение
|2x – 4| = |x – a|
имеет единственный корень.
Решение. Модули двух чисел равны, если эти числа равны или противоположны, поэтому любой корень данного уравнения является либо корнем уравнения 2x – 4 = = x – a, либо корнем уравнения 2x – 4 = – x + a.
При каждом значении a уравнение 2x – 4 = x – a имеет единственный корень x1 = 4 – a, а уравнение
![]() 2x
– 4 = – x + a имеет единственный корень x2 =
2x
– 4 = – x + a имеет единственный корень x2 = ![]() a .
a .
Данное уравнение имеет единственный корень при условии x1 = x2, т. е. при условии 4 – a = 4 3+a . Этому равенству удовлетворяет единственное значение a = 2. Следовательно, условию задачи удовлетворяет единственное значение a = 2.
![]() Замечание. Отметим, что, решая уравнения с
модулем, обычно «распространяют» понятие уравнения, данное для линейных
уравнений, на новую ситуацию. Однако будет лучше, если учитель заметит, что это
уравнения нового типа, отличающиеся от линейных. И решить, например, уравнение
|x| = 7 — это значит найти все такие значения x,
для каждого из которых числовое равенство |x| = 7 верно.
Эти значения x (x1 = 7 и x2
= – 7) и называют корнями рассматриваемого уравнения.
Замечание. Отметим, что, решая уравнения с
модулем, обычно «распространяют» понятие уравнения, данное для линейных
уравнений, на новую ситуацию. Однако будет лучше, если учитель заметит, что это
уравнения нового типа, отличающиеся от линейных. И решить, например, уравнение
|x| = 7 — это значит найти все такие значения x,
для каждого из которых числовое равенство |x| = 7 верно.
Эти значения x (x1 = 7 и x2
= – 7) и называют корнями рассматриваемого уравнения.
25. Докажите свойства 1—6 модуля числа.
1. |–a| = |a|; 2. a |a|;
![]() 3. |a b| =
|a| |b|; 4.
a = a , b 0; b b
3. |a b| =
|a| |b|; 4.
a = a , b 0; b b
5. |a + b| |a| + |b|; 6. |a – b| |a| + |b|.
Свойства 1—2 доказываются рассмотрением случаев: 1) a = 0; 2) a 0; 3) a 0.
Доказательство свойства 3. Если среди чисел a и b есть хотя бы один нуль, то равенство справедливо.
Если среди чисел a и b нет ни одного нуля, то эти числа или одинаковых знаков (оба положительные или оба отрицательные), или разных знаков.
1) Если a 0 и b 0, то a b 0 и |a b| = a b = = |a| |b|, что и требовалось доказать.
2) Если a 0 и b 0, то a b 0 и
|a b| = a b = (–a) (–b) = |–a| |–b| = |a| |b|,
что и требовалось доказать.
3) Если a и b разных знаков — для определённости a 0 и b 0, то a b 0 и |a b| = – (a b) = a (–b) = = |a| |–b| = |a| |b|, что и требовалось доказать.
Аналогичными рассуждениями (с учётом условия b 0) доказывается свойство 4.
Доказательство свойства 5. Если а + b 0, то
|a + b| = a + b |a| + |b| (по свойству 2).
Если же а + b 0, то
|a + b| = – (a + b) = (–a) + (–b) |–a| + |–b| = |a| + |b|
(по свойствам 1 и 2).
Итак, для любых действительных чисел а и b
|a + b| |a| + |b|,
что и требовалось доказать.
Свойство 6 следует из свойства 5. Действительно,
|a – b| = |a + (–b)| |a| + |–b| = |a| + |b|.
![]() Замечание. Доказательство свойства 5 лучше
провести учителю, остальные свойства могут доказать учащиеся при помощи учителя
в составлении плана доказательства (какие случаи надо рассмотреть).
Замечание. Доказательство свойства 5 лучше
провести учителю, остальные свойства могут доказать учащиеся при помощи учителя
в составлении плана доказательства (какие случаи надо рассмотреть).
27. а) Докажите, что расстояние между точками A(x1) и B(x2) вычисляется по формуле AB = |x1 – x2|.
б) Докажите, что координата точки С(x) — середины
отрезка AB, где A(x1) и B(x2), вычисляется по формуле
x1 +x2 x = .
2
Решение. а) Для точек A(x1) и B(x2) возможны три случая: x1 x2, x1 x2 и x1 = x2.
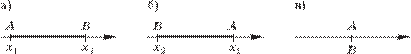
6 Рис. 2
В первом случае AB = x2 – x1 = |x1 – x2| (рис. 2, а).
Во втором случае AB = x1 – x2 = |x1 – x2| (рис. 2, б). В третьем случае AB = 0 = |x1 – x2| (рис. 2, в).
б) Для концов отрезка AB возможны два случая: x1 x2 и x1 x2.
Если x1 x2, то x1 x x2 (рис. 3) и верно равенство
AC = CB. Тогда верно равенство x – x1 = x2 – x, из которого
x1 +x2 . получим x =
2
Если x1 x2, то доказательство проводится аналогично.
28. Докажите, что если точка С(x) принадлежит отрезку AB, где A(x1) и B(x2), и делит этот отрезок в отношении AC : СB = m : n, то координата точки С вычис-
![]() nx1 +mx2 . ляется по формуле x =
nx1 +mx2 . ляется по формуле x =
m n +
Решение. Для концов отрезка AB возможны два случая: x1 x2 и x1 x2.
В первом случае (рис. 4) из равенства AC : СB = m : n
![]() следует, что AC = CB , или x x− 1 = x2 −x . Решив это
уравm n m n
следует, что AC = CB , или x x− 1 = x2 −x . Решив это
уравm n m n
![]() nx1
+mx2 , что и
требонение относительно x, получим x =
nx1
+mx2 , что и
требонение относительно x, получим x =
m n +
валось доказать.
Если x1 > x2, то доказательство проводится аналогично.
![]()
6 Рис. 3 6 Рис. 4
В данном пункте даны определения некоторых числовых множеств: отрезка, интервала, полуинтервала — и приведены примеры изображения таких множеств на координатной оси. В 8 классе при изучении функций эти обозначения будут широко использоваться, поэтому учащимся необходимо их усвоить. Эти обозначения будут применяться также в 9 классе при изучении неравенств.
Отметим, что в последнее время категоричность требования записывать ответ с помощью числовых промежутков снижается. В ответах допускается задание множества чисел неравенством (двойным неравенством). Это стоит учесть при оценивании работ учащихся и не снижать отметки, если ученик, например, вместо интервала (0; + ) напишет неравенство x 0.
Кроме отрезков, интервалов и полуинтервалов множества чисел часто обозначают латинскими буквами A, B, C, … . Некоторые множества имеют специальные обозначения: N, Z, Q, R, R+.
Дополнительная информация по теме имеется в Дополнениях к главе 1. Полезно показать учащимся обозначения для объединения и пересечения множеств, решить несколько задач из Дополнений.
Задания для повторения. При изучении данного пункта можно использовать задания 619—622, 625, 628, 631—633.
35. Принадлежит ли число – 2 множеству чисел (сделайте запись с помощью знаков и ):
а) [–3; 0]; б) (–2; 3); в) (– ; – 2]; г) (–2; + );
д) N; е) Z; ж) Q; з) R?
Ответ. а) – 2 [–3; 0]; б) – 2 (–2; 3); в) – 2 (– ; –2];
г) – 2 (–2; + ); д) – 2 N; е) – 2 Z; ж) – 2 Q;
з) – 2 R.
42. а) Изобразите на координатной оси числовые промежутки [–2; 3] и [0; 2]. Имеют ли они общие точки? Если да, то запишите общую часть (пересечение) этих множеств.
![]() Решение.
Промежутки имеют общие точки, которые составляют отрезок [0; 2] (рис.
5).
Решение.
Промежутки имеют общие точки, которые составляют отрезок [0; 2] (рис.
5).
6 Рис. 5 Промежуточный контроль. С–1.
В данном пункте вводятся понятия системы координат, оси абсцисс, оси ординат, абсциссы и ординаты точки.
Здесь важно подчеркнуть, что между множеством точек плоскости и множеством упорядоченных пар действительных чисел установлено взаимно однозначное соответствие.
Умение определять координаты точки, строить точку по её координатам является обязательным для всех учащихся.
 Задания для
повторения. При изучении данного пункта можно использовать задания 742—744.
Задания для
повторения. При изучении данного пункта можно использовать задания 742—744.
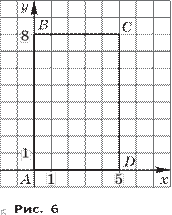
50. а) Постройте прямоугольник ABCD по координатам его вершин: А (0; 0), B (0; 8), С (5; 8), D (5; 0). Найдите периметр и площадь прямоугольника ABCD.
 б) Постройте квадрат ABCD
по координатам трёх его вершин: А (–2; – 1), В (–2;
2), С (1; 2). Найдите координаты вершины D, периметр
и площадь квадрата ABCD.
б) Постройте квадрат ABCD
по координатам трёх его вершин: А (–2; – 1), В (–2;
2), С (1; 2). Найдите координаты вершины D, периметр
и площадь квадрата ABCD.
Решение. а) Прямоугольник ABCD изображён на рисунке 6. Он имеет периметр 2 (5 + 8) = 26 и площадь
5 8 = 40.
б) Квадрат ABCD изображён на рисунке 7. Он имеет периметр
4 3 = 12 и площадь 3 3 = 9, 6 Рис. 7 точка D (1; – 1).
В данном пункте на примерах объясняется понятие функции. Затем даётся определение функции по Лобачевскому и Дирихле, объясняется, что такое аргумент, функция, область определения функции. Приводятся примеры функций, заданных формулой и таблицей, упоминается, что функцию можно задать графиком (это материал следующего пункта). Здесь же вводится обозначение функции y = f(x), определяется понятие значения функции в данной точке и множества значений функции.
Понятие функции является центральным понятием курса алгебры (8—9 классы), алгебры и начал математического анализа (10—11 классы), поэтому оно должно быть усвоено каждым учащимся.
61. Функция задана формулой у = 2х – 5. При каком значении аргумента х значение функции будет равно:
5; – 3; 0; – 5?
Решение. Для нахождения первого значения аргумента х надо решить уравнение 5 = 2х – 5, получится х = 5. Остальные значения аргумента 1; 2,5; 0 находятся аналогично.
62. Какой формулой может быть задана функция, если:
а) значениям х, равным 0, 1, 2, 3, 4, 5, соответствуют
значения у, равные 0, 5, 10, 15, 20, 25;
б) значениям х, равным 1, 2, 3, 4, 5, 6, соответствуют
значения у, равные 2,5, 5, 7,5, 10, 12,5, 15?
Решение. а) Все пары значений x и y удовлетворяют равенству y = 5x, следовательно, функцию можно задать формулой y = 5x;
б) все пары значений x и y удовлетворяют равенству y = 2,5x, следовательно, функцию можно задать формулой y = 2,5x.
В данном пункте вводится понятие графика функции, объясняется, что такое приращение аргумента и приращение функции, какую функцию называют непрерывной на промежутке. Приводится пример функции, имеющей разрыв.
Определение непрерывной функции через непрерывность её графика не требует от учащихся каких-либо особых усилий для его понимания.
Рассматривая непрерывный график, легко убедить учащихся в том, что приведённое определение равносильно и такому определению: функция непрерывна на промежутке, если она определена в каждой точке этого промежутка и малому изменению аргумента x соответствует малое изменение функции. При этом не стоит пытаться как-либо пояснить это аналитически, надо остановиться на интуитивном представлении о том, что такое малое изменение.
На непрерывность функции на промежутке будет обращаться внимание при изучении свойств функций, с опорой на это понятие будет доказываться существование квадратного корня из положительного числа, поэтому каждый ученик должен владеть этим понятием. Введение понятия непрерывности функции на промежутке опирается на интуитивно ясное представление о непрерывной линии. Строгое определение непрерывности функции будет дано только в 11 классе.
68. В 6 ч утра из посёлка на озеро, находящееся в 6 км от посёлка, отправились рыбачить отец и сын. Туда шли пешком, а обратно ехали на попутной машине. На
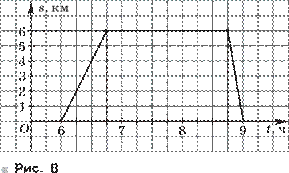
рисунке 8 изображён график их движения. Определите с помощью графика:
а) в какое время рыболовы пришли к озеру;
б) как долго они могли удить рыбу;
в) сколько времени занял у них обратный путь;
г) с какой скоростью они шли пешком;
д) с какой скоростью ехала машина.
Решение. а) Рыболовы пришли к озеру в 6 ч 45 мин;
б) они могли удить рыбу от 6 ч 45 мин до 8 ч 45 мин,
т. е. 2 ч (график не позволяет определить точное время рыбалки, он показывает, что в течение 2 ч рыбаки находились в 6 км от посёлка);
в) обратный путь занял у них 15 мин;
г) они
шли пешком со скоростью 6 : = ![]() 8 (км/ч);
8 (км/ч);
д) машина
ехала со скоростью 6 : = ![]() 24 (км/ч).
24 (км/ч).
![]() Замечание. В рассмотренном задании полезно
обсудить вопрос: является ли система координат, изображённая на рисунке 8, прямоугольной декартовой? Она прямоугольная, но
не декартова, так как её оси взаимно перпендикулярны, но единичные отрезки на
осях различны (они даже выражают различные величины) и нуль на горизонтальной
оси сдвинут влево, а у декартовой системы координат начала отсчёта на осях
должны совпадать.
Замечание. В рассмотренном задании полезно
обсудить вопрос: является ли система координат, изображённая на рисунке 8, прямоугольной декартовой? Она прямоугольная, но
не декартова, так как её оси взаимно перпендикулярны, но единичные отрезки на
осях различны (они даже выражают различные величины) и нуль на горизонтальной
оси сдвинут влево, а у декартовой системы координат начала отсчёта на осях
должны совпадать.
Промежуточный контроль. Т–1.
§ 2.
Функции y = x, y = x2, y = ![]() 1x
1x
Основная цель второго параграфа — изучить три функции разных типов (их графики — прямая, парабола и гипербола), дать учащимся примеры свойств функций, построения их графиков.
В данном пункте рассмотрена биссектриса I и III координатных углов и показано, что если точка A(x; y) принадлежит построенной прямой, то её координаты удовлетворяют уравнению y = x. Показано, что верно и обратное утверждение: если координаты точки удовлетворяют уравнению y = x, то эта точка принадлежит биссектрисе I и III координатных углов.
Каждый ученик должен знать, что график функции y = x — прямая, и уметь его строить.
Задания для повторения. При изучении данного пункта можно использовать задание 745.
70. На биссектрисе II и IV координатных углов отметили точку А(х; у) (рис. 9). Докажите, что для координат этой точки в каждом случае выполняется равенство у = – х.
Доказательство. На рисунке 9, а на данной прямой отмечена точка A, имеющая отрицательную абсциссу x. Пусть прямая, проходящая через точку A и параллельная оси Oy (показана на рисунке пунктиром), пересекает ось Ox в точке A1. Тогда OA1 = – х, AA1 = y. Так как OA — биссектриса II координатного угла, то треугольник OA1A равнобедренный и AA1 = OA1, поэтому верно равенство у = – х.
На рисунке 9, б на данной прямой отмечена точка A, имеющая положительную абсциссу x. Пусть прямая, проходящая через точку A и параллельная оси Oy (показана на рисунке пунктиром), пересекает ось Ox в точке A1. Тогда OA1 = х, AA1 = – y. Так как OA — биссектриса IV координатного угла, то треугольник OA1A равнобедренный и AA1 = OA1, поэтому верно равенство – у = х, откуда следует, что у = – х.
Если x = 0, то y = 0, так как прямая проходит через точку (0; 0). В этом случае равенство у = – х верно, так как 0 = – 0.
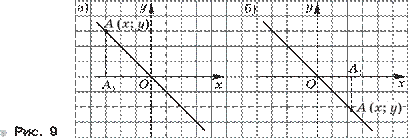
Итак, если точка принадлежит биссектрисе II и IV координатных углов, то её координаты удовлетворяют уравнению у = – х, что и требовалось доказать.
81. Пусть для координат точки А(х; у) выполняется равенство у = – х. Докажите, что эта точка лежит на биссектрисе II и IV координатных углов.
Доказательство. Рассмотрим сначала точку А(х; у), такую, что x 0, тогда y 0, так как у = – х. Обращаясь к
рисунку 9, а, получим, что
OA1 = – x = y = AA1,
т. е. что прямоугольный треугольник OA1A равнобедренный, следовательно, каждый из его острых углов содержит по 45о. Но тогда точка А (х; у) находится на биссектрисе II координатного угла.
Если x 0, то y 0, так как у = – х. Обращаясь к рисунку 9, б, получим, что OA1 = x = – y = AA1, т. е. что прямоугольный треугольник OA1A равнобедренный и поэтому точка A находится на биссектрисе IV координатного угла.
Если же x = 0, то и y = 0, так как у = – х. Точка (0; 0) находится на биссектрисе II и IV координатных углов.
![]()
В данном пункте рассматриваются свойства функции y = x2. Говорится о том, что на промежутке [0; + ) эта функция возрастает, т. е. большему значению аргумента соответствует большее значение функции. Иначе говоря, если 0 x1 x2, y1 =x12 , y2 =x22 , то y1 y2. Доказательство этого факта приводится в учебнике, но там не доказывается, что эта функция убывает на промежутке (– ; 0], поэтому ниже (задание 97) это доказательство приведено.
Здесь же устанавливается, что для функции y = x2 выполняется равенство y (–x) = y (x), и говорится, что такие функции называют чётными. Утверждается, что функция y = x2 непрерывна на промежутке (– ; + ). Приводится обоснование этого утверждения для x 0.
![]() Замечание. Даже у учителей иногда возникает
вопрос: верно ли, что функция y = x2 убывает на
промежутке (– ; 0] и возрастает на
промежутке [0; + )? Сомнения возникают
от кажущегося противоречия: число 0 входит в оба эти промежутка. Но
противоречия здесь нет, так как определения возрастания и убывания функции на
промежутке даются для любых x1 и x2 из
этого промежутка. Подчеркнём, что возрастание (убывание) функции рассматривается
только на промежутке.
Замечание. Даже у учителей иногда возникает
вопрос: верно ли, что функция y = x2 убывает на
промежутке (– ; 0] и возрастает на
промежутке [0; + )? Сомнения возникают
от кажущегося противоречия: число 0 входит в оба эти промежутка. Но
противоречия здесь нет, так как определения возрастания и убывания функции на
промежутке даются для любых x1 и x2 из
этого промежутка. Подчеркнём, что возрастание (убывание) функции рассматривается
только на промежутке.
Обратим внимание на то, что здесь впервые появляются понятия возрастающей (убывающей) на промежутке функции, чётной функции (но нет пока нечётной). Все доказательства должны приводиться учителем, но требовать их от учащихся ещё рано.
В пункте 2.2 сказано, что функция у = х2 непрерывна на промежутке (– ; + ). «Доказательство» непрерывности функции y = x2 на промежутке [0; + ) следует из очевидного факта. Будем считать, что у — это площадь квадрата со стороной х (для х = 0 площадь квадрата считаем равной 0). Ясно, что малое изменение стороны квадрата влечёт малое изменение его площади. Следовательно, для неотрицательных х малому изменению аргумента х соответствует малое изменение функции у. А так как функция определена в каждой точке промежутка [0; + ), то это и означает непрерывность функции y = x2 на промежутке [0; + ).
Непрерывность функции у = х2 на всей оси, т. е. на промежутке (– ; + ), будет следовать из симметрии графика этой функции относительно оси Оу (см. п. 2.3).
Задания для повторения. При изучении данного пункта можно использовать задание 780.
Решения и комментарии
94. Является ли функция у = х2 возрастающей на отрезке [а; b], если:
а) а = – 3; b = 3; в) а = 1; b = 4?
Решение. а) Функция у = х2 не является возрастающей на отрезке [–3; 3], так как можно подобрать такую пару значений, например x1 = – 3 и x2 = 1, из этого отрезка, что из неравенства x1 x2 следует, что y1 y2.
Функция у = х2 не является убывающей на отрезке [–3; 3], так как можно подобрать такую пару значений, например x1 = – 1 и x2 = 1, из этого отрезка, что из неравенства x1 x2 следует, что y1 = y2.
Функция у = х2 является возрастающей на отрезке [0; 3] и убывающей на отрезке [–3; 0].
в) Функция у = х2 является возрастающей на отрезке [1; 4], так как для любых x1 и x2, таких, что
1 x1 x2 4, имеем 1 x12 x22 16, т. е. y1 y2.
97. Докажите, используя определение, что функция у = х2 является убывающей на промежутке (– ; 0].
Доказательство. Пусть x1 и x2 — произвольные числа из промежутка (– ; 0], и пусть верно неравенство x1 x2 0. Докажем, что y1 y2.
Если x1 0, x2 = 0, то у1 = x12 0, а у2 = x22 = 0, т. е. верно неравенство y1 y2.
Если x1 0, x2 0 и x1 x2, то, умножив последнее неравенство на – 1, получим верное неравенство – x1 – x2. Так как для положительных чисел – x1 и – x2 из неравенства – x1 – x2 следует неравенство ( x1)2 ( x2)2 или x12 x22
и у1 = x12 , у2 = x22 , то верно неравенство y1 y2.
Итак, для любой пары чисел x1 и x2 из промежутка
(– ; 0] из неравенства x1 x2 следует неравенство y1 > y2
(большему значению аргумента соответствует меньшее значение функции), т. е. функция у = х2 является убывающей на промежутке (– ; 0], что и требовалось доказать.
В данном пункте вводится понятие графика функции у = х2, объясняется, как его построить. Здесь также приводится соответствующая терминология: парабола, ось симметрии параболы, вершина параболы.
Важно обратить внимание учащихся на то, что свойства функции у = х2 используются при построении графика, а график даёт наглядную иллюстрацию этих свойств. Каждый ученик должен знать, что график функции у = х2 — парабола, и уметь его строить.
102. Принадлежит ли точка A(x; y) графику функции у = х2, если: а) x = 1, y = 5; б) x = 3, y = 9?
Решение. а) Так как при x = 1, y = 5 равенство 5 = 12 неверно, то точка A(1; 5) не принадлежит графику функции у = х2;
б) так как при x = 3, y = 9 равенство 9 = 32 верно, то
точка A (3; 9) принадлежит графику функции у = х2.
103. Дана функция у = х2. На каком промежутке: а) функция возрастает; б) функция убывает?
Ответ. а) [0; + ); б) (– ; 0].
![]() Замечание. Учащиеся могут привести и другие
промежутки возрастания и убывания данной функции. Например, они могут сказать,
что функция возрастает на отрезке [1; 5], а убывает на интервале (–5;
–1). Для доказательства своих утверждений (в задаче доказательство не требуется)
они могут привести рассуждения, похожие на уже разобранные для промежутков [0;
+ ) и (– ;
0].
Замечание. Учащиеся могут привести и другие
промежутки возрастания и убывания данной функции. Например, они могут сказать,
что функция возрастает на отрезке [1; 5], а убывает на интервале (–5;
–1). Для доказательства своих утверждений (в задаче доказательство не требуется)
они могут привести рассуждения, похожие на уже разобранные для промежутков [0;
+ ) и (– ;
0].
Вообще, если промежуток (a; b) (или [a; b], или [a; b), или (a; b]) является частью промежутка [0; + ), на котором по доказанному функция возрастает, то на нём эта функция тоже возрастает. А если этот промежуток является частью промежутка (– ; 0], на котором по доказанному функция убывает, то на этом промежутке функция убывает.
1
В данном пункте рассматриваются свойства функции
y = ![]() 1 для
положительных x. Все эти свойства доказываx
1 для
положительных x. Все эти свойства доказываx
ются. В частности, на промежутке (0;
+ ) «доказательство» непрерывности функции
y = ![]() 1 следует из
приведённых x
1 следует из
приведённых x
в примере учебника рассуждений.
Отсюда делается вывод, что график функции y = ![]() 1 на x
1 на x
промежутке (0; + ) — непрерывная линия.
Задания для повторения. При изучении данного пункта можно использовать задание 789.
109. а) Сравните дроби ![]() и
и
![]() .
.
Решение. Данные дроби можно сравнить, приведя их
к общему знаменателю. А можно воспользоваться тем, что это значения функции y
= ![]() 1 в точках 2
и 3. x
1 в точках 2
и 3. x
Так как числа 2 и 3 принадлежат интервалу (0; + ),
на котором функция y =
![]() 1 убывает, то
из неравенства x
1 убывает, то
из неравенства x
2 3 следует неравенство ![]() .
.
110. а) Дана функция y
= ![]() 1 . Сравните y(1)
и y(2). x
1 . Сравните y(1)
и y(2). x
Решение. Так как числа 1 и 2 принадлежат интервалу
(0; + ), на котором функция y = ![]() 1 убывает, то
из нераx
1 убывает, то
из нераx
венства 1 2 следует неравенство y(1) y(2).
1
В данном пункте с опорой на свойства функции y = ![]() 1 x
1 x
строится график этой функции для положительных x. Затем устанавливается свойство функции
y (–x) = – y(x)
(1) и говорится, что такие функции называют нечётными. Из равенства (1)
следует, что график функции y = ![]() 1 x симметричен относительно начала координат.
Далее строится график функции для x 0, вводится соответствующая
терминология: гипербола, ветви гиперболы. Затем приводятся свойства функции y
=
1 x симметричен относительно начала координат.
Далее строится график функции для x 0, вводится соответствующая
терминология: гипербола, ветви гиперболы. Затем приводятся свойства функции y
= ![]() 1 для x 0.
Доказаx
1 для x 0.
Доказаx
тельства этих свойств опускаются.
![]() Замечание. Отметим,
что непрерывность функции y = 1 на промежутке (– ; 0) следует из симметрии граx
Замечание. Отметим,
что непрерывность функции y = 1 на промежутке (– ; 0) следует из симметрии граx
фика этой функции относительно начала координат.
Каждый ученик должен знать, что график функции
y = ![]() 1 —
гипербола, и уметь его строить.
1 —
гипербола, и уметь его строить.
x
Решения и комментарии 111. д) На каких промежутках
функция y = ![]() 1 непреx
1 непреx
рывна?
Ответ. Функция непрерывна на каждом из
промежутков (– ; 0) и (0; + ). 114. Докажите, что функция y = ![]() 1 является: x
1 является: x
а) нечётной; б) убывающей при x 0.
Решение. а) Область определения функции y =
![]() 1 соx
1 соx
стоит из двух промежутков: (– ; 0) и (0; + ). Поэтому для всякого числа x из области определения этой функции существует число – x, принадлежащее этой области определения. Так как
![]() y (–x) = 1 =
– 1
= – y (x),
y (–x) = 1 =
– 1
= – y (x),
−x x
то функция y = ![]() 1 является нечётной, что и
требовалось x доказать.
1 является нечётной, что и
требовалось x доказать.
б) Пусть x1 и x2 — любые числа из промежутка (– ; 0), для которых верны неравенства x1 x2 0.
Определим знак разности y (x1) – y (x2):
y (x1) – y (x2) = ![]() x11 x12 = x2x x 1 2 x1 .
x11 x12 = x2x x 1 2 x1 .
Так как x1 x2 0, то x2 – x1 0 и x1x2 0, поэтому y (x1) – y (x2) 0, это означает, что y (x1) y (x2).
Итак, при x 0 большему значению аргумента x2
соответствует меньшее значение y (x2), поэтому при x
0 функция y = ![]() 1 является убывающей. x
1 является убывающей. x
Промежуточный контроль. С–2, Т–2, К–1.
Основная цель третьего параграфа — ввести понятие квадратного корня из неотрицательного числа, разобрать свойства квадратных корней, которые будут широко использоваться при дальнейшем изучении математики и смежных предметов.
В данном пункте доказывается, что квадрат любого действительного числа — число неотрицательное, из чего следует, что нет такого действительного числа, квадрат которого — отрицательное число. Далее с опорой на непрерывность параболы y = x2 доказывается существование единственного корня из числа 0 и двух корней из положительного числа, отличающихся только знаками.
Тот факт, что у каждого положительного числа имеется два корня — положительный и отрицательный, позволяет решать уравнения вида x2 = a, где a — квадрат натурального числа. Однако до введения знака арифметического квадратного корня мы пока не можем записывать два корня уравнения x2 = 3, существование которых не вызывает сомнения, но ещё не ясно, как их обозначать. Необходимость научиться их записывать является дополнительным «внутриматематическим» стимулом к изучению материала следующих пунктов учебника.
127. Найдите квадратные корни из числа: а) 10 000;
д) ![]() . Докажите
правильность решения.
. Докажите
правильность решения.
Решение. а) Существует два квадратных корня из числа 10 000. Это числа 100 и – 100, так как 1002 = 10 000,
(–100)2 = 10 000;
д) существует два квадратных корня
из числа ![]() . Это
. Это
![]()
![]() числа и
–
числа и
– ![]() 1 , так как (1)2 = 1 , (
1)2 = 1 .
1 , так как (1)2 = 1 , (
1)2 = 1 .
2 2 4 2 4
129. Решите уравнение:
а) х2 = 4; б) х2 = 9; в) х2 = 16.
Решение. Для каждого из уравнений нетрудно подобрать пару противоположных чисел, квадраты которых равны числу, стоящему в правой части уравнения. Решение уравнения можно записать так:
а) х2 = 4; б) х2 = 9; в) х2 = 16; х1 = 2; х1 = 3; х1 = 4; х2 = –2; х2 = –3; х2 = –4.
Ответ. а) 2; – 2; б) 3; – 3; в) 4; – 4.
В данном пункте вводится понятие арифметического квадратного корня из данного неотрицательного числа b. Это неотрицательное число, квадрат которого равен b.
![]() Заметим, что
такое определение избыточно, так как неотрицательность числа b следует
из утверждения «квадрат любого действительного числа — число неотрицательное»
(п. 3.1). Далее вводится обозначение b для
арифметического квадратного корня из числа b.
Заметим, что
такое определение избыточно, так как неотрицательность числа b следует
из утверждения «квадрат любого действительного числа — число неотрицательное»
(п. 3.1). Далее вводится обозначение b для
арифметического квадратного корня из числа b.
![]() Надо
обратить внимание учащихся на то, что символ b
используется только для обозначения неотрицательного
Надо
обратить внимание учащихся на то, что символ b
используется только для обозначения неотрицательного
квадратного корня из неотрицательного числа b, его и называют арифметическим квадратным корнем из числа b. В дальнейшем при употреблении этого обозначения слово «арифметический» имеют в виду, но часто для краткости опускают.
Задания для повторения. При изучении данного пункта можно использовать задание 725.
Решения и комментарии 143. Решите уравнение:
![]()
![]()
![]() г) 5x 1
= 2; д) 5x 1 = 0; е)
7x 3 = – 1.
г) 5x 1
= 2; д) 5x 1 = 0; е)
7x 3 = – 1.
![]() Решение.
г) Если число x — корень уравнения, то число 5x 1 равно 2. Следовательно, 5x – 1
= 22, откуда получим, что уравнение имеет единственный
корень x = 1;
Решение.
г) Если число x — корень уравнения, то число 5x 1 равно 2. Следовательно, 5x – 1
= 22, откуда получим, что уравнение имеет единственный
корень x = 1;
![]() д) если
число x — корень уравнения, то число 5x
1 равно 0. Следовательно, 5x – 1 = 02,
откуда получим, что уравнение имеет единственный корень x = 0,2;
д) если
число x — корень уравнения, то число 5x
1 равно 0. Следовательно, 5x – 1 = 02,
откуда получим, что уравнение имеет единственный корень x = 0,2;
е) если число x — корень уравнения, то число 7x 3 неотрицательное и оно не может быть равным – 1. Уравнение не имеет корней.
1. Решите уравнение:
а) х2 = 2; б) х2 = 3; в) х2 = 5.
Решение. Для каждого из уравнений нетрудно подобрать пару противоположных чисел, квадраты которых равны числу, стоящему в правой части уравнения.
![]() Ответ. а) 2 ; 2 ; б) 3
; 3 ; в) 5 ; 5 .
Ответ. а) 2 ; 2 ; б) 3
; 3 ; в) 5 ; 5 .
В данном пункте формулируется и доказывается теорема, касающаяся трёх свойств арифметических квадратных корней.
Далее приводятся примеры применения этих свойств для преобразования числовых и буквенных выражений, из которых особо надо выделить вынесение множителя изпод знака корня, внесение множителя под знак корня и освобождение дроби от иррациональности в знаменателе. Желательно, чтобы все учащиеся знали свойства корней и умели их применять для преобразования числовых и буквенных выражений.
Задания для повторения. При изучении данного пункта можно использовать задания 638—642, 739—741.
149.

![]()
![]() Вычислите: е) (3)8 ; ж) a4 ;
з) m6 .
Вычислите: е) (3)8 ; ж) a4 ;
з) m6 .
Решение. е) (3)8 = 812 = |81| = 81;
ж) a4 = (a2 2) = |a2| = a2, так как a2 0;
з) m6 = (m3 2) = |m3| = |m|3, здесь нельзя опустить знак модуля, так как m может быть отрицательным числом.
150. Упростите выражение:
 а) x2 2x 1 ; г) 4 4p p2 ; ж) 4x2 12x 9 . Решение. а) x2 2x 1 = (x 1)2 = x 1
;
а) x2 2x 1 ; г) 4 4p p2 ; ж) 4x2 12x 9 . Решение. а) x2 2x 1 = (x 1)2 = x 1
;
г) 4 4p p2 = (2 p)2 = 2 p ;
ж) 4x2 12x 9 = (2x 3)2 = 2x 3 .
154. Вынесите множитель из-под знака корня:
б) x3 ; г) p7 ; ж) x y4 2 .
Решение. б) x3 = x x2 = x2 x = x x =x x , так как x3 0, поэтому x 0;
г) p7 = p p6 = (p3 2) p = p3 p = p3 p , так как p7 0,
поэтому p 0;
ж) x y4 2 = (x y2 2 2) = (x2 2) y2 = x y2 =x y2 .
157. Внесите множитель под знак корня: б) 3 2 ; ж) 2x 6 , x 0. Решение.
б) 3 2 = 1 3 2 = 1 32 2 = 1 9 2 = 18 ;
ж) 2x 6 = 1 ( 2x) 6 = 1 (2x)2 6 = 1 4x2 6 =
= 24x2 . Здесь под знак корня внесли неотрицательное число – 2x, так как x 0.
171. ![]() а) Освободитесь от иррациональности
в знамена-теле: 1 .
а) Освободитесь от иррациональности
в знамена-теле: 1 .
2 1
\ 2 1
1
Решение. = = = 2 1.
2 1 ( 2 1 )( 2 1 ) 2 1
172. а) Вычислите: 11 4 7 7 .
Решение. 11 4 7 7 = 4 4 7 7 7 =
 =
(2 7)2
7 = 2 7 7 = 2 7 7 =2.
=
(2 7)2
7 = 2 7 7 = 2 7 7 =2.
173. а) Докажите, что значение числового выражения
 = = 1.
= = 1.
174. а) Найдите значение выражения
![]() 4x
9 x2 9 x2 3
при x = 2,5.
4x
9 x2 9 x2 3
при x = 2,5.
Решение. Так как x = 2,5, то
 9 x2 3 0 .
Следовательно,
9 x2 3 0 .
Следовательно,
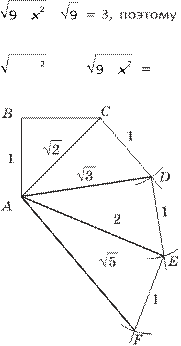 4x 9 x2 9
x2 3 = 4x
9 x 3
4x 9 x2 9
x2 3 = 4x
9 x 3
= 4x + 3 = 4 2,5 + 3 = 13.
175. Дан отрезок единичной длины. С помощью циркуля и линейки постройте отрезок, длина которого равна:
![]()
![]()
![]() а) 2 ; б) 3 ;
в) 5 .
а) 2 ; б) 3 ;
в) 5 .
![]() Решение. Сначала построим
равнобедренный прямоугольный треугольник ABC с катетом 1 (рис.
10). По теореме Пифагора его гипотенуза AC равна 2 .
Решение. Сначала построим
равнобедренный прямоугольный треугольник ABC с катетом 1 (рис.
10). По теореме Пифагора его гипотенуза AC равна 2 .
![]()
![]() Затем
построим прямоугольный треугольник ACD
с катетами AC = 2 и CD =
1. По теореме Пифагора его гипотенуза AD равна 3 . Продолжая процесс построения прямоуголь- 6 Рис. 10 ных треугольников,
как показано на рисунке 10, получим отрезки AE = 2, AF =
5 .
Затем
построим прямоугольный треугольник ACD
с катетами AC = 2 и CD =
1. По теореме Пифагора его гипотенуза AD равна 3 . Продолжая процесс построения прямоуголь- 6 Рис. 10 ных треугольников,
как показано на рисунке 10, получим отрезки AE = 2, AF =
5 .
739.
![]() а)
Найдите значение выражения x (x 10)2
при x = 10,1.
а)
Найдите значение выражения x (x 10)2
при x = 10,1.
Решение. I способ. Вместо x подставим в данное выражение число 10,1:
![]()
![]()
![]() x (x 10)2 = 10,1
– (10,1
10)2 10,1 0,12 =
x (x 10)2 = 10,1
– (10,1
10)2 10,1 0,12 =
= 10,1 – |0,1| = 10,1 – 0,1 = 10.
II способ. Сначала упростим данное выражение, учитывая, что x – 10 0:
![]() x (x 10)2 = x – |x
– 10| = x – (x – 10) = =
x – x + 10 = 10.
x (x 10)2 = x – |x
– 10| = x – (x – 10) = =
x – x + 10 = 10.
740. а) Найдите значение выражения x 4 x 1
![]() x 2 x 1
x 2 x 1
при x = 5.
Решение. I способ. Вместо x подставим в данное выражение число 5:
x 4 x 1 5 4 5 1 1 \ 5 1 4 \ 5 2
 = = = x 2 x 1 5 2 5 1 5 2 5 1
= = = x 2 x 1 5 2 5 1 5 2 5 1
= = 3 5 = 1.
( 5 1 )( 5 2 ) ( 5 1 )( 5 2 ) 3 5 7
II способ. Упростим данное выражение, приведя дроби к общему знаменателю:
x 4 x 1 1 \ x 1 4 \ x 2
 = =
x 2 x 1 x
2 x 1
= =
x 2 x 1 x
2 x 1
= x 1 4 x 8 = 3 x 7 .
( x 1)( x 2) ( x 1)( x 2) 3 x 7
Так как числитель и знаменатель полученной дроби при x = 5 равны и не обращаются в нуль, то дробь равна 1.
III способ. Сначала упростим данное выражение, разложив на множители числители дробей:
x 4 x 1 ( x 2)( x 2) ( x 1)( x 1)
 = =
x 2 x 1 x
2 x 1
= =
x 2 x 1 x
2 x 1
= ( x 2) ( x 1) = x 2 x 1 = 1.
741. в) Найдите значение выражения x 1 1 x 1 при каждом x 3,3.
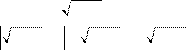 Решение.
Выполнить вычисления при каждом x 3,3 практически невозможно. Упростим
данное выражение, учитывая, что x 1 – 1 0 при каждом x 3,3:
Решение.
Выполнить вычисления при каждом x 3,3 практически невозможно. Упростим
данное выражение, учитывая, что x 1 – 1 0 при каждом x 3,3:
![]() x 1 1 x
1 = x 1 – 1 – x 1 =
– 1.
x 1 1 x
1 = x 1 – 1 – x 1 =
– 1.
Промежуточный контроль. С–3, С–4.
![]() При
изучении данного пункта в обычном классе можно доказать иррациональность числа 3 , но требовать от учащихся этого доказательства не
следует.
При
изучении данного пункта в обычном классе можно доказать иррациональность числа 3 , но требовать от учащихся этого доказательства не
следует.
В классе с углублённым изучением математики это доказательство обязательно для воспроизведения учащимися, так как это первый пример доказательства иррациональности числа. Учащиеся должны уметь проводить это доказательство, а также аналогичные доказательства (задание 180). В сильном классе и в классе с углублённым изучением математики можно разобрать доказательство теоремы, приведённой в учебнике.
ТЕОРЕМА. Если натуральное число n не является
![]() квадратом некоторого
натурального числа, то n —
иррациональное число.
квадратом некоторого
натурального числа, то n —
иррациональное число.
![]() Доказательство.
Предположим противное, что n —
число рациональное, т. е. существуют натуральные числа p и q,
такие, что n = p ,
причём будем считать, что p и q
Доказательство.
Предположим противное, что n —
число рациональное, т. е. существуют натуральные числа p и q,
такие, что n = p ,
причём будем считать, что p и q
q не имеют общих делителей, отличных от 1. Тогда справедливо равенство
p2 n
= ![]() 2 . (1)
q
2 . (1)
q
Если предположить, что q = 1, то n = p2
— квадрат натурального числа, а это противоречит условию теоремы. Значит, q
1. Если предположить, что p = 1, то n = ![]() 12 , т. е. натуq
12 , т. е. натуq
ральное число равно дроби, что невозможно. Значит, p 1. Следовательно, в равенстве (1) p 1 и q 1. Тогда по основной теореме арифметики натуральное число p разлагается на простые множители единственным образом, т. е. p = p1α1 . . . pmαm , где p1, ..., pm — разные простые числа, a1, ..., am — натуральные числа.
По той же теореме q = q1β1 . . . qkβk , где q1, ..., qk — разные простые числа, b1, ..., bk — натуральные числа.
Так как p и q не имеют общих делителей, отличных от 1, то среди чисел q1, ..., qk нет ни одного из чисел p1, ..., pm.
2α1 2αm 2β
Тогда p2 = p1 m q2 = q1 1 ... qk2βk — соглас-
... p ,
но основной теореме арифметики эти разложения единст-
p2 венны и дробь ![]() 2 несократима. Получилось, что натуральq
2 несократима. Получилось, что натуральq
p2 ное число n
равно несократимой дроби ![]() 2 ,
следовательно, q
2 ,
следовательно, q
предположение неверно, что и доказывает теорему.
Задания для повторения. При изучении данного пункта можно использовать задания 632, 634, 635, 729.
179. Докажите, что не существует рационального
числа, квадрат которого равен: а) 5; г) ![]() .
.
Решение. а) В обычном классе можно сослаться на утверждение теоремы, в классе с углублённым изучением математики можно повторить рассуждения, приведённые в учебнике при доказательстве иррациональности числа
![]() 3 ,
но применительно к числу 5 ;
3 ,
но применительно к числу 5 ;
г) предположим, что существует несократимая дробь
p
![]()
![]() p2
p2
, такая, что p и q — натуральные числа и 2 = . Тог-
q q
![]() ⎛ q⎞2 q
⎛ q⎞2 q
![]() да
⎜⎝ p⎟⎠ =
3, т. е. существует рациональное число p ,
равное
да
⎜⎝ p⎟⎠ =
3, т. е. существует рациональное число p ,
равное
![]() 3 ,
что противоречит тому, что число 3 —
иррациональное. Следовательно, не существует рационального числа,
квадрат которого равен
3 ,
что противоречит тому, что число 3 —
иррациональное. Следовательно, не существует рационального числа,
квадрат которого равен ![]() , что и требовалось доказать.
, что и требовалось доказать.
182. Докажите, что значение данного выражения — число рациональное:
![]()
![]()
![]() а) ( 2 1)( 2 1) ; д)
( 2 1)2 ( 2 1)2 .
а) ( 2 1)( 2 1) ; д)
( 2 1)2 ( 2 1)2 .
Решение. Сначала заметим, что здесь и далее применяются формулы сокращённого умножения (a – b)(a + b) = = a2 – b2 и др., доказанные в 7 классе для любых чисел a и b. Теперь некоторые из этих чисел мы научились записывать с помощью арифметического квадратного корня и можем применять к ним доказанные ранее формулы сокращённого умножения.
 а) ( 2 1)( 2 1) = ( 2)2 12 = 1 — число рациональ-
а) ( 2 1)( 2 1) = ( 2)2 12 = 1 — число рациональ-
ное;

![]() д) ( 2 1)2 ( 2 1)2 = ( 2)2 2 2 12
( 2)2 2 2 12
=
д) ( 2 1)2 ( 2 1)2 = ( 2)2 2 2 12
( 2)2 2 2 12
=
= 2 2 2 1 2 2 2 1 = 6 — число рациональное.
![]() 729. а)
Докажите или опровергните утверждение, что для любых положительных чисел a
и b (a b) верно равенство ( a b)2
= a + b.
729. а)
Докажите или опровергните утверждение, что для любых положительных чисел a
и b (a b) верно равенство ( a b)2
= a + b.
Решение. Чтобы убедиться, что это равенство неверно для любых положительных чисел a и b (a b), достаточно привести один пример. Возьмём a = 4, b = 1:
![]() ( 4 1)2= (2
+ 1)2 = 9 4 + 1.
( 4 1)2= (2
+ 1)2 = 9 4 + 1.
![]()
![]() Данный пункт предназначен для
классов с углублённым изучением математики. Если а и b
положительные числа и а2 b2, то по
свойству 7 (п. 1.1) а b. По этому же свойству из неравенств 1 2
4 следует, что истинны неравенства 1 2 4 , или 1
2 2.
Данный пункт предназначен для
классов с углублённым изучением математики. Если а и b
положительные числа и а2 b2, то по
свойству 7 (п. 1.1) а b. По этому же свойству из неравенств 1 2
4 следует, что истинны неравенства 1 2 4 , или 1
2 2.
Аналогично из неравенств 1,42 2 1,52 следует, что
![]() 1,4 2 1,5 и т. д.
1,4 2 1,5 и т. д.
Учащиеся должны сделать для себя вывод, что для любого иррационального числа, записанного с помощью знака корня, на координатной оси можно указать отрезки длины 1, 0,1, 0,01, …, каждому из которых принадлежит это иррациональное число. Это означает, что для любого арифметического квадратного корня из натурального числа можно указать приближение с недостатком с любым количеством цифр после запятой, но для большого количества десятичных знаков приближения этого корня требуются громоздкие вычисления. Здесь важно показать, что для практических нужд бывает достаточно нескольких десятичных знаков, которые можно получить с помощью таблиц или калькулятора.
Задания для повторения. При изучении данного пункта можно использовать задания 636, 637.
![]() 191. Какое число является
более точным приближением 11 : в) 3,31 или
3,32; г) 3,316 или 3,317?
191. Какое число является
более точным приближением 11 : в) 3,31 или
3,32; г) 3,316 или 3,317?

![]() Решение.
в) Найдя приближение числа 11 с недостатком до
третьего знака после запятой: 11 3,316,
получим, что 3,32 является более точным приближением 11
; г) найдя приближение числа 11 с
недостатком до чет-
Решение.
в) Найдя приближение числа 11 с недостатком до
третьего знака после запятой: 11 3,316,
получим, что 3,32 является более точным приближением 11
; г) найдя приближение числа 11 с
недостатком до чет-
вёртого знака после запятой: 11 3,3166, получим, что
![]() 3,317 является более точным
приближением числа 11 .
3,317 является более точным
приближением числа 11 .
Промежуточный контроль. Т–3, К–2.
В данном пункте вводятся понятия множества, элемента множества, подмножества, бесконечного множества, объединения (суммы), пересечения и разности множеств, приводятся соответствующие обозначения множеств. Далее рассказывается о взаимно однозначном соответствии между элементами множеств, о свойстве числового множества быть замкнутым относительно данной операции. Формулируется принцип Дирихле и даётся определение прямого произведения двух множеств.
195. Докажите, что:
а) множества N и Z имеют одинаковую мощность;
б) множества точек двух любых отрезков имеют
одинаковую мощность;
в) множества (0; 1) и R имеют одинаковую мощность.
Решение. а) Выпишем целые и натуральные числа и установим соответствие между ними стрелками:
Z : 0, – 1, 1, – 2, 2, – 3, 3, …
![]()
N : 1, 2, 3, 4, 5, 6, 7, …
Между элементами множеств Z и N установлено взаимно однозначное соответствие, следовательно, множества Z и N имеют одинаковую мощность.
б) Если длины отрезков различны, то изобразим два отрезка, равные данным, друг под другом и установим
между их точками взаимно однозначное соответствие, как на рисунке 11, а. Значит, между точками данных отрезков можно установить взаимно однозначное соответствие. Следовательно, множества точек двух отрезков имеют одинаковую мощность.
Если отрезки равны, то равные им отрезки можно совместить. При этом каждой точке одного отрезка поставим в соответствие совпавшую с ней точку другого отрезка. Очевидно, что и в этом случае множества точек данных отрезков имеют одинаковую мощность.
в) На рисунке 11, б показано, как установить взаимно
однозначное соответствие между точками единичного интервала и прямой. Множества точек единичного интервала и прямой, а следовательно, и числовые множества (0; 1) и R имеют одинаковую мощность.
196. а) Является ли замкнутым относительно операций сложения, вычитания, умножения, деления множество чётных натуральных чисел?
Решение. Множество чётных натуральных чисел является замкнутым относительно операций сложения и умножения, так как сумма и произведение двух чётных натуральных чисел являются чётными натуральными числами.
Множество чётных натуральных чисел не является замкнутым относительно операций вычитания и деления, так как результаты операций 4 – 6 = – 2, 6 : 2 = 3 не принадлежат множеству чётных натуральных чисел.
В данном пункте рассказывается о вкладе Н. И. Лобачевского и П. Дирихле в развитие учения о функциях, а также о роли Р. Декарта в развитии методов аналитической геометрии. Здесь же приводятся некоторые способы вычисления квадратных корней, часть из которых известна ещё по глиняным табличкам Древнего Вавилона, часть опубликована в учебнике арифметики Л. Ф. Магницкого.
Глава 2
Вторая глава начинается изучением квадратного трёхчлена, затем рассматриваются способы решения квадратных уравнений, применение квадратных уравнений к решению задач. Здесь же изучаются способы решения рациональных уравнений и применение рациональных уравнений к решению задач.
Составление уравнений для решения задач способствует не только развитию мышления и речи учащихся, но и обучению их планированию своей деятельности. Так, при решении задач учащиеся должны уметь выделять известные и неизвестные данные, намечать план действий, ставить вопросы, находить ответы на них, проверять, отвечает ли полученный результат условиям задачи. Это важнейшие метапредметные умения, необходимые при изучении математики и других школьных предметов.
Цель изучения главы 2 — научить учащихся решать квадратные и рациональные уравнения и применять их к решению текстовых задач.
Основная цель изучения четвёртого параграфа — научиться решать квадратные уравнения и применять их к решению текстовых задач.
В данном пункте вводятся понятия квадратного трёхчлена и дискриминанта квадратного трёхчлена. Это многочлен ax2 + bx + c, где a, b, c — данные числа, a 0, и число D = b2 – 4ac соответственно. Обратим внимание на то, что позднее число D будем называть ещё и дискриминантом квадратного уравнения, и дискриминантом квадратного неравенства (неравенства второй
степени).
Важную роль в построении теории квадратных уравнений играют теоремы 1—4, доказанные в данном пункте учебника. При их доказательстве используется материал, изученный в 7 классе: понятие тождества, разложение многочлена на множители, выделение полного квадрата, формулы сокращённого умножения многочленов. При необходимости эти вопросы можно повторить до объяснения нового материала.
В данном пункте закладывается основа для изучения материала всего параграфа, поэтому, чем твёрже будут основы, тем успешнее учащиеся будут усваивать следующий материал.
Задания для повторения. При изучении данного пункта можно использовать задания 813, 819.
207. а) Разложите на линейные множители квадратный трёхчлен 2x2 – 5x + 3.
Указание. Воспользуйтесь равенством
ax2 + bx + c = a(x – x1)(x – x2),
![]()
![]() где x1 = b D , x2 = b D , D 0.
где x1 = b D , x2 = b D , D 0.
2a 2a
Решение. Сначала вычислим дискриминант
D = b2 – 4ac = (–5)2 – 4 2 3 = 1 0,
квадратный
трёхчлен имеет корни x1 = ![]() = , x2 =
= , x2 =![]() = 1 и его можно разложить на множители:
= 1 и его можно разложить на множители:
![]() 2x2 – 5x + 3
= 2(x –
2x2 – 5x + 3
= 2(x – ![]() )(x – 1).
)(x – 1).
209. Докажите, что при любых значениях х отличны от нуля значения квадратного трёхчлена:
![]()
![]() а) х2
+ х + 3; б) –х2 + 4х – 5; в) х2
+ 2х + 2. Решение. а) х2
+ х + 3 = х2 + 2 х 1 + 1 + 3
– =
а) х2
+ х + 3; б) –х2 + 4х – 5; в) х2
+ 2х + 2. Решение. а) х2
+ х + 3 = х2 + 2 х 1 + 1 + 3
– =
2 4
= (х + ![]() )2
+ 2,75 0 при любом значении x;
)2
+ 2,75 0 при любом значении x;
б) –х2 + 4х – 5 = –(х2 – 4х + 5) = –(х2 + 4х + 4 + 1) =
= –((х + 2)2 + 1) 0 при любом значении x;
в) х2 + 2х + 2 = х2 + 2х + 1 + 1 = (х + 1)2 + 1 0 при
любом значении x.
210. Докажите, что найдётся такое значение х, при котором значение квадратного трёхчлена х2 – 7х + 6:
а) положительно; б) отрицательно; в) равно нулю.
Решение. а) При x = 0 значение квадратного трёхчлена х2 – 7х + 6 равно 6 — положительно;
б) при x = 2 значение квадратного трёхчлена
х2 – 7х + 6 равно –4 — отрицательно;
в) при x = 1 значение квадратного трёхчлена
х2 – 7х + 6 равно нулю.
790. а) Найдите квадратный трёхчлен, значение которого при x = 0 равно 3, при x = 1 равно 0, при x = 2 равно 1.
Решение. Рассмотрим квадратный трёхчлен f (x) = ax2 +
+ bx + c. По условию задачи
f (0) = a 02 + b 0 + c = c = 3, f (1) = a 12 + b 1 + c = a + b + c = 0, f (2) = a 22 + b 2 + c = 4a + 2b + c = 1.
Так как c = 3, то из двух последних условий получим два уравнения первой степени с двумя неизвестными: a + b = –3, 4a + 2b = –2.
Решив систему этих двух уравнений, получим a = 2, b = –5.
Итак, искомый квадратный трёхчлен есть 2х2 – 5х + 3.
Промежуточный контроль. С–5.
В данном пункте вводятся понятия квадратного уравнения (уравнения второй степени) и дискриминанта квадратного уравнения, напоминается, что такое корень уравнения, что значит решить уравнение и какие уравнения называют равносильными, а также какие равносильные преобразования известны из курса 7 класса.
Задания для повторения. При изучении данного пункта можно использовать задание 812.
217. Проверьте, является ли хотя бы одно из чисел 1 или –1 корнем уравнения:
а) х2 + х = 0; е) х2 – 1 = 0.
Решение. а) При x = 1 имеем: 12 + 1 0, при x = –1 имеем: (–1)2 – 1 = 0, значит, –1 является корнем квадратного уравнения х2 + х = 0;
e) при x = 1 имеем: 12 – 1 = 0, при x = –1 имеем: (–1)2 – 1 = 0, значит, и 1, и –1 являются корнями квадратного уравнения х2 – 1 = 0.
![]() 812.
а) Является ли корнем уравнения х2 – 4х + 2
= 0 число –2 – 2 ?
812.
а) Является ли корнем уравнения х2 – 4х + 2
= 0 число –2 – 2 ?
Решение. При x = –2 – 2 имеем:

![]() (–2 –
2 )2 – 4
(–2 – 2 ) + 2
=
(–2 –
2 )2 – 4
(–2 – 2 ) + 2
=
= 4 + 4 2 + 2 + 8 + 4 2 + 2 0,
значит, это число не является корнем данного уравнения.
![]() Замечание. Приведённое решение не самое изящное,
но учащиеся об этом ещё не догадываются, у них нет другого способа решения.
После изучения теоремы Виета можно вернуться к этому заданию и решить его
иначе.
Замечание. Приведённое решение не самое изящное,
но учащиеся об этом ещё не догадываются, у них нет другого способа решения.
После изучения теоремы Виета можно вернуться к этому заданию и решить его
иначе.
В данном пункте вводится понятие неполного квадратного уравнения как квадратного уравнения ax2 + bx + c = = 0, в котором или b = 0, или c = 0, или b = c = 0, разбираются характерные примеры решения таких уравнений. Главный вывод, который для себя должны сделать учащиеся: любое неполное квадратное уравнение имеет либо два корня, либо один, либо вообще не имеет корней, а начинать поиск корней уравнения надо с попытки разложить его левую часть на множители.
Задания для повторения. При изучении данного пункта можно использовать задания 808—810.
231. Решите уравнение:
а) (х – 1)2 + (х + 1)2 = 2;
в) (3х – 8)2 – (4х – 6)2 + (5х – 2)(х + 2) = 24. Решение. а) (х – 1)2 + (х + 1)2 = 2, х2 – 2х + 1 + х2 + 2х + 1 = 2, 2x2 = 0.
Уравнение имеет единственный корень x = 0. в) (3х – 8)2 – (4х – 6)2 + (5х – 2)(х + 2) = 24,
9х2 – 48х + 64 – (16х2 – 48х + 36) + 5х2 – 2х + 10х – – 4 = 24,
9х2 – 48х + 64 – 16х2 + 48х – 36 + 5х2 – 2х + 10х –
– 4 – 24 = 0,
–2х2 + 8х = 0, –2х(х – 4) = 0, х = 0 или х = 4.
Уравнение имеет два корня: 0 и 4.
235. а) Решите уравнение m2х2 – n2 = 0 относительно x (m и n — данные числа).
Решение. Если m = 0 и n = 0, то корнем уравнения является любое число.
Если m = 0 и n 0, то уравнение не имеет корней.
![]()
![]() Если
m 0, то, разложив левую часть уравнения на множители, перепишем его в
виде m2(х – n )(х + n ) =
0. m m
Если
m 0, то, разложив левую часть уравнения на множители, перепишем его в
виде m2(х – n )(х + n ) =
0. m m
Это уравнение имеет два корня: x1 = mn , x2 = – mn , которые будут различными, если n 0, и будут совпадать, если n = 0.
236. а) Найдите все значения a, при каждом из которых уравнение ax2 – (a + 1)x = 0 имеет единственный корень.
Решение. При a = 0 данное уравнение имеет вид –x = 0 и имеет единственный корень.
Пусть a 0. Перепишем уравнение в виде
(ax – a – 1)x = 0.
При любом a это уравнение имеет корень x = 0. Чтобы данное уравнение имело единственный корень, уравнение ax – a – 1 = 0 должно иметь тот же корень x = 0. Это возможно лишь при a = –1.
Итак, данное уравнение имеет единственный корень при a = 0 и a = –1.
В данном пункте со ссылкой на теоремы из п. 4.1 разбираются способы решения квадратного уравнения общего вида (ax2 + bx + c = 0) для трёх случаев: D 0, D = 0, D 0 — и приводятся характерные примеры решения уравнений для каждого из этих случаев.
Учащиеся должны запомнить формулы корней квад-
![]() ратного уравнения x1 2, = b D , где D =
b2 – 4ac. Эти фор-
ратного уравнения x1 2, = b D , где D =
b2 – 4ac. Эти фор-
2a
мулы на самом деле им уже известны из п. 4.1.
247. Докажите, что корни уравнения ax2 + bx + c = 0 (a 0) при D 0 можно вычислять по формуле
b D
![]()
![]() 2 x1 2, = 2 4 , где D4 = ⎛⎜⎝2b⎞⎟⎠ ac . a
2 x1 2, = 2 4 , где D4 = ⎛⎜⎝2b⎞⎟⎠ ac . a
Решите по этой формуле уравнение:
а) x2 – 8x + 7 = 0; д) 8x2 – 10x + 3 = 0.
Решение. Так как D 0, то корни уравнения вычис-
![]() ляются по формуле x1 2, = b D . Разделив
числитель и
ляются по формуле x1 2, = b D . Разделив
числитель и
2a
знаменатель дроби на 2 и применив свойство арифметического квадратного корня, получим
![]()
![]() x1 2, = 2b 2D = 2b D4 , где D b2 4ac ⎛b⎞2 ac .
x1 2, = 2b 2D = 2b D4 , где D b2 4ac ⎛b⎞2 ac .
= = ⎜
a a 4 4 ⎝2⎟⎠
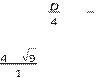
![]() а) x2
– 8x + 7 = 0; = ⎛⎜⎝2b⎠⎞⎟2 ac = ( 4)2 1 7 = 9;
а) x2
– 8x + 7 = 0; = ⎛⎜⎝2b⎠⎞⎟2 ac = ( 4)2 1 7 = 9;
b D
x1 2, = 2 a 4 = = 4 3, x1 = 1, x2 = 7;
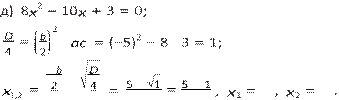 a 8 8
a 8 8 ![]()
![]()
![]() Замечание. Доказанная формула удобна для решения
уравнений с целыми a и c и чётным целым коэффициентом b = 2n
(n Z),
так как в этом случае
Замечание. Доказанная формула удобна для решения
уравнений с целыми a и c и чётным целым коэффициентом b = 2n
(n Z),
так как в этом случае ![]() b =
–n и
b =
–n и
2 ![]() D4 = n2 ac — целые числа.
D4 = n2 ac — целые числа.
248. а) Найдите все значения m, при каждом из которых уравнение x2 + mx + 3 = 0 имеет два совпадающих корня.
Решение. Уравнение имеет два совпадающих корня
(или один корень), если
D = b2 – 4ac = m2 – 4 1 3 = m2 – 12 = 0.
![]()
![]() Решив уравнение m2
– 12 = 0, получим два значения m,
удовлетворяющие условию задачи: m1 = 2 3 , m2 = –2 3 .
Решив уравнение m2
– 12 = 0, получим два значения m,
удовлетворяющие условию задачи: m1 = 2 3 , m2 = –2 3 .
249.
а) Решите уравнение ax2 – 2x
+ 1 = 0, если число a таково, что a 1 и
a 0. Решение. Вычислим ![]() D :
D :
4
![]() D ⎛b⎞2 ac = (–1)2 –
a 1 = 1 – a.
D ⎛b⎞2 ac = (–1)2 –
a 1 = 1 – a.
a a
Если a = 1, то уравнение имеет один корень: x1 = 1.
Если a 1 и a 0, то уравнение имеет два корня:
![]()
![]() x1 = 1 a1 a , x2 =
1 a1 a .
x1 = 1 a1 a , x2 =
1 a1 a .
250. При каких значениях a уравнение x2 + 2x + a = 0: а) имеет два различных корня;
б) имеет единственный корень;
в) не имеет корней?
Решение. Выделив полный квадрат, перепишем уравнение в виде
(x + 1)2 + a – 1 = 0.
а) Если a 1, то уравнение имеет два различных
корня.
б) Если a = 1, то уравнение имеет единственный
корень.
в) Если a 1, то уравнение не имеет корней.
251. а) Решите уравнение x2 – 3ax + 2a2 = 0 для каждого действительного числа a.
Решение. Если a = 0, то уравнение имеет вид x2 = 0 и имеет единственный корень x1 = 0.
Если a 0, то дискриминант этого квадратного уравнения равен D = b2 – 4ac = 9a2 – 8a2 = a2 0 и уравнение
![]() имеет два корня: x1 2, = 3a 2 a2 = 3a 2 a = 3a 2 a .
имеет два корня: x1 2, = 3a 2 a2 = 3a 2 a = 3a 2 a .
![]() Замечание. Знак модуля в записи корней можно
опустить, так как для a 0 верны равенства:
Замечание. Знак модуля в записи корней можно
опустить, так как для a 0 верны равенства:
3a a2 3a a 3a a
x1 = = = = 2a,
2 2 2
 x2 = 3a a2 = 3a a = 3a a = a,
x2 = 3a a2 = 3a a = 3a a = a,
2 2 2
а для a 0 верны равенства:
x1 = 3a a2 = 3a a = 3a a = a,
2 2 2
3a a2 3a a 3a a x2 = = = = 2a.
2 2 2
Следовательно, при «опускании» модуля меняется только номер корня. 252. Решите уравнение:
а) |x2 – 5x + 2| = 2; в) |x2 – 4x + 1| = |x2 – 3x – 10|.
Решение. а) Из определения модуля следует, что
|x2 – 5x + 2| = 2, если или 1) x2 – 5x + 2 = 2, или 2) x2 – 5x + 2 = –2.
Решив уравнение 1), получим два его корня: 0 и 5; решив уравнение 2), получим два его корня: 1 и 4. Следовательно, исходное уравнение имеет четыре корня: 0, 1, 4, 5.
в) Из определения модуля следует, что
|x2 – 4x + 1| = |x2 – 3x – 10|,
если
или 1) x2 – 4x + 1 = x2 – 3x – 10, или 2) x2 – 4x + 1 = –x2 + 3x + 10.
Решив уравнение 1), получим его единственный корень 11; решив уравнение 2), получим два его корня: –1 и 4,5. Следовательно, исходное уравнение имеет три корня:
–1, 4,5, 11.
253. ![]() а) Решите уравнение x2 2x 3
= 0.
а) Решите уравнение x2 2x 3
= 0.
Решение. Числовое значение x2 2x 3 равно 0 лишь
в случае, когда x2 – 2x – 3 = 0. Решив это уравнение, получим два его корня: –1 и 3. Следовательно, исходное уравнение имеет два корня: –1, 3.
254. ![]() а) Решите уравнение x2 3x 3
= 1.
а) Решите уравнение x2 3x 3
= 1.
Решение. Числовое значение x2 3x 3 равно 1, если
x2 3x 3 = 1. Решив это уравнение, получим два его корня: –4 и 1. Следовательно, исходное уравнение имеет два корня: –4, 1.
В данном пункте вводится понятие приведённого квадратного уравнения, т. е. квадратного уравнения с коэффициентом 1 при x2. Его принято записывать в виде
x2 + px + q = 0.
Его корни для D 0 вычисляются по формуле
![]() x1 2, = p D ,
(1)
x1 2, = p D ,
(1)
2
где D = p2 – 4q.
Если число p — чётное, то для D 0 часто применяют другую формулу корней приведённого квадратного уравнения:
![]() x1 2, = p
D , (2)
x1 2, = p
D , (2)
2 4
где D4 =⎛⎜⎝![]() 2p⎞⎟⎠2 q .
2p⎞⎟⎠2 q .
Следует обратить внимание учащихся, что это не новая формула, а другая запись формулы (1).
Задания для повторения. При изучении данного пункта можно использовать задание 811.
258. д) Решите уравнение x2 + 16x + 48 = 0.
Решение. Коэффициент p = 16 — чётное число, поэтому для нахождения корней удобно применить формулу (2).
Так как D4 =⎛⎜⎝2p⎞⎟⎠2 q = 82 – 48 = 16, то
![]() x1 2, = 2p D4 = 8 16 = 8 4 ,
x1
= –12, x2
= –4.
x1 2, = 2p D4 = 8 16 = 8 4 ,
x1
= –12, x2
= –4.
Следовательно, исходное уравнение имеет два корня:
–12 и –4.
259. ж) Решите уравнение x2 + 13x + 22 = 0.
Решение. Коэффициент p = 13 — нечётное число, поэтому для нахождения корней применим формулу (1). Так как D = p2 – 4q = 132 – 4 22 = 81, то
![]() x1 2, = 13 2 81 = 13 92 , x1 = –11, x2 = –2.
x1 2, = 13 2 81 = 13 92 , x1 = –11, x2 = –2.
Cледовательно, исходное уравнение имеет два корня: –11 и –2.
260. Докажите, что если q 0, то уравнение x2 + px + q = 0 имеет два различных корня.
Доказательство. Так как q 0, то D = p2 – 4q 0, поэтому уравнение имеет два различных корня.
В данном пункте доказываются теорема Виета и обратная ей теорема, которые часто используют при решении задач. Здесь также приводятся характерные примеры задач, решаемых при помощи этих теорем.
Желательно, чтобы все учащиеся знали формулировку теоремы Виета для приведённого квадратного уравнения. Для учащихся классов с углублённым изучением математики приводится формулировка теоремы Виета для квадратного уравнения общего вида.
Задания для повторения. При изучении данного пункта можно использовать задания 814, 815.
268. а) Не решая уравнение x2 – 7x + 12 = 0, определите знаки его корней.
Решение. Так как D = p2 – 4q = 49 – 48 = 1 0, то уравнение имеет два различных корня: x1 и x2, причём по теореме Виета x1 + x2 = 7, а x1x2 = 12. Произведение двух чисел x1 и x2 положительно, значит, они одного знака. Сумма этих чисел положительна, значит, оба корня
положительные.
271. а) Один из корней уравнения x2 + 5x – 14 = 0 равен 2. Найдите второй корень.
Решение. Так как один корень существует (x1 = 2), то существует и второй корень x2 (отличный от первого или совпадающий с ним). По теореме Виета x1 + x2 = –5, x1x2 = –14, т. е. 2 + x2 = –5 и 2x2 = –14, следовательно, x2 = –7.
272. Объясните, почему уравнение:
а) 5x2 – 8x – 284 = 0 не имеет корней одного знака;
б) 17x2 – 7x + 354 = 0 не имеет корней разных знаков.
Решение. а) Так как
![]() D4 ⎛⎜⎝2b⎞⎟⎠2 ac = (–4)2 – 5 (–284) 0, =
D4 ⎛⎜⎝2b⎞⎟⎠2 ac = (–4)2 – 5 (–284) 0, =
то уравнение имеет два различных корня x1
и x2, такие, что x1x2 =
– ![]() 0, поэтому уравнение не может
иметь корни одного знака.
0, поэтому уравнение не может
иметь корни одного знака.
б) Так как D = b2 – 4ac = (–7)2 – 4 17 354 0, то уравнение не имеет корней, тем более оно не может иметь корни разных знаков.
273. а) Известно, что x1 = 3 — корень уравнения
2x2 + 16x + a = 0.
Определите второй корень уравнения и число a.
Решение. Так как x1 =
3 — корень уравнения, то по теореме Виета верны равенства: 3 + x2
= –![]() , 3x2 =
, 3x2 = ![]() a2 , где x2
— второй корень уравнения. Из первого равенства получим x2
= –11, из второго равенства получим a = –66. 274.
Составьте квадратное уравнение, корни которого:
a2 , где x2
— второй корень уравнения. Из первого равенства получим x2
= –11, из второго равенства получим a = –66. 274.
Составьте квадратное уравнение, корни которого:
а) равны соответственно сумме и произведению корней
уравнения 3x2 + 2x – 15 = 0;
б) больше корней уравнения 3x2 – 11x + 2 = 0 на еди-
ницу;
в) меньше корней уравнения 2x2 – 13x + 3 = 0 в два
раза.
Решение. а) Так как
D = b2 – 4ac = 22 – 4 3 (–15) 0,
то уравнение имеет два
различных корня: x1 и x2. По теореме Виета x1
+ x2 = – ![]() , x1x2
=
, x1x2
= ![]() 315 =
–5. Если новое уравнение x2 + px + q =
0 имеет корни –
315 =
–5. Если новое уравнение x2 + px + q =
0 имеет корни – ![]() и –5, то по
и –5, то по
![]()
![]() теореме
Виета –p = 5 = , q =
2 ( 5) = 10
теореме
Виета –p = 5 = , q =
2 ( 5) = 10![]() .
.
3 3
Новое уравнение можно записать в виде
![]() x2 ( 17)x 10 = 0 или 3x2
+ 17x + 10 = 0.
x2 ( 17)x 10 = 0 или 3x2
+ 17x + 10 = 0.
3 3
б) Так как D = b2 – 4ac = (–11)2 –4 3 2 0, то уравнение имеет два различных корня: x1 и x2. По теореме
Виета x1 +
x2 = ![]() , x1x2
=
, x1x2
= ![]() . Если новое уравнение x2
+ px + q = 0 имеет корни x1 +
1 и x2 + 1, то по теореме
. Если новое уравнение x2
+ px + q = 0 имеет корни x1 +
1 и x2 + 1, то по теореме
Виета
–p = x1 +
1 + x2 + 1 = x1
+ x2 + 2 = ![]() +
2 =
+
2 = ![]() , q = (x1
+ 1)(x2 + 1) = x1x2
+ x1 + x2 + 1 =
, q = (x1
+ 1)(x2 + 1) = x1x2
+ x1 + x2 + 1 =
![]() +
+ ![]() + 1 =
+ 1 =
![]() . Новое уравнение можно записать в виде x2
–
. Новое уравнение можно записать в виде x2
– ![]() x +
x + ![]() =
0 или 3x2 – 17x + 16 =
0. в) Так как
=
0 или 3x2 – 17x + 16 =
0. в) Так как
D = b2 – 4ac = (–13)2 – 4 2 3 0,
то уравнение имеет два
различных корня: x1 и x2. По теореме Виета x1
+ x2 = ![]() , x1x2
=
, x1x2
= ![]() . Если новое уравнение x2
+ px + q = 0 имеет корни x1 и x2 , то по теореме
. Если новое уравнение x2
+ px + q = 0 имеет корни x1 и x2 , то по теореме
2 2
Виета
–p = x![]() 1 x2 = x1 x2 =
1 x2 = x1 x2 = ![]() , q = x
, q = x![]() 1 x2 x x1 2
1 x2 x x1 2 ![]() 3 .
3 .
Новое уравнение
можно записать в виде x2 – ![]() x +
x +
![]() = 0 или 8x2
– 26x + 3 = 0.
= 0 или 8x2
– 26x + 3 = 0.
275. Числа x1 и x2 — корни уравнения x2 – 2000x + + 1999 = 0. Составьте квадратное уравнение, корни которого –x1 и –x2.
Решение. Так как x1 и x2 — корни уравнения
x2 – 2000x + 1999 = 0,
то по теореме Виета x1 + x2 = 2000, x1x2 = 1999.
Составим квадратное уравнение x2 + px + q = 0, корни которого –x1 и –x2. По теореме Виета
p = –(–x1 – x2) = x1 + x2 = 2000, q = (–x1)(–x2) = x1x2 = 1999.
Искомое квадратное уравнение x2 + 2000x + 1999 = 0.
![]() Замечание. Если заметить, что x1
= 1 — корень данного уравнения, и найти x2 = 1999,
то задачу можно решить проще.
Замечание. Если заметить, что x1
= 1 — корень данного уравнения, и найти x2 = 1999,
то задачу можно решить проще.
Надо обратить внимание учащихся, что корнями квадратного уравнения часто бывает число 1 (в случае a + b + c = 0) или число –1 (в случае a – b + c = 0). Если обнаружен корень квадратного уравнения, то второй корень находится с помощью теоремы, обратной теореме Виета.
276. а) Решите устно квадратное уравнение x2 + 2000x – 2001 = 0.
Решение. Число 1 — корень уравнения, так как 12 + 2000 1 – 2001 = 0.
По теореме Виета 1 + x2 = 2000, 1 x2 = 1999, следова-
тельно, корни уравнения 2 + 3xx 1 –= 11 , = x02 имеет два корня = 1999. x1 и
277. Уравнение x x2. Вычислите:
г) x12 + x22 ; д) x13 + x23 ; е) (x1 – x2)2.
Решение. Так как в приведённом уравнении q 0, т. е. D 0, то оно имеет два различных корня x1 и x2, причём x1 + x2 = –3, x1x2 = –1.
г) x12 + x22 = x12 + 2x1x2 + x22 – 2x1x2 = (x1 + x2)2 –
– 2x1x2 = (–3)2 – 2 (–1) = 11;
д) x13 + x23 = (x1 + x2)( x12 – x1x2 + x22 ) = (x1 + x2)
((x1 + x2)2 – 3x1x2) = (–3) ((–3)2 – 3 (–1)) = –36;
е) (x1 – x2)2 = x12 – 2x1x2 + x22 = (x1 + x2)2 – 4x1x2 = = (–3)2 – 4 (–1) = 13.
Промежуточный контроль. С–6, С–13*.
В данном пункте приводятся два примера применения квадратных уравнений к решению текстовых задач.
Задания для повторения. При изучении данного пункта можно использовать задания 956, 957.
284. а) Одна из цифр двузначного числа на 2 больше другой, а сумма квадратов этого числа и числа, полученного от перестановки его цифр, равна 4034. Найдите это число.
Решение. Пусть x — число десятков, тогда x + 2 — число единиц. Поэтому двузначное число равно 10x + x + + 2 = 11x + 2, а число, полученное от перестановки его цифр, равно 10(x + 2) + x = 11x + 20. Составим уравнение:
(11x + 2)2 + (11x + 20)2 = 4034.
Решив это уравнение, получим единственный его натуральный корень 3. Следовательно, искомое число 35.
Если x — число единиц, а (x + 2) — число десятков, то, повторяя рассуждения, пришли бы к тому же уравнению. В этом случае искомое число 53. Ответ. 35, 53.
285. в) Возможен ли такой прямоугольный треугольник, стороны которого выражаются тремя последовательными натуральными числами? тремя последовательными чётными числами? тремя последовательными нечётными числами?
г) В каком выпуклом многоугольнике число сторон
равно числу его диагоналей?
Решение. в) Пусть n и n + 1 — длины катетов, n + 2 — длина гипотенузы (она больше длины каждого из катетов). По теореме Пифагора составим уравнение:
n2 + (n + 1)2 = (n + 2)2.
Решив это уравнение, получим единственный его натуральный корень n = 3, следовательно, возможен единственный прямоугольный треугольник, стороны которого выражаются тремя последовательными натуральными числами: 3, 4, 5.
Тогда очевидно, что, умножив на 2 длины сторон полученного треугольника, можно найти длины сторон подобного ему прямоугольного треугольника, которые выражаются тремя последовательными чётными числами:
6, 8, 10, и такой треугольник единственный.
Если 2n и 2n + 2 — длины катетов, 2n + 4 — длина его гипотенузы, то (2n)2 + (2n + 2)2 = (2n + 4)2. Это уравнение имеет единственный натуральный корень n = 3.
Если длины сторон двух катетов выражены нечётными числами, то сумма их квадратов чётна. Она не может быть равной квадрату гипотенузы, длина которой выражена нечётным числом. Следовательно, прямоугольный треугольник, стороны которого выражаются тремя последовательными нечётными числами, невозможен.
г) В выпуклом n-угольнике число диагоналей равно
![]()
![]() n n n
n
n n n
n
![]() . Составим уравнение:
. Составим уравнение: ![]() = n.
= n.
2 2
Решив это уравнение, получим единственный его натуральный корень n = 5, следовательно, условие задачи выполнено только в выпуклом пятиугольнике.
286. а) Выпускники одного класса решили после окончания школы обменяться фотографиями — каждый с каждым. Сколько выпускников было в классе, если всего было роздано 930 фотографий?
б) Несколько человек при встрече приветствовали друг друга рукопожатиями. Сколько человек встретилось, если всего рукопожатий было 21?
Решение. а) Пусть было x учащихся, тогда каждый получил по (x – 1) фотографии и всех фотографий было x(x – 1), что по условию задачи равно 930. Составим уравнение: x(x – 1) = 930,
оно имеет два корня: x1 = –30, x2 = 31. Так как x 0, то выпускников было 31.
б) Пусть было x человек, тогда каждый сделал по
![]() x x
x x
(x – 1) рукопожатию.
Рукопожатий было ![]() ,
так как
,
так как
2
каждое рукопожатие в произведении x(x – 1) посчитано дважды. Составим уравнение:
![]() x x
x x
![]() =
21,
=
21,
2
оно имеет два корня: x1 = –6, x2 = 7. Так как x 0, то встретились 7 человек.
288. Оптовый склад покупает товар по 800 р. и продаёт его, повысив цену на некоторое число процентов. Магазин покупает тот же товар на оптовом складе и продаёт его, повысив цену на число процентов, в 1,5 раза большее, чем оптовый склад. В результате цена товара в магазине составляет 1248 р. На сколько процентов увеличивает цену оптовый склад? магазин?
Решение. Пусть оптовый склад повышает цену на x
процентов, а магазин — на 1,5x процентов. Тогда оптовый склад продаёт
товар по 800(1 + ![]() x ) р., а магазин
x ) р., а магазин
100
![]()
![]() продаёт по 800(1 +
x )(1
+ ) р. Составим уравнение: 100
продаёт по 800(1 +
x )(1
+ ) р. Составим уравнение: 100
![]() 800(1 + x )(1 + ) =
1248,
800(1 + x )(1 + ) =
1248,
100
которое перепишем в виде
3x2 + 500x – 11 200 = 0.
Условию задачи удовлетворяет только положительный корень этого квадратного уравнения x = 20; тогда 1,5x = 30, следовательно, оптовый склад повышает цену на 20 %, а магазин ещё на 30 %.
289. Цена товара составляла 500 р. После двух повышений цены товар стоил 546 р. Известно, что во второй раз цена увеличилась на число процентов, меньшее на 1, чем в первый раз. На сколько процентов увеличилась цена в первый раз? во второй раз?
Решение. Пусть первое повышение цены составило x
процентов, а второе — (x – 1) процентов. Составим уравнение:
500(1 + ![]() x )(1 +
x )(1 +
![]() x 1 ) =
546,
x 1 ) =
546,
100 100
которое перепишем в виде x2 + 199x – 1020 = 0.
Условию задачи удовлетворяет только положительный корень этого уравнения x = 5; тогда x – 1 = 4, следовательно, первое повышение цены составило 5 %, а второе — 4 %.
Промежуточный контроль. С–7, С–14*, Т–4, К–3.
Основная цель пятого параграфа — научить учащихся решать рациональные уравнения и применять их к решению текстовых задач. Работа по освоению различных методов решения упражнений и задач способствует достижению таких метапредметных результатов, как умение создавать обобщения, устанавливать аналогии, устанавливать причинно-следственные связи, строить логические рассуждения, умозаключения и делать выводы.
В данном пункте вводится понятие рационального уравнения, напоминается, что такое корень уравнения, что значит решить уравнение и какие уравнения называют равносильными, а также какие равносильные преобразования известны из курса 7 класса.
293. Равносильны ли уравнения:
а) x +
2 = 3 и x + 5 = 6; д)
![]() x2 x = 0 и
x2 x = 0 и ![]() x 1 =
0? x 1 x 1 Решение.
а) Оба уравнения имеют корень — число 1 и других корней не имеют,
следовательно, они равносильны;
x 1 =
0? x 1 x 1 Решение.
а) Оба уравнения имеют корень — число 1 и других корней не имеют,
следовательно, они равносильны;
д) первое уравнение имеет корень 0, а второе уравнение такого корня не имеет, следовательно, уравнения неравносильны.
В данном пункте вводится понятие биквадратного уравнения и разбирается новый приём решения уравнения при помощи замены неизвестного. Рассматриваются характерные примеры решения биквадратных уравнений.
Здесь следует обратить внимание учащихся на терминологию, которая должна стать привычной при устном обосновании решения уравнения: сделаем замену неизвестного
y = …, (1)
получим квадратное уравнение …, решим его, подставим найденные значения y в равенство (1) и решим полученные уравнения относительно x.
Способ замены неизвестного будет применяться и при решении рациональных уравнений, поэтому этим приёмом решения уравнений должны овладеть все учащиеся.
299. Решите уравнение:
а) x4 + 6x2 + 9 = 0; б) x4 – 14x2 – 15 = 0.
Решение. а) Сделаем замену неизвестного y = x2, получим квадратное уравнение y2 + 6y + 9 = 0. Оно имеет единственный корень y = –3.
Теперь решим уравнение x2 = –3. Оно не имеет корней, следовательно, исходное уравнение не имеет корней.
б) Сделаем замену неизвестного y = x2, получим квад-
ратное уравнение y2 – 14y – 15 = 0. Оно имеет два корня:
![]()
![]() y1 =
Теперь решим два уравнения: –1, y2 = 15. x2
= –1 и x2
= 15. Первое из них не имеет корней, второе имеет два корня: – 15 и 15 .
Следовательно, исходное уравнение имеет два корня: – 15
и 15 .
y1 =
Теперь решим два уравнения: –1, y2 = 15. x2
= –1 и x2
= 15. Первое из них не имеет корней, второе имеет два корня: – 15 и 15 .
Следовательно, исходное уравнение имеет два корня: – 15
и 15 .
Замечание. Если в задании «а» учащиеся заметят полный квадрат, то получат более простое решение. Уравнение (x2 + 3)2 = 0 не имеет корней, так как x2 + 3 0 для любого x.
В данном пункте приводится пример решения уравнения вида A (x) B (x) = 0, где A (x) и B (x) — многочлены относительно x. Такие уравнения называют распадающимися. Рассматриваются примеры уравнений, которые после разложения левой части на множители становятся распадающимися.
Учащимся обычного класса достаточно действовать по правилу:
Чтобы решить распадающееся уравнение A (x) B (x) = = 0, где A (x) и B (x) — многочлены, надо решить каждое из уравнений A (x) = 0 и B (x) = 0 и объединить все найденные корни.
В классе с углублённым изучением математики можно ввести понятие совокупности уравнений.
Если даны два уравнения и требуется найти все числа x, каждое из которых является корнем или первого, или второго уравнения, то говорят, что дана совокупность этих уравнений, а каждый корень каждого из уравнений называют решением совокупности данных уравнений.
Используя знак равносильности () и знак совокупности ( [ ), можно записать: если A (x) и B (x) — многочлены, то
![]() A x( ) = 0
A x( ) = 0
A (x) B (x) = 0 B x( ) = 0 .
Задания для повторения. При изучении данного пункта можно использовать задания 806, 826.
304. Решите уравнение:
а) x3 + 5x2 + 6x = 0; в) x4 = 2x3 + 3x2.
Решение. а) Разложим левую часть уравнения на множители: x (x2 + 5x + 6) = 0.
Уравнение x = 0 имеет единственный корень 0, уравнение x2 + 5x + 6 = 0 имеет два корня: –2 и –3.
Следовательно, исходное уравнение имеет три корня:
0, –2, –3.
в) Перенесём все члены уравнения в левую часть, раз-
ложим левую часть уравнения на множители: x2 (x2 – 2x – 3) = 0.
Уравнение x2 = 0 имеет единственный корень 0, уравнение x2 – 2x – 3 = 0 имеет два корня: –1 и 3.
Следовательно, исходное уравнение имеет три корня: –1, 0, 3.
306. Найдите все значения a, при каждом из которых уравнение
(x – 1)(x2 – 6x + a) = 0 (1) имеет ровно два корня.
Решение. Уравнение (1) имеет очевидный корень 1, и ровно два корня оно имеет тогда и только тогда, когда уравнение
x2 – 6x + a = 0 (2)
или имеет два различных корня, один из которых равен 1, или имеет единственный корень, отличный от 1.
1) Уравнение (2) имеет корень 1, если 12 – 6 1 + a = 0,
т. е. при a = 5. В этом случае уравнение (2) имеет корни 1 и 5 и уравнение (1) имеет ровно два корня: 1 и 5.
2)
Уравнение (2) имеет единственный корень, если ![]() D = (3)2
– a = 9 – a = 0, т. е. при a =
9. В этом случае
D = (3)2
– a = 9 – a = 0, т. е. при a =
9. В этом случае
4
уравнение (2) имеет единственный корень 3 и уравнение (1) имеет ровно два корня: 1 и 3. Ответ. 5, 9.
826. Решите уравнение:
б) x3 + x2 + x + 1 = 0; в) 2x4 + 5x3 – 5x – 2 = 0.
Решение. Разложению многочлена на множители помогает наблюдательность. В задании «б» имеется очевидный корень –1, поэтому надо стараться выделить множитель x + 1. В заданиях «б» и «в» группировку слагаемых подсказывают коэффициенты.
б) Разложив левую часть уравнения на множители,
перепишем уравнение в виде
(x + 1)(x2 + 1) = 0.
Уравнение x + 1 = 0 имеет единственный корень –1, уравнение x2 + 1 = 0 не имеет корней, поэтому исходное уравнение имеет единственный корень –1.
в) Разложим левую часть уравнения на множители:
2x4 + 5x3 – 5x – 2 = 2(x4 – 1) + 5x(x2 – 1) = = 2(x2 – 1)(x2 + 1) + 5x(x2 – 1) = (x2 – 1)(2x2 + 5x + 2). Перепишем уравнение в виде
(x2 – 1)(2x2 + 5x + 2) = 0.
Уравнение x2 – 1 =
0 имеет два корня: –1 и 1, уравнение 2x2 + 5x
+ 2 = 0 имеет два корня: –2 и – ![]() , поэтому
исходное уравнение имеет четыре корня: –2, –1, –
, поэтому
исходное уравнение имеет четыре корня: –2, –1, – ![]() , 1.
, 1.
В данном пункте разбираются характерные примеры решения уравнений вида
![]() P x( ) = 0,
(1)
P x( ) = 0,
(1)
Q x( )
где P(x) и Q(x) — многочлены относительно x.
При решении уравнения (1) учащимся обычного класса достаточно следовать правилу, сформулированному в учебнике.
В классе с углублённым изучением математики можно дать следующее определение:
Если дано уравнение P(x) = 0 и неравенство Q(x) 0, где P(x) и Q(x) — многочлены относительно x, и требуется найти все корни уравнения P(x) = 0, удовлетворяющие неравенству Q(x) 0, то говорят, что надо решить систему, состоящую из этого уравнения и неравенства. Эту систему записывают так:
⎧ P(x) = 0,
⎨⎩Q(x) 0.
Решить такую систему — значит найти все корни уравнения P(x) = 0, удовлетворяющие неравенству Q(x) 0.
Для учащихся класса с углублённым изучением математики можно сформулировать следующее утверждение:
P(x)
Уравнение ![]() = 0, где P(x) и Q(x)
— многочлены
= 0, где P(x) и Q(x)
— многочлены
Q(x)
относительно x, равносильно системе ⎨⎩Q(x) 0.
Это утверждение можно записать с использованием знаков равносильности и системы:
P(x) ⎧P(x) = 0, ![]() Q(x) = 0 ⎨⎩Q(x)
0.
Q(x) = 0 ⎨⎩Q(x)
0.
а) ![]() x 7 = 0;
в)
x 7 = 0;
в) ![]() x2 7x 5
= 0.
x2 7x 5
= 0.
Решение. а) Уравнение x2 – 2x + 1 = 0 имеет единственный корень 1. При x = 1 знаменатель дроби отличен от нуля. Следовательно, исходное уравнение имеет единственный корень 1;
в) уравнение x2 – 2x + 3 = 0 не имеет корней. Следо-
вательно, исходное уравнение не имеет корней.
315. Найдите все значения a, при каждом из которых уравнение
x2 4x a
![]() = 0 (1)
x 1
= 0 (1)
x 1
имеет единственный корень.
Решение. Уравнение (1) имеет единственный корень тогда и только тогда, когда уравнение
x2 – 4x + a = 0 (2)
или имеет два различных корня, один из которых равен –1 (он обращает знаменатель дроби в нуль и не является корнем уравнения (1)), или имеет единственный корень, отличный от –1.
1) Уравнение (2) имеет корень –1, если (–1)2 – 4 (–1) + + a = 0, т. е. при a = –5. В этом случае уравнение (2) имеет два корня: –1 и 5, а уравнение (1) имеет единственный корень 5.
2) Уравнение (2) имеет единственный корень, если
![]() D = (–2)2
– a = 4 – a = 0,
D = (–2)2
– a = 4 – a = 0,
4
т. е. при a = 4. В этом случае уравнение (2) имеет единственный корень 3 и уравнение (1) имеет единственный корень 3.
Ответ. –5, 4.
В данном пункте разбираются характерные примеры решения рациональных уравнений, приводимых к виду
P x( )
![]() = 0, где P(x) и Q(x)
— многочлены относительно x.
= 0, где P(x) и Q(x)
— многочлены относительно x.
Q x( )
Эти решения обобщены в виде правила, следуя которому учащиеся должны решать уравнения.
После правила в учебнике приводится замечание, говорящее о том, что отклонение от этого правила может привести к потере корней или к приобретению посторонних корней.
Здесь можно привести такие примеры. Пример 1. Решим уравнение
![]() x2 3x =
x2 3x = ![]() . (1) x 3 x 3
. (1) x 3 x 3
Если решать уравнение (1) не по правилу, а сократить дроби в обеих частях уравнения на x – 3, то получится уравнение x = 3, не равносильное исходному уравнению. Такое «решение» приводит к приобретению постороннего корня 3, так как на самом деле уравнение (1) корней не имеет.
Пример 2. Решим уравнение
![]() x2 2x = 35 . (2) x 7 x 7
x2 2x = 35 . (2) x 7 x 7
Некоторые учащиеся для решения этого уравнения применяют такой «способ решения». Умножив обе части уравнения на x + 7, получают уравнение
x2 + 2x = 35. (3)
Решив уравнение (3), находят два его корня: x1 = 5 и x2 = –7. Эти два числа по ошибке считают корнями и уравнения (2), хотя x2 не является корнем уравнения (2), так как обращает знаменатели дробей в двух частях уравнения в нуль.
Ошибка происходит из-за того, что переход от уравнения (2) к уравнению (3) не является равносильным переходом, т. е. уравнение (3) неравносильно уравнению (2). Уравнение (3) является следствием уравнения (2). Об уравнениях-следствиях будет рассказано в п. 5.8.
Задания для повторения. При изучении данного пункта можно использовать задания 831, 832.
Решения и комментарии 317. Равносильны ли уравнения:
б) ![]() = 0 и x 2 =
0; x 5 x 5
= 0 и x 2 =
0; x 5 x 5
![]()
![]() в) x 3 = 0 и = 0;
x 1 x
1
в) x 3 = 0 и = 0;
x 1 x
1
г) 2x = x и 2 = 1? x 1 x 1
Решение. б) Если второе уравнение умножить на число 2, то получим первое уравнение. Так как умножение уравнения на число, отличное от нуля, — это равносильное преобразование, то уравнения равносильны;
в) если записать левую часть первого уравнения в виде дроби (сложить алгебраические дроби), то получим второе уравнение. Следовательно, данные уравнения равносильны;
г) уравнения неравносильны, так как первое уравне-
ние имеет корень 0, который не является корнем второго уравнения.
324. а) Решите уравнение
![]() x 40 x 39 = 39 40 .
x 40 x 39 = 39 40 .
39 40 x 40 x 39
Решение. Сложив дроби в обеих частях уравнения и перенеся все члены полученного уравнения в левую часть, перепишем его в виде
![]() (79x 3121)(x2 79x) = 0. (4)
(79x 3121)(x2 79x) = 0. (4)
![]()
Уравнение (79x – 3121)(x2
– 79x) = 0 имеет три корня: x1
= 39 ![]() , x2 = 0,
x3 = 79. Ни одно из этих чисел не обращает в
нуль знаменатель 39 40 (x – 40)(x – 39)
дроби в уравнении (4). Следовательно, эти числа являются корнями уравнения (4),
а значит, и равносильного ему исходного уравнения.
, x2 = 0,
x3 = 79. Ни одно из этих чисел не обращает в
нуль знаменатель 39 40 (x – 40)(x – 39)
дроби в уравнении (4). Следовательно, эти числа являются корнями уравнения (4),
а значит, и равносильного ему исходного уравнения.
Промежуточный контроль. С–8.
В данном пункте рассматриваются две задачи, решения которых приводят к рациональным уравнениям.
За время, отведённое на изучение данного пункта, скорее всего, не удастся решить все задачи из этого пункта, да это и не надо. Следует отобрать наиболее поучительные, по мнению учителя, задачи, а остальные использовать для организации текущего повторения при изучении следующих пунктов учебника.
Отметим, что на этапе первоначального обучения решению текстовых задач, приводящих к уравнению вида
P x( )
![]() =
0, желательно не нарушать процедуру решения та-
=
0, желательно не нарушать процедуру решения та-
Q x( )
кого уравнения, т. е. находить все корни уравнения P(x) = 0 и выбирать из них те, которые не обращают в нуль знаменатель дроби Q(x). Только после этого отбирать корни, удовлетворяющие условиям задачи.
327. а) Расстояние между двумя населёнными пункта-ми 50 км. Из этих пунктов одновременно навстречу друг другу выехали мотоциклист и велосипедист. Скорость мотоциклиста на 30 км/ч больше скорости велосипедиста. Встретились они на расстоянии 10 км от одного из населённых пунктов. Какова скорость велосипедиста?
Решение. Встреча произошла в 10 км от пункта, из которого выехал велосипедист, так как за одно и то же время мотоциклист, двигавшийся с большей скоростью, проехал большее расстояние. Итак, велосипедист проехал 10 км, а мотоциклист 50 – 10 = 40 (км).
Пусть скорость велосипедиста x км/ч, тогда время его
движения 10![]() ч. Скорость
мотоциклиста (x + 30) км/ч, тогx
ч. Скорость
мотоциклиста (x + 30) км/ч, тогx
да время
его движения ![]() 40 ч. До встречи они
затрати-
40 ч. До встречи они
затрати-
x 30
ли одинаковое время. Составим уравнение:
|
которое перепишем в виде |
|
(1) |
![]()
![]() = 0.
(2) x x
= 0.
(2) x x![]()
Уравнение 30x – 300 = 0 имеет единственный корень x1 = 10. Число x1 не обращает в нуль знаменатель дроби в уравнении (2), следовательно, x1 — корень уравнения (2), а значит, и равносильного ему уравнения (1), следовательно, скорость велосипедиста равна 10 км/ч.
328. Расстояние между городами А и В 60 км. Из города А в город В выезжают одновременно две автомашины. Скорость первой на 20 км/ч больше скорости второй. И она прибывает в город В на полчаса раньше. Определите скорость каждой автомашины.
Решение. Пусть скорость второй автомашины x
км/ч и она проехала 60 км за ![]() 60 ч, тогда скорость первой автоx
60 ч, тогда скорость первой автоx
машины (x + 20)
км/ч и она проехала 60 км за ![]() 60 ч, x 30
60 ч, x 30
![]()
![]() что на ч меньше, чем
60
ч. Составим уравнение: x
что на ч меньше, чем
60
ч. Составим уравнение: x
![]() 60 –
60
= , (3) x
x 20
60 –
60
= , (3) x
x 20
которое перепишем в виде
![]() x2 20x 2400 = 0. (4)
x2 20x 2400 = 0. (4)
2x x( 20)
Уравнение x2 + 20x – 2400 = 0 имеет корни 40 и –60, которые не обращают в нуль знаменатель 2x(x + 20) дроби, следовательно, это корни уравнения (4), а значит, и равносильного ему уравнения (3). Но скорость движения положительна, следовательно, скорость второй автомашины 40 км/ч, а скорость первой машины 60 км/ч.
При кратком оформлении решения текстовых задач иногда используют таблицу. Учащимся полезно запомнить, что сначала они должны заполнить два столбца таблицы, затем при помощи этих столбцов заполнить третий. А при помощи третьего столбца они должны составить уравнение.
330. а) На обработку одной детали первый рабочий затрачивает на 1 мин меньше, чем второй. Сколько деталей обработает каждый из них за 4 ч, если первый рабочий обрабатывает за это время на 8 деталей больше, чем второй?
Решение. Пусть за 4 ч второй рабочий сделал x деталей.
|
|
Время работы, ч |
Число деталей |
Время, затраченное на 1 деталь, ч |
|
1-й рабочий |
4 |
x + 8 |
4
x 8 |
|
2-й рабочий |
4 |
x |
4
x |
Первый рабочий на обработку одной
детали затрачивал на ![]() ч меньше, чем второй. Составим уравнение:
ч меньше, чем второй. Составим уравнение:
![]()
![]() 4 –
4
= , (5) x
x 8
4 –
4
= , (5) x
x 8
которое перепишем в виде
x2 8x 1920
![]() = 0.
(6)
= 0.
(6)
60x x( 8)
Уравнение x2 + 8x – 1920 = 0 имеет корни 40 и –48, которые не обращают в нуль знаменатель 60x(x + 8) дроби, следовательно, это корни уравнения (6), а значит, и равносильного ему уравнения (5). Так как число деталей положительно, то второй рабочий за 4 ч обрабатывает 40 деталей, а первый 40 + 8 = 48 (деталей).
332. б) Автомашина должна была пройти 840 км. В середине пути водитель остановился на обед, а через час продолжил путь. Чтобы прибыть вовремя в пункт назначения, пришлось увеличить скорость на 10 км/ч. Сколько времени занял весь путь, включая время на остановку?
Решение. Пусть x ч — время движения по плану на участке длиной 420 км.
|
|
Путь, км |
Время движения, ч |
Скорость, км/ч |
|
По плану |
420 |
x |
420
x |
|
Фактически |
420 |
x – 1 |
420
x 1 |
Скорость движения была увеличена на 10 км/ч по сравнению с планом, составим уравнение:
![]() 420 –
420
= 10, (7) x 1 x
420 –
420
= 10, (7) x 1 x
которое перепишем в виде
x2 x 42
![]() = 0.
(8) x x( 1)
= 0.
(8) x x( 1)
Уравнение x2 – x – 42 = 0 имеет корни 7 и –6, которые не обращают в нуль знаменатель x(x – 1) дроби, следовательно, это корни уравнения (8), а значит, и уравнения (7). Время движения — величина положительная, т. е. на вторую половину пути по плану должно быть затрачено 7 ч. На весь путь с остановкой затрачено в 2 раза больше времени, т. е. 14 ч.
333. Первый пешеход может пройти расстояние между двумя пунктами на 5 ч быстрее, чем второй. Если пешеходы выйдут из этих пунктов одновременно навстречу друг другу, то встретятся через 6 ч. За сколько часов каждый из них может пройти это расстояние?
Решение. Пусть второй пешеход может пройти всё
расстояние за x ч, тогда первый может пройти это расстояние за x +
5 ч. В час второй пешеход проходит ![]() 1 , x
1 , x
![]() первый
—
первый
— ![]() 1 , а
вместе они проходят часть этого
1 , а
вместе они проходят часть этого
x 5
расстояния. Составим уравнение:
![]()
![]() 1 +
1
= , (9) x
x 5
1 +
1
= , (9) x
x 5
которое перепишем в виде
x2 7x 30
![]() = 0. (10)
= 0. (10)
6x x( 5)
Уравнение x2 – 7x – 30 = 0 имеет корни 10 и –3, не обращающие в нуль знаменатель 6x(x + 5) дроби, следовательно, это корни уравнения (10), а значит, и уравнения (9). Условиям задачи удовлетворяет корень 10, т. е. второй пешеход может пройти всё расстояние за 10 ч, а первый — за 10 + 5 = 15 (ч).
337. Задача Безу. Некто купил лошадь и спустя некоторое время продал её за 24 пистоля. При этой продаже он теряет столько процентов, сколько стоила ему лошадь. Спрашивается: за какую сумму он её купил?
![]() Решение.
Пусть некто купил лошадь за x пистолей. Продав её за 24 пистоля, он
потерял на этой продаже x – 24 пистоля. Выразим убыток в
процентах: x 24 100. x
Решение.
Пусть некто купил лошадь за x пистолей. Продав её за 24 пистоля, он
потерял на этой продаже x – 24 пистоля. Выразим убыток в
процентах: x 24 100. x
По условию задачи он равен x. Составим уравнение:
![]() x 24 100 = x, (11) x
x 24 100 = x, (11) x
которое перепишем в виде
x2 100x 2400
![]() = 0.
(12) x
= 0.
(12) x
Уравнение x2 – 100x + 2400 = 0 имеет корни 40 и 60, которые не обращают в нуль знаменатель x дроби, следовательно, это корни уравнения (12), а значит, и равносильного ему уравнения (11). Оба корня удовлетворяют условиям задачи, следовательно, задача имеет два решения: лошадь стоит или 40, или 60 пистолей.
Промежуточный контроль. С–9, К–4.
В данном пункте на характерных примерах разбирается способ решения рациональных уравнений при помощи замены неизвестного. Пункт предназначен для классов с углублённым изучением математики. Стоит обратить внимание на п. 10 дидактических материалов. Там разобраны решения достаточно сложных задач.
Замену неизвестного при решении уравнений полезно обсудить и в обычном классе, ограничив сложность рассматриваемых примеров.
Задания для повторения. При изучении данного пункта можно использовать задания 817, 824, 825, 828.
Решения и комментарии 340. Решите уравнение:
![]() а) ⎛⎜⎝
а) ⎛⎜⎝![]() 2x x 1⎞⎟⎠2 2 ⎛⎝⎜
2x x 1⎞⎟⎠2 2 ⎛⎝⎜![]() 2x x 1⎟⎠⎞ = 3; б) 2x x 1 2x x 1 = 2.
2x x 1⎟⎠⎞ = 3; б) 2x x 1 2x x 1 = 2.
Решение. а) Сделаем замену неизвестного: y = 2x 1,
x
получим квадратное уравнение y2 – 2y = 3, которое имеет два корня: –1 и 3. Теперь найдём корни исходного уравнения, решив два уравнения:
1) ![]() 2x 1 = –1 и 2)
2x 1 = –1 и 2) ![]() 2x 1 =
3. x x
2x 1 =
3. x x
Уравнение 1) имеет единственный корень – ![]() , уравнение
2) имеет единственный корень 1. Эти числа и являются корнями исходного
уравнения.
, уравнение
2) имеет единственный корень 1. Эти числа и являются корнями исходного
уравнения.
б)
Сделаем замену неизвестного: y = ![]() x ,
тогда
x ,
тогда
2x 1
2x 1 1
![]() = . Получим
уравнение x y
= . Получим
уравнение x y
y
+ ![]() 1 =
2. (1) y
1 =
2. (1) y
Уравнение (1) имеет единственный корень 1.
Теперь решим уравнение
![]() x = 1.
(2)
x = 1.
(2)
2x 1
Уравнение (2) имеет единственный корень –1, следовательно, число –1 является корнем исходного уравнения. 341. Решите уравнение:
а) x(x + 2)(x + 3)(x + 5) = 72;
в) x2 – 9x + 13 + ![]() x2 91x 15
= 0.
x2 91x 15
= 0.
Решение. а) Если раскрыть скобки в левой части уравнения, то получится уравнение четвёртой степени, которое трудно решить. Попробуем заменой неизвестного привести исходное уравнение к квадратному. Умножим первый множитель на четвёртый, а второй на третий. Получим уравнение
(x2 + 5x)(x2 + 5x + 6) = 72. (3)
Сделаем замену неизвестного: y = x2 + 5x, получим уравнение
y(y + 6) = 72. (4)
Уравнение (4) имеет два корня: y1 = 6, y2 = –12.
Чтобы найти корни исходного уравнения, решим два уравнения:
1) x2 + 5x = 6 и 2) x2 + 5x = –12.
Уравнение 1) имеет два корня: 1 и –6, уравнение 2) не имеет корней. Следовательно, исходное уравнение имеет два корня: 1 и –6.
в) Сделаем замену неизвестного: y = x2 – 9x + 15, по-
лучим уравнение
1 y
+ ![]() –
2 = 0. (5) y
–
2 = 0. (5) y
Уравнение (5) имеет единственный корень y1 = 1.
Чтобы найти корни исходного уравнения, решим уравнение
x2 – 9x + 15 = 1. (6)
Уравнение (6) имеет два корня: 2 и 7. Следовательно, исходное уравнение имеет два корня: 2 и 7.
342.
в) Решите уравнение ![]() xx22 xx 13 xx22 xx
42 = 5.
xx22 xx 13 xx22 xx
42 = 5.
Решение. Чтобы упростить решение уравнения, сначала выделим целую часть каждой дроби:
![]() xx22 xx 13
xx22 xx 42 = x2x 2 x x 1 1 2 x2x 2
x x 2 2 =
xx22 xx 13
xx22 xx 42 = x2x 2 x x 1 1 2 x2x 2
x x 2 2 =
= 1 x2 2x 1 1 x2 2x 2 = 2 x2 2x 1 x2 2x 2 .
Теперь уравнение запишется проще: ![]() x2 2x 1 x2
2x 2 = 3. (7)
x2 2x 1 x2
2x 2 = 3. (7)
Сделаем замену неизвестного: y = x2 – x + 1, получим уравнение
![]() 2 2 = 3. (8)
2 2 = 3. (8)
y y 1
Уравнение (8) имеет два корня: y1
= 1, y2 = – ![]() .
.
Чтобы найти корни исходного уравнения, решим два уравнения:
1) x2 – x + 1 = 1
и 2) x2 – x + 1 = – ![]() .
.
Уравнение 1) имеет два корня: 0 и 1, уравнение 2) не имеет корней. Следовательно, исходное уравнение имеет два корня: 0 и 1.
![]() 828. а) Решите
уравнение x 6
x
=
5 .
828. а) Решите
уравнение x 6
x
=
5 .
![]() Решение.
Сделаем замену неизвестного: y = x
, получим уравнение
Решение.
Сделаем замену неизвестного: y = x
, получим уравнение
y2 – 6y + 5 = 0. (9)
Уравнение (9) имеет два корня: y1 = 1, y2 = 5.
Чтобы найти корни исходного уравнения, решим два уравнения:
![]()
![]() 1) x = 1 и 2) x = 5.
1) x = 1 и 2) x = 5.
Уравнение 1) имеет единственный корень 1, уравнение 2) имеет единственный корень 25. Следовательно, исходное уравнение имеет два корня: 1 и 25. Промежуточный контроль. С–10*.
В данном пункте, предназначенном для классов с углублённым изучением математики, вводится понятие уравнения-следствия и приводятся три способа перехода к уравнению-следствию:
1) освобождение уравнения от знаменателя, т. е. заме-
на уравнения f x( ) = 0 уравнением f(x) = 0 (f(x) и g(x) — g x( )
многочлены относительно x);
2) приведение подобных членов уравнения, т. е. замена разности f(x) – f(x) нулём;
3) возведение уравнения в квадрат, т. е. замена уравнения f(x) = g(x) уравнением f2(x) = g2(x).
Важно отметить, что если при решении уравнения был выполнен переход к уравнению-следствию, то необходимо проверить, являются ли корни полученного уравнения корнями исходного уравнения.
343. а) Решите уравнение
![]() x2 2x 15 =0. x 3
x2 2x 15 =0. x 3
Решение. Освобождая уравнение от знаменателя, получим уравнение-следствие
x2 + 2x – 15 = 0. (1)
Уравнение (1) имеет два корня: 3 и –5. Проверка показывает, что из этих чисел только число 5 является корнем исходного уравнения. Следовательно, исходное уравнение имеет единственный корень 5. 344. Решите уравнение:
![]() а) x2 x x 1 = 6 x
1 ;
а) x2 x x 1 = 6 x
1 ;
в) 5x2 1 = 30x 1 .
x 6 x 6
Решение. а) Перенеся все члены уравнения в левую часть и приведя подобные члены, получим следствие данного уравнения:
x2 – x – 6 = 0. (2)
Уравнение (2) имеет два корня: –2 и 3. Проверка показывает, что из этих чисел только число 3 является корнем исходного уравнения. Следовательно, исходное уравнение имеет единственный корень 3.
в) Перенеся все члены уравнения в левую часть и приведя подобные члены, получим следствие данного уравнения:
5x2 – 30x = 0. (3)
Уравнение (3) имеет два корня: 0 и 6. Проверка показывает, что из этих чисел только число 0 является корнем исходного уравнения. Следовательно, исходное уравнение имеет единственный корень 0. 347. Решите уравнение:
а) 2x2 x 3 = x 3 ;
![]() и) 2x2 3x 9 = x2
4x 1 .
и) 2x2 3x 9 = x2
4x 1 .
Решение. а) Возведя уравнение в квадрат, получим следствие данного уравнения:
2x2 + x + 3 = x2 + 6x + 9. (4)
Уравнение (4) имеет два корня: –1 и 6. Проверка показывает, что каждое из этих чисел является корнем исходного уравнения. Следовательно, исходное уравнение имеет два корня: –1 и 6.
и) Возведя уравнение в квадрат, получим следствие
данного уравнения:
2x2 – 3x – 9 = x2 + 4x – 1. (5)
Уравнение (5) имеет два корня: 8 и –1. Проверка показывает, что число 8 является корнем исходного уравнения, а число –1 нет. Следовательно, исходное уравнение имеет единственный корень 8. 348. Решите уравнение:
а) |x – 2| = 2x – 1; в) |x2 – 4x + 1| = 2x – 4.
Решение. а) Возведя уравнение в квадрат, получим следствие данного уравнения:
x2 – 4x + 4 = 4x2 – 4x + 1. (6)
Уравнение (6) имеет два корня: –1 и 1. Проверка показывает, что число 1 является корнем исходного уравнения, а число –1 нет. Следовательно, исходное уравнение имеет единственный корень 1.
в) Возведя уравнение в квадрат, получим следствие
данного уравнения:
(x2 – 4x + 1)2 = (2x – 4)2. (7)
Перенеся все члены уравнения в его левую часть и применив формулу разности квадратов, перепишем уравнение (7) в виде
(x2 – 6x + 5)(x2 – 2x – 3) = 0. (8)
Уравнение (8) имеет четыре корня: –1, 1, 3 и 5. Проверка показывает, что числа 3 и 5 являются корнями исходного уравнения, а числа –1 и 1 нет. Следовательно, исходное уравнение имеет два корня: 3 и 5.
Промежуточный контроль. С–12, К–4.
В данном пункте вводится операция деления многочлена на двучлен с остатком, показывается способ деления многочлена на двучлен уголком. Затем формулируются и доказываются теорема Безу и две теоремы о целых корнях многочлена с целочисленными коэффициентами. Вся эта теоретическая база должна подвести учащихся к выводу: если у многочлена с целочисленными коэффициентами есть целый корень, то его следует искать среди делителей свободного члена, а это даёт алгоритм поиска корней некоторых уравнений более высоких, чем вторая, степеней.
При решении уравнения Pn (x) = 0, где Pn (x) — многочлен степени n с целочисленными коэффициентами, сначала надо найти корень a этого уравнения. Затем разделить с остатком многочлен Pn (x) на двучлен (x – a). Из теоремы Безу следует, что остаток от деления равен 0. Теперь исходное уравнение можно записать в виде
(x – a) Pn – 1 (x) = 0, где Pn – 1 (x) — многочлен степени n – 1.
Описанный способ разложения многочлена на множители может повторяться несколько раз, пока не получится многочлен второй степени. Далее останется найти корни этого многочлена второй степени и указать все корни исходного уравнения.
В учебнике приводятся примеры деления многочлена на двучлен уголком и примеры использования разложения многочлена на множители для решения уравнений.
Можно дополнить теоретические сведения данного пункта, сформулировав и доказав теорему, которая даёт дополнительные возможности при решении уравнений.
ТЕОРЕМА 3. Если все коэффициенты а0, а1, ..., аn(аn 0) многочлена
Рn (х) = аnхn + аn – 1хn – 1 + ... + а1х + а0 (1)
![]() p p целые числа
и рациональное число ( — несократимая q q
p p целые числа
и рациональное число ( — несократимая q q
![]() дробь, р Z, q N) является корнем многочлена, то
коэффициент а0 делится на р, а коэффициент ап
делится на q. Доказательство. Пусть рациональное число p ( p — q q
дробь, р Z, q N) является корнем многочлена, то
коэффициент а0 делится на р, а коэффициент ап
делится на q. Доказательство. Пусть рациональное число p ( p — q q
несократимая дробь, р Z, q N) есть корень многочлена Рп (х), т. е. пусть справедливо числовое равенство
pn pn 1 p аn ![]() n + аn – 1
n + аn – 1 ![]() qn 1 + ...
+ а1
qn 1 + ...
+ а1 ![]() q + а0 = 0. (2) q
q + а0 = 0. (2) q
Умножим равенство (2) на qn:
аnpn + аn – 1pn – 1q + ... + а1pqn – 1 + а0qn = 0. (3)
Все слагаемые в левой части равенства (3) — целые числа. Ясно, что их сумма (число 0), а также сумма всех слагаемых, кроме последнего, делятся на р. Следовательно, последнее слагаемое а0qn делится на p, но тогда а0 делится на р, так как числа р и q не имеют общих простых делителей и поэтому qn не делится на р. Сумма всех слагаемых делится на q, а также сумма всех слагаемых, кроме первого, делится на q, следовательно, первое слагаемое апрп делится на q, но тогда ап делится на q, так как рп не делится на q. Что и требовалось доказать.
При доказательстве теорем 2 и 3 использовалось утверждение:
Если натуральные числа p и q не имеют общих простых делителей, то числа pn и q (а также p и qn) не имеют общих простых делителей.
Приведём его доказательство.
По основной теореме арифметики натуральное число p разлагается на простые множители единственным образом, т. е. p = p1α1 ... pmαm , где p1, ..., pm — разные простые числа, a1, ..., am — натуральные числа.
По той же теореме q = q1β1 ... qkβk , где q1, ..., qk — разные простые числа, b1, ..., bk — натуральные числа.
Так как p и q не имеют общих простых делителей, то все числа q1, ..., qk разные.
Так как pn = p1nα1 ... pmnαm — единственное разло-
жение числа pn на простые множители, то оно содержит только множители p1nα1, ..., pmnαm , среди которых нет степеней чисел q1, ..., qk. Следовательно, pn и q не имеют общих простых делителей, что и требовалось доказать.
350. а) Не выполняя деления, определите остаток от деления многочлена 5x3 – 3x2 + 2 на двучлен x – 1, на двучлен x + 1.
Решение. По теореме Безу остаток от деления многочлена P3 (x) = 5x3 – 3x2 + 2 на двучлен x – 1 равен значению этого многочлена в точке 1:
P3 (1) = 5 – 3 + 2 = 4,
а остаток от деления многочлена P3 (x) на двучлен x + 1 равен значению этого многочлена в точке –1:
P3 (–1) = –5 – 3 + 2 = –6.
351. а) Разложите на множители многочлен x3 – x2 – x – 2.
Решение. Коэффициент многочлена 3 равен 1. По теореме 2 если этот многочлен P3 (x) = x3 – x2 –
– x – 2 при x
имеет рациональный корень, то этот корень целый и является делителем свободного члена –2. Будем искать корень многочлена среди делителей свободного члена: 1, –1, 2, – 2.
Если x = 1, то P3 (1) = 1 – 1 – 1 – 2 0; если x = –1, то P3 (–1) = –1 – 1 + 1 – 2 0; если x = 2, то P3 (2) = 8 – 4 – 2 – 2 = 0.
Итак, x = 2 — корень многочлена P3 (x).
Далее можно разделить многочлен P3 (x) на двучлен x – 2 уголком, как показано в учебнике, а можно разложить P3 (x) на множители, группируя слагаемые так, чтобы получить общий множитель x – 2:
x3 – x2 – x – 2 = x3 – 2x2 + x2 – 2x + x – 2 = = (x – 2) (x2 + x + 1).
Так как многочлен x2 + x + 1 не имеет корней (его дискриминант отрицателен), то многочлен P3 (x) имеет единственный корень 2 и его разложение на множители уже получено:
P3 (x) = (x – 2)(x2 + x + 1).
352. а) Решите уравнение x3 + 2x2 – x – 2 = 0.
Решение. Коэффициент многочлена 3 равен 1. По теореме 2 если этот многочлен P3 (x) = x3 + 2x2 –
– x – 2 при x
имеет рациональный корень, то этот корень целый и является делителем свободного члена –2. Будем искать корень многочлена среди делителей свободного члена: 1, –1, 2, – 2.
Если x = 1, то P3 (1) = 1 + 2 – 1 – 2 = 0.
Итак, x = 1 — корень многочлена P3 (x).
Далее разложим многочлен P3 (x) на множители, группируя слагаемые так, чтобы получить общий множитель x – 1:
![]() x3 + 2x2
– x – 2 =
x3 – x2
+ 3x2– 3x +
2x – 2 = = (x
– 1)(x2 + 3x
+ 2).
x3 + 2x2
– x – 2 =
x3 – x2
+ 3x2– 3x +
2x – 2 = = (x
– 1)(x2 + 3x
+ 2).
Так как многочлен x2 + 3x + 2 имеет корни –1 и –2, то многочлен P3 (x) имеет три корня: 1, – 1 и –2. Следовательно, исходное уравнение имеет те же корни.
Дополнительное задание. Разложите на множители многочлен 12x3 – 8x2 – 3x + 2.
Решение. Пусть многочлен имеет рациональный корень p (р Z, q N). По теореме 3 число 2 делится на p, а
q
число 12 делится на q.
Число р содержится среди чисел: 1, –1, 2, –2, число q содержится среди чисел: 1, 2, 3, 4, 6, 12,
![]()
![]() число p содержится
среди чисел: 1, –1, 2, –2, 1 , – 1 , q 2 2
число p содержится
среди чисел: 1, –1, 2, –2, 1 , – 1 , q 2 2
1 1 2 2 1 1 1 1 1 1
, – , , – , , – , , – , , – .
3 3 3 3 4 4 6 6 12 12
![]() Если
x = 1, то P3 (1)
= 12 – 8 –
3 + 2 0; если x =
–1, то P3 (–1) = –12
– 8 + 3 +
2 0; если x = 2, то P3
(2) = 96 – 32
– 6 + 2 0;
если x = –2, то P3 (–2)
= –96 – 32 +
6 + 2 0; если x =
Если
x = 1, то P3 (1)
= 12 – 8 –
3 + 2 0; если x =
–1, то P3 (–1) = –12
– 8 + 3 +
2 0; если x = 2, то P3
(2) = 96 – 32
– 6 + 2 0;
если x = –2, то P3 (–2)
= –96 – 32 +
6 + 2 0; если x =
![]() , то P3 (
12 ) =
, то P3 (
12 ) =
![]() 2 = 0 .
2 = 0 .
Здесь можно продолжить поиск рационального корня, но
проще разложить данный многочлен на два множителя: x – ![]() и
квадратный трёхчлен, затем разложить известным способом на множители квадратный
трёхчлен:
и
квадратный трёхчлен, затем разложить известным способом на множители квадратный
трёхчлен:
12x3 – 8x2 – 3x + 2 = 12x3 – 6x2 – 2x2 + x – 4x + 2 =
= (x –
![]() )(12x2 –
2x – 4) = 12(x
–
)(12x2 –
2x – 4) = 12(x
– ![]() )(x +
)(x + ![]() )(x
–
)(x
– ![]() ) =
) =
= (2x – 1)(2x + 1)(3x – 2).
Промежуточный контроль. С–11.
В данном пункте множество действительных чисел расширяется до множества комплексных чисел. Изложение материала весьма краткое (обоснованное изложение теории комплексных чисел предусмотрено в 11 классе).
Здесь вводятся понятия мнимой единицы, комплексного числа, мнимого числа, сопряжённых комплексных чисел, рассматриваются арифметические операции с комплексными числами. С помощью мнимой единицы i, действительных чисел и знаков арифметических действий составляют буквенные выражения (комплексные числа), эти буквенные выражения преобразуют как обычные буквенные выражения, однако при этом считают, что i2 = –1.
Далее приводятся примеры вычислений с комплексными числами и пример выражения корней квадратного уравнения с отрицательным дискриминантом при помощи комплексных чисел.
357. Выполните указанные действия:
а) (2 – 3i) + (5 + i); б) (7 – 2i) – (4 – 3i);
в) (3 – 5i)(4 – 6i); г) (40 + i) : (3 – i).
Решение. а) (2 – 3i) + (5 + i) = 2 – 3i + 5 + i = 7 – 2i; б) (7 – 2i) – (4 – 3i) = 7 – 2i – 4 + 3i = 3 + i;
в) (3 – 5i)(4 – 6i) = 12 – 20i – 18i + 30i2 = 12 – 38i – 30 =
= –18 – 38i;
![]() г)
(40 + i) : (3 –
i)
= = 120
г)
(40 + i) : (3 –
i)
= = 120![]() 3i 42 i i2
=
3i 42 i i2
=
9 i
![]()
= ![]() i = 11 9, 4 3, i .
i = 11 9, 4 3, i .
10
358. Решите квадратное уравнение:
а) x2 + 1 = 0; д) x2 + x + 1 = 0.
Решение. а) Разложим левую часть уравнения на множители:
x2 + 1 = x2 – (–1) = x2 – i2 = (x – i)(x + i).
Теперь очевидно, что данное уравнение имеет два корня: –i и i.
д) Вычислим дискриминант квадратного уравнения: D = b2 – 4ac = 1 – 4 = –3.
Корни квадратного уравнения можно найти по формуле
![]() b i D
b i D
x1 2, =:
2a
![]()
![]() x1 = 1 2 i 3 , x2 =
1 2 i 3 .
x1 = 1 2 i 3 , x2 =
1 2 i 3 .
В данном пункте рассказывается об истории использования квадратных уравнений в древние времена, о вкладе Ф. Виета, Р. Декарта и И. Ньютона в теорию квадратных уравнений. Приводятся примеры задач из «Арифметики» Л. Ф. Магницкого, сводящиеся к квадратным уравнениям. Здесь говорится о вкладе российских учёных в науку о числе и даётся информация об использовании комплексных чисел. Это способствует воспитанию российской гражданской идентичности: привитию уважения к Отечеству, формированию знания об истории, культуре своего народа, основах культурного наследия народов России и человечества. Материал, представленный в данном пункте, помогает также формированию целостного мировоззрения, объясняет роль разных народов в истории математики, воспитывает уважительное отношение к разным народам мира.
Глава 3
Третья глава посвящена изучению линейной, квадратичной
и дробно-линейной функций. Изложение материала опирается на знание учащимися
функций y = x, y =
x2, y = ![]() 1 , их
свойств и графиков. Обобщение и систематизация x
1 , их
свойств и графиков. Обобщение и систематизация x
изученных ранее сведений помогают формированию устойчивых познавательных интересов учащихся, способствуют развитию критичности мышления, формированию коммуникативных компетенций в обучении.
Цель изучения главы — усвоить свойства линейной, квадратичной и дробно-линейной функций, научиться строить их графики.
Основная цель шестого параграфа — научить учащихся строить графики линейных функций и решать задачи, связанные с линейными функциями.
В данном пункте рассматривается функция y = kx, называемая прямой пропорциональностью. Вводится понятие коэффициента пропорциональности. Учащиеся должны по формуле, которой задана функция, научиться определять коэффициент пропорциональности, по заданному значению x находить соответствующее значение y и по заданному значению y находить соответствующее значение x, заполнять таблицы соответствующих значений данной функции. Все эти умения пригодятся при изучении других функций.
365. Определите, одинаковые или разные знаки имеют x (x 0) и соответствующее ему y, если функция задана формулой:
в) y = kx, k 0;
е) y = kx, k 0. Решение. в)
Так как k = ![]() y 0, то числа x и y
одного x знака;
y 0, то числа x и y
одного x знака;
е) так как k = ![]() y 0, то
числа x и y разных знаков.
y 0, то
числа x и y разных знаков.
x
В данном пункте на примере функции y = 2x показывается, что графиком функции y = kx является прямая, проходящая через начало координат и точку (1; k). Доказательство этого факта приводится в Дополнениях к главе 3.
Учащиеся должны научиться строить прямую y = kx по двум точкам: (0; 0) и (1; k), твёрдо усвоить расположение прямой y = kx для k 0 (I и III четверти), для k 0 (II и IV четверти), для k = 0 (ось Ox).
В классе с углублённым изучением математики следует
обратить внимание на дополнительные задания, связанные с перпендикулярностью
графиков y = kx и y = –
![]() 1 x (k
0). k Задания
для повторения. При изучении данного пункта можно использовать задания 746—750,
753, 754, 770.
1 x (k
0). k Задания
для повторения. При изучении данного пункта можно использовать задания 746—750,
753, 754, 770.
376. а) Задана функция у = 1
![]() х.
Точка (6; а) принадлежит графику этой функции. Найдите
а.
х.
Точка (6; а) принадлежит графику этой функции. Найдите
а.
б) Задана функция у = –2,7х. Точка (b; –3) принадле-
жит графику этой функции. Найдите b.
в) Точка (6; 4) принадлежит графику функции у = kх. Найдите k.
Решение. а) Так как точка (6;
а) принадлежит прямой у = 1 ![]() х,
то a = 1
х,
то a = 1 ![]() 6, т. е. a = 8.
6, т. е. a = 8.
б) Так как точка (b; –3) принадлежит прямой у = –2,7х,
то –3 = –2,7b,
откуда b = 1![]() .
.
в) Так как точка (6; 4) принадлежит прямой у = kх,
то 4 = 6k,
откуда k = ![]() .
.
379. На рисунке 12 изображён график функции у = kх.
Определите коэффициент k.
Решение. а) Точка (1; 1) принадлежит прямой, следовательно, 1 = k 1, т. е. k = 1.
б) Точка ( ![]() ; 1)
принадлежит прямой, следовательно,
; 1)
принадлежит прямой, следовательно,
1 = k ![]() ,
т. е. k = 3.
,
т. е. k = 3.
в) Точка (–2; 1)
принадлежит прямой, следовательно, 1 = k (–2),
т. е. k = – ![]() .
.
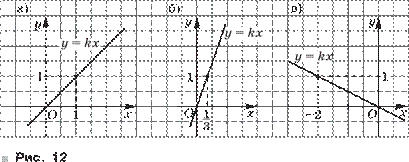
![]() Замечание. При решении задачи полезно
предварительно определять знак углового коэффициента. Например, в заданиях «а»
и «б» прямая проходит через I и III координатные углы, поэтому k 0, в
задании «в» прямая проходит через II и IV координатные углы, поэтому k 0.
Замечание. При решении задачи полезно
предварительно определять знак углового коэффициента. Например, в заданиях «а»
и «б» прямая проходит через I и III координатные углы, поэтому k 0, в
задании «в» прямая проходит через II и IV координатные углы, поэтому k 0.
Учащиеся должны научиться определять знак коэффициента пропорциональности k по данному графику функции у = kх. Это умение пригодится в дальнейшем.
380. а) В одной системе координат постройте
графики функций y = 2x и y = – ![]() x.
Определите угол между этими прямыми.
x.
Определите угол между этими прямыми.
Решение. I способ. На
прямой y = 2x отметим точку A (1;
2), а на прямой y = – ![]() x — точку B
(2; –1) (рис. 13).
x — точку B
(2; –1) (рис. 13).
Пусть D и C — основания перпендикуляров, проведённых к оси Ox из точек A и B соответственно. Так как AD = OC = 2, OD = BC = 1, ADO = OCB = 90о, то AOD = OBC по двум сторонам и углу между ними. Из равенства треугольников следует, что AOD = OBC. А так как в прямоугольном треугольнике сумма острых углов равна 90о, то
AOB = AOD + BOC = OBC + BOC = 90о.
![]() Значит, угол между
прямыми, являющимися графиками функций y = 2x и y
= –
Значит, угол между
прямыми, являющимися графиками функций y = 2x и y
= – ![]() x, равен 90о.
x, равен 90о.
II способ. Из курса геометрии известна формула расстояния между двумя точками:
![]() AB
= (x1
x2)2 (y1 y2)2,
AB
= (x1
x2)2 (y1 y2)2,
6 Рис. 13
где A (x1; y1), B (x2; y2). Для точек O (0; 0), A (1; 2),
![]()
![]() B (2; –1)
вычислим расстояния: AB = 10 , OA = 5 ,
B (2; –1)
вычислим расстояния: AB = 10 , OA = 5 ,
![]() OB = 5 . Так как AB2 =
OA2 + OB2,
то по теореме, обратной теореме Пифагора, AOB = 90о.
Значит, угол между прямыми, являющимися графиками функций y = 2x
и y = –
OB = 5 . Так как AB2 =
OA2 + OB2,
то по теореме, обратной теореме Пифагора, AOB = 90о.
Значит, угол между прямыми, являющимися графиками функций y = 2x
и y = – ![]() x, равен 90о. 381.
Докажите, что прямые y = kx и y = –
x, равен 90о. 381.
Докажите, что прямые y = kx и y = – ![]() 1 x (k
0) k перпендикулярны.
1 x (k
0) k перпендикулярны.
Доказательство. Рассмотрим точки O (0; 0), A (1; k) на
прямой y = kx, B (k; –1) на прямой y = – 1 x. Пользуясь k
формулой расстояния между двумя точками:
AB = (x1 x2)2 (y1 y2)2 ,
![]() где A (x1;
y1), B (x2; y2),
вычислим расстояния: AB = (k
1)2 ( 1 k)2 = 2k2 2
,
где A (x1;
y1), B (x2; y2),
вычислим расстояния: AB = (k
1)2 ( 1 k)2 = 2k2 2
,
![]() OA = (1 0)2 (k 0)2 = k2
1 ,
OA = (1 0)2 (k 0)2 = k2
1 ,
OB = (k 0)2 ( 1 0)2 = k2 1 .
Так как AB2 = OA2 + OB2, то по теореме, обратной теореме Пифагора, AOB = 90о, что и требовалось доказать.
Замечание. Для решения задачи в общем виде удобнее применить второй способ доказательства предыдущей задачи, так как в этом случае не требуется обсуждать различное положение точек A и B при k 0 и при k 0.
В данном пункте сначала вводится понятие линейной функции как функции, заданной формулой y = kx + b. Затем на примере функции y = 2x + 4 показывается, что её график можно получить параллельным переносом графика функции y = 2x на 4 единицы вверх. Учащиеся должны усвоить, что график функции y = kx + b можно построить по двум точкам или при помощи параллельного переноса графика функции y = kx на |b| единиц вверх (если b 0) или вниз (если b 0).
Необязательным для освоения всеми учащимися является способ построения графика функции y = 2(x + 2) при помощи параллельного переноса прямой y = 2x на 2 единицы влево. Но эта идея будет использована при изучении других функций, поэтому с ней можно ознакомить всех учащихся.
Задания для повторения. При изучении данного пункта можно использовать задания 755—761.
399. а) Задана функция у = –4х + 3. Точка (1; а) принадлежит графику этой функции. Найдите а.
б) Задана функция у = 12х – 1. Точка (b; –3) принад-
лежит графику этой функции. Найдите b.
в) Определите угловой коэффициент k функции у = kх + 1, если точка A (2; 5) принадлежит её графику.
Решение. а) Так как точка (1; а) принадлежит прямой у = –4х + 3, то a = –4 1 + 3 = –1.
б) Так как точка (b; –3)
принадлежит прямой y = 12х – 1,
то 12b – 1 = –3, откуда b
= – ![]() .
.
в) Так как точка (2; 5) принадлежит прямой у = kх + 1,
то 5 = 2k + 1, откуда k = 2.
400. а) Точки А (6; 5) и B (12; 11) принадлежат графику функции у = kх + b. Определите угловой коэффициент k.
Решение. Пусть заданы, но пока не известны числа k и b. Подставив в формулу у = kх + b вместо x число 6, а вместо y число 5, получим верное числовое равенство 5 = 6k + b. Аналогично получим верное числовое равенство 11 = 12k + b.
Чтобы найти неизвестные числа k и b, решим систему двух уравнений 6k + b = 5 и 12k + b = 11 с неизвестными k и b. Получим k = 1 и b = –1.
401. Точки А (х1; у1) и В (х2; y2) принадлежат графику функции у = kх + b. Выразите угловой коэффициент k через х1, х2, у1, y2, если известно, что х1 х2.
Решение. Пусть заданы, но пока не известны числа k и b. Подставив в формулу у = kх + b вместо x число х1, а вместо y число у1, получим верное числовое равенство у1 = kх1 + b. Аналогично получим верное числовое равенство у2 = kх2 + b.
Чтобы найти неизвестные числа k и b, решим систему двух уравнений у1 = kх1 + b и у2 = kх2 + b с неизвестными k и b. Получим k = y1 y2 и b = x y1 2 y x1 2 .
402. Какой из графиков, приведённых на рисунке 14, является графиком функции:
а) у = 2х – 1; б) у = –х + 3; в) у = 5;
г) у = 4х; д) у = х + 2; е) у = –х?
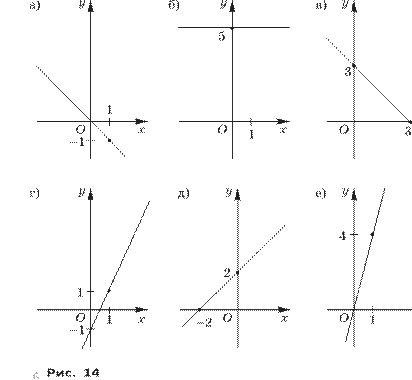
Решение. При решении задачи учащиеся должны соотнести, т. е. установить соответствие объектов: формул, которыми заданы функции, и графиков функций. Похожая форма заданий используется в ГИА-9.
а) График функции у = 2х – 1 проходит через точки (0; –1) и (1; 1) (рис. 14, г).
б) График функции у = –х + 3 проходит через точки (0; 3) и (3; 0) (рис. 14, в).
в) График функции у = 5 — прямая, параллельная оси Ox, проходящая через точку (0; 5) (рис. 14, б).
г) График функции у = 4х проходит через точки (0; 0)
и (1; 4) (рис. 14, е).
д) График функции у = х + 2 проходит через точки
(0; 2) и (–2; 0) (рис. 14, д).
е) График функции у = –х проходит через точки (0; 0)
и (1; –1) (рис. 14, а).
403. На рисунке 15 изображены прямые а, b, c и d. Какой формулой задана каждая из них?
![]() Решение. Для
каждой прямой можно найти координаты двух точек и повторить рассуждения из
задания 400. Но сначала проще найти ординату точки пересечения прямой с
осью Oy — это значение свободного члена b в формуле у =
kх + b.
Решение. Для
каждой прямой можно найти координаты двух точек и повторить рассуждения из
задания 400. Но сначала проще найти ординату точки пересечения прямой с
осью Oy — это значение свободного члена b в формуле у =
kх + b.
Например, прямая a проходит через точки (0; 1) и (–1; 0). Решив
⎧0k b = 1,
систему уравнений ⎨⎩ k b = 0, получим b = 1, k = 1, следовательно, прямая задаётся уравнением у = х + 1.
Аналогично рассуждая, получим ответы в других заданиях. 6 Рис. 15
Для прямой b: у = 0,5х + 5, для
![]() прямой c: у
= –х + 7, для прямой d: у = –2х
+ 3.
прямой c: у
= –х + 7, для прямой d: у = –2х
+ 3.
![]() 1. (ГИА)
Графика какой из перечисленных функций нет на рисунке 16?
1. (ГИА)
Графика какой из перечисленных функций нет на рисунке 16?
![]() 1)
у = х – 2 2)
у = х – 2
1)
у = х – 2 2)
у = х – 2
3) у = 2 – х 4) у = х + 2
Решение. 1) Прямая у = х – 2 проходит через точки (0; –2) и
![]() (2; 0)
— такая прямая на рисунке 6 Рис.
16 есть.
(2; 0)
— такая прямая на рисунке 6 Рис.
16 есть.
2) Прямая у = х – 2 проходит через точки (0; –2) и
(3; 0) — такой прямой нет.
3)
![]() Прямая у = 2 – х
проходит через точки (0; 2) и (2; 0) — такая прямая
есть.
Прямая у = 2 – х
проходит через точки (0; 2) и (2; 0) — такая прямая
есть.
4) Прямая у = х + 2 проходит через точки (0; 2) и
(3; 3) — такая прямая есть.
Ответ. На рисунке нет прямой 2.
Промежуточный контроль. С–15.
В данном пункте на двух примерах рассматриваются графики равномерного движения точки. Главный вывод, к которому надо подвести учащихся: график движения точки на заданном промежутке времени — отрезок. С графиком движения, заданным ломаной линией, учащиеся уже встречались в п. 1.6. Теперь к заданию 72 из п. 1.6 можно вернуться при изучении «кусочного» способа задания функции — на каждом отрезке значений x функция задаётся своей формулой (см. задание 70).
Задания для повторения. При изучении данного пункта можно использовать задания 762—769.
408. На рисунке 17 изображён график движения точки. Менялась ли координата точки в промежуток времени от 0 до 3? В какой момент времени началось движение точки и с какой скоростью?
Решение. Координата s точки в промежуток времени от 0 до 3 не менялась, она оставалась равной нулю. В момент времени t = 3 началось движение точки со cкоростью 2 м/с, так как приращению времени t = 4 – 3 = 1 (с) соответствует приращение координаты s = 2 – 0 = 2 (м).
409. Функция, задающая зависимость координаты s от времени t, выражена формулой
s(t) = ⎧⎨⎩20t, если6, если0 t t 33,.
Ей соответствует график, изображённый на рисунке 17. Напишите формулу, которой задаётся функция s(t), график которой изображён на рисунке 18.
Решение. На промежутке 0 t < 2 координата s не изменяется: s = 0, а на промежутке t 2 координата s меняется по закону s = 3t – 6 (так как точки (2; 0) и (3; 3) принадлежат графику функции s = kt + b, то k = 3, b = –6). Формула зависимости s(t) имеет вид
s(t) = ⎧⎨⎩30t, если6, если0 t t 22,.
410. Напишите формулу зависимости s(t), график которой изображён на рисунке 19.
Решение. а) Так как точки (0; 5) и (5; 0) принадлежат графику функции s = kt + b, то k = –1, b = 5, т. е. s = –t + 5.
6 Рис. 17 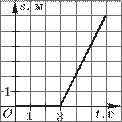 6 Рис. 18
6 Рис. 18 
мула зависимости s(t) имеет вид
⎧5, если 0 t 2, s(t) = ⎨ 2 5, t 10, если 2 t 4. ⎩
В данном пункте вводится функция у = |х|, формулируются её свойства и строится её график. Построение графика функции у = |х – x0| + y0 выделено в учебнике как необязательный материал. В данном пункте подробно разбираются приёмы построения графика этой функции для всех характерных случаев: параллельный перенос вверх-вниз, вправо-влево, последовательное выполнение этих переносов.
Этот материал можно не требовать от всех учащихся в обычном классе, но показать перенос графика функции у = |х| полезно всем, так как тот же приём будет использоваться при параллельном переносе параболы, а затем и гиперболы, к чему и готовит материал данного пункта.
![]() В классе с
углублённым изучением математики можно использовать примеры 1—6 из п. 1
Дополнений к главе 3
В классе с
углублённым изучением математики можно использовать примеры 1—6 из п. 1
Дополнений к главе 3
и задания 510—512.
512. а) Постройте график функции у = |х| + х.
Решение. Если х 0, то по определению модуля |х| = х и функция задаётся формулой у = 2х.
Если х < 0, то по определению модуля |х| = –х и функция задаётся формулой у = 0.
График функции у = |х| + х изображён на рисунке 20. 6 Рис. 20 Дополнительное задание. Постройте график функции:
|
x |
2 |
|
x |
2 |
|
x |
2 |
|
x |
2 |
|
x |
1 |
|
x |
1 |
|
x |
1 |
|
x |
1 |
x 1 x 1 ; б) у = x 2 x 2 ;
а) у =
в) у = ; г) у = . x 1 x 1 x 2 x 2
Решение. а) Отметим, что при x = 1 и при x = –1 функция не определена. Построим график функции на каждом из промежутков: x –1, –1 x 1 и x 1.
![]() Если x –1,
то |х – 1| = –(х – 1),
|х + 1| = –(х +
1) и x 1 x 1 (x
1) (x 1)
Если x –1,
то |х – 1| = –(х – 1),
|х + 1| = –(х +
1) и x 1 x 1 (x
1) (x 1)
= = –1 – 1 = –2, x 1 x 1 x 1 x 1
поэтому функция задаётся формулой у = –2.
Если –1 х 1, то |х – 1| = –(х – 1), |х + 1| = х + 1 и
![]() x 1 x
1 (x 1) x 1
x 1 x
1 (x 1) x 1
= = –1 + 1= 0, x 1 x 1 x 1 x 1
поэтому функция задаётся формулой у = 0.
![]() Если x 1, то |х – 1|
= х – 1, |х + 1|
= х + 1 и
Если x 1, то |х – 1|
= х – 1, |х + 1|
= х + 1 и  =
=
6 Рис. 21 изображён на рисунке 21.
Промежуточный контроль. Т–6.
В данном пункте вводится понятие целой и дробной части числа, строятся графики функций у = [х] и у = {х}. Отметим, что функция у = {х} является первой функцией, отличной от константы, значения которой периодически повторяются. Это свойство функции полезно обсудить, использовать при построении графиков, но здесь понятие периодической функции вводить ещё рано.
Отметим, что равенство x = [х] + {х} справедливо для любого x.
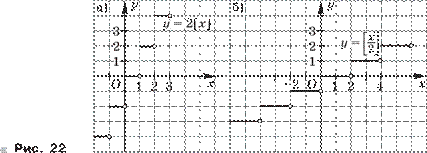
Покажем, как из равенства [х] + {y} = –3,13 можно определить [х] и {y}. Так как [х] Z, а {y} [0; 1), то [х] = –4, {y} = 0,87.
420. Постройте график функции:
|
а) у = 2[х]; |
г) у = ⎡⎢⎣ |
ж) у = –3{х}; |
|
к) у = { }x ; |
о) у = [х] – {х}; |
п) у = {х}2. |
2
Решение. а) Для каждого значения аргумента x, такого, что n x n + 1, где n — целое число, [х] = n. Если n умножить на 2, то получится соответствующее значение функции у = 2[х]. График функции у = 2[х] изображён на рисунке 22, а.
г) Для каждого значения аргумента x,
такого, что 2n x 2n + 2, где n — целое число, ⎡⎢⎣![]() x2⎤⎥⎦
= n. График функции у = ⎡⎢⎣
x2⎤⎥⎦
= n. График функции у = ⎡⎢⎣![]() x2⎤⎥⎦
изображён на рисунке 22, б.
x2⎤⎥⎦
изображён на рисунке 22, б.
ж) Для каждого значения аргумента x, такого, что n x n + 1, где n — целое число, значение функции у = –3{х} получим умножением на –3 соответствующего значения функции у = {х}. График функции у = –3{х} изображён на рисунке 23, а.
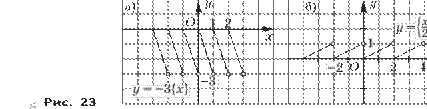

к) Для каждого значения аргумента x, такого, что
0 x 2, верно неравенство 0 ![]() x 1,
поэтому { }x =
x 1,
поэтому { }x = ![]() x .
x .
2 2 2
На промежутке [0; 2) график функции y = { }x совпадает
2
с графиком функции y =
![]() x . Если
значения аргумента
x . Если
значения аргумента
2
отличаются на чётное целое число, то соответствующие им значения функции y = { }x совпадают. График функции
2 у = { }x изображён на рисунке 23, б.
2
о) В одной системе координат построим графики функций у = [х] и у = –{х} (рис. 24, а). Для каждого значения аргумента x сложим соответствующие значения функций, получим значение функции у = [х] – {х}.
График функции у = [х] – {х} изображён на рисунке 24, б.
п) На промежутке 0 x 1 верно равенство {х} = х, поэтому верно равенство {х}2 = х2. Следовательно, график функции у = {х}2 на этом промежутке совпадает с графиком функции у = х2. Если значения аргумента отличаются на целое число, то соответствующие им значения функции у = {х}2 совпадают. График функции у = {х}2 изображён на рисунке 25.
![]() 421. Решите
уравнение:
421. Решите
уравнение:
б) х = [х] – {х};
в) [х]2 – {х}2 = 3,75.
Решение. б) Перепишем уравнение в виде
[х] + {х} = [х] – {х}. 6 Рис. 25
Теперь очевидно, что {х} = 0, следовательно, х — любое целое число.
в) Перепишем уравнение в виде
[х]2 = {х}2 + 3,75.
Так как {x} [0; 1), то {x}2 [0; 1), а [х]2 — целое число, поэтому {x}2 = 0,25, {x} = 0,5. Тогда [х]2 = 4, следовательно, [х] = –2 или [х] = 2.
Итак, либо х = [х] + {х} = –2 + 0,5 = –1,5, либо х = [х] + {х} = 2 + 0,5 = 2,5. 422. Решите систему уравнений:
а) ⎧⎨⎩[[хy]] ++ {{xy}} == –2,13,3,5; б) ⎨⎩⎧xy ++ {[xy]} == 6–5,6;,1,
⎪⎧ [х] + {y} + z = –0,8,
в) ⎨ [y] + {z} + x = 4,95,
⎪⎩ [z] + {x} + y = 0,75.
Решение. а) Как отмечалось выше, из первого уравнения системы следует, что [х] = –3, {y} = 0,87. Аналогично из второго уравнения следует, что [y] = 3, {x} = 0,5.
Следовательно, х = [х] + {х} = –3 + 0,5 = –2,5, y = [y] + {y} = 3 + 0,87 = 3,87.
б) Перепишем систему уравнений в виде
⎧[х] + {x} + [y] = 6,1,
⎨⎩[y] + {y} + {x} = –5,6.
Так как [х] и [y] — целые числа, то {х} = 0,1. Подставив это число во второе уравнение системы, получим, что y = [y] + {y} = –5,7. Следовательно, [y] = –6. Подставив {х} = 0,1 и [y] = –6 в первое уравнение системы, получим, что [х] = 12. Тогда
х = [х] + {х} = 12 + 0,1 = 12,1.
Следовательно, (12,1; –5,7) — решение системы.
в) Оставив без изменения второе и третье уравнения
системы и заменив первое уравнение суммой первого уравнения, умноженного на –1, второго и третьего уравнений, получим равносильную исходной систему
⎧⎪⎨ 2{[y]х }+ + { z2[} +y] x= = 6 ,5,4,95,
⎪⎩ [z] + {x} + y = 0,75.
Из первого уравнения системы получим [y] + {x} = 3,25, откуда следует, что [y] = 3, {x} = 0,25.
Используя эти результаты, из второго и третьего уравнений системы получим
[x] + {z} = 1,7, откуда следует, что [x] = 1, {z} = 0,7; [z] + {y} = –2,5, откуда следует, что [z] = –3, {y} = 0,5.
Теперь найдём х, y, z: х = [х] + {х} = 1,25, y = [y] + {y} = 3,5, z = [z] + {z} = –2,3.
Итак, (1,25; 3,5; –2,3) — единственное решение системы.
423. Некто измерил стороны прямоугольника. Он умножил целую часть длины на целую часть ширины и получил 48; умножил целую часть длины на дробную часть ширины и получил 3,2; умножил дробную часть длины на целую часть ширины и получил 1,5. Определите площадь прямоугольника.
Решение. Пусть x — длина прямоугольника, y — ширина прямоугольника. По условию задачи составим уравнения
[x] [y] = 48, (1) [x] {y} = 3,2, (2) {x} [y] = 1,5. (3)
Площадь S прямоугольника вычислим следующим образом:
S = xy = ([х] + {х})([y] + {y}) = [х] [y] + {х} [y] +
+ [х] {y} + {х} {y} = 48 + 3,2 + 1,5 + {х} {y} = 52,7 + + {х} {y}.
Осталось найти произведение {х} {y}.
Из уравнения (1) получим
|
[y] =
⎡⎣x⎤⎦ Из уравнения (2) получим |
(4) |
|
[x] =
|
(5) |
![]() Тогда, подставив [x]
= 3,2 в уравнение (4), получим,
Тогда, подставив [x]
= 3,2 в уравнение (4), получим,
что [y] = 15{y}. Подставив 15{y} в уравнение (3) вместо [y], получим
15{х} {y} = 1,5,
откуда следует, что {х} {y} = 0,1.
Теперь найдём площадь прямоугольника:
S = 52,7 + {х} {y} = 52,7 + 0,1 = 52,8. Ответ. 52,8.
![]() Замечание. В задаче 423 не требовалось
найти значения x и y, но можно подобрать такую пару чисел x
= 8,25 и y = 6,4, которая
действительно является решением системы.
Замечание. В задаче 423 не требовалось
найти значения x и y, но можно подобрать такую пару чисел x
= 8,25 и y = 6,4, которая
действительно является решением системы.
Промежуточный контроль. С–16.
Основная цель седьмого параграфа — научить учащихся строить графики квадратичных функций и решать задачи, связанные с этими функциями.
![]()
В данном пункте рассматривается функция y = ax2 для a 0, формулируются и доказываются её свойства. Из сравнения графиков функций y = x2 и y = 2x2 делается вывод о том, что второй график можно получить из первого растяжением в 2 раза вдоль оси Oy. Далее этот вывод обобщается для функций y = x2 и y = ax2 (a 0). В обычном классе рассуждения о растяжении и сжатии графиков можно опустить.
439. а) Задана функция у = 3x2. Точка (–2; a) принадлежит графику этой функции. Найдите a.
б) Задана функция у = 3x2. Точка (b; 12) принадлежит
графику этой функции. Найдите b.
в) Точка (1; 8) принадлежит графику функции у = ах2. Определите a.
Решение. а) Так как точка (–2; a) принадлежит графику функции у = 3x2, то a = 3 (–2)2, т. е. a = 12.
б) Так как точка (b; 12) принадлежит графику функции у = 3x2, то 12 = 3b2. Решив это уравнение, получим b1 = 2, b2 = –2.
в) Так как точка (1; 8) принадлежит графику функции
у = аx2, то 8 = a 12, откуда следует, что а = 8.
440. На рисунке 26 представлены графики функций у = х2 и у = ах2. Определите a.
Эта задача решается так же, как предыдущая, только учащиеся сами должны найти на рисунке точку с известными координатами. Аналогично выполняются задания 441, 442.
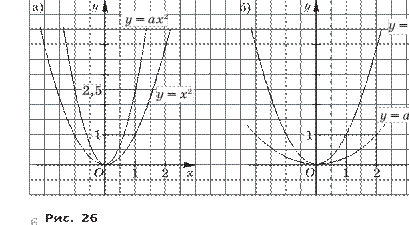
Решение. а) Точка (1; 2,5) принадлежит графику функции у = ах2, поэтому 2,5 = a 12, откуда следует, что а = 2,5.
б) Точка (2; 1) принадлежит графику функции у = ах2,
поэтому 1 = a 22, откуда следует, что а = 0,25.
![]()
В данном пункте рассматривается функция у = ах2 для а 0, вводятся понятия вершины параболы и оси симметрии параболы. От всех учащихся надо добиться понимания расположения параболы в зависимости от знака коэффициента a.
452. а) Дана функция у = –3x2. Точка (t; –3) принадлежит графику этой функции. Определите t.
б) Дана функция у = –0,2x2. Точка (–0,2; t) принад-
лежит графику этой функции. Определите t.
Решение. а) Точка (t; –3) принадлежит графику функции у = –3x2, поэтому –3 = –3t2. Решив это уравнение, получим t1 = 1, t2 = –1.
б) Точка (–0,2; t) принадлежит графику функции у = –0,2x2, поэтому t = –0,2 (–0,2)2, т. е. t = –0,008.
453. а) Прямая y = 8 пересекает параболу y = ax2 в двух точках, расстояние между которыми равно 6. Найдите число a.
б) Прямая y = –8 пересекает параболу y = ax2 в двух точках, расстояние между которыми равно 4. Найдите число a.
Решение. а) Так как точки пересечения прямой y
= 8, параллельной оси Ox, с параболой y =
ax2 симметричны относительно оси Oy и
расстояние между ними равно 6, то эти точки пересечения имеют абсциссы –3 и 3,
т. е. точки (–3; 8) и (3; 8) принадлежат графику
функции у = аx2, поэтому 8 =
a 32. Решив это уравнение, получим а = ![]() .
.
б) Так как точки пересечения прямой y = –8, па-
раллельной оси Ox, с параболой y = ax2 симметричны относительно оси Oy и расстояние между ними равно 4, то эти точки пересечения имеют абсциссы –2 и 2, т. е. точки (–2; –8) и (2; –8) принадлежат графику функции у = аx2, поэтому –8 = a 22. Решив это уравнение, получим а = –2.
В данном пункте на примере переноса параболы у = 2x2 разбирается способ построения графиков функций у = 2x2 – 2, у = 2(x – 2)2, у = 2(x – 2)2 + 3 при помощи параллельного переноса графика исходной функции вправовлево, или вверх-вниз, или при помощи двух этих переносов. Выводы, полученные при решении конкретных задач, обобщаются в виде правил, с помощью которых решаются аналогичные задачи на построение графиков функций данного вида.
Задания для повторения. При изучении данного пункта можно использовать задание 776.
463. Какой формулой задана функция, график которой получен из параболы у = x2 с помощью:
а) сжатия по оси Oy в 2 раза и переноса вершины в
точку (5; 0);
б) растяжения по оси Oy в 5 раз и переноса вершины
в точку (–4; 0)?
Решение. а) При сжатии по оси Oy в 2 раза
параболы у = x2 получится парабола у = ![]() x2
с вершиной (0; 0). При переносе этой параболы вершина переместится в
точку
x2
с вершиной (0; 0). При переносе этой параболы вершина переместится в
точку
(5; 0), получится парабола у
= ![]() (x – 5)2.
(x – 5)2.
б) При растяжении по оси Oy в 5 раз параболы у = x2 получится парабола у = 5x2 с вершиной (0; 0). При переносе этой параболы вершина переместится в точку (–4; 0), получится парабола у = 5(x + 4)2.
472. а) Какой формулой задана функция, график которой получен параллельным переносом параболы у = 2x2 так, что её вершина есть точка (5; –1)?
Решение. Вершина (0; 0) параболы у = 2x2 перенесена в точку (5; –1), следовательно, функция задана формулой у = 2(x – 5)2 – 1.
473. Парабола у = a(x – 3)2 + 2 пересекает ось Oy в точке (0; –16). В каких точках эта парабола пересекает ось Ox?
Решение. Так как точка (0; –16) принадлежит параболе у = a(x – 3)2 + 2, то верно равенство –16 = a(0 – 3)2 + 2, откуда следует, что a = –2.
Парабола у = –2(x – 3)2 + 2 пересекает ось Ox в точках, ордината y которых равна 0. Решив уравнение 0 = –2(x – 3)2 + 2, получим x1 = 2, x2 = 4. Следовательно, парабола пересекает ось Ox в точках (2; 0) и (4; 0).
В данном пункте рассматривается функция у = ax2
+ + bx + c (a 0), называемая квадратичной функцией. Здесь
доказывается теорема о том, что графиком квадратичной функции у = ax2
+ bx + c является парабола с вершиной в точке (x0;
y0), полученная параллельным переносом параболы у = ax2,
где x0 = ![]() 2ba , y0
=
2ba , y0
= ![]() 4Da , D
= b2 – 4ac. Далее разбираются примеры
построения парабол. Приводится пример доказательства возрастания (убывания)
функции на промежутке.
4Da , D
= b2 – 4ac. Далее разбираются примеры
построения парабол. Приводится пример доказательства возрастания (убывания)
функции на промежутке.
Задания для повторения. При изучении данного пункта можно использовать задания 781—787.
480. а) Найдите наименьшее значение функции у = x2 – 10x + 1.
Решение. Так как x2 – 10x + 1 = (x – 5)2 – 24, то функция достигает наименьшего значения (–24) в точке x = 5.
481. а) Найдите наибольшее значение функции у = –x2 – 4x + 8.
Решение. Так как –x2 – 4x + 8 = –(x + 2)2 + 12, то функция достигает наибольшего значения 12 в точке x = –2.
![]() Замечание. Абсцисса точки, в которой функция у
= ax2 + bx + c достигает своего наибольшего
(наименьшего) значения, вычисляется по формуле x0 =
Замечание. Абсцисса точки, в которой функция у
= ax2 + bx + c достигает своего наибольшего
(наименьшего) значения, вычисляется по формуле x0 =
![]() 2ba .
2ba .
482. а) Докажите, что функция у = x2 – 2x – 3 возрастает на промежутке [1; + ) и убывает на промежутке (– ; 1].
Доказательство. Пусть x1 и x2 — произвольные числа, такие, что 1 x1 x2. Вычислим разность y1 – y2: y1 – y2 = (x12 – 2x1 – 3) – (x22 – 2x2 – 3) =
= (x1 – x2) (x1 + x2 – 2).
Так как x1 x2, то x1 – x2 0. Так как x1 1, x2 1, то x1 + x2 2 и x1 + x2 – 2 0, следовательно, y1 – y2 0, т. е. y1 y2. Итак, большему значению аргумента (x2) со-
ответствует большее значение функции (2 – 2x – 3 возрастает на промежутке y2), следователь-
но, функция у = x
[1; + ).
Пусть теперь x1 и x2 — произвольные числа, такие, что x1 x2 1. Вычислим разность y1 – y2:
y1 – y2 = (x1 – x2)(x1 + x2 – 2).
Так как x1 x2, то x1 – x2 0. Так как x1 1, x2 1, то x1 + x2 2 и x1 + x2 – 2 0, следовательно, y1 – y2 0, т. е. y1 y2. Итак, большему значению аргумента (x2) соответствует меньшее значение функции (2 – 2x – 3 убывает на промежуткеy2), следова- тельно, функция у = x
(– ; 1].
784. По графику функции у = ax2 + bx + c определите знаки a, b, c (рис. 27).
6 Рис. 27
Решение. а) Так как ветви
параболы направлены вверх, то a 0. Так как у(0) 0, то c
= у(0) 0. Абсцисса вершины параболы x0 0.
Так как x0 = ![]() 2 ab и a
0, то b 0.
2 ab и a
0, то b 0.
б) a 0, c 0, b 0 (обоснование, как в пункте «а»).
в) Так как ветви параболы направлены вверх, то a 0.
Так как у(0) 0, то c 0. Абсцисса вершины параболы x0
0. Так как x0 = ![]() 2 ab и a
0, то b 0.
2 ab и a
0, то b 0.
г) Так как ветви параболы направлены вверх, то
a 0. Так как у(0) 0,
то c 0. Абсцисса вершины параболы x0 0. Так
как x0 = ![]() 2 ab и a 0, то
b 0.
2 ab и a 0, то
b 0.
д) Так как ветви параболы направлены вниз, то
a 0. Так как у(0) 0,
то c 0. Абсцисса вершины параболы x0 0. Так
как x0 = ![]() 2 ab и a 0, то b 0.
2 ab и a 0, то b 0.
е) a 0, c 0, b 0 (обоснование, как в пункте «д»).
Промежуточный контроль. С–17, Т–7.
Основная цель восьмого параграфа — научить учащихся строить графики дробно-линейных функций и решать задачи, связанные с этими функциями.
В данном пункте рассматривается функция y = ![]() k , где x
k , где x
k — данное не равное нулю
число. Говорят также, что переменная y обратно пропорциональна
переменной x с коэффициентом пропорциональности k, эту функцию
называют обратной пропорциональностью. Главное назначение данного пункта
заключается в обучении учащихся определять, является ли данная функция обратной
пропорциональностью, для заданной функции y = ![]() k
заполнять x
k
заполнять x
таблицы значений x и y, а также по заданной паре значений x и y определять k.
489. Определите, одинаковые или разные знаки имеют x(x 0) и соответствующее ему y, если функция задана формулой:
в) y = ![]() k , где k
0; е) y =
k , где k
0; е) y = ![]() k , где k 0. x x
k , где k 0. x x
Решение. в) Так как xy = k 0, то числа x и y имеют одинаковые знаки.
е) Так как xy = k 0, то числа x и y имеют разные
знаки.
k
В данном пункте рассматривается функция y = ![]() k , где x
k , где x
k 0, формулируются и доказываются свойства этой функции, объясняется построение графика функции, называемого гиперболой.
Рассуждения про сжатие и растяжение графика в обычном классе можно не рассматривать.
495. Принадлежат ли точки A и B
одной и той же гиперболе y = ![]() k , если: x
k , если: x
в) A(2; 10), B(–20; –1); д) A(0,5; 10), B(2; 5)?
![]() Решение. в)
Точка A принадлежит гиперболе с коэффициентом k = xy = 20,
и точка B принадлежит гиперболе с коэффициентом k = 20.
Точки A и B принадлежат одной и той же гиперболе y =
Решение. в)
Точка A принадлежит гиперболе с коэффициентом k = xy = 20,
и точка B принадлежит гиперболе с коэффициентом k = 20.
Точки A и B принадлежат одной и той же гиперболе y = ![]() 20 . x
20 . x
д) Точка B принадлежит гиперболе с коэффициентом
k = xy = 5, а точка
B принадлежит гиперболе с коэффициентом k = xy = 10.
Точки A и B не принадлежат одной и той же гиперболе y =
![]() k .
k .
x k
В данном пункте рассматривается функция y = ![]() k , где x
k , где x
k 0. Стоит отметить, что случай
k = 0 не рассматривается, так как в этом случае функция y =
![]() k не
определена в x
k не
определена в x
единственной точке x = 0,
а в остальных она равна 0. Каждый учащийся должен усвоить связь между знаком k
и расположением ветвей гиперболы. Далее делается вывод о симметричности графиков
функций y = ![]() k и y = – k
k и y = – k
x x
относительно оси Ox. Из свойств
функции y = ![]() k , где
k , где
x
k 0, отмечаются её убывание при k 0 на каждом промежутке (– ; 0) и (0; + ) и возрастание при k 0 на каждом промежутке (– ; 0) и (0; + ), а также её нечётность, а следовательно, симметричность графика относительно начала координат.
Решения и комментарии 505. Докажите, что функция
y = ![]() k , где k
0, являетx ся
нечётной.
k , где k
0, являетx ся
нечётной.
Доказательство. Область определения функции:
(– ; 0)![]() ). Пусть число x
принадлежит одному из промежутков (– ; 0)
или (0; + ). Тогда число –x
принадлежит другому из этих промежутков и верны равенства
). Пусть число x
принадлежит одному из промежутков (– ; 0)
или (0; + ). Тогда число –x
принадлежит другому из этих промежутков и верны равенства
y(–x) = k = – k = –y(x).
x x
![]() Следовательно, функция y =
k ,
где k 0, является x
Следовательно, функция y =
k ,
где k 0, является x
нечётной, что и требовалось доказать.
В данном пункте рассматривается функция
y =
![]() x k
+ у0, где k, x0, y0
— данные числа и k 0. Да-
x k
+ у0, где k, x0, y0
— данные числа и k 0. Да-
x0
![]() лее
разбираются два примера построения графика функции y =
лее
разбираются два примера построения графика функции y = ![]() x kx0 +
у0 и делается вывод о построении графика функции такого вида при
помощи параллельного переноса гиперболы y = k .
x kx0 +
у0 и делается вывод о построении графика функции такого вида при
помощи параллельного переноса гиперболы y = k .
Формулу y = x x0 + у0 можно привести к виду
y = ![]() ax b .
Функцию вида y =
ax b .
Функцию вида y = ![]() ax b ,
где b ac, называют x x0 x c
ax b ,
где b ac, называют x x0 x c
дробно-линейной. Ограничение b
aс необходимо для того, чтобы исключить случай, когда y = а
для всех x, кроме x = c, и чтобы для функции y = ![]() x kx0 +
у0
x kx0 +
у0
исключить случай, когда k = 0.
Задания для повторения. При изучении данного пункта можно использовать задание 791.
508. Постройте график функции:
а) y =
![]() 2x 4 ;
б) y =
2x 4 ;
б) y = ![]() x 1 .
x 1 x 3
x 1 .
x 1 x 3
Решение. а) Так как
![]()
![]() 2x 4 = 2(x 1) 6
= 2 6 = 6 2, x 1 x 1 x
1 x 1
2x 4 = 2(x 1) 6
= 2 6 = 6 2, x 1 x 1 x
1 x 1
то заданную функцию запишем в виде y = 6 2. x 1
Искомый график получим параллельным переносом
гиперболы y = ![]() 6 на 1
единицу влево и на 2 единицы вниз x (рис. 28).
6 на 1
единицу влево и на 2 единицы вниз x (рис. 28).
б) Так как
![]() x 1 = (x 3) 2 = 2 1 ,
x 1 = (x 3) 2 = 2 1 ,
x 3 x 3 x 3
то заданную функцию запишем в
виде y = ![]() 2 1.
Искоx 3
2 1.
Искоx 3
мый график получим параллельным
переносом гиперболы y = ![]() 2 на 3 единицы вправо и на 1 единицу
вниз (рис. 29).
2 на 3 единицы вправо и на 1 единицу
вниз (рис. 29).
x
509. Является ли дробно-линейной функция:
а) y =
![]() x 1 ; б) y
=
x 1 ; б) y
= ![]() 3x 1 ; в)
y =
3x 1 ; в)
y = ![]() 2x 4 ? x 2 2x 2 x
2
2x 4 ? x 2 2x 2 x
2
Постройте график каждой из этих функций.
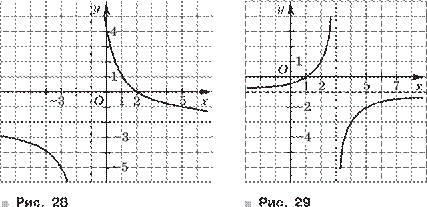
Решение.
Каждая из функций «а», «б» и «в» записана в виде y = ![]() ax b . x c
ax b . x c
а) Здесь a = 1, b = 1, c = 2, условие b ac выполнено, следовательно, данная функция является дробно-линейной.
Так как
![]() x 1 = x 2 1 = 1 1 , x 2 x 2 x 2
x 1 = x 2 1 = 1 1 , x 2 x 2 x 2
то искомый график получим параллельным
переносом гиперболы y = ![]() 1 на 2 единицы вправо и на 1 единицу x
1 на 2 единицы вправо и на 1 единицу x
вверх (рис. 30, а).
б) Так как
![]() 3x 1 =
1 5, x
0 5,
= 1 5, x ( 0 5, ) ,
3x 1 =
1 5, x
0 5,
= 1 5, x ( 0 5, ) ,
![]() x 1 x
( 1)
x 1 x
( 1)
то здесь a = –1,5, b = –0,5, c = –1, условие b ac выполнено, следовательно, данная функция является дробнолинейной. Так как
1 5, x 0 5, 1 5, (x 1) 2 2 2
![]()
![]() = = 1 5, = 1 5, , x 1 x 1 x 1 x
1
= = 1 5, = 1 5, , x 1 x 1 x 1 x
1
то искомый график получим параллельным
переносом гиперболы y = ![]() 2 на 1 единицу влево и на 1,5 единицы
x
2 на 1 единицу влево и на 1,5 единицы
x
вниз (рис. 30, б).
в) Здесь a = 2, b = 4, c = 2, условие b aс не выполнено,
так как 4 = 2 2. Следовательно, данная функция не является дробно-линейной.
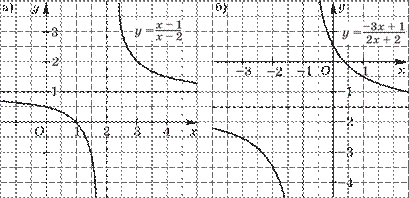
6 Рис. 30
![]() Данную функцию можно
записать в виде y =
Данную функцию можно
записать в виде y = ![]()
![]() . Её гра-
. Её гра-
x 2
фиком является прямая y = 2 без точки, соответствующей значению аргумента x = 2, для которого функция не определена (рис. 31).
Промежуточный контроль. С–18, Т–8, К–5.
![]()
![]() В данном пункте
рассматриваются приёмы построения графиков функций, содержащих модули. Для построения
таких графиков сначала раскрывают модули на тех промежутках, на которых
выражения, содержащиеся под знаком модуля, сохраняют знак. Затем строят на этих
промежутках графики получившихся функций. Разбирается построение графиков
функций y = f x( ) и y = f x() .
В данном пункте
рассматриваются приёмы построения графиков функций, содержащих модули. Для построения
таких графиков сначала раскрывают модули на тех промежутках, на которых
выражения, содержащиеся под знаком модуля, сохраняют знак. Затем строят на этих
промежутках графики получившихся функций. Разбирается построение графиков
функций y = f x( ) и y = f x() .
Задания для повторения. При изучении данного пункта можно использовать задания 788, 790.
514. Постройте график функции:
|
x |
1 |
|
x |
1 |
![]() а) y = x 1 ; б)
y = x 1 ; в)
y = ; x 1 x
1
а) y = x 1 ; б)
y = x 1 ; в)
y = ; x 1 x
1
|
x |
1 |
|
x |
1 |
![]() x2 4 x
1
x2 4 x
1
г) y = ; ж) y = x 2 ; к) y = x2 1 ;
![]()
![]() л) у = { }x 1 . 2
л) у = { }x 1 . 2
![]() Решение. а)
Так как x 1 = x 1 2 = 2 + 1, то x 1 x 1 x
1
Решение. а)
Так как x 1 = x 1 2 = 2 + 1, то x 1 x 1 x
1
искомый график получим параллельным
переносом гиперболы y = ![]() 2 на 1 единицу влево и на 1 единицу
вверх x
2 на 1 единицу влево и на 1 единицу
вверх x
(рис. 32, а).
б) Часть графика функции y = ![]() x 1 , для
точек кото-
x 1 , для
точек кото-
x 1
рого y 0, оставим без изменения. Другую часть графика

этой функции (для точек которого y 0) симметрично отразим относительно оси Ox. Получим график функции
y
![]() =
x 1 (рис.
32, б).
=
x 1 (рис.
32, б).
x 1
в) Часть графика функции y = ![]() x 1 , для
точек кото-
x 1 , для
точек кото-
x 1
|
x |
1 |
|
x |
1 |
рого x 0, оставим без изменения. Затем отразим эту часть графика относительно оси Oy. Получим график функции y = (рис. 33, а).
|
x |
1 |
|
x |
1 |
г) Часть графика функции y = , для точек кото-
|
x |
1 |
|
x |
1 |
рого y 0, оставим без
изменения. Ту часть графика этой функции, для точек которого y 0,
симметрично отразим относительно оси Ox. Получим график функции y
= ![]()
(рис. 33, б).
ж) Так как функция определена для всех x –2, то
рассмотрим два случая: x –2 и x –2.
1) Если
x –2, то x2 4 = ![]() = x 2 .
= x 2 .
|
x |
2 |
|
x2 |
4 |
2) Если
x –2, то = ![]() = x 2 .
= x 2 .

x2 4
Получим график функции y = с областью опре-
![]() x 2
x 2
деления (– ;
–2)∪
(–2; ![]() ) (рис. 34, а).
) (рис. 34, а).
к) Функция определена для всех x, кроме x = 1, x = –1. Рассмотрим два случая: x –1 и x –1.
![]() x 1 x
1 1
x 1 x
1 1
1) ![]() Если x –1,
то x2 1 = =
x 1 , поэтому
график функции на этом промежутке есть часть гиперболы у =
Если x –1,
то x2 1 = =
x 1 , поэтому
график функции на этом промежутке есть часть гиперболы у = ![]() 1 .
1 .
![]() x 1 x 1
(x 1) 1
x 1 x 1
(x 1) 1
2) ![]() Если x –1,
то x2 1 = =
x 1 , поэтому
график функции на этом промежутке есть часть гиперболы у =
Если x –1,
то x2 1 = =
x 1 , поэтому
график функции на этом промежутке есть часть гиперболы у = ![]() 1 .
1 .
![]() x 1 x 1
x 1 x 1
График функции y = x2 1 изображён на рисунке
34, б.
л) Построим последовательно графики
функций: у = {х} (рис. 35, а); перенесём его на ![]() единицы
вниз, получим
единицы
вниз, получим
6 Рис. 35
график функции у = {х}
– ![]() (рис. 35, б); теперь отразим
отрицательную часть графика функции у = {х} –
(рис. 35, б); теперь отразим
отрицательную часть графика функции у = {х} – ![]() относительно
оси Ox, получим график функции у = |{х} –
относительно
оси Ox, получим график функции у = |{х} – ![]() |
|
(рис. 35, в).
1. Придумайте функции, содержащие модули, и постройте их графики.
2. (ЕГЭ, 2010, С5). Найдите все значения а, такие, что уравнение
|x + 3| – 1 = |2x – a| (1) имеет единственное решение.
Решение. Сначала построим в системе координат xOy графики функций y = |x + 3| – 1 и y = 2|x| (рис. 36). Ясно, что эти графики имеют две общие точки. Следовательно, уравнение |x + 3| – 1 = 2|x| имеет два решения. Если график y = 2|x| передвигать вправо, оставляя вершину угла на оси Ох в точке (b; 0), то новый график будет иметь две общие точки с графиком y = |x + 3| – 1. Следовательно, уравнение
|x + 3| – 1 = 2|x – b| (2) будет иметь два решения.
Если график y = 2|x| передвигать влево, оставляя вершину угла на оси Ох в точке (b; 0), то новый график также будет иметь две общие точки с графиком y = |x + 3| – 1 до тех пор, пока вершина не попадёт в точку (–2; 0). Если вершина угла попадёт в точку (–2; 0), то уравнение (2), где b = –2, имеет единственное решение.
![]() Рассуждая аналогично,
получим, что если вершина угла будет в точке (b; 0), где –4 <
b < –2, то уравнение (2) не имеет решений, если вершина попадёт в
точку (b; 0), где b = –4, то уравнение (2) имеет
единственное решение, если вершина будет в точке (b; 0), где b
< –4, то уравнение (2) имеет два решения.
Рассуждая аналогично,
получим, что если вершина угла будет в точке (b; 0), где –4 <
b < –2, то уравнение (2) не имеет решений, если вершина попадёт в
точку (b; 0), где b = –4, то уравнение (2) имеет
единственное решение, если вершина будет в точке (b; 0), где b
< –4, то уравнение (2) имеет два решения.
Следовательно, уравнение (2) имеет единственное решение при b = –2 и при b = –4.
Переписав уравнение (1) в
![]() виде
виде
![]() x 3
x 3![]() 1 = 2 x a ,
полу-
1 = 2 x a ,
полу-
2
6 Рис. 36 чаем, что это
уравнение имеет единственное решение при ![]() a = –2 и при
a = –2 и при ![]() a = –4,
т. е. если
a = –4,
т. е. если
2 2
a = –4 или a = –8.
Ответ. a = –4, a = –8.
![]() Замечание. Отметим, что при решении задания 2
мы воспользовались тем, что график функции y = |x| есть
угол, равный 90о, а график функции y = 2|x|
есть угол, меньший 90о.
Замечание. Отметим, что при решении задания 2
мы воспользовались тем, что график функции y = |x| есть
угол, равный 90о, а график функции y = 2|x|
есть угол, меньший 90о.
Промежуточный контроль. С–19*, С–20*.
В данном пункте доказывается, что графиком функции y = 2x является прямая, что уравнение ax + by + c = 0, где a и b не равны нулю одновременно, задаёт на координатной плоскости xOy некоторую прямую. Здесь же доказывается, что уравнение окружности с центром A(a; b) и радиусом R имеет вид
(x – a)2 + (y – b)2 = R2.
Задания для повторения. При изучении данного пункта можно использовать задания 792, 793.
516. а) Напишите уравнение прямой, все точки которой одинаково удалены от точек A(2; 3) и B(4; 5).
Решение. Пусть M(x; y) — произвольная точка прямой. Так как все точки прямой одинаково удалены от точек A и B, то верно равенство MA2 = MB2, которое перепишем в виде
(x – 2)2 + (y – 3)2 = (x – 4)2 + (y – 5)2.
Раскрыв скобки и перенеся все члены уравнения в левую часть, получим уравнение 4x + 4y – 28 = 0, или x + y – 7 = 0.
Верно и обратное утверждение: если точка (x; y) принадлежит прямой x + y – 7 = 0, то MA2 = MB2. Действительно,
MA2 = (x – 2)2 + (y – 3)2 = (x – 2)2 + (7 – x – 3)2 = = (x – 2)2 + (4 – x)2,
MB2 = (x – 4)2 + (y – 5)2 = (x – 4)2 + (7 – x – 5)2 = = (x – 4)2 + (2 – x)2.
Итак, искомое уравнение прямой имеет вид x + y – 7 = 0.
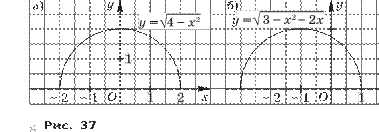
519. Постройте график функции:
![]()
![]() а) y = 4 x2 ; б)
y = 3 x2
2x .
а) y = 4 x2 ; б)
y = 3 x2
2x .
![]() Решение.
а) Пусть M(x; y) — произвольная точка искомого графика,
тогда числа x и y удовлетворяют неравенству y 0 и
равенству y = 4 x2 .
Но тогда они удовлетворяют равенству y2 = 4 –
x2, которое перепишем в виде x2 + y2
= 4. Итак, координаты точки M удовлетворяют уравнению
окружности с центром O(0; 0) и радиусом 2, следовательно, точка M
принадлежит этой окружности. Но так как y 0, то точка M
принадлежит верхней полуокружности с центром O(0; 0) и радиусом
2.
Решение.
а) Пусть M(x; y) — произвольная точка искомого графика,
тогда числа x и y удовлетворяют неравенству y 0 и
равенству y = 4 x2 .
Но тогда они удовлетворяют равенству y2 = 4 –
x2, которое перепишем в виде x2 + y2
= 4. Итак, координаты точки M удовлетворяют уравнению
окружности с центром O(0; 0) и радиусом 2, следовательно, точка M
принадлежит этой окружности. Но так как y 0, то точка M
принадлежит верхней полуокружности с центром O(0; 0) и радиусом
2.
![]() Верно и обратное
утверждение: если точка (x; y) принадлежит верхней полуокружности
с центром O(0; 0) и радиусом 2, то она удовлетворяет равенству y
= 4 x2 .
Действительно, любая точка верхней полуокружности (x; y)
удовлетворяет уравнению x2 + y2 =
4 и неравенству y 0, значит, она удовлетворяет и равенству y =
4 x2 .
Верно и обратное
утверждение: если точка (x; y) принадлежит верхней полуокружности
с центром O(0; 0) и радиусом 2, то она удовлетворяет равенству y
= 4 x2 .
Действительно, любая точка верхней полуокружности (x; y)
удовлетворяет уравнению x2 + y2 =
4 и неравенству y 0, значит, она удовлетворяет и равенству y =
4 x2 .
![]() Итак, график функции y =
4 x2 есть верхняя
полуокружность с центром O(0; 0) и радиусом 2 (рис. 37, а).
Итак, график функции y =
4 x2 есть верхняя
полуокружность с центром O(0; 0) и радиусом 2 (рис. 37, а).
![]() б)
Так как 3 x2 2x
= 4 (x 1)2 , то искомый график получим при помощи параллельного
переноса графика функции y = 4 x2
на 1 единицу влево (рис. 37, б).
б)
Так как 3 x2 2x
= 4 (x 1)2 , то искомый график получим при помощи параллельного
переноса графика функции y = 4 x2
на 1 единицу влево (рис. 37, б).
В данном пункте рассказывается о том, что некоторые свойства параболы были установлены ещё Архимедом, о вкладе Г. Галилея в изучение равноускоренного движения тел под действием силы тяжести, о применении квадратичной функции к решению задач о движении тел под действием силы тяжести.
Глава 4
Четвёртая глава посвящена изучению способов решения систем рациональных уравнений. Здесь используются понятия, изученные в 7 классе и применявшиеся ранее к системам линейных уравнений, что даёт возможность повторить изученное и научиться действовать в новой ситуации. Это понятия: решения уравнения с двумя (тремя) неизвестными, системы уравнений с двумя (тремя) неизвестными, равносильности уравнений, систем уравнений.
Составление систем уравнений для решения задач способствует не только развитию мышления и речи учащихся, но и обучению их планированию своей деятельности. Так, при решении задач учащиеся должны уметь выделять известные и неизвестные данные, намечать план действий, ставить вопросы, находить ответы на них, проверять, отвечает ли полученный результат условиям задачи. Это важнейшие метапредметные умения, необходимые при изучении математики и других школьных предметов.
Цель изучения главы 4 — усвоить перечисленные понятия, научиться решать системы рациональных уравнений и применять их к решению текстовых задач.
Основная цель изучения девятого параграфа заключается в том, чтобы, опираясь на известные понятия, связанные с уравнениями и системами линейных уравнений, научиться решать системы рациональных уравнений и применять их к решению текстовых задач.
В данном пункте вводятся понятия рационального уравнения с двумя (тремя) неизвестными и его решения, определяется, что значит решить систему уравнений, приводятся утверждения о равносильности систем уравнений.
Основными заданиями данного пункта являются задания на установление того, что данная пара (тройка) чисел является решением системы. Задание 536 рубрики «Исследуем» приучает учащихся к решению задач с параметрами.
Задания для повторения. При изучении данного пункта можно использовать задания 834—836.
534. Является ли решением системы уравнений
⎧x2 xy 3 = 0, ⎨⎩x 5 = y
пара чисел: а) (0; 3); б) (–3; 2)?
Решение. а) Так как 0 + 5 3, то пара чисел (0; 3) не является решением второго уравнения системы, а значит, не является и решением системы уравнений;
б) так как –3 + 5 = 2, (–3)2 + (–3) 2 – 3 = 0, то пара
чисел (–3; 2) является решением системы уравнений.
535. Является ли решением системы уравнений
⎪x y z = 2, ⎪⎩xy z2 = 2
тройка чисел: а) (1; –1; 1); б) (1; 1; 1)?
Решение. а) Так как 1 – 1 + 1 3, то тройка чисел (1; –1; 1) не является решением первого уравнения системы, а значит, не является и решением системы уравнений;
б) так как 1 + 1 + 1 = 3, 1 – 1 – 1 –2, то тройка чисел (1; 1; 1) не является решением второго уравнения системы, а значит, не является решением системы уравнений.
536. При каком значении a пара чисел (2; –1) являет-
⎧a x2 ay = 21, ся решением системы уравнений ⎨ 2
⎩5x ay = a 4?
Решение. Пусть a — некоторое число, для которого пара чисел (2; –1) является решением системы уравнений, тогда верны два числовых равенства:
1) 2a2 + a = 21 и 2) 10 + a = a2 + 4,
которые можно рассматривать как уравнения относительно a. Уравнение 2) имеет два корня: a1 = 3, a2 = –2. Число a1 является корнем уравнения 1), а число a2 нет, следовательно, при a = 3 пара чисел (2; –1) является решением системы уравнений. И других значений а, удовлетворяющих условию задачи, нет.
В данном пункте на четырёх примерах показывается, как можно решать способом подстановки системы рациональных уравнений, в которых имеется хотя бы одно уравнение первой степени.
⎧⎪1 1 = ![]() 1 ,
1 ,
547. г) Решите систему уравнений ⎨x y 12
⎪⎩x y = 1.
Решение. Выразим x через y из второго уравнения системы и подставим y + 1 вместо x в первое уравнение системы:
![]() 1 1 =
1 1 = ![]() 1 . (1) y 1 y 12
1 . (1) y 1 y 12
Уравнение (1) имеет два корня: y1 = –4 и y2 = 3. Подставив эти числа в равенство x = y + 1, получим соответствующие им значения x: x1 = –3 и x2 = 4. Ответ. (–3; –4), (4; 3).
Промежуточный контроль. С–21.
В данном пункте разбираются примеры решения систем рациональных уравнений способом сложения уравнений, способом введения новых неизвестных, способом выделения полных квадратов, способом разложения на множители. При этом используются равносильные преобразования уравнений. Иногда решению системы помогает знание того, что сумма квадратов двух чисел равна нулю тогда и только тогда, когда эти числа нули.
Задания для повторения. При изучении данного пункта можно использовать задание 848.
⎧x2 y2 = 5,
548. а) Решите систему уравнений ⎨⎩xy = 2.
Решение. Обычно решение такой системы записывают, заменяя данную систему равносильными ей системами:
⎧⎨⎩xxy2 = y2 2=; 5, ⎩⎧⎨2xxy2 =y2 =4;5, ⎩⎧⎨xx22 2yxy2 = 5,y2 = 1;
⎧x2 y2 = 5,
⎨⎩(x y)2 = 1. (1)
Знаки равносильности ( ) поставлены для учителя, но в классе с углублённым изучением математики их вполне можно использовать.
Решениями второго уравнения последней из систем (1) являются такие пары чисел (x; y), которые являются решениями хотя бы одного из уравнений:
1) x + y = 1 и 2) x + y = –1.
Поэтому все решения исходной системы есть объединение всех решений двух систем
⎧x2 y2 = 5, ⎧x2 y2 = 5, 3) ⎨⎩x y = 1 и 4) ⎨⎩x y = 1.
Решив системы 3) и 4), получим все решения исходной системы: (–1; 2), (2; –1), (1; –2), (–2; 1).
Ответ. (–1; 2), (2; –1), (1; –2), (–2; 1).
549. а) Решите систему уравнений
⎧x2 12y = 68,
⎨⎩y2 4x = 28.
Решение. Заменим в системе первое уравнение суммой двух уравнений этой системы. Получим систему, равносильную исходной:
⎧x2 4x y2 12y = 40,
⎨⎩y2 4x = 28. (2)
Теперь выделим полные квадраты в первом уравнении системы (2):
⎧(x 2)2 (y 6)2 = 0,
⎨⎩y2 4x = 28. (3)
Так как сумма квадратов двух чисел равна нулю тогда и только тогда, когда эти числа нули, то первое уравнение системы (3) имеет единственное решение (2; –6). Проверкой убеждаемся, что эта пара чисел является решением второго уравнения системы (3), следовательно, она является решением системы (3) и равносильной ей исходной системы.
Ответ. (2; –6).
550. Решите систему уравнений:
![]()
а) ⎧⎪⎩⎪⎨xy22 64xy = x214 1;4y = 2, в) ⎧⎨⎩99xyx2 44xyy2 == 1,2.
Решение. а) Введя новое неизвестное a =
x2 – 4y, перепишем первое уравнение системы
в виде a ![]() 1 = 2 .
Оно
1 = 2 .
Оно
a
имеет единственный корень a = 1. Это означает, что данная система равносильна системе
⎧x2 4y = 1,
⎨⎩y2 6x = 14. (4)
Сложив уравнения системы (4) и заменив полученным уравнением первое уравнение системы, получим новую систему, равносильную системе (4), а значит, и исходной системе:
⎧x2 6x y2 4y = 13,
⎨⎩y2 6x = 14. (5)
Выделив в первом уравнении системы (5) полные квадраты, перепишем систему (5) в виде
⎧(x 3)2 (y 2)2 = 0,
⎨⎩y2 6x = 14. (6)
Теперь очевидно, что первое уравнение системы (6) имеет единственное решение: x = 3, y = 2. Проверка показывает, что эта пара чисел является решением второго уравнения системы (6), а значит, она является решением системы (6) и равносильной ей исходной системы.
Итак, исходная система имеет единственное решение
(3; 2).
в) Перепишем систему в виде
⎧x x(9 4y) = 1,
⎨⎩y x(9 4y) = 2. (7)
Если пара чисел (x0; y0) — решение системы (7), то верны числовые равенства x0(9x0 + 4y0) = 1 и y0(9x0 + 4y0) = –2. Заметим, что обе части этих числовых равенств не нули, поэтому, разделив первое равенство на второе почленно, получим новое числовое равенство:
xy00 = ![]() .
Откуда следует, что y0 = –2x0.
То есть искомые решения системы (7) являются решениями системы
.
Откуда следует, что y0 = –2x0.
То есть искомые решения системы (7) являются решениями системы
⎧x x(9 4y) = 1,
⎨⎩y = 2x. (8)
Решив систему (8), получим два её решения: (1; –2), (–1; 2).
Проверкой убеждаемся, что обе эти пары чисел действительно являются решениями исходной системы.
Ответ. а) (3; 2); в) (1; –2), (–1; 2).
![]() Замечание. Отметим, что мы не доказали в процессе
решения задания «в» равносильность системы (8) и исходной системы, но из
проведённого рассуждения следует, что любое решение исходной системы является
решением системы (8) (т. е. система (8) является следствием исходной системы),
поэтому необходимо проверить, является ли каждое решение системы (8) решением
исходной системы. И эта проверка является обязательной частью решения системы.
На самом деле система (8) равносильна исходной системе, что следует из
утверждения, доказанного ниже (дополнительное задание 1).
Замечание. Отметим, что мы не доказали в процессе
решения задания «в» равносильность системы (8) и исходной системы, но из
проведённого рассуждения следует, что любое решение исходной системы является
решением системы (8) (т. е. система (8) является следствием исходной системы),
поэтому необходимо проверить, является ли каждое решение системы (8) решением
исходной системы. И эта проверка является обязательной частью решения системы.
На самом деле система (8) равносильна исходной системе, что следует из
утверждения, доказанного ниже (дополнительное задание 1).
551. Решите систему уравнений:
⎧x2 6x y2 2y 10 = 0,
a) ⎨⎩15x 44y = 1;
⎧x2 4x 4y2 4y 5 = 0,
б) ⎨⎩1005 5, x 4024y = 1.
Решение. а) Выделив полные квадраты в первом уравнении, перепишем его в виде
(x – 3)2 + (y – 1)2 = 0. (9)
Теперь очевидно, что первое уравнение системы имеет единственное решение: x = 3, y = 1. Проверкой убеждаемся, что эта пара является решением второго уравнения, а значит, и решением системы уравнений.
б) Рассуждая аналогично, получим единственное ре-
шение системы (–2; 0,5).
Ответ. а) (3; 1); б) (–2; 0,5).
1. Докажите утверждение: если f(x, y) и g(x, y) — многочлены относительно x и y, a и b — числа, b 0, то равносильны системы
![]() 1)
⎧⎨⎩f x yg x y(( ,,
)) == ab, и 2) ⎪⎧⎪⎩⎨g x yg x yf x y((( ,, , )) )= =abb,.
1)
⎧⎨⎩f x yg x y(( ,,
)) == ab, и 2) ⎪⎧⎪⎩⎨g x yg x yf x y((( ,, , )) )= =abb,.
Доказательство. 1. Пусть пара чисел (x0; y0) — решение системы 1), тогда верны числовые равенства f(x0, y0) = a и g(x0, y0) = b. Так как b 0, то и g(x0, y0) 0, поэтому
![]() верно числовое равенство f x y( 0, 0) = a . Это означает, что g x y( 0, 0)
b
верно числовое равенство f x y( 0, 0) = a . Это означает, что g x y( 0, 0)
b
любое решение системы 1) является решением системы 2).
2. Пусть теперь пара чисел (x0; y0) — решение систе-
![]() мы 2), тогда верны числовые
равенства f x y( 0, 0) = a и g x y( 0, 0) b
мы 2), тогда верны числовые
равенства f x y( 0, 0) = a и g x y( 0, 0) b
g(x0, y0) = b. Так как b 0, то и g(x0, y0) 0, поэтому, умножив обе части первого числового равенства на отличное от нуля число g(x0, y0), получим новое верное числовое равенство f(x0, y0) = a. Это означает, что любое решение системы 2) является решением системы 1).
3. Предположим, что система 1) не имеет решения, а система 2) имеет решение. Тогда из п. 2 доказательства, проведённого выше, следует, что система 1) имеет решение. Полученное противоречие показывает, что сделанное предположение неверно. Значит, если система 1) не имеет решения, то и система 2) не имеет решения.
Аналогично доказывается, что если система 2) не имеет решения, то и система 1) не имеет решения.
Из приведённого доказательства следует, что системы 1) и 2) равносильны, что и требовалось доказать.
2. Решите систему уравнений:
a) ⎧⎨x y2 3 = 8, ⎧xy x = 4, ⎪⎧xyyz == 2,4, ⎩x y3 2 = 4; ⎩x y2 x2 = 4; ⎨⎪⎩xz = 2.
б) ⎨ в)
Решение. а) Исходная система равносильна системе
⎧⎪y = 2,
⎨x
⎪⎩x y3 2 = 4,
которую перепишем в виде
⎧y = 2x,
⎨⎩x y3 2 = 4. (10)
Система (10) имеет единственное решение (1; 2). Следовательно, и исходная система имеет единственное решение (1; 2).
б) Исходную систему перепишем в виде
⎧x y( 1) = 4,
⎨⎩x y2( 1) = 4.
Эта система равносильна системе
⎧x = 1,
⎨⎩x y( 1) = 4. (11)
Система (11) имеет единственное решение (–1; –5). Следовательно, и исходная система имеет единственное решение (–1; –5).
в) Исходная система равносильна системе
⎧⎪ ![]() xz = 2,
xz = 2,
|
или системе |
⎨ yz = 4, ⎪ xz = 2, ⎩ |
|
|
|
⎧⎪z = = 2x4,, ⎨yz |
(12) |
⎪⎩xz = 2.
Система (12) имеет два решения: (1; 2; –2), (–1; –2; 2).
Следовательно, и исходная система имеет два решения:
(1; 2; –2), (–1; –2; 2).
Ответ. а) (1; 2); б) (–1; –5); в) (1; 2; –2), (–1; –2; 2).
Промежуточный контроль. С–22, С–23, С–24*.
В данном пункте разбираются решения текстовых задач, приводящие к системам рациональных уравнений. Начать объяснение нового материала можно с более простых задач 552—555.
Задания для повторения. При изучении данного пункта можно использовать задания 848, 983.
552. а) Разложите число 171 на два множителя, сумма которых была бы равна 28.
Решение. Пусть x — первый множитель, y — второй
⎧xy = 171,
множитель. Составим систему уравнений ⎨⎩x y = 28.
Решив систему, получим два её решения: x1 = 9, y1 = 19 и x2 = 19, y2 = 9. Порядок множителей в задаче не важен, поэтому искомые множители 9 и 19. Ответ. 9 и 19.
554. а) Если к квадрату первого числа прибавить удвоенное второе число, то получится (–7), а если из первого числа вычесть второе, то получится 11. Найдите эти числа.
Решение. Пусть x — первое число, y — второе число. По условиям задачи составим два уравнения: x2 + 2y = –7 и x – y = 11. Решив систему этих уравнений, получим два её решения: (–5; –16), (3; –8).
Ответ. –5 и –16 или 3 и –8.
555. а) Найдите двузначное число, если цифра десятков на 2 больше цифры единиц, а произведение числа на сумму его цифр равно 640.
![]()
Решение. Пусть xy = 10x + y — искомое двузначное число, тогда выполняются равенства
x = y + 2 и (10x + y)(x + y) = 640.
Решив систему этих уравнений, получим два её реше-
![]() ния: (6; 4) и ⎜⎝⎛ 1153; 7511⎞⎟⎠
.
ния: (6; 4) и ⎜⎝⎛ 1153; 7511⎞⎟⎠
.
Так как по смыслу задачи x и y — целые числа и
1 x 9 и 0 y 9, то условию задачи удовлетворяют лишь x = 6 и y = 4, т. е. искомое число 64. Ответ. 64.
557. б) Двое рабочих, работая вместе, выполнили всю работу за 5 дней. Если бы первый рабочий работал в два раза быстрее, а второй — в два раза медленнее, то всю работу они выполнили бы за 4 дня. За сколько дней выполнил бы эту работу первый рабочий?
Решение. I способ. Пусть за x и y дней выполнят всю работу первый и второй рабочие соответственно. При совместной работе они выполнят работу за 5 дней. Составим
первое уравнение: ![]() 1 1 =
1 1 = ![]() 1 .
1 .
x y 5
Если бы первый работал в 2 раза быстрее, а второй —
![]() в 2 раза медленнее, то в
день они выполняли бы 2 и 1 x 2y
в 2 раза медленнее, то в
день они выполняли бы 2 и 1 x 2y
всей работы соответственно и всю работу выполнили бы за 4 дня. Составим второе уравнение:
2![]()
![]() 1 = . x 2y
1 = . x 2y
Для получения ответа надо решить систему из двух составленных уравнений, что можно сделать, введя новые
неизвестные a = ![]() 1 и b =
1 и b = ![]() 1 . Поэтому можно
было бы с x y
1 . Поэтому можно
было бы с x y
самого начала ввести эти неизвестные.
![]()
![]() II
способ. Пусть a и b — части работы, выполняемые за день
первым и вторым рабочими соответственно. Составим два уравнения: a b =
и 2a b =.
II
способ. Пусть a и b — части работы, выполняемые за день
первым и вторым рабочими соответственно. Составим два уравнения: a b =
и 2a b =.
2
Решив систему из этих двух уравнений,
получим a
= ![]() и b =
и b = ![]() .
.
Первый рабочий выполнит всю работу
за 1 ![]() =
=
= 10 (дней).
Ответ. 10 дней.
983. Если продать 20 коров, то заготовленного сена хватит на десять дней дольше, если же прикупить 30 коров, то запас сена исчерпается десятью днями раньше. Сколько было коров и на сколько дней заготовлено сена?
Решение. Пусть для x коров заготовлено сена на y дней. Запишем кратко условие задачи:
|
число коров |
число дней |
|
x |
y |
|
x – 20 |
y + 10 |
|
x + 30 |
y – 10 |
Так как при постоянном запасе сена число дней обратно пропорционально числу коров, то составим два уравнения:
![]() x = y 10
и x 30 = y . x 20 y x y 10
x = y 10
и x 30 = y . x 20 y x y 10
Система этих уравнений имеет единственное решение:
x = 120, y = 50. То есть для 120 коров было запасено сена на 50 дней.
Ответ. 120 коров; 50 дней.
Промежуточный контроль. С–25, Т–9.
Основная цель изучения десятого параграфа заключается в том, чтобы, опираясь на знания о графиках функций, научиться решать графическим способом уравнения и системы уравнений. Здесь рассматривается приём, который обычно называют графическим способом решения систем уравнений. Этот приём состоит в построении графиков соответствующих функций, в выяснении, пересекаются ли они, т. е. имеет ли система уравнений решения и сколько.
Вообще говоря, этим способом не всегда можно найти точные решения, но в отдельных случаях удаётся их найти. Чтобы проверить, что решения найдены точно, надо их подставить в каждое уравнение системы и убедиться, что получатся верные числовые равенства.
В пункте 10.1 разбираются примеры решения систем уравнений графическим способом и задача, ответ к которой графическим способом можно получить только приближённо.
В пункте 10.2 проводится исследование и устанавливаются соотношения между коэффициентами двух уравнений первой степени с двумя неизвестными для трёх случаев:
1) система имеет единственное решение;
2) система не имеет решений;
3) система имеет бесконечно много решений.
Эти соотношения полезно помнить, так как они позволяют определять не только наличие решений системы двух уравнений первой степени с двумя неизвестными, но и их количество.
Задания для повторения. При изучении данного пункта можно использовать задание 846.
571. Пересекает ли обе оси координат прямая ax + by + + c = 0, если оба числа a и b отличны от нуля?
Решение. Если y = 0, то из уравнения
прямой следует, что x = ![]() c , т. е. прямая пересекает
ось Ox в точке a
c , т. е. прямая пересекает
ось Ox в точке a
( ![]() c ; 0). Аналогично
показывается, что прямая пересекает a ось Oy в точке (0;
c ; 0). Аналогично
показывается, что прямая пересекает a ось Oy в точке (0; ![]() c ). b
c ). b
578. При каких a и b прямые x + y = –b и x – ay = 2:
а) пересекаются в точке (1; 4); б) параллельны; в) совпадают?
Решение. а) Прямые пересекаются в точке (1; 4), если эта точка принадлежит каждой прямой, т. е. если верны равенства 1 + 4 = –b и 1 – 4a = 2. Из этих равенств находим, что a = –0,25, b = –5.
б) Прямые параллельны, если их коэффициенты при
x и y пропорциональны, но не пропорциональны свобод-
![]()
![]() ным членам, т. е.
если = 1 b , откуда находим, что
ным членам, т. е.
если = 1 b , откуда находим, что
a 2
a = –1, b –2.
![]()
![]() в) Прямые совпадают, если
в) Прямые совпадают, если
![]() их коэффициенты при x,
y и свободные члены пропорциональны, т. е. если =
1 = b , откуда
их коэффициенты при x,
y и свободные члены пропорциональны, т. е. если =
1 = b , откуда
a 2
находим, что a = –1, b = –2.
580. а) Решите графическим способом систему уравнений
6 Рис. 38 ⎧⎪⎨2xx yy =14=, 0,
⎪⎩y = 2.
Решение. Построим в одной системе координат три прямые (рис. 38). Они пересекаются в точке (1; 2), следовательно, система имеет единственное решение (1; 2). Проверка показывает, что решение найдено точно.
![]() Замечание. Если учащиеся заметят, что данная
система уравнений легко решается устно, то найденное ими решение надо
использовать для проверки нового для них графического способа решения систем.
Замечание. Если учащиеся заметят, что данная
система уравнений легко решается устно, то найденное ими решение надо
использовать для проверки нового для них графического способа решения систем.
581. Найдите все значения a, при каждом из которых система уравнений
⎧(3 2 )a x (1 a y) a2 = 0, ⎨⎩7x 3y 4 = 0
имеет бесконечно много решений.
Решение. Система имеет бесконечно много решений тогда, когда прямые совпадают, т. е. если коэффициенты при x и y и свободные члены пропорциональны:
3 2a = 1 a = a2 .
7 3 4
![]() Равенство
3 2a = 1 a
выполняется лишь при a = –2.
Равенство
3 2a = 1 a
выполняется лишь при a = –2.
7 3
![]() При этом значении a
выполняется и равенство 1 a = a2,
При этом значении a
выполняется и равенство 1 a = a2,
3 4
следовательно, лишь при a = –2 система имеет бесконечно много решений.
582. Найдите все значения a, при каждом из которых система уравнений
⎧a x2 (2a 1)y (5a 3) = 0,
⎨⎩4x 5y 13 = 0
не имеет решений.
![]() Решение.
Система не имеет решений тогда, когда прямые параллельны, т. е. если
коэффициенты при x и y пропорциональны, но не пропорциональны
свободным членам:
Решение.
Система не имеет решений тогда, когда прямые параллельны, т. е. если
коэффициенты при x и y пропорциональны, но не пропорциональны
свободным членам:
a2 = (2a 1) (5a 3) .
![]() 4 5
13
4 5
13
a2 (2a 1)
Равенство = вы-
4 5 Рис. 39
6
полняется
при a = – ![]() и при
и при
![]()
![]() a = 2.
При a = – условие (2a 1) (5a 3)
выполняет-
a = 2.
При a = – условие (2a 1) (5a 3)
выполняет-
5 13
ся, а при
a = 2 нет. Следовательно, лишь
при a = – ![]() система не имеет решений.
система не имеет решений.
1. (ГИА). Две прямые пересекаются в точке С (рис. 39). Вычислите координаты точки C. Решение. Решим систему уравнений
⎧3x y = 1, ⎨⎩x 3y = 7.
Она имеет единственное решение: (1; –2), следовательно, эта пара чисел и есть координаты точки C. Ответ. (1; –2).
В данном пункте разбираются примеры решения графическим способом систем уравнений первой и второй степени.
Задания для повторения. При изучении данного пункта можно использовать задание 839.
584. д) Решите графическим способом систему уравне-
⎧y = x2 2x 1, ний ⎨ 2
⎩y = x 4x 1.
![]() Решение. Так
как x2 – 2x + 1 = (x
– 1)2, то графиком функции y = x2
– 2x + 1 является парабола с вершиной (1; 0), ветви
которой направлены вверх (a = 1 >
0). Так как
Решение. Так
как x2 – 2x + 1 = (x
– 1)2, то графиком функции y = x2
– 2x + 1 является парабола с вершиной (1; 0), ветви
которой направлены вверх (a = 1 >
0). Так как
–x2 + 4x + 1 = –(x – 2)2 + 5, то графиком функции y = –x2 + 4x + 1 является парабола с вершиной (2; 5), ветви которой направлены вниз (a = –1 < 0).
Графики функций (рис. 40) пересекаются в точках (0; 1) и (3; 4).
Проверка показывает, что решения
6 Рис. 40 найдены точно. Следовательно, система имеет два решения: (0; 1) и (3; 4).
586. Говорят, что прямая y = kx + l касается параболы y = ax2 + bx + с, если прямая и парабола имеют единственную общую точку. То есть если система уравнений
⎧y = ax2 bx c, ⎨⎩y = kx l
имеет единственное решение. Найдите все значения k, при каждом из которых:
а) прямая y = kx касается параболы y = 0,5x2 – x + 4,5;
б) прямая y = kx – 4k – 2 касается параболы y = 0,5x2 – – 3x + 6,5.
Решение. а) Прямая y = kx касается параболы y = 0,5x2 – x + 4,5, если система уравнений
⎧y = 0 5, x2 x 4 5, ,
![]() имеет единственное
решение, т. е. если уравнение
имеет единственное
решение, т. е. если уравнение
0,5x2 – x + 4,5 = kx (1) имеет единственный корень.
Квадратное уравнение (1) имеет единственный корень, если дискриминант этого уравнения D равен нулю:
(k + 1)2 – 4 0,5 4,5 = 0. (2)
Из равенства (2) следует, что D = 0 только в двух случаях: k1 = 2 и k2 = –4.
Итак, парабола y = 0,5x2 – x + 4,5 имеет две касательные вида y = kx.
Это прямые y = 2x и y = –4x
6 Рис. 41 (рис. 41).
б) Прямая y = kx – 4k – 2 касается параболы
y = 0,5x2 – 3x + 6,5, если система уравнений
⎧y = 0 5, x2 3x 6 5, , ⎨⎩y = kx 4k 2
имеет единственное решение, т. е. если уравнение
0,5x2 – 3x + 6,5 = kx – 4k – 2 (3) имеет единственный корень.
Квадратное уравнение (3) имеет единственный корень, если дискриминант этого уравнения D равен нулю:
(k + 3)2 – 4 0,5 (8,5 + 4k) = 0. (4)
Из равенства (4) следует, что D = 0 только в двух случаях: Итак, парабола k1 = –2 и k2 = 4.y = 0,5x2 – 3x + 6,5 имеет две каса-
тельные вида y = kx – 4k – 2. Это прямые y = –2x + 6 и y = 4x – 18.
587. Говорят, что прямая y = kx + b касается окружности (x – x0)2 + (y – y0)2 = R2, если прямая и окружность имеют единственную общую точку, т. е. если система
уравнений ⎧⎨⎩(yx = kxx0 )2 b (y y0)2 = R2, имеет единственное
решение. Найдите все значения k, при каждом из которых:
а) прямая y = kx + 3 касается окружности (x + 2)2 +
+ y2 = 9;
б) прямая y = k(x – 5) + 5 касается окружности
(x – 1)2 + (y – 2)2 = 25.
Решение. а) Прямая y = kx + 3 касается окружности
(x + 2)2 + y2 = 9, если система уравнений
⎧(x 2)2 y2 = 9, ⎨⎩y = kx 3
имеет единственное решение, т. е. если уравнение
(x + 2)2 + (kx + 3)2 = 9 (5) имеет единственный корень.
Перепишем квадратное уравнение в виде
(1 + k2)x2 + 2(3k + 2)x + 4 = 0. (6)
Квадратное уравнение (6) имеет единственный корень, если дискриминант этого уравнения D равен нулю:
4(3k + 2)2 – 4 (1 + k2) 4= 0. (7)
Из равенства (7) следует, что D = 0 только в двух случаях: k1 = 0 и k2 = –2,4.
Имеются две касательные вида y = kx + 3 к окружности (x + 2)2 + y2 = 9. Это прямые y = 3 и y = –2,4x + 3.
б) Прямая y = k(x – 5) + 5 касается окружности
(x – 1)2 + (y – 2)2 = 25, если система уравнений
⎧(x 1)2 (y 2)2 = 25, ⎨⎩y = k x( 5) 5
имеет единственное решение, т. е. если уравнение
(x – 1)2 + (kx – 5k + 3)2 = 25 (8) имеет единственный корень.
Перепишем квадратное уравнение в виде
(1 + k2)x2 – 2(5k2 – 3k + 1)x + 25k2 – 30k – 15 = 0. (9)
Квадратное уравнение (9) имеет единственный корень,
если четверть дискриминанта этого
уравнения ![]() D равна
D равна
4 нулю:
(5k2
– 3k + 1)2 – (1 + k2)(25k2
– 30k – 15) = (3k + 4)2
= 0. Из последнего равенства следует, что ![]() D = 0 только
D = 0 только
4
при k = – ![]() .
.
Итак, имеется единственная касательная вида y =
k(x – 5) + 5 к окружности (x – 1)2
+ (y – 2)2 = 25. Это прямая y
= – ![]() (x – 5) + 5.
(x – 5) + 5.
В данном пункте разбираются примеры решения уравнения графическим способом. Если учащиеся научились графическим способом решать системы двух уравнений с двумя неизвестными, то они легко освоят и графический способ решения уравнений. Надо только обратить их внимание на разницу в постановке задачи: решая систему уравнений с двумя неизвестными х и у, ищем пары чисел (х; у), а решая графическим способом уравнение с одним неизвестным х, мы сами вводим второе неизвестное у, но ищем только значение х.
Стоит подчеркнуть, что графический способ решения уравнений позволяет определить число корней уравнения, а сами корни находятся лишь приближённо. Чтобы убедиться, что корни уравнения найдены точно, необходимо выполнить проверку.
588. На рисунке 42 изображены графики функций у = у = 2х – 1.
а) Укажите несколько значе-
ний х, при которых эти функции принимают различные значения.
б) Укажите корни уравнения
![]() 1 =
2х – 1. (1) 6
Рис. 42 x
1 =
2х – 1. (1) 6
Рис. 42 x
|
и (1; 1), следовательно, уравнение |
|
|
(1) имеет два корня: x1 = –0,5 и x = 1. |
6 Рис. 43 |
![]() Являются ли найденные
корни точными или приближёнными?
Являются ли найденные
корни точными или приближёнными?
Решение. а) При х = –2; –1; 0,5; 2 функции принимают различные значения.
б) Графики данных функций пересекаются в точках (–0,5; –2)
2
Оба корня найдены точно, так как верны равенства
![]() 1
1
![]() =
2 (–0,5) – 1 и = 2 1
– 1.
=
2 (–0,5) – 1 и = 2 1
– 1.
0 5,
592. а) Используя графики функций (рис. 43), решите уравнение ах2 = –bх – с и определите а, b и c.
Решение. Графики функций y = ах2 и y = –bх – с пересекаются в точках (1; 2) и (–0,5; 0,5). Поэтому числа 1 и –0,5 удовлетворяют уравнению ах2 = –bх – с, т. е. уравнение имеет два корня: x1 = 1 и x2 = –0,5.
Подставив пару чисел 2, получим а = 2. Подставив в формулу х1 = 1 и y1 = 2 в формулу y = –bх – с
y = ах
сначала пару чисел х1 = 1 и y1 = 2, а затем пару чисел х2 = –0,5 и y2 = 0,5, получим два уравнения с неизвестными b и с:
![]() 2
= –b – с, 0,5 = 0,5b – с.
(2)
2
= –b – с, 0,5 = 0,5b – с.
(2)
Решив систему уравнений (2), получим b = –1, с = –1.
594. Найдите все значения a, при каждом из которых урав-
![]()
![]() нение 4 x2 = x a
нение 4 x2 = x a
а) имеет единственный ко-
рень; б) имеет два корня; в) не
имеет корней. 6 Рис. 44
![]() Решение.
а) График функции y = 4 x2
есть верхняя полуокружность с центром (0; 0) и радиусом 2. При каждом значении
a график функции y = x a есть пара лучей с вершиной на оси Ox:
y = x – a при x a и y = –x +
a при x a, которые образуют с положительным направлением оси Ox
углы 45º и 135º. На рисунке 44 изображён такой угол с вершиной A,
касающийся полуокружности. Из равнобедренного прямоугольного треугольника
Решение.
а) График функции y = 4 x2
есть верхняя полуокружность с центром (0; 0) и радиусом 2. При каждом значении
a график функции y = x a есть пара лучей с вершиной на оси Ox:
y = x – a при x a и y = –x +
a при x a, которые образуют с положительным направлением оси Ox
углы 45º и 135º. На рисунке 44 изображён такой угол с вершиной A,
касающийся полуокружности. Из равнобедренного прямоугольного треугольника
![]()
![]() OBA найдём OA =
2 2 . В этом случае a = 2 2 .
OBA найдём OA =
2 2 . В этом случае a = 2 2 .
Аналогично для угла с вершиной C, касающегося полуокружности, получим, что a = –2 2 .
![]() Итак,
при a = 2 2 и a = –2 2 исходное уравнение имеет единственный корень.
Итак,
при a = 2 2 и a = –2 2 исходное уравнение имеет единственный корень.
![]()
![]() б) Нетрудно убедиться, что
если вершина угла лежит внутри отрезка AC, т. е. если –2 2 a 2 2 ,
то стороны угла пересекают полуокружность в двух точках, следова-
б) Нетрудно убедиться, что
если вершина угла лежит внутри отрезка AC, т. е. если –2 2 a 2 2 ,
то стороны угла пересекают полуокружность в двух точках, следова-
![]() тельно, при –2 2 a 2 2
исходное уравнение имеет два корня.
тельно, при –2 2 a 2 2
исходное уравнение имеет два корня.
в) Если вершина угла находится левее точки С или
![]()
![]() правее точки A, т. е.
если a –2 2 или a 2 2 , то исходное уравнение не имеет корней.
правее точки A, т. е.
если a –2 2 или a 2 2 , то исходное уравнение не имеет корней.
Промежуточный контроль. С–27, С–28, Т–10, К–6.
В данном пункте даётся определение диофантова уравнения, говорится о том, что в 7 классе приводились примеры решения линейных диофантовых уравнений. Далее даётся определение частного и общего решения линейного диофантова уравнения, показывается, как найти общее решение диофантова линейного уравнения.
Затем добавляются диофантовы уравнения второй степени. На примерах показывается, как решать диофантовы уравнения при помощи:
1) разложения многочлена на множители;
2) перебора всех возможных случаев;
3) выражения одного неизвестного через другое и выяснения, когда это выражение будет целым числом.
Задания для повторения. При изучении данного пункта можно использовать задание 852.
597. Решите уравнение x2 – y2 = 5:
а) в целых числах; б) в натуральных числах.
Решение. а) Разложим левую часть уравнения на множители:
(x – y)(x + y) = 5.
Произведение двух целых чисел равно 5 в каждом из четырёх случаев:
|
⎧x y = 1, 1) ⎨x y = 5; ⎩ |
⎧x y = 5, 2) ⎨x y = 1; ⎩ |
|
⎧x y = 1, 3) ⎨x y = 5; ⎩ |
⎧x y = 5, 4) ⎨x y = 1. ⎩ |
Системы 1)—4) имеют решения (3; 2), (3; –2), (–3; –2), (–3; 2) соответственно.
б) Из решения пункта «а» следует, что уравнение име-
ет единственное решение (3; 2) в натуральных числах. Тот же результат можно получить иначе.
Так как x и y — натуральные числа и 5 0, то x + y и x – y — натуральные числа и x + y x – y. Тогда произведение 5 может получиться в единственном случае: x + y = 5, x – y = 1, откуда получается единственное решение данного уравнения в натуральных числах: (3; 2).
598. а) Решите уравнение xy + 5x – 3y = 18 в целых числах.
Решение. Перепишем уравнение в виде x(y + 5) – 3y – 15 = 3, x(y + 5) – 3(y + 5) = 3, (x – 3)(y + 5) = 3.
Произведение двух целых чисел равно 3 в каждом из четырёх случаев:
|
⎧x 3 = 1, 1) ⎨y 5 = 3; ⎩ |
⎧x 3 = 1, 2) ⎨y 5 = 3; ⎩ |
|
⎧x 3 = 3, 3) ⎨y 5 = 1; ⎩ |
⎧x 3 = 3, 4) ⎨y 5 = 1. ⎩ |
Системы 1)—4) имеют решения (4; –2), (2; –8), (6; –4), (0; –6) соответственно.
599. а) Докажите, что уравнение x2 – 6x + y2 + 4y + + 13 = 0 имеет единственное целочисленное решение. Доказательство. Перепишем уравнение в виде
(x – 3)2 + (y + 2)2 = 0.
Это уравнение имеет единственное решение: x1 = 3, y1 = –2. Это единственное целочисленное решение уравнения, что и требовалось доказать.
602. Один рабочий на новом станке производит за 1 ч целое число деталей, большее 8, а на старом станке — на 3 детали меньше. На новом станке один рабочий выполняет норму за целое число часов, а два рабочих вместе выполняют норму на старых станках на 1 ч быстрее. Из какого количества деталей состоит дневная норма?
Решение. Пусть х деталей один рабочий производит на новом станке за час (х 8) и выполняет весь заказ за t ч, тогда на старом станке один рабочий производит за час (х – 3) детали, а весь заказ состоит из tх или 2(х – 3)(t – 1) деталей. Составим уравнение: tх = 2(х – 3)(t – 1),
![]() так как x
8, то можно выразить t через x из этого уравнения: t =
так как x
8, то можно выразить t через x из этого уравнения: t =
![]() = 2
= 2 ![]() 6 .
6 .
x 6 x 6
Так как х 8, то t является натуральным числом в двух случаях: при х = 9 и при х = 12. В том и в другом случае tх = 36, т. е. дневная норма состоит из 36 деталей.
603. Пастух заметил, что произведение числа баранов на число его баранов, уменьшенное на единицу, ровно на 15 больше, чем произведение его собственного возраста на число его баранов, уменьшенное на 2. Сколько лет пастуху?
Решение. Пусть было n баранов и пастуху было a лет.
Тогда верно равенство
n(n – 1) = 15 + a(n – 2).
Выразим a через n из этого равенства:
n2 n 15 n n( 2) n 2 13
a = = =
![]() n 2
n 2
= =
= n 1 ![]() 13 .
13 .
n 2 n 2 n 2 n 2
Так как число a натуральное, то n – 2 — делитель числа 13. Это возможно лишь при натуральных n1 = 3 и n2 = 15. Но для n1 число a не натуральное, а для n2 — натуральное. Следовательно, n = 15. Тогда a = 15, т. е. пастуху было 15 лет.
604. Иван Петрович приобрёл в начале года k акций банка «Надежда», часть из которых — простые, а другая часть — привилегированные. За год доход по одной простой акции составил 16 условных денежных единиц, а доход по одной привилегированной акции — 21 условную денежную единицу. Сколько привилегированных акций купил Иван Петрович, если доход за год по купленным акциям составил 269 условных денежных единиц?
Решение. Пусть Иван Петрович приобрёл в начале года х привилегированных акций, тогда простых акций он купил (k – х) штук. Доход за год по всем акциям составил 21х + 16(k – х), или 269 условных денежных единиц. Составим уравнение:
21х + 16(k – x) = 269,
![]()
которое перепишем в виде х = k .
Итак,
Иван Петрович купил ![]() привилегиро-
привилегиро-
5 ванных акций.
Задача почти решена. Но ответ выражен через k,
значение которого в условии задачи не дано. Заметим, что количество акций —
число натуральное. Оно больше ![]() ,
,
![]()
![]() но меньше
но меньше ![]() ,
так как первая дробь даёт наименьшее число акций (если все акции
привилегированные), а вторая — их наибольшее число (если все акции простые).
Так как 12
,
так как первая дробь даёт наименьшее число акций (если все акции
привилегированные), а вторая — их наибольшее число (если все акции простые).
Так как 12 ![]() 13 и 16
13 и 16 ![]() 17,
то 13 k 16. В этом промежутке только при k = 14 число k
является натуральным. Итак, Иван Петрович купил =
17,
то 13 k 16. В этом промежутке только при k = 14 число k
является натуральным. Итак, Иван Петрович купил =
5
= ![]() = 9
привилегированных акций.
= 9
привилегированных акций.
Ответ. 9 привилегированных акций.
605. Купил Роман раков: вчера мелких — по цене 51 к. за штуку, а сегодня — по 99 к., но очень крупных. Всего на раков он истратил 25 р. 20 к., из них переплаты из-за отсутствия сдачи в сумме составили от 16 до 20 к. Определите, сколько раков купил Роман вчера и сколько сегодня.
Решение. Пусть Роман купил вчера х, а сегодня у раков и переплата составила р к. Тогда справедливо равенство
51х + 99y + р = 2520.
Так как числа 51, 99, 2520 делятся на 3, то и р делится на 3. Но по условию задачи 16 р 20, следовательно, р = 18. Тогда справедливо равенство
51х + 99y = 2502.
Выразим x через y из этого уравнения:
x = ![]() 834 33y
= 49 2y
834 33y
= 49 2y ![]() y 1 .
y 1 .
17 17
Число х является целым числом при у = 16 + 17k, где k — целое неотрицательное число, и х — натуральное число лишь при у = 16. Следовательно, у = 16 и х = 18 — единственная пара значений х и у, удовлетворяющая условиям задачи.
Ответ. Вчера 18 раков, сегодня 16 раков.
852. а) В каком двузначном числе удвоенная сумма цифр равна их произведению?
б) Найдите все целые значения a, при каждом из ко-
a3 1 торых дробь ![]() принимала бы
целые значения.
принимала бы
целые значения.
a 1
![]()
Решение. а) Пусть xy = 10x + y — двузначное число, записанное при помощи цифр x и y. Надо найти такие
x и y, чтобы выполнялось равенство 2(x + y) = xy.
Выразим из этого равенства x через y:
x
= ![]() 2y . (1)
2y . (1)
y 2
Так как x и y цифры, то, учитывая равенство (1), получаем, что 3 y 9. Найдём x для каждого целого y: при y = 3 получим x = 6, при y = 4 получим x = 4, при y = 6 получим x = 3. Условиям задачи удовлетворяют числа 63, 44 или 36. При остальных значениях y число x дробное, т. е. при y, равном 5, 7, 8, 9, не существует чисел, удовлетворяющих условиям задачи.
Итак, имеется три двузначных числа, удовлетворяющие условиям задачи: 36, 44 и 63.
б) Преобразуем данную дробь:
![]() a3 1 = a3 1 2 =
a3 1 = a3 1 2 = ![]() a a2 a 1) 2 = a 1 a 1
a a2 a 1) 2 = a 1 a 1
= a a a 1
Данная дробь принимает целые значения
при тех же значениях a (a 1), при которых дробь ![]() 2 является
це-
2 является
це-
a 1
лым числом, т. е. если или a – 1 = –2, или a – 1 = –1, или a – 1 = 1, или a – 1 = 2.
Следовательно, условиям задачи удовлетворяют четыре числа: –1, 0, 2 и 3.
1. На доске написано 20 целых чисел. Их среднее арифметическое равно –2, среднее арифметическое положительных чисел равно 40, среднее арифметическое отрицательных чисел равно –100. Определите количество отрицательных чисел.
Решение. Пусть написано p положительных и q отрицательных чисел (p и q — натуральные числа), остальные числа (их 20 – p – q) были нулями. Сумма всех положительных чисел равна 40p, сумма всех отрицательных чисел равна –100q, сумма нулей — нуль, а сумма всех чисел равна –2 20 = –40. Тогда верно равенство
40p – 100q = –40,
которое перепишем в виде
5q = 2(p + 1).
Так как левая часть этого равенства делится на 5, то p — число, которое при делении на 5 даёт остаток 4. Так как p + q 20, то p может принимать только значения 4, 9, 14, 19. Тогда соответствующие значения q: 2, 4, 6, 8. Рассмотрим все случаи:
p = 4, q = 2, p + q = 6; p = 9, q = 4, p + q = 13; p = 14, q = 6, p + q = 20; p = 19, q = 8, p + q = 27.
Только три первые пары p и q удовлетворяют неравенству p + q 20. Следовательно, отрицательных чисел было или 2, или 4, или 6.
2. На доске написано n целых чисел (8 n 29). Их среднее арифметическое равно 6, среднее арифметическое положительных чисел равно 45, среднее арифметическое отрицательных чисел равно –90. Определите:
а) число n;
б) каких чисел было больше: положительных или от-
рицательных;
в) наибольшее возможное количество положительных
чисел.
Решение. Пусть было p положительных и q отрицательных чисел (p и q — натуральные числа), остальные n – p – q числа были нулями. Сумма всех положительных чисел равна 45p, сумма всех отрицательных чисел равна –90q, сумма нулей — нуль, а сумма всех чисел равна 6n.
Тогда верно равенство
45p – 90q = 6n,
которое перепишем в виде
2n = 15(p – 2q). (*)
Из этого равенства следует, что число p —
чётное, а число n делится на 15. В промежутке 8 n 29 такое n
единственное: n = 15. Тогда равенство (*) можно переписать в виде
2 = p – 2q, откуда q = ![]() p – 1.
p – 1.
2
Так как q 1, то p 4. Рассмотрим все возможные случаи, учитывая, что p + q 15: если p = 4, то q = 1 и p + q 15; если p = 6, то q = 2 и p + q 15; если p = 8, то q = 3 и p + q 15; если p = 10, то q = 4 и p + q 15.
Если p 12, то p + q 15.
Во всех возможных случаях положительных чисел было больше, чем отрицательных.
Получены ответы на вопросы задачи: а) n = 15;
б) положительных чисел было больше, чем отрицательных; в) наибольшее возможное количество положительных чисел 10.
![]() Замечание. Ответ на вопрос «б» можно получить
проще. Так как 2n 0, то p – 2q 0, откуда следует,
что p 2q q. Это означает, что положительных чисел было больше,
чем отрицательных.
Замечание. Ответ на вопрос «б» можно получить
проще. Так как 2n 0, то p – 2q 0, откуда следует,
что p 2q q. Это означает, что положительных чисел было больше,
чем отрицательных.
Промежуточный контроль. С–26.
В данном пункте и в упражнениях к нему приводятся сведения об использовании уравнений и систем уравнений в древнем Вавилоне, в «Арифметике» Диофанта, а также рассматриваются старинные задачи на решение систем (Диофант, аль-Хорезми, аль-Караджи, Л. Пизанский, К. Рудольф). Этот материал способствует формированию ответственного отношения к учению, готовности и способности учащихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов.
Описание работы с текстовыми задачами помещено в конец данной книги, так как затруднительно «разложить» по пунктам учебника рекомендации по использованию текстовых задач при изучении алгебры. Причина в том, что разные учителя в разных классах могут по-разному планировать работу с текстовыми задачами, так как классы имеют различные стартовые возможности в начале учебного года, а также различные цели обучения.
Текстовые задачи в учебнике решаются различными способами, что позволяет учащимся самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения этих задач. Работа с текстовыми задачами развивает умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации.
В 8 классе специально изучалось решение текстовых задач при помощи квадратных и рациональных уравнений, их систем. Выделим несколько типов текстовых задач, кроме упомянутых, которые полезно изучить со всеми учащимися, и несколько идей решения задач, которые учащимся полезно освоить. Здесь есть содержательное пересечение с задачным материалом, рекомендованным для изучения в 7 классе. Это следует повторить, а задачи на смеси и сплавы стоит объяснить заново.
1. Необходимо повторить арифметические способы решения задач и применение линейных уравнений для решения задач:
• на части;
• на нахождение двух чисел по их сумме и разности;
• на дроби;
• на совместную работу;
• на движение по реке;
• на движение;
• на деление числа на части, пропорциональные данным числам;
• на пропорции и проценты;
• на смеси и сплавы;
• на применение линейных уравнений.
2. Необходимо продолжить применение нескольких «нестандартных» способов решения задач, которые уже использовались в 7 классе, и показать новые — решение задач в общем виде, метод подобия. Эти способы окажутся полезными при решении олимпиадных, конкурсных задач, задач из ОГЭ и ГВЭ:
• обратный ход;
• переформулировка задачи;
• использование вспомогательных букв (неизвестных); • решение задачи в общем виде;
• метод подобия.
Примеры этих задач, кроме задач на смеси и сплавы, и задач, решаемых в общем виде и методом подобия, приведены в методических рекомендациях для 7 класса.
Сначала остановимся на задачах, в которых можно применить какой-то из перечисленных методов, например, можно решить задачу арифметически или с помощью уравнения. Отметим, что каждый раз, когда задачу удаётся решить несколькими методами, это надо обязательно использовать, так как решение одной задачи несколькими способами намного полезнее решения нескольких задач одним способом.
858. Одновременно были зажжены две свечи одинаковой длины: одна свеча потолще (сгорающая за 4 ч), другая потоньше (сгорающая за 2 ч). Через некоторое время обе свечи потушили. Оказалось, что огарок толстой свечи в 3 раза длиннее огарка тонкой свечи. Сколько времени горели свечи?
Решение. I способ. Изобразим свечи прямоугольниками одинаковой высоты (рис. 45, а). Так как тонкая свеча сгорает в 2 раза быстрее, то в любой момент времени сгоревшая часть тонкой свечи в 2 раза больше, чем сгоревшая часть толстой свечи. Поэтому, когда свечи погасли (рис. 45, б), сгоревшая часть тонкой свечи (AC) в 2 раза больше сгоревшей части толстой свечи (MK).
По условию задачи оставшаяся часть тонкой свечи (CB)
в 3 раза меньше оставшейся части толстой свечи (KN). Тогда CB =
![]() KN =
KN = ![]() DB =
DB =
![]() AB, а AC =
AB, а AC = ![]() AB.
Сле-
AB.
Сле-
довательно, тонкая свеча горела ![]() 2
= 1,6 (ч).
2
= 1,6 (ч).

II способ. За 1 ч сгорает ![]() толстой
свечи и
толстой
свечи и ![]() тонкой.
тонкой.
Пусть свечи горели x ч, огарок толстой свечи
составляет 1 – ![]() x , а огарок тонкой 1 –
x , а огарок тонкой 1 –
![]() x их
первоначальной длины.
x их
первоначальной длины.
4 2
По условию задачи
первый огарок в 3 раза больше второго. Составим уравнение: 1 – ![]() x = 3
(1 –
x = 3
(1 – ![]() x ), откуда x =
1,6.
x ), откуда x =
1,6.
4 2
Ответ. 1,6 ч.
Здесь и далее при решении задач несколькими способами полезно сопоставлять их, выявлять преимущество того или иного способа для решения конкретной задачи.
864. Морская вода содержит 5% (по массе) соли. Сколько килограммов пресной воды нужно добавить к 50 кг морской воды, чтобы содержание соли в полученной воде составило 2%?
Решение. I способ. 50 кг морской воды содержит 0,05 50 = 2,5 (кг) соли. Чтобы содержание соли составляло 2%, морской воды должно быть 2,5 : 0,02 = 125 (кг), т. е. надо добавить 125 – 50 = 75 (кг) пресной воды.
![]() II способ.
Пусть добавили x кг пресной воды, тогда морской воды с содержанием соли
2% стало (50 + x) кг, а количество соли в ней не изменилось.
Вычислим это количество двумя способами и составим уравнение:
II способ.
Пусть добавили x кг пресной воды, тогда морской воды с содержанием соли
2% стало (50 + x) кг, а количество соли в ней не изменилось.
Вычислим это количество двумя способами и составим уравнение:
0,05 50 = 0,02 (50 + x),
откуда x = 75.
Ответ. 75 кг.
865. а) До просушки зерна влажность его была 20%. 10 ц этого зерна просушили, после чего его масса уменьшилась на 100 кг. Определите влажность зерна после просушки.
Решение. I способ. После просушки получилось 10 – 1 = 9 (ц) зерна. Содержание воды уменьшилось с 0,2 10 = 2 до 2 – 1 = 1 центнера и составило
![]() = 11
= 11![]() (%) .
(%) .
II способ. Пусть содержание воды в зерне после просушки составляет p%. До просушки масса сухого вещества составляла 100 – 20 = 80 (%), или 0,8 10 = 8 (ц), а после
![]() просушки — 100 p 9 (ц). Приравняв полученные резуль-
просушки — 100 p 9 (ц). Приравняв полученные резуль-
100
![]() таты, составим уравнение: 100 p 9 = 8, откуда p = 11.
таты, составим уравнение: 100 p 9 = 8, откуда p = 11.
100
Ответ. 11![]() %.
%.
866. а) При проверке влажность зерна оказалась рав-ной 23%, а после просушки 12%. На сколько процентов стало легче зерно после просушки?
б) Семена попали под дождь и стали на 20% тяжелее. Когда их просушили, они потеряли в массе 20%. Вернулись ли они к первоначальной массе?
Решение. а) Пусть первоначально было m кг зерна. Сухое вещество в нём составляло 100 – 23 = 77 (%) массы зерна, т. е. 0,77m кг. После просушки масса сухого вещества составляет 100 – 12 = 88 (%) массы просушенного
зерна, которая равна 0 77, m = 7m (кг). Масса зерна умень-
0 88, 8
![]()
![]() шилась на m –
= m (кг), или на
шилась на m –
= m (кг), или на ![]() m 100 % = 12,5%.
m 100 % = 12,5%.
8 8 m
б) Пусть первоначальная масса зерна m кг, она уве-
личилась на 20% и составила (1 + 0,2)m = 1,2m (кг). При сушке эта масса уменьшилась на 20% и составила (1 – 0,2) 1,2m = 0,96m (кг). То есть масса зерна после просушки уменьшилась (на 4%).
Ответ. а) На 12,5%; б) нет.
867. а) Время изготовления некоторой детали умень-шилось на 40 %. На сколько процентов увеличилась производительность труда?
б) Объём строительных работ увеличился на 80%. На сколько процентов нужно увеличить число рабочих для выполнения этой работы за то же время, если производительность труда будет увеличена на 20%?
Решение. а) I способ. Время изготовления
детали уменьшилось на 40% (было 100%, стало 60%), или уменьшилось в 100 :
60 = ![]() раза. Производительность труда
увеличилась во столько же раз и составляет теперь 100
раза. Производительность труда
увеличилась во столько же раз и составляет теперь 100 ![]() =
166
=
166 ![]() (%), т. е. увеличилась на 66
(%), т. е. увеличилась на 66 ![]() %.
%.
II способ. Пусть 1 деталь изготавливали за t
мин и производительность труда выражалась дробью 1![]() , теперь её t
, теперь её t
изготавливают за 0,6t мин и производительность труда выражается дробью 1 = 5 . Производительность труда уве-
0 6, t 3t
5 1
![]() личилась
на 3t 1 t 100% =
личилась
на 3t 1 t 100% = ![]() % = 66
% = 66![]() %.
%.
t
б) Объём работ увеличился на 80%, т. е. в 1,8 раза, поэтому число рабочих надо увеличить в 1,8 раза. Производительность труда будет увеличена на 20%, т. е. в 1,2 раза, поэтому число рабочих надо уменьшить в 1,2 раза. Таким образом, число рабочих надо увеличить в 1,8 : 1,2 = 1,5 раза, или на 50%.
Ответ.
а) На 66 ![]() %; б) на 50%.
%; б) на 50%.
868. а) Цена книги снизилась на столько процентов, на сколько копеек она снизилась. Какова первоначальная цена книги?
Решение. Пусть старая цена книги x к., а
новая — y к. (x y). Так как снижение цены в процентах и в
копейках одинаково, составим уравнение: ![]() (x y) 100 = x y . x Так как x y и x 0,
то x = 100. Ответ. 1 р.
(x y) 100 = x y . x Так как x y и x 0,
то x = 100. Ответ. 1 р.
Уметь решать задачи в общем виде очень полезно для того, чтобы не решать одну и ту же задачу с разными числовыми данными несколько раз. Иногда бывает полезно решать задачу в общем виде, если числовые данные громоздки. В общем виде решают задачи при изучении геометрии и физики. Кроме того, заменяя числовые данные буквами, мы готовим учащихся к решению задач с параметрами.
870. Найдите процентное содержание p олова в сплаве, полученном из двух кусков массами m1 и m2, содержащих соответственно p1 и p2 процента олова, если:
а) m1 = 15, p1 = 40, m2 = 35, р2 = 20;
б) m1 = 35, р1 = 40, m2 = 15, р2 = 20.
Решение. Запишем, как можно вычислить массу олова до и после сплавления (единицы измерения должны быть одинаковые, например граммы). Так как масса олова до и после сплавления не изменилась, то выполняется равенство
![]()
![]() m1 100p1 + m2 100p2 = (m1 + m2) 100
m1 100p1 + m2 100p2 = (m1 + m2) 100![]() p .
p .
Перепишем его в виде
m1 p1 + m2 p2 = (m1 + m2) p.
Выразим p из этого равенства: p = m p1 1 m p2 2 .
m1 m2
а) При m1 = 15, p1 = 40, m2 = 35, p2 = 20
p = ![]() = 26.
= 26.
б) При m1 = 35, p1 = 40, m2 = 15, p2 = 20
p = ![]() = 34.
= 34.
Ответ. m p1 1 m p2 2 %; а) 26%; б) 34%.
m1 m2
871. Докажите, что в предыдущей задаче из условия р2 р1 следует, что р2 р р1.
Доказательство. Так как p2 p1, то верно двойное неравенство
m1 p2 + m2 p2 m1 p1 + m2 p2 m1 p1 + m2 p1.
Вынесем за скобки общие множители в левой и правой частях двойного неравенства
(m1 + m2) p2 m1 p1 + m2 p2 (m1 + m2) p1.
Разделим почленно двойное неравенство на положи-
тельную сумму m1 + m2: р2 m p1 1m1 m pm2 22 p1 и, заменив
m p1 1m1 m pm2 22 на p, получим р2 p p1, что и требовалось до-
казать.
872. Имеется два куска сплава олова и свинца. Первый массой m1 г содержит р1% олова, второй содержит р2% олова. Сколько граммов от второго куска надо добавить к первому, чтобы получить сплав с содержанием олова р%, если:
а) m1 = 300, р1 = 40, р2 = 60, р = 56;
б) m1 = 180, р1 = 45, р2 = 70, р = 60?
Решение. Пусть надо добавить m2 г от второго сплава, тогда верно равенство
![]()
![]() m1 100p1 + m2 100p2 = (m1 + m2) 100
m1 100p1 + m2 100p2 = (m1 + m2) 100![]() p ,
p ,
из которого выразим m2:
m2 = m p1p(2 pp1) . (1)
а) При m1 = 300, р1 = 40, р2 = 60, p = 56 имеем
m2 = ![]() = 1200.
= 1200.
б) При m1 = 180, р1 = 45, р2 = 70, p = 60 имеем
m2 = ![]() = 270.
= 270.
Ответ. m p1( p1) г; а) 1200 г; б) 270 г.
p2 p
873. Кусок сплава меди и цинка массой 36 кг содержит 45% меди. Сколько килограммов меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 60% меди?
Решение. Пусть надо добавить x кг меди, тогда содержание меди в сплаве составит (0,45 36 + x) кг, или 0,6 (36 + x) кг. Получим, что верно равенство 0,45 36 + x = 0,6 (36 + x), откуда x = 13,5.
Ответ. 13,5 кг.
![]() Замечание. Эта задача похожа на задачу 872 и
может быть решена по формуле (1):
Замечание. Эта задача похожа на задачу 872 и
может быть решена по формуле (1):
m2
= m p1p(2 pp1) = ![]() .
.
877. Имеются два куска, содержащие 60% и 40% оло-ва. По скольку граммов от каждого куска надо взять, чтобы получить 600 г сплава, содержащего 45% олова?
Решение. Пусть от первого куска надо взять x г, тогда от второго надо взять (600 – x) г. Подсчитав содержание олова в полученном сплаве двумя способами, составим уравнение:
0,6 x + 0,4 (600 – x) = 0,45 600,
откуда x = 150, а 600 – x = 450.
Ответ. 150 и 450 г.
878. Имеются два куска, содержащие р1 и р2 процента олова. По скольку граммов от каждого куска надо взять, чтобы получить m г сплава, содержащего р% олова, если:
а) m = 450, p1 = 70, р2 = 40, р = 60;
б) m = 600, p1 = 80, р2 = 65, р = 75?
Решение. Пусть от первого куска надо взять x г, тогда от второго надо взять (m – x) г. Составим уравнение:
x
p1 + (m – x) p2 = m ![]() p ,
p ,
100 100 100
![]()
![]() откуда x = m p( p2) , m – x =
m p( 1 p) .
откуда x = m p( p2) , m – x =
m p( 1 p) .
p1 p2 p1 p2
а) При m =
450, p1 = 70, p2 =
40, p = 60 имеем x = ![]() = 300, m
– x = 450 – 300 = 150.
= 300, m
– x = 450 – 300 = 150.
б) При m =
600, p1 = 80, p2 =
65, p = 75 имеем x = ![]() = 400, m
– x = 600 – 400 = 200.
= 400, m
– x = 600 – 400 = 200.
![]() Ответ. m p( p2) и m p( 1 p) г; а)
300 и 150 г; б) 400 и
Ответ. m p( p2) и m p( 1 p) г; а)
300 и 150 г; б) 400 и
p1 p2 p1 p2
200 г.
879. Из «Арифметики» Л.Ф. Магницкого. У некоторого человека были для продажи вина двух сортов. Первое ценою 10 гривен ведро, второе же по 6 гривен. Захотелось ему сделать из тех двух вин, взяв по части, третье вино, чтобы ему цена была по 7 гривен. Какие части надлежит из тех двух вин взять к наполнению ведра третьего вина ценою в 7 гривен?
![]() Решение. Пусть
для составления требуемой смеси надо взять x частей ведра вина I сорта (x
1) и (1 – x) частей ведра вина II сорта. Первая часть вина
стоит 10x гривен, а вторая — 6(1 – x) гривен. Составим уравнение:
Решение. Пусть
для составления требуемой смеси надо взять x частей ведра вина I сорта (x
1) и (1 – x) частей ведра вина II сорта. Первая часть вина
стоит 10x гривен, а вторая — 6(1 – x) гривен. Составим уравнение:
![]()
![]() 10x + 6(1 – x) = 7,
10x + 6(1 – x) = 7,
![]() откуда x = ,
1 – x = .
откуда x = ,
1 – x = .
Ответ. ведра по 10 гривен и ведра по 6 гривен.
888. Через первую трубу бассейн наполняется за а мин, через вторую трубу — за b мин. За сколько минут наполнится бассейн через обе эти трубы? Решите задачу в общем виде, получите ответ для указанных значений а и b:
а) а = 12, b = 36; б) а = 14, b = 35.
![]() Решение. I способ.
Решим задачу по действиям: 1) 1 : a = 1 (басс.) —
наполняет первая труба за 1 мин; a 2) 1 : b = 1 (басс.) —
наполняет вторая труба за 1 мин; b
Решение. I способ.
Решим задачу по действиям: 1) 1 : a = 1 (басс.) —
наполняет первая труба за 1 мин; a 2) 1 : b = 1 (басс.) —
наполняет вторая труба за 1 мин; b
3) 1 + 1 = a b (басс.) — наполняют обе трубы за a b ab
1 мин;
![]()
![]() 4) 1
: a b
= ab (мин) — время наполнения
бассей-
4) 1
: a b
= ab (мин) — время наполнения
бассей-
ab a b
на через две трубы.
а) При a = 12, b = 36 имеем ab = = 9;
a b
![]()
![]() б) при a = 14,
b = 35 имеем ab = =
10. a b
б) при a = 14,
b = 35 имеем ab = =
10. a b
II способ. Пусть две трубы при совместной работе наполнят бассейн за x мин, тогда за 1 мин они наполнят
1 ![]() бассейна. Составим уравнение:
бассейна. Составим уравнение:
x
![]() 1 1 =
1 1 = ![]() 1 .
1 .
a b x
Выразим x через a и b:
x
= ![]() ab .
ab .
a b
Вычисления для случаев «а» и «б» аналогичны. Ответ. ![]() ab мин;
а) 9 мин; б) 10 мин. a b
ab мин;
а) 9 мин; б) 10 мин. a b
892. Некоторое расстояние автомобиль преодолева-ет в гору со скоростью а км/ч, а с горы — со скоростью b км/ч. Какова средняя скорость движения автомобиля на всём участке пути, если:
а) а = 40, b = 60; б) а = 30, b = 45? Решение. Пусть s км — длина участка пути.
1) ![]() s s = s a( b) (ч) —
время движения в оба конца; a b ab
s s = s a( b) (ч) —
время движения в оба конца; a b ab
2) 2s s a( b) = 2ab (км/ч) — средняя скорость.
ab a b
![]()
![]() а) При a = 40,
b = 60 2ab = = 48 (км/ч); a b
а) При a = 40,
b = 60 2ab = = 48 (км/ч); a b
![]() б) при a = 30,
b = 45 2ab = = 36 (км/ч). a b
б) при a = 30,
b = 45 2ab = = 36 (км/ч). a b
Ответ. а) 48 км/ч; б) 36 км/ч.
893. Лодка от А до В плывёт по течению а ч, а от В до А (против течения) b ч. Сколько часов будет плыть бревно от А до В, если: а) а = 3, b = 4; б) а = 2, b = 3? Решение. I способ.
1)
1 : a = ![]() 1 (расст.) — проплывает лодка за 1 ч
по a течению;
1 (расст.) — проплывает лодка за 1 ч
по a течению;
2)
1 : b = 1![]() (расст.) — проплывает лодка за 1 ч
против b течения;
(расст.) — проплывает лодка за 1 ч
против b течения;
3)
⎜⎝⎛![]() 1a 1b⎞⎟⎠ 2 =
1a 1b⎞⎟⎠ 2 = ![]() b2 aba
(расст.) — проплывает бревно за 1 ч;
b2 aba
(расст.) — проплывает бревно за 1 ч;
4) ![]() 1 : b a
= 2ab
(ч) — время движения бревна.
1 : b a
= 2ab
(ч) — время движения бревна.
2ab b a
![]() а) При a = 3,
b = 4 имеем 2ab =
а) При a = 3,
b = 4 имеем 2ab = ![]() = 24
(ч); b a
= 24
(ч); b a
б) при a = 2, b = 3 имеем 2ab = 12 (ч).
b a
II способ. Пусть бревно проплывёт расстояние AB за
x ч, тогда за 1 ч
оно проплывает ![]() 1 этого
расстояния, что x
1 этого
расстояния, что x
равно ⎜⎝⎛![]() 1a 1b⎞⎟⎠ 2.
Составим уравнение:
1a 1b⎞⎟⎠ 2.
Составим уравнение:
![]() x1 = ⎛⎜⎝1a 1b⎞⎟⎠ 2,
x1 = ⎛⎜⎝1a 1b⎞⎟⎠ 2,
откуда x = ![]() 2ab . b a
2ab . b a
Вычисления для случаев «а» и «б» аналогичны. Ответ. ![]() 2ab ч;
а) 24 ч; б) 12 ч. b a
2ab ч;
а) 24 ч; б) 12 ч. b a
919. Две бригады грузчиков должны были
разгрузить баржу в течение 6 ч. Первая бригада выполнила ![]() всей
работы, вторая бригада закончила разгрузку. Вся работа была выполнена за 12 ч.
Сколько часов требуется каждой бригаде в отдельности для разгрузки баржи?
всей
работы, вторая бригада закончила разгрузку. Вся работа была выполнена за 12 ч.
Сколько часов требуется каждой бригаде в отдельности для разгрузки баржи?
![]()
![]() Решение. Пусть
первая бригада может разгрузить баржу за x ч, вторая — за y ч, а
обе вместе — за 6 ч. Составим первое уравнение: 1 + 1 =
. x y
Решение. Пусть
первая бригада может разгрузить баржу за x ч, вторая — за y ч, а
обе вместе — за 6 ч. Составим первое уравнение: 1 + 1 =
. x y
На ![]() всей работы первая
бригада потратит
всей работы первая
бригада потратит ![]() x ч, на
x ч, на
1
![]()
![]() –
3
= 2
всей работы вторая бригада потратит y ч, а
–
3
= 2
всей работы вторая бригада потратит y ч, а
5 5
всего 12 ч. Составим второе уравнение:
![]() x +
x + ![]() y = 12.
y = 12.
Решив систему этих двух уравнений, получим два её решения: x1 = 10, y1 = 15 и x2 = 12, y2 = 12.
Ответ. 10 и 15 ч или 12 и 12 ч.
922. Брат и сестра собирали малину в двухлитровые бидоны. Брат собирал ягоды быстрее сестры. Через некоторое время он решил ей помочь и поменялся с ней бидонами. Момент для обмена бидонами был выбран удачно — ребята наполнили их ягодами одновременно. Сколько литров ягод они набрали вместе до того, как поменялись бидонами?
Решение. I способ. Пусть брат до обмена бидонами собрал x л, а сестра собрала y л ягод (x y), тогда после обмена брат собрал (2 – y) л, а сестра собрала (2 – x) л ягод. Брат собирал ягоды быстрее сестры в одно и то же число раз до и после обмена бидонами, поэтому x больше y во столько же раз, во сколько (2 – y) больше, чем (2 – x). Составим уравнение:
2
![]() y = x .
y = x .
2 x y
Второе уравнение составить не удаётся, что и вызывает затруднение у учащихся. Преобразуем данное уравнение:
(x y x)( y 2) = 0.
![]()
![]() x y
x y
Числитель дроби равен нулю, если x – y = 0 или x + y – 2 = 0. Первое равенство невозможно, так как x y, следовательно, x + y – 2 = 0, т. е. x + y = 2. При этом знаменатель дроби не обращается в нуль, так как x 2 и y 0. Найти x и y не удалось, но этого и не требовалось. Мы получили ответ на вопрос задачи: до обмена бидонами ребята собрали 2 л ягод.
II способ. Брат должен поменяться с сестрой бидонами в тот момент, когда ему останется собрать столько ягод, сколько к этому моменту собрала сестра. Тогда после обмена бидонами каждый из них соберёт столько же ягод, сколько до обмена, а вместе они соберут половину от объёма двух бидонов, т. е. 2 л. Ответ. 2 л.
923. Дед и внук начали одновременно собирать клюк-ву в одинаковые лукошки. Дед собирает быстрее внука. Когда им надо поменяться лукошками, чтобы оба лукошка наполнились одновременно?
Решение. Рассуждая так же, как при решении задачи 922, получим ответ: дед и внук должны поменяться лукошками тогда, когда деду останется собрать столько ягод, сколько к тому моменту собрал внук.
924. Брат и сестра собирали малину. Корзина брата вмещала 5 л, а корзина сестры — 4 л. Брат собирал ягоды быстрее сестры, поэтому, когда она набрала половину своей корзины, они поменялись корзинами и через некоторое время наполнили их одновременно. Сколько литров ягод собрал брат?
Решение. Пусть сначала брат набрал x л, а
сестра — 2 л ягод. Из условия задачи следует, что x 2. После обмена
корзинами брат набрал ещё 2 л, а сестра набрала (5 – x) л ягод.
Брат собирал ягоды быстрее сестры в одно и то же число раз до и после обмена
корзинами. Составим уравнение: x = ![]() 2 . Оно имеет
два корня: 4 и 1. Так как
2 . Оно имеет
два корня: 4 и 1. Так как
2 5 x
x 2, то x = 4.
Всего брат собрал 4 + 2 = 6 (л).
Ответ. 6 л.
925.
Брат и сестра собирали малину. Когда сестра со-брала ![]() своего
двухлитрового бидона, трёхлитровый бидон брата был почти полон. Ребята
поменялись бидонами и через некоторое время одновременно закончили сбор ягод.
Во сколько раз брат работал быстрее сестры?
своего
двухлитрового бидона, трёхлитровый бидон брата был почти полон. Ребята
поменялись бидонами и через некоторое время одновременно закончили сбор ягод.
Во сколько раз брат работал быстрее сестры?
Решение. Сначала сестра собрала ![]() 2
=
2
= ![]() л малины.
л малины.
![]()
![]() Пусть брат собрал в k
раз больше (k 1), т. е.
Пусть брат собрал в k
раз больше (k 1), т. е. ![]() k л. Потом сестра собрала (3 –
k л. Потом сестра собрала (3 –
![]() k) л, а брат опять в k раз
больше, т. е. (3k – k2) л, что составило 2 –
4
= 2
л. Составим
k) л, а брат опять в k раз
больше, т. е. (3k – k2) л, что составило 2 –
4
= 2
л. Составим
3 3
уравнение: 3k – ![]() k2
=
k2
= ![]() . Оно имеет два корня: 2 и
. Оно имеет два корня: 2 и ![]() . Так
. Так
как k 1, то k = 2.
Ответ. В 2 раза.
926. Отец и сын принялись косить два соседних луга, площади которых относятся как 8 : 7. Когда отец скосил три четверти большего луга, а сын скосил больше половины меньшего, они присели отдохнуть и подсчитали, что если будут работать с той же производительностью, но поменяются местами, то закончат работу одновременно. Во сколько раз отец косил быстрее сына?
Решение. Пусть площади лугов равны 7k и 8k некоторых единиц площади, где k 0. Из условия задачи следует, что отец скосил 6k единиц площади. Пусть сын скосил y тех же единиц площади (y 3,5k). После отдыха отец скосил 7k – y, а сын — оставшиеся 2k единиц площади.
Отец косил в ![]() 6k ,
или в 7
6k ,
или в 7![]() k y ,
раза быстрее сына. Приy 2k
k y ,
раза быстрее сына. Приy 2k
равняв эти дроби, составим уравнение:
6k = 7k y , (1) y 2k
![]() 2 2 y 7ky 12k которое
перепишем в виде = 0.
2 2 y 7ky 12k которое
перепишем в виде = 0.
2yk
![]() Уравнение y2
– 7ky + 12k2 = 0 имеет
корни y1 = 3k и y2 =
4k. Так как k 0, то оба корня не обращают в нуль знаменатель
дроби в уравнении (1), следовательно, это корни уравнения (1) при любом k 0.
Корень 3k не удовлетворяет условию y 3,5k. Это означает,
что отец работал быстрее сына в 6k = 6k =
1,5 (раза). y 4k
Уравнение y2
– 7ky + 12k2 = 0 имеет
корни y1 = 3k и y2 =
4k. Так как k 0, то оба корня не обращают в нуль знаменатель
дроби в уравнении (1), следовательно, это корни уравнения (1) при любом k 0.
Корень 3k не удовлетворяет условию y 3,5k. Это означает,
что отец работал быстрее сына в 6k = 6k =
1,5 (раза). y 4k
Ответ. В 1,5 раза.
927. Сулико подошла к роднику с двумя кувшинами. Один вмещал 5 л, а другой — 4 л. Вода из родника текла двумя струями — одна сильнее, другая слабее. Сулико поставила одновременно кувшины под струи и, когда набралась половина меньшего кувшина, поменяла кувшины местами. Как это ни удивительно, но кувшины наполнились одновременно. Во сколько раз больше воды даёт одна струя, чем другая?
Решение. I способ. Пусть Сулико поставила больший кувшин под сильную струю, а меньший — под слабую. Пусть одна струя даёт в x раз больше воды, чем другая (x 1). Сначала в меньший кувшин набралось 2 л, а в больший — 2x л воды. Сулико поменяла местами кувшины. В меньший кувшин набралось 2 л, а в больший —
2 ![]() л воды. Всего в больший кувшин
набралось 5 л воды. x
л воды. Всего в больший кувшин
набралось 5 л воды. x
Составим уравнение:
2x + 2 = 5, (2)
x
![]() которое перепишем в виде 2x2 5x 2 = 0. x
которое перепишем в виде 2x2 5x 2 = 0. x
Уравнение 2x2 – 5x +
2 = 0 имеет корни x1 = 2 и x2
= ![]() , которые не обращают в нуль знаменатель
дроби x, следовательно, это корни уравнения (2). Так как x 1, то
условиям задачи удовлетворяет только x1.
, которые не обращают в нуль знаменатель
дроби x, следовательно, это корни уравнения (2). Так как x 1, то
условиям задачи удовлетворяет только x1.
Если же кувшины поставить наоборот — больший под слабую, а меньший под сильную струю, то всё равно получится уравнение (2).
II способ. Пусть сначала в меньший кувшин набралось 2 л, а в больший — x л воды. Сулико поменяла местами кувшины. В меньший кувшин набралось 2 л, а в больший — (5 – x) л воды. Одна струя даёт больше воды в одно и то же число раз. Составим уравнение:
![]() 2 = 5 x , (3)
x 2
2 = 5 x , (3)
x 2
x2 5x 4 которое
перепишем в виде ![]() =
0.
=
0.
2x
Уравнение x2 – 5x + 4 = 0 имеет корни x1 = 1 и x2 = 4, которые не обращают в нуль знаменатель дроби 2x, следовательно, это корни уравнения (3). Два корня соответствуют двум возможностям — поставить меньший кувшин под сильную струю или под слабую. В обоих случаях ответ на вопрос задачи один и тот же: одна струя даёт в 2 раза больше воды, чем другая, так как в первом случае 2 : 1 = 2, а во втором случае 4 : 2 = 2.
Ответ. В 2 раза.
931. Один мастер оклеит комнату обоями за а ч, а другой — за b ч. Если же они будут работать вместе, то производительность труда каждого повысится на р%. За сколько часов они оклеят комнату, работая вместе, если:
а) а = 6, b = 4, р = 20; б) а = 3, b = 7, р = 40?
Решение. Пусть время совместной работы без повышения производительности труда равно x ч. Из уравнения
1 1 1 ab
![]() + =
выразим x через a и b: x =
+ =
выразим x через a и b: x = ![]() . a b x a b
. a b x a b
Если производительность труда повысится на p%, т. е.
![]() в 1 + p = 100 p
раза, то время работы уменьшится во
в 1 + p = 100 p
раза, то время работы уменьшится во
100 100
столько же раз и составит
ab 100 p = 100ab ч. a b 100 (a b)(100 p)
![]() а) При a = 6, b
= 4, p = 20 имеем =
2 (ч).
а) При a = 6, b
= 4, p = 20 имеем =
2 (ч).
![]() б) При a =
3, b = 7, p = 40 имеем = 1,5
(ч). Ответ.
б) При a =
3, b = 7, p = 40 имеем = 1,5
(ч). Ответ. ![]() 100ab ч; а) 2 ч; б) 1,5
ч.
100ab ч; а) 2 ч; б) 1,5
ч.
(a b)(100 p)
984. Если продать 20 коров, то заготовленного сена хватит на двадцать дней дольше, если же уменьшить выдачу сена на одну корову в день на 20%, заменив сено другими кормами, то сена хватит на пятнадцать дней дольше запланированного. Сколько было коров и на сколько дней заготовлено сена?
Решение. Пусть для x коров на y дней запасено по z кг сена на день, т. е. всего xyz кг. Весь запас сена подсчитаем ещё двумя способами: (x – 20)(y + 20) z и x (y + 15) 0,8z кг. Составим систему двух уравнений с тремя неизвестными:
⎧(x 20)(y 20) z = xyz, ⎨⎩x (y 15) 0, z = xyz.
Так как z 0, x 0, то система равносильна системе
⎧(x 20)(y 20) = xy, ⎨⎩(y 15) 0 8, = y.
Решение системы: x = 80, y = 60.
Ответ. 80 коров; на 60 дней.
Метод подобия заключается в том, что, используя графики равномерных процессов и подобие треугольников, составляется уравнение для решения задачи. Для примера возьмём задачу из учебника 7 класса и решим её двумя новыми способами: с помощью уравнения с неизвестным в знаменателе (стандартный школьный метод, изученный в 8 классе) и с помощью метода подобия.
1. Две старушки вышли одновременно навстречу друг другу из двух городов. Они встретились в полдень и достигли каждая чужого города: первая — в 4 ч пополудни, а вторая — в 9 ч. Узнайте, когда они вышли из своих городов.
Решение. I способ. Пусть до встречи
старушки шли х ч. Тогда на весь путь первая затратила (х + 4) ч,
а вторая — (х + 9) ч. Первая проходила в час 1 , вторая — ![]() 1 часть
1 часть
x 4 x 9
![]() пути, вместе они проходили 1 часть пути.
Составим уравx
пути, вместе они проходили 1 часть пути.
Составим уравx
![]() нение: 1 +
1
= 1 .
нение: 1 +
1
= 1 .
x 4 x 9 x
Это уравнение имеет два корня: x1 = 6, x2 = –6. Так как по смыслу задачи x 0, то до встречи старушки были в пути 6 ч, т. е. вышли из своих городов в 6 ч утра (12 – 6 = 6).
II способ. Пусть по-прежнему старушки шли до встречи х ч. Построим графики движения первой и второй старушек: PP1 и VV1 соответственно (рис. 46). Моменту их встречи соответствует точка M графиков.
Из условия задачи следует, что NP1 = 4, KV1 = 9, а требуется найти PK = x. Из подобия двух пар треугольников VMN и V1MK, MPK и MP1N получим пропорции
x MN MN 4
= и = ,
![]() 9 MK MK x
9 MK MK x
откуда получим, что x = 4 .
![]() Последнее (более
простое) уравнение также имеет два корня: x1 = 6,
x2 = –6. Так как по смыслу задачи x 0,
то до встречи старушки были в пути 6 ч, т. е. вышли из своих городов в 6 ч утра
(12 – 6 = 6).
Последнее (более
простое) уравнение также имеет два корня: x1 = 6,
x2 = –6. Так как по смыслу задачи x 0,
то до встречи старушки были в пути 6 ч, т. е. вышли из своих городов в 6 ч утра
(12 – 6 = 6).
Ответ. В 6 ч утра.
Применение метода подобия 6 Рис. 47 предполагает использование графиков равномерных процессов,
что ценно само по себе, так как если ученик освоит этот метод, то сможет применять графики при решении задач и в том случае, когда это помогает анализу условий и поиску идеи решения задачи, не связанного с подобными треугольниками.
2. Из города А в город В вышел пешеход. Через некоторое время после выхода пешехода из города В ему навстречу выехал велосипедист. Через час после выхода пешехода вслед за ним выехал мотоциклист. Все участники двигались равномерно и встретились в одной точке маршрута. Мотоциклист прибыл в город В через 3 ч после выезда из него велосипедиста, но за 2 ч до прибытия туда пешехода. Через сколько часов после выезда мотоциклиста велосипедист прибыл в город А?
Решение. Построим графики движения пешехода, велосипедиста и мотоциклиста: АP, BUV и ANM соответственно (рис. 47). Моменту их встречи в одной точке маршрута соответствует точка O графиков.
Из условия задачи следует, что MP = 2, UM = 3, AN = 1, а требуется найти NV = x. Из подобия двух пар треугольников UOM и VON, POM и AON получим пропорции
![]() x NO NO
x NO NO
= и =,
![]() 3 OM OM
3 OM OM
откуда получим, что x = .
3
Решив это уравнение, получим его единственный корень x = 1,5.
Итак, через 1,5 ч после выезда мотоциклиста велосипедист прибыл в город А. Ответ. Через 1,5 ч.
3. Пешеход, велосипедист и мотоциклист движутся по шоссе с постоянными скоростями в одном и том же направлении. Велосипедист догнал пешехода в тот момент, когда мотоциклист отставал от них на 6 км. Мотоциклист догнал пешехода, когда велосипедист был впереди них на 2 км. На каком расстоянии мотоциклист был впереди пешехода в тот момент, когда он догнал велосипедиста?
Решение. I способ. Построим схематически графики движения пешехода, велосипедиста и мотоциклиста: AF, AE и BE соответственно (рис. 48). По условию задачи AB = 6, CD = 2, требуется найти EF.
![]() Из подобия
треугольников ABE и CDE следует, что
Из подобия
треугольников ABE и CDE следует, что
AE AB
= = = 3,
![]() CE CD
CE CD
![]() 6 Рис. 48
6 Рис. 48
AC CE = 3,
CE откуда AC = 2CE, AE = 3CE.
Из подобия треугольников EFA и CDA следует, что
EF AE 3CE 3
![]() = = = .
= = = .
![]() CD AC 2CE 2
CD AC 2CE 2
Так как CD = 2, то EF = 2 = 3.
Итак, мотоциклист был впереди пешехода на 3 км.
II способ. Пусть от момента обгона велосипедистом пешехода до момента обгона мотоциклистом пешехода прошло t1 мин, а от момента обгона мотоциклистом пешехода до момента обгона мотоциклистом велосипедиста прошло t2 мин. Тогда за t1 мин мотоциклист приблизился к велосипедисту на 6 – 2 = 4 (км), а за t2 мин он приблизился к велосипедисту на 2 км — на расстояние, в 2 раза меньшее, следовательно, t1 = 2t2.
За t1 мин велосипедист удалился от пешехода на 2 км, а за t2 мин он удалился от пешехода на расстояние, в 2 раза меньшее, т. е. на 1 км. Тогда велосипедист (и мотоциклист) был впереди пешехода на 2 + 1 = 3 (км).
Ответ. 3 км.
1. Задача Ариабхаты (476 — ок. 550). Два лица имеют равные капиталы, причём каждый состоит из известного числа вещей одинаковой стоимости и известного числа монет. Но как число вещей, так и суммы денег у каждого различны. Какова ценность вещи?
Указание. Считайте, что у первого лица а вещей и b монет, а у второго лица с вещей и d монет (а с, b d).
Решение. Пусть каждая вещь стоит x монет. Составим уравнение: ax + b = cx + d.
Перепишем это уравнение в виде (a – c)x = d – b.
Так как a c, то уравнение имеет единственный
корень x = ![]() d b ,
т. е. вещь стоит
d b ,
т. е. вещь стоит ![]() d b
монет.
d b
монет.
a c a c
2. Число 20 представьте в виде суммы двух слагаемых так, чтобы их произведение оказалось наибольшим.
Решение. Пусть первое слагаемое x, тогда второе слагаемое 20 – x. Преобразуем полученное произведение x(20 – x), используя выделение полного квадрата: x(20 – x) = 20x – x2 = –(x – 10)2 + 100.
Чтобы произведение x(20 – x) имело наибольшее значение, выражение x – 10 должно равняться нулю. Это возможно лишь при x = 10. Тогда число 20 надо записать в виде суммы равных слагаемых: 20 = 10 + 10.
3. Найдите число, которое даёт наименьшую сумму со своим квадратом.
Решение. Пусть это число x, а его квадрат — x2. Найдём x, при котором сумма x + x2 принимает наименьшее значение. Выделим полный квадрат:
x + x2 = (x + 0,5)2 – 0,25.
Чтобы сумма x + x2 была наименьшей, выражение x + 0,5 должно равняться нулю. Это возможно лишь при x = –0,5. Тогда искомое число есть –0,5.
4. Число 18 представьте в виде суммы двух слагаемых так, чтобы сумма удвоенного первого из них и квадрата второго была наименьшей.
Решение. Пусть первое слагаемое x, тогда второе слагаемое 18 – x. Найдём x, при котором сумма 2x + (18 – x)2 принимает наименьшее значение. Выделим полный квадрат:
2x + (18 – x)2 = x2 – 34x + 324 = (x – 17)2 + 35.
Чтобы выражение 2x + (18 – x)2 оказалось наименьшим, выражение x – 17 должно равняться нулю. Это возможно лишь при x = 17. Тогда число 18 надо записать в виде суммы: 18 = 17 + 1.
5. Число 16 представьте в виде суммы двух слагаемых так, чтобы сумма кубов этих слагаемых оказалась наименьшей.
Решение. Пусть первое слагаемое x, тогда второе слагаемое 16 – x. Найдём x, при котором сумма x3 + (16 – x)3 принимает наименьшее значение. Преобразуем выражение:
x3 + (16 – x)3 = (x + 16 – x)(x2 – x(16 – x) + (16 – x)2) = = 16(3x2 – 48x + 256) = 16(3(x – 8)2 + 64).
Чтобы значение выражения x3 + (16 – x)3 оказалось наименьшим, выражение x – 8 должно равняться нулю. Это возможно лишь при x = 8. Тогда число 16 надо записать в виде суммы равных слагаемых: 16 = 8 + 8.
6. Проволока длиной 100 см согнута так, что получился прямоугольник наибольшей возможной площади. Определите его размеры.
Решение. Пусть длина прямоугольника x см, тогда его ширина (50 – x) см. Найдём x, при котором выражение x(50 – x) принимает наибольшее значение. Преобразуем полученное выражение:
x(50 – x) = 50x – x2 = –(x2 – 50x) = –(x – 25)2 + 625.
Чтобы значение выражения x(50 – x) оказалось наибольшим, выражение x – 25 должно равняться нулю. Это возможно лишь при x = 25. Тогда этот прямоугольник является квадратом со стороной 25 см.
7. В понедельник акции компании А подорожали на некоторое число процентов, а во вторник подешевели на то же число процентов. В результате они стали стоить на 16% дешевле, чем при открытии торгов в понедельник. На какое число процентов подорожали акции компании А в понедельник?
Решение. Пусть акции компании А, стоившие a р., в понедельник подорожали на p%, а во вторник подешевели на p%. Тогда они стали стоить
![]() a (1 100p )(1 p ) = a ⎛⎜⎝1 10000
a (1 100p )(1 p ) = a ⎛⎜⎝1 10000![]() p2 ⎞⎟
(р.).
p2 ⎞⎟
(р.).
100
По условию задачи они стали стоить на 16% дешевле,
т. е. a (1 ![]() 16 )
р. Составим уравнение:
16 )
р. Составим уравнение:
100
a ⎜⎝1 10000![]() p2 ⎞⎟⎠ =
a (1 100
p2 ⎞⎟⎠ =
a (1 100![]() 16 ) . ⎛
16 ) . ⎛
Разделив обе части уравнения на неравное нулю число
![]() p2 a, получим
уравнение 1
p2 a, получим
уравнение 1 ![]() = 1 , имеющее единст-
= 1 , имеющее единст-
10000
венный положительный корень p = 40.
Следовательно, акции компании А подорожали в понедельник на 40%.
8. Заработная плата некоторой категории служащих повышалась два раза, причём процент повышения во второй раз был в два раза больше, чем в первый раз. Определите, на сколько процентов повышалась зарплата каждый раз, если до первого повышения зарплата была 1400 р., а после второго повышения составила 1848 р.
Решение. Пусть зарплату повышали первый раз на p%, тогда во второй — на 2p %. После первого повышения
![]()
![]() зарплата составила 1400 (1
зарплата составила 1400 (1 ![]() p )
р., а после второго — 100
1400 1 p )(1 2p ) р., что составляет 1848 р. Соста-
p )
р., а после второго — 100
1400 1 p )(1 2p ) р., что составляет 1848 р. Соста-
100 100
![]() вим уравнение: 1400 (1 p )(1 2p )
= 1848.
вим уравнение: 1400 (1 p )(1 2p )
= 1848.
100 100
Разделив обе части этого уравнения на 56 и сделав
замену неизвестного x = ![]() p , перепишем уравнение в
виде
p , перепишем уравнение в
виде
100
25(1 + x)(1 + 2x) = 33.
Это уравнение имеет единственный положительный корень x = 0,1, следовательно, p = 10.
Итак, заработная плата в первый раз повысилась на 10%, а во второй — на 20%.
9. Два брата купили акции разных компаний на равные суммы. В понедельник акции старшего брата подорожали, а акции младшего брата подешевели на p%. Во вторник акции старшего брата подешевели, а акции младшего брата подорожали на q%. Чьи акции после торгов во вторник стоили дороже, если: а) p = q; б) p q?
Решение. Пусть каждый из братьев купил акций на a р. Тогда после торгов во вторник акции старшего брата стоили (в рублях)
![]()
![]() a1 = a(1 100p )(1 100q ) = a(1 100pq2) 100a (p q),
a1 = a(1 100p )(1 100q ) = a(1 100pq2) 100a (p q),
а акции младшего брата стоили
![]()
![]() a2 = a(1 100p )(1 100q ) = a(1 100pq2) 100a (p q) .
a2 = a(1 100p )(1 100q ) = a(1 100pq2) 100a (p q) .
а) Если p = q, то акции братьев стоили одинаково.
б) Если p q, то акции старшего брата стоили дороже.
10. Инвестор купил 171 акцию известной компании по 342 р. за штуку. Через некоторое время разразился финансовый кризис, акции упали в цене и инвестор продал их на p% дешевле, чем купил сам. А когда кризис закончился, инвестор решил вложить все деньги, вырученные от неудачной продажи акций, в покупку большего числа тех же акций, которые со времени неудачной продажи стали дешевле на q%. Сколько акций купил инвестор во второй раз, если: а) q = 43; б) q = 25?
Решение. Чтобы избежать громоздких записей,
обозначим a = 171, b = 342. Первоначально инвестор
потратил на покупку акций ab р. Акции были проданы первый раз по b(1 ![]() p ) р. за акцию на сумму ab(1 p )
р.
p ) р. за акцию на сумму ab(1 p )
р.
100 100
![]() Второй раз акции
были куплены по b(1 p )(1 q )
р.
Второй раз акции
были куплены по b(1 p )(1 q )
р.
100 100
![]() за акцию на сумму ab
1
за акцию на сумму ab
1 ![]() p )
р., поэтому было куплено
p )
р., поэтому было куплено
100
![]() ab⎛⎜⎝1 100p ⎞⎟⎠ = a = 17100 (акций).
ab⎛⎜⎝1 100p ⎞⎟⎠ = a = 17100 (акций).
b⎛⎜⎝1 100p ⎞⎟⎠⎛⎜⎝1 100q ⎞⎟⎠ 1 100q 100 q
Как видим, ответ не зависит от значений b и p.
а) Если q = 43, то 17100 = 300 (акций).
100 q
![]() б) Если q = 25,
то 17100
= 228 (акций).
б) Если q = 25,
то 17100
= 228 (акций).
100 q
Ответ. а) 300 акций; б) 228 акций.
11. По условиям задания 10 ответьте на вопрос: на какое наименьшее целое число процентов должна вырасти цена акций с момента второй покупки, чтобы акции стоили не меньше той суммы, которую инвестор первоначально потратил на покупку акций, если: а) p = 22; б) p = 16?
Решение. Пусть с момента второй покупки цена акций увеличилась на x% и каждая акция стоит
b(1 p )(1 q )(1 x ) р.
100 100 100
![]() Тогда все a
акций, купленные во второй раз,
Тогда все a
акций, купленные во второй раз,
q
1
100
![]() стоят ab1 p )(1 x ) р.
стоят ab1 p )(1 x ) р.
100 100
Эта сумма равна первоначально вложенной сумме ab р., если x является корнем уравнения
|
( |
![]() 1
p )(1 x ) = 1,
1
p )(1 x ) = 1,
100 100
![]() т. е. если x = 100p .
Если же x
т. е. если x = 100p .
Если же x ![]() 100p ,
100p ,
100 p 100 p
![]() то (1 p )(1 x ) 1,
то (1 p )(1 x ) 1,
100 100
т. е. при x 100p эта сумма больше
100 p
6 Рис. 49 первоначально вложенной суммы ab р.
Итак, чтобы акции стали стоить не
меньше суммы, которую инвестор первоначально потратил на покупку акций, должно выполняться неравенство
100p
x ![]() .
.
100 p
а)
Если p = 22, то x ![]() 100p 28,2,
т. е. наименьшее
100p 28,2,
т. е. наименьшее
100 p
число процентов равно 29.
б)
Если p = 16, то x ![]() 100p 19,04,
т. е. наимень-
100p 19,04,
т. е. наимень-
100 p
шее число процентов равно 20.
Ответ. а) На 29%; б) на 20%.
12. Сечение туннеля имеет форму прямоугольника, сверху завершённого полукругом (рис. 49). Периметр сечения 18 м. При каком радиусе полукруга сечение туннеля наибольшее?
Решение. Сначала выразим через R удвоенную высоту 2h стены туннеля до закругления:
2h = (18 – pR – 2R) м.
Теперь вычислим площадь сечения туннеля:
S = 0,5pR2 + 2Rh = 0,5pR2 + R(18 – pR – 2R) = = –(0,5p + 2)R2 + 18R.
Найдём R, при котором выражение –(0,5p + 2)R2 + + 18R принимает наибольшее значение. Преобразуем это выражение, используя выделение полного квадрата:
–(0,5p + 2)R2 + 18R =
![]() ⎛( 9 ) 2 ( 9 ) 2⎞
⎛( 9 ) 2 ( 9 ) 2⎞
= –(0,5p + 2)⎜⎝ R 0 5, π 2 0 5, π 2 ⎟⎠.
Чтобы значение выражения –(0,5p + 2)R2
+ 18R оказалось наибольшим, выражение R – ![]() должно
равняться нулю. Это возможно лишь при R =
должно
равняться нулю. Это возможно лишь при R = ![]() .
.
Если считать, что p » 3,14, то R » ![]() » 2,52 (м).
» 2,52 (м).
![]() Следовательно, при
радиусе полукруга R »
2,52 м сечение туннеля наибольшее.
Следовательно, при
радиусе полукруга R »
2,52 м сечение туннеля наибольшее.
13. Из пунктов А и В (рис. 50), расстояние между которыми 20 км, вышли одновременно в указанных направлениях два пешехода. Скорость пешехода, вышедшего из пун- 6 Рис. 50 кта А, 4 км/ч, а скорость пешехода,
вышедшего из пункта В, 6 км/ч. Через какое время расстояние между ними станет наименьшим?
Решение. Пусть прошло x ч и пешеход A удалился от пункта A на 4x км, а пешеходу B до пункта A осталось пройти (20 – 6x) км. Тогда квадрат расстояния между ними (по теореме Пифагора) равен
(4x)2 + (20 – 6x)2 = 52x2 – 240x + 400.
![]() Так как положительное
расстояние между пешеходами будет наименьшим тогда, когда квадрат этого
расстояния будет наименьшим, то осталось найти значение x, при котором
выражение 52x2 – 240x + 400
достигает наименьшего значения. Выделим полный квадрат:
Так как положительное
расстояние между пешеходами будет наименьшим тогда, когда квадрат этого
расстояния будет наименьшим, то осталось найти значение x, при котором
выражение 52x2 – 240x + 400
достигает наименьшего значения. Выделим полный квадрат:
![]()
![]() 52x2 – 240x + 400
= 52 x 30)2 52 (30)2 400.
52x2 – 240x + 400
= 52 x 30)2 52 (30)2 400.
13 13
![]()
![]()
![]()
![]() Чтобы
значение выражения 52x2 – 240x + 400
оказалось наименьшим, выражение x должно равняться нулю. Это возможно лишь при x =. Тогда
искомое время равно 2 ч.
Чтобы
значение выражения 52x2 – 240x + 400
оказалось наименьшим, выражение x должно равняться нулю. Это возможно лишь при x =. Тогда
искомое время равно 2 ч.
Ответ. Через 2 ч.
![]()
![]() Замечание. Выше
приведены способы решения задач, основанные на выделении полного квадрата. Но
можно решать эти задачи, используя свойство квадратичной функции y =
ax2 + bx + c достигать в точке x0
= 2ab при a
0 наименьшего значения, а при a 0 наибольшего значения.
Максимальный выигрыш от применения этого способа получится при решении задачи 12.
Замечание. Выше
приведены способы решения задач, основанные на выделении полного квадрата. Но
можно решать эти задачи, используя свойство квадратичной функции y =
ax2 + bx + c достигать в точке x0
= 2ab при a
0 наименьшего значения, а при a 0 наибольшего значения.
Максимальный выигрыш от применения этого способа получится при решении задачи 12.
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Примерное тематическое планирование работы
по учебнику «Алгебра, 8» . . . . . . . . . . . . . . . . . . . . . . . 17
Глава 1. Простейшие функции. Квадратные корни 20
Глава 2. Квадратные и рациональные уравнения . . . 48
Глава 3. Линейная, квадратичная
и дробно-линейная функции . . . . . . . . . . . . . . . . . . . . . 83
Глава 4. Системы рациональных уравнений . . . . . . . . 113 Обучение решению текстовых задач . . . . . . . . . . . . . . 137
Задания на исследование . . . . . . . . . . . . . . . . . . . . . . . . 154
У ч е б н о е и з д а н и е
Серия «МГУ — школе» Потапов Михаил Константинович
Шевкин Александр Владимирович
Алгебра
8 класс
Учебное пособие для общеобразовательных организаций
Центр естественно-математического образования
Редакция математики и информатики
Зав. редакцией Т. А. Бурмистрова
Редактор Т. Г. Войлокова
Младший редактор Е. В. Трошко
Художник О. П. Богомолова
Художественный редактор О. П. Богомолова
Компьютерная графика И. В. Губиной
Техническое редактирование и компьютерная вёрстка Н. А. Разворотневой
Корректор О. В. Крупенко
Налоговая льгота — Общероссийский классификатор продукции ОК 005-93—953000. Изд. лиц. Серия ИД № 05824 от 12.09.01. Подписано в печать 14.03.16. Формат 60901/16. Бумага газетная. Гарнитура SchoolBookCSanPin. Уч.-изд. л. 8,20. Тираж 50 экз. Заказ № . Акционерное общество «Издательство «Просвещение». 127521, Москва, 3-й проезд Марьиной рощи, 41.
Отпечатано в типографии «Onebook» ООО «Сам Полиграфист».
129090, Москва, Протопоповский пер., 6. Тел.: +7(495) 545-37-10.
E-mail: info@onebook.ru
Сайт: www.onebook.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.