

![]()
УДК 373.5.016:512 16+
ББК 74.262.21
П64
Серия «МГУ — школе» основана в 1999 году
Потапов М. К.
П64 Алгебра. Методические рекомендации. 9 класс : учеб. пособие для общеобразоват. организаций / М. К. Потапов, А. В. Шевкин. — 2-е изд. — М. : Просвещение, 2019. — 191 с. : ил. — (МГУ—школе). — ISBN 978-5-09-070988-0.
Эта книга адресована учителям, работающим по учебнику серии «МГУ — школе» «Алгебра. 9 класс» авторов С. М. Никольского, М. К. Потапова, Н. Н. Решетникова, А. В. Шевкина. В ней дана характеристика курса алгебры 9 класса, приведены примерное тематическое планирование, методические рекомендации по всем темам и решения наиболее трудных задач.
УДК 373.5.016:512 ББК 74.262.21
ISBN 978-5-09-070988-0 © Издательство «Просвещение», 2016, 2019
© Художественное оформление.
Издательство «Просвещение», 2016, 2019
Все права защищены
О книге для учителя
Данная книга предназначена для учителей, работающих по учебнику «Алгебра. 9 класс» серии «МГУ — школе» (авторы С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин). Этот учебник является частью учебного комплекта для 7—9 классов, рекомендованного Министерством образования и науки Российской Федерации, он продолжает учебники тех же авторов «Алгебра. 7 класс» и «Алгебра. 8 класс» серии «МГУ — школе». В учебный комплект для 9 класса входят:
· Алгебра. 9 класс: учебник для общеобразоват. организаций / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. — М.: Просвещение, 2014— 2019;
· Алгебра. Дидактические материалы. 9 класс / М. К. Потапов, А. В. Шевкин. — М.: Просвещение, 2010—2019;
· Алгебра. Тематические тесты. 9 класс / П. В. Чулков, Т. С. Струков. — М.: Просвещение, 2010—2019;
· Алгебра. Методические рекомендации. 9 класс / М. К. Потапов, А. В. Шевкин. — М.: Просвещение, 2019.
В данной книге рассмотрены концепция учебников алгебры серии «МГУ — школе» и структура учебника для 9 класса, приведено примерное тематическое планирование, даны методические рекомендации по изучению основных тем курса алгебры 9 класса и комментарии к решению некоторых трудных задач. Здесь же даны рекомендации по использованию дидактических материалов. Практически для всех пунктов учебника в книге имеются рубрики Решения и комментарии и Промежуточный контроль, к некоторым пунктам даётся рубрика Задания для повторения. В первой из них приведены условия многих задач из учебника и их решения или даны рекомендации, как найти решение с пояснениями, помогающими обучению школьников. Во второй рубрике даны номера самостоятельных и контрольных работ по дидактическим материалам, а также номера тестов из сборника тематических тестов. В последней рубрике приводятся номера упражнений из раздела «Задания для повторения» учебника, которые можно использовать при изучении данного пункта.
Следует обратить внимание на то, что в пособии для учителей (как и в учебнике) рассмотрены вопросы обучения алгебре в 9 классе как в общеобразовательных классах, так и в классах с углублённым изучением математики. При этом сначала обсуждаются вопросы для общеобразовательных классов, затем для классов с углублённым изучением математики.
В комментариях для учителя не выделяются необязательные задания, так как в учебнике есть соответствующие обозначения. При этом не обсуждается время, отводимое на изучение пункта, так как при разных вариантах планирования могут быть различия. Во многих пунктах книги для учителя методические комментарии даны в расчёте на возможно более глубокое изучение вопроса, поэтому при подготовке к уроку учитель должен отобрать главное, что будет изложено учащимся на уроке, решить, каким будет закрепление материала в классе и дома, когда и каким будет контроль изученного. При этом не надо стремиться донести до учащихся все подробности и тонкости изучаемого материала, если учащиеся существенно ограничены во времени изучения темы.
Об учебниках математики серии «МГУ — школе»
В серии «МГУ — школе» издательство «Просвещение» издаёт учебники «Математика» для 5 и 6 классов, «Алгебра» для 7, 8 и 9 классов, «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа» для 10 и 11 классов (авторы С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин). Эти учебники полностью отвечают требованиям Федерального государственного образовательного стандарта. Они рекомендованы министерством в качестве учебников для любых типов общеобразовательных организаций. Их издание является составной частью программы «МГУ — школе», разработанной по инициативе ректора Московского государственного университета академика В. А. Садовничего и нацеленной на сохранение и развитие лучших традиций отечественного математического образования.
Авторами учебников разработана концепция многоуровневых учебников математики. Приведём основные положения этой концепции.
· Математика едина и может быть изложена в одном учебнике для работы по разным программам. Содержание учебника должно соответствовать научной точке зрения на изучаемые вопросы.
· Учебник должен сочетать в себе научность, стройность, экономность и логичность изложения материала с доступностью для учащихся его учебных текстов.
· Учебник не должен ограничиваться интересами среднего ученика, он должен удовлетворять интересам всех учащихся — от слабых до сильных — для обеспечения их индивидуальной образовательной траектории.
· Учебник должен быть пригоден для организации дифференцированного обучения и обеспечивать любой желаемый уровень глубины изучения материала с учётом устойчивых познавательных интересов.
· Способ изложения материала в учебнике, организация учебных текстов и системы упражнений должны обеспечивать достижение разных целей обучения при работе по разным программам.
Структура учебников серии «МГУ — школе» и их методический аппарат отвечают положениям этой концепции.
Учебники серии «МГУ — школе» составляют три независимых цикла — для 5—6, 7—9 и 10—11 классов. Обучение в каждом цикле можно начинать независимо от того, по каким учебникам учились школьники в предыдущие годы, так как в первом учебнике каждого цикла проводится повторение и систематизация изученного за предыдущие годы.
Учебники для 5—6 классов ориентированы на развитие интереса к математике в процессе обучения, в них много материала, нацеленного на повышенный уровень математической подготовки.
Учебники для 7—9 классов предназначены как для общеобразовательных классов, так и для классов с углублённым изучением математики.
Учебники для 10—11 классов охватывают содержание курса алгебры и начал математического анализа для всех профилей старшей школы.
Авторы учебников уверены, что не следует упрощать обучение за счёт сокращения числа изучаемых вопросов и необходимо сохранить фундаментальность изложения теории в учебниках, оставляя за учителем право более или менее глубокого изложения теоретического материала на уроке в зависимости от уровня подготовки класса и целей обучения. В учебниках коротко, ясно и доступно, без долгих введений излагается суть вопроса. Мотивировать появление тех или иных понятий, определений при необходимости должен учитель, так как в разных классах это надо делать по-разному.
Учебники серии «МГУ — школе» имеют высокий научный и методический потенциал. Они отличаются расположением учебного материала в естественной логической последовательности, позволяющей излагать материал более глубоко, экономно и строго. В соответствии с требованиями ФГОС учебники не только нацелены на формирование навыков, но и учат действовать осознанно. Обычно обучение больше ориентировано на вопрос «как?», на действия по образцу, требует многократных повторений для поддержания навыков. В учебниках серии «МГУ — школе» уделяется достаточно внимания вопросу «почему?», имеющему большой развивающий потенциал для достижения личностных результатов освоения ООП основного общего образования. Учебники позволяют интенсифицировать процесс обучения, что в условиях уменьшения числа учебных часов особенно важно. Они полностью обеспечивают обучение тех школьников, которые хотят и могут обучаться основам наук.
Главный методический принцип, положенный в основу изложения теоретического материала, заключается в том, что ученик за один раз должен преодолевать не более одной трудности. Поэтому каждое новое понятие формируется, каждое новое умение отрабатывается сначала в чистом виде, затем трудности совмещаются, что позволяет учащимся контролировать процесс и результат учебной деятельности.
Аналогично выстроена и система упражнений. Сложность заданий в каждом пункте нарастает линейно: учитель определяет сам, на какой ступеньке лестницы сложности он может остановиться со своим классом или с конкретным учеником.
Одна из особенностей системы упражнений в учебниках заключается в том, что для каждого нового действия или приёма решения в учебниках имеется достаточное число упражнений, которые не перебиваются упражнениями на другие темы. Только тогда, когда новый материал освоен, можно подключать задания на соединение этого материала с ранее изученным, задания на повторение, не связанные с новым материалом, в итоге формируется умение контролировать процесс и результат учебной математической деятельности.
Важную роль в формировании первоначальных представлений о зарождении и развитии математики играют исторические сведения, завершающие каждую главу учебников. Этот материал способствует формированию представления о математической науке как сфере человеческой деятельности, об этапах её становления, о её значимости для развития цивилизации. Работа со старинными задачами — одна из сильных сторон учебников, она может много дать в воспитании уважения к традициям и истории, в развитии общеучебных умений.
Учебники серии «МГУ — школе» полностью обеспечивают обучение тех школьников, которые могут и хотят учиться основам наук. Они нацелены на повышенный уровень математической подготовки учащихся. Учебники можно использовать и в классах с обычной программой по математике, если не изучать сверхпрограммный материал и пропускать сложные задачи, а также выбирать уровень полноты изложения теоретического материала на уроке и уровень предъявления требований к знаниям и умениям учащихся в соответствии с поставленными целями обучения и возможностями конкретного класса, оставаясь при этом на уровне не ниже обязательных требований к математической подготовке учащихся. При таком подходе у сильных учащихся будет возможность с помощью учебника более глубоко разобраться в любом вопросе, чего они часто лишены, если учебник написан в расчёте на среднего ученика.
Основные идеи курса алгебры 7—9 классов
Алгебра играет в математике большую роль, теперь существует даже тенденция «алгебраизации» математики. Наряду с фундаментальной ролью внутри математики алгебра имеет и прикладное значение. Достаточно отметить её выходы в физику, кибернетику, математическую экономику. Поэтому изучение алгебры в школе является важной частью фундамента естественно-научного образования.
Для учебников алгебры возможны два способа распределения учебного материала по годам обучения. Первый — в каждом классе дают понемножку буквенных выражений, уравнений, неравенств, функций и т. п., так как детям якобы скучно долго изучать одни и те же вопросы. При использовании такого способа распределения учебного материала страдают научная аккуратность и строгость изложения, появляются порочные логические круги, недомолвки и несуразности, что в первую очередь сказывается на обучении и воспитании сильных учащихся.
Так происходит, например, когда действительные числа рассматриваются после изучения тождеств, функций и их графиков. Реализация этого первого подхода к построению курса алгебры в процессе обучения чаще ориентирована на формирование навыков.
Но есть и второй способ распределения учебного материала по годам обучения, основанный на его внутренней логике. Он диктует последовательность появления в учебнике тех или иных вопросов, позволяет в каждом учебном году ставить главную задачу. Этот способ, принятый в учебниках серии «МГУ — школе», позволяет излагать материал в строгой логической последовательности, без ненужных повторов и недомолвок, что делает изложение даже сложных вопросов ясным и доступным. Учебники серии «МГУ — школе» обеспечивают системную подготовку по предмету, требуют меньше, чем обычно, времени, позволяют ориентировать процесс обучения на формирование результатов обучения и освоения содержания курса, требуемых ФГОС. Как показывает опыт работы по ним, интерес к предмету возникает у учащихся не от многообразия и частого чередования тем, а от того, что учащиеся имеют возможность «вжиться» в каждый элемент содержания, постепенно углубляя его понимание. Изложение материала в учебниках связное — подряд излагаются большие темы, нет чересполосицы мелких вопросов, нарушающих логику изложения крупных тем. Это позволяет каждый раз сосредоточиваться на одном вопросе и поэтому изучить его более глубоко и в то же время более экономно. Отдельные темы программы изучаются один раз и в полном объёме, чтобы потом к ним не возвращаться в теоретической части учебника. Дальнейшее закрепление и повторение, а иногда и развитие изученного ведутся через линию упражнений.
Содержание курса алгебры диктует порядок изложения основного учебного материала: сначала должны изучаться чисто алгебраические вопросы (алгебраические выражения) как более доступные в этом возрасте, а уж затем функциональные вопросы. Поэтому материал 7 класса посвящён алгебраическим выражениям, а изучение функций начинается лишь в 8 классе.
Школьный курс алгебры 7—9 классов на самом деле лишь наполовину является алгеброй, другая его половина приходится на вопросы математического анализа, изучаемые традиционно в курсе алгебры (длина отрезка, действительные числа, функции). Желательно различать эти составляющие и излагать алгебраические вопросы алгебраическими методами. Например, к буквенным выражениям часто подходят как к функциям многих переменных (функциональный подход), хотя естественнее говорить о них как о множестве объектов, подчинённых явно выписанным законам (алгебраический подход). Поэтому при изложении темы «Алгебраические выражения» авторы считают необходимым оставаться на чисто алгебраической точке зрения. Одночлен определяется как произведение некоторых чисел и букв, многочлен — как сумма одночленов, алгебраическая дробь — как отношение многочлена к ненулевому многочлену. Приводятся правила, которым они подчинены. Например, в одночлене можно поменять местами множители, в многочлене можно привести подобные члены, алгебраическую дробь можно сократить на ненулевой многочлен и т. д. Эти свойства мотивируются по мере их введения, отмечается, что при замене букв числами в рассматриваемых буквенных равенствах последние превращаются в верные числовые равенства (за исключением случаев деления на нуль).
В учебниках для 7—9 классов достаточно внимания уделено решению уравнений, неравенств и их систем, построению графиков элементарных функций, решению текстовых задач, в том числе в общем виде, что необходимо для изучения курсов геометрии и физики.
Учебники алгебры серии «МГУ — школе» содержат весь материал программ как для классов с обычной программой по математике, так и для классов с углублённым изучением математики. Авторы считают принципиально важным иметь общий учебник для всех этих классов, что позволяет учащимся переходить без особых трудностей с одной программы обучения на другую, а учителям проводить уровневую дифференциацию обучения как для разных классов, так и для отдельных учащихся. Такой учебник позволяет сильному учащемуся обычного класса разобраться в любом вопросе, изучить математику вплоть до уровня углублённого изучения. Учитель, работающий в классах с разной подготовкой, ведя обучение по одному учебнику в рамках одной авторской концепции, может лишь менять в зависимости от класса глубину погружения в теоретические и технические подробности.
В общеобразовательных классах дополнительные материалы и сложные задачи обычно не рассматриваются. Если же учитель имеет достаточно часов и его класс проявляет интерес к математике, то за счёт Дополнений к главам учебников, а также пунктов и отдельных задач со звёздочкой, необязательных в обычных общеобразовательных классах, можно расширить и углубить содержание изучаемого материала до объёма, предусмотренного программой для классов с углублённым изучением математики.
Об учебнике «Алгебра. 9 класс» серии «МГУ — школе» Учебник «Алгебра. 9 класс» содержит пять глав:
1. Неравенства.
2. Степень числа.
3. Последовательности.
4. Тригонометрические формулы.
5. Элементы приближённых вычислений, статистики, комбинаторики и теории вероятностей.
В первом параграфе главы 1 рассматриваются линейные неравенства и системы таких неравенств, а во втором параграфе — неравенства второй степени. При решении линейных и квадратичных неравенств приводится графическая их иллюстрация.
Параграф 3 главы 1 посвящён решению рациональных неравенств, подробно рассматриваются метод интервалов и решение систем рациональных неравенств. Отметим, что согласно новым стандартам, утверждённым Министерством образования и науки, рациональные неравенства являются необязательными для всех учащихся, они перенесены в старшую школу. Подчеркнём, что в этой главе в основном решаются строгие неравенства. Решению нестрогих неравенств посвящён лишь последний пункт. Мы считаем, что решение нестрогих неравенств должно состоять из двух этапов: 1) решение уравнения; 2) решение строгого неравенства. А затем в ответе надо объединить решения уравнения и строгого неравенства. Попытки отойти от этого правила и просто записать решение нестрогого неравенства как решение строгого, только с заменой интервалов на отрезки, часто приводят к ошибкам. Метод интервалов обосновывается свойством двучлена x – a, что не требует явного обращения к непрерывности функции.
В качестве Дополнений к этой главе рассматриваются доказательства числовых неравенств и понятие производной линейной и квадратичной функций. Производные вводятся для многочленов с опорой на интуитивное понятие предела, их введение связано с тем, что производные необходимы при изучении курса физики.
В результате изучения главы 1 учащиеся должны научиться решать линейные и квадратные неравенства, системы неравенств.
В главе 2 в основном изучается корень степени n и его свойства. Следует отметить, что согласно новым стандартам в основной школе оставлено лишь изучение квадратных и кубических корней, изучение остальных корней натуральной степени n перенесено в старшую школу.
В качестве дополнения к этой главе приведено понятие степени с рациональным показателем. Отметим, что существование и единственность, в частности, корня третьей степени из любого действительного числа показывается в этой главе графически, с опорой на непрерывность графика функции у = х3.
В результате изучения главы 2 учащиеся должны овладеть понятием корня степени n и уметь применять его основные свойства.
Глава 3 посвящена в основном изучению арифметической и геометрической прогрессий. Сначала вводится понятие числовой последовательности и рассматриваются её свойства, затем изучаются арифметические и геометрические прогрессии, формулы общего члена, формулы суммы первых n членов и свойства прогрессий.
В качестве необязательного материала рассматривается бесконечно убывающая геометрическая прогрессия.
В Дополнениях к этой главе разбирается метод математической индукции. Это связано с тем, что доказательства формул для арифметической и геометрической прогрессий требует применения данного метода.
В результате изучения главы 3 учащиеся должны овладеть понятиями арифметической и геометрической прогрессий и уметь применять их свойства при решении задач.
Глава 4 посвящена изучению синуса, косинуса, тангенса и котангенса любого угла. Угол вводится как поворот вектора, рассматриваются градусная и радианная меры угла, и тогда каждому действительному числу соответствует угол, градусная или радианная мера которого равна этому числу. После этого вводятся понятия синуса, косинуса, тангенса и котангенса любого угла и выводятся основные формулы для них. В Дополнениях к этой главе приводятся формулы синусов и косинусов суммы углов, двойных и половинных углов.
Отметим, что согласно новым стандартам весь материал этой главы перенесён в старшую школу, но он по традиции изучается в 9 классах с углублённым изучением математики. Авторы учебника считают, что материал этой главы желательно изучить в 9 классе, так как это существенно облегчит его изучение в старшей школе. Кроме того, тригонометрические формулы дают пример построения алгебры со своими правилами преобразования буквенных выражений, что полезно в плане общего развития школьников.
В результате изучения главы 4 учащиеся должны освоить понятие угла с любой градусной или радианной мерой, знать определение и свойства синусов, косинусов и тангенсов любых углов, уметь преобразовывать тригонометрические выражения и доказывать тригонометрические тождества с применением формул.
Глава 5 замыкает линию изучения чисел в основной школе. В ней речь идёт о приближениях чисел, вводятся понятия абсолютной и относительной погрешностей приближения числа и понятия приближения числа с точностью до указанного разряда после запятой либо до какойто значащей цифры. Далее изучаются вопросы описательной статистики, комбинаторики и теории вероятностей.
В Дополнениях к этой главе рассматриваются бином Ньютона и треугольник Паскаля.
В результате изучения главы 5 учащиеся должны научиться применять правила приближённых вычислений, получить представление о способах задания числовых данных и их характеристиках, научиться решать несложные комбинаторные задачи и задачи на вычисление вероятностей.
При организации повторения курса алгебры 7—9 классов необходимо обратить особое внимание на наиболее трудные темы курса, постараться учесть индивидуальные пробелы учащихся при подготовке к основному государственному экзамену (ОГЭ).
При повторении теории необходимо выделять основные теоретические факты, изученные в 7—9 классах, давая иллюстрации их применения на наиболее характерных примерах. При этом можно использовать задачи из раздела «Задания для повторения».
Система упражнений в учебнике построена в соответствии с принципом «от простого к сложному». После каждого учебного текста идут вопросы по изученной теории, затем упражнения по новому материалу, которые не перебиваются заданиями на повторение. Упражнения нацелены на освоение изученного, формирование умений, предусмотренных стандартом. В курсе алгебры много заданий, выполняемых по образцам, рекомендованным в учебнике или учителем, но в 9 классе надо больше внимания уделить формированию более сложных умений, связанных с доказательством и исследованием. Соответствующие упражнения выделены в особые рубрики «Доказываем» и «Исследуем».
Умение доказывать особенно важно при обучении по программе с углублённым изучением математики, поэтому, кроме вопросов теории, связанных с доказательствами, надо обратить внимание на более сложные упражнения из рубрики «Доказываем». Работа с этими заданиями способствует достижению таких метапредметных результатов, как умение создавать обобщения, устанавливать аналогии, устанавливать причинно-следственные связи, строить логические рассуждения, умозаключения и делать выводы.
Многие задания из рубрики «Исследуем» связаны с поиском значений параметра, при которых выполнено некоторое условие. Тем самым у учащихся формируются важные умения исследовать ситуацию, описанную в задаче, в зависимости от значения этой величины. Термин «параметр» в учебнике сознательно не используется, но подразумевается, а учащиеся фактически решают задачи, которые выносятся на итоговый контроль ОГЭ и ГВЭ, встречаются в дополнительных испытаниях при поступлении в вузы. Разбор решений этих задач позволит подготовить учащихся к решению олимпиадных задач, а также будет способствовать формированию компетентности в проведении учебно-исследовательской деятельности. Обсуждение решений этих задач помогает обобщению знаний и сотрудничеству со сверстниками и учителем. Выполнение заданий данной рубрики поможет учащимся в развитии таких метапредметных умений, как умение самостоятельно планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных задач; умение осуществлять контроль своей деятельности, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией; умение оценивать правильность выполнения учебной задачи, собственные возможности её решения; умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач.
Развитию способностей учащихся искать и использовать информацию, связанную с изучаемым материалом, будут способствовать задания рубрики «Ищем информацию». Часть из этих заданий можно выполнить в виде небольших сообщений (докладов) для одноклассников или поместив в математические газеты.
К данному курсу существует Электронная форма учебника (ЭФУ) — соответствующая по структуре, содержанию и художественному оформлению печатной форме учебника и включающая в себя интерактивные ссылки, расширяющие и дополняющие материал печатного учебника.
Функциональными особенностями ЭФУ является:
— удобный и понятный интерфейс и навигация по
ЭФУ;
— работа в онлайн- и офлайн-режимах;
— тестовые задания к каждой теме, разделу учебника;
— возможность добавления материалов, созданных учителем;
— инструменты изменения размера шрифта, создания заметок и закладок.
Использование ЭФУ предоставляет учителю следующие возможности:
— организовать контроль и самоконтроль по результатам изучения темы;
— реализовать технологии мобильного, дистанционного или смешанного обучения;
— реализовать требования ФГОС по формированию информационно-образовательной среды системой электронных образовательных ресурсов и др.
Об использовании дидактических материалов и сборника тестов
Дидактические материалы содержат три раздела:
I. Материалы для подготовки к самостоятельным ра-ботам.
II. Самостоятельные работы.
III. Контрольные работы.
В разделе I разобраны решения заданий, похожих на задания из самостоятельной работы и готовящих учащихся к выполнению соответствующей работы. Практика показывает, что учащиеся не любят читать учебник, полагаясь на то, что поняли всё, что требуется, из рассказа учителя, а подготовка к самостоятельной работе по первой части дидактических материалов, разбор решений задач, похожих на задания из самостоятельной работы, дают шанс овладеть умением читать математическую литературу и повышают результативность работы. Кроме того, такая работа хотя бы для части учащихся уменьшит вредную тягу к поиску готовых домашних заданий.
Дидактические материалы используются для промежуточного контроля по теме и итоговой контрольной работы. Следует учесть, что провести все самостоятельные работы с выставлением отметки со всем классом, скорее всего, не удастся, да это и не требуется. Некоторые из работ можно использовать как домашние задания на отметку или как дополнительные задания для наиболее заинтересованных учащихся. Самостоятельные работы отнесены к соответствующим темам, но могут использоваться и при изучении других тем (например, для организации повторения изученного через некоторый промежуток времени).
В обязательную часть самостоятельных работ на отметку можно включать не все задания, ориентируясь на уровень подготовки класса и на отводимое для работы время. Необязательные задания можно оценивать дополнительной отметкой.
В обычном классе в обязательную часть контрольных работ можно не включать последнее задание.
Виды контроля полезно разнообразить. Для этого можно использовать сборник «Алгебра. Тематические тесты. 9 класс» авторов П. В. Чулкова, Т. С. Струкова. Тестовый контроль интересен небольшой затратой времени на его проведение и оперативностью получения информации о качестве знаний и умений школьников. Тесты удобно использовать для организации текущего повторения, для дополнительного опроса учащихся, желающих исправить отметки по изученной теме или в четверти.
О решении текстовых задач
В учебнике «Алгебра. 9 класс» решение текстовых задач при помощи рациональных уравнений и их систем проводится только при текущем и итоговом повторении. Основной целью решения текстовых задач является развитие у учащихся умения моделировать с помощью уравнения или системы уравнений ситуацию, описанную в задаче, делать логически правильные выводы на основе анализа имеющихся данных задачи и использовать эти данные для её решения. Решая текстовые задачи, учащиеся учатся планировать свою работу, выполнять её согласно намеченному плану, проверять полученный ответ на соответствие условиям задачи. Эти умения являются метапредметными, действия, их формирующие, называют универсальными учебными действиями. Этим действиям уделяется особое внимание в новых стандартах по математике.
Авторы считают, что решение текстовых задач является наиболее эффективным способом развития логического мышления и речи учащихся, повышает результативность обучения математике и другим предметам.
Обратим внимание на то, что решение текстовых задач является важным видом учебной деятельности школьников, умения, формируемые при решении текстовых задач, выносятся на итоговый контроль. В каждом классе работа с текстовыми задачами будет вестись в своём темпе, поэтому её нельзя заранее спланировать для всех классов и дать рекомендации по использованию задач по всем пунктам. В связи с этим рекомендации по работе с задачами разных видов даны в конце данного пособия. Предполагается, что учитель сам будет планировать момент включения работы с текстовыми задачами в учебный процесс.
Здесь можно дать только один совет, которому полезно следовать. Работа с текстовыми задачами на повторение не должна вклиниваться в изучение нового материала до тех пор, пока основные умения по этому материалу не сформированы. Желательно, чтобы эта работа была связана с повторением изученного, которое проводится под руководством учителя, и подготовкой к итоговой аттестации. Задачи должны разнообразить формы учебной деятельности, делать изучение математики более живым и интересным.
О работе в классах с углублённым изучением математики
В учебнике «Алгебра. 9 класс» серии «МГУ — школе» материал, предназначенный только для классов с углублённым изучением математики, специально выделен. Это доказательства некоторых теорем, дополнительные вопросы, изложенные в пунктах, отмеченных звёздочками и в Дополнениях к главам учебника, а также более сложные задачи.
В классе с углублённым изучением математики используются и дидактические материалы. При этом все задания считаются обязательными только для классов с углублённым изучением математики. Кроме того, в дидактических материалах имеются самостоятельные работы, отмеченные звёздочками, которые предназначены только для классов с углублённым изучением математики.
В классе с углублённым изучением математики следует больше внимания уделять решению задач из олимпиад и конкурсов, участию учащихся в различных турнирах. Ниже к ряду пунктов сделаны специальные замечания о работе с такими задачами.
Из двух вариантов тематического планирования вариант I (3 ч в неделю, всего 102 ч) предназначен для классов, работающих по обычной программе, а вариант II (4 ч в неделю, всего 136 ч) — для классов с углублённым изучением математики. Справа от параграфа или пункта указано число часов, отведённых на его изучение для каждого варианта планирования.
|
|
I II |
|
Глава 1. Неравенства |
31 36 |
|
§ 1. Линейные неравенства с одним неизвестным 1.1. Неравенства первой степени |
9 10 |
|
с одним неизвестным 1.2. Применение графиков к решению неравенств |
2 2 |
|
первой степени с одним неизвестным |
1 1 |
|
1.3. Линейные неравенства с одним неизвестным 1.4. Системы линейных неравенств |
3 2 |
|
с одним неизвестным 1.5*. Неравенства, содержащие неизвестное |
3 3 |
|
под знаком модуля § 2. Неравенства второй степени |
— 2 |
|
с одним неизвестным 2.1. Понятие неравенства второй степени |
11 11 |
|
с одним неизвестным 2.2. Неравенства второй степени |
1 1 |
|
с положительным дискриминантом 2.3. Неравенства второй степени |
3 3 |
|
с дискриминантом, равным нулю 2.4. Неравенства второй степени |
2 2 |
|
с отрицательным дискриминантом 2.5. Неравенства, сводящиеся к неравенствам |
2 2 |
|
второй степени |
2 2 |
|
Контрольная работа № 1 |
1 1 |
|
§ 3. Рациональные неравенства |
11 11 |
|
3.1. Метод интервалов |
3 3 |
|
3.2. Решение рациональных неравенств |
2 2 |
|
3.3. Системы рациональных неравенств |
2 2 |
|
3.4. Нестрогие неравенства |
3 2 |
3.5*. Замена неизвестного при решении неравенств — 1
|
Контрольная работа № 2 |
1 1 |
|
Дополнения к главе 1 |
— 4 |
|
1. Доказательство числовых неравенств 2. Производные линейной и квадратичной |
— 2 |
|
функций |
— 2 |
|
3. Исторические сведения |
— — |
|
Глава 2. Степень числа |
15 24 |
|
|
§ 4. Функция y = xn |
3 3 |
|
|
4.1. Свойства и график функции y = xn, x 0 4.2. Свойства и графики функций y = x2m |
1 1 |
|
|
и y = x2m + 1 |
2 2 |
|
|
§ 5. Корень степени n |
12 17 |
|
|
5.1. Понятие корня степени n |
2 2 |
|
|
5.2. Корни чётной и нечётной степеней |
3 3 |
|
|
5.3. Арифметический корень степени n |
3 2 |
|
|
5.4. Свойства корней степени n |
3 3 |
|
|
|
— 2 |
|
|
5.6*. Корень степени n из натурального числа |
— 2 |
|
|
5.7*. Иррациональные уравнения |
— 2 |
|
|
Контрольная работа № 3 |
1 1 |
|
|
Дополнения к главе 2 |
— 4 |
|
|
1. Понятие степени с рациональным показателем |
— 2 |
|
|
2. Свойства степени с рациональным показателем — 2 |
|
|
|
3. Исторические сведения |
— — |
|
|
Глава 3. Последовательности |
18 22 |
|
|
§ 6. Числовые последовательности и их свойства |
4 4 |
|
|
6.1. Понятие числовой последовательности |
2 2 |
|
|
6.2. Свойства числовых последовательностей |
2 2 |
|
|
§ 7. Арифметическая прогрессия |
7 7 |
|
|
7.1. Понятие арифметической прогрессии 7.2. Сумма первых n членов арифметической |
3 3 |
|
|
прогрессии |
3 3 |
|
|
Контрольная работа № 4 |
1 1 |
|
|
§ 8. Геометрическая прогрессия |
7 9 |
|
|
8.1. Понятие геометрической прогрессии 8.2. Сумма первых n членов геометрической |
3 3 |
|
|
прогрессии 8.3*. Бесконечно убывающая геометрическая |
3 3 |
|
|
прогрессия |
— 2 |
|
|
Контрольная работа № 5 |
1 1 |
|
|
Дополнения к главе 3 |
— 2 |
|
|
1. Метод математической индукции |
— 2 |
|
|
2. Исторические сведения |
— — |
|
|
Глава 4. Тригонометрические формулы |
— 22 |
|
|
§ 9*. Угол и его мера |
— 5 |
|
|
9.1*. Понятие угла |
— 1 |
|
|
9.2*. Градусная мера угла |
— 2 |
|
|
9.3*. Радианная мера угла |
— 2 |
|
|
§ 10*. Синус, косинус, тангенс и котангенс угла |
— 6 |
|
|
10.1*. Определение синуса и косинуса угла |
— 2 |
|
|
10.2*. Основные формулы для sina и cosa |
— 2 |
|
|
10.3*. Тангенс и котангенс угла |
— 2 |
|
|
Дополнения к главе 4 |
— 11 |
|
|
1. Косинус разности и косинус суммы двух углов |
— 2 |
|
|
2. Формулы для дополнительных углов |
— 1 |
|
|
3. Синус суммы и синус разности двух углов |
— 2 |
|
|
4. Сумма и разность синусов и косинусов |
— 2 |
|
|
5. Формулы для двойных и половинных углов |
— 2 |
|
|
6. Произведение синусов и косинусов |
— 1 |
|
|
7. Исторические сведения |
— — |
|
|
Контрольная работа № 6 |
— 1 |
|
Глава 5. Элементы приближённых вычислений, статистики, комбинаторики и теории вероятностей 19 21
§ 11. Приближения чисел 4 5
11.1. Абсолютная погрешность приближения 1 1
11.2. Относительная погрешность приближения 1 1
11.3*. Приближения суммы и разности 1 1
11.4*. Приближение произведения и частного 1 1 11.5*. Приближённые вычисления и калькулятор — 1
§ 12. Описательная статистика 2 2
12.1. Способы представления числовых данных 1 1 12.2. Характеристики числовых данных 1 1
§ 13. Комбинаторика 5 5
13.1. Задачи на перебор всех возможных вариантов 1 1
13.2. Комбинаторные правила 1 1
13.3. Перестановки 1 1
13.4. Размещения 1 1 13.5. Сочетания 1 1
§ 14. Введение в теорию вероятностей 8 8
14.1. Случайные события 2 2
14.2. Вероятность случайного события 2 2
14.3. Сумма, произведение и разность
случайных событий 1 1
14.4. Несовместные события. Независимые события 1 1
14.5. Частота случайных событий 1 1
Контрольная работа № 7 1 1
Дополнения к главе 5 — 2
1. Бином Ньютона. Треугольник Паскаля — 1
2. Высказывания — 1
3. Исторические сведения — —
Повторение курса 7—9 классов 19 10
Повторение 18 9
Итоговая контрольная работа № 8 1 1
Первая глава посвящена изучению методов решения рациональных неравенств с одним неизвестным. Сначала изучаются линейные неравенства, затем неравенства второй степени и, наконец, рациональные неравенства.
Многие упражнения данной главы решаются разными способами, что позволяет развивать критичность мышления, формировать коммуникативные компетенции в обучении, умение формулировать свои мысли, аргументировать их, отстаивать свою точку зрения.
Цель изучения главы 1 — освоить методы решения линейных неравенств, неравенств второй степени и их систем, кроме того, особенно в классах с углублённым изучением математики, научиться решать хотя бы несложные рациональные неравенства.
§ 1. Линейные неравенства с одним неизвестным
Основное назначение первого параграфа — обучение школьников решению линейных неравенств и их систем. Сначала изучаются способы решения неравенств первой степени с одним неизвестным. Показывается применение графиков к решению неравенств. Затем вводятся понятия линейного неравенства и равносильности неравенств. На примерах демонстрируется решение линейных неравенств. Наконец, изучаются системы неравенств. В качестве необязательного материала для классов с углублённым изучением математики рассматривается решение неравенств, содержащих неизвестное под знаком модуля и сводящихся к решению линейных неравенств и их систем.
1.1. Неравенства первой степени с одним неизвестным
Перед изучением этого пункта желательно повторить материал 7—8 классов, связанный с понятием многочлена первой степени, понятие координатной оси, изображение числовых промежутков на координатной оси, затем выполнить задания 1—3.
Стоит отметить, что неравенство вида kx + b 0 (kx + b 0), где k 0, называют неравенством первой степени, так как в его левой части находится многочлен первой степени.
В обычном классе учащиеся должны освоить предлагаемый в примере 2 учебного текста способ решения неравенства первой степени, понимать, что такое решение неравенства, что значит решить неравенство.
В классе с углублённым изучением математики можно требовать обоснования способа решения неравенства, как это сделано в примере 1 учебного текста. Этот способ доказательства называют рассуждениями с числовыми значениями — он используется и при решении сложных задач.
9. Можно ли указать:
а) наименьшее решение неравенства x 0;
в) наименьшее целое решение неравенства x –5;
г) наибольшее целое решение неравенства x 1?
Решение. а) Наименьшее решение неравенства x
0 указать нельзя. Если учащиеся считают иначе, надо выяснить, какое решение
они считают наименьшим (например, 1), показать, что есть бесконечно много
других решений, меньших указанного. В нашем случае ![]() =
= ![]() — новое решение неравенства (процесс
нахождения координаты середины отрезка можно продолжать бесконечно).
— новое решение неравенства (процесс
нахождения координаты середины отрезка можно продолжать бесконечно).
в) Наименьшим целым решением неравенства x –5
является число –4.
г) Наибольшим целым решением неравенства x 1 яв-
ляется число 0.
![]() Замечание.
Здесь и далее можно придерживаться такого порядка распределения заданий на
классные и домашние. В классе решаются задания а), в), д), ... (через букву), а
дома — оставшиеся задания. Разумеется, если требуется, то из этого правила
делаются исключения.
Замечание.
Здесь и далее можно придерживаться такого порядка распределения заданий на
классные и домашние. В классе решаются задания а), в), д), ... (через букву), а
дома — оставшиеся задания. Разумеется, если требуется, то из этого правила
делаются исключения.
11. а) Решите неравенство x – 1 0. Решение. а) x – 1 0, | +1 x 0 + 1, x 1.
Ответ. (1; + ).
![]() Замечание
1. Формулируя правило «перенесём слагаемое...», учащиеся должны
понимать, что этим кратким объяснением они заменяют фразу «справа и слева
прибавим число...». Чтобы добиться понимания именно второго объяснения, полезно
фиксировать справа от неравенства выполняемое действие (далее будут и другие
действия). Кроме прочего, это поможет учащимся восстанавливать порядок решения
по своим записям.
Замечание
1. Формулируя правило «перенесём слагаемое...», учащиеся должны
понимать, что этим кратким объяснением они заменяют фразу «справа и слева
прибавим число...». Чтобы добиться понимания именно второго объяснения, полезно
фиксировать справа от неравенства выполняемое действие (далее будут и другие
действия). Кроме прочего, это поможет учащимся восстанавливать порядок решения
по своим записям.
![]() Замечание 2. Обратим внимание на форму записи ответа. В учебнике
практически все ответы записаны в виде числовых промежутков. Но если ученик
оставляет ответ в виде x 1 (задание 11, а), то это нельзя
считать ошибкой. В данном пособии мы будем использовать обе формы записи
ответа, что рекомендуем делать и в тетрадях учащихся.
Замечание 2. Обратим внимание на форму записи ответа. В учебнике
практически все ответы записаны в виде числовых промежутков. Но если ученик
оставляет ответ в виде x 1 (задание 11, а), то это нельзя
считать ошибкой. В данном пособии мы будем использовать обе формы записи
ответа, что рекомендуем делать и в тетрадях учащихся.
14. б) Решите неравенство x
+ 1![]() 199. Решение. б) x
+
199. Решение. б) x
+ ![]() 199, | –
199, | – ![]() x
199 –
x
199 – ![]() , x 198
, x 198 ![]() .
.
Ответ. x 198
![]() .
.
16. а) Решите неравенство 2x 4. Решение. а) 2x 4, | : 2 x 2.
Ответ. x 2.
25. а) Решите неравенство 0,3x – 20 0. Решение.
![]()
![]()
![]() а)
0,3x – 20 0, | + 2020\10
а)
0,3x – 20 0, | + 2020\10
0,3x 20, | :
0,3 20 : 0,3 = ![]() = 66= .
= 66= .
0 3,
x 66 ![]() .
.
Ответ. x 66
![]() .
.
![]() Замечание.
Вычисления, необходимые для решения неравенства, можно делать справа от столбца
с записью решения, отделив их вертикальной чертой.
Замечание.
Вычисления, необходимые для решения неравенства, можно делать справа от столбца
с записью решения, отделив их вертикальной чертой.
1.2. Применение графиков к решению неравенств первой степени с одним неизвестным
Перед изучением данного пункта желательно повторить построение графика линейной функции в декартовой системе координат по двум точкам, выполнить задания 26 и 27. Желательно, чтобы учащиеся освоили идею решения неравенств f(x) 0 и f(x) 0 пока для линейной функции f(x). Это поможет в дальнейшем освоить применение графиков к решению неравенств и для других функций f(x). Задания для повторения. При изучении данного пункта можно использовать задания 1010, 1015 (а—в).
29. Решите неравенство, используя график линейной функции:
е) – ![]() x + 5
0; ж) 400x + 100 0.
x + 5
0; ж) 400x + 100 0.
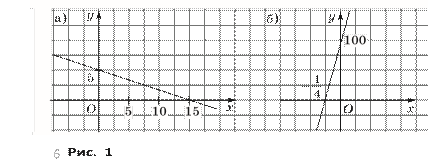
Решение. е) Построим график функции y = –
![]() x
+ 5
x
+ 5
по двум точкам (0; 5) и (15; 0) (рис. 1, а). Определим по графику, что y 0 при всех x 15.
ж) Построим график функции y = 400x + 100 по двум
точкам (0; 100) и (– ![]() ; 0) (рис.
1, б). Определим по графику, что y 0 при всех x –
; 0) (рис.
1, б). Определим по графику, что y 0 при всех x – ![]() .
.
Ответ. е) (15; + ); ж) (– ![]() ;
+ ).
;
+ ).
![]() Замечание.
В задании 29 показано применение прямоугольной декартовой системы
координат (см. рис. 1, а) и прямоугольной системы координат, которая не
является декартовой (см. рис. 1, б). В обоих случаях оси координат
перпендикулярны, начала осей координат совпадают, но в первом случае единичные
отрезки по осям равны, а во втором нет.
Замечание.
В задании 29 показано применение прямоугольной декартовой системы
координат (см. рис. 1, а) и прямоугольной системы координат, которая не
является декартовой (см. рис. 1, б). В обоих случаях оси координат
перпендикулярны, начала осей координат совпадают, но в первом случае единичные
отрезки по осям равны, а во втором нет.
1.3. Линейные неравенства с одним неизвестным
В данном пункте вводится понятие линейного неравенства с одним неизвестным x — это неравенство, левая и правая части которого многочлены степени не выше первой или числа. Поэтому сначала надо повторить понятие степени многочлена, рассмотрев, например, многочлены 3x + 5 (первая степень), 3x2 + 5x – 7 (вторая степень), 0x + 2 (нулевая степень). Напомним, что степень нулевого многочлена, т. е. числа 0, не определена (0 = 0x1 = 0x2 = ...).
Далее вводятся понятия члена неравенства, решения линейного неравенства. В обычном классе будет достаточно, если учащиеся запомнят и будут правильно применять правила 1—4 для решения неравенств, а в классе с углублённым изучением математики учащиеся должны научиться обосновывать эти правила с помощью рассуждений с числовыми значениями (как при решении примера
1 из п. 1.1.).
Итог изучения данного пункта должен быть таков:
Любое линейное неравенство после преобразования будет иметь вид
1) kx + b 0 или 2) kx + b 0.
Если k 0, то неравенство является неравенством первой степени и решается, как показано в п. 1.1.
Если k = 0 и b = 0, то оба неравенства 1) и 2) не имеют решений.
Если k = 0 и b 0, то любое x является решением неравенства 1), а неравенство 2) не имеет решений.
Если k = 0 и b 0, то неравенство 1) не имеет решений, а решением неравенства 2) является любое x.
В классе с углублённым изучением математики надо по дидактическим материалам научить учащихся решать линейные неравенства с параметром (С–2*).
Задания для повторения. При изучении данного пункта можно использовать задание 997.
42. а) Докажите, что данное неравенство равносильно линейному неравенству, и найдите все его решения: x(2 – x) (3 – x)(3 + x).
Решение. Применим к данному неравенству преобразования, в результате каждого из которых получается неравенство, равносильное исходному.
x(2 – x) (3 – x)(3 + x),
2x – x2 9 – x2, | + x2
2x 9, x 4,5.
Линейное неравенство x 4,5 и равносильное ему исходное неравенство имеют множество решений (– ; 4,5). Ответ. (– ; 4,5).
![]() Замечание.
В приведённой выше записи каждое следующее неравенство равносильно всем
предыдущим неравенствам, следовательно, последнее неравенство равносильно
исходному. Здесь мы считаем, что равносильность таких переходов доказана ранее.
Но доказательство можно провести без ссылки на ранее изученные факты с помощью
рассуждений с числовыми значениями.
Замечание.
В приведённой выше записи каждое следующее неравенство равносильно всем
предыдущим неравенствам, следовательно, последнее неравенство равносильно
исходному. Здесь мы считаем, что равносильность таких переходов доказана ранее.
Но доказательство можно провести без ссылки на ранее изученные факты с помощью
рассуждений с числовыми значениями.
1) Пусть число x0 — решение исходного неравенства, тогда верно числовое неравенство
x0(2 – x0) (3 – x0)(3 + x0).
В обеих частях верного числового неравенства применим распределительный закон, получим верное числовое неравенство
2x0 – x02 9 – x02 . | + x02
Справа и слева прибавим одно и то же число x02 , получим новое верное числовое неравенство 2x0 9.
Наконец, разделим обе части верного числового неравенства на 2, получим ещё одно верное числовое неравенство x0 4,5.
Итак, если x0 — решение исходного неравенства, то оно является решением неравенства x 4,5.
2) Проведя рассуждения в обратном порядке, убедимся, что если число x0 — решение неравенства x 4,5, то это число является решением исходного неравенства.
Итак, любое решение исходного неравенства является
решением неравенства x 4,5, а любое решение неравенства x 4,5
является решением исходного неравенства, следовательно, эти неравенства
равносильны. 43. а) Решите неравенство ![]() x – 1 1.
x – 1 1.
3
Решение. ![]() x – 1 1,
| · 3
x – 1 1,
| · 3
3
x – 1 3,| + 1 x 4.
Ответ. (– ; 4).
44. Может ли неравенство первой степени с одним не-известным: а) быть верным при любом значении неизвестного; б) не иметь решений?
Решение. а) Неравенство первой степени с одним неизвестным x имеет вид kx + b 0 или kx + b 0, здесь k 0. Сначала рассмотрим случай k 0.
Неравенство kx + b 0 (k 0) равносильно неравенст-
ву x – ![]() b . Но
это неравенство первой степени с одним неk известным, оно не может быть верным
при любом x. На-
b . Но
это неравенство первой степени с одним неk известным, оно не может быть верным
при любом x. На-
b
пример, число – ![]() – 1
не является его решением. k
– 1
не является его решением. k
Неравенство kx + b 0 (k 0) равносильно неравенст-
ву x – ![]() b . Но
это неравенство первой степени с одним неk известным, оно не может быть верным
при любом x. На-
b . Но
это неравенство первой степени с одним неk известным, оно не может быть верным
при любом x. На-
b
пример, число – ![]() + 1
не является его решением. k
+ 1
не является его решением. k
Аналогично можно рассуждать и при k 0, следовательно, неравенство первой степени не может быть верным при любом значении неизвестного.
б) Из рассуждений в задании а) следует, что ни при каких b и k 0 неравенство первой степени не может не иметь решений.
45. Может ли линейное неравенство с одним неизвестным: а) быть верным при любом значении неизвестного; б) не иметь решений?
Решение. а) Линейное неравенство может быть верным при любом значении x. Приведём пример: неравенство 0x –1 верно при любом значении x.
б) Линейное неравенство может не иметь решений.
Приведём пример: неравенство 0x 1 не имеет решений.
Промежуточный контроль. С–1, С–2*.
1.4. Системы линейных неравенств с одним неизвестным
В данном пункте вводится понятие системы линейных неравенств с одним неизвестным x и объясняется, что значит решить систему (найти множество всех решений данной системы). Перед объяснением нового материала полезно повторить изображения числовых множеств на координатной прямой и нахождение пересечения числовых промежутков. Желательно, чтобы каждый учащийся научился решать системы линейных неравенств.
В классе с углублённым изучением математики надо научить учащихся решать системы линейных неравенств с параметром (С–4*).
Задания для повторения. При изучении данного пункта можно использовать задание 1082.
56. а) Найдите все х, для каждого из которых значение функции у = 2х – 3 больше значения функции у = –х + 4. Решение. Решив неравенство
2х – 3 –х + 4,
получим, что х ![]() . Итак, для
каждого х
. Итак, для
каждого х ![]() значение
значение
функции у = 2х – 3 больше значения функции у = –х + 4.
57. а) Найдите все х, для каждого из которых функции у = 3х и у = 1 + х одновременно принимают отрицательные значения.
Решение. Решив систему неравенств
м3x 0, но1 + x 0,
получим, что её решениями будут все х –1. Итак, для каждого х –1 функции у = 3х и у = 1 + х одновременно принимают отрицательные значения.
Промежуточный контроль. С–3.
1.5. Неравенства, содержащие неизвестное под знаком модуля
В данном пункте разобрано несколько способов решения неравенств, содержащих неизвестное под знаком модуля. Перед объяснением нового материала полезно повторить определение модуля числа, построение графиков функций y = |x|, y = |x – a|, y = |x – a| + b. Далее в учебнике рассматриваются примеры решения неравенств (от простого к сложному):
|x| 3, |x| 5, |x – 3| 4, |2x – 3| 3, |2|x| – 5| 4, |x + 2| 0,5x + 4.
Задания для повторения. При изучении данного пункта можно использовать задания 1075—1078. Решения и комментарии
67. Решите неравенство: а) |2|x| – 3| 5; в) |2|x| – 3| 5.
Решение. а) I способ. Множество решений неравенства |2|x| – 3| 5 есть множество всех x, удовлетворяющих или неравенству 1) 2|x| – 3 5, или неравенству 2) 2|x| – 3 –5. Решив неравенства 1) и 2), надо объединить множества их решений.
Неравенство 1) равносильно неравенству 2|x| 8, множество его решений есть объединение промежутков (– ; –4) и (4; + ).
Неравенство 2) равносильно неравенству 2|x| –2, которое не имеет решений.
Следовательно, все решения исходного неравенства составляют множество (– ; –4)И (4; + ).
II способ. Построив графики функций y = |2|x| – 3| и y = 5, найдём все значения x, для каждого из которых точки первого графика расположены выше точек второго графика (рис. 2, а). Получим то же множество (– ; –4)И И (4; + ).

6 Рис. 2
в) I способ. Множество решений неравенства |2|x| – 3| 5 есть множество всех x, удовлетворяющих двойному неравенству –5 2|x| – 3 5, или, что то же самое, системе неравенств:
мп2 x – –5,3
н (1)
по2 x – 5.3
Система (1) равносильна системе
мп x –1,
![]() нпо x 4. (2)
нпо x 4. (2)
Решением первого неравенства системы (2) является любое число x, множество решений второго неравенства системы (2) есть интервал (–4; 4). Поэтому множество решений системы (2) и равносильного ей неравенства |2|x| – 3| 5 есть интервал (–4; 4).
II способ. Построив графики функций y = |2|x| – 3| и y = 5, найдём все значения x, для каждого из которых точки первого графика расположены ниже точек второго графика (рис. 2, б). Получим то же множество (–4; 4).
Ответ. а) (– ; –4)И (4; + ); в) (–4; 4).
68. Решите неравенство:
а) |x – 3| x + 1; в) |x – 3| x + 1.
Решение. При решении каждого неравенства рассмотрим три случая:
x = 3, x 3, x 3
и объединим все найденные решения.
а) Очевидно, что число 3 не является решением исход-
ного неравенства.
Все остальные решения исходного неравенства являются решениями:
мx 3,
или системы 1) ноx 3 x 1,
мx 3,
или системы 2) но x 3 x 1.
Система 1) не имеет решений, система 2) имеет множество решений (– ; 1).
Следовательно, исходное неравенство имеет множество решений (– ; 1).
в) Очевидно, что число 3 является решением исходного неравенства.
Все решения x 3 исходного неравенства являются решениями:
мx 3,
или системы 1) ноx 3 x 1,
мx 3,
или системы 2) но x 3 x 1.
Система 1) имеет множество решений (3; + ).
Система 2) имеет множество решений (1; 3).
Объединив все найденные решения, получим, что исходное неравенство имеет множество решений (1; + ). Ответ. а) (– ; 1); в) (1; + ).
![]() Замечание.
Тот же результат можно получить, используя графики функций y = |x
– 3| и y = x + 1.
Замечание.
Тот же результат можно получить, используя графики функций y = |x
– 3| и y = x + 1.
69. При каких значениях а неравенство:
а) |2x – a| x + 1 не имеет решений;
б) |3x – a| 3 – 3x имеет множество решений (1; + )?
![]()
![]() Решение.
а) Разделим обе части исходного неравенства на 2, получим равносильное ему
неравенство |x –
Решение.
а) Разделим обе части исходного неравенства на 2, получим равносильное ему
неравенство |x – ![]() a |
x + .
a |
x + .
2
Сначала построим график функции y = g(x),
где g(x) = ![]() x +
x + ![]() ,
он пересекает ось Ox в точке с абсциссой x = –1 (рис. 3, а).
Затем построим график функции y = f(x), где f(x)
= |x –
,
он пересекает ось Ox в точке с абсциссой x = –1 (рис. 3, а).
Затем построим график функции y = f(x), где f(x)
= |x – ![]() a | для
a | для ![]() a = –1, т. е. для a
= –2 (см.
a = –1, т. е. для a
= –2 (см.
2 2
рис. 3, а). В этом случае исходное неравенство не имеет решений, так как для любого x верно неравенство f(x) g(x).
Если a –2, то вершина угла, являющегося графиком функции y = f(x), находится на оси Ox левее точки x = –1

6 Рис. 3

(рис. 3, б). В этом случае исходное неравенство не имеет решений, так как для любого x верно неравенство f(x) g(x).
Если же a –2, то вершина угла, являющегося графиком функции y = f(x), находится на оси Ox правее точки x = –1 (рис. 3, в). В этом случае исходное неравенство имеет решения — все x, заключённые между абсциссами точек пересечения графиков. Находить эти решения не требуется.
Итак, при a –2 неравенство |2x – a| x + 1 не имеет решений.
б) Разделим обе части исходного
неравенства на 3, получим равносильное ему неравенство |x – ![]() a | 1 –
x.
a | 1 –
x.
3
Сначала построим график функции y = g(x), где g(x) = 1 – x, он пересекает ось Ox в точке с абсциссой x = 1 (рис. 4, а).
Затем построим график функции y = f(x), где f(x) =
= |x – ![]() a | для
a | для ![]() a = 1, т. е. для a
= 3 (см. рис. 4, а). В этом
a = 1, т. е. для a
= 3 (см. рис. 4, а). В этом
3 3
случае исходное неравенство имеет множество решений (1; + ), так как для любого x 1 верно неравенство f(x) g(x).
![]() Если a 3, то
вершина угла, являющегося графиком функции y = f(x),
находится на оси Ox левее точки x = 1 (рис. 4, б).
В этом случае имеются решения неравенства f(x) g(x),
не входящие в интервал (1; + ), например числа из промежутка a +
; 1 1щ.
Если a 3, то
вершина угла, являющегося графиком функции y = f(x),
находится на оси Ox левее точки x = 1 (рис. 4, б).
В этом случае имеются решения неравенства f(x) g(x),
не входящие в интервал (1; + ), например числа из промежутка a +
; 1 1щ.
6 2 ы
Если же a 3, то вершина угла, являющегося графиком функции y = f(x), находится на оси Ox правее точки x = 1 (рис. 4, в). В этом случае исходное неравенство f(x) g(x) выполняется для любых x, т. е. множество решений исходного неравенства — интервал (– ; + ).
Итак, лишь при a = 3 неравенство |3x – a| 3 – 3x имеет множество решений (1; + ).
Ответ. а) При a –2; б) при a = 3.
Промежуточный контроль. С–4*.
§ 2. Неравенства второй степени с одним неизвестным
Основное назначение второго параграфа — обучение школьников решению неравенств второй степени с одним неизвестным. Сначала вводится понятие неравенства второй степени с одним неизвестным, показывается применение графиков к решению неравенств. Затем последовательно изучается решение таких неравенств с положительным дискриминантом, дискриминантом, равным нулю, отрицательным дискриминантом. Далее рассматриваются неравенства, сводящиеся к неравенствам второй степени с одним неизвестным. По-прежнему рассматриваются только строгие неравенства.
2.1. Понятие неравенства второй степени с одним неизвестным
В этом пункте вводится понятие неравенства второй степени с одним неизвестным. Эти неравенства называют так потому, что в левой их части стоит многочлен второй степени с неизвестным x. Отметим, что эти неравенства называют ещё квадратными. Вводится необходимая терминология, объясняется, что значит решить неравенство второй степени с одним неизвестным, сообщается, что при решении неравенств второй степени используют утверждения 1—4, сформулированные в п. 1.3. В обычных классах этот факт просто сообщается, в классе с углублённым изучением математики это надо доказать. Здесь же показывается, что любое неравенство второй степени с отрицательным коэффициентом при x2 равносильно неравенству второй степени с положительным коэффициентом при x2, что позволяет в дальнейшем рассматривать только неравенства второй степени с положительным коэффициентом при x2.
Задания для повторения. При изучении данного пункта можно использовать задания 1053, 1054, 1056, 1057.
73. а) Вычислите дискриминант неравенства x2 – 7x + 10 0.
Решение. Вычислим дискриминант неравенства
D = b2 – 4ac = 49 – 4 · 1 · 10 = 9.
76. а) Напишите неравенство с положительным коэф-фициентом при x2, равносильное неравенству –x2 + 5x + 7 0.
Решение. Умножив исходное неравенство на (–1), получим равносильное ему неравенство с положительным коэффициентом при x2:
–x2 + 5x + 7 0, | · (–1) x2 – 5x – 7 0.
77.
а) Напишите неравенство с коэффициентом 1 при x2,
равносильное неравенству – ![]() x2 + 3x
– 5 0.
x2 + 3x
– 5 0.
Решение. Умножив исходное неравенство на (–2), получим равносильное ему неравенство с коэффициентом 1 при x2:
– ![]() x2
+ 3x – 5 0, | · (–2) x2
– 6x + 10 0.
x2
+ 3x – 5 0, | · (–2) x2
– 6x + 10 0.
2.2. Неравенства второй степени с положительным дискриминантом
Перед изучением данного пункта следует повторить изображение числовых промежутков на координатной оси и график квадратичной функции.
В данном пункте рассматривается решение неравенств
1) ax2 + bx + c 0 и 2) ax2 + bx + c 0 при условиях a 0 и D = b2 – 4ac 0. При этих условиях левую часть неравенства можно разложить на множители, а так как a 0, то неравенства 1) и 2) равносильны соответственно неравенствам
(x – x1)(x – x2) 0 и (x – x1)(x – x2) 0, где x1 и x2 — корни трёхчлена ax2 + bx + c.
Учитывая, что случай x1 = x2 невозможен, так как D 0, отметим корни x1 и x2 на координатной оси (считая, что x1 x2), определим знак левой части неравенства на каждом из интервалов (– ; x1), (x1; x2), (x2; + ) и запишем ответ. Отметим, что для a 0 чередование знаков «+, –, +» на интервалах объясняется тем, что:
1) если x x2, то из неравенств x x2 и x2 x1 следует, что x x1. Поэтому (x – x1)(x – x2) 0;
2) если x1 x x2, то из неравенств x x2 и x x1 следует, что (x – x1)(x – x2) 0;
3) если x x1, то из неравенств x x1 и x1 x2 следует, что x x2. Поэтому (x – x1)(x – x2) 0.
Далее показывается применение графиков квадратичной функции к решению неравенств 1) и 2).
Задания для повторения. При изучении данного пункта можно использовать задание 1084 (а, б, д, е).
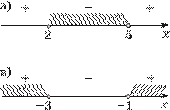 Решения и комментарии
Решения и комментарии82. Составьте неравенство второй степени с одним неизвестным, все решения которого отмечены на рисунке 5 штриховкой.
Решение. а) Неравенство можно записать или в виде
6 Рис. 5 x(x 2 –– 2)(7x x +– 10 5) 0 0. , или в виде
в) Неравенство можно записать или в виде
(x – (–3))(x – (–1)) 0,
или в виде x2 + 4x + 3 0.
88. а) Решите неравенство 0,5x2 – x 0.
Решение. Исходное неравенство равносильно неравенству x2 – 2x 0, которое можно переписать в виде x(x – 2) 0,
множество решений последнего неравенства есть интервал (0; 2). Следовательно, исходное неравенство имеет те же решения.
Ответ. (0; 2).
91. а) Решите неравенство 0,25x2 – 4x + 12 0.
Решение. Исходное неравенство равносильно неравенству x2 – 16x + 48 0, которое можно переписать в виде (x – 4)(x – 12) 0, множество решений последнего неравенства есть объединение промежутков (– ; 4)И (12; + ). Следовательно, исходное неравенство имеет те же решения.
Ответ. (– ; 4)И (12; + ).
![]() Замечание.
Обратим внимание на то, что многие учащиеся решают неравенства строго по
алгоритму: вычислим D, найдём корни трёхчлена x1 и x2,
разложим левую часть неравенства на множители и т. д., но находятся и такие
учащиеся, которые в простых случаях умеют подбирать корни многочлена, используя
теорему, обратную теореме Виета. Вряд ли нужно требовать, чтобы они подробно
следовали описанному выше алгоритму, но что нужно делать обязательно (во
избежание ошибок), так это проверять правильность разложения многочлена на
множители раскрытием скобок.
Замечание.
Обратим внимание на то, что многие учащиеся решают неравенства строго по
алгоритму: вычислим D, найдём корни трёхчлена x1 и x2,
разложим левую часть неравенства на множители и т. д., но находятся и такие
учащиеся, которые в простых случаях умеют подбирать корни многочлена, используя
теорему, обратную теореме Виета. Вряд ли нужно требовать, чтобы они подробно
следовали описанному выше алгоритму, но что нужно делать обязательно (во
избежание ошибок), так это проверять правильность разложения многочлена на
множители раскрытием скобок.
93. а) Укажите все значения x, при каждом из которых квадратичная функция y = x2 + 1,5x – 1 принимает положительные значения; отрицательные значения.
Решение. Квадратный трёхчлен x2 + 1,5x – 1 имеет корни x1 = –2, x2 = 0,5. Функция y = x2 + 1,5x – 1 принимает положительные значения на интервалах (– ; –2) и (0,5; + ); отрицательные значения на интервале (–2; 0,5).
Ответ. y 0 при x (– ; –2)И (0,5; + ); y 0 при x (–2; 0,5).
94. Найдите значение k, при котором неравенство:
а) x2 – 3x + k 0 верно только для x (1; 2);
б) –x2 + x + k 0 верно только для x (–2; 3).
Решение. а) Неравенство x2 – 3x + k 0 верно только для x (1; 2), если x1 = 1 и x2 = 2 — корни квадратного трёхчлена x2 – 3x + k (здесь a = 1 0), т. е. при k = 1 · 2 = 2.
б) Умножив неравенство на (–1), получим равносиль-
ное ему неравенство x2 – x – k 0. Это неравенство верно только для x (–2; 3), если x1 = –2 и x2 = 3 — корни квадратного трёхчлена x2 – x – k, т. е. при –k = –6, k = 6.
Ответ. а) k = 2; б) k = 6.
2.3. Неравенства второй степени с дискриминантом, равным нулю
В данном пункте рассматривается решение неравенств
1) ax2 + bx + c 0 и 2) ax2 + bx + c 0 при условиях a 0 и D = b2 – 4ac = 0, также показывается применение графиков квадратичной функции к решению неравенств 1) и 2).
Учащимся полезно помнить, что если D = 0, то при a 0 квадратный трёхчлен является полным квадратом.
Задания для повторения. При изучении данного пункта можно использовать задание 1055 (а, б, д, е).
98. Существуют ли x, при которых выражение: а) –x2;
в) (2 – x)2 принимает положительное значение?
Решение. а) Так как x2 0 при любом значении x, то –x2 0 при любом значении x. Поэтому нет таких значений x, при которых –x2 0.
в) Так как (2 – x)2 0 при любом значении x, то су-
ществуют такие значения x, при которых (2 – x)2 0. Это все x 2.
101. Решите неравенство:
а) x2 – 4x + 4 0; в) x2 + 10x + 25 0.
Решение. а) Так как x2 – 4x + 4 = (x – 2)2, то исходное неравенство имеет множество решений — все x, кроме x = 2, т. е. (– ; 2)И (2; + ).
в) Так как x2 + 10x + 25 = (x + 5)2 0 при любом значении x, то неравенство x2 + 10x + 25 0 не имеет решений.
Ответ. а) (– ; 2)И (2; + ); б) решений нет.
![]() Замечание.
Желательно также показать решение неравенств с использованием графиков
квадратичной функции.
Замечание.
Желательно также показать решение неравенств с использованием графиков
квадратичной функции.
104. Найдите все значения k, при каждом из которых неравенство:
а) x2 – 24x + k 0 верно при всех x, кроме x = 12;
б) 64x2 +
kx + 9 0 верно при всех x, кроме x = – ![]() .
.
Решение. а) Здесь требуется найти значение k, при котором неравенство можно записать в виде (x – 12)2 0.
Условию задачи удовлетворяет лишь k = 144.
б) Здесь требуется найти значение k, при котором неравенство можно записать в виде
64(x + ![]() )2 0.
)2 0.
Условию задачи удовлетворяет лишь k = 48.
Ответ. а) k = 144; б) k = 48.
105. а) Найдите все x, при каждом из которых неверно неравенство
x2 + 8x + 16 0.
Решение. Решив неравенство
x2 + 8x + 16 0,
получим, что оно верно при всех x, кроме x = –4. Следовательно, это неравенство неверно лишь при x = –4.
Ответ. –4.
2.4. Неравенства второй степени с отрицательным дискриминантом
В данном пункте рассматривается решение неравенств
1) ax2 + bx + c 0 и 2) ax2 + bx + c 0 при условиях a 0 и D = b2 – 4ac 0, также показывается применение графиков квадратичной функции к решению неравенств 1) и 2).
Задания для повторения. При изучении данного пункта можно использовать задания 1086 (а, б), 1088, 1089.
110. а) Решите неравенство 0,2x2 – x + 100 0.
Решение. Так как a = 0,2 0 и D = 1 – 4 · 0,2 · 100 0, то любое число является решением данного неравенства.
Ответ. (– ; + ).
112. Найдите все значения m, при каждом из которых неравенство верно при любом значении x:
а) 2x2 – x + m 0; б) 3x2 + 2x + m 0.
Решение. а) Так как a = 2 0,
то, чтобы неравенство было верно при любом значении x, дискриминант D
должен быть отрицательным: 1 – 4 · 2 · m
0. Следовательно, условию задачи удовлетворяют все значения m ![]() .
.
б) Так как a = 3 0, то, чтобы неравенство было вер-
но при любом значении x,
дискриминант D должен быть отрицательным: 4 – 4 ·
3 · m 0. Следовательно, условию задачи удовлетворяют все
значения m ![]() .
.
Ответ. а) m ![]() ;
б) m
;
б) m ![]() .
.
В классах с углублённым изучением математики следует по дидактическим материалам изучить тему «Неравенства второй степени с параметром», затем провести самостоятельную работу С–6*.
Промежуточный контроль. С–5, С–6*.
2.5. Неравенства, сводящиеся к неравенствам второй степени
В данном пункте рассматривается решение неравенств, обе части которых многочлены и которые равносильными преобразованиями, отмеченными ранее, сводятся к неравенству второй степени.
115. Приведите неравенство:
а) 7 3x – 5x2; б) 2x –3 + 2x2
к виду ax2 + bx + c 0 или ax2 + bx + c 0.
Решение. а) Перенеся все члены неравенства в левую часть, получим неравенство
5x2 – 3x + 7 0,
равносильное исходному.
б) Перенеся все члены неравенства в левую часть, получим неравенство
–2x2 + 2x + 3 0,
равносильное исходному неравенству. Это неравенство можно переписать также в виде 2x2 – 2x – 3 0.
122. Решите неравенство:
![]() а)
x – 1 + 0 2, x2 1; в) (x –
1)(x – 2)
x +
1 – x .
а)
x – 1 + 0 2, x2 1; в) (x –
1)(x – 2)
x +
1 – x .
3 15 5 3
Решение. а) Перенеся все члены неравенства в левую часть, умножив обе части неравенства на 15 и приведя подобные члены многочлена, получим неравенство
3x2 + 5x – 20 0,
равносильное исходному. Так как a = 3 0 и D = 265 0, x1 = – 5 – 265 , x2 = – 5 + 265 , то множество всех реше-
6 6
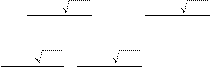 ний исходного неравенства
есть интервал ж
– – 5 265
; – + 5 265 цч . зи 6 6 ш
ний исходного неравенства
есть интервал ж
– – 5 265
; – + 5 265 цч . зи 6 6 ш
в) Перенеся все члены неравенства в левую часть, ум-
ножив обе части неравенства на 15 и приведя подобные члены многочлена, получим неравенство x2 – x – 1 0,
равносильное
исходному. Так как a = 1 0 и D = 5 0,
x1 = ![]() , x2 =
, x2 = ![]() ,
то множество всех решений исход-
,
то множество всех решений исход-
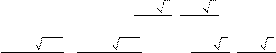 ного неравенства есть
интервал зж1 – 5; 1 + 5 цч .
ного неравенства есть
интервал зж1 – 5; 1 + 5 цч .
и 2 2 ш
Ответ. а) зжи – – 5 6 265 ; – + 5 6 265 цчш ; в) жзи1 – 2 5; 1 + 2 5 чшц .
123. Решите неравенство:
а) |x2 – 6x + 8| 3; в) 4 |x2 – 2x – 4| 11.
Решение. а) I способ. Исходное неравенство равносильно системе неравенств
 мx2 – 6x + 8 3, ноx2 – 6x + –8 3.
мx2 – 6x + 8 3, ноx2 – 6x + –8 3.
Первое неравенство системы имеет множество решений (1; 5), второе неравенство — (– ; + ), следовательно, система, а значит, и равносильное ей исходное неравенство имеют множество решений (1; 5).
II способ. Построив графики функций y = f(x) и y = g(x), где f(x) = |x2 – 6x + 8| и g(x) = 3 (рис. 6), найдём все x, для каждого из которых f(x) g(x), получим множество решений ис6 Рис. 6 ходного неравенства (1; 5).
 в) I способ.
Все решения ис-
в) I способ.
Все решения ис-
ходного неравенства являются или решениями системы
мx2 – 2 – x 4 11,
1) ноx2 – 2 – x 4 4,
или решениями системы
мп–(x2 – 2 – x 4) 11,
2) нпо–(x2 – 2 – x 4) 4.
Решив каждую из систем 1) и 2) и объединив все полученные решения, получим все решения исходного неравенства. 6 Рис. 7
Система 1) имеет множество решений (–3; –2)И (4; 5), система 2) имеет множество решений (0; 2), поэтому исходное неравенство имеет множество решений: (–3; –2)И (0; 2)И (4; 5).
II способ. Построив графики функций y = f(x), y = g(x) и y = h(x), где f(x) = |x2 – 2x – 4|, g(x) = 4 и h(x) = 11 (рис. 7), найдём все x, для каждого из которых g(x) f(x) h(x),
получим множество решений исходного неравенства (–3; –2) И (0; 2)И (4; 5).
Ответ. а) (1; 5); в) (–3; –2)И (0; 2)И (4; 5).
124. Найдите область определения функции:
4 x2 – 4x
а) y = ; г) y = ;
![]() x2 – 4
x2 – 4
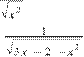 ж) y = .
ж) y = .
Решение. а) Функция определена для любых x таких, что x 0, следовательно, область определения функции есть множество (– ; 0)И (0; + ).
г) Функция определена для любых x, таких, что x2 – 4 0. Решив это неравенство, получим, что область определения функции есть (– ; –2)И (2; + ).
ж) Функция определена для любых x, таких, что 3x – 2 – x2 0. Решив это неравенство, получим, что область определения функции есть множество (1; 2).
Ответ. а) (– ; 0)И (0; + ); г) (– ; –2)И (2; + ); ж) (1; 2).
Промежуточный контроль. К–1.
§ 3. Рациональные неравенства
Основное назначение этого параграфа — обучение школьников решению рациональных неравенств и их систем. Сначала рассматривается метод интервалов решения неравенств вида
A(x) 0 и A(x) 0, (1) где A(x) — многочлен относительно x. Затем показывается, что решение любого строгого рационального неравенства сводится к решению неравенства вида (1). После этого рассматриваются системы рациональных неравенств.
Все неравенства, приводимые в параграфах 1—2 и в пунктах 3.1—3.3, являются строгими. В п. 3.4 рассматривается решение нестрогих неравенств. В заключение параграфа разбирается способ применения замены неизвестного при решении рациональных неравенств.
Отметим, что тема «Рациональные неравенства» в программу 9 общеобразовательного класса не входит, поэтому в обычных классах пункты 3.1—3.4 можно изучать только применительно к линейным неравенствам и неравенствам второй степени и решать задания, которые не отмечены звёздочкой. Материал этот достаточно прост, а его осознание существенно расширит представления школьников о решении неравенств, позволит сформировать необходимые умения по рассматриваемой теме.
В классе с углублённым изучением математики следует изучить весь материал полностью, добавив к этому изучение по дидактическим материалам (раздел I) содержания работ 7—12. Это поможет учащимся быть более успешными в различных олимпиадах и конкурсах.
3.1. Метод интервалов
В этом пункте рассматривается решение неравенств вида
1) A(x) 0 и 2) A(x) 0,
где А(х) — многочлен относительно х.
Для решения любого из неравенств 1) и 2) надо найти корни многочлена А(х) и отметить их на координатной оси, в каждом из получившихся интервалов определить знак многочлена А(х). Тогда объединение всех интервалов, где многочлен положителен, составит множество решений неравенства 1), а объединение всех интервалов, где многочлен отрицателен, составит множество решений неравенства 2).
В примере 1 подробно разбирается решение этим способом неравенства
(х + 2)(х – 3)(х4 + 1) 0,
для решения которого надо «вручную» определить знаки многочлена на каждом из трёх интервалов (– ; –2), (–2; 3), (3; + ).
Далее отмечается, что во многих случаях процесс решения неравенства можно упростить, действуя по правилу, называемому методом интервалов.
В качестве примера рассматривается многочлен
А(х) = (х – х1)(х – х2) ... (х – хn),
где х1 х2 ... хn.
Для вывода правила проводятся обоснованные рассуждения, опирающиеся на свойство двучлена x – x0, которое заключается в следующем: двучлен x – x0 равен нулю при x = x0, положителен при x x0 и отрицателен при x x0.
Далее на оси x отмечаются числа х1, х2, ..., хn, затем над правым интервалом ставится знак «+» и, начиная с него, чередуются знаки «+», «–», «+», «–», ... над интервалами справа налево; затем записывается ответ. Методом интервалов решается пример 2.
Затем обсуждается необязательный для обычных классов пример 3 решения неравенства
(х – 1)3(х – 2)2(х – 3)4(х – 4) 0
и формулируется общий метод интервалов для решения неравенств вида 1) или 2), если
А(х) = (x – x1 ) (k1 x – x2 )k2 ... (x – xm )km ,
причём х1 х2 ... хm и хотя бы одно из чисел ki 2.
На оси x отмечаются числа х1, х2, ..., хm, затем над правым интервалом ставится знак «+», затем при переходе через любое xi сохраняется знак, если ki чётно, и меняется знак, если ki нечётно.
Далее этим методом решается пример 4.
В обычных классах достаточно, если учащиеся запомнят метод интервалов и научатся его применять. В классах с углублённым изучением математики учащиеся должны уметь обосновывать общий метод интервалов, а также метод решения неравенств 1) и 2) для
А(х) = c x( – x1 )k1 ... (x – xm)km (x2 + p x1 + q1 ) ...
... (x2 + p xn + qn) ,
где c 0 и квадратные трёхчлены имеют отрицательные дискриминанты, и применять их для решения неравенств. Задания для повторения. При изучении данного пункта можно использовать задание 1083 (а, в, д).
134. а) Решите неравенство методом интервалов:
(x – 1)(x – 3)(x – 5) 0.
Решение. Отметим корни многочлена[1] 1, 3, 5 на координатной оси и расставим знаки по методу интервалов. Решениями неравенства будут значения x из тех интервалов, над которыми стоит знак «+» (рис. 8).
Итак, исходное неравенство имеет множество решений (1; 3)И (5; + ).
Ответ. (1; 3)И (5; + ).
135. а) Решите неравенство методом интервалов:
(x2 + x)(5x – 5) 0.
Решение. Сначала разложим на линейные множители многочлен, записанный в левой части неравенства 5(x + 1)(x – 0)(x – 1) 0.
Отметим корни многочлена –1, 0, 1 на координатной оси и расставим знаки по методу интервалов. Решениями неравенства будут значения x из тех интервалов, над которыми стоит знак «–» (рис. 9).
Итак, исходное неравенство имеет множество решений (– ; –1)И (0; 1).
Ответ. (– ; –1)И (0; 1).
139. к) Решите неравенство методом интервалов:
(–x2 + 6x – 10)(x2 – 5x + 6)(x – 2) 0.
Решение. Разложив на множители трёхчлен
x2 – 5x + 6, перепишем неравенство в виде
–(x2 – 6x + 10)(x – 2)2(x – 3) 0.
Это неравенство равносильно неравенству
(x2 – 6x + 10)(x – 2)2(x – 3) 0.
Так как дискриминант трёхчлена x2 – 6x + 10 отрицательный, то этот трёхчлен не имеет корней. Его коэффициент при старшем члене положительный, поэтому при любом значении x этот трёхчлен принимает положительные значения. К тому же выводу можно прийти другим путём: x2 – 6x + 10 = (x – 3)2 + 1 0 при любом значении x.
![]()
 6
Рис.
9
6
Рис.
9
6 Рис. 10 6 Рис. 11
Отметим корни многочлена 2 и 3 на координатной оси, определим знаки многочлена на интервалах, получим, что знак «–» стоит над двумя интервалами (– ; 2) и (2; 3) (рис. 10).
Итак, исходное неравенство имеет множество решений (– ; 2)И (2; 3).
Ответ. (– ; 2)И (2; 3).
140. а) При каких значениях а множество решений неравенства (х – 3)(х – 5)(х – а)2 0 состоит из двух интервалов? из трёх интервалов?
Решение. 1) Если a 5, то многочлен имеет три корня: 3, 5 и a. Отметим эти корни многочлена на координатной оси и, применив общий метод интервалов, определим знак многочлена на интервалах (рис. 11). Получим, что множество решений исходного неравенства состоит из трёх интервалов.
2) Если a = 5, то исходное неравенство перепишется в виде
(х – 3)(х – 5)3 0. (1)
3) Если 3 a 5, то многочлен имеет три корня: 3, a и 5. Отметим эти корни многочлена на координатной оси и, применив общий метод интервалов, определим знак многочлена на интервалах (рис. 13). Получим, что множество решений неравенства состоит из двух интервалов.
4) Если a = 3, то исходное неравенство перепишется в виде
(х – 3)3(х – 5) 0. (2)
Отметим корни 3 и 5 многочлена на координатной оси и, применив общий метод интервалов, определим знак многочлена на интервалах (см. рис. 12). Получим, что множество решений неравенства (2), а значит, и исходного неравенства состоит из двух интервалов.
![]()
6 Рис. 12 6 Рис. 13
6 Рис. 14 6 Рис. 15
5) Если a 3, то многочлен имеет три корня: a, 3 и 5. Отметим эти корни многочлена на координатной оси и, применив общий метод интервалов, определим знак многочлена на интервалах (рис. 14). Получим, что множество решений исходного неравенства состоит из трёх интервалов.
Объединяя все рассмотренные случаи, запишем ответ.
Ответ. Если 3 a 5, то множество решений исходного неравенства состоит из двух интервалов; если a 3 или a 5, то множество решений исходного неравенства состоит из трёх интервалов.
3.2. Решение рациональных неравенств
В данном пункте, пользуясь понятием равносильности неравенств, решение любого строгого рационального неравенства сводится к решению неравенства A(x) 0 или A(x) 0, где A(x) — многочлен относительно x.
Задания для повторения. При изучении данного пункта можно использовать задания 1092 (а—г), 1093 (а, б), 1094.
Решения и комментарии 146. Решите неравенство:
![]() а)
а) ![]() (x – 1)(x + 2) 0; в) 0.
(x – 1)(x + 2) 0; в) 0.
x – 3
Решение. а) Исходное неравенство равносильно неравенству
(x – (–2))(x – 1)(x – 3) 0. (1)
Отметим корни многочлена –2, 1, 3 на координатной оси и, применив метод интервалов, расставим знаки «+» и «–» над полученными интервалами (рис. 15).
Получим, что неравенство (1), а значит, и равносильное ему исходное неравенство имеют множество решений (–2; 1)И (3; + ).
6 Рис. 16 6 Рис. 17
в) Исходное неравенство равносильно неравенству
(x – (–8))(x – (–1))(x – 5)(x – 7) 0. (2)
Отметим корни многочлена –8, –1, 5, 7 на координатной оси и, применив метод интервалов, определим знаки многочлена на интервалах (рис. 16). Получим, что неравенство (2), а значит, и равносильное ему исходное неравенство имеют множество решений (– ; –8)И (–1; 5)И И (7; + ).
Ответ. а) (–2; 1)И (3; + ); в) (– ; –8)И (–1; 5)И И (7; + ).
150. а) Решите
неравенство ![]() x22 – + x 2 0.
x22 – + x 2 0.
x – 7 + x 6
Решение. Исходное неравенство равносильно неравенству
(x2 – x + 2)(x – 1)(x – 6) 0. (3)
Получим, что неравенство (3), а значит, и равносильное ему исходное неравенство имеют множество решений (1; 6).
Ответ. (1; 6).
x2 – 6x + 4 0.
153. а) Решите
неравенство ![]()
x – 1
Решение. Исходное неравенство равносильно неравенству
![]()
![]() (x – 3 – 5())(x – 1)(x – (3 + 5)) 0. (4)
(x – 3 – 5())(x – 1)(x – (3 + 5)) 0. (4)
![]() Отметим
корни многочлена 3 – 5 , 1 и 3
+ 5 на координатной оси, применив
метод интервалов, расставим знаки «+» и «–» над полученными интервалами (рис.
18).
Отметим
корни многочлена 3 – 5 , 1 и 3
+ 5 на координатной оси, применив
метод интервалов, расставим знаки «+» и «–» над полученными интервалами (рис.
18).
![]()
![]() Получим, что нераве нство (4), а
значит, и равносильное ему исходное неравенство имеют множество решений (3 –
5 ; 1)И (3
+ 5 ; + ).
Получим, что нераве нство (4), а
значит, и равносильное ему исходное неравенство имеют множество решений (3 –
5 ; 1)И (3
+ 5 ; + ).
Ответ.
(3 – 5 ; 1)И ![]()
И (3 + 5 ; + ).
6 Рис. 18
![]()
6 Рис. 19 6 Рис. 20
155. Решите неравенство:
(x + 1) (2 x – 2)
а) ![]() 2 0; г)
2 0; г) ![]() (x + x1 + )(x + 3 2)3 0.
(x + x1 + )(x + 3 2)3 0.
(x + 3)
Решение. а) Исходное неравенство равносильно неравенству
(x + 3)2(x + 1)2(x – 2) 0. (5)
Отметим корни многочлена –3, –1 и 2 на координатной оси, применив общий метод интервалов, расставим знаки «+» и «–» над полученными интервалами (рис. 19).
Получим, что неравенство (5), а значит, и равносильное ему исходное неравенство имеют множество решений (2; + ).
г) Исходное неравенство равносильно неравенству
(x + 3)(x + 2)3(x + 1) 0. (6)
Отметим корни многочлена –3, –2 и –1 на координатной оси, применив общий метод интервалов, расставим знаки «+» и «–» над полученными интервалами (рис. 20).
Получим, что неравенство (6), а значит, и равносильное ему исходное неравенство имеют множество решений (–3; –2)И (–1; + ).
Ответ. а) (2; + ); г) (–3; –2)И (–1; + ).
156. а) При каких значениях а множество решений
неравенства ![]() (x + 5)(x – 2 3) 0 состоит из двух
интервалов?
(x + 5)(x – 2 3) 0 состоит из двух
интервалов?
(x – a)
из трёх интервалов?
Решение. При любом значении a исходное неравенство равносильно неравенству
(x + 5)(x – 3)(x – a)2 0. (7)
1) Если a 3, то многочлен имеет три корня: –5, 3 и a. Отметим эти корни на координатной оси и, применяя общий метод интервалов, расставим знаки «+» и «–» над полученными интервалами (рис. 21).
![]() Получим, что
множество решений неравенства (7), а значит, и исходного неравенства состоит из
трёх интервалов.
Получим, что
множество решений неравенства (7), а значит, и исходного неравенства состоит из
трёх интервалов.
Рис. 21
![]()
6 Рис. 22 6 Рис. 23
2) Если a = 3, то исходное неравенство перепишется в виде
(x + 5)(x – 3)3 0. (8)
Многочлен имеет два корня: –5 и 3. Отметим эти корни на координатной оси и, применяя общий метод интервалов, расставим знаки «+» и «–» над полученными интервалами (рис. 22).
Получим, что множество решений неравенства (8), а значит, и исходного неравенства состоит из двух интервалов.
3) Если –5 a 3, то многочлен имеет три корня: –5, a и 3. Отметим эти корни на координатной оси и, применяя общий метод интервалов, расставим знаки «+» и «–» над полученными интервалами (рис. 23).
Получим, что множество решений неравенства (7), а значит, и исходного неравенства состоит из двух интервалов.
4) Если a = –5, то исходное неравенство перепишется в виде
(x + 5)3(x – 3) 0. (9)
Многочлен имеет два корня: –5 и 3. Отметим эти корни на координатной оси и, применяя общий метод интервалов, расставим знаки «+» и «–» над полученными интервалами (см. рис. 22).
Получим, что множество решений неравенства (9), а значит, и исходного неравенства состоит из двух интервалов.
![]() 5) Если a –5,
то многочлен имеет три корня: a, –5 и 3. Отметим эти корни на
координатной оси и, применяя общий метод интервалов, расставим знаки «+» и «–»
над полученными интервалами (рис. 24). Получим, что множество решений
неравенства (7), а значит, и исходного неравенства состоит из трёх интервалов.
5) Если a –5,
то многочлен имеет три корня: a, –5 и 3. Отметим эти корни на
координатной оси и, применяя общий метод интервалов, расставим знаки «+» и «–»
над полученными интервалами (рис. 24). Получим, что множество решений
неравенства (7), а значит, и исходного неравенства состоит из трёх интервалов.
Объединяя все рассмотренные выше случаи, можно запи- Рис. 24 сать ответ. 6
Ответ. а) Если –5 a 3, то множество решений исходного неравенства состоит из двух интервалов; если a –5 или a 3, то множество решений исходного неравенства состоит из трёх интервалов.
Промежуточный контроль. С–7, С–8*.
3.3. Системы рациональных неравенств
Данный пункт должен быть изучен в каждом классе — обычном и с углублённым изучением математики, так как здесь рассматриваются практически только задания с квадратными неравенствами. Системы рациональных неравенств, отмеченные звёздочкой, не сложны, но решение таких рациональных неравенств считается необязательным для общеобразовательных классов.
Задания для повторения. При изучении данного пункта можно использовать задание 1096.
162. а) Решите систему неравенств
мп(x – 5)(x + 1) 0, н 2 по(x – 10) 0.
Решение. Первое неравенство системы имеет множество решений (– ; –1)И (5; + ). Второе неравенство системы имеет множество решений (– ; 10)И (10; + ). Общей частью этих множеств является множество (– ; –1)И
И (5; 10)И (10; + ). Это и есть множество решений системы неравенств (рис. 25).
Ответ. (– ; –1)И (5; 10)И (10; + ).
163. а) Решите систему неравенств
пм(x – 2)(x – 3) 0,
![]() x + 2 0.
x + 2 0.
по(x – 4)(x + 4)
Решение. Исходная система неравенств равносильна системе
мп(x – 2)(x – 3) 0,
нпо(x + 4)(x + 2)(x – 4) 0 (1)
Первое неравенство системы (1) имеет множество решений (– ; 2)И (3; + ) (рис. 26, а). Второе неравенство системы неравенств (1) имеет множество решений
![]() (–4; –2)И (4; + ) (рис. 26, б). Множество решений системы
неравенств (1), а значит, и равносильной ей исходной системы неравенств есть
(–4; –2)И И (4; + ) (рис. 26, в).
(–4; –2)И (4; + ) (рис. 26, б). Множество решений системы
неравенств (1), а значит, и равносильной ей исходной системы неравенств есть
(–4; –2)И И (4; + ) (рис. 26, в).
Рис. 25 Ответ. (–4; –2)И (4; + ).
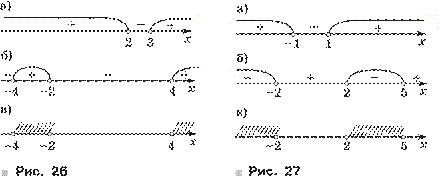
![]() 164. в) Решите
систему неравенств мпнпxxx222 – + – 514 00,.
164. в) Решите
систему неравенств мпнпxxx222 – + – 514 00,.
оx – 4
Решение. Исходная система неравенств равносильна системе
мп(x + 1)(x – 1)(x2 + 4) 0,
н (2) по(x + 2)(x – 2)(x – 5) 0.
Первое неравенство системы (2) имеет множество решений (– ; –1)И (1; + ) (рис. 27, а). Второе неравенство системы (2) имеет множество решений (– ; –2)И (2; 5) (рис. 27, б). Множество решений системы (2), а значит, и равносильной ей исходной системы есть (– ; –2)И (2; 5) (рис. 27, в).
Ответ. (– ; –2)И (2; 5).
Промежуточный контроль. С–9.
3.4. Нестрогие неравенства
Данный пункт должен быть изучен в каждом классе — и в обычном, и с углублённым изучением математики. В обычных классах желательно проработать по дидактическим материалам п. 10 и провести самостоятельную работу С–10.
В классах с углублённым изучением математики следует рассмотреть ещё задания со звёздочкой и проработать по дидактическим материалам п. 11 и провести самостоятельную работу С–11.
Отметим важную особенность решения нестрогих неравенств. Для решения, например, неравенства A(x) 0 предлагается сначала решить уравнение A(x) = 0, затем строгое неравенство A(x) 0, после чего объединить все найденные решения уравнения и неравенства. Такой подход обеспечивает осознание учеником отличия нестрогого неравенства от строгого, понимание, что умение решать нестрогое неравенство опирается на умения решать уравнения и решать строгие неравенства.
Если же учащиеся решают строгие и нестрогие неравенства по одной и той же схеме, закрашивая во втором случае точки на координатной оси и ставя квадратные скобки вместо круглых, то такое следование единому алгоритму для разных по своей природе неравенств нередко приводит к ошибкам.
Особое внимание следует уделить тому, что, например,
![]() x –
1 0 не равносильно неравенству
неравенство
x –
1 0 не равносильно неравенству
неравенство
x – 5
(x – 1)(x – 5) 0, так как число 5, обращающее знаменатель дроби в нуль, не является решением первого неравенства, но является решением второго. Поэтому нельзя начинать решение нестрогого неравенства с перехода к равносильному неравенству с многочленом, как это делалось при решении строгих неравенств.
После изучения нестрогих неравенств можно использовать для контроля знаний или для повторения через некоторое время тесты Т–1, Т–2 из сборника тематических тестов.
Задания для повторения. При изучении данного пункта можно использовать задания 1083 (г, д, е), 1084 (в, г), 1085 (в, г), 1086 (в, г), 1092 (д, е).
167. а) Решите неравенство
x2 – 12x + 32 0.
Решение. Сначала решим уравнение
x2 – 12x + 32 = 0, (1) оно имеет корни x1 = 4 и x2 = 8 (рис. 28, а).
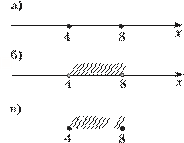 Затем
решим неравенство x2 – 12x + 32
0, (2)
Затем
решим неравенство x2 – 12x + 32
0, (2)
оно имеет множество решений
(4; 8) (рис. 28, б).
Объединив множества решений уравнения (1) и неравенства (2), получим, что множество решений исходного неравенства есть отрезок [4; 8] (рис. 28, в).
Рис. 28 Ответ. [4; 8].
1 0 .
171. а) Решите неравенство
x – 1
![]() Решение. Очевидно,
что уравнение 1
= 0 корней не x – 1
Решение. Очевидно,
что уравнение 1
= 0 корней не x – 1
имеет. Решим неравенство ![]() 1 0,
оно имеет множество
1 0,
оно имеет множество
x – 1
решений (1; + ).
Следовательно, множество решений исходного неравенства есть интервал (1; + ).
Ответ. (1; + ).
172.
а) Решите неравенство ![]() x2 – 24x + 3 0. x – 9
x2 – 24x + 3 0. x – 9
Решение. Сначала решим уравнение
x2 – 4x + 3
![]() 2 = 0, (3)
2 = 0, (3)
x – 9
оно имеет единственный корень x1 = 1 (рис. 29, а). Затем решим неравенство
x2 – 4x + 3
![]() 2 0, (4)
2 0, (4)
x – 9
оно равносильно неравенству (x + 3)(x – 1)(x – 3)2 0 и имеет множество решений (– ; –3)И (1; 3)И (3; + )
(рис. 29, б).
Объединив множества решений уравнения (3) и неравенства (4), получим, что множество решений исходного неравенства есть (– ; –3)И [1; 3)И (3; + ) (рис. 29, в). Ответ. (– ; –3)И [1; 3)И (3; + ).
![]() Замечание.
Стоит обратить внимание учащихся на необходимость следования указанному в п.
3.2 алгоритму решения рациональных неравенств. Например, иногда учащиеся
находят более экономное «решение» неравенст-
Замечание.
Стоит обратить внимание учащихся на необходимость следования указанному в п.
3.2 алгоритму решения рациональных неравенств. Например, иногда учащиеся
находят более экономное «решение» неравенст-
2
ва, чем приведённое выше. Они
неравенство ![]() x – 24x + 3
0
x – 24x + 3
0
x – 9
переписывают в виде ![]() 0 , сокращают алгебра-
0 , сокращают алгебра-
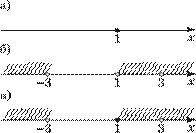
![]() ическую
дробь в левой части x – 1 0 , а занеравенства:
ическую
дробь в левой части x – 1 0 , а занеравенства:
x + 3
тем решают полученное неравенство, считая, что оно равносильно исходному. Между тем полученное неравенство не равносильно исходному, так как имеет решение 3, которого исходное неравенство
не имеет. Рис. 29
6
175. Решите неравенство:
а) |x2 – 6x + 7| 2; б) |x2 – 9x + 19| 1.
Решение. а) Все решения исходного неравенства являются или решениями неравенства 1) x2 – 6x + 7 2, или решениями неравенства 2) x2 – 6x + 7 –2.
Неравенство 1) имеет множество решений (– ; 1]И И [5; + ).
Неравенство 2) равносильно неравенству
(x – 3)2 0,
оно имеет единственное решение x1 = 3.
![]() Объединив множества
решений неравенств 1) и 2), получим, что множество решений исходного
неравенства есть (– ;
1]И
Объединив множества
решений неравенств 1) и 2), получим, что множество решений исходного
неравенства есть (– ;
1]И
6 Рис. 30 И {3}И [5; + ) (рис. 30).
б) Все решения исходного
неравенства являются и решениями неравенства x2 – 9x + 19 1,
и решениями неравенства x2 – 9x + 19 –1,
т. е. исходное неравенство равносильно системе неравенств
 мx2 – 9x + 19 1,
мx2 – 9x + 19 1,
ноx2 – 9x + 19 – 1. (5)
Первое неравенство системы перепишем в виде
(x – 3)(x – 6) 0,
оно имеет множество решений [3; 6] (рис. 31, а).
Второе неравенство системы перепишем в виде
6 Рис. 31 (x – 4)(x – 5) 0,
оно имеет множество решений (– ; 4]И [5; + ) (рис. 31, б).
Система (5) и равносильное ей исходное неравенство имеют множество решений [3; 4]И [5; 6] (рис. 31, в).
Ответ. а) (– ; 1]И {3}И [5; + ); б) [3; 4]И [5; 6].
178. д) Решите систему неравенств
м(x + 1)(x2 – – x 6) 0, ппн(x – 1)(x2 – 5 + x 6) 0, ппо(x + 3)(x2 – 4) 0.
 Решение. Перепишем
систему в виде
Решение. Перепишем
систему в виде
м(x + 2)(x + 1)(x – 3) 0, пн(x – 1)(x – 2)(x – 3) 0, (6) по(x + 3)(x + 2)(x – 2) 0.
Первое неравенство системы имеет множество решений [–2; –1]И [3; + ) (рис. 32, а). Второе неравенство системы имеет множество решений (– ; 1]И [2; 3] (рис. 32, б).
Третье неравенство системы 6 Рис. 32 имеет множество решений
[–3; –2]И [2; + ) (рис. 32, в). Общая часть этих трёх множеств состоит из двух чисел –2 и 3 (рис. 32, г).
Ответ. {–2; 3}.
1. (Подготовка к К–2.) Докажите, что для любых чисел x справедливо неравенство:
а) x2 – 20x + 101 0;
б) x2 + 2x – 2|x + 1| –2.
Найдите все значения x, для которых левая часть неравенства б) равна правой.
Решение. а) Перепишем исходное неравенство, выделив полный квадрат в левой его части:
(x – 10)2 + 1 0,
так как (x – 10)2 0 для любого x, то полученное неравенство справедливо для любого x, что и доказывает исходное неравенство.
б) Перепишем исходное неравенство в виде
|x + 1|2 – 2|x + 1| + 1 0,
или в виде
(|x + 1| – 1)2 0.
Так как последнее неравенство справедливо для любого числа x, то и исходное неравенство справедливо для любого числа x.
Левая часть исходного неравенства равна правой, если |x + 1| = 1, т. е. при x = 0 и при x = –2.
Промежуточный контроль. С–10, С–11*, Т–3, К–2 (обычные классы).
3.5. Замена неизвестного при решении неравенств
В данном пункте на примерах показывается решение рациональных неравенств способом замены неизвестного. Этот пункт не является обязательным для обычных классов, но в классах с углублённым изучением математики он должен быть хорошо проработан, так как замена неизвестного довольно часто применяется при решении более сложных задач.
В классах с углублённым изучением математики надо проработать по дидактическим материалам п. 12 и провести самостоятельную работу С–12, а затем контрольную работу К–2.
179. Решите неравенство:
а) (x – 3)4 – 5(x – 3)2 + 4 0;
в) (x + 1)4 – 5(x + 1)2 + 4 0.
Решение. а) Введя новое неизвестное t = (x – 3)2, перепишем исходное неравенство в виде
t2 – 5t + 4 0. (1)
Неравенству (1) удовлетворяют все t, такие, что 1 t 4, поэтому множество решений исходного неравенства есть множество решений двойного неравенства:
1 (x – 3)2 4. (2)
Двойное неравенство (2) имеет множество решений (1; 2)И (4; 5), следовательно, и исходное неравенство имеет то же множество решений.
в) Введя новое неизвестное t = (x + 1)2, перепишем ис-
ходное неравенство в виде
t2 – 5t + 4 0. (3)
Неравенству (3) удовлетворяют все t, такие, что t 1 или t 4, поэтому все решения исходного неравенства являются или решениями неравенства 1) (x + 1)2 1, или решениями неравенства 2) (x + 1)2 4.
Множество решений неравенства 1) есть [–2; 0], а множество решений неравенства 2) есть (– ; –3]И [1; + ).
Следовательно, множество решений исходного неравенства есть (– ; –3]И [–2; 0]И [1; + ).
![]() Ответ. а) (1; 2)И (4; 5); в) (– ; –3]И [–2; 0]И [1; + ). 181. а) Решите неравенство x2 + 4x – – 2 2 15 0. x + 4x
Ответ. а) (1; 2)И (4; 5); в) (– ; –3]И [–2; 0]И [1; + ). 181. а) Решите неравенство x2 + 4x – – 2 2 15 0. x + 4x
Решение. Введя новое неизвестное t = x2 + 4x, перепишем исходное неравенство в виде
![]() t – 2 – 15 0 . (4) t
t – 2 – 15 0 . (4) t
Неравенству (4) удовлетворяют все t, такие, что t –3, а также все t, такие, что 0 t 5, поэтому все решения исходного неравенства есть или решения неравенства 1) x2 + 4x –3, или решения двойного неравенства 2) 0 x2 + 4x 5.
Неравенство 1) имеет множество решений [–3; –1], двойное неравенство 2) имеет множество решений
[–5; –4)И (0; 1], следовательно, исходное неравенство имеет множество решений [–5; –4)И [–3; –1]И (0; 1]. Ответ. [–5; –4)И [–3; –1]И (0; 1].
182. а) Решите неравенство |x + 4|2 – 7|x + 4| 0.
Решение. а) Введя новое неизвестное t = |x + 4|, перепишем исходное неравенство в виде
t2 – 7t 0. (5)
Неравенству (5) удовлетворяют лишь все t, такие, что t 0, а также все t, такие, что t 7, поэтому все решения исходного неравенства есть или решения неравенства 1) |x + 4| 0, или решения неравенства 2) |x + 4| 7.
Неравенство 1) имеет единственное решение x1 = –4, неравенство 2) имеет множество решений (– ; –11]И
И [3; + ), следовательно, исходное неравенство имеет множество решений (– ; –11]И {–4}И [3; + ). Ответ. (– ; –11]И {–4}И [3; + ).
 мx2 – 3 x + 2 0, п
мx2 – 3 x + 2 0, п
184. а) Решите систему неравенств н 10 0.
по3 – x
Решение. Введя новое неизвестное t = |x|, перепишем исходную систему неравенств в виде
мпt2 – 3t + 2 0,
н ![]() 10 0. (6)
10 0. (6)
по3 – t
Системе (6) удовлетворяют лишь все t, такие, что t 1, а также все t, такие, что 2 t 3, поэтому все решения исходной системы есть или решения неравенства 1) |x| 1, или решения двойного неравенства 2) 2 |x| 3.
Неравенство 1) имеет множество решений (–1; 1), неравенство 2) имеет множество решений (–3; –2)И (2; 3), следовательно, исходное неравенство имеет множество решений (–3; –2)И (–1; 1)И (2; 3).
Ответ. (–3; –2)И (–1; 1)И (2; 3).
Промежуточный контроль. С–12*, С–13*.
Дополнения к главе 1
1. Доказательство числовых неравенств
В данном пункте сначала приводятся известные ещё из курса 8 класса пять свойств числовых неравенств, которые в дальнейшем будут применяться при доказательстве других числовых неравенств. Далее разбирается много примеров на доказательство числовых неравенств, в том числе доказательство неравенства между средним арифметическим и средним геометрическим двух положительных чисел и доказательство неравенства x + 1 2 (для x > 0). x
Следует предостеречь учащихся от ошибочных доказательств, например от такого «доказательства»:
Докажем, что для любых чисел a и b справедливо неравенство
![]() a2 b2 ab. (1)
a2 b2 ab. (1)
2
Из неравенства (1) следует неравенство
a2 + b2 2ab. (2)
Из неравенства (2) следует неравенство a2 + b2 – 2ab 0, которое можно переписать в виде
(a – b)2 0. (3)
Так как неравенство (3), очевидно, справедливо (квадрат числа неотрицателен), то справедливо и неравенство
(1).
Ученики обычно удивляются, что приведённое «доказательство» доказательством неравенства (1) не является. На самом деле доказано, что из справедливости неравенства (1) следует справедливость неравенства (3), но ведь не требовалось доказать, что (a – b)2 0.
Приведённое рассуждение всего лишь «анализ», помогающий найти путь доказательства. Настоящее доказательство требует проведения рассуждений в обратном порядке: рассмотрим неравенство, справедливое для любых чисел a и b:
(a – b)2 0,
применим формулу квадрата разности:
a2 – 2ab + b2 0,
в полученном верном неравенстве прибавим к каждой части число 2ab, получим новое верное неравенство a2 + b2 2ab.
Разделив обе части неравенства на положительное число 2, получим верное неравенство
![]() a2 + b2 ab,
a2 + b2 ab,
2
что и требовалось доказать.
Доказательство может содержать приведённые выше шаги:
2 2
![]() a + b ab, (4)
a + b ab, (4)
2
a2 + b2 2ab, a2 – 2ab + b2 0,
(a – b)2 0, (5)
но тогда оно должно заканчивается фразой «рассуждая в обратном порядке, из справедливости неравенства (5) получим справедливость неравенства (4), что и требовалось доказать».
Данный пункт обязательно изучается в классах с углублённым изучением математики, но и в обычном классе было бы полезно показать учащимся доказательства нескольких неравенств.
Как отмечается в учебнике, не существует общего метода доказательства неравенств. Поэтому при доказательстве каждого данного неравенства нужно сделать несколько попыток доказательств разными способами и в конце концов выбрать то доказательство, справедливость которого не вызывает сомнений. При этом иногда помогает «анализ» возможного доказательства, как в приведённом выше примере.
185. Докажите неравенство, где a, b, c — действительные числа:
б) a3 + b3 a2b + ab2 (a + b 0);
г) ![]() 1 +
a –2 (a
0). a
1 +
a –2 (a
0). a
Доказательство. б) Приведём доказательство неравенства, не проводя «анализ». Рассмотрим разность A = a3 + b3 – (a2b + ab2). Так как A = a3 – a2b + b3 – ab2 = = a2(a – b) – b2(a – b) = (a – b)(a2 – b2) = (a – b)2(a + b), то, учитывая, что (a – b)2 0 для любых a и b и по условию a + b 0, получим, что A 0. Следовательно, доказано неравенство a3 + b3 – (a2b + ab2) 0.
Прибавляя к обеим частям этого неравенства число a2b + ab2, получим, что справедливо неравенство a3 + b3 a2b + ab2,
что и требовалось доказать.
![]() Замечание.
Выше записано доказательство неравенства б) так, как его можно было бы
обсуждать с учащимися. Записать доказательство неравенства в тетрадях можно
короче:
Замечание.
Выше записано доказательство неравенства б) так, как его можно было бы
обсуждать с учащимися. Записать доказательство неравенства в тетрадях можно
короче:
Сначала проведём «анализ», помогающий найти доказательство неравенства. Из неравенства
a3 + b3 a2b + ab2 (1) следует неравенство
a3 – a2b + b3 – ab2 0,
которое можно переписать в виде
(a – b)2(a + b) 0. (2)
«Анализ» закончен. Перейдём к доказательству. Так как (a – b)2 0 и a + b 0, то для любых таких a и b справедливо неравенство (2). Рассуждая в обратном порядке, из справедливости неравенства (2) получим справедливость неравенства (1), что и требовалось доказать.
г) Сначала проведём «анализ», помогающий найти до-
казательство неравенства.
Перенеся все члены неравенства в левую часть, получим неравенство
![]() 1 + a + 2 0.
(3)
1 + a + 2 0.
(3)
a
Приведя дроби к общему знаменателю, получим неравенство
![]() a2 + 2a + 1 0. (4) a
a2 + 2a + 1 0. (4) a
Применяя формулу квадрата суммы двух чисел, получим неравенство
![]() (a + 1)2 0. (5)
(a + 1)2 0. (5)
a
«Анализ» закончен. Перейдём к доказательству. Рассуждаем в обратном порядке. Так как (a + 1)2 0 для любого числа a и по условию a 0, то для a 0 справедливо неравенство (5).
Применяя формулу квадрата суммы двух чисел, получим, что справедливо неравенство (4).
Так как a 0, то, разделив члены многочлена a2 + 2a + 1 на a, получим, что справедливо неравенство
(3).
Прибавляя к обеим частям этого неравенства число –2, получим, что справедливо исходное неравенство, что и требовалось доказать.
![]() Замечание.
Неравенство г) можно доказать, ссылаясь
Замечание.
Неравенство г) можно доказать, ссылаясь
![]() 1 2 (b 0). на ранее доказанное неравенство + b
1 2 (b 0). на ранее доказанное неравенство + b
b
![]() 1 2 (b 0) на отрицательУмножив неравенство + b b
1 2 (b 0) на отрицательУмножив неравенство + b b
![]() ное
число –1, получим, что справедливо неравенство –1 + –( b) – 2 (b 0). Обозначив a = –b,
перепишем полуb
ное
число –1, получим, что справедливо неравенство –1 + –( b) – 2 (b 0). Обозначив a = –b,
перепишем полуb
![]() 1 2 (a 0), что и треченное неравенство в виде + –a a
1 2 (a 0), что и треченное неравенство в виде + –a a
бовалось доказать.
186. Докажите неравенство, где a, b, c — действительные числа:
![]() а) ab 2ab (a 0, b 0); a + b
а) ab 2ab (a 0, b 0); a + b
г) 2a2 + b2 + c2 2a(b + c).
Доказательство. а) Проведём «анализ», помогающий найти доказательство неравенства. Перенесём все члены неравенства в левую часть, приведём дроби к общему знаменателю, вынесем в числителе дроби общий множитель за скобки и применим формулу квадрата разности:
 ab 2ab ,
(6) a + b
ab 2ab ,
(6) a + b
ab – 2ab 0 ,
a + b
ab a( + b) – 2ab
0 ,
a + b
ab a( + – b 2 ab)
0 ,
a + b
2
ab( a – b)
0 . (7) a + b
«Анализ» закончен. Перейдём к доказательству. При условиях a 0 и b 0 неравенство (7) справедливо, так
2
![]()
![]() как ab 0, a + b 0 и ( a – b)
0. Рассуждая в обратном порядке, получим, что при условиях a 0 и b
0 из справедливости неравенства (7) следует справедливость неравенства (6),
что и требовалось доказать.
как ab 0, a + b 0 и ( a – b)
0. Рассуждая в обратном порядке, получим, что при условиях a 0 и b
0 из справедливости неравенства (7) следует справедливость неравенства (6),
что и требовалось доказать.
г) Проведём «анализ», помогающий найти доказательство неравенства. Перенесём все члены неравенства в левую часть, раскроем скобки и применим формулу квадрата разности:
2a2 + b2 + c2 2a(b + c), (8)
2a2 + b2 + c2 – 2a(b + c) 0,
2a2 + b2 + c2 – 2ab – 2ac 0,
(a – b)2 + (a – c)2 0. (9)
Неравенство (9) справедливо, так как (a – b)2 0 и (a – c)2 0. Рассуждая в обратном порядке, получим, что из справедливости неравенства (9) следует справедливость неравенства (8), что и требовалось доказать.
187. Докажите неравенство, где a, b, c — действительные числа:
а) a2 + b2 + c2 ab + ac + bc;
б) ab + ac + bc + + a b c (a 0, b 0, c 0); c b a
![]()
![]() в)
– 2 + 2 a b , если a2 + b2 = 1;
в)
– 2 + 2 a b , если a2 + b2 = 1;
г) 9a + 4 12 (a 0).
a
Доказательство. а) Проведём «анализ», помогающий найти доказательство неравенства. Перенесём все члены неравенства в левую часть, умножим обе части неравенства на 2 и применим формулу квадрата разности:
a2 + b2 + c2 ab + ac + bc, (10) a2 + b2 + c2 – ab – ac – bc 0, 2a2 + 2b2 + 2c2 – 2ab – 2ac – 2bc 0,
(a – b)2 + (b – c)2 + (a – c)2 0. (11)
«Анализ» закончен. Перейдём к доказательству. Неравенство (11) справедливо для любых a, b и c, так как (a – b)2 0, (b – c)2 0 и (a – c)2 0. Рассуждая в обратном порядке, получим, что из справедливости неравенства (11) следует справедливость неравенства (10), что и требовалось доказать.
б) Проведём «анализ», помогающий найти доказатель-
![]() ство неравенства. Умножим
доказываемое неравенство на положительное число 2abc:
ство неравенства. Умножим
доказываемое неравенство на положительное число 2abc: ![]() ab + ac + bc
+ + a b c , (12) c b a
ab + ac + bc
+ + a b c , (12) c b a
2a2b2 + 2a2c2 + 2b2c2 2a2bc + 2ab2c + 2abc2.
Перенесём все члены неравенства в левую часть и применим формулу квадрата разности:
(ab – ac)2 + (ab – bc)2 + (ac – bc)2 0. (13)
«Анализ» закончен. Перейдём к доказательству. Неравенство (13) справедливо, так как (ab – ac)2 0,
(ab – bc)2 0, (ac – bc)2 0. Рассуждая в обратном порядке, получим, что из справедливости неравенства (13) следует справедливость неравенства (12), что и требовалось доказать.
в) Рассмотрим A = (a + b)2. Применяя формулу ква-
драта суммы, имеем
A = (a + b)2 = a2 + 2ab + b2 a2 + b2 + 2|a||b|.
Применяя неравенство между средним арифметическим и средним геометрическим двух неотрицательных чисел, получим, что
![]() a2 + b2 2 a b2 2
= 2 a b ,
a2 + b2 2 a b2 2
= 2 a b ,
откуда следует, что
A 2(a2 + b2).
Так как a2 + b2 = 1, то получаем, что справедливо неравенство (a + b)2 2. Перепишем это неравенство в виде
2
![]() |a +
b|2 – ( 2) 0.
|a +
b|2 – ( 2) 0.
Применяя формулу разности квадратов, перепишем это неравенство в виде
![]()
![]() (|a +
b| – 2 )(|a +
b| + 2 ) 0.
(14)
(|a +
b| – 2 )(|a +
b| + 2 ) 0.
(14)
![]() Так как
для любых a и b имеем |a + b| + 2 2 0,
то из справедливости неравенства (14) следует, что
Так как
для любых a и b имеем |a + b| + 2 2 0,
то из справедливости неравенства (14) следует, что
|a + b| – 2 0.
Последнее неравенство можно переписать в виде
|a + b| 2
 или, используя определение
абсолютной величины числа, в виде
или, используя определение
абсолютной величины числа, в виде
![]() – 2 a
+ b 2 ,
– 2 a
+ b 2 ,
что и требовалось доказать.
![]() г) Из неравенства между
средним арифметическим и средним геометрическим следует, что если a 0,
то для положительных чисел 9a и
г) Из неравенства между
средним арифметическим и средним геометрическим следует, что если a 0,
то для положительных чисел 9a и ![]() 4 справедливы
соотношения: a 9a + 4 2 9a 4 , т. е. что справедливо
неравенство a a
4 справедливы
соотношения: a 9a + 4 2 9a 4 , т. е. что справедливо
неравенство a a
9a + 1 ,4 2 что и требовалось доказать.
a
188. Докажите неравенство, где a, b, c — действительные числа:
а) |a + b| |a| + |b|; б) |a – b| |a| + |b|;
в) ||a| – |b|| |a – b|.
Доказательство. а) Докажем справедливость неравенства в каждом из рассмотренных ниже случаев.
Если a 0 и b 0, то a + b 0, поэтому |a + b| =
= a + b = |a| + |b|.
Если a 0 и b 0, то a + b 0, поэтому |a + b| =
= –(a + b) = –(–|a| – |b|) = |a| + |b|.
Если a 0 и b 0 и |a| |b|, то |a + b| = ||a| – |b|| =
= |a| – |b| |a| + |b|.
Если a 0 и b 0 и |a| |b|, то |a + b| = ||a| – |b|| =
= ||b| – |a|| = |b| – |a| |a| + |b|.
Если a 0 и b 0 и |a| |b|, то |a + b| = |–|a| + |b|| =
= ||a| – |b|| = |a| – |b| |a| + |b|.
Если a 0 и b 0 и |a| |b|, то |a + b| = |–|a| + |b|| =
= ||b| – |a|| = |b| – |a| |a| + |b|.
Таким образом, во всех рассмотренных случаях доказываемое неравенство справедливо.
б) Из неравенства, доказанного в задании а), следует,
что
|a – b| = |a + (–b)| |a| + |–b| = |a| + |b|,
что и требовалось доказать.
в) Докажем справедливость неравенства в каждом из
рассмотренных ниже случаев.
Если a 0 и b 0, то ||a| – |b|| = |a – b|.
Если a 0 и b 0, то ||a| – |b|| = |–a + b| = |a – b|.
Если a 0 и b 0 и |a| |b|, то ||a| – |b|| = |a| – |b|
||a| + |b|| = |a – b|.
Если a 0 и b 0 и |a| |b|, то ||a| – |b|| = ||b| – |a|| = = |b| – |a| |b| + |a| = ||b| + |a|| = |–b + a| = |a – b|.
Если a 0 и b 0 и |a| |b|, то ||a| – |b|| = |a| – |b| |a| + |b| = ||a| + |b|| = |–a + b| = |a – b|.
Если a 0 и b 0 и |a| |b|, то ||a| – |b|| = ||b| – |a|| = = |b| – |a| |a| + |b| = ||a| + b|| = |–a + b| = |a – b|.
Таким образом, во всех рассмотренных случаях доказываемое неравенство справедливо.
189. Докажите, что:
а) сумма кубов катетов прямоугольного треугольника
меньше куба гипотенузы;
б) an bn, если n — натуральное число и 0 a b.
Доказательство. а) Для катетов а, b и гипотенузы c прямоугольного треугольника верно равенство a2 + b2 = с2. Умножив обе части этого равенства на с, получим новое верное равенство a2с + b2с = с3. Так как a с и b с, то a3 + b3 a2с + b2с. Из справедливости этого неравенства следует, что справедливо неравенство a3 + b3 с3, что и требовалось доказать.
б) I способ. Так как 0 a b и
bn – an = (b – a)(bn – 1 + bn – 2a + ... + ban – 2 + an – 1),
то отсюда следует, что справедливо неравенство bn – an 0. Прибавляя к обеим частям последнего неравенства число an, получим, что справедливо неравенство bn an, что и требовалось доказать.
II способ. Докажем неравенство при помощи свойства 3 умножения одноимённых неравенств с положительными членами: если 0 a b и 0 c d, то ac bd.
Умножив два одноимённых неравенства с положительными членами a b и a b, получим a2 b2. Умножив неравенство a2 b2 на a b, получим неравенство a3 b3. Умножив неравенство a3 b3 на a b, получим неравенство a4 b4 и т. д. Выполнив (n – 1) раз операцию умножения, получим an bn, что и требовалось доказать.
![]() Замечание.
Здесь проведено доказательство неравенства для некоторого конкретного
натурального числа n. Доказательство справедливости этого неравенства
для любого натурального числа n будет приведено позже с помощью метода
математической индукции.
Замечание.
Здесь проведено доказательство неравенства для некоторого конкретного
натурального числа n. Доказательство справедливости этого неравенства
для любого натурального числа n будет приведено позже с помощью метода
математической индукции.
191. Задача Евклида (IV в. до н. э.). Докажите,
что если а, b, c, d — положительные числа и а
— наибольшее число в пропорции ![]() a = c , то
верно неравенство b d
a = c , то
верно неравенство b d
a + d b + c.
Доказательство. Так как по условию задачи a c,
то из верного равенства a = c ![]() b
следует, что
b
следует, что ![]() b 1, откуда d d
b 1, откуда d d
получаем, что b d. Аналогично
показывается, что из верного равенства a = b ![]() c следует, что с d.
d
c следует, что с d.
d
Умножим обе части верного числового неравенства b d на положительное число с – d, получим верное неравенство b(с – d) d(с – d), которое перепишем в виде bс + d2 dс + bd. Заменим в этом последнем неравенстве произведение bс равным ему произведением аd, получим неравенство аd + d2 dс + bd.
Разделим обе части этого верного неравенства на положительное число d и получим верное неравенство а + d с + b,
что и требовалось доказать.
![]() Замечание.
Во времена Евклида многие факты в математике доказывались геометрическим
способом. Приведём изящное геометрическое доказательство того же неравенства.
Замечание.
Во времена Евклида многие факты в математике доказывались геометрическим
способом. Приведём изящное геометрическое доказательство того же неравенства.
![]() На отрезке AD,
длина которого равна a + d, отметим точку М так, чтобы AM
= a, DM = d. Построим окружность с диаметром AD
(рис. 33). Так как a d, то центр O окружности принадлежит
отрезку AM. Так как a b, то, построив новую окружность с центром
M и радиусом b, получим точку B на окружности, BM =
b. На пересечении прямой BM с первой окружностью получим точку С.
Из теоремы о пересекающихся хордах следует, что
На отрезке AD,
длина которого равна a + d, отметим точку М так, чтобы AM
= a, DM = d. Построим окружность с диаметром AD
(рис. 33). Так как a d, то центр O окружности принадлежит
отрезку AM. Так как a b, то, построив новую окружность с центром
M и радиусом b, получим точку B на окружности, BM =
b. На пересечении прямой BM с первой окружностью получим точку С.
Из теоремы о пересекающихся хордах следует, что
6 Рис. 33 ad чи следует, что = b MC, а из условия зада-ad = bc, поэтому
MC = c.
Так как длина хорды, не проходящей через центр окружности, меньше её диаметра, то AD BC, т. е.
a + d b + c, что и требовалось доказать.
Промежуточный контроль. К–2.
2. Производные линейной и квадратичной функций
В данном пункте приводится материал, который нужно рассматривать только в классах с углублённым изучением математики, если это требуется для изучения физики.
На конкретных примерах вводятся понятия средней скорости, мгновенной скорости. Понятие производной вводится с опорой на интуитивное представление о пределе функции, производные вычисляются по определению для линейной и квадратичной функций. Вводится понятие первообразной функции для линейной функции.
3. Исторические сведения
В данном пункте рассказана история возникновения понятий равенства и неравенства чисел, применения знаков равенства и неравенства.
Исторические сведения играют важную роль в формировании первоначальных представлений о зарождении и развитии математики. Этот материал способствует формированию представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации. Он помогает также формированию целостного мировоззрения, объясняет роль разных народов в истории математики, воспитывает уважительное отношение к разным народам мира.
![]() Вторая
глава посвящена в основном изучению корней степени n из числа. Сначала
рассматриваются функции y = xn, где n —
натуральное число, их свойства и графики. Затем вводится понятие корня степени n
из числа и для «доказательства» существования корней из числа и выяснения их количества
применяются графики функции y = xn. После чего
изучаются свойства корней, рассматривается функция y = n x и решение иррациональных уравнений. В
Дополнениях к главе рассматривается степень числа с рациональным показателем и
её свойства.
Вторая
глава посвящена в основном изучению корней степени n из числа. Сначала
рассматриваются функции y = xn, где n —
натуральное число, их свойства и графики. Затем вводится понятие корня степени n
из числа и для «доказательства» существования корней из числа и выяснения их количества
применяются графики функции y = xn. После чего
изучаются свойства корней, рассматривается функция y = n x и решение иррациональных уравнений. В
Дополнениях к главе рассматривается степень числа с рациональным показателем и
её свойства.
При изучении данного материала полезно приучать школьников к самоконтролю, с помощью которого можно обнаружить допущенные ошибки. Для этого нужно проверять, действительно ли найденное число является корнем степени n из данного числа. Использование преобразований и упрощений выражений способствует развитию мышления учащихся, обучению их планированию своей деятельности, осознанному выбору наиболее эффективных способов решения.
Цель изучения главы 2 — освоить понятие корня степени n из числа (хотя бы для n = 2, n = 3) и научиться использовать свойства корней для преобразования числовых и буквенных выражений.
При углублённом изучении математики материал изучается без ограничения n 3.
§ 4. Функция y = xn
Основное назначение четвёртого параграфа — обучить школьников строить графики функций y = xn с использованием свойств этих функций. Функции y = xn (n 2) сначала изучаются для x 0, затем для x R.
4.1. Свойства и график функции y = xn, x 0
![]()
В данном пункте формулируются и доказываются свойства, общие для функций y = x2, y = x3, y = x4, ..., рассматриваемых на промежутке [0; + ), при этом обосновывается их взаимное расположение при изображении в одной системе координат.
Задания для повторения. При изучении данного пункта можно использовать задания 1030, 1031, 1034 (а—в).
213. а) Дана функция y = x4 (x 0). При каких значениях x значения функции равны 0; 1; 16; 81?
б) Дана функция y = x3 (x 0). При каких значениях
x значения функции равны 0; 1; 8; 64?
Решение. а) y = 0, если x = 0; y = 1, если x = 1; y = 16, если x = 2; y = 81, если x = 3.
б) y = 0, если x = 0; y = 1, если x = 1; y = 8, если
x = 2; y = 64, если x = 4.
214. При каких значениях x (x 0) выполняется неравенство y1(x) y2(x), если:
а) y1(x) = x6, y2(x) = x3; б) y1(x) = x2, y2(x) = x5?
Решение. а) y1(x) y2(x) при x 0, если x (0; 1), так как для 0 x 1 имеем y1(x) – y2(x) = x6 – x3 = x3(x3 – 1) =
= x3(x – 1)(x2 + x + 1) 0.
б) y1(x) y2(x) при x 0, если x (1; + ), так как
для x 1 имеем y1(x) – y2(x) = x2 – x5 = x2(1 – x3) = = x2(1 – x)(x2 + x + 1) 0.
4.2. Свойства и графики функций y = x2m и
![]()
В данном пункте функции y = xn рассматриваются на всей области своего существования, т. е. на R, выявляется различие графиков функции для чётного и нечётного n, находятся промежутки возрастания и убывания для чётного и нечётного n.
Возрастание функций y = x2m и y = x2m + 1 на промежутке [0; + ) обосновывается в п. 4.1. Из чётности функции y = x2m следует, что на промежутке (– ; 0] эта функция убывает. Из нечётности функции y = x2m + 1 следует, что на промежутке (– ; 0] эта функция возрастает.
Доказательство возрастания функции y = x2m + 1 на промежутке (– ; + ) обычно вызывает затруднения у учащихся. Поэтому приведём его (для классов с углублённым изучением математики).
Пусть x1 x2, докажем, что x12m + 1 x22m + 1 .
Если 0 x1 x2, то неравенство x12m + 1 x22m + 1 доказано в п. 4.1.
Если x1 x2 0, то |x1| |x2| 0, поэтому по доказанному |x1|2m+1 |x2|2m+1, т. е. x12m + 1 x22m + 1 .
Если x1 0 x2, то по доказанному выше x12m + 1 0 и 0 x22m + 1 , откуда по свойству транзитивности нера-
венств следует, что x12m + 1 x22m + 1 .
Так как рассмотрены все случаи, то неравенство x12m + 1 x22m + 1 доказано для любых x1 x2.
Задания для повторения. При изучении данного пункта можно использовать задания 1036, 1037.
231. а) Сравните значения функций y = x и y = x5 при значениях аргумента 0 x 1.
Решение. Если 0 x 1, то x x5, так как x – x5 = x(1 – x)(1 + x)(1 + x2) 0
для 0 x 1.
Можно рассуждать иначе. Если 0 x 1, то, умножив неравенство 1 x на положительное число x, получим, что x x2, далее, последовательно умножая получаемые неравенства на положительное число x, получим x x2, x2 x3, x3 x4, x4 x5, поэтому по свойству транзитивности неравенств имеем x x5.
![]() Замечание.
Выводы при решении рассмотренного задания можно делать из взаимного
расположения графиков функций, так как оно обосновано в п. 4.2. В классах с
углублённым изучением математики можно попросить доказать неравенства без
ссылки на графики функций, как это сделано в задании 231(а).
Замечание.
Выводы при решении рассмотренного задания можно делать из взаимного
расположения графиков функций, так как оно обосновано в п. 4.2. В классах с
углублённым изучением математики можно попросить доказать неравенства без
ссылки на графики функций, как это сделано в задании 231(а).
233. Дана функция y = x12. Сравните: а) y(1) и y(2);
б) y(–2) и y(–1).
Решение. а) Так как функция y = x12 возрастает на промежутке [0; + ), числа 1 и 2 принадлежат этому промежутку и 1 2, то y(1) y(2).
б) Так как функция y = x12 убывает на промежутке (– ; 0], числа –2 и –1 принадлежат этому промежутку и –2 –1, то y(–2) y(–1).
![]() Замечание.
В задании б) можно рассуждать иначе: так как функция y = x12
чётная, то y(–2) = y(2) y(1) = y(–1),
а неравенство y(2) y(1) доказано в пункте а). 234. Дана
функция y = x9. Сравните:
Замечание.
В задании б) можно рассуждать иначе: так как функция y = x12
чётная, то y(–2) = y(2) y(1) = y(–1),
а неравенство y(2) y(1) доказано в пункте а). 234. Дана
функция y = x9. Сравните:
а) y(–1) и y(1); б) y(–2) и y(0); в) y(4) и y(–5).
Решение. а) y(–1) = –1, y(1) = 1; –1 1, следовательно, y(–1) y(1).
б) y(–2) = (–2)9 0; y(0) = 09 = 0, следовательно,
y(–2) y(0).
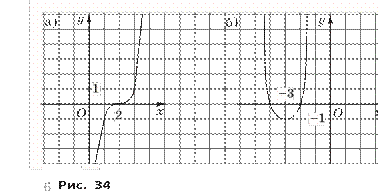
в) y(4) = 49 0, а y(–5) = (–5)9 0, следовательно,
y(4) y(–5).
Дополнительное задание. Постройте график функции:
а) y = (x – 2)3; б) y = (x + 3)4 – 1.
Решение. а) График функции y = x3 перенесём на 2 единицы вправо, получим график функции y = (x – 2)3 (рис. 34, а).
б) График функции y = x4 перенесём на 3 единицы влево и на 1 единицу вниз, получим график функции y = (x + 3)4 – 1 (рис. 34, б).
§ 5. Корень степени n
![]() Основное
назначение пятого параграфа — научить школьников пользоваться свойствами корней
степени n. Сначала вводится понятие корня степени n, затем
рассматриваются корни чётной и нечётной степеней, вводятся обозначения корней,
изучаются свойства арифметических корней степени n, рассматривается
функция y = n x (x
0), обсуждается вопрос извлечения корня степени n из натурального
числа, наконец, разбираются методы решения иррациональных уравнений.
Основное
назначение пятого параграфа — научить школьников пользоваться свойствами корней
степени n. Сначала вводится понятие корня степени n, затем
рассматриваются корни чётной и нечётной степеней, вводятся обозначения корней,
изучаются свойства арифметических корней степени n, рассматривается
функция y = n x (x
0), обсуждается вопрос извлечения корня степени n из натурального
числа, наконец, разбираются методы решения иррациональных уравнений.
Отметим, что по действующей программе в обычном классе достаточно изучать корни 2-й и 3-й степеней. Однако здесь же требуется научиться решать уравнения типа xn = 2. Кажется странным, что ученик основной школы должен уметь решать уравнения x2 = 2 и x3 = 2, а уравнение x5 = 2 — нет. Поэтому в данном параграфе изучаются корни степени n 2 и их свойства без ограничения n 3. Учитель в конкретном классе сам решает, изучать ли весь материал, или отобрать только то, что относится к квадратным и кубическим корням. В обычном классе так можно поступить, но надо бы изучить хотя бы пп. 5.1–5.3.
В классах с углублённым изучением математики следует изучить весь материал этого параграфа, а также материал Дополнений к главе 2, так как это облегчит обучение в старших классах, где программа перегружена после переноса туда тригонометрии и добавления элементов статистики и теории вероятностей на фоне уменьшения числа учебных часов. Кроме того, изучаемый в данном параграфе материал традиционно входит в программу классов с углублённым изучением математики, он окажется полезным для участия в олимпиадах и других соревнованиях.
5.1. Понятие корня степени n 5.2. Корни чётной и нечётной степени
В пункте 5.1 приводится словесное определение корня степени n (n N, n 2) из числа. С помощью определения вычисляются корни степени n из некоторых чисел. Эти примеры показывают, что надо рассматривать два случая: n — чётное число и n — нечётное число. Из приведённых примеров, получается вывод:
а) нет корней чётной степени из отрицательного числа;
б) существует единственный корень из числа нуль,
равный нулю;
в) существует ровно два корня чётной степени из положительного числа: один положительный b1, другой отрицательный b2 (b2 = –b1);
г) существует единственный корень нечётной степени
из любого действительного числа.
В п. 5.2 этот вывод доказывается графическим методом.
![]() Затем вводятся обозначения
для корня степени n из числа a: n
a . По определению:
Затем вводятся обозначения
для корня степени n из числа a: n
a . По определению:
1) ![]()
![]()
![]()
![]() обозначение 2k a
используют только для a 0, причём если a = 0, то 2k 0
= 0, если a 0, то обозначение 2k
a используют только
для положительного числа b1, такого, что b1
= 2k a , но тогда b2 = –
2k a ;
обозначение 2k a
используют только для a 0, причём если a = 0, то 2k 0
= 0, если a 0, то обозначение 2k
a используют только
для положительного числа b1, такого, что b1
= 2k a , но тогда b2 = –
2k a ;
2) обозначение 2k + 1 a используют для любого действительного числа a.
Пользуясь определением и обозначениями для корня степени n, можно написать решения следующих уравнений:
1) ![]()
![]() уравнение x2k
= a (a 0) имеет два корня: x1 = 2k a ,
x2 = – 2k a ;
уравнение x2k
= a (a 0) имеет два корня: x1 = 2k a ,
x2 = – 2k a ;
2) ![]() уравнение x2k+1
= a (a — любое число) имеет единственный корень x1
= 2k + 1 a .
уравнение x2k+1
= a (a — любое число) имеет единственный корень x1
= 2k + 1 a .
Желательно, чтобы эти понятия и обозначения были усвоены учащимися в любом классе.
Задания для повторения. При изучении данного пункта можно использовать задания 865—868.
248. Проверьте, является ли число:
а) 6 корнем шестой степени из числа 46 656;
б) –3 корнем седьмой степени из числа 2187;
в) –3 корнем седьмой степени из числа –2187;
г) –0,4 корнем пятой степени из
числа ![]() .
.
Решение. а) Так как 6 0 и 66 = 46 656, то 6 является корнем шестой степени из числа 46 656.
б) –3 не является корнем седьмой степени из числа 2187, так как (–3)7 0, а 2187 0.
в) Так как (–3)7 = –2187, то –3 является корнем седь-
мой степени из числа –2187.
г) –0,4 не является корнем пятой степени из числа ![]() ,
так как (–0,4)5 0, а
,
так как (–0,4)5 0, а ![]() 0.
0.
261. Верно ли равенство:
![]()
![]() а) 3 –27 =
–3; б) 4 –6 = –2; г) 4 625 =
–5?
а) 3 –27 =
–3; б) 4 –6 = –2; г) 4 625 =
–5?
Решение. а) Равенство 3 –27 = –3 верно, так как

6 Рис. 35
![]()
![]() г) Равенство 4 625 =
–5 неверно, так как 4 625 0, а –5 0.
г) Равенство 4 625 =
–5 неверно, так как 4 625 0, а –5 0.
266. Решите уравнение, используя график функции: а) x3 = 8; в) x3 = –27.
Решение. а) Построим графики функций y = x3 и y = 8 (рис. 35, а). Они пересекаются в единственной точке с абсциссой 2 (23 = 8). Поэтому уравнение имеет единственный корень x1 = 2.
в) Построим графики функций y = x3 и y = –27 (рис. 35, б). Они пересекаются в единственной точке с абсциссой –3 ((–3)3 = –27). Поэтому уравнение имеет единственный корень x1 = –3.
![]() 275. Вычислите: а) 5
+ 4 1 ; в) 4 16 – 1; д) 3 27 – 4 81 . Решение. а) 5 +
4 1
= 5 + 1 = 6; в) 4 16 –
1 = 2 – 1 = 1; д) 3 27 – 4 81
= 3 – 3 = 0.
275. Вычислите: а) 5
+ 4 1 ; в) 4 16 – 1; д) 3 27 – 4 81 . Решение. а) 5 +
4 1
= 5 + 1 = 6; в) 4 16 –
1 = 2 – 1 = 1; д) 3 27 – 4 81
= 3 – 3 = 0.
5.3. Арифметический корень степени n
![]()
![]() В данном пункте вводится
понятие арифметического корня: неотрицательный корень степени n из
неотрицательного числа a называют арифметическим корнем степени n
из числа a. Далее приводятся свойства арифметических корней. Желательно,
чтобы эти свойства знали все учащиеся. Желательно также, чтобы все учащиеся
усвоили свойство 2k + 1 –a = – 2k + 1 a
, справедливое для любого действительного числа a.
В данном пункте вводится
понятие арифметического корня: неотрицательный корень степени n из
неотрицательного числа a называют арифметическим корнем степени n
из числа a. Далее приводятся свойства арифметических корней. Желательно,
чтобы эти свойства знали все учащиеся. Желательно также, чтобы все учащиеся
усвоили свойство 2k + 1 –a = – 2k + 1 a
, справедливое для любого действительного числа a.
Задания для повторения. При изучении данного пункта можно использовать задание 872.
280. Является ли следующая запись записью арифметического корня:
![]()
![]()
![]() а)
3 –2 ;
б) – 4 3 ; в) 3 (–2)2 ; г) 4 (–3)3 ?
а)
3 –2 ;
б) – 4 3 ; в) 3 (–2)2 ; г) 4 (–3)3 ?
Решение. а) Запись 3 –2 не является записью арифметического корня, так как это отрицательное число.
б) Запись – 4 3 не является записью арифметического
корня, так как это отрицательное число.
в) Запись 3 (–2)2 является записью арифметического
корня, так как это корень из положительного числа 4.
![]() г) Запись 4 (–3)3 не является
записью арифметическо-
г) Запись 4 (–3)3 не является
записью арифметическо-
го корня, так как это выражение не имеет смысла (корень чётной степени из отрицательного числа не существует). 281. Вычислите арифметические корни:
![]() ;
;
Замечание. Здесь и далее, формируя умения преобразовывать числовые и буквенные выражения с корнями, не нужно стремиться быстро перейти к устному вынесению множителя из-под знака корня или выполнению устно других операций. Подробные записи, приведённые выше, позволяют учащимся осмысленно применять свойства корней, что повышает надёжность усвоения нового материала. 295. Упростите выражение:
![]() в) 3 48 – 3 750 + 3 6 + 3 162
; е) 303 + 7 3 2 + 53 144 .
в) 3 48 – 3 750 + 3 6 + 3 162
; е) 303 + 7 3 2 + 53 144 .
2 3
Решение. в) 3 48 – 3 750 + 3 6 + 3 162 =
= 3 8 · – 6 3 125 · 6 + 3 6 + 3 27 · 6 =
= 3 8 · 3 6 – 3 125 · 3 6 + 3 6 + 3 27 · 3 6 =
= 2 63 – 53 6 + 3 6 + 33 6 = 3 6 ;
![]()
![]() целое число,
что и требовалось доказать.
целое число,
что и требовалось доказать.
302. а) Решите уравнение х4 – 3х2 – 4 = 0.
Решение. Введя новое неизвестное t = х2, перепишем исходное уравнение в виде
t2 – 3t – 4 = 0. (1)
Уравнение (1) имеет два корня: t1 = –1, t2 = 4. Следовательно, все корни исходного уравнения есть объединение корней уравнений: 1) х2 = –1 и 2) х2 = 4. Так как уравнение 1) не имеет корней, а уравнение 2) имеет два корня x1 = –2, x2 = 2, то и исходное уравнение имеет те же два корня.
Ответ. –2; 2.
303. Укажите все значения а, для каждого из которых уравнение х4 = а имеет два корня; имеет единственный корень; не имеет корней.
![]()
![]() Решение. Если a 0,
то уравнение х4 = а имеет два корня: x1
= – 4 a , x2 = 4 a .
Решение. Если a 0,
то уравнение х4 = а имеет два корня: x1
= – 4 a , x2 = 4 a .
Если a = 0, то уравнение х4 = а имеет единственный корень x0 = 0.
Если a 0, то уравнение х4 = а не имеет корней, так как х4 0, а a 0.
5.4. Свойства корней степени n
В данном пункте приводятся дополнительные свойства арифметических корней. Все эти свойства можно не изучать в обычном классе, однако две формулы, справедливые для любого числа a, желательно знать каждому учащемуся:
![]() 2k 2k 2k
+ 1 2k + 1
2k 2k 2k
+ 1 2k + 1
![]() a = |a| и a = a.
a = |a| и a = a.
Задания для повторения. При изучении данного пункта можно использовать задания 873—875.
309. Вынесите множитель из-под знака корня:
е) 4 16c d5 6 , если c 0, d 0;
ж) 4 5x4 , если x 0.
Решение. е) Так как c 0, d 0, то
4 16c d5 6 4 (2cd)4 · 4 cd2 = 2cd cd4 2 = 2cd cd4 2 .
=
ж) Так как x 0, то 4 5x4 = 4 x4 · 4 5 = x 4 5 = –x4 5 .
a2 b x2
![]() 313. г) Внесите
множитель под знак корня: b 4 a7 ,
313. г) Внесите
множитель под знак корня: b 4 a7 ,
если Решение.b 0. Так как b
0, то ![]() a2 0 (a 0, так как в
a2 0 (a 0, так как в
b
знаменателе подкоренного выражения не может быть нуль), и поэтому
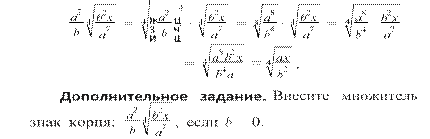 = Решение. Так как b
0, то
= Решение. Так как b
0, то ![]() a2 0 , а
a2 0 , а ![]() a2 0 (a 0),
a2 0 (a 0),
b –b
4
![]()
![]() b
b
г)
д)
е)
=
а)
в) 5
Решение.
2
![]() а) (4 a – 1)(4 a + 1) =
(4 a) – = 1 4 a2 – = 1 a
– 1;
а) (4 a – 1)(4 a + 1) =
(4 a) – = 1 4 a2 – = 1 a
– 1;
в) (3 m – 4 m)(4 m + 3 m) = (3 m – 4 m)(3 m + 4 m) =
2 2
= (3 m) – (4 m) = 3 m2 – m .
Промежуточный контроль. С–14, С–15*.
5.5. Функция y = n x , x 0
![]() В
данном пункте рассматриваются свойства функции y = n x , где n N, n
2, определённой на промежутке [0; + ), и её график. Авторы не вводят понятие обратной функции,
поэтому для доказательства некоторых свойств этой функции и построения её
графика используются следующие рассуждения.
В
данном пункте рассматриваются свойства функции y = n x , где n N, n
2, определённой на промежутке [0; + ), и её график. Авторы не вводят понятие обратной функции,
поэтому для доказательства некоторых свойств этой функции и построения её
графика используются следующие рассуждения.
Рассматривается множество точек координатной плоскости xOy, которое можно задать двумя способами:
![]() 1) {y = n x x, , 0 y 0}
и 2) {x = yn,
, x 0 y 0}.
1) {y = n x x, , 0 y 0}
и 2) {x = yn,
, x 0 y 0}.
![]() Вторым
способом задана функция x = yn, которая в координатной
плоскости yOx для y 0 имеет непрерывный график (рис. 36, а).
Так как в первом случае записана функция y = n x (x 0), то эта
функция в системе координат yOx имеет тот же график, что на рисунке 36, а.
Вторым
способом задана функция x = yn, которая в координатной
плоскости yOx для y 0 имеет непрерывный график (рис. 36, а).
Так как в первом случае записана функция y = n x (x 0), то эта
функция в системе координат yOx имеет тот же график, что на рисунке 36, а.
![]() Из свойств функции x
= yn следует, что функция y = n x (x 0) является
непрерывной и возрастающей на промежутке x [0; + ) линией. Однако система координат
Из свойств функции x
= yn следует, что функция y = n x (x 0) является
непрерывной и возрастающей на промежутке x [0; + ) линией. Однако система координат
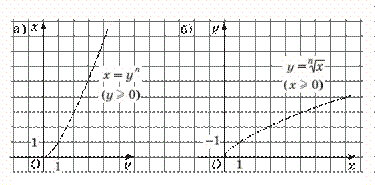
6 Рис. 36
![]() расположена непривычно: ось x
направлена вверх, а ось y — вправо. Это неудобство легко устранить.
Выполним осевую симметрию системы координат и графика относительно оси y
= x, получим систему координат xOy и график той же функции y = n x
(x 0) в более привычном расположении (рис. 36, б).
расположена непривычно: ось x
направлена вверх, а ось y — вправо. Это неудобство легко устранить.
Выполним осевую симметрию системы координат и графика относительно оси y
= x, получим систему координат xOy и график той же функции y = n x
(x 0) в более привычном расположении (рис. 36, б).
Задания для повторения. При изучении данного пункта можно использовать задания 1025—1027.
![]() 334. Известно, что: а) 3 a 1;
б) 3 a 1.
334. Известно, что: а) 3 a 1;
б) 3 a 1.
Верно ли, что a больше единицы? больше нуля?
![]()
![]()
![]()
![]() Решение. Рассмотрим
графики функций y = 3 x (x 0) и y =
1 (рис. 37). Так как функция y = 3 x возрастает на промежутке
[0; + ),
то значение y = 1 она принимает лишь в одной точке x = 1.
Для x 1 график функции y = 3 x лежит выше прямой y =
1, а для 0 x
1 график функции y = 3 x лежит ниже прямой y =
1. Это означает, что 3 a 1 для a 1 и 0 3 a 1
для 0 a
1.
Решение. Рассмотрим
графики функций y = 3 x (x 0) и y =
1 (рис. 37). Так как функция y = 3 x возрастает на промежутке
[0; + ),
то значение y = 1 она принимает лишь в одной точке x = 1.
Для x 1 график функции y = 3 x лежит выше прямой y =
1, а для 0 x
1 график функции y = 3 x лежит ниже прямой y =
1. Это означает, что 3 a 1 для a 1 и 0 3 a 1
для 0 a
1.
![]() Ответ. а) Верно, что a
1 и что a 0; б) неверно, что a 1, и неверно, что a 0,
так как 3 a = 0 для a = 0.
Ответ. а) Верно, что a
1 и что a 0; б) неверно, что a 1, и неверно, что a 0,
так как 3 a = 0 для a = 0.
337. Докажите неравенство: а) 3 10 2; в) 7 4 16 .
![]() Решение. а) В силу
возрастания функции y = 3 x на промежутке [0; + ) из неравенства
10 8 следует, что 3 3 3
Решение. а) В силу
возрастания функции y = 3 x на промежутке [0; + ) из неравенства
10 8 следует, что 3 3 3
![]() 10
8 = 2, т. е. что справедливо
неравенство 10 2, что и требовалось
доказать.
10
8 = 2, т. е. что справедливо
неравенство 10 2, что и требовалось
доказать.
в) Заметим, что 4 16 = 4 . В силу возрастания фун-
![]() кции y = x на промежутке [0; + ) из неравенства 7
4, следует, что 7 4 = 4 16 , т. е. справедливо неравенство 7 4 16 , что и требовалось доказать.
кции y = x на промежутке [0; + ) из неравенства 7
4, следует, что 7 4 = 4 16 , т. е. справедливо неравенство 7 4 16 , что и требовалось доказать.
338. Сравните числа: а) 2 и 3 4
7; б) 12 и 2.
Решение. а) Так как 2 = 3 8 и 3 8 3 7 , то из возрастания функции y = 3 x следует, что
2 3 7 . 6 Рис. 37
![]() б) Так как 2 = 4 16 и 4 12 4 16 , то из
возрастания
б) Так как 2 = 4 16 и 4 12 4 16 , то из
возрастания
функции y = 4 x следует, что 4 12 2.
339.
![]() а)
Найдите два последовательных натуральных числа, между которыми заключено число 3 3 .
а)
Найдите два последовательных натуральных числа, между которыми заключено число 3 3 .
![]()
![]() Решение. Так как
ближайшие к числу 3 кубы натуральных чисел — это 1 = 13
и 8 = 23, то в силу возрастания функции y = 3 x
на промежутке [0; + ) из неравенства 13 3 23
следует неравенство 1 3 3 2.
Решение. Так как
ближайшие к числу 3 кубы натуральных чисел — это 1 = 13
и 8 = 23, то в силу возрастания функции y = 3 x
на промежутке [0; + ) из неравенства 13 3 23
следует неравенство 1 3 3 2.
340. Сравните натуральные числа m (m 2) и n (n 2), если:
![]() а) m 5 n 5 ; в) m 0,2 n 0,2 .
а) m 5 n 5 ; в) m 0,2 n 0,2 .
Решение. а) Перепишем неравенство в виде
![]() mn 5n
mn 5m .
(1)
mn 5n
mn 5m .
(1)
Так как функция y = mn x возрастает на промежутке [0; + ), то неравенство (1) выполняется, только если 5n 5m, т. е. если n m.
в) Перепишем неравенство в виде
![]() mn 0,2n
mn 0,2m .
(2)
mn 0,2n
mn 0,2m .
(2)
Так как функция y = mn x возрастает на промежутке [0; + ), то неравенство (2) выполняется, только если
0,2n 0,2m, т. е. если n m.
341. а) Сравните с единицей положительное число a,
![]() если 3 a 4 a .
если 3 a 4 a .
Решение. Перепишем неравенство в виде
![]() 12 a4 12 a3 .
(3)
12 a4 12 a3 .
(3)
Так как функция y = 12 x возрастает на промежутке [0; + ), то неравенство (3) выполняется, только если a4 a3. Так как a 0, то, разделив неравенство a4 a3 на a3, получим, что a 1.
Ответ. a 1.
342.
![]() а) Каким
может быть натуральное число n (n 2), если n 16 4?
а) Каким
может быть натуральное число n (n 2), если n 16 4?
Решение. Перепишем неравенство в виде
![]()
![]() n 42
n 4n .
(4) Так как функция y = n x возрастает на
промежутке [0; + ), то неравенство (4) выполняется, только если
n 42
n 4n .
(4) Так как функция y = n x возрастает на
промежутке [0; + ), то неравенство (4) выполняется, только если
42 4n, т. е. если 2 n.
Ответ. n 2.
343. Найдите область определения функции:
![]()
![]() а) y
= 3x ; б) y
= 3 –5x .
а) y
= 3x ; б) y
= 3 –5x .
![]()
![]() Решение. а) Так как
функция y = t (t =
3x) определена на множестве неотрицательных чисел, то справедливо
неравенство 3x 0, которое имеет множество решений [0; + ). Следовательно,
область определения функции y = 3x
есть промежуток [0; + ).
Решение. а) Так как
функция y = t (t =
3x) определена на множестве неотрицательных чисел, то справедливо
неравенство 3x 0, которое имеет множество решений [0; + ). Следовательно,
область определения функции y = 3x
есть промежуток [0; + ).
![]()
![]() б) Так как функция y =
3t
(t = –5x) определена на множестве всех неотрицательных
чисел t, то справедливо неравенство –5x 0, которое имеет
множество решений (–
; 0]. Следовательно, область определения функции y = 3 –5x
есть промежуток (– ;
0].
б) Так как функция y =
3t
(t = –5x) определена на множестве всех неотрицательных
чисел t, то справедливо неравенство –5x 0, которое имеет
множество решений (–
; 0]. Следовательно, область определения функции y = 3 –5x
есть промежуток (– ;
0].
В данном пункте приводится пример вычисления корня третьей степени из числа 17, указывается способ, по которому можно найти любое количество знаков после запятой в десятичной записи этого числа.
Формулируется утверждение: арифметический корень степени n (n 2) из натурального числа может быть или натуральным числом, или иррациональным числом.
![]() В учебнике
не приводится доказательство этого утверждения, но в простых случаях учащиеся
должны научиться его доказывать. Например, доказывать иррациональность числа 3 2 (задание 351,
а). Но сам учитель должен владеть и общим доказательством этого утверждения
(оно приведено ниже в Замечании к заданию 351).
В учебнике
не приводится доказательство этого утверждения, но в простых случаях учащиеся
должны научиться его доказывать. Например, доказывать иррациональность числа 3 2 (задание 351,
а). Но сам учитель должен владеть и общим доказательством этого утверждения
(оно приведено ниже в Замечании к заданию 351).
![]() Данный
пункт предназначен для классов с углублённым изучением математики, но и
учащиеся обычного класса должны знать без доказательства, что 5 , 3 3 , ... — иррациональные числа.
Данный
пункт предназначен для классов с углублённым изучением математики, но и
учащиеся обычного класса должны знать без доказательства, что 5 , 3 3 , ... — иррациональные числа.
Задания для повторения. При изучении данного пункта можно использовать задания 876, 877, 893.
Решения и комментарии
![]() 351. а) Докажите
иррациональность числа 3 2 .
351. а) Докажите
иррациональность числа 3 2 .
![]() Доказательство.
Предположим, что число 3 2 рациональное, т. е. предположим, что существует
несократимая дробь
Доказательство.
Предположим, что число 3 2 рациональное, т. е. предположим, что существует
несократимая дробь ![]() p , такая, что справедливо равенство 3 2 =
p ,
где q q
p , такая, что справедливо равенство 3 2 =
p ,
где q q
p N, q N. Тогда справедливо равенство
2q3 = p3. (1)
Так как левая часть равенства (1) делится на 2, то и правая часть равенства, т. е. p3, делится на 2. Докажем, что если p3 делится на 2, то и p делится на 2.
Число p при делении на 2 может иметь только два остатка: 1 или 0.
Если p = 2n + 1, где n N, то равенство 2q3 = 8n3 + + 12n2 + 6n + 1 не выполняется ни при каком натуральном q, так как левая его часть делится на 2, а правая нет. Следовательно, число p при делении на 2 не может иметь остаток 1, т. е. p делится на 2.
Если p = 2n, где n N, то равенство (1) перепишется в виде 4n3 = q3. Аналогично показывается, что число q при делении на 2 не может иметь остаток 1, т. е. и оно делится на 2.
![]() Следовательно,
каждое из чисел p и q делится на 2. Получилось противоречие с
предположением, что в равенстве 3 2 = p дробь
Следовательно,
каждое из чисел p и q делится на 2. Получилось противоречие с
предположением, что в равенстве 3 2 = p дробь ![]() p — несократимая.
Следовательно, q q
p — несократимая.
Следовательно, q q
предположение неверно, а верно утверждение, что число
3
2 — иррациональное.
Замечание. Доказательство иррациональности числа
3
29 тем же способом окажется громоздким, так как потребуется рассмотреть не два случая, как в предыдущем задании, а 29. Поэтому приведём другой способ доказательства иррациональности корней степени n из натуральных чисел, не являющихся n-й степенью натурального числа.
![]() Теорема.
Если натуральное число m не является n-й степенью (n N, n
2) какого-либо натурального числа, то n m — иррациональное число.
Теорема.
Если натуральное число m не является n-й степенью (n N, n
2) какого-либо натурального числа, то n m — иррациональное число.
![]() Доказательство.
Предположим противное, т. е. предположим, что n m — число рациональное. Это означает,
Доказательство.
Предположим противное, т. е. предположим, что n m — число рациональное. Это означает,
![]() p N, q N), тачто существует несократимая дробь (p
q
p N, q N), тачто существует несократимая дробь (p
q
![]() кая, что n m = p . Но тогда справедливо
равенство q
кая, что n m = p . Но тогда справедливо
равенство q
qnm = pn. (2)
Если q = 1, то m = pn, что противоречит условию теоремы, следовательно, q 1.
Если p = 1, то pn = 1, но тогда из равенства qnm = 1 следует, что произведение двух чисел, каждое из которых больше 1, равно 1, чего быть не может, следовательно, p 1.
Если p 1, то по основной теореме арифметики число p разлагается на простые множители
p = p1a1 p2a2 ... pkak , (3)
где p1, p2, ..., pk — различные простые числа, a1, a2, ..., ak — натуральные числа.
Так как число q 1, то оно имеет делитель d, где
p
d — простое число. Но так как дробь ![]() несократимая,
то q
несократимая,
то q
среди чисел p1, p2, ..., pk нет числа d.
Из равенства (3) следует равенство
pn = p1na1 p2na2 ... pknak . (4)
По основной теореме арифметики разложение каждого натурального числа на простые множители единственно. Поэтому правая часть равенства (4) есть (единственное) разложение числа pn на простые множители. Так как среди чисел p1, p2, ..., pk нет числа d, то pn не делится на d. Тогда из равенства (2) следует, что его левая часть делится на простое число d, а правая нет.
![]() Полученное противоречие
означает, что сделанное предположение неверно, т. е. n m — иррациональное число.
Полученное противоречие
означает, что сделанное предположение неверно, т. е. n m — иррациональное число.
354. Найдите приближённое значение кубического корня с точностью до 0,1 из следующих чисел: а) 3; б) 6.
![]()
![]()
![]()
![]()
![]() Решение. а) Так как
1,43 = 2,744 3 1,53 = 3,375, то 1,4 3 3 1,5.
Заметим, что 1,4 — приближённое значение числа 3
3 с точностью до 0,1 с
недостатком, а 1,5 — приближённое значение числа 3
3 с точностью до 0,1 с избытком.
В качестве приближённого значения числа 3 3 можно взять любое из чисел 1,4 и 1,5, они
отличаются от числа 3 3 не более чем на 0,1. Аналогично рассуждая,
получим, что 1,44 3 3 1,45, поэтому более точным приближением из
двух чисел 1,4 и 1,5 является число 1,4.
Решение. а) Так как
1,43 = 2,744 3 1,53 = 3,375, то 1,4 3 3 1,5.
Заметим, что 1,4 — приближённое значение числа 3
3 с точностью до 0,1 с
недостатком, а 1,5 — приближённое значение числа 3
3 с точностью до 0,1 с избытком.
В качестве приближённого значения числа 3 3 можно взять любое из чисел 1,4 и 1,5, они
отличаются от числа 3 3 не более чем на 0,1. Аналогично рассуждая,
получим, что 1,44 3 3 1,45, поэтому более точным приближением из
двух чисел 1,4 и 1,5 является число 1,4.
![]()
![]() б) Так как 1,83
= 5,832 6 1,93 = 6,859, то
1,8 3 6 1,9. Заметим, что 1,8 — приближённое
значение числа 3 6 с точностью до 0,1 с недостатком, а 1,9 —
приближённое значение числа 3 6 с точностью до 0,1 с избытком. Аналогично
рассуждая, получим, что
б) Так как 1,83
= 5,832 6 1,93 = 6,859, то
1,8 3 6 1,9. Заметим, что 1,8 — приближённое
значение числа 3 6 с точностью до 0,1 с недостатком, а 1,9 —
приближённое значение числа 3 6 с точностью до 0,1 с избытком. Аналогично
рассуждая, получим, что
1,81 3 6 1,82, поэтому более точным приближением из двух чисел 1,8 и 1,9 является число 1,8.
В данном пункте вводится понятие иррационального уравнения и напоминается понятие уравнения-следствия, на конкретных примерах показывается решение иррациональных уравнений переходом к уравнению-следствию, объясняется, что если при решении уравнения был выполнен переход к его следствию, то требуется проверить, все ли корни уравнения-следствия являются корнями исходного уравнения. Этот метод уже был рассмотрен в 8 классе в других ситуациях.
В конце пункта разбирается приём решения уравнений вида f(x) g(x) = 0, где хотя бы одна из функций f(x) и g(x) содержит неизвестное под знаком корня.
Здесь стоит рассмотреть п. 13 дидактических материалов, в котором приводится пример решения иррационального уравнения при помощи замены неизвестного.
Данный пункт предназначен для классов с углублённым изучением математики.
Задания для повторения. При изучении данного пункта можно использовать задания 991, 996. Решения и комментарии
362. ![]() а) Решите уравнение 5x + 11 = x + 1.
а) Решите уравнение 5x + 11 = x + 1.
Решение. Возведём исходное уравнение в квадрат, получим его следствие:
5x + 11 = x2 + 2x + 1. (1)
![]() Уравнение (1) имеет два
корня: x1 = 5 и x2 = –2. Проверка
показывает, что число x1 является корнем исходного уравнения,
так как 5 · 5 + 11 = 6 и 5 + 1 = 6, а x2
не является, так как 5 · –2 + ( ) 11 = 1, а –2 + 1 = –1.
Следовательно, исходное уравнение имеет единственный корень x1.
Уравнение (1) имеет два
корня: x1 = 5 и x2 = –2. Проверка
показывает, что число x1 является корнем исходного уравнения,
так как 5 · 5 + 11 = 6 и 5 + 1 = 6, а x2
не является, так как 5 · –2 + ( ) 11 = 1, а –2 + 1 = –1.
Следовательно, исходное уравнение имеет единственный корень x1.
Ответ. 5.
363. ![]() а) Решите уравнение
3x – = 7 2x
– 5 .
а) Решите уравнение
3x – = 7 2x
– 5 .
Решение. Возведём исходное уравнение в квадрат, получим его следствие:
3x – 7 = 2x – 5. (2)
Уравнение (2) имеет единственный корень: x1 = 2. Проверка показывает, что число x1 не является корнем
![]() исходного уравнения, так как
выражение 3 · 2 – 7 не имеет смысла.
Следовательно, исходное уравнение не имеет корней.
исходного уравнения, так как
выражение 3 · 2 – 7 не имеет смысла.
Следовательно, исходное уравнение не имеет корней.
Ответ. Нет корней.
364. а) Решите уравнение x – 2 + x + 3 = 3 + 7x .
Решение. Возведём исходное уравнение в квадрат, получим его следствие:
![]() x – 2 + 2 x – 2 x + 3 + x + 3 = 3x
+ 7. (3) Уравнение (3) равносильно уравнению
x – 2 + 2 x – 2 x + 3 + x + 3 = 3x
+ 7. (3) Уравнение (3) равносильно уравнению
2 x – 2 x + 3 = x + 6. (4)
Возведём уравнение (4) в квадрат, получим его следствие, а значит, и следствие исходного уравнения:
4x2 + 4x – 24 = x2 + 12x + 36. (5)
![]() Уравнение (5) имеет два
корня: x1 = 6 и x2 = –
Уравнение (5) имеет два
корня: x1 = 6 и x2 = –![]() . Проверка
показывает, что число x1 является корнем исходного уравнения,
так как 6 – 2 + 6 + 3 = 5 и
. Проверка
показывает, что число x1 является корнем исходного уравнения,
так как 6 – 2 + 6 + 3 = 5 и
3 · 6 + 7 = 5, а x2 не является, так как выражение
![]() –
– 2 не имеет смысла. Следовательно, исходное уравнение имеет
единственный корень x1.
–
– 2 не имеет смысла. Следовательно, исходное уравнение имеет
единственный корень x1.
Ответ. 6.
365. Решите уравнение:
![]()
![]() в) 3x + 1 = |2x – 1|; д)
3 x – 1 = x – 1.
в) 3x + 1 = |2x – 1|; д)
3 x – 1 = x – 1.
Решение. в) Возведя исходное уравнение в квадрат, получим его следствие:
3x + 1 = 4x2 – 4x + 1. (6)
Уравнение (6) имеет два корня: x1
= 0 и x2 = ![]() . Проверка показывает, что оба числа x1
и x2 являются корнями исходного уравнения. Следовательно,
исходное уравнение имеет только эти два корня.
. Проверка показывает, что оба числа x1
и x2 являются корнями исходного уравнения. Следовательно,
исходное уравнение имеет только эти два корня.
д) Возведя исходное уравнение в нечётную третью степень, получим равносильное ему уравнение: x – 1 = (x – 1)3,
которое перепишем в виде
(x – 1)((x – 1)2 – 1) = 0. (7)
Уравнение (7) имеет три корня: x1 = 0, x2 = 1 и x3 = 2, следовательно, и равносильное ему исходное уравнение имеет те же три корня.
Ответ. в) 0; ![]() ; д) 0; 1;
2.
; д) 0; 1;
2.
366. Решите уравнение:
а) x2 + 2x + 10 + x2 + 2x + 17 = 7;
![]() д) 1 + 2 = 2.
д) 1 + 2 = 2.
x2 – 6x + 10 x2 – 6x + 13
Решение. а) Уравнение можно решить переходом к уравнению-следствию. Для этого надо один из корней перенести в правую часть уравнения:
![]() x2 + 2x +
17 = 7 – x2 + 2x
+ 10 , (8) затем возвести в квадрат:
x2 + 2x +
17 = 7 – x2 + 2x
+ 10 , (8) затем возвести в квадрат:
x2 + 2x + 17 = 49 – 14 x2 + 2x + 10 + x2 + 2x + 10,
в полученном уравнении надо привести подобные члены, уединив корень в левой части уравнения и разделив полученное уравнение на 14:
![]() x2 + 2x + 10 = 3. (9)
x2 + 2x + 10 = 3. (9)
Возведя уравнение (9) в квадрат, получим его следствие, являющееся также следствием исходного уравнения: x2 + 2x + 10 = 9. (10)
Уравнение (10) имеет единственный корень: x1 = –1. Проверкой убеждаемся, что он является и корнем исходного уравнения. Следовательно, исходное уравнение имеет единственный корень –1.
![]() Замечание 1.
При решении уравнения из задания 366 (а) можно применить два
разных способа замены неизвестного, обозначив буквой t или x2
+ 2x + 10, или x2 + 2x +
10 .
Замечание 1.
При решении уравнения из задания 366 (а) можно применить два
разных способа замены неизвестного, обозначив буквой t или x2
+ 2x + 10, или x2 + 2x +
10 .
В первом случае придём к уравнению t + t + 7 = 7,
![]() а во втором — к уравнению t + t2
+ 7 = 7. Второй способ предпочтительнее, так как потребуется лишь один
раз возводить уравнение в квадрат.
а во втором — к уравнению t + t2
+ 7 = 7. Второй способ предпочтительнее, так как потребуется лишь один
раз возводить уравнение в квадрат.
![]() Замечание
2. Отметим, что более эффектное решение этого уравнения получится у
наблюдательных учащихся, которые перепишут исходное уравнение в виде
Замечание
2. Отметим, что более эффектное решение этого уравнения получится у
наблюдательных учащихся, которые перепишут исходное уравнение в виде
![]() (x + 1)2 + 9 + (x + 1)2 + 16 = 7.
(11)
(x + 1)2 + 9 + (x + 1)2 + 16 = 7.
(11)
Теперь очевидно, что при x = –1 оба корня достигают своих наименьших значений 3 и 4 соответственно. Так как при этом уравнение (11) обращается в верное числовое равенство, то число x1 = –1 — корень уравнения (11) и исходного уравнения. Других корней уравнение (11) не име-
![]()
![]() 2 ет, так как при x –1 верны
неравенства (x + 1) + 9 3, (x + 1)2 + 16 4
и (x + 1)2 + 9 +
(x + 1)2 + 16 7.
2 ет, так как при x –1 верны
неравенства (x + 1) + 9 3, (x + 1)2 + 16 4
и (x + 1)2 + 9 +
(x + 1)2 + 16 7.
д) В этом уравнении лучше не переходить к уравне-
нию-следствию, так как его решение будет громоздким.
Приведём более простое решение. Перепишем исходное уравнение в виде
1 + 2 = 2. (12)
![]() (x – 3)2 + 1 (x – 3)2 + 4
(x – 3)2 + 1 (x – 3)2 + 4
Теперь очевидно, что при x = 3 уравнение (12) обращается в верное числовое равенство, т. е. число x1 = 3 — корень уравнения (12) и исходного уравнения. Других корней уравнение не имеет, так как при x 3 верно неравенство
1 + 2 2 .
(x – 3)2 + 1 (x – 3)2 + 4
Ответ. а) –1; д) 3.
367. ![]() а) Решите уравнение
(x2 – 4)( x + 1 – 2) =
0.
а) Решите уравнение
(x2 – 4)( x + 1 – 2) =
0.
Решение. Уравнение
x2 – 4 = 0
имеет два корня: x1 = 2 и x2 = –2. Из них только для числа x1 имеет смысл второй множитель в левой части исходного уравнения, следовательно, x1 — корень исходного уравнения, а x2 нет. Уравнение
![]() x + 1 – 2
= 0
x + 1 – 2
= 0
имеет единственный корень: x3 = 3. При этом значении x первый множитель в левой части исходного уравнения имеет смысл, следовательно, x3 — корень исходного уравнения.
Итак, исходное уравнение имеет два корня x1 и x3.
Ответ. 2; 3.
368. а) Решите уравнение
13x + 3 x + 3
![]() + 25 –
10 = 0.
+ 25 –
10 = 0.
![]()
![]() x + 3 13x + 3 Решение.
Введя новое неизвестное t = 13x + 3 , пере-
x + 3 13x + 3 Решение.
Введя новое неизвестное t = 13x + 3 , пере-
x + 3
пишем уравнение в виде
t
+ ![]() 25 – 10 = 0.
(13) t
25 – 10 = 0.
(13) t
Уравнение (13) имеет единственный корень: t1 = 5, следовательно, все корни исходного уравнения являются корнями уравнения
![]() 13x + 3
= 5. (14)
13x + 3
= 5. (14)
x + 3
Возведя уравнение (14) в квадрат, получим его следствие, являющееся также следствием исходного уравнения:
13![]() x + 3 = 25.
(15)
x + 3 = 25.
(15)
x + 3
Уравнение (15) имеет единственный корень: x1 = –6.
Следовательно, исходное уравнение имеет тот же корень.
Ответ. –6.
Промежуточный контроль. С–13*, К–3.
Дополнения к главе 2
1. Понятие степени с рациональным показателем 2. Свойства степени с рациональным показателем
В пункте 1 Дополнений вводится понятие степени по-
p
ложительного числа а с рациональным показателем ![]() , где q
, где q
p — целое число, q — натуральное число, q 2, и с помощью свойств корня степени q доказываются первые свойства степени с рациональным показателем:
p
![]() p 1 p pk ж ц
p 1 p pk ж ц ![]()
1) aq = зaq ч , 2) aq = aqk (k N), з ч и ш
pq
![]()
3) ap = a q (q N, q 2).
Рассмотрим «доказательство» софизма «–1 = 1»:
![]()
![]() 2
2 ![]() 1
1
–1 = (–1)1 = (–1)2 = –1(( )2 ) = 12 = 1.
Попросите учащихся найти ошибку в рассуждениях.
Ответ. Здесь переход после второго знака равенства совершён неверно: определение степени с рациональным показателем применено для отрицательного числа –1.
Подчеркнём, что рациональная степень числа a определена только для положительного числа a. Однако если рациональное число r положительно, то, применив к нему определение степени с рациональным показателем, получим, что p
![]() 0r
= 0q = q 0p
= q 0 = 0.
0r
= 0q = q 0p
= q 0 = 0.
Напомним, что записи 00 и 0–r (r 0) не имеют смысла. Также не имеет смысла запись ar, где a 0 и r — рациональное число, не являющееся целым числом.
При выполнении задания 378 используется это замечание.
В пункте 2 доказываются теоремы о свойствах степени с рациональным показателем, из которых следует, что свойства степеней, известные ранее для целых показателей, справедливы и для рациональных показателей.
Решения и комментарии 376. Вычислите:
а) ( )2 · (![]() 49);
б) (0 01, )–2 · (6 25, )–0 5, .
49);
б) (0 01, )–2 · (6 25, )–0 5, .
7 25
![]() –2
–2 ![]() 2
2
Решение. а) ( )2 · (![]() 49)
= ( ) · 49 = 49 · 7 = ;
49)
= ( ) · 49 = 49 · 7 = ;
7 25 25 4 5
![]()
![]()
![]() 1 –1 1 1 –
1 –1 1 1 – ![]()
![]() б) (0 01, )–
б) (0 01, )–![]() 2 · (6 25, )–0 5, = 1 ) 2 · ( ) 2 = 1002
· ( ) =
2 · (6 25, )–0 5, = 1 ) 2 · ( ) 2 = 1002
· ( ) =
100 = 10 · ![]() = 4.
= 4.
![]() 378. При каких
значениях a уравнение (ax)
378. При каких
значениях a уравнение (ax)![]() = 3 a : а) имеет единственный
корень;
= 3 a : а) имеет единственный
корень;
б) имеет бесконечное множество корней;
в) не имеет корней?
Решение. 1. Если a = 0, то для любого x R имеем
(0x)![]() = 0
= 0![]() ,
,
![]() так как
так как ![]() 0, и 3 0 = 0 по определению корня третьей
0, и 3 0 = 0 по определению корня третьей
степени. Следовательно, в этом случае любое число x R является корнем исходного уравнения, т. е. уравнение имеет бесконечное множество корней.
2. ![]() Если a 0, то 3 a 0.
Для любого x 0 имеем аx 0. Поэтому запись (ax)
Если a 0, то 3 a 0.
Для любого x 0 имеем аx 0. Поэтому запись (ax)![]() не имеет
смысла, т. е. среди x 0 нет корней исходного уравнения. Для x =
0 имеем
не имеет
смысла, т. е. среди x 0 нет корней исходного уравнения. Для x =
0 имеем
![]() аx
= 0 и (ax)
аx
= 0 и (ax)![]() = 0 3 a 0,
= 0 3 a 0,
![]() т.
е. x = 0 не является корнем исходного уравнения. Для любого x
0 по определению степени с рациональным показателем перепишем уравнение в
виде 3 3
т.
е. x = 0 не является корнем исходного уравнения. Для любого x
0 по определению степени с рациональным показателем перепишем уравнение в
виде 3 3
ax = a
или в виде
![]() 3 a · 3 x = 3 a , (1)
3 a · 3 x = 3 a , (1)
откуда следует, что для любого a 0 уравнение (1) имеет единственный корень x1 = 1.
3. ![]() Если a 0, то 3 a 0,
а левая часть исходного уравнения отрицательной быть не может, так как в
положительную рациональную степень можно возвести только неотрицательное число ax.
Поэтому в этом случае уравнение не имеет корней.
Если a 0, то 3 a 0,
а левая часть исходного уравнения отрицательной быть не может, так как в
положительную рациональную степень можно возвести только неотрицательное число ax.
Поэтому в этом случае уравнение не имеет корней.
Следовательно, исходное уравнение: а) имеет единственный корень 1 для каждого a 0; б) имеет бесконечное множество корней для a = 0; в) не имеет корней для каждого a 0.
384. е) Вычислите
![]()
![]()
![]() жж 2 1 цж 2
жж 2 1 цж 2 ![]() 1 цц
1 цц ![]() зз33 + 73 чз93 – 3 · 7 + 493 чч . з
зз33 + 73 чз93 – 3 · 7 + 493 чч . з
ии ши шш
Решение. Преобразуем данное выражение, применив формулу суммы кубов и свойства степени с рациональным показателем:
![]() жж 2 1 цж 2
жж 2 1 цж 2 ![]() 1 цц
1 цц![]()
![]()
![]() ззз33 + 73 чз93 – 3 · 7 + 493 чч = ии ши шш
ззз33 + 73 чз93 – 3 · 7 + 493 чч = ии ши шш
![]()
![]()
![]()
![]() = жзжз323 цч3 + жз713 цч3 цч = (32 + 7)
= жзжз323 цч3 + жз713 цч3 цч = (32 + 7)![]() = 1643 = жз(16)
= 1643 = жз(16)![]() 14 чц3
= 8. ии ш и
ш чш и ш
14 чц3
= 8. ии ш и
ш чш и ш
з
389. Упростите выражение:
1 –
![]() а) a a a · a 8 ; б)
а) a a a · a 8 ; б)
![]() Решение. а)
Сначала преобразуем выражение применив определение и свойства степени с
рациональным показателем, затем умножим полученный результат на a
Решение. а)
Сначала преобразуем выражение применив определение и свойства степени с
рациональным показателем, затем умножим полученный результат на a![]() .
.
![]()
![]()
![]()
![]() a a a = ж ж 1 ц12
цж ж 3 ц12 цч зa · ч з
a a a = ж ж 1 ц12
цж ж 3 ц12 цч зa · ч з
![]() Так как з зa a · 2 ч ч = зa · зa2 ч ч =
Так как з зa a · 2 ч ч = зa · зa2 ч ч =
з и ш ч з и ш ч и ш и ш
![]()
![]()
![]()
![]() ж
ж ![]() 3 ц
3 ц![]() ж 7 ц –
ж 7 ц –![]() 1
1
= зa a · 4 ч = зa4 ч = a, то a · a 8 = a = a. и ш и ш
![]()
![]() ж ж 1 12 12 цч
ж ж 1 12 12 цч
з
![]() б) Так как x
x x x = зз ж ц цч ч =
б) Так как x
x x x = зз ж ц цч ч =
з зз зиx x · 2 чш чч ч x · x ·
з и ш ч ![]() и ш
и ш
3
![]()
![]()
![]()
![]()
![]() жззx · ззжx · жзx2 цч12 цчч12 чччц = жзззx · жзиx x · 43 шцч12 ччцч = жзззx · жизx74 цшч12 чччц =
жззx · ззжx · жзx2 цч12 цчч12 чччц = жзззx · жзиx x · 43 шцч12 ччцч = жзззx · жизx74 цшч12 чччц =
=
з з и ш ч
з и ш ч и ш и ш и ш
![]() ж 7
ж 7![]() ц
ц![]() ж 15
ж 15![]() ц
ц![]()
= зx x · 8 ч = зx 8 ч = x, и ш и ш
![]()
![]()
![]() 3 15 ж 3
ц
3 15 ж 3
ц
![]() –
– –з ч
–
– –з ч
то x : x 16 = x16 и 16 ш = x = x.
Промежуточный контроль. С–16*.
3. Исторические сведения
В данном пункте излагается история изучения корней и степени с рациональным показателем.
Этот материал способствует формированию ответственного отношения к учению, готовности и способности учащихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов.
В этой главе вводится понятие числовой последовательности, разбираются основные способы задания числовой последовательности, главное внимание уделяется рассмотрению двух видов числовых последовательностей — арифметической и геометрической прогрессий.
В материалах для классов с углублённым изучением математики рассматриваются бесконечно убывающая геометрическая прогрессия и метод математической индукции, используемый для доказательства математических утверждений.
Цель изучения главы 3 — добиться, чтобы учащиеся овладели понятиями: числовая последовательность, арифметическая прогрессия, геометрическая прогрессия — и научились пользоваться основными формулами для арифметической и геометрической прогрессий. Кроме того, в классах с углублённым изучением математики учащиеся должны освоить доказательство математических утверждений с помощью метода математической индукции, что способствует достижению таких метапредметных результатов, как умение создавать обобщения, устанавливать аналогии, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение и делать выводы.
§ 6. Числовые последовательности и их свойства
В этом параграфе сначала вводится понятие числовой последовательности, а затем изучаются её свойства.
Основная цель изучения шестого параграфа — научить школьников понимать, что такое числовая последовательность и каковы способы её задания.
6.1. Понятие числовой последовательности
В данном пункте даются определения числовой последовательности, членов последовательности, её общего члена, приводятся примеры числовых последовательностей. Для классов с углублённым изучением математики рассматривается пример рекуррентного способа задания последовательности.
Задания для повторения. При изучении данного пункта можно использовать задание 1097.
409. Запишите формулу общего члена последовательности:
д) 1, –1, 1, –1, 1, –1, ...; е) –1, 1, –1, 1, –1, 1, ... .
Решение. д) Общий член последовательности имеет вид an = (–1)n + 1.
е) Общий член последовательности имеет вид bn = (–1)n.
411. Найдите сумму первых шести членов последова-тельности, заданной формулой общего члена:
а) an = 3n + 2; б) an = (–1)n · n.
Решение. По формуле общего члена последовательности найдём шесть первых членов последовательности, затем вычислим их сумму:
а) a1 = 5, a2 = 8, a3 = 11, a4 = 14, a5 = 17, a6 = 20,
5 + 8 + 11 + 14 + 17 + 20 = 75;
б) a1 = –1, a2 = 2, a3 = –3, a4 = 4, a5 = –5, a6 = 6, –1 + 2 – 3 + 4 – 5 + 6 = 3.
412. Числовая последовательность задана формулой общего члена xn = 10 + 2n.
а) Найдите x1, x10, x100.
б) Запишите последующий и предыдущий члены для xn (n 2).
в) Запишите член последовательности, имеющий но-
мер n + 2.
Решение. а) По формуле общего члена последовательности найдём x1 = 12, x10 = 30, x100 = 210.
б) xn + 1 = 10 + 2(n + 1) = 12 + 2n; xn – 1 = 10 + 2(n – 1) = 8 + 2n.
в) xn + 2 = 10 + 2(n + 2) = 14 + 2n.
414. Последовательность задана первыми членами: 1, 5, 9, ... . Запишите формулу её общего члена.
Решение. Учитывая, что члены последовательности увеличиваются на 4, можно составить формулу общего члена так:
xn = 1 + 4(n – 1),
или
xn = 4n – 3.
По этой формуле запишем первые пять членов последовательности: 1, 5, 9, 13, 17.
Однако это не единственное решение. Заметим, что первый и третий члены — квадраты чисел 1 и 3 (номеров членов). Для этих членов подошла бы формула общего члена xn = n2. Чтобы не менять значения первого и третьего члена и увеличить второй член на 1, добавим в эту
1 + –( 1)n
формулу слагаемое ![]() .
Для n = 2 это слагаемое рав-
.
Для n = 2 это слагаемое рав-
2
но 1, для нечётных номеров n оно равно 0. Итак, формула общего члена с теми же тремя первыми членами имеет вид n
1 + –( 1)
2
xn
= n + ![]() .
.
2
По этой формуле запишем первые пять членов последовательности: 1, 5, 9, 17, 25.
Две построенные последовательности различны, но три первые члена у них совпадают с тремя первыми членами заданной последовательности.
415. а) Последовательность задана рекуррентным спо-собом: a1 = 2, an + 1 = an + 3. Запишите первые пять её членов.
Решение. Подставляя в формулу an + 1 = an + 3 вместо n числа 1, 2, 3, 4 и заменив a1 числом 2, получим члены последовательности со второго по пятый, выпишем первые пять членов этой последовательности: 2, 5, 8, 11, 14.
416. а) Последовательность задана рекуррентным спо-собом: a1 = 3, an + 1 = an + 2. Задайте последовательность формулой n-го члена, вычислите первые пять её членов.
Решение. Подставляя в формулу an + 1 = an + 2 вместо n числа 1, 2, 3, 4 и заменив a1 числом 3, получим члены последовательности со второго по пятый, выпишем первые пять членов этой последовательности: 3, 5, 7, 9, 11. Учитывая, что члены последовательности увеличиваются на 2, можно составить формулу её n-го члена: xn = 3 + 2(n – 1),
или
xn = 2n + 1.
419. Числовая последовательность задана формулой n-го члена:
n
а) an =
5n; б) bn = 27 · ( )![]() .
.
Задайте последовательность рекуррентным способом.
Решение. а) Подставляя в формулу an = 5n вместо n числа 1, 2, 3, 4, ..., получим члены последовательности: 5, 10, 15, 20, ... . Так как каждый следующий член последовательности можно получить из предыдущего прибавлением числа 5, то последовательность можно задать рекуррентным способом: a1 = 5, an + 1 = an + 5.
n
б) Подставляя в формулу bn
= 27 · (
)![]() вместо n числа
вместо n числа
1, 2, 3, 4, ..., получим члены последовательности: 9, 3, 1,
![]() , ... . Так как
каждый следующий член последовательности можно получить из предыдущего
умножением на
, ... . Так как
каждый следующий член последовательности можно получить из предыдущего
умножением на ![]() , то последовательность можно задать
рекуррентным способом: a1
= 9, an
+ 1 = an ·
, то последовательность можно задать
рекуррентным способом: a1
= 9, an
+ 1 = an · ![]() .
.
420. а) Последовательность задана формулой n-го члена an = 177 – 3n. Сколько положительных членов у этой последовательности?
Решение. Найдём все натуральные числа n, для каждого из которых an 0. Для этого решим неравенство 177 – 3n 0.
Это неравенство равносильно неравенству n 59. Следовательно, у этой последовательности 58 положительных членов.
423. а) Найдите наименьший член последовательно-сти, заданной формулой общего члена
an = n2 – 19,8n + 113.
Решение. Рассмотрим функцию
y = x2 – 19,8x + 113 = (x – 9,9)2 + 14,99, которая при натуральных значениях x принимает значения, совпадающие с членами данной последовательности. Эта функция достигает наименьшего значения в точке x0 = 9,9. Так как число 9,9 не натуральное и 9 9,9 10, то наименьшим членом последовательности будет или a9, или a10.
Так как a9 = 92 – 19,8 · 9 + 113 = 15,8,
а
a10 = 102 – 19,8 · 10 + 113 = 15
и 15 15,8, то 15 — наименьший член последовательности.
424. а) Найдите все значения a, при каждом из которых последовательность, заданная формулой общего члена yn = n2 – 20n + 100 – a,
имеет единственный отрицательный член.
Решение. Запишем формулу общего члена в виде
yn = (n – 10)2 – a. (1)

Для каждого значения a рассмотрим функцию y = (x – 10)2 – a,
которая при натуральных значениях x принимает значения, совпадающие с членами данной последовательности. Отрицательные члены в этой последовательности будут только в случае, если выполнено неравенство
(x – 10)2 a. (2)
Рассмотрев для функции вида y = (x – 10)2 – a случаи:
1) a 0 (рис. 38, а);
2) a = 0 (рис. 38, б);
3) 0 a 1 (рис. 38, в);
4) a = 1 (рис. 38, г);
5) a 1 (рис. 38, д), определим, что при натуральных значениях x функция имеет единственное отрицательное значение только в случаях 3) и 4). Следовательно, данная последовательность имеет единственный отрицательный член при 0 a 1. Ответ. 0 a 1.
426. а) Докажите, что для любых натуральных n последовательность чисел Фибоначчи {un} обладает свойством:
u1 + u2 + ... + un = un + 2 – 1. (3)
Доказательство. Последовательность чисел Фибоначчи задаётся рекуррентно следующим образом: u1 = u2 = 1,
uk + 2 = uk + 1 + uk, (4) где k = 1, 2, 3, ... .
Подставим в равенство (4) значения k от 1 до n, получим n равенств:
u3 = u2 + u1, u4 = u3 + u2, u5 = u4 + u3,
. . . . . . . . . . . .
un + 1 = un + un – 1, un + 2 = un + 1 + un.
Сложив эти n равенств и вычтя из обеих частей полученного равенства одинаковые слагаемые, получим верное равенство:
un + 2 = u2 + u1 + u2 + u3 + ... + un – 1 + un. (5)
Заменив в правой части равенства (5) число u2 на 1 и вычтя из обеих частей равенства (5) по 1, получим верное равенство:
un + 2 – 1 = u1 + u2 + u3 + ... + un – 1 + un, что и доказывает равенство (3).
6.2. Свойства числовых последовательностей
В данном пункте даются определения монотонной последовательности и ограниченной последовательности, приводятся примеры монотонных и немонотонных последовательностей, а также примеры ограниченных последовательностей. Вводится понятие конечной последовательности. Отметим, что любая последовательность бесконечна, но если рассматриваются только несколько её первых членов, то в этом случае говорят, что последовательность конечна и у неё есть последний член.
Изучение этого материала поможет общему развитию учащихся, а также облегчит понимание аналогичного материала для функций.
Задания для повторения. При изучении данного пункта можно использовать задание 1098.
435. а) Последовательность
задана формулой n-го члена an = ![]() n – 1n .
Докажите, что последовательность является возрастающей и ограниченной.
n – 1n .
Докажите, что последовательность является возрастающей и ограниченной.
Решение. Для любого натурального n найдём члены последовательности с номерами n и n + 1:
an = ![]() n – 1n , an + 1 =
n – 1n , an + 1 = ![]() n + 1n .
n + 1n .
Вычислим разность:
n n – 1 1
![]() an + 1 – an = n + 1 – n = n n(
+ 1) .
an + 1 – an = n + 1 – n = n n(
+ 1) .
Так как для любого натурального n эта разность положительна, то an + 1 an для любого натурального n, т. е.
по определению эта последовательность возрастающая. Так как
n – 1 1
![]()
![]() =
1 – n n
=
1 – n n
для любого натурального n, то выполняется двойное неравенство 0 an 1.
Следовательно, последовательность является и ограниченной сверху, и ограниченной снизу, поэтому эта последовательность является ограниченной по определению.
438. Укажите все значения b, при которых последова-
1999n + b тельность,
заданная формулой an = ![]() 2000n ,
является:
2000n ,
является:
а) возрастающей; б) убывающей.
Решение. Так как для любого натурального n верны
![]() равенства an = 19992000 + 2000b n и an +
1 – an
=
равенства an = 19992000 + 2000b n и an +
1 – an
= ![]() 2000n n–(b + 1) , то последовательность будет возрастающей, если an
+ 1 – – an 0, т. е. при b
0; последовательность будет убывающей, если an + 1
– an 0, т. е. при b 0.
2000n n–(b + 1) , то последовательность будет возрастающей, если an
+ 1 – – an 0, т. е. при b
0; последовательность будет убывающей, если an + 1
– an 0, т. е. при b 0.
Если же b = 0, то последовательность не является ни возрастающей, ни убывающей, все её члены совпадают.
Ответ. а) При b 0; б) при b 0. Промежуточный контроль. С–17.
§ 7. Арифметическая прогрессия
В этом параграфе сначала вводится понятие арифметической прогрессии, затем изучаются её свойства.
Основная цель изучения седьмого параграфа — овладеть понятием арифметической прогрессии, изучить её свойства и научиться их использовать.
7.1. Понятие арифметической прогрессии 7.2. Сумма первых n членов арифметической прогрессии
В пункте 7.1 даются определения арифметической прогрессии, её разности и рассматриваются основные свойства арифметической прогрессии. Следует обратить внимание на задачу, с помощью которой выводится формула простых процентов.
В пункте 7.2 приведена формула суммы первых n членов арифметической прогрессии. Этим материалом должны овладеть все учащиеся.
Обратим внимание на то, что рассуждения в тексте учебника лишь подводят к гипотезе о формулах n-го члена арифметической прогрессии и суммы первых n членов арифметической прогрессии (эти рассуждения часто принимают за доказательства). Полные доказательства этих формул можно провести в классе с углублённым изучением математики после изучения метода математической индукции.
Задания для повторения. При изучении данного пункта можно использовать задания 1101—1106.
443. Является ли арифметической прогрессией после-довательность:
а) –5; –2; 1; 1; 4; 7; 10; ...;
в) 1 ![]() ; 1
; 1 ![]() ; 1
; 1 ![]() ; 1
; 1
![]() ;
1
;
1 ![]() ; ...?
; ...?
Решение. а) Так как a3 – a2 a4 – a3, то последовательность не является арифметической прогрессией.
в) Так как a2 – a1 a3 – a2, то последовательность не
является арифметической прогрессией.
444. Запишите первые четыре члена арифметической прогрессии, если a1 = 2, d = –3.
Решение. По определению арифметической прогрессии имеем a2 = a1 + d = –1, a3 = a2 + d = –4, a4 = a3 + d = –7.
Ответ. 2, –1, –4, –7.
447. Докажите, что в арифметической прогрессии {an}
am – ak разность d можно вычислить по формуле d = , m – k
m k.
Решение. По формуле n-го члена арифметической прогрессии имеем
am = a1 + (m – 1)d, ak = a1 + (k – 1)d,
am – ak = (m – 1 – k + 1)d = (m – k)d.
Так как m k, то d = am – ak , что и требовалось докаm – k зать.
451. Является ли число 12 членом арифметической прогрессии:
б) –11; –8; –5; ...; г) 44,5; 43; 41,5; ...?
Решение. б) Сначала найдём разность арифметической прогрессии:
d = –8 – (–11) = 3.
Если 12 является членом арифметической прогрессии с номером n, то верно равенство
12 = –11 + (n – 1) · 3,
из которого следует, что n =
8 ![]() . Так как номер члена арифметической
прогрессии — число натуральное, то число 12 не является членом этой
арифметической прогрессии.
. Так как номер члена арифметической
прогрессии — число натуральное, то число 12 не является членом этой
арифметической прогрессии.
г) Сначала найдём разность арифметической прогрессии: d = 43 – 44,5 = –1,5.
Если 12 является членом арифметической прогрессии с номером n, то верно равенство
12 = 44,5 + (n – 1) · (–1,5),
из которого следует, что n =
22 ![]() . Так как номер члена арифметической
прогрессии число натуральное, то число 12 не является членом арифметической
прогрессии.
. Так как номер члена арифметической
прогрессии число натуральное, то число 12 не является членом арифметической
прогрессии.
453. а) Сколько положительных членов имеет арифметическая прогрессия 3,8; 3,5; 3,2; ...?
Решение. Сначала найдём разность арифметической прогрессии:
d = 3,5 – 3,8 = –0,3.
По формуле n-го члена арифметической прогрессии имеем
an = 3,8 + (n – 1) · (–0,3) = 4,1 – 0,3n.
Найдём все натуральные n, для которых верно
неравенство 4,1 – 0,3n 0. Решив это неравенство, получим, что n 13
![]() .
Так как решениями этого неравенства являются лишь натуральные числа от 1 до 13,
то эта арифметическая прогрессия имеет 13 положительных членов.
.
Так как решениями этого неравенства являются лишь натуральные числа от 1 до 13,
то эта арифметическая прогрессия имеет 13 положительных членов.
455. Докажите, что последовательность, заданная формулой общего члена:
а) an = 3n – 7; б) an = –3n + 5,
является арифметической прогрессией.
Решение. а) Так как для данной последовательности
{an} для любого натурального n разность
an + 1 – an = 3(n + 1) – 7 – (3n – 7) = 3
число постоянное, то эта последовательность является арифметической прогрессией с разностью d = 3.
б) Так как для данной последовательности {an} для лю-
бого натурального n разность
an + 1 – an = –3(n + 1) + 5 – (–3n + 5) = –3
число постоянное, то эта последовательность является арифметической прогрессией с разностью d = –3.
457. Предприниматель взял в банке кредит на сумму а р. при условии, что в конце каждого месяца его долг перед банком будет увеличиваться на р% от суммы взятого кредита. Предприниматель вернул деньги банку сполна в сумме b р. через n месяцев.
а) Какую сумму предприниматель вернул банку, если
а = 500 000, р = 2, n = 10?
б) На какую сумму предприниматель взял кредит, если р = 2, n = 12, b = 992 000?
в) Через сколько месяцев предприниматель вернул
банку деньги, если а = 600 000, р = 3, b = 852 000?
г) Под какой процент в месяц предприниматель взял
кредит, если а = 700 000, n = 6, b = 910 000?
Решение. а) Предприниматель вернул банку 500 000 р.
и ещё по 2% от этой суммы за каждый из 10 месяцев, т. е.
500 000 · · 2 10
500 000
+ ![]() = 600 000
(р.).
= 600 000
(р.).
100
б) Так как за 12 месяцев предприниматель выплатил дополнительно 12 · 2 = 24 (%) взятой в кредит суммы, то 992 000 р. составляет 100 + 24 = 124 (%) взятой в кредит суммы, которая равна
![]() = 800 000 (р.).
= 800 000 (р.).
в) Так как 852 000 р. от 600 000 составляют
![]() = 142 (%)
= 142 (%)
взятой в кредит суммы, то за пользование кредитом предприниматель вернул банку 142 – 100 = 42 (%) взятой в кредит суммы. Предприниматель вернул кредит через 42 : 3 = 14 (месяцев).
г) Так как 910 000 р. от 700 000 составляют
![]() = 130 (%)
= 130 (%)
взятой в кредит суммы, то за пользование кредитом предприниматель вернул банку 130 – 100 = 30 (%) взятой в кредит суммы. Предприниматель взял кредит под 30 : 6 = 5 (%) в месяц.
Ответ. а) 600 000 р.; б) 800 000 р.; в) 14 месяцев;
г) 5%.
458. Покажите, как ответ к каждой задаче из предыдущего номера можно получить с помощью формулы общего члена арифметической прогрессии.
Решение. После первого месяца долг предпринимателя
pa pa увеличится на ![]() р. и станет равным a +
р. и станет равным a + ![]() р. Суммы
р. Суммы
100 100
долга в конце каждого месяца образуют арифметическую
pa
прогрессию с первым членом a1 = a + 100![]() (р.) и разностью pa
(р.) и разностью pa
![]() р.,
поэтому после n месяцев сумма его долга может
р.,
поэтому после n месяцев сумма его долга может
100 быть получена как n-й член этой прогрессии, т. е.
ap pn
![]() b = an = a1
+ (n – 1)d = a + 100 ·
n = a 1 + ( 100) (р.).
b = an = a1
+ (n – 1)d = a + 100 ·
n = a 1 + ( 100) (р.).
![]()
![]() Таким образом, b =
a 1 + ) (р.). pn
Таким образом, b =
a 1 + ) (р.). pn
100
Далее в каждой из задач предыдущего номера по известным значениям трёх величин можно получить значение четвёртой величины.
464. а) Определите сумму первых 40 чётных натуральных чисел.
б) Определите сумму всех трёхзначных натуральных
чисел.
Решение. а) Здесь требуется определить сумму первых членов арифметической прогрессии, у которой a1 = 2, d = 2. По формуле суммы первых n членов арифметической прогрессии для n = 40 имеем
![]() 2a1 + (40
– 1)d
2a1 + (40
– 1)d
S40
= ![]() 2 · 40
= · 40 =
1640.
2 · 40
= · 40 =
1640.
Итак, сумма первых 40 чётных натуральных чисел равна 1640.
б) Здесь требуется определить сумму чисел от 100 до 999, т. е. сумму первых 900 членов арифметической прогрессии, у которой a1 = 100, d = 1. По формуле суммы первых n членов арифметической прогрессии (n = 900) имеем
2a1 + (900 – 1)d
S900
= ![]() 2 · 900
=
2 · 900
=
= ![]() · 900
= 494 550.
· 900
= 494 550.
Итак, сумма всех трёхзначных натуральных чисел равна 494 550.
Ответ. а) 1640; б) 494 550.
466. Сложили несколько первых членов арифметической прогрессии {аn} и получили 430. Сколько членов сложили, если а1 = –7, d = 3?
Решение. Применяя формулу суммы первых n членов арифметической прогрессии, имеем
2a1 + (n – 1)d –14 + (n – 1 · ) 3
![]() Sn = 2 · n =
Sn = 2 · n = ![]() 2 · n
= 430.
2 · n
= 430.
Уравнение
–14 + (n – 1 · ) 3
![]() · n
= 430
· n
= 430
2
имеет два корня: n1
= –14 ![]() , n2 = 20.
Так как номер члена
, n2 = 20.
Так как номер члена
арифметической прогрессии может быть только натуральным числом, то сложили 20 членов арифметической прогрессии.
Ответ. 20.
471. Для арифметической прогрессии {аn} вычислите S2001, если а1001 = 2000.
Решение. По формуле суммы первых n членов арифметической прогрессии для n = 2001 имеем
2a1 + (2001 – 1)d
![]() S2001 = 2 · 2001 =
S2001 = 2 · 2001 =
= (a1 + 1000d) · 2001 = а1001 · 2001 = = 2000 · 2001 = 4 002 000.
Ответ. 4 002 000.
473. Задача из папируса Ахмеса (XVIII—XVII
вв. до н. э.). Разделите 10 мер хлеба на 10 человек, если разность между
количеством хлеба у каждого человека и ему предшествующего составляет ![]() меры.
меры.
Решение. Сначала найдём первый
член арифметической прогрессии, у которой 10 членов, d = ![]() и
сумма де-
и
сумма де-
сяти членов равна 10. По формуле суммы первых n членов арифметической прогрессии для n = 10 имеем
![]()
![]() 2a1 + (10
– 1 · ) 18 · 10 = (a1 + 9 ) · 10 .
2a1 + (10
– 1 · ) 18 · 10 = (a1 + 9 ) · 10 .
S10 = 2 16
Уравнение
![]() (a1 + 9 ) · 10 = 10
(a1 + 9 ) · 10 = 10
16
имеет единственный корень a1
= ![]() .
.
Итак, первому надо дать ![]() меры, а каждому
следующему на
меры, а каждому
следующему на ![]() меры больше.
меры больше.
474. В арифметической прогрессии сумма первых m членов равна сумме первых n членов (m n). Докажите, что сумма первых (m + n) членов равна нулю.
Доказательство. По условию задачи сумма первых m членов равна сумме первых n членов (m n), т. е. верно равенство 2a1 + (m – 1)d 2a1 + (n – 1)d
![]()
![]() · m
= · n ,
· m
= · n ,
2 2
из которого получим, что
(m – n)(2a1 + (m + n – 1)d) = 0.
Так как m n, то, разделив последнее равенство на m – n 0, получим, что
2a1 + (m + n – 1)d = 0. (1) Применив формулу суммы первых (m + n) членов арифметической прогрессии, получим
2a1 + (m + – 1n )d
![]() Sm
+ n = 2 · (m + n) . (2)
Sm
+ n = 2 · (m + n) . (2)
Из равенства (1) следует, что числитель дроби в равенстве (2) равен 0, следовательно, Sm + n = 0, что и требовалось доказать.
Дополнительное задание. Сумма членов арифметической прогрессии со второго по шестой на 15 больше суммы членов той же прогрессии с первого по пятый. Найдите разность этой арифметической прогрессии.
Решение. I способ. По условию a1 + a2 + a3 + a4 + a5 + 15 = a2 + a3 + a4 + a5 + a6,
следовательно, a6 – a1 = 15. Так как a6 = a1 + 5d, то из равенства a1 + 5d – a1 = 15
найдём, что d = 3.
II способ. Каждый член суммы a2 + a3 + a4 + a5 + a6 на d больше соответствующего члена суммы a1 + a2 +
+ a3 + a4 + a5, поэтому
5d = 15,
откуда найдём, что d = 3.
Ответ. d = 3.
Промежуточный контроль. С–18, К–4.
§ 8. Геометрическая прогрессия
В этом параграфе сначала вводится понятие геометрической прогрессии, затем изучаются её свойства.
Основная цель изучения восьмого параграфа — овладеть понятием геометрической прогрессии, изучить её свойства и научиться их использовать.
В классах с углублённым изучением математики следует изучить бесконечно убывающую геометрическую прогрессию.
В пункте 8.1 даются определения геометрической прогрессии, её знаменателя и рассматриваются основные свойства геометрической прогрессии. В пункте 8.2 приводится формула суммы первых n членов геометрической прогрессии. Этим материалом должны овладеть все учащиеся.
Особое внимание надо обратить на задачу, с помощью которой выводится формула сложных процентов.
Следует подчеркнуть, что существуют два способа процентного роста — по формуле простых процентов и по формуле сложных процентов, и объяснить, чем эти способы различаются. При этом учащиеся должны понимать, что если, например, вкладывать деньги в банк под один и тот же процент и на один и тот же срок, то прирост вклада по формуле сложных процентов будет большим за счёт процентов на процентные деньги.
Действительно, если при вкладе на простые проценты после n месяцев вклад в a р. под p% в месяц превратится
p в a(1 + nd) р.,
где d = ![]() , то при вкладе
на сложные про-
, то при вкладе
на сложные про-
100
центы он
превратится в a(1 + d)n = a(1 +
nd + ![]() n n( – 1) · d2
+ ... + dn) р.
n n( – 1) · d2
+ ... + dn) р.
2
Здесь в скобках записано разложение (1 + d)n по формуле бинома Ньютона (см. Дополнения к главе 5).
Обратим внимание на то, что рассуждения в тексте учебника лишь подводят к гипотезе о формулах n-го члена геометрической прогрессии и суммы первых n членов геометрической прогрессии (эти рассуждения часто принимают за доказательства). Полные доказательства этих формул можно провести в классе с углублённым изучением математики после изучения метода математической индукции.
Задания для повторения. При изучении данного пункта можно использовать задания 1118, 1120, 1123—1125.
Решения и комментарии
478. Является ли геометрической прогрессией последовательность:
а) 1; 8; 15; 21; 26; ...; б) 4; 2; 1; 0,5; 0,25; ...?
Решение. а) Так как a2 : a1 a3 : a2, то последовательность не является геометрической прогрессией.
б) Так как a2 : a1 = a3 : a2 = a4 : a3 = a5 : a4 = 0,5, то последовательность может являться геометрической прогрессией со знаменателем q = 0,5, если последующие члены прогрессии будут получаться по формуле 4 · (0,5)n–1.
482. Даны три последовательных члена геометрической прогрессии:
а) 7; x; 63. Найдите x, если x 0;
б) 2; x; 18. Найдите x, если x 0.
![]() Решение.
а) Пользуясь свойством геометрической прогрессии с положительными членами,
имеем an + 1 = an · an
+ 2 = 7 · 63
= 21, т. е. x = 21.
Решение.
а) Пользуясь свойством геометрической прогрессии с положительными членами,
имеем an + 1 = an · an
+ 2 = 7 · 63
= 21, т. е. x = 21.
б) Так как для геометрической прогрессии с произ-
вольными членами верно равенство an + 1 : an = an + 2 : an + 1, то число x является корнем уравнения x : 2 = 18 : x. Это уравнение имеет два корня: x1 = –6, x2 = 6. Так как x 0, то x = –6.
Ответ. а) 21; б) –6.
483. а) Найдите a1 и q геометрической прогрессии {аn}, если a4 – a2 = 18 и a5 – a3 = 36.
Решение. Перепишем данные равенства, используя a1 и q:
a1q3 – a1q = 18 и a1q4 – a1q2 = 36.
Для решения задачи надо решить систему полученных уравнений с неизвестными a1 и q. Вынеся за скобки q во втором уравнении и заменив a1q3 – a1q числом 18, получим уравнение 18q = 36. Оно имеет единственный корень q = 2. Теперь, подставив вместо q число 2 в первое уравнение, получим уравнение 8a1 – 2a1 = 18, которое имеет единственный корень a1 = 3.
Ответ. a1 = 3, q = 2.
484. а) Докажите, что для любой геометрической про-
грессии {bn} верно равенство bb97 + + bb109 = bb119 + + bb1112 .
Доказательство. Перепишем доказываемое равенство, используя b1 и q:
![]() b q1 8 + b q1 9 = b q1 10 + b q1 11 . (1)
b q1 8 + b q1 9 = b q1 10 + b q1 11 . (1)
6 8 8 10 b q1 + b q1 b q1 + b q1
Так как b1 0 и q 0, то дробь в левой части равенства (1) можно сократить на b1q6, а дробь в правой части — на b1q8. Получится равенство
q2 + q3 q2 + q3
![]() 2 = 2 . (2)
2 = 2 . (2)
1 + q 1 + q
Так как равенство (2) выполняется для любых q, то, рассуждая в обратном порядке, из справедливости равенства (2) получим, что справедливо равенство (1), что и требовалось доказать.
487. а) Задача И. Ньютона (1643–1727). Даны четыре последовательных члена геометрической прогрессии. Сумма двух крайних членов равна 13, двух средних равна 4. Определите эти члены.
Решение. Пусть даны четыре члена геометрической
прогрессии: an, an + 1, an + 2, an + 3. По условию задачи верны два равенства:
an + an + 3 = 13 и an + 1 + an + 2 = 4,
т. е. an + anq3 = 13 и anq + anq2 = 4.
Для решения задачи надо решить систему полученных уравнений с двумя неизвестными an и q. Перепишем эти уравнения в виде
an(1 + q)(1 – q + q2) = 13 и anq(1 + q) = 4.
Так как q 0, то, найдя из
второго уравнения системы, что an(1 + q) =
![]() 4q , и подставив в первое
уравнение
4q , и подставив в первое
уравнение ![]() 4q вместо an(1
+ q), получим уравнение
4q вместо an(1
+ q), получим уравнение
4 1( – + q q2)
= 13, q
имеющее два корня: q1
= 4, q2 = ![]() .
.
Если q = 4, то из
второго уравнения получим, что an = ![]() , т. е.
искомые члены геометрической прогрессии:
, т. е.
искомые члены геометрической прогрессии:
![]()
![]() 1 4 16 , , , .
1 4 16 , , , .
5 5 5
Если q = ![]() , то из второго
уравнения получим, что
, то из второго
уравнения получим, что
![]()
![]() an =
64 ,
т. е. искомые члены геометрической прогрессии: 5 , 16 , 4 , 1 .
an =
64 ,
т. е. искомые члены геометрической прогрессии: 5 , 16 , 4 , 1 .
5 5 5
![]()
![]()
![]()
![]() Мы получили
в двух случаях одни и те же члены, но они различаются порядком: в первом случае
они являются членами возрастающей прогрессии, во втором — убывающей. Ответ.
1 ,
4 ,
16 ,
или , 16 ,
4 ,
1 .
Мы получили
в двух случаях одни и те же члены, но они различаются порядком: в первом случае
они являются членами возрастающей прогрессии, во втором — убывающей. Ответ.
1 ,
4 ,
16 ,
или , 16 ,
4 ,
1 .
5 5 55 5 5
488. В начале месяца вкладчик положил на счёт в банке а р. при условии, что в конце каждого месяца на его счёт будет начисляться р% от той суммы вклада, которая будет находиться на его счёте в начале этого месяца. Вкладчик не снимал деньги со счёта n месяцев, а в начале (n + 1)-го месяца снял со счёта все деньги в сумме b р.
а) Какую сумму вкладчик снял со счёта, если а = 600 000, р = 1, n = 2?
б) Какую сумму вкладчик положил на счёт, если
b = 530 604, р = 2, n = 3?
в) Покажите, как ответ к каждой из задач а) и б) можно получить с помощью формулы общего члена геометрической прогрессии.
Решение. а) В конце первого месяца сумма 600
000 р. увеличится на ![]() = 6000 (р.) и превратится в
600 000 +
= 6000 (р.) и превратится в
600 000 +
+ 6 000 = 606
000 (р.). В конце второго месяца сумма 606 000 р. увеличится на ![]() =
6060 (р.) и превратит-
=
6060 (р.) и превратит-
ся в 606 000 + 6060 = 612 060 (р.), т. е. вкладчик снял со счёта 612 060 р.
б) В конце первого месяца сумма a р. увеличится на
a · 2
![]() =
0,02a (р.) и превратится в a + 0,02a = 1,02a
(р.),
=
0,02a (р.) и превратится в a + 0,02a = 1,02a
(р.),
100
т. е. увеличится в 1,02 раза. В конце второго месяца сумма 1,02a р. увеличится на 2%, т. е. в 1,02 раза, и превратится в a · 1,022 р. В конце третьего месяца сумма a · 1,022 р. увеличится ещё раз на 2%, т. е. в 1,02 раза, и превратится в a · 1,023 = 1,061208a р., что по условию задачи равно 530 604 р. Из уравнения
1,061208a = 530 604
найдём его единственный корень a = 500 000, т. е. вкладчик положил на счёт 500 000 р.
в) Суммы на счёте в начале 1-го, 2-го, ..., n-го, (n + 1)-го месяцев образуют геометрическую прогрессию с
p первым членом a и знаменателем
q = 1 + ![]() , так
как
, так
как
100
p каждая следующая сумма больше
предыдущей в 1 + ![]()
100 раза:
1 2 n
![]()
![]()
![]()
![]() a, a1 + ) ,
a(1 + ) , ..., a(1 + ) . p p p
a, a1 + ) ,
a(1 + ) , ..., a(1 + ) . p p p
100 100 100
В заданиях а) и б) сумму b р. сняли через n месяцев,
т. е. в начале (n + 1)-го месяца, поэтому верно равенство:
n
![]() p
p
![]() b
= a1 + ) . (1)
b
= a1 + ) . (1)
100
Далее в каждом из пунктов а) и б) по известным значениям трёх величин из равенства (1) можно получить значение четвёртой величины.
493. а) Вычислите сумму первых десяти членов геометрической прогрессии –32; 16; –8; 4; ... .
Решение. Сначала найдём знаменатель q геометрической прогрессии {аn}:
q = a2 : a1
= 16 : (–32) = – ![]() .
.
Теперь вычислим сумму:
( ) –32 · жз1 – –жз 1 цч10 цчч
![]()
![]() a1 1 – qn = зи и 2ш ш = –. S10 = 1 – q 1 +
a1 1 – qn = зи и 2ш ш = –. S10 = 1 – q 1 + ![]()
Ответ. – ![]() .
.
496. Сумма первых десяти членов геометрической прогрессии равна 64, произведение первого и десятого членов равно 16. Найдите сумму чисел, обратных этим десяти членам геометрической прогрессии.
Решение. По условиям задачи для геометрической прогрессии {аn} составим два равенства:
a1 + a1q + a1q2 + a1q3 + a1q4 +
+ a1q5 + a1q6 + a1q7 + a1q8 + a1q9 = 64,
a1 · a1q9 = 16.
Вынесем в левой части первого равенства за скобки число a q12 9 :
![]() жзи 1 9 + 1 8
+ 1 7 + 1 6 + 1 5
+ 1 4 + 1 3 + 1 2
+ a q11 + a11 цчш a q1 a q1 a q1 a q1 a q1 a q1 a q1 a q1
жзи 1 9 + 1 8
+ 1 7 + 1 6 + 1 5
+ 1 4 + 1 3 + 1 2
+ a q11 + a11 цчш a q1 a q1 a q1 a q1 a q1 a q1 a q1 a q1
a q12 9 = 64,
затем, заменив в полученном равенстве a q12 9 на 16 и разделив полученное равенство на 16, перепишем его в виде
1 1 1 1 1 1 1 1 1 1
![]()
![]() + + + + + + + + + = 4. a10 a9 a8 a7 a6 a5 a4 a3 a2 a1
+ + + + + + + + + = 4. a10 a9 a8 a7 a6 a5 a4 a3 a2 a1
Итак, найдена сумма десяти чисел, обратных первым десяти членам данной геометрической прогрессии. Ответ. 4.
Промежуточный контроль. С–19, С–20*.
В данном пункте вводятся понятия бесконечно убывающей геометрической прогрессии и её суммы. Приводятся примеры вычисления суммы бесконечно убывающей геометрической прогрессии.
Материал этого пункта предназначен для классов с углублённым изучением математики, однако при наличии времени хотя бы часть этого материала можно разобрать и в обычном классе. Дело в том, что некоторые задания на вычисление суммы бесконечно убывающей геометрической прогрессии имеют наглядные иллюстрации и доступны в обычном классе, а вычисление суммы бесконечного ряда — новый шаг в постижении математики, интересный всем учащимся.
Задания для повторения. При изучении данного пункта можно использовать задания 1137, 1138, 1140.
Решения и комментарии
499. Обратите в обыкновенную дробь бесконечную пе-риодическую десятичную дробь: а) 0,(3); г) 0,(13).
Решение. а) Так как 0,(3) = 0,3 + 0,03 + 0,003 + ... — сумма бесконечно убывающей геометрической прогрессии {аn}, у которой a1 = 0,3, q = 0,1, то
![]() a1 =
0 3, = 1 .
a1 =
0 3, = 1 .
S =
1 – q 1 – 0,1 3
г) Так как 0,(13) = 0,13 + 0,0013 + 0,000013 + ... — сумма бесконечно убывающей геометрической прогрессии {аn}, у которой a1 = 0,13, q = 0,01, то
![]() a1 =
0 13, = 13 .
a1 =
0 13, = 13 .
S =
1 – q 1 – 0,01 99
500. Задача П. Ферма (1601—1665). Докажите, что для бесконечно убывающей геометрической прогрессии
S a1
{аn}, имеющей сумму
S, выполняется равенство ![]() S – a1 = a2 .
S – a1 = a2 .
Решение. Выразим левую часть доказываемого равенства через a1 и q, затем заменим a1q на a2:
a1
![]() S = 1 – q = a1 = a1 = a1 ,
S = 1 – q = a1 = a1 = a1 ,
S – a1 a1 – a1 a1 – a1(1 – q) a q1 a2
1 – q
что и требовалось доказать.
501. а) Найдите сумму бесконечно убывающей геоме-трической прогрессии:
![]() ; 1;
; 1; ![]() ; …
; …
Решение. Сначала найдём знаменатель q геометрической прогрессии {аn}:
q = a3 : a2
= ![]() :
1 =
:
1 = ![]() .
.
Теперь вычислим сумму бесконечно убывающей геометрической прогрессии:

Ответ. ![]() .
.
502.
![]() а) Дан острый угол, величина которого равна a. На его стороне на
расстоянии l от вершины отметили точку А1. Из неё
провели перпендикуляр А1А2 ко второй
стороне угла, из точки А2
провели перпендикуляр А2А3 к
первой стороне и т. д. (рис. 39). Получилась ломаная с бесконечным числом
звеньев. Вычислите её длину, если l = 1 м, a = 45°.
а) Дан острый угол, величина которого равна a. На его стороне на
расстоянии l от вершины отметили точку А1. Из неё
провели перпендикуляр А1А2 ко второй
стороне угла, из точки А2
провели перпендикуляр А2А3 к
первой стороне и т. д. (рис. 39). Получилась ломаная с бесконечным числом
звеньев. Вычислите её длину, если l = 1 м, a = 45°.
Решение. I способ. В прямоугольных треугольниках А1А2А3, А2А3А4, ... имеются острые углы, равные углу А1АA2 (острые углы с взаимно перпендикулярными сторонами). Выразим сумму
S = А1А2 + А2А3 + А3А4 + ... 6 Рис. 39 через l и a:
S = l · sin a + l · sin a · cos a + l · sin a · cos2a + ... .
![]()
![]() Теперь вычислим сумму
бесконечно убывающей геометрической прогрессии со знаменателем q
= cos a
и первым членом l · sin a
(|q| 1, так как угол a
острый):
Теперь вычислим сумму
бесконечно убывающей геометрической прогрессии со знаменателем q
= cos a
и первым членом l · sin a
(|q| 1, так как угол a
острый):
II способ. Из вершины угла A проведём два луча, перпендикулярные сторонам данного угла, и продолжим звенья ломаной до пересечения с этими лучами (рис. 40).
Так как перпендикуляры, проведённые к одной прямой, параллельны, то образуются параллелограммы А1А2C2C1, А2А3B2B1, ... . По свойству параллелограмма имеем А1А2 = C1C2, А2А3 = B1B2, ... . Все звенья ломаной отложатся на построенных лучах, и длина ломаной с бесконечным числом звеньев равна сумме длин двух отрезков AB1 и AС1, причём AB1 = А2А3 + А4А5 + ... и
![]() AС1
= А1А2 + А3А4+
... . Тогда в пря- 6 Рис. 40 моугольном треугольнике А1AB1
с острым углом B1, равным a,
AB1 = tg la = tg145 = 1,
а в прямоугольном треугольнике А1АC1 с
острым углом С1, равным a,
AС1
= А1А2 + А3А4+
... . Тогда в пря- 6 Рис. 40 моугольном треугольнике А1AB1
с острым углом B1, равным a,
AB1 = tg la = tg145 = 1,
а в прямоугольном треугольнике А1АC1 с
острым углом С1, равным a,
![]()
![]() AС1 = sinl a = sin145 = 2 ,
AС1 = sinl a = sin145 = 2 ,
т. е. S = AB1 + AС1 = 2 + 1 (м).
![]() Ответ. 2
+ 1 (м).
Ответ. 2
+ 1 (м).
![]() Замечание.
Если решить задачу вторым способом в общем виде, то получится результат
Замечание.
Если решить задачу вторым способом в общем виде, то получится результат
l · (1 + cos a)
S
= ![]() ,
,
sin a
который нетрудно привести к виду
l · sin a
S
= ![]() ,
,
1 – cos a
чтобы убедиться, что получился тот же ответ.
Промежуточный контроль. К–5.
Дополнения к главе 3
Методом математической индукции называют способ доказательства истинности для любого натурального n некоторого утверждения. Этот способ основан на принципе математической индукции, сформулированном в учебном тексте. Прежде чем приступить к обсуждению способа изложения материала на уроке, приведём шуточный пример, обсуждение которого помогает учащимся понять суть нового метода доказательства.
Представьте, что вы подошли к кинотеатру и видите огромную очередь желающих купить билет на новый фильм. Вы становитесь в конец очереди, и к вам подходит человек со словами: «Я прошёл от начала очереди до конца и заметил, что в очереди после каждой женщины стоит женщина». Можно ли на основании услышанного утверждать, что в очереди стоят одни женщины? Обычно учащиеся легко справляются с этим вопросом, отвечая, что для истинности утверждения «В очереди стоят только женщины» надо быть уверенным, что первая в очереди женщина. Тогда после каждой женщины стоит женщина и утверждение «В очереди стоят только женщины» будет истинным. Но если первым в очереди стоит мужчина, то это утверждение будет ложным.

Вторым примером, которым можно предварить объяснение нового материала, может быть разбор решения задачи 516.
516. На один из трёх штырьков насажены n различных колец так, что большее кольцо лежит ниже меньшего (на рисунке 41 n = 3). За один ход разрешается перенести одно кольцо с одного штырька на другой, при этом не разрешается большее кольцо класть на меньшее. Докажите, что наименьшее число ходов, за которое можно перенести все кольца с одного штырька на другой, равно 2n – 1.
Если условие этой задачи учитель сформулирует без последнего предложения, т. е. без формулы 2n – 1, выражающей зависимость числа ходов от числа колец, то у учащихся будет возможность поучаствовать в поиске этой формулы. В процессе обсуждения они убеждаются, что могут проверить справедливость формулы лишь для нескольких первых значений n, но не могут доказать её для любого натурального n, так как натуральных чисел бесконечно много.
Рассуждения можно провести так.
Одно кольцо (n = 1) можно перенести на новый штырёк за 1 ход.
Два кольца (n = 2) можно перенести за 3 хода — первое кольцо перенести на второй штырёк, второе — на третий, затем первое — на третий.
Три кольца (n = 3) можно перенести за 3 + 1 + 3 = 7 ходов, перенеся сначала два верхних кольца за 3 хода на второй штырёк, потом нижнее кольцо за 1 ход на третий штырёк, потом снова два кольца за 3 хода на третий штырёк (рис. 42).
Аналогично можно перенести 4, 5, 6 колец за
7 + 1 + 7 = 15, 15 + 1 + 15 = 31, 31 + 1 + 31 = 63 хода соответственно.
Наблюдательные учащиеся могут заметить, что для n колец число ходов меньше n-й степени числа 2 на единицу, т. е. выражается формулой 2n – 1.
Следовательно, получена гипотеза о выражении числа ходов через n, которую ещё нужно доказать для любого натурального n. Но что значит доказать формулу для лю-
бого натурального n? Очевидно, что проверить истинность формулы для всех n невозможно. Необходимо соглашение, позволяющее считать, что при выполнении некоторых условий доказываемое утверждение считается истинным для любого натурального n.
После обсуждения рассмотренных примеров учащиеся будут подготовлены к тому, что если истинность некоторого утверждения, зависящего от натурального n, установлена для n = 1 и доказано, что из истинности этого утверждения для некоторого n = k следует истинность этого утверждения для следующего значения n, равного k + 1, то считается, что это утверждение истинно для любого натурального n (это соглашение и называют принципом математической индукции).
Пример 1 из учебного текста (доказать по индукции, что 0n = 0 для любого натурального n) достаточно прост, чтобы, не отвлекаясь на технические сложности, освоить идею доказательства методом математической индукции.
В других примерах показываются доказательства методом математической индукции различных равенств и неравенств, здесь же приводятся доказательства формулы общего члена арифметической прогрессии и формулы суммы первых n членов геометрической прогрессии.
Полезно отметить, что недопустимо пропускать любой из двух шагов в доказательстве методом математической индукции, и рассказать об ошибках, к которым может привести такой пропуск.
Хотя материал данного пункта предназначен для классов с углублённым изучением математики, но и в обычных классах полезно на простых примерах показать применение метода математической индукции, чтобы учащиеся знали, каким методом можно доказать формулы n-го члена и суммы первых n членов арифметической и геометрической прогрессий.
Решения и комментарии
507. в) Докажите методом математической индукции, что для любого натурального n выполняется равенство
1 + 3 + 5 + ... + (2n – 1) = n2.
Доказательство. При n = 1 справедливо равенство 1 = 12.
Предположим, что для некоторого натурального числа n = k справедливо равенство
1 + 3 + 5 + ... + (2k – 1) = k2, (1)
и докажем, что для n = k + 1 тогда справедливо равенство
1 + 3 + 5 + ... + (2k – 1) + (2k + 1) = (k + 1)2. (2)
Используя равенство (1), имеем
1 + 3 + 5 + ... + (2k – 1) + (2k + 1) =
= k2 + (2k + 1) = (k + 1)2,
что и доказывает равенство (2).
Согласно принципу математической индукции, равенство
1 + 3 + 5 + ... + (2n – 1) = n2
справедливо для любого натурального n.
![]() Замечание.
При обсуждении задания 507 можно упомянуть, что выдающийся
математик XX столетия А. Н. Колмогоров (1903—1987) ещё в детстве проявлял
необыкновенные математические способности. В возрасте пяти лет он установил,
что 1 + 3 = 22, 1 + 3 +
5 = 32, 1 + 3 + 5 +
7 = 42 и т. д., т. е. выдвинул гипотезу, что сумма
первых n нечётных натуральных чисел равна n2.
Замечание.
При обсуждении задания 507 можно упомянуть, что выдающийся
математик XX столетия А. Н. Колмогоров (1903—1987) ещё в детстве проявлял
необыкновенные математические способности. В возрасте пяти лет он установил,
что 1 + 3 = 22, 1 + 3 +
5 = 32, 1 + 3 + 5 +
7 = 42 и т. д., т. е. выдвинул гипотезу, что сумма
первых n нечётных натуральных чисел равна n2.
508. Докажите методом математической индукции, что для любого натурального n выполняется неравенство:
а) 1 + 2 + 3 + ... + n n2; д) 4n 7n – 5.
Доказательство. а) При n = 1 справедливо неравенство 1 12.
Предположим, что для некоторого натурального числа n = k справедливо неравенство
1 + 2 + 3 + ... + k k2, (3)
и докажем, что тогда для n = k + 1 справедливо неравенство
1 + 2 + 3 + ... + k + (k + 1) (k + 1)2. (4) Используя неравенство (3), имеем
1 + 2 + 3 + ... + k + (k + 1) k2 + (k + 1) (k + 1)2, что и доказывает неравенство (4).
Согласно принципу математической индукции, неравенство
1 + 2 + 3 + ... + n n2
справедливо для любого натурального n.
д) При n = 1 справедливо неравенство 41 7 – 5, при n = 2 справедливо неравенство 42 14 – 5.
Предположим, что для некоторого натурального числа n = k (k 2) справедливо неравенство
4k 7k – 5, (5) и докажем, что тогда для n = k + 1 справедливо неравенство
4k + 1 7(k + 1) – 5. (6)
Используя неравенство (5), имеем
4k + 1 = 4k · 4 (7k – 5) · 4 = 28k – 20 = = 7(k + 1) – 5 + (21k – 22).
Итак, для k 2 верно неравенство 4k + 1 7(k + 1) – 5.
Тем самым неравенство (6) доказано для k 2.
Согласно принципу математической индукции, неравенство 4k 7k – 5 справедливо для любого натурального n 2. Так как оно верно и при n = 1, то неравенство справедливо для любого натурального n.
![]() Замечание.
При доказательстве неравенства д) был использован более общий метод
математической индукции.
Замечание.
При доказательстве неравенства д) был использован более общий метод
математической индукции.
Он заключён в следующем.
Если свойство, зависящее от натурального n, во-первых, верно при n = n0 (n0 1) и, во-вторых, из предположения его верности при n = k (k n0) следует, что оно верно при n = k + 1, то считают, что это свойство верно для любого натурального n n0.
510. Докажите, что для любого натурального n выполняется равенство
2 2
3 3 3 3 n n( + 1)
1 + 2 + 3
+ ... + n = ![]() .
(7)
.
(7)
4
Доказательство. При n = 1 справедливо равенство
13
= 1![]() 2 • 22 .
2 • 22 .
4
Предположим, что для некоторого натурального числа n = k справедливо равенство
2 2
3 3 3 3 k k( + 1)
1
+ 2 + 3 + ... + k =
![]() , (8)
, (8)
4
и докажем, что тогда для n = k + 1 справедливо равенство
2 2
3 3 3 3 3 (k + 1) (k + 2)
1 + 2 + 3 + ...
+ k + (k + 1) = ![]() . (9)
. (9)
4 Используя равенство (8), имеем
k k2( + 1)2 3 3 3 3 3 3
1 + 2 + 3 + ... + k + (k + 1) = + (k + 1) =
4
![]() (k + 1)2(k2 + 4(k + 1)) (k + 1) (2 k + 2)2
(k + 1)2(k2 + 4(k + 1)) (k + 1) (2 k + 2)2
= = ,
4 4
что и доказывает равенство (9).
Согласно принципу математической индукции, равенство (7) справедливо для любого натурального n.
512. Задача аль-Каши (XIV—XV вв.) Докажите, что для любого натурального n выполняется равенство
14 +
24 + 34 + ... +
n4 = ![]() (6n5 + 15n4
+ 10n3 – n). (10)
(6n5 + 15n4
+ 10n3 – n). (10)
Доказательство. При n = 1 справедливо равенство
14 = ![]() (6 + 15
+ 10 – 1).
(6 + 15
+ 10 – 1).
Предположим, что для некоторого натурального числа n = k справедливо равенство
14 + 24
+ 34 + ... + k4
= ![]() (6k5 + 15k4
+ 10k3 – k), (11) и докажем, что
тогда для n = k + 1 справедливо равенство
(6k5 + 15k4
+ 10k3 – k), (11) и докажем, что
тогда для n = k + 1 справедливо равенство
14 + 24 + 34 + ... + k4 + (k + 1)4 =
= ![]() (6(k + 1)5 +
15(k + 1)4 + 10(k + 1)3
– (k + 1)). (12)
(6(k + 1)5 +
15(k + 1)4 + 10(k + 1)3
– (k + 1)). (12)
Используя равенство (11), имеем
14 + 24 + 34 + ... + k4 + (k + 1)4 =
= ![]() (6k5
+ 15k4 + 10k3 –
k) + (k + 1)4 = =
(6k5
+ 15k4 + 10k3 –
k) + (k + 1)4 = = ![]() (6k5
+ 15k4 + 10k3 –
k + 30(k4 + 4k3
+ 6k2 + 4k + 1)) =
(6k5
+ 15k4 + 10k3 –
k + 30(k4 + 4k3
+ 6k2 + 4k + 1)) =
= ![]() (6k5 + 45k4
+ 130k3 + 180k2
+ 119k + 30).
(6k5 + 45k4
+ 130k3 + 180k2
+ 119k + 30).
Убедимся, что правая часть равенства (12) преобразуется к тому же виду
![]() (6(k + 1)5
+ 15(k + 1)4 + 10(k +
1)3 – (k + 1)) =
(6(k + 1)5
+ 15(k + 1)4 + 10(k +
1)3 – (k + 1)) =
= ![]() (6(k5 + 5k4
+ 10k3 + 10k2 +
5k + 1) +
(6(k5 + 5k4
+ 10k3 + 10k2 +
5k + 1) +
+ 15(k4
+ 4k3 + 6k2 +
4k + 1) + 10(k3 + 3k2
+ 3k + 1) – k – 1) = = ![]() (6k5
+ 45k4 + 130k3 +
180k2 + 119k + 30).
(6k5
+ 45k4 + 130k3 +
180k2 + 119k + 30).
Итак, равенство (12) доказано, следовательно, согласно принципу математической индукции, равенство (10) справедливо для любого натурального n.
![]() Замечание.
Иногда при доказательстве равенства (неравенства) приходится отдельно
преобразовывать его левую и правую части, что и сделано при разборе задания 512.
Замечание.
Иногда при доказательстве равенства (неравенства) приходится отдельно
преобразовывать его левую и правую части, что и сделано при разборе задания 512.
514. Докажите, что для любого натурального n:
а) 5n + 3 делится на 4; в) 4n + 6n – 1 делится на 9. Доказательство. а) При n = 1 число 5 + 3 = 8 делится на 4.
Предположим, что для некоторого натурального числа n = k число 5k + 3 делится на 4, и докажем, что тогда для n = k + 1 число 5k + 1 + 3 делится на 4.
Перепишем число 5k + 1 + 3 в виде 5 · 5k + 3 = 5 · (5k + 3) – 12.
Так как числа 5 · (5k + 3) и 12 делятся на 4, то их разность — число 5k + 1 + 3 — также делится на 4.
Следовательно, согласно принципу математической индукции, число 5n + 3 делится на 4 для любого натурального n.
в) При n = 1 число 4 + 6 – 1 = 9 делится на 9.
Предположим, что для некоторого натурального числа n = k число 4k + 6k – 1 делится на 9, и докажем, что тогда для n = k + 1 число 4k + 1 + 6(k + 1) – 1 делится на 9. Перепишем число 4k + 1 + 6(k + 1) – 1 в виде 4 · 4k + 6k + 5 = 4 · (4k + 6k – 1) – 18k + 9 = = 4 · (4k + 6k – 1) – 9 · (2k – 1).
Так как числа 4 · (4k + 6k – 1) и 9 · (2k – 1) делятся на
9, то их разность — число 4k + 1 + 6(k + 1) – 1 — также делится на 9.
Следовательно, согласно принципу математической индукции, число 4n + 6n – 1 делится на 9 для любого натурального n.
Приведём доказательство методом математической индукции формулы 2n – 1 из задания 516.
Доказательство. При n = 1 формула справедлива, так как одно кольцо можно перенести за 21 – 1 = 1 ход.
Предположим, что для некоторого натурального числа n = k «пирамиду» из k колец можно перенести за 2k – 1 ходов, и докажем, что тогда «пирамиду» из (k + 1) кольца можно перенести за 2k + 1 – 1 ходов.
По нашему предположению, «пирамиду» из k колец можно перенести за 2k – 1 ходов на второй штырёк. Нижнее (k + 1)-е кольцо можно перенести за 1 ход на третий штырёк, потом снова пирамиду из k колец можно перенести за 2k – 1 ходов на третий штырёк.
Всего для переноса «пирамиды» из (k + 1) кольца потребовалось (2k – 1) + 1 + (2k – 1) = 2k + 1 – 1 ходов, что и требовалось доказать.
Согласно принципу математической индукции, наименьшее число ходов, за которое можно перенести все кольца с одного штырька на другой, равно 2n – 1.
В этом пункте приведена история изучения прогрессий,
известная задача-легенда о шахматной доске и другие факты, связанные с
прогрессиями. Этот материал способствует формированию ответственного отношения
к учению, готовности и способности учащихся к саморазвитию и самообразованию на
основе мотивации к обучению и познанию, выбору дальнейшего образования на базе
ориентировки в мире профессиональных предпочтений, осознанному построению
индивидуальной образовательной траектории с учётом устойчивых познавательных
интересов.
Глава 4
В этой главе изучаются формулы для синусов, косинусов, тангенсов и котангенсов любых углов. Сначала обобщается известное из геометрии понятие угла, вводятся градусная и радианная меры угла, даётся определение синуса, косинуса, тангенса и котангенса произвольного угла; изучаются их основные свойства.
В Дополнениях к главе приводятся формулы для синусов и косинусов суммы и разности двух углов и формулы для суммы, разности и произведения синусов и косинусов.
Цель изучения главы 4 — понять, что такое угол в тригонометрии, что такое синус, косинус, тангенс и котангенс любого угла.
Следует отметить, что материал этой главы перенесён из 9 класса в 10 класс и не входит в итоговый контроль (ГИА), но по традиции он изучается в классах с углублённым изучением математики.
Авторы считают, что даже беглое изучение этого материала в обычных классах расширит кругозор учащихся, даст им пример «другой» алгебры, в которой скобки в выражении sin (x + y) «раскрываются» совсем не так, как кажется некоторым учащимся. Кроме того, такое предварительное изучение тригонометрии позволит повысить эффективность её изучения в 10 классе.
§ 9. Угол и его мера
В данном параграфе сначала вводится понятие угла поворота, затем изучаются его градусная и радианная меры.
Основная цель изучения параграфа — усвоить понятие угла как поворота подвижного вектора, освоить градусную и радианную меры любого угла, научиться переводить величины углов из одной меры в другую.
В пункте 9.1 вводятся понятия подвижного вектора, полного оборота, положительных и отрицательных углов, нулевого угла. Если в геометрии рассматривались неотрицательные углы, меньшие развёрнутого, то теперь рассматриваются также углы, большие развёрнутого и отрицательные.
В пункте 9.2 вводится понятие градусной меры угла.
Говорят, что градусная мера угла равна 1 градусу (1°), если подвижный угол совершил поворот,
равный ![]() пол-
пол-
ного оборота. Утверждается, что для любого действительного числа a существует, и притом единственный, угол, градусная мера которого равна этому числу a.
Далее приводятся примеры построения углов, имеющих ту или иную градусную меру. Здесь удобно использовать окружность единичного радиуса, которая в пункте 9.3 будет названа единичной окружностью. Учащимся следует показать приём построения «табличных» углов (30°, 45°, 60°, 90°) и связанных с ними углов без транспортира, что позволит в дальнейшем быстрее находить значения синусов, косинусов, тангенсов и котангенсов углов, сводимых к их значениям для «табличных» углов.
Покажем, как это можно сделать. Учащиеся должны сначала научиться отмечать на единичной окружности точки, соответствующие:
а) углам 0°, 90°, 180°, 270° (точки лежат на пересечении осей координат с единичной окружностью) (рис. 43, а); б) углам 45°, 135°, 225°, 315° (точки лежат на пересечении биссектрис координатных углов с единичной окружностью) (рис. 43, б);
в) углам 30°, 150°, 210°, 330° (точки лежат на пересе-
чении прямых y = ![]() и y
= –
и y
= – ![]() с единичной окружностью)
с единичной окружностью)
(рис. 43, в);
6 Рис. 43
г) углам 60°, 120°, 240°, 300° (точки лежат на пересе-
чении прямых x = ![]() и x
= –
и x
= – ![]() с единичной окружностью)
с единичной окружностью)
(рис. 43, г).
Умея строить указанные точки, легко построить соответствующие им углы и тем самым выполнить задание 526. При этом нужно отметить требуемые углы дугами (как на рисунках в учебнике) или, обозначив построенные точки буквами, сделать поясняющие записи в виде РAOB = 90° (см. рис. 43, а).
Чтобы обосновать, что точка B, изображённая на рисунке 43, в, соответствует углу 30°, достаточно опустить из этой точки перпендикуляр ВС на ось Ox (рис. 43, д). Тогда в прямоугольном треугольнике BOC катет ВС равен половине гипотенузы ОB, поэтому угол СOB, лежащий против этого катета, равен 30°. Аналогично даётся обоснование для рисунка 43, г.
Задания для повторения. При изучении данного пункта можно использовать задания 1, 2 из рубрики «Задания для самоконтроля».
Решения и комментарии
527. Укажите несколько положительных и отрицательных углов, образованных такими поворотами, при каждом из которых угол между начальным и конечным положением подвижного вектора равен 30°, –45°, 60°, –90°.
Решение. 1) 30°, 30° + 360° = 390°, 30° – 360° = –330°, 30° + 360° · 2 = 750°, 30° – 360° · 2 = –690°;
2) –45°, –45° + 360° = 315°, –45° – 360° = –405°, –45° + 360° · 2 = 675°, –45° – 360° · 2 = –765°;
3) 60°, 60° + 360° = 420°, 60° – 360° = –300°, 60° + 360° · 2 = 780°, 60° – 360° · 2 = –660°;
4) –90°, –90° + 360° = 270°, –90° – 360° = –450°, –90° + 360° · 2 = 630°, –90° – 360° · 2 = –810°.
528. Укажите наименьший по абсолютной величине угол среди данных углов: д) 400° + 360° · n, где n Z; е) –700° + 360° · n, где n Z.
Решение. д) При n = –1 имеем 400° + 360° · n = 40°. При увеличении или уменьшении числа n абсолютная величина угла увеличивается.
е) При n = 2 имеем –700° + 360° · n = 20°. При увели-
чении или уменьшении числа n абсолютная величина угла увеличивается.
529. Представьте следующие углы в виде a + 360° · n, где 0° a 360°, n — некоторое целое число: в) 600°; г) –900°.
Решение. в) 600° = 240° + 360° · 1; г) –900° = 180° + 360° · (–3).
В данном пункте вводится понятие радианной меры угла. Говорят, что радианная мера угла равна 1 радиану, если подвижный угол совершил такой поворот, что его конечная точка при движении по окружности описала дугу, длина которой равна радиусу окружности. Утверждается, что для любого действительного числа a существует, и притом единственный, угол, радианная мера которого равна этому числу a.
Далее приводятся примеры построения углов, имеющих ту или иную радианную меру. Наконец, выясняется связь между градусной и радианной мерой.
При изучении данной темы обычно наблюдается недопонимание учащимися необходимости выражать радианную меру угла через число p. Чтобы снять всякие сомнения на этот счёт, можно провести такое рассуждение.
Отметим на единичной окружности точки, соответствующие углам в 1, 2, 3, 4, 5, 6 радиан. Для этого надо откладывать от точки А в направлении против часовой стрелки на окружности 1, 2, 3, 4, 5, 6 раз дугу, длина которой равна радиусу окружности. Так как длина окружности радиуса 1 равна 2p ≈ 6,28, то полный оборот содержит больше 6 радиан (рис. 44, а).
Если продолжить откладывание в том же направлении на этой окружности дуг длиной в 1 радиус, то возникает иллюзия, что через некоторое (возможно, большое) число шагов новое деление на окружности, соответствующее углу в некоторое число радиан, совпадёт с каким-нибудь из отмеченных ранее делений. Однако этого не произойдёт, как бы долго мы ни продолжали откладывать в том же направлении эти дуги. Докажем это методом от противного.
Предположим, что на n-м шаге мы отметили на окружности точку N, соответствующую углу в n радиан, n — натуральное число (рис. 44, б). Затем продолжили откладывание в том же направлении дуг длиной в 1 радиус

6 Рис. 44
и на каком-то шаге обнаружили, что точка, соответствующая углу в m радиан, совпала c уже отмеченной точкой N. Для этого пришлось сделать k (k ≠ 0) полных оборотов. Тогда справедливо равенство
m – n = 2kp, k N,
из которого следует, что p = ![]() m – n .
m – n .
2k
Получено противоречие: число p оказалось равным обыкновенной дроби. Но, как известно, число p — иррациональное число, т. е. оно не может быть равным рациональному числу. Следовательно, предположение, что на каком-то шаге новое деление, соответствующее углу в m радиан, совпадёт со старым делением, соответствующим углу в n радиан (m и n — натуральные числа), неверно. Такое рассуждение можно провести при решении задания 555.
![]() Замечание. В
приведённом рассуждении мы нигде не пользовались тем, что m и n —
натуральные числа, т. е. если точка N получена при откладывании p
раз
Замечание. В
приведённом рассуждении мы нигде не пользовались тем, что m и n —
натуральные числа, т. е. если точка N получена при откладывании p
раз ![]() 1 части q
1 части q
дуги в 1 радиан, то она не может совпасть ни с какой
другой точкой, полученной при
откладывании r раз 1![]() ча-
ча-
s
![]() p r сти
дуги в 1 радиан ( ≠
, где p, q, r, s — натуральные q s
p r сти
дуги в 1 радиан ( ≠
, где p, q, r, s — натуральные q s
числа).
![]() Теперь становится
ясным, что при использовании радианной меры без числа p и его долей обойтись невозможно. На
рисунке 44, в показаны точки, которые на рисунке 43, а
соответствовали углам в 0°,
90°, 180°, 270°. Теперь они
соответствуют углам в
Теперь становится
ясным, что при использовании радианной меры без числа p и его долей обойтись невозможно. На
рисунке 44, в показаны точки, которые на рисунке 43, а
соответствовали углам в 0°,
90°, 180°, 270°. Теперь они
соответствуют углам в ![]() p ,
p, , 2p радиан. Запоми-
p ,
p, , 2p радиан. Запоми-
2
нанию этих углов (и следующих за ними) помогает «считалочка»: показывая точки на окружности, говорим: «раз пи на два, два пи на два, три пи на два, …». Аналогичный приём помогает при поиске точек, соответствующих углам
![]() в p, 2p = p,
3p,
4p = p, …
(радиан).
в p, 2p = p,
3p,
4p = p, …
(радиан).
4 4 2 4 4
Теперь, установив равенство 180° = p радиан и разделив его сначала на p, потом на 180, получим соотношения, которые надо запомнить:
180o p
![]() =
1 радиан; 1°
=
=
1 радиан; 1°
= ![]() радиан.
радиан.
p 180
![]() С их помощью можно
переводить градусную меру в радианную и наоборот. Например, 135° = 135
· 1°
= 135 ·
С их помощью можно
переводить градусную меру в радианную и наоборот. Например, 135° = 135
· 1°
= 135 · ![]() p радиан = радиан;
p радиан = радиан;
180
![]() 5p 5p 5p 180o
5p 5p 5p 180o ![]() радиан =
радиан =
![]() · 1 радиан =
· = 150°.
· 1 радиан =
· = 150°.
6 6 6 p
![]() В
этих равенствах слово «радиан» обычно опускают и пишут коротко: 135° = 3p , 5p
= 150°.
В
этих равенствах слово «радиан» обычно опускают и пишут коротко: 135° = 3p , 5p
= 150°.
4 6
Задания для повторения. При изучении данного пункта можно использовать задание 3 из рубрики «Задания для самоконтроля».
Решения и комментарии
532. Выразите в радианах величину угла, градусная мера которого равна:
а) 360°, 180°, 90°, 270°, 0°; в) 60°, 120°, 240°, 300°.
![]() Решение. а)
360° = 2p, 180° = p, 90° = p , 270°
= ,
Решение. а)
360° = 2p, 180° = p, 90° = p , 270°
= ,
2
![]() 0° = 0; 180o p 2p 4p 5p
0° = 0; 180o p 2p 4p 5p
![]() в) 60°
= = , 120°
=
в) 60°
= = , 120°
= ![]() , 240° = , 300° =
, 240° = , 300° = ![]() .
.
3 3 3 3 3
533. Выразите в градусах величину угла, радианная ме-
![]() ра
которого равна: б) , 3p , 5p , 7p ; г) ,
5p , 7p , 11p .
ра
которого равна: б) , 3p , 5p , 7p ; г) ,
5p , 7p , 11p .
4 4 4 6 6
Решение. б) p = = 45°, 3p = 135°, 5p = 225°,
4 4 4 4
7p
![]() =
315°;
=
315°;
4
p 180o 5p 7p 11p
![]() г) = = 30°,
г) = = 30°, ![]() = 150°,
= 150°, ![]() = 210°,
= 210°, ![]() = 330°.
= 330°.
6 6 6 6 6
Промежуточный контроль. С–21*, С–22*.
§ 10. Синус, косинус, тангенс и котангенс угла
В данном параграфе сначала определяются синус и косинус угла и изучаются их свойства, потом определяются тангенс и котангенс угла и также изучаются их свойства. Желательно, чтобы эти понятия и свойства освоили все учащиеся, так как этот материал будет в дальнейшем использоваться ими при обучении в старшей школе.
Основная цель изучения параграфа — овладеть понятиями синуса, косинуса, тангенса и котангенса угла, изучить их свойства и научиться применять их.
В данном пункте вводится единичная окружность, на ней отмечают точку, соответствующая углу a, коротко: точку a. Тогда ординату точки a называют синусом угла a, а абсциссу — косинусом угла a. Эти определения нужно мотивировать, связав их с известными учащимся из курса геометрии определениями синуса и косинуса угла, не превосходящего развёрнутого.
Из определения синуса и косинуса угла можно сделать выводы:
а) для любого угла a существует sin a, притом един-
ственный;
б) для любого угла a существует cos a, притом един-
ственный.
Далее разбираются примеры вычисления синусов и косинусов углов, приводится таблица значений синуса и косинуса «табличных» углов первой четверти. Эти значения учащиеся должны выучить, опираясь на рисунок 45.
Если учащиеся выучат эти значения, то с учётом знаков синуса и косинуса они будут легко находить значения синуса и косинуса для углов, связанных с точками, отмеченными на рисунках 43, а—г.
Задания для повторения. При изучении данного пункта можно использовать задание 4 из рубрики «Задания для самоконтроля».
Решения и комментарии 553. Верно ли равенство:
а) sin (– ![]() p) = –sin
p) = –sin ![]() p ; б) cos (–
p ; б) cos (– ![]() p) = cos
p) = cos ![]() p ?
p ?
2 2 4 4
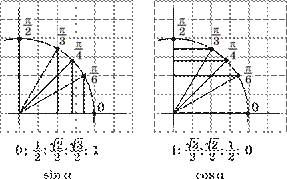
6 Рис. 45
![]() Решение. а) sin (– p) — это ордината точки B единич2
Решение. а) sin (– p) — это ордината точки B единич2
ной окружности, а sin p — это ордината точки A единич-
2
ной окружности (рис. 46, а), равенство верно, так как ординаты различаются только знаком.
![]() б)
cos (– p) — это абсцисса точки B единичной окруж4 p ности, а cos — это абсцисса точки A
единичной окруж4
б)
cos (– p) — это абсцисса точки B единичной окруж4 p ности, а cos — это абсцисса точки A
единичной окруж4
ности (рис. 46, б), равенство
верно, так как абсциссы равны. 556. Определите знак числа: а) sin 4;
б) cos ![]() 3p .
3p .
4
Решение. а) Так как
p
4 ![]() ,
,
то точка 4 принадлежит третьей четверти, поэтому sin 4 0.
б) Так как
p 3p
![]() p,
p,
2 4
то точка ![]() 3p принадлежит второй четверти, поэтому
3p принадлежит второй четверти, поэтому
4
cos ![]() 0.
0.
557. Выполняется ли равенство cos a = sin a при каком-нибудь a? Проиллюстрируйте своё решение на рисунке.
Решение. Рассмотрим точки a и b единичной окружности, лежащие на биссектрисе I и III четвертей (рис. 47). Координаты точки a равны, поэтому верно равенство cos a = sin a, координаты точки b равны, поэтому верно равенство cos b = sin b.

6 Рис. 46 6 Рис. 47
Все углы a можно задать формулой p
a = ![]() + 2pk, где k
— целое число.
+ 2pk, где k
— целое число.
4
Все углы b можно задать формулой
b = ![]() +
2pk,
где k — целое число.
+
2pk,
где k — целое число.
Все углы a и b можно задать формулой p
a = ![]() + pk, где k
— целое число.
+ pk, где k
— целое число.
4
559. Что больше:
p
а) sin 40° или sin ![]() ;
;
4
p
б) cos ![]() или cos 60°;
или cos 60°;
3
ж) sin (–300°) или cos 120°;
з) cos 13![]() p
или sin (–
p
или sin (– ![]() p) ?
p) ?
4 2
p
Решение. а)
Углы 40° и ![]() принадлежат I четверти,
принадлежат I четверти,
4
где с увеличением угла синус
увеличивается. Так как 40°
45° =
p , то sin 40°
sin ![]() p .
p .
![]() 4 4
4 4
p p
б) Углы и 60° равны, поэтому cos
![]() = cos 60°.
= cos 60°.
3 3
ж) Так как на единичной окружности точки –300° и –300° + 360° = 60° совпадают, то sin (–300°) = sin 60° 0, а cos 120° 0, поэтому sin (–300°) cos 120°.
з) Так как на единичной окружности
точки 13![]() p
и
p
и
4
13p 5p
![]() – 2p =
– 2p = ![]() совпадают, то
совпадают, то
4 4
cos
![]() = cos
= cos ![]() ,
,
![]() sin
(– p) = –1 и – –1,
sin
(– p) = –1 и – –1,
2
![]() поэтому cos 13
поэтому cos 13![]() p
sin (– p) .
p
sin (– p) .
4 2
Промежуточный контроль. С–23*.
В данном пункте с опорой на ранее изученные факты (уравнение окружности, свойства координат точек единичной окружности, симметричных относительно оси Ox, относительно начала координат) доказывается основное тригонометрическое тождество
sin2a + cos2a = 1 (1) и формулы
sin (–a) = –sin a, (2) cos (–a) = cos a, (3) sin (a + 2pk) = sin a, k Z, (4) cos (a + 2pk) = cos a, k Z, (5) sin (p + a) = – sin a, (6) cos (p + a) = – cos a. (7)
Некоторые другие формулы, например sin (p – a) = = sin a, cos (p – a) = – cos a, могут быть доказаны как следствия формул (2)—(7) (задание 586).
Например,
sin (p – a) = sin (p + (–a)) = –sin (–a) = sin a.
Умение доказывать тригонометрические формулы проверяется в самостоятельной работе С–24. Кроме того, там проверяется умение школьников находить значения одной из заданных функций (sin a или cos a) по заданному значению другой и выполнять упрощения выражений с применением формул (1)—(7).
Задания для повторения. При изучении данного пункта можно использовать задание 5 из рубрики «Задания для самоконтроля».
Решения и комментарии
568. Существует ли такой угол a, для которого:
а) sin a = –1,
cos a =
![]() ; в) sin a =
; в) sin a = ![]() ,
cos a =
,
cos a =
![]() ?
?
Решение. а) Так как sin2a + cos2a = 1 +
![]() 1, то такой угол a не существует.
1, то такой угол a не существует.
в) Так как sin2a + cos2a = ![]() +
+
![]() = 1, то такой угол
= 1, то такой угол
a существует.
569. Возможно ли равенство:
![]()
![]() а)
sin a =
– 3 ; б) cos a = 3 – 1?
а)
sin a =
– 3 ; б) cos a = 3 – 1?
Решение. а) Так как |sin a| = 3 1, то такое равенство невозможно.
![]() б) Так как |cos a| = 3 – 1 1, то такое равенство воз-
б) Так как |cos a| = 3 – 1 1, то такое равенство воз-
![]() можно. 570. а)
Вычислите sin a,
если cos a
= , 0 a
можно. 570. а)
Вычислите sin a,
если cos a
= , 0 a
![]() p .
p .
![]() 2
Решение. Так как sin2a
= 1 – cos2a
= 1 –
2
Решение. Так как sin2a
= 1 – cos2a
= 1 – ![]() =
= ![]() и 0 a
и 0 a ![]() p ,
то sin a
0. Поэтому sin a
= .
p ,
то sin a
0. Поэтому sin a
= .
2
![]()
![]() Замечание.
При выполнении этого задания лучше избегать записи: sin a = ± 1 – cos2 a , так как, имея опыт вычисления корней квадратного
уравнения по формуле
Замечание.
При выполнении этого задания лучше избегать записи: sin a = ± 1 – cos2 a , так как, имея опыт вычисления корней квадратного
уравнения по формуле
![]() –b± D
–b± D
, учащиеся могут подумать, что имеется два значе-
2a ния sin a, отвечающих условию задачи, а это не так.
577. Если 0 a ![]() p
и sin a
= 1 + b, то какие значения
p
и sin a
= 1 + b, то какие значения
2
может принимать b?
Определите cos a.
Решение. Так как 0 a ![]() p ,
то 0 sin
a 1, т. е. 2
p ,
то 0 sin
a 1, т. е. 2
0 1 + b 1, откуда следует, что –1 b 0. Так как
0 a p , то cos a 0 и
![]() 2 cos a = 1 – sin2 a = 1 – (1 + b)2 = –2 – b b2 .
2 cos a = 1 – sin2 a = 1 – (1 + b)2 = –2 – b b2 .
582. а) Расположите в порядке возрастания числа sin (–55°), sin 600°, sin 1295°.
Решение. Выразим синусы данных углов через синус углов из первой четверти: sin (–55°) = –sin 55°,
sin 600° = sin (240° + 360°) = sin 240° =
= sin (180° + 60°) = –sin 60°, sin 1295° = sin (215° + 3 · 360°) = sin 215° = = sin (180° + 35°) = –sin 35°.
Так как углы 55°, 60° и 35° принадлежат первой четверти, в которой большему углу соответствует больший синус, то sin 35° sin 55° sin 60°.
Но тогда –sin 35° –sin 55° –sin 60°, поэтому sin 600° sin (–55°) sin 1295°.
583. а) Сравните sin 91° и sin 92°.
Решение. 91° и 92° — углы второй четверти, в которой большему углу соответствует меньший синус. Так как 91° 92°, то sin 91° sin 92°.
584. а) Сравните cos 101° и cos 157°.
Решение. 101° и 157° — углы второй четверти, в которой большему углу соответствует меньший косинус. Так как 101° 157°, то cos 101° cos 157°.
585. а) Сравните cos 1,6p и cos 1,68p.
Решение. 1,6p и 1,68p — углы четвёртой четверти, в которой большему углу соответствует больший косинус.
Так как 1,6p 1,68p, то cos 1,6p cos 1,68p.
Промежуточный контроль. С–24*.
В данном пункте учебника вводятся понятия тангенса и котангенса угла a как отношения синусов и косину-
сов этого угла: tg a = ![]() sina
и ctg a
=
sina
и ctg a
= ![]() cosa ,
выписываются cosa sina
cosa ,
выписываются cosa sina
углы a, для каждого из которых не определён tg a или ctg a. Подчёркивается, что для тех углов a, для которых определён tg a, он единственный; для тех углов a, для которых определён ctg a, он единственный.
Здесь, как и при введении синуса и косинуса угла, желательно начать с определений tg a и ctg a для острого угла прямоугольного треугольника, получить все «табличные» значения tg a и ctg a для острого угла a.
Если учащиеся выучат эти значения, то с учётом знака тангенса и котангенса они будут легко находить значения тангенса и котангенса для углов, связанных с точками, отмеченными на рисунках 43, а—д.
С помощью определений тангенса и котангенса угла и свойств синуса и косинуса угла доказываются основные свойства тангенса и котангенса угла:
tg a
· ctg a
= 1, a ![]() pk , k
Z,
pk , k
Z,
2
tg (–a) = –tg a,
tg (a + pn) = tg a, n Z, ctg (–a) = ctg a,
ctg (a + pn) = ctg a, n Z.
![]() Свойства tg2a + 1 =
cos12 a , a
Свойства tg2a + 1 =
cos12 a , a ![]() 2p
+ pk,
k Z,
2p
+ pk,
k Z,
ctg2a + 1 = 12 , a pk, k Z sin a
можно доказать при выполнении задания 598.
Желательно, чтобы материал этого пункта усвоили все учащиеся.
Задания для повторения. При изучении данного пункта можно использовать задание 6 из рубрики «Задания для самоконтроля».
Решения и комментарии
597. а) Определите знак выражения:
tg 71° tg 139° tg 235° tg 304° tg (–393°) tg 1000°.
Решение. tg 71° 0, так как 71° — угол первой четверти, где тангенс положительный; tg 139° 0, так как 139° — угол второй четверти, где тангенс отрицательный;
tg 235° = tg (235° – 180°) = tg 55° 0, так как 55° —
угол первой четверти, где тангенс положительный; tg 304° = tg (304° – 180°) = tg 124° 0, так как 124° —
угол второй четверти, где тангенс отрицательный; tg (–393°) = tg (–393° + 2 · 180°) = tg (–33°) = = –tg 33° 0, так как 33° — угол первой четверти, где тангенс положительный; tg 1000° = tg (100° + 5 · 180°) = tg 100° 0, так как 100° — угол второй четверти, где тангенс отрицательный.
Произведение содержит 4 отрицательных множителя,
остальные положительные, следовательно, произведение положительно. 599. в)
Вычислите sin a,
tg a и ctg
a, если p a ![]() 3p
3p
2 и cos a = –0,6.
Решение. Так как cos a = –0,6, то sin2a = 1 – cos2a =
= 1 – 0,36 = 0,64; так как p a 3p , то sin a 0, поэтому
![]() 2 sin a
= – 0,64 = –0,8;
2 sin a
= – 0,64 = –0,8;
sin a –0 8, 4
tg a = = = ; cos a –0 6, 3
1 3
ctg a = = .
tg a 4
![]() Замечание.
Здесь также лучше избегать записи sin a
= ± 1 – cos2 a по описанной выше причине.
Замечание.
Здесь также лучше избегать записи sin a
= ± 1 – cos2 a по описанной выше причине.
601. Упростите выражение:
tg + tga b cos2a – ctg2a
ж) ![]() ; з) 2 2 .
ctg + ctga b sin a – tg a
; з) 2 2 .
ctg + ctga b sin a – tg a
tg + tg a b ж sin a sin bц ж cos a cos bц
Решение. ж) = з + ч : з + ч =
ctg + ctg a b и cos a cos bш и sin a sin bш
sin cos + sin cos a b b a sin cos + b a sin cos a b
= : =
cos cos a b sin sin a b
(sin cos + sin cos a b b a) sin sin a b sin sin a b
= = = tg a · tg b. cos cos sin a b( a cos + sin cos b b a) cos cos a b
cos a – ctg a 2 cossin2aa = cos2a 1 – жз 12 цч =
![]() 2 2 cos a
– 2 и sin
aш з) sin2a 2a =
2 sin2 ж 1
ц
2 2 cos a
– 2 и sin
aш з) sin2a 2a =
2 sin2 ж 1
ц
– tg sin a – cos2aa sin2a 1 – зи cos2aчш
cos2a sin( 2a – 1) cos2a cos4a –cos( 2a) 6
a
![]() = sin2a cos( 2a – 1) sin2a = sin4a –sin( 2a) = cossin6a =
ctg6 a.
= sin2a cos( 2a – 1) sin2a = sin4a –sin( 2a) = cossin6a =
ctg6 a.
605. а) Упростите выражение
sin 2 – ( p a) sin (a – p) cos (a – 2p)
![]() .
.
cos 2 – ( p a) ctg 2 – ( p a) tg 3 – ( p a)
sin 2 – ( p a) sin (a – p) cos (a – 2p)
Решение.
![]() =
=
cos 2 – ( p a) ctg 2 – ( p a) tg 3 – ( p a)
sin –( a) –sin ( (p – a)) cos a (–sin a)(–sin a) cos a 2
![]() =
= = sin a.
cos –( a) ctg –( a) tg –( a) cos · a 1
=
= = sin a.
cos –( a) ctg –( a) tg –( a) cos · a 1
606. Упростите выражение:
1 – cos4a – sin4a cos3a – sin3a
![]() а)
sin4a
– 2sin2a
+ 1 ; б) 1
+ sin cosa a . 1 – cos4a
– sin4a
а)
sin4a
– 2sin2a
+ 1 ; б) 1
+ sin cosa a . 1 – cos4a
– sin4a
Решение. а) 4 2 =
sin a – 2sin a + 1 2
![]() (sin2a + cos2a
– cos4a – sin4a 2 2 2
(sin2a + cos2a
– cos4a – sin4a 2 2 2
2sin a cos a 2sin a 2
![]() = 2 = 4 = 2 = 2tg a.
= 2 = 4 = 2 = 2tg a.
(1 – sin2a) cos a cos a
cos3a – sin3a (cos – sin a a)(cos2a + sin cos + sina a 2a)
б) = =
![]() 1 + sin cos a a 1 + sin cos a a
1 + sin cos a a 1 + sin cos a a
(cos – sin a a)(1 + sin cos a a)
= = cos a – sin a.
1 + sin cos a a
Промежуточный контроль. С–25*, К–6.
1. Косинус разности и косинус суммы двух углов 2. Формулы для дополнительных углов 3. Синус суммы и синус разности двух углов
В трёх первых пунктах Дополнений к главе 4 доказываются формулы синусов и косинусов разности и суммы двух углов.
Отметим, что основной формулой, из которой получаются остальные, является формула cos (a – b) = = cos a cos b + sin a sin b. Она доказывается с помощью скалярного произведения векторов. Доказательство этой формулы достаточно сложное, его следует разобрать с классом и можно не требовать от учащихся его воспроизведения. Для доказательства формулы cos (a + b) достаточно выполнить преобразование cos (a + b) = cos (a – (–b)), затем применить формулу косинуса разности двух углов и свойства синуса и косинуса.
Остановимся на способе запоминания этих двух формул: cos (a – b) = cos a cos b + sin a sin b, (1) cos (a + b) = cos a cos b – sin a sin b. (2)
Если обратить внимание учащихся на чередование функций[2] «косинус-косинус, синус-синус» в правых частях формул (1) и (2) и на то, что знаки в левых и в правых частях этих формул различны, то это поможет запомнить формулы.
Забегая вперёд, отметим, что на чередование функций можно будет опираться при запоминании формулы cos 2a = cos2a – sin2a, которая получается из формулы (2) заменой b на a.
Следствиями формул (1) и (2) являются формулы для дополнительных углов:
![]() cos p – a) = sin a,
(3)
cos p – a) = sin a,
(3)
2
![]()
![]() sin
p – a) = cos a.
(4)
sin
p – a) = cos a.
(4)
2
Их доказательство приводится в пункте 2 Дополнений.
Эти формулы очень часто используются в дальнейшем.
В пункте 3 с использованием формул (3) и (4) доказываются формулы синуса суммы и синуса разности двух углов:
sin (a – b) = sin a cos b – cos a sin b, sin (a + b) = sin a cos b + cos a sin b.
Если эти формулы записать в виде sin (a – b) = sin a cos b – sin b cos a, (5) sin (a + b) = sin a cos b + sin b cos a, (6) то, обратив внимание учащихся на чередование функций «синус-косинус, синус-косинус» в правых частях формул (5) и (6) и на то, что знаки в левых и правых частях формул (5) и (6) одинаковы, мы облегчим запоминание этих формул.
Забегая вперёд, отметим, что на чередование функций можно будет опираться при запоминании формулы sin 2a = 2sin a cos a, которая получается из формулы (6) заменой b на a.
Дополнительно к материалам учебника по дидактическим материалам можно изучить формулы приведения для синуса и косинуса (С–27).
608. а) Вычислите, не пользуясь таблицей или калькулятором, cos 15°.
Решение. cos 15° = cos (45° – 30°) = cos 45° · cos 30°+
![]() + sin 45°
· sin 30°
= · + · 1 =
.
+ sin 45°
· sin 30°
= · + · 1 =
.
2 2
613. Докажите справедливость равенства:
3p 3p
а) cos ( ![]() – a) = –sin
a; б)
cos (
– a) = –sin
a; б)
cos ( ![]() + a) = sin
a.
+ a) = sin
a.
2 2
Решение.
3p 3p 3p
а) cos ( ![]() – a) = cos
– a) = cos
![]() · cos a + sin
· cos a + sin
![]() · sin a =
· sin a =
2 2 2
= 0 · cos a + (–1) · sin a = –sin a.
3p 3p 3p
б) cos ( ![]() + a) = cos
+ a) = cos
![]() · cos a – sin
· cos a – sin
![]() · sin a =
· sin a =
2 2 2
= 0 · cos a – (–1) · sin a = sin a.
618. а) Вычислите cos 75° + cos 15°.
Решение. cos 75° + cos 15° = cos (45° + 30°) + + cos (45° – 30°) = cos 45° · cos 30° – sin 45° · sin 30° +
+ cos 45° · cos 30° + sin 45° · sin 30° = 2cos 45° · cos 30° =
= 2 · ![]() · = .
· = .
619. Упростите выражение:
p p p p
а) cos ( +
a) ·
cos ( – a)
– sin ( ![]() – a) · sin
(
– a) · sin
( ![]() + a);
+ a);
4 4 4 4
![]()
![]()
![]() б) cos 2p + a) + cos (2p – a) + cos a.
б) cos 2p + a) + cos (2p – a) + cos a.
3 3
Решение.
p p p p
а) cos ( +
a) ·
cos ( – a)
– sin ( ![]() – a) · sin
(
– a) · sin
( ![]() + a) =
+ a) =
![]()
![]() 4 4 4 4 p p p
4 4 4 4 p p p
= cos ( ![]() +
a +
– a)
= cos = 0.
+
a +
– a)
= cos = 0.
4 4 2
![]()
![]() б) cos 2p + a) + cos (2p – a) + cos a
= cos · cos a
–
б) cos 2p + a) + cos (2p – a) + cos a
= cos · cos a
–
3 3
![]() – sin
– sin ![]() ·
sin a
+ cos
·
sin a
+ cos ![]() · cos a + sin
· cos a + sin
![]() · sin a + cos
a = =
2 cos · cos a
+ cos a
= 2 · (–
· sin a + cos
a = =
2 cos · cos a
+ cos a
= 2 · (–![]() 1)
· cos a
+ cos a
= 0.
1)
· cos a
+ cos a
= 0.
2
627. Приведите числовое выражение к виду синуса или косинуса положительного угла, не превышающего 45°:
б) sin 70°; в) cos 82°.
Решение. б) sin 70° = sin (90° – 20°) = cos 20°; в) cos 82° = cos (90° – 8°) = sin 8°.
628. Приведите числовое выражение к виду синуса или косинуса положительного угла, не превышающего p p 5p
![]() : б) cos
: б) cos ![]() ; в) sin .
; в) sin .
4 3 7
![]() Решение. б) cos p = cos жзp – pцч =
sin p ;
Решение. б) cos p = cos жзp – pцч =
sin p ;
3 и 2 6 ш 6
![]() в) sin 5
в) sin 5![]() p
= sin жзp – –жз
p
= sin жзp – –жз ![]() 3pчццч =
cos жз–3pцч
= cos
3pчццч =
cos жз–3pцч
= cos ![]() 3p .
3p .
7 и 2 и 14 шш и 14 ш 14
635. Упростите выражение:
![]() а) sin a –
а) sin a – ![]() cos a; б)
cos a; б) ![]() (cos
a –
sin a).
(cos
a –
sin a).
Решение.
а) sin a – ![]() 1 cos a = cos
1 cos a = cos ![]() p
sin a
– sin
p
sin a
– sin ![]() p cos a
=
p cos a
=
2 2 6 6
= sin (a – p);
6
![]()
![]()
![]() б) (cos a – sin
a) =
cos a
– sin a
= = cos p cos a – sin
p sin a
= cos p + a) .
б) (cos a – sin
a) =
cos a
– sin a
= = cos p cos a – sin
p sin a
= cos p + a) .
4 4 4
Промежуточный контроль. С–26*, С–27*.
4. Сумма и разность синусов и косинусов 5. Формулы для двойных и половинных углов 6. Произведение синусов и косинусов
В трёх последних пунктах Дополнений к главе 4 доказываются формулы суммы, разности и произведения синусов и косинусов, а также формулы для двойных и половинных углов.
В пункте 4 приводятся доказательства формул:
a + b a – b sin a + sin b = 2 sin cos ; (1)
2 2
![]() a – b a + b sin a – sin
b =
2 sin cos ; (2)
a – b a + b sin a – sin
b =
2 sin cos ; (2)
2 2
a + b a – b cos a + cos b = 2 cos cos ; (3)
2 2
a – b a + b cos a – cos b = –2 sin sin . (4)
2 2
Для лучшего запоминания этих формул надо обратить внимание учащихся на то, что в левой части каждой из них стоят суммы или разности одноимённых функций от a и b, а справа — удвоенные произведения двух функций от полусуммы или полуразности этих углов. Воспроизводить эти формулы будет легче, если учащиеся запомнят идею их доказательства: надо сложить или вычесть sin (x + y) и sin (x – y) или cos (x + y) и cos (x – y). В первом случае получим чередование функций «синус-косинус» и при сложении, и при вычитании, а во втором случае получим чередование функций «косинус-косинус» при сложении и «синус-синус» при вычитании.
В правой части каждой из формул (1)—(4) знак между a и b в числителе первого аргумента совпадает со знаком между функциями в левой части формулы. Не рекомендуем правую часть формулы (4) писать без минуса:
b – a a + b
![]() 2sin sin
. Учащиеся должны запомнить, что знак
2sin sin
. Учащиеся должны запомнить, что знак
2 2
«–» в правой части формул (1)—(4) ставится только при вычитании косинусов.
В пункте 5 доказываются формулы:
sin2a = 2sin a cos a, (5)
cos2a = cos2a – sin2a, (6)
sin2 a = 1 – cos a , (7)
2 2
![]() cos2 a
= 1 +
cos a . (8)
cos2 a
= 1 +
cos a . (8)
2 2
Учащиеся обязательно должны понять идею доказательства формул (5) и (6) — в формулах для sin (a + b) и cos (a + b) надо заменить b на a, тогда, помня чередование функций для формул sin (a + b) и cos (a + b), они легко запомнят формулу (5): два раза «синус-косинус» и формулу (6): «косинус-косинус минус синус-синус».
Не рекомендуем формулы (7) и (8) писать в виде sin a = 1 – cos a , cos a = 1 + cos a ,
2 2 2 2
![]() так как учащиеся могут
подумать, что для каждого a
существует два значения sin a
или cos a , а это не так.
так как учащиеся могут
подумать, что для каждого a
существует два значения sin a
или cos a , а это не так.
2 2
В пункте 6 приводятся доказательства трёх формул:
sin a cos b = 1 (sin (a + b) + sin (a – b)),
2
![]() cos
a cos
b =
1(cos
(a +
b) +
cos (a
– b)),
sin a sin
b =
cos
a cos
b =
1(cos
(a +
b) +
cos (a
– b)),
sin a sin
b =
![]() (cos (a – b) – cos (a + b)).
(cos (a – b) – cos (a + b)).
Эти формулы относятся к таким, которые проще вывести заново, если они не запомнились надёжно. И здесь запоминанию формул способствует опора на чередование функций для синуса и косинуса суммы или разности двух углов.
644. а) Докажите справедливость равенства
sin 50° + sin 10° – cos 20° = 0.
Доказательство. sin 50° + sin
10° –
cos 20°
= = 2sin 30°cos
20° –
cos 20°
= 2 · ![]() cos 20° – cos 20° =
cos 20° – cos 20° =
= cos 20° – cos 20° = 0, что и требовалось доказать.
645. а) Докажите справедливость равенства
cos ![]() + cos
+ cos ![]() =
0.
=
0.
Доказательство. cos 5![]() p
+ cos
p
+ cos ![]() 7p
= 2cos
7p
= 2cos ![]() p cos
зж–
p cos
зж– ![]() p цч = 2 · 0 · cos
зж–
p цч = 2 · 0 · cos
зж– ![]() p чц =
0,
p чц =
0,
12 12 2 и 12ш и 12ш что и требовалось доказать.
75o 15o
646. ![]() в) Вычислите: cos cos
.
в) Вычислите: cos cos
.
2 2
Решение. Заметим, что данные углы можно представить в виде полусуммы и полуразности углов 45° и 30°:
75o 45o + 30o 15o 45o – 30o
![]() = ,
= .
= ,
= .
2 2 2 2
Воспользуемся формулой суммы косинусов:
![]()
![]()
![]() 75o 15o1
75o 15o1
cos cos = (cos 45° + cos 30°) = + ) =
2 22 2
= .
651. а) Докажите справедливость равенства
(sin a
+ sin b)2
+ (cos a
+ cos b)2
= 4cos2 ![]() a – b .
a – b .
2
Доказательство. (sin a + sin b)2 + (cos a + cos b)2 =
= (2sin a + b cos a – b )2 + (2cos a + b cos a – b )2 =
2 2 2 2
![]() =
4sin2 a
+ b cos2 a
– b + 4cos2 a + b cos2 a
– b =
=
4sin2 a
+ b cos2 a
– b + 4cos2 a + b cos2 a
– b =
2 2 2 2
= 4cos2 a – b (sin2 a + b + cos2 a + b ) =
2 2 2
= 4cos2 a – b · 1 = 4cos2 a – b , что и требовалось дока-
2 2
зать.
![]() 657. а)
Вычислите sin2a,
если sin a
= , 0 a
657. а)
Вычислите sin2a,
если sin a
= , 0 a
![]() p .
p .
2
Решение. Так как 0 a p , то cos a 0 и
2
2
![]() cos a = 1
– sin2 a = 1 – ( ) = 3 ,
cos a = 1
– sin2 a = 1 – ( ) = 3 ,
2
sin2a = 2sin a cos a = 2 · 1 · 3 = .
2 2
661. Если 0 a ![]() p ,
то что больше:
p ,
то что больше:
2
а) cos2a или 2cos a; б) sin2a или 2sin a? Решение. а)
Так как 0 a
![]() p ,
то 0 2a
p и a 2a.
p ,
то 0 2a
p и a 2a.
2
С увеличением угла от 0 до p значения косинуса
уменьшаются, поэтому cos2a
cos a,
а так как cos a
2cos a,
то для 0 a
![]() p
справедливо неравенство cos2a
2cos a.
p
справедливо неравенство cos2a
2cos a.
2
б) Так как 0 a ![]() p ,
то 0 sin a
1, 0 cos a
1 и
p ,
то 0 sin a
1, 0 cos a
1 и
2
sin2a = 2sin a cos a 2sin a · 1 2sin a,
т. е. sin2a 2sin a.
662. Существуют ли углы a, для которых выполняется равенство sin2a = 2sin
a (0
a ![]() p )?
p )?
2
Решение. Так как sin2a = 2sin a cos a, то равенство sin2a = 2sin a
выполняется лишь при условии cos a = 1. Это возможно только для угла a = 0.
679. в) Докажите справедливость равенства sin2a (sin2a + sin2b) + cos2a (cos2a + cos2b) =
= 2cos2(a – b). Доказательство.
sin2a (sin2a + sin2b) + cos2a (cos2a + cos2b) =
= sin22a + sin2asin2b + cos22a + cos2acos2b =
= 1 + cos (2a – 2b) = 1 + cos2 (a – b) =
![]()
![]() = 1
+ cos2(a
– b)
– sin2(a
– b)
= 2cos2(a
– b),
что и требовалось доказать. 680. а) Вычислите: cos
= 1
+ cos2(a
– b)
– sin2(a
– b)
= 2cos2(a
– b),
что и требовалось доказать. 680. а) Вычислите: cos ![]() p
cos cos .
p
cos cos .
9
Решение. Для решения этой задачи умножим и разде-
лим данное выражение на 8sin
![]() p
и преобразуем получен9
p
и преобразуем получен9
![]() ную дробь, применяя
три раза формулу синуса двойного угла:
ную дробь, применяя
три раза формулу синуса двойного угла:
9
=
Применение рассмотренного приёма в следующем задании не так очевидно.
2p 3p
![]()
![]() Дополнительное
задание. Вычислите: cos – sin .
Дополнительное
задание. Вычислите: cos – sin .
5 10
Решение. Сначала приведём данное выражение к разности одноимённых функций:
![]()
![]()
![]()
![]()
![]()
![]() cos
2p – sin 3p = sinзжp – 2pцч – sin 3p
= sin p – sin 3p .
cos
2p – sin 3p = sinзжp – 2pцч – sin 3p
= sin p – sin 3p .
5 10 и 2 5 ш 10 10 10
![]()
![]()
![]()
![]() Теперь,
применив формулу разности синусов, получим sin p
– sin 3p = 2sinжз– p цч cos 2p =
–2sin p cos 2p .
Теперь,
применив формулу разности синусов, получим sin p
– sin 3p = 2sinжз– p цч cos 2p =
–2sin p cos 2p .
10 10 и 10 ш 10 10 10
Умножим и разделим полученное произведение на p
![]() 2cos и применим два раза
формулу синуса двойного
2cos и применим два раза
формулу синуса двойного
10 угла:
![]() p
p
2 2 sin cos cos
|
Заметив, что |
10 |
10 |
![]() sin
sin
![]() 4p =
sinжзp – p цч = cos
4p =
sinжзp – p цч = cos ![]() p ,
p ,
10 и 2 10 ш 10
имеем
![]() 2p 3p 1 cos
2p 3p 1 cos ![]() – sin = – .
– sin = – .
5 10 2
682. а) Преобразуйте в сумму или разность: cos 3a cos a.
Решение. cos 3acos a = ![]() (cos
(3a +
a) +
cos (3a
– a))
=
(cos
(3a +
a) +
cos (3a
– a))
=
= ![]() (cos 4a + cos
2a) =
(cos 4a + cos
2a) =
![]() cos 4a +
cos 4a + ![]() cos 2a.
cos 2a.
683. а) Докажите, что
![]()
![]() sin 9p cos 5p – sin 6p cos p = 1 –
1 sin
p .
sin 9p cos 5p – sin 6p cos p = 1 –
1 sin
p .
28 28 35 35 2 2 5
Доказательство.
![]()
![]() 9p 5p p sin cos
– sin
9p 5p p sin cos
– sin
28
![]() = 1 (sin( p + 5p )
+ sin(
= 1 (sin( p + 5p )
+ sin(
2 28 28
– 1 (sin( 6p + p ) + sin(
2 35 35
= (sin p + sin p ) – 1 (sin p + sin p
2 7 2 5 7
что и требовалось доказать.
Промежуточный контроль. С–28*, С–29*, С–30*, К–7.
7. Исторические сведения
В данном пункте рассказывается об истории возникновения тригонометрии — от Клавдия Птолемея до Леонарда Эйлера. Этот материал способствует формированию представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации, о вкладе разных народов в её развитие.
элементы приближённых вычислений, статистики, комбинаторики и теории вероятностей
Пятая глава посвящена изучению приближённых вычислений, статистики, комбинаторики и теории вероятностей. Здесь рассматриваются различные способы представления числовых данных с помощью таблицы, круговой и столбчатой диаграмм, вводятся новые понятия и способы решения задач в теории вероятностей.
Выполнение заданий, приведённых в данной главе, поможет учащимся в развитии таких метапредметных умений, как умение самостоятельно планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных задач; умение осуществлять контроль своей деятельности, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией; умение оценивать правильность выполнения учебной задачи, собственные возможности её решения; умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач.
Цель изучения главы 5 — освоить методы приближённых вычислений и решения задач комбинаторики и теории вероятностей.
Основная цель изучения данного параграфа — усвоить понятия абсолютной и относительной погрешностей, оценки погрешности.
11.1. Абсолютная погрешность приближения
![]()
![]()
![]() В данном пункте вводятся
понятия приближения числа, абсолютной погрешности приближённого равенства a a (это число a – a ),
оценки погрешности приближения (всякое такое число h, что h a – a ).
Далее приводятся примеры применения этих понятий.
В данном пункте вводятся
понятия приближения числа, абсолютной погрешности приближённого равенства a a (это число a – a ),
оценки погрешности приближения (всякое такое число h, что h a – a ).
Далее приводятся примеры применения этих понятий.
Задания для повторения. При изучении данного пункта можно использовать задание 7 из рубрики «Задания для самоконтроля».
690. Укажите абсолютную погрешность приближения для следующего приближённого равенства: а) 2,7 ≈ 3; б) 5,789 ≈ 5,79.
Решение. а) Абсолютная погрешность приближённого равенства 2,7 ≈ 3 равна |2,7 – 3| = 0,3.
б) Абсолютная погрешность приближённого равенства 5,789 ≈ 5,79 равна |5,789 – 5,79| = 0,001.
![]() 694. Укажите
на координатной оси все приближения числа 2,185 с точностью до: а) 1; б) 0,1.
694. Укажите
на координатной оси все приближения числа 2,185 с точностью до: а) 1; б) 0,1.
Решение. а) Искомые приближения — это все числа x, для которых верно неравенство |x – 2,185| 1. Решив это неравенство, получим множество его решений: [1,185; 3,185] 6 Рис. 48
(рис. 48, а).
б) Искомые приближения — это все числа x, для которых верно неравенство |x – 2,185| 0,1. Решив это неравенство, получим множество его решений: [2,085; 2,285] (рис. 48, б).
![]() Замечание.
Выполняя задание 694, учащиеся могут не решать неравенство, а
отступить на координатной оси вправо и влево от числа 2,185 на 1 или 0,1
соответственно. Тогда любое число x из образовавшегося числового отрезка
отличается от числа 2,185 не более чем на 1 и 0,1 соответственно.
Замечание.
Выполняя задание 694, учащиеся могут не решать неравенство, а
отступить на координатной оси вправо и влево от числа 2,185 на 1 или 0,1
соответственно. Тогда любое число x из образовавшегося числового отрезка
отличается от числа 2,185 не более чем на 1 и 0,1 соответственно.
11.2. Относительная погрешность приближения
![]() В
данном пункте вводится понятие относительной погрешности приближённого
равенства a a
(это число
В
данном пункте вводится понятие относительной погрешности приближённого
равенства a a
(это число
a – a
![]() ), приводятся примеры
вычисления относительной a
), приводятся примеры
вычисления относительной a
погрешности, формулируются правила оценки относительной погрешности приближения:
1. Если заменить положительное число его приближением с точностью до k-й значащей цифры с недостатком, то относительная погрешность этого приближения не превышает 10–(k – 1).
2. Если заменить
положительное число его приближением с точностью до k-й значащей цифры с
округлением, то относительная погрешность этого приближения не превышает ![]() ·
10–(k – 1).
·
10–(k – 1).
Далее разбираются примеры оценки относительной погрешности округления, подтверждающие эти правила.
Задания для повторения. При изучении данного пункта можно использовать задание 8 из рубрики «Задания для самоконтроля».
698. Определите абсолютную и относительную погреш-ности приближения: а) 127 130; б) 17 20.
Решение. а) Абсолютная погрешность приближения
равна |127 – 130| = 3, относительная погрешность
приближения равна ![]() .
.
б) Абсолютная погрешность приближения равна |17 –
20| = 3, относительная погрешность приближения равна ![]() .
.
699. Округлите число до одной цифры после запятой и определите абсолютную и относительную погрешности приближения: а) 0,48; б) 1,324.
Решение. а) 0,48 0,5, абсолютная и относительная погрешности приближения равны соответственно
![]() |0,48 – 0,5| = 0,02
и 0 02, = 1 .
|0,48 – 0,5| = 0,02
и 0 02, = 1 .
0 48, 24
б) 1,324 1,3, абсолютная и относительная погрешно-
![]() сти приближения равны
соответственно |1,324 – 1,3| = 0,024 и 0 024, = 6 .
сти приближения равны
соответственно |1,324 – 1,3| = 0,024 и 0 024, = 6 .
1 324, 331
700. Оцените относительную погрешность приближён-ного равенства:
а) 23 392 23 000; г) 0,000578 0,0006.
Решение. а) Число 23 392 заменено приближением
23 000 = 2,3 ·
104 с точностью до 2-й значащей цифры с округлением, поэтому по
правилу 2 относительная погрешность этого приближения не превышает ![]() ·
10–(2 – 1) =
·
10–(2 – 1) =
= ![]() .
.
г) Число 0,000578 заменено приближением 0,0006 =
= 6 · 10–4 с точностью до 1-й значащей цифры с
округлением, поэтому по правилу 2 относительная погрешность этого
приближения не превышает ![]() · 10–(1 – 1)
=
· 10–(1 – 1)
= ![]() .
.
Промежуточный контроль. С–31*.
11.3. Приближение суммы и разности
В данном пункте доказываются теоремы о приближении суммы и разности двух чисел и о приближении суммы конечного числа слагаемых, разбираются примеры применения этих теорем.
Задания для повторения. При изучении данного пункта можно использовать задания 9, 10 из рубрики «Задания для самоконтроля».
705. а) Оцените абсолютную погрешность приближённого равенства
123 784,5 – 3897 124 000 – 4000 = 120 000.
Решение. Так как абсолютная погрешность данного приближённого равенства не превышает суммы абсолютных погрешностей приближённых равенств:
123 784,5 124 000 и 3897 4000,
то искомая абсолютная погрешность не превышает суммы
|123 784,5 – 124 000| + |3897 – 4000| = = 215,5 + 103 = 318,5.
710. Какое округление чисел 0,378561; 2,235622; 3,789012; 4,251617 необходимо провести, чтобы их сумма была получена с точностью до 0,1? Выполните сложение данных чисел приближённо с точностью до 0,1.
Решение. Округлим слагаемые до первой цифры после запятой:
0,378561 0,4; 2,235622 2,2; 3,789012 3,8; 4,251617 4,3.
По теореме о погрешности приближения суммы конечного числа слагаемых, погрешность приближённого равенства
0,378561 + 2,235622 + 3,789012 + 4,251617
0,4 + 2,2 + 3,8 + 4,3 = 10,7
не превышает суммы погрешностей слагаемых:
|0,378561 – 0,4| + |2,235622 – 2,2| +
+ |3,789012 – 3,8| + |4,251617 – 4,3| = = 0,021439 + 0,035622 + 0,010988 + 0,048383 = = 0,116432 0,1.
Округлим слагаемые до второй цифры после запятой:
0,378561 0,38; 2,235622 2,24; 3,789012 3,79; 4,251617 4,25.
По теореме о погрешности приближения суммы конечного числа слагаемых, погрешность приближённого равенства
0,378561 + 2,235622 + 3,789012 + 4,251617
0,38 + 2,24 + 3,79 + 4,25 = 10,66
не превышает суммы погрешностей слагаемых:
|0,378561 – 0,38| + |2,235622 – 2,24| +
+ |3,789012 – 3,79| + |4,251617 – 4,25| = = 0,001439 + 0,004378 + 0,000988 + 0,001617 = = 0,008422 0,1.
Итак, данные слагаемые надо округлить до двух значащих цифр. Сумма этих цифр приближённо с точностью до 0,1 равна 10,66.
711. Пол комнаты состоит из 17 досок, ширина каждой из которых 35 см с точностью до 0,5 см. Какую возможную ошибку мы сделаем, если будем считать, что ширина комнаты (в направлении ширины досок) равна приближённо 35 · 17 см?
Решение. По теореме о погрешности приближения суммы конечного числа слагаемых погрешность приближения 35 · 17 к истинной ширине равна 0,5 · 17 = 8,5. Ошибка может составить 8,5 см.
11.4. Приближение произведения и частного
11.5. Приближённые вычисления и калькулятор
В пункте 11.4 доказываются теоремы о приближении произведения и частного двух чисел, разбираются примеры применения этих теорем. Оказывается, что относительная погрешность произведения (частного) двух чисел не превышает суммы относительных погрешностей этих чисел. При этом относительные погрешности чисел надо стараться сделать равными.
В пункте 11.5 на примере калькулятора с восьмиразрядным дисплеем рассказывается о том, как надо пользоваться калькулятором при выполнении приближённых вычислений. На изучение этого пункта следует обратить особое внимание, так как учащиеся, пользуясь калькулятором, обычно полагают, что все цифры получаемых ими результатов верные, а это не всегда так.
Задания для повторения. При изучении данного пункта можно использовать задание 11 из рубрики «Задания для самоконтроля».
713. а) Вычислите приближённо с относительной погрешностью, меньшей 0,001, произведение двух чисел 0,12345678... и 2,(7).
Решение. Округлим каждое число до четырёх значащих цифр:
a = 0,12345678... 0,1235, b = 2,(7) 2,778.
Тогда a · b 0,1235 · 2,778 = 0,343083 0,3431.
Относительная погрешность найденного произведения не
превосходит ![]() · 10–(4 – 1)
+
· 10–(4 – 1)
+ ![]() · 10–(4 – 1)
= 0,001.
· 10–(4 – 1)
= 0,001.
716. а) Вычислите приближённо с относительной погрешностью, меньшей 0,01, частное двух чисел 0,12345678... и 2,(17).
Решение. Округлим каждое число до трёх значащих цифр:
a = 0,12345678... 0,123, b = 2,(17) 2,17.
Тогда a : b 0,123 : 2,17 = 0,05668... 0,0567.
Относительная погрешность найденного частного не
превосходит ![]() · 10–(3 – 1)
+
· 10–(3 – 1)
+ ![]() · 10–(3 – 1)
= 0,01.
· 10–(3 – 1)
= 0,01.
Промежуточный контроль. С–32*.
Основная цель изучения данного параграфа — усвоить способы представления различных числовых характеристик.
12.1. Способы представления числовых данных
В данном пункте рассматриваются способы представления числовых данных с помощью таблицы, круговой и столбчатой диаграмм. Этот материал должен быть хорошо знаком учащимся из предыдущих классов и личного опыта (учебная литература, СМИ).
Задания для повторения. При изучении данного пункта можно использовать задание 12 из рубрики «Задания для самоконтроля».
720. На рисунке 49 жирными точками показана цена олова на момент закрытия биржевых торгов во все рабочие дни с 12 по 28 ноября 2007 г. По горизонтали указываются числа месяца, по вертикали — цена тонны олова в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку:
а) наименьшую цену олова на момент закрытия торгов
в указанный период;
б) день, в который цена олова на момент закрытия торгов в указанный период была наибольшей;
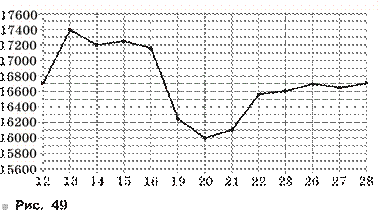
в) день, в который цена олова на момент закрытия торгов снизилась по сравнению с предыдущим днём на наибольшую величину.
Решение. а) Наименьшая цена олова на момент закрытия торгов в указанный период составила 16 000 долларов за тонну.
б) 13 ноября 2007 г. цена олова на момент закрытия
торгов в указанный период была наибольшей.
в) 19 ноября 2007 г. цена олова на момент закрытия торгов снизилась по сравнению с предыдущим днём на наибольшую величину.
![]() 724. В
некотором царстве, в некотором государстве в ходе выборов в парламент по
телевидению показали итоги голосования в одном из избирательных округов (рис.
50). Объясните, почему представленная информация о числе голосов избирателей,
поданных за партии, не является достоверной.
724. В
некотором царстве, в некотором государстве в ходе выборов в парламент по
телевидению показали итоги голосования в одном из избирательных округов (рис.
50). Объясните, почему представленная информация о числе голосов избирателей,
поданных за партии, не является достоверной.
Решение. Сумма процентов
6 Рис. 50 голосов, отданных за все партии, должна быть равна 100, а здесь
17,4 + 26,3 + 59,7 + 21,8 = 125,2 100.
Поэтому представленная информация о числе голосов избирателей не является достоверной.
12.2. Характеристики числовых данных
В данном пункте на конкретных примерах рассматриваются следующие числовые характеристики: среднее арифметическое данных чисел, мода, размах, медиана и дисперсия. Приводятся примеры применения этих понятий.
Задания для повторения. При изучении данного пункта можно использовать задание 13 из рубрики «Задания для самоконтроля».
725. За первый час были проданы мужские рубашки новой коллекции следующих цветов: розовый, белый, зелёный, зелёный, белый, голубой, голубой, белый, голубой, белый. Определите моду этой совокупности.
Решение. Так как белый цвет встречается чаще других цветов, то белый цвет — мода данной совокупности.
Ответ. Белый.
726. Определите среднее число очков, выпадающих на игральном кубике, на котором точками отмечены числа 1, 2, 3, 4, 5, 6. Какая из характеристик (среднее арифметическое, мода, медиана, размах) указывает на это число?
Решение. Интуитивно ясно, что при достаточно большом числе испытаний каждое число очков, изображённое на гранях «правильного» кубика, выпадает одинаково часто. Обозначим это число n. Тогда среднее число очков, выпадающих в одном испытании, равно
1 · + 2 · + 3 · + 4 · + 5 · n n n n n + · 6 n
![]() = 3 5, .
= 3 5, .
6 · n
Тот же результат даёт среднее арифметическое шести
1 + + + + + 2 3 4 5 6
![]() чисел: = ,3 5. Медианой данной совокуп-
чисел: = ,3 5. Медианой данной совокуп-
6
![]() ности
является среднее арифметическое двух чисел: = ,3 5.
ности
является среднее арифметическое двух чисел: = ,3 5.
Размах 6 – 1 = 5 не указывает на среднее число очков в одном испытании.
730. Шериф полиции, только вступивший в должность, упомянул о резком росте преступности в округе при старом шерифе и для убедительности показал диаграмму числа преступлений за два года, предшествующие его назначению
(рис. 51). Действительно ли преступность резко возросла?
Решение. Шериф полиции явно сгустил краски, так как
6 Рис. 51
рост преступности на ![]() · 100% 4 5, % вряд ли можно назвать резким. А разница в
высоте столбцов была бы совсем маленькой, если бы они были изображены без
разрыва.
· 100% 4 5, % вряд ли можно назвать резким. А разница в
высоте столбцов была бы совсем маленькой, если бы они были изображены без
разрыва.
732*. Докажите свойства дисперсии:
а) если все числовые значения совокупности умень-
шить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится;
б) если все числовые значения совокупности уменьшить (увеличить) в k раз, то дисперсия уменьшится (увеличится) в k2 раз.
Доказательство. а) Если каждую величину увеличить на b, то среднее арифметическое также увеличится на b:
![]() (a1 + b) + ... + (an + b) = a1 + ... + an + · n b = a1 + ... + an + b.
(a1 + b) + ... + (an + b) = a1 + ... + an + · n b = a1 + ... + an + b.
n n n
Поэтому отклонения величин от среднего значения не изменятся:
![]()
![]()
![]()
![]() (ai + b) – a1 + ... + an + b) = ai – a1 + ... + an. nn
(ai + b) – a1 + ... + an + b) = ai – a1 + ... + an. nn
Следовательно, не изменится и дисперсия.
б) Если каждую величину увеличить в k раз, то сред-
нее арифметическое также увеличится в k раз:
![]() ka1 + ... + kan = k a( 1 + ... + an) = · k a + ... + an .
ka1 + ... + kan = k a( 1 + ... + an) = · k a + ... + an .
![]()
n n n
Поэтому отклонение каждой из величин от среднего значения также увеличится в k раз, квадрат каждого отклонения увеличится в k2 раз, поэтому и дисперсия (среднее арифметическое квадратов всех отклонений) увеличится в k2 раз.
Основная цель изучения данного параграфа — усвоить понятия и способы решения задач в комбинаторике.
13.1. Задачи на перебор всех возможных вариантов
В данном пункте рассматриваются примеры задач, в которых требуется осуществить перебор всех возможных вариантов или подсчитать их число. Желательно научить всех школьников решению таких задач.
Задания для повторения. При изучении данного пункта можно использовать задание 15 из рубрики «Задания для самоконтроля».
737. Четыре друга купили 4 билета в кино. Сколькими различными способами они могут занять свои места в зрительном зале?
Решение. Имеется 4 способа занять первое место (его может занять любой из четырёх приятелей) и в каждом из них — 3 способа занять второе место (его может занять любой из оставшихся трёх приятелей), всего — 4 · 3 способа. В каждом из них третье место можно занять двумя способами (его может занять любой из оставшихся двух приятелей), всего — 4 · 3 · 2 способа. Наконец, последнее место может занять один оставшийся приятель одним способом. Поэтому число способов занять 4 места равно
4 · 3 · 2 · 1 = 24.
Ответ. 24.
739. Бросили два игральных кубика. Сколькими раз-личными способами могут выпасть очки на этих кубиках?
Решение. На первом кубике очки могут выпасть шестью различными способами, в каждом из них на втором кубике очки могут выпасть также шестью способами, всех способов 6 · 6 = 36.
Ответ. 36 способами.
740. а) На окружности отметили 7 точек. Сколько получится отрезков, если соединить каждую точку с каждой?
Решение. Из каждой из 7 точек можно провести 6
отрезков. Так как каждый отрезок относится к двум точкам, то число отрезков
равно ![]() = 21.
= 21.
Решим задачу вторым способом. Из первой точки проведено 6 отрезков, из второй точки — 5 новых отрезков, из третьей — 4, из четвёртой — 3, из пятой — 2 отрезка, из шестой — 1, из седьмой точки уже нельзя провести ни одного нового отрезка. Итого, имеется 6 + 5 + 4 + 3 + 2 + + 1 = 21 отрезок.
Ответ. 21 отрезок.
742. а) Встретились несколько друзей, каждый пожал руку каждому. Вова Веселов был так рад встрече, что пожал руку дважды некоторым из своих друзей, но не всем. Всего было 30 рукопожатий. Сколько друзей встретилось?
б) Встретились несколько друзей, каждый пожал ру-
ку каждому. Последним пришёл Петя Угрюмов, он пожал руку не всем своим друзьям. Всего было 30 рукопожатий. Сколько друзей встретилось?
Решение. а) Если бы друзей было 7 и каждый
пожал руку каждому из друзей по одному разу, то всего рукопожатий было бы ![]() =
21. Даже если Вова пожал руки всем друзьям по два раза, то это добавит 6
рукопожатий, а их общее число будет меньше 30. Следовательно, число друзей
больше 7.
=
21. Даже если Вова пожал руки всем друзьям по два раза, то это добавит 6
рукопожатий, а их общее число будет меньше 30. Следовательно, число друзей
больше 7.
Если бы друзей было 8 и каждый пожал руку каждому из
друзей по одному разу, то всего рукопожатий было бы ![]() = 28.
Так как общее число рукопожатий на
= 28.
Так как общее число рукопожатий на
30 – 28 = 2 больше, то по два раза Вова пожал руку двум друзьям. То есть число друзей могло быть равным 8.
Если бы друзей было 9 и каждый пожал руку каждому из
друзей по одному разу, то всего рукопожатий было бы ![]() = 36,
что больше 30. Следовательно, число друзей
= 36,
что больше 30. Следовательно, число друзей
меньше 9.
б) Если бы друзей было 8 и каждый пожал руку каждому
из друзей по одному разу, то всего рукопожатий было бы ![]() = 28.
Так как Петя пожал руку не всем дру-
= 28.
Так как Петя пожал руку не всем дру-
зьям, то число рукопожатий должно быть меньше 28. Следовательно, число друзей больше 8.
Если друзей было 9 и каждый пожал руку каждому из друзей по одному разу, то всего рукопожатий было бы
![]() = 36,
что на 36 – 30 = 6 больше, чем 30, следователь-
= 36,
что на 36 – 30 = 6 больше, чем 30, следователь-
но, шести из своих восьми друзей Петя не пожал руку. То есть число друзей могло быть равным 9.
Если бы друзей было 10, то даже без Петиных рукопожатий общее число рукопожатий было бы равно
![]() = 36,
что больше 30. Следовательно, число друзей
= 36,
что больше 30. Следовательно, число друзей
меньше 10.
Ответ. а) 8 друзей; б) 9 друзей.
13.2. Комбинаторные правила
В данном пункте вводится понятие комбинаторной задачи и рассматриваются комбинаторные правила сложения и умножения. Желательно научить всех школьников решению таких задач.
Задания для повторения. При изучении данного пункта можно использовать задание 15 из рубрики «Задания для самоконтроля».
743. На тарелке лежит 5 мандаринов и 4 апельсина. Сколькими способами можно выбрать или мандарин, или апельсин?
Решение. По правилу сложения один фрукт можно выбрать 5 + 4 = 9 способами.
Ответ. 9 способами.
744. На тарелке лежит 5 мандаринов и 4 апельсина. Сколькими способами можно выбрать один мандарин и один апельсин?
Решение. По правилу умножения выбрать пару «мандарин и апельсин» можно 5 · 4 = 20 способами.
Ответ. 20 способами.
746. В классе 12 мальчиков и 15 девочек. Нужно выбрать старосту класса и его заместителя. Сколькими способами можно осуществить выбор, если это должны быть:
а) два мальчика;
в) мальчик-староста и девочка-заместитель;
д) мальчик и девочка (старостой может быть и маль-
чик, и девочка)?
Решение. а) Старосту из 12 мальчиков можно выбрать 12 способами, в каждом из них из оставшихся 11 мальчиков можно выбрать одного заместителя 11 способами. Поэтому выбрать старосту класса и его заместителя из 12 мальчиков можно 12 · 11 = 132 способами.
в) Старосту из 12 мальчиков можно выбрать 12 способами, в каждом из них из 15 девочек можно выбрать одного заместителя 15 способами. Поэтому выбрать мальчика — старосту и девочку — заместителя из 12 мальчиков и 15 девочек можно 12 · 15 = 180 способами.
д) Если староста мальчик, а его заместитель девочка, то число способов равно 180 (см. задание в). Если староста девочка, а её заместитель мальчик, то, рассуждая аналогично, получим 15 · 12 = 180 способов. А всего способов 180 + 180 = 360.
Ответ. а) 132 способами; в) 180 способами; д) 360 способами.
747. б) Сколькими способами 3 человека могут разместиться на четырёхместной скамейке?
Решение. Имеется 4 способа оставить одно место свободным, в каждом из них 3 человека могут занять оставшиеся 3 места 3 · 2 · 1 = 6 способами. А всего способов 4 · 6 = 24.
Ответ. 24 способами.
748.
![]() Сколько различных автомобильных номеров мож-но получить,
используя три буквы из 30 букв русского алфавита (без ь, ъ, ы) и четыре из
десяти цифр (от 0 до 9), если цифры и буквы повторять не разрешается и номер
должен иметь вид, как на рисун-
Сколько различных автомобильных номеров мож-но получить,
используя три буквы из 30 букв русского алфавита (без ь, ъ, ы) и четыре из
десяти цифр (от 0 до 9), если цифры и буквы повторять не разрешается и номер
должен иметь вид, как на рисун-
ке 52? 6 Рис. 52
Решение. Имеется 30 · 29 · 28 = 24 360 способов выбрать 3 буквы без повторения, в каждом из них имеется 10 · 9 · 8 · 7 = 5040 способов выбрать 4 цифры без повторения. А всего способов получить автомобильные номера 24 360 · 5040 = 122 774 400.
Ответ. 122 774 400 номеров.
750. В кафе предлагают два первых блюда: борщ, рас-сольник, четыре вторых блюда: гуляш, котлеты, сосиски, пельмени и три третьих блюда: чай, кофе, компот. Сколько вариантов обеда предлагают в кафе?
Решение. Имеется 2 способа выбрать первое блюдо, в каждом из них имеется 4 способа выбрать второе блюдо, т. е. имеется 2 · 4 = 8 способов выбрать первое и второе блюда. В каждом из них имеется 3 способа выбрать третье блюдо. А всего способов выбрать обед из трёх блюд 8 · 3 = 24.
Ответ. 24 способа.
751. а) Сколько решений в натуральных числах имеет система уравнений
мa + = b 4, ноc + = d 5?
Решение. Первое уравнение системы имеет 3 решения в натуральных числах: a = 1, b = 3; a = 2, b = 2; a = 3, b = 1. Для каждого из них второе уравнение системы имеет 4 решения в натуральных числах: c = 1, d = 4; c = 2, d = 3; c = 3, d = 2; c = 4, d = 1. Поэтому система имеет 3 · 4 = 12 решений.
Ответ. 12 решений.
13.3. Перестановки 13.4. Размещения 13.5. Сочетания
Материал пунктов 13.3—13.5 обычно вызывает затруднения у учащихся, которые плохо понимают, чем размещения из n элементов по k отличаются от сочетаний из n элементов по k. Следует отметить, что для первых важна последовательность выбранных k элементов, а для вторых эта последовательность не важна. При этом можно воспользоваться примерами, дающими запоминающиеся образы:
P4 — количество мелодий, которые можно сыграть, используя 4 различные ноты (без повторения);
A74 — количество мелодий, которые можно сыграть, используя 4 различные ноты из данных семи нот (без повторения);
C74 — количество аккордов, которые можно сыграть, используя 4 различные ноты из данных семи нот (без повторения). Ноты в аккорде звучат одновременно, порядок следования нот не важен.
Чтобы подготовить учащихся к введению определений и формул для вычисления числа перестановок из n элементов, числа размещений из n элементов по k, числа сочетаний из n элементов по k, необходимо, следуя учебнику, решить приведённые в учебном тексте простые задачи с двумя, тремя, четырьмя элементами.
Например, формула подсчёта числа перестановок из n элементов может быть получена сначала для нескольких чисел n.
Для n = 3 рассуждение можно вести так. На первое место можно поставить любой из трёх элементов (3 возможности). Если один элемент мы уже поставили на первое место, то на второе место можно поставить один из двух оставшихся элементов (2 возможности). Тогда первые два места можно занять шестью способами (3 · 2 = 6), в каждом из которых оставшееся третье место можно занять одним способом одним оставшимся элементом (1 возможность). Тогда число перестановок из трёх элементов равно P3 = 3 · 2 · 1 = 6. Приведённое рассуждение учащиеся легко применят для четырёх элементов и могут выдвинуть гипотезу, что справедлива формула
Pn = n · (n – 1) · (n – 2) · ... · 3 · 2 · 1 = n!.
Эту гипотезу можно доказать методом математической индукции.
Задания для повторения. При изучении данного пункта можно использовать задания 16—19 из рубрики «Задания для самоконтроля».
756. Проказница-Мартышка, Осёл, Козёл да Косолапый Мишка затеяли сыграть квартет. Выясните, сколькими способами они могут сесть со своими инструментами на четыре места.
Решение. Число способов равно числу перестановок из 4 элементов:
P4 = 4 · 3 · 2 · 1 = 24.
Ответ. 24 способами.
759. а) Вычислите P10 : P9.
10 · · 9 ... · 1
Решение.
P10 : P9 = ![]() 9 · ... · 1 = 10.
9 · ... · 1 = 10.
Ответ. 10.
760. У кассира автобуса имеются для продажи биле-ты на автобус с номерами от 000000 до 999999. Сколько номеров билетов из этого набора записаны цифрами 1, 2, 3, 4, 5, 6 без повторения?
Решение. Число таких билетов равно числу перестановок из 6 элементов:
P6 = 6
· 5 · 4 · 3 · 2 ·
1 = 720. Ответ. 720. 763. Докажите формулу: Ank
= ![]() n! .
n! .
(n – k)!
Доказательство. Для 1 k n имеем
Ank = n · (n – 1) · ... · (n – k + 1) =
n · (n – 1 · ) ... · (n – + 1 · k ) (n – k) · ... · 1 n!
![]() = =
.
= =
.
(n – k) · ... · 1
Для k = 1 формула A =
(n – 1)!
![]() Для k = n, как
показано в учебнике, Ann = n!. Чтобы записать требуемую
формулу для k = n, принято считать, что 0! = 1.
Тогда формула Ann = n! = n! = n! = n!
Для k = n, как
показано в учебнике, Ann = n!. Чтобы записать требуемую
формулу для k = n, принято считать, что 0! = 1.
Тогда формула Ann = n! = n! = n! = n!
(n – n)! 0! 1
верна.
Тем самым формула доказана для 1 k n.
764. а) Сколькими различными способами можно распределить между шестью лицами две разные путёвки?
Решение. Число способов распределить две разные путёвки между шестью лицами равно
A62 = 6 · 5 = 30
(первую путёвку можно распределить шестью способами; в каждом из них вторую путёвку можно распределить пятью способами среди лиц, не получивших первую путёвку).
Ответ. 30.
766. У билетного кассира имеются для продажи билеты на автобус с номерами от 000000 до 999999. Сколько номеров билетов из этого набора записаны разными цифрами?
Решение. Поставив одну из десяти цифр на первое место, на второе место можно поставить одну из оставшихся девяти цифр, ..., на шестое место — одну из оставшихся пяти цифр, поэтому разными цифрами можно записать
A106 = 10 · 9 · 8 · 7 · 6 · 5 = 151 200 номеров.
Ответ. 151 200 номеров.
767. У билетного кассира имеются для продажи билеты на автобус с номерами от 000000 до 999999. Сколько номеров билетов из этого набора записаны без нулей?
Решение. Поставив одну из девяти цифр (нули исключены) на первое место, на второе место можно поставить одну из оставшихся восьми цифр, ..., на шестое место — одну из оставшихся четырёх цифр, поэтому разными цифрами можно записать
A96 = 9 · 8 · 7 · 6 · 5 · 4 = 60 480 номеров.
Ответ. 60 480 номеров. 771.
Докажите формулу: Cnk = ![]() n! .
n! .
k n! ( – k)!
Доказательство. Для 1 k n имеем
k (n – 1 · ... · ) (n – + 1k )
n ·
Cn = =
k!
![]() n · (n – 1 · ... · ) (n – + 1 · k ) (n – k)
· ... · 1 n!
n · (n – 1 · ... · ) (n – + 1 · k ) (n – k)
· ... · 1 n!
= = .
k! · (n – k) · ... · 1 k n! ( – k)!
Для k = 1 имеем
1 n n n ( – 1)! n!
![]() Cn =
Cn = ![]() =
n = = .
=
n = = .
1 1! (n – 1)! 1! (n – 1)!
Для k = n имеем
n ( – 1 · ... · ) (n – + 1n ) n n
Cn = ![]() =
1.
=
1.
n!
Чтобы написать требуемую формулу для k = n, принято считать, что 0! = 1. Тогда для k = n имеем
![]() Cnn = n n(
– 1 · ... · ) (n – + 1n ) = n! .
Cnn = n n(
– 1 · ... · ) (n – + 1n ) = n! .
n! n n! ( – n)!
Тем самым формула доказана для 1 k n.
772. Докажите, что Cnk = Cnn – k . Вычислите:
а) C109 ; в) C1210 ; е) C19981997 .
Доказательство.
Для 1 k
n имеем Cnk
= ![]() n!
=
n!
=
k n! ( – k)!
= ![]() = Cn , что и
требовалось доказать.
= Cn , что и
требовалось доказать.
(n – k k) ! !
![]() а)
C109 = C1010 – 9 = C101 = 10! = 10 · 9! =
10; 1! (10
– 1)
! 9 !
а)
C109 = C1010 – 9 = C101 = 10! = 10 · 9! =
10; 1! (10
– 1)
! 9 !
в) C1210 = C1212 – 10 = C122 = ![]() =
=
![]() = 66;
= 66;
е)C19981997 = C19981998 – 1997 = C19981 = ![]() 1998 · 1997! = 1 1998!(
– 1)!
1998 · 1997! = 1 1998!(
– 1)!
= ![]() = 1998.
= 1998.
773. а) Сколькими способами можно распределить две одинаковые путёвки между пятью лицами?
Решение. а) Число способов распределить две
одинаковые путёвки между пятью лицами равно C52
= ![]() = 10
= 10
(оно в 2 раза меньше числа способов распределить две разные путёвки между пятью лицами, так как порядок получения путёвок не важен).
Ответ. 10 способами.
775. Из 27 учащихся класса нужно выбрать двух дежурных. Сколькими способами это можно сделать?
Решение. Число способов выбрать двух дежурных
из 27 учащихся равно C272 = ![]() = 351.
= 351.
Ответ. 351 способом.
Основная цель изучения данного параграфа — усвоить понятия и способы решения задач в теории вероятностей, научиться применять полученные знания в жизненных ситуациях, приводящих к вероятностным задачам.
14.1. Случайные события
В данном пункте вводятся понятия случайного опыта, равновозможных исходов, случайного события, элементарного события, исхода, благоприятствующего событию A, невозможного события и достоверного события.
Далее разбираются примеры применения этих понятий и материал, посвящённый обсуждению введённых понятий на языке теории множеств.
Задания для повторения. При изучении данного пункта можно использовать задание 20 из рубрики «Задания для самоконтроля».
781. В опыте подбрасывают две монеты. Сколько всего исходов в этом опыте? Сколько исходов благоприятствует событию:
а) A — «выпало два герба»;
б) B — «выпало две решки»;
в) C — «выпали герб и решка»?
Какие исходы опыта благоприятствуют каждому из событий A, B, C. Какие из этих событий являются элементарными событиями?
Решение. В этом опыте 4 исхода: (О, О), (Р, Р), (О, Р), (Р, О).
а) Событию A благоприятствует одно событие с исходом (О, О).
б) Событию B благоприятствует одно событие с исхо-
дом (Р, Р).
в) Событию C благоприятствуют два события с исхо-
дами (О, Р), (Р, О).
События A и B — элементарные, каждому из них благоприятствует один исход. Событие C не является элементарным, ему благоприятствуют два исхода.
782. В опыте из колоды в 36 карт извлекают две карты. Сколько исходов благоприятствует событию:
а) A — «извлечены две карты чёрной масти»;
в) C — «извлечены две карты: одна чёрной масти, дру-
гая красной»?
Решение. а) Из 18 карт чёрной масти извлечь две карты можно P182 = 18 · 17 = 306 способами.
в) Из 18 карт чёрной масти извлечь одну можно
18 способами, из 18 карт красной масти извлечь одну можно 18 способами. По комбинаторному правилу умножения событию C благоприятствует 18 · 18 = 324 события. Ответ. а) 306; в) 324.
783. Сколько событий может произойти в опыте подбрасывания игрального кубика?
Решение. В этом опыте 6 исходов, следовательно, может произойти 26 = 64 события.
Ответ. 64 события.
14.2. Вероятность случайного события
В данном пункте вводятся понятие равновозможных событий, обозначения для достоверного и невозможного событий, для несовместных событий и вероятности события. Далее подробно разбираются примеры вычисления вероятностей событий.
Задания для повторения. При изучении данного пункта можно использовать задание 21 из рубрики «Задания для самоконтроля».
784. Ваня, Маша и Петя хотят купить три билета в кино на соседние места. Какова вероятность того, что место Маши окажется посередине, если она выберет один билет из трёх случайным образом?
Решение. Число всех равновозможных исходов
равно P3 = 3 · 2 · 1
= 6. Число исходов, благоприятствующих событию «Маша окажется
посередине», равно 2 (ВМП, ПМВ), поэтому вероятность этого события равна ![]() =
=
![]() .
.
Ответ. ![]() .
.
785. Три карты: валет (В), дама (Д), король (К) — перемешали и положили в ряд «рубашкой» вверх. Какова вероятность того, что после переворачивания карт:
а) они окажутся в порядке ВДК;
б) на первом месте окажется Д;
г) на всех трёх местах окажется Д?
Решение. Число всех равновозможных исходов в опыте равно P3 = 3 · 2 · 1 = 6.
а) Число исходов, благоприятствующих событию «карты
окажутся в порядке ВДК», равно 1, поэтому вероятность этого события равна ![]() .
.
б) Число исходов, благоприятствующих событию «на
первом месте окажется Д», равно 2 (ДВК, ДКВ), поэтому вероятность этого события
равна ![]() =
= ![]() .
.
г) Событие «на всех трёх местах окажется Д»
невозможное, ему благоприятствуют 0 исходов, поэтому вероятность этого события
равна ![]() = 0.
= 0.
Ответ. а) ![]() ; б)
; б) ![]() ;
г) 0.
;
г) 0.
789. В лотерее предлагается угадать n чисел из k. Определите, в какой лотерее вероятность выигрыша больше: в лотерее «6 из 49» или «5 из 36».
Решение. Выясним, сколько существует способов угадать 6 чисел из 49 (событие А). Так как порядок угаданных чисел не важен, то искомое число способов равно
![]() C496 =
=
C496 =
= ![]() 49 · 48 · 47 · 46 · 45 · 44 =
13 983 816.
49 · 48 · 47 · 46 · 45 · 44 =
13 983 816.
· · · 6 5 4 3 · · 2 1
Аналогично число способов угадать 5 чисел из 36 (событие B) есть число сочетаний из 36 по 5. Оно равно
![]() C365 = 36! =
36 · 35 ·
34 · 33 · 32 = 2 235 552.
C365 = 36! =
36 · 35 ·
34 · 33 · 32 = 2 235 552.
5 · 31! · · · · 5 4 3 2 1
В первом опыте возможны 13 983 816 исходов, все эти
исходы равновозможны, и требуется определить вероятность события A,
поэтому Р(А) = ![]() .
.
Во втором опыте возможны 2 235 552 исхода, все эти
исходы равновозможны, и требуется определить вероятность события В,
поэтому Р(B) = ![]() .
.
Так как ![]()
![]() , то вероятность
выигрыша больше в лотерее «5 из 36».
, то вероятность
выигрыша больше в лотерее «5 из 36».
Ответ. Вероятность выигрыша больше в лотерее «5 из 36».
790. В некотором царстве, в некотором государстве разбойника приговорили к смертной казни, и он подал царю прошение о помиловании. Добрый царь, большой знаток теории вероятностей, сказал: «Доверимся случаю, пусть разбойник сам решит свою судьбу. Выдайте ему мешок с полным набором костей домино и две игральные кости. Пусть он вытащит из мешка не глядя одну кость домино или бросит две игральные кости — по своему выбору. Если полученная в этом испытании сумма очков окажется равной числу, которое он назовёт до начала испытания, то быть по сему — пусть живёт». Какой вид испытания должен выбрать разбойник и какую сумму назвать, чтобы вероятность остаться живым оказалась наибольшей?
![]() Решение.
В полном наборе костей домино 28 костей, поэтому число всех равновозможных
исходов опыта «вынуть из мешка кость домино» равно 28. Событию A —
«вынуть кость с суммой очков 6» благоприятствуют 4 случая, а каждому из событий
«вынуть кость с суммой очков n», где n 6, благоприятствует
меньше случаев, поэтому вероятность события A наибольшая в этом опыте,
она равна 4
= 1 .
Решение.
В полном наборе костей домино 28 костей, поэтому число всех равновозможных
исходов опыта «вынуть из мешка кость домино» равно 28. Событию A —
«вынуть кость с суммой очков 6» благоприятствуют 4 случая, а каждому из событий
«вынуть кость с суммой очков n», где n 6, благоприятствует
меньше случаев, поэтому вероятность события A наибольшая в этом опыте,
она равна 4
= 1 .
28 7
При бросании двух игральных костей имеется 6 ·
6 = 36 равновозможных исходов опыта «бросить две игральные
кости». Событию B — «получить сумму очков 7» благоприятствуют 6 случаев,
а каждому из событий «получить сумму очков n», где n 7,
благоприятствует меньше случаев, поэтому вероятность события B
наибольшая в этом опыте, она равна ![]() =
= ![]() .
.
![]() Так
как 1
1 ,
то разбойник должен выбрать опыт с
Так
как 1
1 ,
то разбойник должен выбрать опыт с
6 7
двумя игральными костями и назвать число 7. В этом случае вероятность сохранить жизнь больше, чем в опыте с костями домино.
14.3. Сумма, произведение и разность случайных событий
В данном пункте вводятся понятия суммы, произведения и разности двух случайных событий, а также понятия события, противоположного событию A, и противопо-
![]()
ложных событий A и A , устанавливается их свойство
![]()
A + A = W (сумма противоположных событий есть достоверное событие), а также свойство вероятностей противоположных событий (сумма их вероятностей равна 1):
![]()
P(A) +P( A ) = 1.
Задания для повторения. При изучении данного пункта можно использовать задание 22 из рубрики «Задания для самоконтроля».
793. Спортивный комментатор оценил вероятность
победы лыжника Иванова в 90%. Какова вероятность (по оценке спортивного
комментатора) того, что Иванов не победит? ![]()
Решение. События А — «победит Иванов» и A — «не победит Иванов» противоположные, поэтому
сумма их вероятностей равна 1 (![]() ). Так как вероятность события A
). Так как вероятность события A
![]()
![]()
![]() равна , то
вероятность события A равна 1 –
90
= 10
.
равна , то
вероятность события A равна 1 –
90
= 10
.
100 100
Ответ. 10%.
795. В опыте бросают игральный кубик. Какова вероятность события:
а) M — «не выпало простое число очков»;
б) N — «не выпало число очков, кратное 3»;
в) K — «не выпало число очков, кратное 2 или 3»?
Решение. Число всех равновозможных исходов в
опыте равно 6. ![]()
а) Событию M — «выпадет простое число очков» благоприятствует 3 исхода (2, 3, 5 очков), следовательно,
![]() P( M ) =
P( M ) =
![]() =
= ![]() .
.
Тогда
вероятность противоположного события M равна 1 – ![]() =
=
![]() .
.
![]()
б) Событию N — «выпадет число очков, кратное 3» благоприятствует 2 исхода (3, 6 очков), следовательно,
![]() P( N ) =
P( N ) =
![]() =
= ![]() .
.
Тогда
вероятность противоположного события N равна 1 – ![]() =
=
![]() .
.
![]()
в) Событию K — «выпадет число очков, кратное 2
или 3» благоприятствует 4 исхода (2,
3, 4, 6 очков), следовательно, ![]()
P( K ) =
![]() =
= ![]() .
.
Тогда вероятность противоположного события K равна
Ответ. а) ![]() ; б)
; б) ![]()
1 – ![]() =
= ![]() .
.
; в) ![]() .
.
14.4. Несовместные события. Независимые события
В данном пункте вводится понятие несовместных событий, устанавливаются свойства:
1) произведение несовместных событий A и B является невозможным событием;
2) вероятность суммы несовместных событий A и B равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B). (1)
Формула (1) является частным случаем более общей формулы для вероятности суммы событий A и B, не являющихся несовместными событиями:
P(A + B) = P(A) + P(B) – P(A · B). (2)
Далее вводится понятие независимых событий, т. е. событий A и B, таких, что
P(A · B) = P(A) · P(B). (3)
Заметим, что при решении практических задач редко проверяют равенство (3), а обычно пользуются интуитивными соображениями, основанными на опыте. Поэтому в практических задачах независимость событий заранее оговаривают.
Задания для повторения. При изучении данного пункта можно использовать задание 23 из рубрики «Задания для самоконтроля».
798. В опыте из колоды (36 карт) случайным образом извлекают карту. Рассматриваются события A — «извлечён король» и B — «извлечён валет». Определите вероятность события C = A + B.
Решение. Так как события A и B несовместные и
P(A) = P(B)
= ![]() =
= ![]() , то по формуле (1)
имеем
, то по формуле (1)
имеем
P(A + B) = P(A) +
P(B) = ![]() +
+ ![]() =
= ![]() .
.
Тот же результат можно получить без формулы (1). Так
как валетов и тузов вместе 8, то вероятность вынуть одну из этих карт равна ![]() =
=
![]() .
.
801. В опыте из непрозрачного мешка наудачу вынимают кость домино. Рассматриваются события A — «извлечена кость с суммой очков, кратной 2», B — «извлечена кость с суммой очков, кратной 3», C — «извлечена кость с суммой очков, кратной 6». Определите вероятности событий A, B, C. Используя найденные вероятности, вычислите вероятность события D — «извлечена кость с суммой очков, кратной или 2, или 3».
Решение. Из 28 костей домино сумму очков, кратную 2, имеют 16 костей, сумму очков, кратную 3, — 10, сумму очков, кратную 6, — 6. Поэтому
P(A) = ![]() =
=
![]() , P(B) =
, P(B) = ![]() =
=
![]() , P(C) =
, P(C) = ![]() =
=
![]() .
.
![]()
![]()
![]() Так
как события A и B не являются несовместными (можно вынуть кость с
суммой 6 очков, кратной и 2, и 3), событие C есть произведение событий A
и B, а событие D есть сумма событий A и B, тогда по
формуле (2) имеем P(D) = P(A + B) =
P(A) + P(B) – P(A · B)
= = P(A) + P(B) – P(C)
= + 5 – 3 = .
Так
как события A и B не являются несовместными (можно вынуть кость с
суммой 6 очков, кратной и 2, и 3), событие C есть произведение событий A
и B, а событие D есть сумма событий A и B, тогда по
формуле (2) имеем P(D) = P(A + B) =
P(A) + P(B) – P(A · B)
= = P(A) + P(B) – P(C)
= + 5 – 3 = .
14 14
14.5. Частота случайных событий
В данном пункте вводится понятие относительной частоты события А, рассказывается об опытном определении относительной частоты выпадения герба в опытах Ж. Бюффона и К. Пирсона и на этом примере утверждается, что относительная частота выпадания герба мало отличается от вероятности выпадания герба в указанном эксперименте, равной 0,5.
Учащиеся должны понимать, что не всегда удаётся
определить вероятность р события, как это имеет место с бросанием монеты
или игральной кости (например, без опыта невозможно определить приближённо
вероятность того, что кнопка, подброшенная вверх, упадёт остриём вверх). Но
если возможно опыт повторить п раз, то при большом п
относительная частота события ![]() m может
расn
m может
расn
сматриваться как приближённое значение вероятности m
( ![]() ≈ p) этого
события. n
≈ p) этого
события. n
При большом количестве опытов относительная частота события, как правило, мало отличается от вероятности этого события.
Эту закономерность называют статистической устойчивостью относительных частот.
![]() Замечание.
Если относительную частоту события принять по определению за приближённое
значение вероятности этого события, то получим так называемое статистическое
определение вероятности.
Замечание.
Если относительную частоту события принять по определению за приближённое
значение вероятности этого события, то получим так называемое статистическое
определение вероятности.
Далее в учебнике объясняется разница между классическим и аксиоматическим определениями вероятности, элементарной и общей теорией вероятностей.
Задания для повторения. При изучении данного пункта можно использовать задание 24 из рубрики «Задания для самоконтроля».
805. Пятеро учащихся при бросании монеты 50 раз получили данные, приведённые в таблице:
|
Ученик |
Число бросаний |
Число выпаданий герба |
Относительная частота выпадания герба |
|
1 |
50 |
27 |
0,54 |
|
2 |
50 |
28 |
0,56 |
|
3 |
50 |
23 |
0,46 |
|
4 |
50 |
26 |
0,52 |
|
5 |
50 |
24 |
0,48 |
Вычислите относительную частоту выпадания герба во всех 250 опытах.
Решение. Относительная частота выпаданий герба
во всех 250 опытах равна ![]() = 0,512.
= 0,512.
Дополнительное задание. Определите приближённое значение вероятности события «кнопка, подброшенная вверх, упадёт остриём вверх», подбросив кнопку 50 раз.
Итоговый контроль. К–8.
1. Бином Ньютона. Треугольник Паскаля
В этом пункте рассматриваются формулы (а + b)n для n = 1, 2, 3, 4, затем рассказывается о способе получения коэффициентов многочлена (а + b)n с помощью треугольника Паскаля и приводится формула бинома Ньютона:
(а + b)n = аn + Cn1 аn – 1b + ... + Cnn – 1 аbn – 1 + bn, (1) где Cnk — число сочетаний из п по k.
3. Исторические сведения
В этом пункте рассказывается об истории приближённых вычислений, статистики и теории вероятностей, о роли российских учёных в развитии этих наук. Это способствует воспитанию российской гражданской идентичности: уважение к Отечеству, знание истории, культуры своего народа, основ культурного наследия народов России и человечества. Материал, представленный в данном пункте, помогает также формированию целостного мировоззрения, объясняет роль разных народов в истории математики, воспитывает уважительное отношение к разным народам мира.
Описание работы с текстовыми задачами помещено в конец данной книги, так как затруднительно «разложить» по пунктам учебника рекомендации по использованию текстовых задач при изучении алгебры в 9 классе: разные учителя в разных классах могут по-разному планировать эту работу, так как классы могут иметь различные стартовые возможности в начале учебного года.
В 9 классе решение текстовых задач специально не изучается, все «школьные» приёмы решения текстовых задач уже изучены в предыдущие годы, к новым можно отнести только решение некоторых задач на последовательности.
Решение текстовых задач различными способами позволяет учащимся самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения. Работа с текстовыми задачами развивает умение понимать и использовать математические средства наглядности (чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации.
Выделим несколько типов текстовых задач, примеры которых можно найти в методических рекомендациях для 7 и 8 классов и которые полезно повторить со всеми учащимися. Это задачи:
· на части;
· на нахождение двух чисел по их сумме и разности;
· на дроби;
· на совместную работу;
· на движение по реке;
· на движение;
· на деление числа на части, пропорциональные данным числам;
· на пропорции и на проценты;
· на смеси и сплавы;
· на применение линейного уравнения или системы линейных уравнений;
· на применение рационального уравнения или системы рациональных уравнений.
Необходимо повторить некоторые «нестандартные» способы решения задач, они окажутся полезными при решении олимпиадных задач и задач из ГИА-9 и ЕГЭ-11:
· обратный ход;
· переформулировка задачи;
· использование вспомогательных букв (неизвестных); · решение задачи в общем виде; · метод подобия.
Приведём решения нескольких интересных задач из раздела «Задания для повторения» в «хронологическом» порядке, не группируя их по методам решения.
1192.
Из «Арифметики» Л. Ф. Магницкого. Верёвкой длиною 5
аршин связали 100 копий. Спрашивается, сколько таких же копий можно связать
другой верёвкой длиною 7 ![]() аршина (предполагается, что пучки копий
обвя-
аршина (предполагается, что пучки копий
обвя-
зывают верёвкой по окружности).
Решение. Пусть радиус первой окружности r,
тогда её длина 2pr,
а площадь круга, ограниченного этой окружностью, pr2.
Если длину окружности увеличить в 7 ![]() : 5 = 1,5
раза, то её радиус увеличится в 1,5 раза, а площадь круга увеличится в 1,52
= 2,25 раза. Если первая окружность вмещала 100 копий, то вторая
окружность вмещает 2, 25 · 100 = 225 копий.
: 5 = 1,5
раза, то её радиус увеличится в 1,5 раза, а площадь круга увеличится в 1,52
= 2,25 раза. Если первая окружность вмещала 100 копий, то вторая
окружность вмещает 2, 25 · 100 = 225 копий.
Ответ. 225 копий.
1193. Могут ли три человека преодолеть расстояние 36 км не более чем за 6 ч, если скорость пешехода равна 5 км/ч, но у них имеется велосипед (рассчитанный только на одного человека), на котором можно передвигаться со скоростью 15 км/ч? Если могут, то покажите как; если нет, то объясните почему.
Решение. Заметим, что если разбить весь путь (36 км) на три равных отрезка (по 12 км) и каждый человек два отрезка пройдёт пешком и один отрезок проедет на велосипеде, то каждый из них затратит на весь путь
![]() +
+ ![]() = 5,6 (ч), т. е. меньше чем
6 ч.
= 5,6 (ч), т. е. меньше чем
6 ч.
Пусть все трое одновременно отправляются в путь — двое пешком, третий на велосипеде. Проехав первый отрезок, человек положит велосипед на дорогу с таким расчётом, чтобы следующий отрезок второй человек проехал на велосипеде, так же и третий человек должен проехать третий отрезок пути.
Ответ. Могут.
Отметим, что каждый раз, когда задачу удаётся решить несколькими методами, это надо обязательно использовать, так как решение задачи несколькими способами намного полезнее решения нескольких задач одним методом. Вот пример такой задачи.
1196. Задача П. Л. Чебышёва. Мальчик сказал: «Если мне дадут ещё 40 орехов, то у меня будет столько же, сколько у моего брата. А если мне дадут 90 орехов, то у меня станет в 2 раза больше, чем у моего брата». Сколько орехов у каждого?
Решение. I способ (арифметический). Если мальчику дадут 40 орехов, то у него станет столько орехов, сколько у брата. А если дадут на 90 – 40 = 50 орехов больше, то у него станет в 2 раза больше орехов, чем у брата, значит, у брата 50 орехов, тогда у мальчика 50 – 40 = 10 орехов.
II способ (алгебраический, составление уравнения). Если у мальчика x орехов, то у его брата (x + 40) орехов. Так как (x + 90) орехов — это в два раза больше, чем у брата, то составим уравнение
2(x + 40) = x + 90.
Оно имеет единственный корень x = 10, поэтому у мальчика 10 орехов, а у его брата 10 + 40 = 50 орехов.
III способ (алгебраический, составление системы уравнений). Если у мальчика x орехов, а у его брата y орехов, то можно составить два уравнения: x + 40 = y и x + 90 = 2y. Решив систему этих уравнений, получим её единственное решение: x = 10, y = 50.
Следовательно, у мальчика 10 орехов, а у его брата 50 орехов.
Ответ. У мальчика 10 орехов, у брата 50 орехов.
1197. Старинная задача (Китай, I в.). Сообща покупают вещь. Если каждый человек внесёт по 8 (денежных единиц), то избыток равен 3. Если каждый человек внесёт по 7, то недостаток равен 4. Спрашивается количество людей и стоимость вещи.
Решение. I способ (арифметический, переформулировка задачи). Представим, что сначала каждый человек внесёт по 7 и недостаток равен 4. Если после этого каждый добавит по одной денежной единице (значит, внесёт по 8), то избыток будет равен 3. Следовательно, добавление каждым человеком одной денежной единицы увеличивает собранную сумму на 3 + 4 = 7 денежных единиц. Следовательно, было 7 человек, вещь стоила 7 · 8 – 3 = 53 денежные единицы.
II способ (алгебраический, составление уравнения). Пусть было x человек, тогда вещь стоила или 8x – 3, или
7x + 4 денежные единицы. Составим уравнение 8x – 3 = 7x + 4.
Оно имеет единственный корень x = 7, поэтому было 7 человек, вещь стоила 7 · 8 – 3 = 53 денежные единицы.
III способ (алгебраический, составление системы уравнений). Пусть было x человек и вещь стоила y денежных единиц. Составим два уравнения: 8x = y + 3 и 7x = y – 4. Решив систему этих уравнений, получим её единственное решение: x = 7, y = 53.
Следовательно, было 7 человек, вещь стоила 53 денежные единицы.
Ответ. 7 человек, 53 денежные единицы.
1202. Участникам школьной математической виктори-ны было предложено 30 вопросов. За каждый правильный ответ засчитывалось 7 очков, а за неправильный списывалось 12 очков. Сколько верных ответов дал участник викторины, если он набрал 77 очков?
Решение. Пусть было x верных ответов, тогда неверных ответов было 30 – x. Составим уравнение 7x – 12(30 – x) = 77.
Оно имеет единственный корень x = 23, поэтому было 23 верных ответа.
Ответ. 23 верных ответа.
1203. Сумма трёх чисел равна 254,772. Если в одном из чисел перенести запятую на две цифры вправо, то получится большее из чисел, а если перенести запятую в том же числе на одну цифру влево, то получится меньшее число. Найдите эти числа.
Решение. Пусть x — среднее число, тогда 100x — большее число, а 0,1x — меньшее число. Составим уравнение x + 100x + 0,1x = 254,772.
Оно имеет единственный корень x = 2,52, три числа таковы:
0,252; 2,52; 252.
Ответ. 0,252; 2,52; 252.
1205. На термометре Цельсия температуры таяния льда и кипения воды обозначаются соответственно 0° и 100°. На термометре Фаренгейта эти температуры обозначены соответственно –32° и 212°. При какой температуре оба термометра будут показывать одинаковое число градусов?
Решение. Пусть искомая температура составляет x градусов. Обе шкалы термометра являются координатными осями с равномерными шкалами, поэтому точки D и K делят отрезки AB и MN в одном и том же отношении
(рис. 53). Составим уравнение
![]() 100 – x 212
– x
100 – x 212
– x
![]() = .
= .
x – 0 x – –( 32)
Оно имеет единственный корень x = 22 ![]() ,
поэтому искомая температура равна 22
,
поэтому искомая температура равна 22 ![]() градуса.
градуса.
Ответ. 22 ![]() градуса.
6 Рис. 53
градуса.
6 Рис. 53
1206. а) Обнаружив в 64 м от себя уползающую черепаху, Ахиллес начал её преследовать. Сократив расстояние до черепахи в 8 раз и осознав своё превосходство, он прекратил погоню. Какой путь проделал Ахиллес с начала погони, если его скорость в 15 раз больше скорости черепахи, причём движение Ахиллеса и черепахи происходило по прямой?
Решение. Это задача конкурсного экзамена в МГУ прошлых лет. Так как скорость Ахиллеса в 15 раз больше скорости черепахи, то за одно и то же время он пробежал путь, в 15 раз больший, чем черепаха. Пусть путь черепахи x м, тогда путь Ахиллеса 15x м. Расстояние от начального положения Ахиллеса до конечного положения черепахи равно
15x + 64 : 8 = 15x + 8, или 64 + x м.
Составим уравнение
15x + 8 = 64 + x.
Оно имеет единственный корень x = 4, следовательно, Ахиллес проделал путь в 60 м.
Ответ. 60 м.
1208. Под посев пшеницы отведено 3 участка
пашни, общая площадь которых в 3 раза больше площади второго участка. За день
были засеяны половина первого, ![]() вто-
вто-
рого и весь третий участок. Площадь, оставшаяся незасеянной, в 2 раза меньше площади третьего участка. Какую часть отведённой под посев площади составляет площадь, засеянная за день?
Решение. Так как площадь трёх участков в 3 раза больше, чем площадь второго участка, то сумма площадей первого и третьего участков в 2 раза больше площади второго участка.
Пусть площадь первого участка x, второго участка y, тогда площадь третьего участка равна 2y – x, площадь трёх участков 3y (площади измеряются одними и теми же единицами).
За день были
засеяны пшеницей ![]() x +
x + ![]() y + (2y
– x) =
y + (2y
– x) = ![]() y –
y – ![]() x (ед.
площади).
x (ед.
площади).
Остались незасеянными
3y – ( ![]() y –
y – ![]() x)
=
x)
= ![]() x +
x + ![]() y (ед.
площади),
y (ед.
площади),
что в 2 раза меньше, чем 2y – x (ед. площади). Следовательно, справедливо равенство
2( ![]() x +
x + ![]() y) =
2y – x.
y) =
2y – x.
Из этого равенства выразим x
через y: x = ![]() y.
y.
8 1
![]() y – x
y – x
Требуется найти 3 2 . 3y
![]() 1 8 1
1 8 1
y – x y – y
![]()
![]() 2 =
3 3
= .
2 =
3 3
= .
3y 3y
Ответ. ![]() .
.
1209. Велосипедист проехал расстояние от пункта А до пункта В и обратно с постоянной скоростью. Мотоциклист проехал расстояние АВ со скоростью, в n раз большей, чем скорость велосипедиста. Он оставил мотоцикл в пункте В и вернулся в пункт А пешком со скоростью в n раз меньшей, чем скорость велосипедиста. Кто из них был дольше в пути и во сколько раз, если: а) п = 2; б) n = 5?
Решение. Пусть скорость велосипедиста v км/ч, а расстояние между пунктами А и В равно s. Тогда на путь
2s туда и обратно велосипедист
потратил t1 = ![]() v (ч), а
мото-
v (ч), а
мото-
s n ( 2 + 1)
![]() циклист t2 = nsv + nsv = nv (ч).
циклист t2 = nsv + nsv = nv (ч).
Покажем, что t2 t1 при любом n 1. Действительно
s n( 2 + 1) s n ( – 1)2
![]() 2s t2 –
t1 = nv – v = nv
0 при n 1,
2s t2 –
t1 = nv – v = nv
0 при n 1,
т. е. t2 t1 при n 1, следовательно, при n 1 мотоциклист будет в пути дольше велосипедиста. Определим, во сколько раз:
s n ( 2 + 1) 2
2s n + 1
![]() : = . nv
v 2n
: = . nv
v 2n
n2 + 1
![]() а) При п = 2 имеем =
1,25;
а) При п = 2 имеем =
1,25;
2n
n2 + 1
б) при п = 5 имеем = 2,6.
2n
Ответ. Мотоциклист; а) в 1,25 раза; б) в 2,6 раза.
![]() Замечание.
По смыслу задачи n 1. Однако интересно дополнительно рассмотреть
ситуации: 0 n 1 и n = 1.
Замечание.
По смыслу задачи n 1. Однако интересно дополнительно рассмотреть
ситуации: 0 n 1 и n = 1.
Если 0 n 1, то ответ останется тот же: «мотоциклист», хотя ситуация окажется необычной: мотоциклист проехал расстояние AB со скоростью, меньшей, чем скорость велосипедиста, а вернулся пешком в пункт A со скоростью, большей, чем скорость велосипедиста; хотя если он хороший бегун и плохо едет на мотоцикле, то такая ситуация возможна.
Если же n = 1, т. е. велосипедист, мотоциклист на мотоцикле и мотоциклист пешком имели одинаковую скорость, то они были в пути одно и то же время.
1210.
Латунь состоит из меди и цинка. Кусок латуни весом 124 г,
погружённый в воду, теряет в весе 15 г, а кусок меди весом 89 г, погружённый в
воду, теряет в весе 10 г. Кроме того, известно, что кусок цинка, погружённый в
воду, теряет ![]() веса. Определите, сколько меди и
веса. Определите, сколько меди и
сколько цинка содержится в 124 г латуни.
Решение. Пусть в латуни содержится x г меди и (124 – x) г цинка. Тогда при погружении в воду медь и
цинк теряют 10![]() x г и 124
x г и 124![]() – x г соответственно, что в
сум-
– x г соответственно, что в
сум-
89 7
ме составляет 15 г. Составим уравнение
10x 124 – x
![]() +
= 15.
+
= 15.
89 7
Это уравнение имеет единственный корень x = 89, следовательно, меди было 89 г, а цинка 124 – 89 = 35 (г). Ответ. 89 г меди и 35 г цинка.
1211. Нарисовали ромбы и прямоугольники. Ромбов в 2 раза больше, чем прямоугольников. Число ромбов, не являющихся прямоугольниками, в 3 раза больше числа прямоугольников, не являющихся ромбами.
а) Определите наименьшее возможное число фигур.
б) Во сколько раз квадратов было меньше, чем ром-
бов?
в) Сколько квадратов нарисовали, если всего нарисо-
вали 20 фигур?
Решение. Пусть было x прямоугольников, не являющихся ромбами, и y прямоугольников, являющихся ромбами (то есть квадратами). Тогда было 3x ромбов, не являющихся прямоугольниками. Следовательно, всего фигур было 4x + y, среди них было x + y прямоугольников и 3x + y ромбов. Так как ромбов в два раза больше, чем прямоугольников, то верно равенство
3x + y = 2(x + y),
из которого следует, что x = y.
а) Наименьшее возможное число фигур получим при
x = y = 1. Это число равно 4x + y = 5.
б) Квадратов, т. е. прямоугольников, являющихся ромбами, было y, а всего ромбов 4x. Квадратов было в
4x 4x
![]() = = 4 раза
меньше, чем ромбов.
= = 4 раза
меньше, чем ромбов.
y x
в) Если всего нарисовали 4x + y = 5y = 20 фигур, то
квадратов нарисовали 4.
Ответ. а) 5; б) в 4 раза; в) 4.
1212. Грузовая машина выехала из пункта А в пункт В. Спустя 2 ч из пункта В в пункт А выехала легковая машина, которая прибыла в пункт А на час позже, чем грузовая машина в пункт В. Сколько часов была в пути грузовая машина, если к моменту встречи она проехала всего пути?
Решение. I способ. Пусть грузовая машина ехала до встречи t ч, тогда вдвое меньший путь она проехала за
t 3t
ч и была в пути ![]() ч. Легковая машина ехала до встре-
ч. Легковая машина ехала до встре-
2 2
чи (t – 2) ч, тогда вдвое больший путь она проехала за 2(t – 2) ч и была в пути 3(t – 2) ч, что на 1 ч меньше времени движения грузовой машины. Составим уравнение
3t
![]() – 3(t – 2)
= 1,
– 3(t – 2)
= 1,
2
откуда t = ![]() .
Время движения грузовой машины равно
.
Время движения грузовой машины равно
3t
= 5 (ч).
2
![]()
![]()
![]() II
способ. Воспользуемся методом подобия. Построим графики движения машин OF
и GCD (рис. 54). Пусть грузовая машина была в пути x ч. Тогда ОЕ
= x, ОD = x + 1, CF = x – 2.
Из подобия треугольников OMD и FMC следует, что
II
способ. Воспользуемся методом подобия. Построим графики движения машин OF
и GCD (рис. 54). Пусть грузовая машина была в пути x ч. Тогда ОЕ
= x, ОD = x + 1, CF = x – 2.
Из подобия треугольников OMD и FMC следует, что
OD MK
![]() = ,
= ,
CF MN
![]() MK
MK
но ![]() = (это
отношение расстояний, пройденных гру-
= (это
отношение расстояний, пройденных гру-
MN
зовой и легковой машинами до встречи). Составим уравнение
![]() x + 1
x + 1
![]() = ,
= ,
x – 2
![]() откуда x = 5,
т. е. время движения грузовой машины равно 5 ч.
откуда x = 5,
т. е. время движения грузовой машины равно 5 ч.
Ответ. 5 ч.
1214. Задача Л. Н. Толстого. На 100 р. купили 100 скотин — телят по полтине, коров по 3 р., быков по 10 р. Сколько купили телят, коров и быков в отдельности?
Решение. Пусть купили x быков, y коров и 100 – x – y телят. 6 Рис. 54 Составим уравнение:
10x + 3y + 0,5(100 – x – y) = 100,
которое перепишем в виде
19x + 5y = 100.
Решим это уравнение в натуральных числах. Так как при любом y число 5y делится на 5, то 19x = 100 – 5y делится на 5. А так как число 19 не делится на 5, то число x делится на 5.
Если x = 5, то получим y = 1. Если x 5, то значения y не являются натуральными, т. е. уравнение имеет единственное решение в натуральных числах: x = 5, y = 1. Тогда 100 – x – y = 94. Итак, купили 5 быков, 1 корову и 94 телёнка.
Ответ. 5 быков, 1 корову и 94 телёнка.
1222. Среди абитуриентов, выдержавших приёмные экзамены в вуз, оценку «отлично» получили: по математике — 96 абитуриентов, по физике — 74, по русскому языку — 84, по математике или физике — 150, по математике или русскому языку — 152, по физике или русскому языку — 132, по всем трём предметам — 8. Сколько абитуриентов получили хотя бы одну пятёрку? Сколько среди них получивших одну пятёрку?
Решение. Получили «отлично» ровно по двум предметам:
1) 96 + 74 – 150 – 8 = 12 (абитуриентов) — по математике и физике;
2) 96 + 84 – 152 – 8 = 20 (абитуриентов) — по математике и русскому языку;
3) 84 + 74 – 132 – 8 = 18 (абитуриентов) — по физике и русскому языку.
Получили хотя бы одну пятёрку:
4) 150 + 84 – 20 – 18 – 8 = 188 (абитуриентов). Получили одну (ровно одну) пятёрку:
5) 188 – 20 – 12 – 18 – 8 = 130 (абитуриентов).
Ответ: 188 абитуриетов; 130 абитуриентов.
1224. Для производства одного электродвигателя типа А используется 2 кг сплава, содержащего 20% свинца и 80% меди. Для производства одного электродвигателя типа В используется 2 кг сплава, содержащего 60% свинца и 40% меди. Прибыль от производства одного электродвигателя типа А или типа В составляет соответственно 8 р. или 12 р. Сколько нужно изготовить электродвигателей каждого типа, чтобы получить 1000 р. прибыли, израсходовав при этом не более 84 кг свинца и не более 111 кг меди?
Решение. Для производства одного электродвигателя типа А используется 0,2 · 2 = 0,4 кг свинца и 0,8 · 2 = 1,6 кг меди. Для производства одного электродвигателя типа В используется 0,6 · 2 = 1,2 кг свинца и 0,4 · 2 = 0,8 кг меди. Пусть нужно изготовить x электродвигателей типа А и y электродвигателей типа В. Составим уравнение 8x + 12y = 1000.
Выразим x через y:
x = 125 – 1,5y.
Чтобы было израсходовано не более 84 кг свинца и не более 111 кг меди, должны выполняться неравенства:
0,4x + 1,2y 84 и 1,6x + 0,8y 111.
Подставив в эти неравенства вместо x выражение 125 – 1,5y, получим два линейных неравенства относительно y:
0,4(125 – 1,5y) + 1,2y 84 и 1,6(125 – 1,5y) + 0,8y 111.
Решив систему
этих двух неравенств, получим, что 55,625 y
56
![]() .
.
Этому двойному неравенству удовлетворяет единственное целое значение y (число моторов не может быть дробным), это y = 56. Теперь найдём соответствующее значение x:
x = 125 – 1,5 · 56 = 41.
Итак, нужно изготовить 41 электродвигатель типа А и 56 электродвигателей типа B.
Ответ: 41 электродвигатель типа А, 56 электродвигателей типа В.
1232. Шесть мальчиков и четыре девочки организовали турнир по шашкам. Каждый участник турнира сыграл с каждым по одной партии. За выигрыш присуждали 2 очка, за ничью — 1 очко, за проигрыш — 0 очков. Девочки вместе набрали 40 очков. Кто выиграл больше очков: мальчики у девочек или девочки у мальчиков — и на сколько?
Решение. Участников турнира было 6 + 4 = 10. Они сыграли
![]() = 45 (партий)
= 45 (партий)
и набрали
45 · 2 = 90 (очков)
независимо от исходов отдельных партий. По условию задачи девочки набрали 40 очков, тогда мальчики набрали 90 – 40 = 50 (очков). Чтобы ответить на вопрос задачи, рассмотрим «турнир в турнире» — игры девочек между собой. В них сыграно
![]() = 6 (партий)
= 6 (партий)
и набрано
6 · 2 = 12 (очков).
Остальные 40 – 12 = 28 (очков) девочки выиграли у мальчиков.
Аналогично мальчики в играх между собой набрали
30 очков, значит, мальчики выиграли у девочек 50 – 30 = 20 (очков).
Итак, девочки выиграли у мальчиков на
28 – 20 = 8 (очков)
больше, чем мальчики у девочек.
Ответ: Девочки выиграли у мальчиков на 8 очков больше.
1247. Материальная точка движется с поверхности земли вертикально вверх с начальной скоростью 20 м/с. Сколько времени точка будет находиться в движении и на какую высоту от поверхности земли она поднимется? Сопротивлением воздуха пренебречь.
Решение. Пусть материальная точка движется вдоль координатной оси, направленной вертикально вверх, тогда её координата h определяется по формуле
2
h = h0 + v0t
– ![]() gt ,
gt ,
2
а скорость v — по формуле
v = v0 – gt.
Здесь h0 = 0 м, v0 = 20 м/с, g 10 м/с2, поэтому
2 h = 20t – ![]() gt 20t – 5t2,
v 20 – 10t.
gt 20t – 5t2,
v 20 – 10t.
2
Так как в наивысшей точке траектории движения материальной точки v = 0, то на наибольшую высоту точка поднимется при t 2 с, и эта высота будет равна h 20 м. Ответ. 2 с; 20 м.
1249. Спелеолог для выяснения глубины подземной полости бросил вниз без начальной скорости камень. Звук от падения камня на дно полости дошёл до спелеолога через 3 с. Какова глубина подземной полости, если принять скорость звука равной 330 м/с и пренебречь сопротивлением воздуха? Считать, что g 9,8 м/с2.
Решение. Пусть через t с камень достиг дна подземной полости. За это время он пролетел расстояние, равное
gt2
![]() м. Звук от падения камня на дно
полости дошёл до
м. Звук от падения камня на дно
полости дошёл до
2
gt2 спелеолога
через t + ![]() с, что по
условию задачи равно 660
с, что по
условию задачи равно 660
3 с. Составим уравнение
gt2 t + ![]() =
3.
=
3.
660
Это уравнение имеет единственный положительный
корень t 2,88, для которого ![]() gt2 40,6, т. е. глубина
gt2 40,6, т. е. глубина
2
подземной полости приближённо равна 40,6 м. Ответ. 40,6 м.
1250. Парашютист покинул летящий самолёт на высоте 3 км и через 3 мин приземлился. Определите время его снижения до раскрытия парашюта и с раскрытым парашютом, если средняя скорость снижения с раскрытым парашютом равна 6 м/с. Сопротивлением воздуха при снижении без парашюта пренебречь. Считать, что g 9,8 м/с2.
Решение. Пусть парашютист снижался до раскрытия
gt2 парашюта t с и пролетел ![]() м, тогда с раскрытым пара-
м, тогда с раскрытым пара-
2
шютом он снижался (180 – t) с и пролетел 6(180 – t) м. Составим уравнение:
gt2
![]() + 6(180 –
t) = 3000.
+ 6(180 –
t) = 3000.
2
Это уравнение имеет единственный положительный корень t 20,4, следовательно, время снижения парашютиста до раскрытия парашюта равно 20,4 с, а с раскрытым парашютом
180 – 20,4 = 159,6 (с).
Ответ. 20,4 с; 159,6 с.
1255. Колонна солдат длиной l м движется со скоростью х м/мин. Из конца колонны в её начало отправляется сержант со скоростью у м/мин, затем с той же скоростью он возвращается в конец колонны. На путь туда и обратно сержант затратил t мин.
а) Выразите t, l, х, у через остальные величины.
б) Вычислите t, если l = 510, х = 70, у = 100.
Решение. а) По смыслу задачи у х, тогда время t движения сержанта в оба конца равно
![]()
![]() l l 2yl y – x + y + x = y2 – x2
(мин).
l l 2yl y – x + y + x = y2 – x2
(мин).
Из равенства
2yl
t
= ![]() 2 2
2 2
y – x
выразим величины l, х, у через остальные величины:
![]()
![]() t y( 2 – x2) 2ly
l + l2
+ t x2 2 l =
t y( 2 – x2) 2ly
l + l2
+ t x2 2 l = ![]() ,
х = y2 – , у = .
,
х = y2 – , у = .
2y t t
б) Если l = 510, х = 70, у = 100, то 2yl 2 • 100 • 510
![]() t
= 2 2
= 2 2
= 20 (мин). y – x 100 – 70
t
= 2 2
= 2 2
= 20 (мин). y – x 100 – 70
Ответ. в) 20 мин.
1256. Колонна солдат длиной l движется с постоянной скоростью по шоссе. Курьер из конца колонны отправился в её начало. Достигнув начала колонны, он тут же повернул обратно и пошёл в конец колонны с той же скоростью. За это время колонна прошла расстояние s. Определите расстояние, которое прошёл курьер в оба конца, если:
а) l = 400 м, s = 300 м; б) l = 300 м, s = 400 м.
Решение. Пусть скорость колонны равна х м/мин, а скорость курьера — у м/мин (у х). Тогда время движения курьера в оба конца равно
![]()
![]() l l 2yl y – x + y + x = y2 – x2
(мин).
l l 2yl y – x + y + x = y2 – x2
(мин).
2yl 2xyl
За это время колонна прошла 2 2 • x
= ![]() 2 2 ,
y – x y – x
2 2 ,
y – x y – x
или s м. Составим уравнение
2xyl
![]() 2 2 = s. (1) y – x
2 2 = s. (1) y – x
Курьер за время движения в оба конца прошёл путь,
y sy
в ![]() раз
больший, чем s, т. е.
раз
больший, чем s, т. е. ![]() м. Чтобы найти
эту веx x
y личину, нужно из уравнения (1) найти
м. Чтобы найти
эту веx x
y личину, нужно из уравнения (1) найти ![]() . x
. x
y
Введём новое неизвестное п =
![]() и перепишем уравнеx
и перепишем уравнеx
ние (1) в виде
2nl
![]() 2
= s (2)
2
= s (2)
n – 1
или в виде
sn2 – 2nl – s
![]() 2 = 0. (3) n – 1
2 = 0. (3) n – 1
Числитель дроби в левой части уравнения (3) обраща-
![]() l l2 – s2 ется в нуль при п1,2
= s
, а так как у х, то п 1 и знаменатель дроби в
левой части уравнения (3) в нуль не обращается. Уравнение (3), а значит, и
уравнение (2) имеют единственный положительный корень
l l2 – s2 ется в нуль при п1,2
= s
, а так как у х, то п 1 и знаменатель дроби в
левой части уравнения (3) в нуль не обращается. Уравнение (3), а значит, и
уравнение (2) имеют единственный положительный корень
![]() l + l2
+ s2 n1 = s .
l + l2
+ s2 n1 = s .
Тогда искомое расстояние равно
![]() l + l2
+ s2 2 2
l + l2
+ s2 2 2
![]() · = + s l l + s
(м).
· = + s l l + s
(м).
s
а) Если l = 400 м, s = 300 м, то курьер прошёл в оба
конца
![]() 400 + 4002 + 3002 = 900
(м);
400 + 4002 + 3002 = 900
(м);
б) если l = 300 м, s = 400 м, то курьер прошёл в оба
конца
300 + 3002 + 4002 = 800 (м).
Ответ. а) 900 м; б) 800 м.
![]() Замечание.
Чтобы избежать введения третьего неизвестного, равного отношению
двух уже введённых неизвестных, можно через n обозначить число,
показывающее, во сколько раз скорость курьера больше скорости колонны.
Замечание.
Чтобы избежать введения третьего неизвестного, равного отношению
двух уже введённых неизвестных, можно через n обозначить число,
показывающее, во сколько раз скорость курьера больше скорости колонны.
Пусть скорость колонны равна х м/мин, а скорость курьера в n раз больше скорости колонны, т. е. nх м/мин. Тогда время движения курьера в оба конца равно
l l 2nl
![]()
![]() + = (мин).
+ = (мин).
nx – x nx + x x n( 2 – 1)
За это время колонна прошла путь
2nl 2nl
![]() · x =
· x = ![]() 2 (м), x n( 2 – 1) n – 1
2 (м), x n( 2 – 1) n – 1
что по условию задачи равно s м. Далее составим уравнение (2), решив которое относительно n, получим тот же результат.
1263. Проценты содержания (по массе) красителя в трёх растворах образуют геометрическую прогрессию. Если смешать первый, второй и третий растворы в отношении 2 : 3 : 4, то получится раствор, содержащий 32% красителя. Если же смешать их в отношении 3 : 2 : 1, то получится раствор, содержащий 22% красителя. Сколько процентов красителя содержит первый раствор?
Решение. Пусть в первом, втором и третьем растворах содержится (по массе) p%, pq%, pq2% красителя соответственно.
Если смешать 2x, 3x, 4x одинаковых единиц массы первого, второго и третьего растворов соответственно, то содержание красителя составит 32%. Составим уравнение
ж p pq pq2 ц
![]() ззи100 · 2x + 100 · 3x + 100 · 4xччш · 100
ззи100 · 2x + 100 · 3x + 100 · 4xччш · 100
= 32,
2x + 3x + 4x
которое перепишем в виде
2p + 3pq + 4pq2 = 288.
Если смешать 3y, 2y, y одинаковых единиц массы первого, второго и третьего растворов соответственно, то содержание красителя составит 22%. Составим уравнение
ж p pq pq2 ц
![]() зз100
· 3y + 100 · 2y + 100 · yччш · 100 и
зз100
· 3y + 100 · 2y + 100 · yччш · 100 и
= 22,
3y + 2y + y
которое перепишем в виде
3p + 2pq + pq2 = 132.
Решив систему двух уравнений относительно p и q, получим единственное положительное решение этой системы: p = 12, q = 2.
Ответ. 12%.
1264. Два пешехода одновременно вышли навстречу друг другу из пунктов А и В, расстояние между которыми 34 км. В 4 км от пункта А первый пешеход (вышедший из пункта А) сделал остановку на 1 ч 30 мин. После остановки он увеличил скорость на 2 км/ч и встретил второго пешехода в 18 км от пункта В. Если бы первый пешеход не делал остановки и шёл всё время с первоначальной скоростью, то пешеходы встретились бы на полпути. Определите скорость второго пешехода.
Решение. Если бы первый пешеход не делал остановки и шёл всё время с первоначальной скоростью, то пешеходы встретились бы на полпути, следовательно, они шли с одинаковыми скоростями. Пусть скорость каждого пешехода в начале пути x км/ч.
Встреча пешеходов произошла в 18 км от пункта В,
до этой встречи второй пешеход был в пути 18![]() ч, а перx
ч, а перx
вый (с учётом остановки)
4 34 – 18 – 4
![]() + 1 5, + ч. x x + 2
+ 1 5, + ч. x x + 2
Составим уравнение
4 34 – 18 – 4 18
![]() + 1 5, + = .
+ 1 5, + = .
x x + 2 x
Решив это уравнение, получим его единственный положительный корень x = 4. Следовательно, скорость второго пешехода равна 4 км/ч.
Ответ. 4 км/ч.
1266. Проливной дождь лил несколько часов подряд. Когда он наполнил некоторую часть открытого бассейна, включили насос для откачки воды. Он откачал воду за 5 ч, на протяжении которых дождь продолжал лить. Если бы вместо первого насоса включили второй, мощность которого в 2 раза больше, то он откачал бы воду за 2 ч. За сколько часов откачали бы воду два насоса при совместной работе? Считайте процессы наполнения бассейна и откачки воды равномерными.
Решение. Пусть до включения насоса в бассейне было x л воды, за 1 ч наливалось в бассейн y л воды, за 1 ч первый насос откачивал из бассейна z л воды в час, два насоса откачали бы воду из бассейна за t ч. По условиям задачи составим систему уравнений
мx + 5y = 5z, п
нx + 2y = 2 · 2z, поx + ty = · t 3 .
В получившейся системе неизвестных больше, чем уравнений, поэтому все её решения найти не удастся, но это и не требуется. Выразим t из третьего уравнения системы:
t
= ![]() x .
x .
3z – y
Вычтем второе уравнение из первого, получим z = 3y.
Из первого уравнения имеем
x = 5z – 5y,
следовательно, x = 10y. Теперь вычислим t:
![]()
![]() t = x =
10y = 1.
t = x =
10y = 1.
3z – y 9y – y
Следовательно, два насоса откачают воду за 1 ч 15 мин.
Ответ. За 1 ч 15 мин.
1267. а) На лугу растёт трава. 20 коров съедят всю траву за 21 день, а 30 коров — за 7 дней. За сколько дней всю траву на лугу могли бы съесть 22 коровы?
Решение. Пусть первоначальный объём травы на лугу t ед., трава растёт равномерно, т. е. ежедневно прирастает один и тот же объём травы x ед., каждая корова съедает в день один и тот же объём y ед. травы (объём травы измеряется некоторой общей для всех величин единицей).
А 22 коровы съедят всю траву на лугу за d дней.
Составим систему уравнений:
мt + 21x = 21 · 20 · y,
п
нt + 7x = 30 · · 7 y, поt + dx = 22 · · .d y
Умножим первое уравнение системы на –1, второе — на 3, сложим полученные уравнения:
2t = 210y,
откуда t = 105y. Теперь из второго уравнения имеем
x = 30y – ![]() t,
t,
следовательно, x = 15y. Из третьего уравнения получим
![]() d = t =
105y
= 15.
d = t =
105y
= 15.
22y – x 22y – 15y
Следовательно, 22 коровы съедят всю траву на лугу за 15 дней.
Ответ. 15 дней.
Ниже приведены условия задач на исследование, связанных с уравнениями, системами уравнений, неравенствами; текстовые задачи: на проценты, на движение по реке, на совместную работу; задачи на исследование свойств нового объекта (чётные и нечётные факториалы).
Особо выделим задачи с изменением величины на несколько процентов. Эта тематика задач требует основательного знания процентных расчётов. Такие задачи встречались и в предыдущих классах, но здесь сделан упор на сочетании практической направленности расчётов с идеей решения задач в общем виде, что позволяет не только затронуть тематику задач, выносимых на итоговый контроль в ОГЭ и ГВЭ, но и сформулировать несколько задач для исследования. При решении задач иногда оказывается удобным не вести расчёты с данными значениями величин, а обозначить эти значения буквами. Самостоятельный поиск решений предложенных задач и разбор их решений в классе позволят подготовить учащихся к итоговому контролю и к участию в олимпиадах, а также будет способствовать формированию компетентности в проведении учебно-исследовательской деятельности. Обсуждение решений этих задач способствует обобщению знаний и сотрудничеству со сверстниками и учителем. Выполнение заданий данной рубрики поможет учащимся в развитии таких метапредметных умений, как умение самостоятельно планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных задач; умение осуществлять контроль своей деятельности, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией; умение оценивать правильность выполнения учебной задачи, собственные возможности её решения; умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач.
1. а) Найдите все значения a, при каждом из которых уравнение
ax2 – (4a + 1)x + 9a = 0
имеет единственный корень; имеет два различных корня; не имеет корней.
Решение. Если a = 0, то уравнение имеет вид –x = 0, оно имеет единственный корень.
Если a 0, то квадратное уравнение имеет дискриминант
D = (4a + 1)2 – 36a2.
Уравнение имеет единственный корень, если D = 0,
т. е. если a = –0,1 или a = 0,5. Уравнение имеет два различных корня, если D 0, т. е. если a (–0,1; 0)И (0; 0,5). Уравнение не имеет корней, если D 0, т. е. если a (– ; –0,1)И (0,5; + ).
Ответ. а) Единственный корень при a = –0,1, при a = 0 и при a = 0,5; два различных корня при a (–0,1; 0)И
И(0; 0,5); не имеет корней при a (– ; –0,1)И(0,5; + ).
2. Найдите наименьшее значение суммы x2 + y2, если (x; y) — решение системы уравнений
мx – 3y = a, но3x – = + y a 2.
При каком значении а достигается это наименьшее значение?
Решение. Для любого значения a система уравнений имеет решения:
x
= ![]() a + 3 , y =
a + 3 , y = ![]() – + a 1 .
– + a 1 .
4 4
Найдём наименьшее значение суммы x2 + y2:
x2 + y2 = a2 + 6a + 9 + a2 – 2a + 1 = a2 + 2a + 5 =
![]()
8
При a = –1 верно равенство x2 + y2 = 0,5, при a –1 верно неравенство x2 + y2 0,5.
Ответ. 0,5; при a = –1.
3. Найдите все значения a, для каждого из которых неравенство
ax2 – (2a + 1)x + a 0 (1) не имеет решений.
Решение. 1) При a = 0 неравенство (1) имеет вид –x 0. Это неравенство имеет решения.
2) При каждом значении a 0 исходное неравенство является квадратным и дискриминант квадратного трёхчлена равен D = 4a + 1.
а) Если а 0, то D = 4a + 1 0 и исходное неравенство
имеет решения.
б) Если а 0 и D 0, то исходное неравенство имеет
решения.
в) Если а 0 и D 0, то исходное неравенство не име-
ет решений.
г) Если а 0 и D = 0, то исходное неравенство не имеет решений.
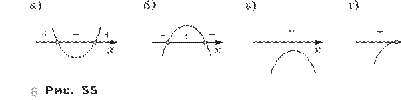
Иллюстрациями для приведённых ответов служат графики квадратичных функций y = ax2 – (2a + 1)x + a (рис. 55).
Следовательно, при a 0 исходное неравенство не имеет решений только для тех значений a, которые удовлетворяют системе
мa 0, но4a + 1 0,
т. е. только для а – ![]() .
.
Ответ. При а – ![]() .
.
4. а) При каких значениях а система неравенств
м4x – 4a 2ax – 5,
н6x – 2a 3ax + 5, (2)
о
имеет решения?
Решение. Перепишем систему (2) в виде
мп(4 – 2a x) 4a – 5,
нпо(6 – 3a x) 2a + 5. (3)
1) При a = 2 система (3) не имеет решений, так как первое неравенство системы 0x 3 не имеет решений. 2) При a 2 система (3) имеет вид
мx 4a – 5, п 4 – 2a
![]() н 2a + 5. (4)
н 2a + 5. (4)
поx 6 – 3a
![]() Система (4) имеет решения, если
4a
– 5 2a + 5
Система (4) имеет решения, если
4a
– 5 2a + 5
![]() 4 – 2a 6 – 3a
(рис. 56). Решив это неравенство, получим все его решения: a (– ; 2)И (3
4 – 2a 6 – 3a
(рис. 56). Решив это неравенство, получим все его решения: a (– ; 2)И (3 ![]() ;
+ ), из
;
+ ), из
которых условию a 2 удовлетворяют лишь все a (– ; 2).
6 Рис. 56
3) При a 2 систему (2) перепишем в виде
|
поx 6 – 3a |
(5) |
![]() Система (5) имеет решение,
если 2a
+ 5 4a – 5
Система (5) имеет решение,
если 2a
+ 5 4a – 5
6 – 3a 4 – 2a
(рис. 57). Решив это
неравенство, получим все его решения: a (2; 3 ![]() ). Все они
удовлетворяют условию a 2.
). Все они
удовлетворяют условию a 2.
Итак, система (2) имеет решения при a
(– ; 2)И И (2; 3 ![]() ).
).
Ответ. При a (– ; 2)И (2; 3
![]() ).
).
5. а) При каких значениях а система неравенств
м9x – 5a 3ax + 2,
![]()
![]() но6x + 2a 2ax – 7 ([3]) не имеет решений?
но6x + 2a 2ax – 7 ([3]) не имеет решений?
Решение. Перепишем систему (6) в виде
мп(9 – 3a x) 5a + 2,
н( ) 2a – 7. (7)
по [4] – 2a x –
1) При a = 3 система (7) не имеет решений, так как первое неравенство системы 0x 17 не имеет решений. 2) При a 3 система (7) имеет вид
мпx 59 – a + 3a2,
![]() н –2a – 7. (8)
н –2a – 7. (8)
поx 6 – 2a
Система (8) не имеет решений, если
–2a – 7 5a + 2
![]() 3) При a 3
система (7) имеет вид
3) При a 3
система (7) имеет вид
мx 5a + 2,
![]() пн –9 – 2a – 3a7. (9) 6 Рис. 59 поx 6 – 2a
пн –9 – 2a – 3a7. (9) 6 Рис. 59 поx 6 – 2a
Система (9) не имеет решений, если
5a + 2 –2a – 7
![]()
9 – 3a 6 – 2a
(рис. 59). Решив это
неравенство, получим все его решения: a (– ; – ![]() ]И (3; + ), из которых условию a 3 удовлетворяют лишь все a
(3;
+ ).
]И (3; + ), из которых условию a 3 удовлетворяют лишь все a
(3;
+ ).
Итак, система (6) не имеет решений
при a [
– ![]() ;
3) И {3}И (3; + ), т. е. при a [ –
;
3) И {3}И (3; + ), т. е. при a [ – ![]() ; + ).
; + ).
Ответ. При a [ – ![]() ; + ).
; + ).
6. В период бурного роста цен с 1 октября 1993 г. за хранение денег на депозитном вкладе Сбербанк России в течение 12, 6 и 3 месяцев выплачивал доход в размере 150%, 130% и 120% годовых соответственно. Какой доход можно было получить за год:
а) при двукратном вложении денег на 6 месяцев;
б) при четырёхкратном вложении денег на 3 месяца?
Решение. Если на счёт положить a р. на 12 месяцев под 150% годовых, то через год на счёте окажется
![]() a(1 + 150) р., или 2,5a р.
a(1 + 150) р., или 2,5a р.
100
а) Если на счёт положить a р. на 6 месяцев под 130% годовых (при этом за 6 месяцев выплачивается доход 130 : 2 = 65%), то через год (за 2 срока по 6 месяцев) на
2
![]()
![]() счёте окажется a1 + 65 )
р., или 2,7225a р., что больше 100
счёте окажется a1 + 65 )
р., или 2,7225a р., что больше 100
2,5a р. Доход составит 2,7225a – a = 1,7225a р., или 172,25%.
б) Если на счёт положить a р. на 3 месяца под 120% годовых (при этом за 3 месяца выплачивается доход 120 : 4 = 30%), то через год (за 4 срока по 3 месяца) на
4
![]()
![]() счёте окажется a1 + 30 ) р., или 2,8561a
р., что больше 100
счёте окажется a1 + 30 ) р., или 2,8561a
р., что больше 100
2,7225a р. Доход составит 2,8561a – a = 1,8561a р., или 185,61%.
Ответ. а) 172,25%; б) 185,61%.
7. Каким наибольшим целым числом x должен выражаться процент годовых для депозитных вкладов на 6 месяцев, чтобы двукратное использование этого вклада приносило доход меньший, чем вклад на 1 год под р% годовых? Каким наибольшим целым числом y должен выражаться процент годовых для вкладов на 3 месяца, чтобы двукратное использование этого вклада приносило доход меньший, чем вклад на 6 месяцев?
Решите задачу в общем виде, проведите расчёты для p = 150.
Решение. Определим наибольшее целое число х, которым должен выражаться процент годовых для вкладов на 6 месяцев, чтобы двукратное использование этого вклада приносило доход, меньший р%.
Пусть в начале года положили а р. под р% годовых.
![]()
![]() В
конце года получат сумму a1 + )
р. Если положили p
100
В
конце года получат сумму a1 + )
р. Если положили p
100
а р. под х%
годовых на 6 месяцев, полученную через полж ![]() x ц
x ц
года сумму aз1 + 2 ч р. ещё раз положили на 6 месяцев,
з 100 ч
и ш x ц2
ж ![]()
в конце года получат aз1 + 2 ч р. По условию задачи
з 100 ч и ш
первая сумма должна быть больше второй, т. е. должно выполняться неравенство 2
ж ![]() x ц
x ц
![]()
![]() a1 + p ) aз1 + 2 ч ,
a1 + p ) aз1 + 2 ч ,
100 з 100 ч и ш
которое перепишем в виде
х2 + 400х – 400р 0. (10)
Вычислим теперь корни квадратного трёхчлена х2 + 400х – 400р.
D
Так как = 40000 + 400р = 400(100 + р), то
4
x1 = –200 – 20 p + 100 , х2 = –200 + 20 p + 100 .
![]() Поэтому
решения неравенства (10) составляют промежуток
Поэтому
решения неравенства (10) составляют промежуток
–200 – 20 p + 100 х –200 + 20 p + 100 .
![]() Условию
задачи удовлетворяет наибольшее натуральное число n, такое, что n –200
+ 20 p + 100 .
Условию
задачи удовлетворяет наибольшее натуральное число n, такое, что n –200
+ 20 p + 100 .
![]()
![]() При р = 150
имеем х –200 + 20 p + 100 = –200 + 20 250 = 116,2...,
При р = 150
имеем х –200 + 20 p + 100 = –200 + 20 250 = 116,2...,
откуда наибольшее целое значение х равно 116.
Отметим, что двукратное вложение денег на 6 месяцев
2 ж 116![]() ц
ц
под 116% годовых увеличит вклад в з1 + 2 ч = 2,49... ра-
з 100 ч и ш
за, т. е. меньше, чем на 150%, а под 117% годовых уве-
2 ж 117![]() ц
ц
личит вклад в з1 + 2 ч = 2,51... раза, т. е. больше, чем
з 100 ч и ш
на 150%.
Пусть теперь известна процентная ставка х по вкладам на 6 месяцев. Определим наибольшее целое число y, которым должен выражаться процент годовых для вкладов на 3 месяца, чтобы двукратное использование этого вклада приносило доход, меньший х%. Дальше можно полностью повторить приведённые выше рассуждения и получить двойное неравенство
![]() –400 – 20 2x + 400 y –400 + 20 2x + 400 .
–400 – 20 2x + 400 y –400 + 20 2x + 400 .
![]()
![]() Условию задачи удовлетворяет
наибольшее натуральное число n, такое, что n –400 + 20
2x + 400 . При х = 116
имеем у –400 + 20 232 + 400
= –400 + 20 632 =
102,7...,
Условию задачи удовлетворяет
наибольшее натуральное число n, такое, что n –400 + 20
2x + 400 . При х = 116
имеем у –400 + 20 232 + 400
= –400 + 20 632 =
102,7...,
откуда наибольшее целое значение у равно 102.
Отметим, что двукратное вложение денег на 3 месяца
2 ж 102![]() ц
ц
под 102% годовых увеличит вклад в з1 + 4 ч = 1,57... ра-
з 100 ч и ш
за, т. е. меньше, чем на 116% = 58%, а под 103% годовых
ж ![]()
увеличит вклад в з1 + 4 ч = 1,581... раза, т. е. больше,
з 100 ч и ш
чем на 58%.
Ответ. Для p = 150 имеем x = 116 и y = 102.
![]()
![]()
![]() Замечание.
Отметим, что, например, при p = 300 х –200 + 20
p + 100
= –200 + 20 400 =
200, следовательно, условию задачи удовлетворяет х = 199.
Замечание.
Отметим, что, например, при p = 300 х –200 + 20
p + 100
= –200 + 20 400 =
200, следовательно, условию задачи удовлетворяет х = 199.
Если бы в условии задачи вместо слов «доход меньший, чем...» было написано «доход не больший, чем...», то ответ выражался бы формулой
![]() n = й–200 + 20 p + 100щ . лы
n = й–200 + 20 p + 100щ . лы
8. Из пункта A в пункт B по течению реки надо отбуксировать два плота с помощью катера, собственная скорость которого 20 км/ч. Найдите наименьшее время, за которое можно отбуксировать оба плота из A в B, если скорость течения реки 3 км/ч, а расстояние AB равно 58 км.
Решение. Наименьшее время буксировки плотов будет только в том случае, если оба плота прибудут в пункт B одновременно, так как только в этом случае будет максимально использована «помощь» реки. Чтобы два плота прибыли в пункт B одновременно, катер должен буксировать каждый плот одно и то же время — x ч. Пусть на возвращение ко второму плоту (после буксировки первого) катер затратит y ч, тогда за (x + y) ч второй плот удалится от пункта A на 3(x + y) км, а катер за то же время удалится от пункта A на (23x – 17y) км (сначала удалится на 23x км с первым плотом, потом возвратится за первым плотом, сокращая это удаление на 17y км). Так как в момент начала буксировки второго плота катер и второй плот были удалены от A на одно и то же расстояние, то составим первое уравнение
3(x + y) = 23x – 17y. (11)
Так как второй плот проплыл без буксировки 3(x + y) км и с буксировкой 23x км, а расстояние AB равно 58 км, то составим второе уравнение
3(x + y) + 23x = 58. (12)
Решив систему уравнений
![]() (11) и (12), найдём,
что x = y = 2. Тогда наименьшее время буксировки обоих
плотов равно x + y + x = 6 (ч).
(11) и (12), найдём,
что x = y = 2. Тогда наименьшее время буксировки обоих
плотов равно x + y + x = 6 (ч).
Это решение можно проиллюстрировать графиками движения двух плотов и катера: ACE — график движения первого плота, ADE — график движения второго плота, ACDE — график движения катера (рис. 60). Ответ. 6 ч.
6 Рис. 60
9. а) Теплоход по течению реки от A до B идёт a ч, а от B до A он идёт b ч. Расстояние AB равно 36 км, скорость течения реки равна 3 км/ч. Если 3 a 4, то какому числовому промежутку принадлежат значения b?
Решение. Скорость теплохода по течению реки равна
36 36
![]() км/ч,
против течения — км/ч, тогда скорость теa b
км/ч,
против течения — км/ч, тогда скорость теa b
![]()
![]()
![]() чения равна 36 – 36) : = 2 18 – 18 (км/ч),
или 3 км/ч. Из a b a b
чения равна 36 – 36) : = 2 18 – 18 (км/ч),
или 3 км/ч. Из a b a b
равенства 18 – 18 = 3 получим, что ![]() 6 = – 6 1. a b b a
6 = – 6 1. a b b a
Так как 3 a 4, то 3 6 2, откуда следует, что a
![]() верно двойное неравенство 6 –
1 1,
а также двойное a
верно двойное неравенство 6 –
1 1,
а также двойное a
неравенство
![]()
![]() 6 1.
6 1.
b
Все решения этого неравенства есть b [6; 12].
Ответ. b [6; 12].
10. а) Пешеход может пройти расстояние AB за a ч, а велосипедист может проехать то же расстояние за b ч. Однажды они отправились одновременно навстречу друг другу — пешеход из A, велосипедист из B — и встретились через t ч. Если 20 ≤ a ≤ 24, 5 ≤ b ≤ 8, то какому числовому промежутку принадлежат значения t?
Решение. Расстояние AB пешеход может
пройти за a ч, а велосипедист может проехать за b ч,
следовательно, за 1 ч пешеход проходит ![]() 1 расстояния AB,
а велосипедист a
1 расстояния AB,
а велосипедист a
![]() проезжает 1 расстояния AB.
А вместе за 1 ч они преодоb
проезжает 1 расстояния AB.
А вместе за 1 ч они преодоb
![]() левают 1 +
1 ,
или 1
расстояния AB, поэтому верно раa b t
левают 1 +
1 ,
или 1
расстояния AB, поэтому верно раa b t
венство
1 + 1 = 1 . (13) a b t
Так как 20 a 24, 5 b 8, то
![]()
![]()
![]()
![]()
![]() 1 1 , 1 1 и 1 +
1
. a 20 8 ba b
1 1 , 1 1 и 1 +
1
. a 20 8 ba b
![]()
![]() Следовательно, 1 . t
Следовательно, 1 . t
Все решения этого неравенства есть t [4; 6].
Ответ. t [4; 6].
![]() Замечание.
Если из равенства (13) выразить t, то из формулы t =
Замечание.
Если из равенства (13) выразить t, то из формулы t = ![]() ab получится более грубая
оценка для t: a + b
ab получится более грубая
оценка для t: a + b
t [3,125; 7,68].
Назовём чётным факториалом число n!! — произведение всех чётных натуральных чисел, не превосходящих n, а нечётным факториалом число n!!! — произведение всех нечётных натуральных чисел, не превосходящих n (n 4).
Например, 6!! = 2 · 4 · 6 = 48, 6!!! = 1 · 3 · 5 = 15, 7!! = 2 · 4 · 6 = 48, 7!!! = 1 · 3 · 5 · 7 = 105.
11. Определите последнюю цифру в записи числа
2007!!!.
Решение. Записи всех множителей числа 2007!!! оканчиваются нечётными цифрами и среди них есть 5, поэтому запись числа 2007!!! оканчивается цифрой 5.
Ответ. 5.
12. Определите, сколько нулей в конце записи числа 100!!.
Решение. В произведении 100!! множителей 2 больше, чем множителей 5, поэтому число нулей в конце записи числа 100!! равно числу множителей 5 в произведении чисел: 10 · 20 · 30 · 40 · 50 · 60 · 70 · 80 · 90 · 100.
Это произведение содержит 12 множителей 5, поэтому в конце записи числа 100!! ровно 12 нулей.
Ответ. 12 нулей.
13. Определите последнюю отличную от нуля цифру в записи числа 30!!.
Решение. Будем последовательно определять последнюю отличную от нуля цифру в произведении 30!!. Ниже в первой строке записаны множители числа 30!!, а во второй записана последняя отличная от нуля цифра, полученная после умножения на этот множитель:
2 · 4 · 6 · 8 · 10 · 12 · 14 · 16 · 18 · 20 · 22 · 24 · 26 · 28 · 30.
8 8 4 4 8 2 2 6 2 4 6 6 8 4
Ответ. 4.
Докажите (14—18):
14. n!! · n!!! = n!, если n — натуральное число и n 4.
Доказательство. n!! — это произведение всех чётных чисел, не превосходящих n, а n!!! — это произведение всех нечётных чисел, не превосходящих n. В этих произведениях множители не повторяются, поэтому n!! · n!!! — это произведение всех чётных и всех нечётных чисел, не превосходящих n, т. е. это n!, что и требовалось доказать.
15. Если n — чётное число, большее 4, то n!! n!!!. Доказательство. Так как n — число чётное, то
n!! = 2 · 4 · 6 · ... · n, n!!! = 1 · 3 · 5 · ... · (n – 1).
В этих произведениях равное число множителей, каждый множитель первого произведения больше соответствующего множителя второго произведения, поэтому n!! n!!!, что и требовалось доказать.
![]() Замечание.
Утверждение «если два произведения содержат равное число множителей и каждый
множитель первого произведения больше соответствующего множителя второго
произведения, то первое произведение больше второго» кажется очевидным, но в
старших классах это утверждение надо доказывать.
Замечание.
Утверждение «если два произведения содержат равное число множителей и каждый
множитель первого произведения больше соответствующего множителя второго
произведения, то первое произведение больше второго» кажется очевидным, но в
старших классах это утверждение надо доказывать.
16. Если n — нечётное число, большее 4, то n!! n!!!. Доказательство. Так как n — число нечётное, то n!! = 2 · 4 · 6 · ... · (n – 1), n!!! = 1 · 3 · 5 · ... · n.
Во втором произведении на один множитель больше, но если переписать их так:
n!! = 2 · 4 · 6 · ... · (n – 1), n!!! = 3 · 5 · 7 · ... · n,
то в этих произведениях равное число множителей, каждый множитель первого произведения меньше соответствующего множителя второго произведения, поэтому n!! n!!!, что и требовалось доказать.
17. Если n!! n!!! и n — натуральное число, n 4, то n — чётное число.
Доказательство. (От противного.) Предположим, что число n — нечётное, тогда из доказанного выше (задание 16) следует, что верно неравенство n!! n!!!, противоречащее условию, следовательно, n — чётное натуральное число, что и требовалось доказать.
18. Если n!! n!!! и n — натуральное число, n 4, то n — нечётное натуральное число.
Доказательство. (От противного.) Предположим, что число n — чётное, тогда из доказанного выше (задание 15) следует, что верно неравенство n!! n!!!, противоречащее условию, следовательно, n — нечётное натуральное число, что и требовалось доказать.
19.
Сколько лет Васе, если чётный факториал его возраста больше
нечётного факториала его возраста в ![]() раза?
раза?
![]()
![]() Решение.
Пусть Васе исполнилось n лет, тогда =
Решение.
Пусть Васе исполнилось n лет, тогда = ![]() n!! . Так как 1,
то n!! n!!!, тогда n — чётn!!!
n!! . Так как 1,
то n!! n!!!, тогда n — чётn!!!
ное число (см. задание 17).
Так как число n!!! не содержит чётных множителей, то на 2 дробь ![]() n!! не
сокращалась и
n!! не
сокращалась и
n!!!
все множители 2 из разложения числа n!! на простые мно-
жители содержатся в разложении на простые множители числителя дроби 1024 = 210. Составим произведение чётных чисел, взятых подряд, начиная с 2, и содержащее 10 множителей 2:
2 · 4 · 6 · 8 · 10 · 12.
Следовательно, n = 12.
Ответ. 12 лет.
20. Сколько лет Дусе, если нечётный факториал
её возраста больше чётного факториала её возраста в ![]() раза?
раза?
![]()
![]() Решение.
Пусть Дусе исполнилось n лет, тогда =
Решение.
Пусть Дусе исполнилось n лет, тогда = ![]() n!!! . Так
как 1, то n!!! n!!, тогда n — нечётn!!
n!!! . Так
как 1, то n!!! n!!, тогда n — нечётn!!
ное число (см. задание 18).
Так как число n!!! не содержит чётных множителей, то на 2 дробь ![]() n!!! не
сокращалась и n!!
n!!! не
сокращалась и n!!
все множители 2 из разложения числа n!! на простые множители содержатся в разложении на простые множители знаменателя дроби 1024 = 210. Составим произведение чётных чисел, взятых подряд, начиная с 2, и содержащее 10 множителей числа 2:
2 · 4 · 6 · 8 · 10 · 12.
Следовательно, n = 13.
Ответ. 13 лет.
Оглавление
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Примерное тематическое планирование работы
по учебнику «Алгебра. 9 класс» . . . . . . . . . . . . . . 16 Глава 1. Неравенства . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 Глава 2. Степень числа . . . . . . . . . . . . . . . . . . . . . . . . . 63 Глава 3. Последовательности . . . . . . . . . . . . . . . . . . . . 88
Глава 4. Тригонометрические формулы . . . . . . . . . . . . 116
Глава 5. Элементы приближённых
вычислений, статистики, комбинаторики и теории вероятностей 138 Обучение
решению текстовых задач . . . . . . . . . . . . . . 162 Задания для
исследования . . . . . . . . . . . . . . . . . . . . . . . 179

У ч е б н о е и з д а н и е
Серия «МГУ — школе»
Потапов Михаил Константинович
Шевкин Александр Владимирович
Алгебра
Методические рекомендации
9 класс
Учебное пособие для общеобразовательных организаций
Редакция математики и информатики
Заведующий редакцией Е. В. Эргле
Ответственный за выпуск И. В. Рекман
Редакторы Т. Г. Войлокова, И. В. Рекман
Младший редактор Е. А. Андреенкова
Художник О. П. Богомолова
Художественный редактор Т. В. Глушкова
Компьютерная графика А. Г. Вьюниковской
Техническое редактирование и компьютерная вёрстка Н. А. Разворотневой
Корректоры О. Н. Леонова, А. В. Рудакова
Налоговая льгота — Общероссийский классификатор продукции ОК 005-93—953000. Изд. лиц. Серия ИД № 05824 от 12.09.01. Подписано в печать 15.05.19. Формат 60901/16. Бумага газетная. Гарнитура SchoolBookCSanPin. Уч.-изд. л. 9,88. Тираж 1000 экз. Заказ № .
Акционерное общество «Издательство «Просвещение».
Российская Федерация, 127473, г. Москва, ул. Краснопролетарская, д. 16, стр. 3, этаж 4, помещение I.
Предложения по оформлению и содержанию учебников — электронная почта «Горячей линии» — fpu@prosv.ru.
Отпечатано в России.
Отпечатано по заказу АО «ПолиграфTрейд» в типографии филиала АО «ТАТМЕДИА» ПИК «Идел-Пресс». 420066, г. Казань, ул. Декабристов, 2.
[1] Далее вместо слов «корни многочлена, записанного в левой части неравенства» будем писать коротко: «корни многочлена».
[2] Понятие «тригонометрическая функция» будет введено только в 10 классе, но для упрощения речи правомерно использовать термин «функция», так как, например, каждому углу a соответствует единственное значение sin a.
[3] 6 – 2a 9 – 3a
(рис. 58). Решив это неравенство, получим все его решения: a
[ – ![]() ; 3), все они удовлетворяют условию a
3.
; 3), все они удовлетворяют условию a
3.
[4] Рис. 57 6 Рис. 58
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.