
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ЧЕЧЕНСКОЙ РЕСПУБЛИКИ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ГРОЗНЕНСКИЙ ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ»
Утверждаю
Директор ГБПОУ «ГПК»
Мусхаджиев Р.Х.
_______________________
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
к лабораторным и практическим занятиям
по учебной дисциплине
ЕН.01 ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ
Специальность: 09.02.07. Информационные системы и программирование
2020г.
|
Рассмотрена Согласовано на заседании цикловой комиссии Зам.директора по УР Протокол от «____»________20___г. №___ Ганчаев М.С Председатель_________ Орцуева Д.Н. «____»________20___г.
|
Методические рекомендации к лабораторным и практическим занятиям предназначены для закрепления теоретических знаний и приобретение необходимых практических навыков и умений по программе учебной дисциплины ЕН.01 Элементы высшей математики составлены в соответствии с учебным планом и рабочей программой учебной дисциплины по специальности среднего профессионального образования 09.02.07. Информационные системы и программирование
|
Организация разработчик: |
- государственное бюджетное профессиональное образовательное учреждение «Грозненский политехнический колледж»
|
|
Разработчик: |
Преподаватель: Сулиманова Х.Ш. |
Пояснительная записка
Методические рекомендации по проведению лабораторных и практических занятий по учебной дисциплине ЕН.01 Элементы высшей математики составлены в соответствии с учебным планом и рабочей программой дисциплины по специальности среднего профессионального образования 09.02.07. Информационные системы и программирование для студентов очной формы обучения.
В соответствии с рабочей программой ЕН.01 Элементы высшей математики
на изучение учебной дисциплины предусмотрено 72 часа, из которых 28 часов на проведение лабораторных работ и практических занятий, 14 часов на (внеаудиторную) самостоятельную работу.
Цель проведения практических (лабораторных) занятий: формирование практических умений, необходимых в последующей профессиональной и учебной деятельности.
Задачи:
- обобщение, систематизация, углубление, закрепление полученных теоретические знания по конкретным темам;
- формирование умения применять полученные знания на практике;
- выработка при решении поставленных задач таких профессионально значимых качеств, как самостоятельность, ответственность, точность, творческая инициатива.
Освоение содержания учебной дисциплины ЕН.01 Элементы высшей математики
обеспечивает достижение студентами следующих результатов:
|
Код |
Умения |
Знания |
|
ОК 1, ОК 5,
|
Выполнять операции над матрицами и решать системы линейных уравнений Решать задачи, используя уравнения прямых и кривых второго порядка на плоскости Применять методы дифференциального и интегрального исчисления Решать дифференциальные уравнения Пользоваться понятиями теории комплексных чисел |
Основы математического анализа, линейной алгебры и аналитической геометрии Основы дифференциального и интегрального исчисления Основы теории комплексных чисел |
Перечень практических и/или лабораторных занятий ЕН.01 Элементы высшей математики
|
Наименование раздела (темы) |
Практическая работа |
Содержание практической работы |
Кол-во часов |
|
Тема. Теория пределов |
ПЗ № 1 |
Вычисление пределов |
2 |
|
Тема. Дифференциальное исчисление функции одной действительной переменной |
ПЗ № 2 |
Вычисление производных функций |
2 |
|
Тема. Интегральное исчисление функции одной действительной переменной |
ПЗ № 3 |
Вычисление интегралов |
2 |
|
Тема. Дифференциальное исчисление функции нескольких действительных переменных |
ПЗ № 4 |
Задача о наибольшем и наименьшем значениях |
2 |
|
Тема. Интегральное исчисление функции нескольких действительных переменных |
ПЗ № 5 |
Вычисление двойного интеграла |
2 |
|
Тема. Теория рядов |
ПЗ № 6 |
Решение задач на вычисление суммы ряда, на исследование сходимости числового ряда |
2 |
|
Тема. Обыкновенные дифференциальные уравнения |
ПЗ № 7 |
Решение дифференциальных уравнений 2-го порядка |
2 |
|
Тема. Матрицы и определители |
ПЗ № 8 |
Действия с матрицами |
2 |
|
Тема. Матрицы и определители |
ПЗ № 9 |
Нахождение обратной матрицы |
2 |
|
Тема. Системы линейных уравнений |
ПЗ № 10 |
Решение систем линейных уравнений различными методами |
2 |
|
Тема. Векторы и действия с ними |
ПЗ № 11 |
Прямоугольные координаты на плоскости |
2 |
|
Тема. Аналитическая геометрия на плоскости |
ПЗ № 12 |
Решение простейших задач аналитической геометрии на плоскости |
2 |
|
Контрольная работа: «Интегральное исчисление функции нескольких действительных переменных» |
Кр № 1 |
Интеграл |
2 |
|
Контрольная работа: «Действия над векторами» |
Кр № 2 |
Действия над векторами |
2 |
|
ИТОГО |
14 |
|
28 |
Общие методические рекомендации и рекомендации по проведению практических/ лабораторных занятий
При выполнении каждой практической/лабораторной работы необходимо придерживаться следующих правил:
1. Внимательно прочитайте инструкцию по выполнению практической /лабораторной работы.
2. Пользуясь рекомендациями к работе, выполните предложенные задания.
3. Оформите письменный отчет по выполненной практической/лабораторной работе.
Требования к содержанию и оформлению отчета
по практической/лабораторной работе
-название и цель работы;
-оборудование;
-ход работы (краткое описание порядка выполнения работы, результаты эксперимента, расчета, наблюдения оформляются в виде таблицы. В таблицу заносятся все экспериментальные данные и результаты расчетов. Все расчеты производятся ниже таблицы. К отчету прилагаются графики в случае необходимости графической интерпретации полученных результатов или другие материалы);
-вывод по работе, соответствующий полученным результатам (Например, можно начать следующим образом: из полученных данных можно сделать следующие выводы: (и перечисляем, к каким выводам в результате проделанной работе вы пришли).
Критерии оценки результатов выполнения практической/лабораторной работы
Критериями оценки результатов выполнения практической (лабораторной) работы являются:
-степень реализации цели работы;
-качество оформления отчета;
-степень соответствия результатов работы заданным требованиям.
Оценка выполнения практической (лабораторной) работы
Отметка 5– «отлично» выставляется, если студент имеет глубокие знания учебного материала по теме практической (лабораторной)работы, показывает усвоение взаимосвязи основных понятий, используемых в работе, самостоятельно выполнил все рекомендации по выполнению практической работе, смог ответить на контрольные вопросы, дает правильный алгоритм решения задачи, выполнены поставленные цели работы.
Отметка 4– «хорошо» выставляется, если студент показал знание учебного материала, допускает небольшие неточности при выполнении экспериментальных заданий и расчетов, смог ответить почти полно на все контрольные вопросы.
Отметка 3– «удовлетворительно» выставляется, если студент в целом освоил материал практической работы, но затрудняется с выполнением всех заданий практической (лабораторной) работы без помощи преподавателя, ответил не на все контрольные вопросы.
Отметка 2– «неудовлетворительно» выставляется студенту, если он имеет существенные пробелы в знаниях основного учебного материала практической (лабораторной)работы, не может самостоятельно выполнить задания практической (лабораторной)работы, не раскрыл содержание контрольных вопросов.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ СТУДЕНТОВ К
ПРАКТИЧЕСКИМ ЗАНЯТИЯМ
Практическое занятие 1
1.Название темы Вычисление пределов
2. Учебная цель: Используя теоретический материал и образцы решения задач, решить примеры по теме: «Вычисление пределов»
3. Продолжительность занятия: 2 часа.
4. Материалы, оборудование, ТСО, программное обеспечение, оснащение, раздаточный материал ПК, проектор, сборник задач, карточки с алгоритмом решения задач
5. Литература, информационное обеспечение Элементы высшей математики Гончаренко В.М. и др.
6.Методические рекомендации по выполнению работы: изучите краткие теоретические и учебно-методические материалы по теме практического занятия. При выполнении работы соблюдайте последовательность действий.
7.Порядок выполнения работы:
Краткая теория
Краткие теоретические сведения
Предел рациональной функции
Определение: Целой рациональной функцией![]() называется
функция вида
называется
функция вида
![]()
Теорема 1.Предел целой рациональной функции при ![]() , равен значению
этой функции в точке
, равен значению
этой функции в точке ![]() , т.е.
, т.е.![]() .
.
Предел дробно-рациональной функции
Определение: дробно-рациональной функцией![]() называется
функция вида
называется
функция вида
![]() ,
где
,
где ![]() –целые
рациональные функции.
–целые
рациональные функции.
Теорема 2: предел дробно-рациональной функции при ![]() , если при этом
знаменатель не обращается в нуль, равен значению функции в точке
, если при этом
знаменатель не обращается в нуль, равен значению функции в точке ![]() , т.е.
, т.е. ![]()
Определение: функция ![]() называется
бесконечно малой при
называется
бесконечно малой при![]() , если
, если
![]() .
.
Определение:функция ![]() называется
бесконечно большой при
называется
бесконечно большой при![]() , если
, если ![]() .
.
Теорема 3: отношение функции, имеющий конечный
предел при ![]() , не равный нулю, к функции
бесконечно малой при
, не равный нулю, к функции
бесконечно малой при![]() есть величина бесконечно большая.
есть величина бесконечно большая.
Задача. Вычислить ![]()
Решение. Предел знаменателя в точке ![]() равен нулю,
поэтому теорема 2 не применима. Найдем отдельно предел числителя и предел
знаменателя при
равен нулю,
поэтому теорема 2 не применима. Найдем отдельно предел числителя и предел
знаменателя при ![]() .
.
![]() ,
,
![]() .
.
Предел числителя конечен, предел знаменателя равен нулю,
используя теорему 3, получим![]() .
.
Раскрытие неопределенности вида ![]()
Задача. Вычислить ![]() .
.
Пределы на бесконечность
Определение: предел целой рациональной функции при![]() равен
равен ![]() .
.
Теорема 4: отношение функции, имеющий конечный
предел при![]() к
функции бесконечно большой, есть величина бесконечно малая.
к
функции бесконечно большой, есть величина бесконечно малая.
Задача. Вычислить ![]()
Решение. Предел числителя равен 5, предел
знаменателя равен![]() ,т.е. имеем отношение
конечного предела к функции бесконечно большой, поэтому, применив теорему 4
получим
,т.е. имеем отношение
конечного предела к функции бесконечно большой, поэтому, применив теорему 4
получим ![]() .
.
Задача.Вычислить ![]()
Предел дробно-рациональной функции при ![]() равен
равен
1) 0, если степень числителя ниже степени знаменателя;
2) отношению коэффициентов при старших степенях ![]() , если степени
числителя и знаменателя равны;
, если степени
числителя и знаменателя равны;
3)![]() , если степень
числителя выше степени знаменателя.
, если степень
числителя выше степени знаменателя.
Порядок выполнения работы:
Используя теоретические сведения выполнить предложенное преподавателем задание.
Содержание работы
Задача 1. ![]()
Задача 2. ![]()
Задача 3. ![]()
Задача 4.![]()
Задача 5.![]()
Критерии оценивания
Оценка «5» - все задачи решены верно.
Оценка «4» -все задачи решены верно, но допущены неточности или несущественные ошибки.
Оценка «3» - все задачи решены, но допущены существенные ошибки и неточности.
Оценка «2» - задачи не решены.
8.Форма отчета: выполнение заданий в тетрадях для практических занятий.
9. Место проведения самоподготовки: читальный зал библиотеки.
Практическое занятие 2
1. Название темы Вычисление производных функций
2. Учебная цель: Используя теоретический материал и образцы решения задач, решить примеры по теме «Вычисление производных и дифференциалов высших порядков»
3. Продолжительность занятия: 2 часа.
4.Материалы, оборудование, ТСО, программное обеспечение, оснащение, раздаточный материал ПК, проектор, сборник задач, карточки с алгоритмом решения задач
5. Литература, информационное обеспечение Элементы высшей математики Гончаренко В.М. и др.
6.Методические рекомендации по выполнению работы: изучите краткие теоретические и учебно-методические материалы по теме практического занятия. При выполнении работы соблюдайте последовательность действий.
7.Порядок выполнения работы:
Краткая теория
Краткие теоретические сведения:
Правила дифференцирования
1) ![]() ;
;
2) ![]() , в частности
, в частности ![]() ;
;
3) ![]() ;
;
4) ![]() , если
, если![]() ;
;
5) ![]() ,
если
,
если ![]() и
и ![]() .
.
Формулы дифференцирования
![]()
![]() в частности,
в частности, ![]()
![]() в частности,
в частности, ![]()
![]() в частности,
в частности, ![]()
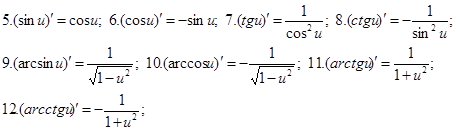
Производная сложной и обратной функций
Определение. Пусть ![]() и
и
![]() , тогда
, тогда ![]() -
сложная функция с промежуточным аргументом
-
сложная функция с промежуточным аргументом ![]() и
независимым аргументом
и
независимым аргументом ![]() .
.
Теорема. Если функция ![]() имеет
производную
имеет
производную ![]() в точке
в точке ![]() ,
а функция
,
а функция ![]() имеет производную
имеет производную ![]() в соответствующей точке
в соответствующей точке ![]() , то сложная функция
, то сложная функция ![]() имеет производную
имеет производную ![]() в точке
в точке ![]() которая
находится по формуле
которая
находится по формуле ![]() .
.
Правило нахождения производной сложной функции:
Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Дифференциал функции
Определение. Если функция ![]() дифференцируема
в точке
дифференцируема
в точке ![]() , т.е. имеет в этой точке конечную
производную
, т.е. имеет в этой точке конечную
производную![]() , то ее приращение
, то ее приращение ![]() можно записать в виде
можно записать в виде ![]() , где
, где ![]() .
.
Главная, линейная относительно ![]() часть
часть
![]() приращения функции называется
дифференциалом функции и обозначается
приращения функции называется
дифференциалом функции и обозначается![]()
![]() :
:
![]() .
. ![]()
При достаточно малых ![]() приращение
функции приближенно равно ее дифференциалу т.е.
приращение
функции приближенно равно ее дифференциалу т.е. ![]() .
.
Примеры:
Найти дифференциал функции у = ![]() .
.
Решение:
Используя формулу, ![]() получаем dy = (-sinx+10x)dx.
получаем dy = (-sinx+10x)dx.
2. Для функции ![]() найти приращение
найти приращение![]() при
при ![]() и
и![]() .
.
Решение:
Используя формулу, ![]() получаем
получаем ![]() (
(![]() )
)![]()
![]() =
=
=(![]() )
)![]() . Выполняя подстановку
. Выполняя подстановку ![]() и
и![]() , находим приращение
, находим приращение![]() :
:
![]() =(3
=(3![]()
![]() )
)![]() =0,05
=0,05
Ответ: ![]() =0,05
=0,05
Порядок проведения работы:
Используя теоретические сведения выполнить предложенное преподавателем задание
Содержание работы
1.Найдите производную функции:
![]()
![]()
![]()
![]()
![]()
|
2.Найдите дифференциал функции:
|
|
8.Форма отчета: выполнение заданий в тетрадях для практических занятий.
9. Место проведения самоподготовки: читальный зал библиотеки.
Практическое занятие 3
1. Название темы Вычисление интегралов
2. Учебная цель: Используя теоретический материал и образцы решения задач, сформировать умение и навык вычисления интегралов
3. Продолжительность занятия: 2 часа.
4.Материалы, оборудование, ТСО, программное обеспечение, оснащение, раздаточный материал ПК, проектор, сборник задач, карточки с алгоритмом решения задач
5. Литература, информационное обеспечение Элементы высшей математики Гончаренко В.М. и др.
6.Методические рекомендации по выполнению работы: изучите краткие теоретические и учебно-методические материалы по теме практического занятия. При выполнении работы соблюдайте последовательность действий.
7.Порядок выполнения работы:
Краткие теоретические сведения:
Определенный интеграл
Определение. Если существует конечный предел интегральной
суммы ![]() , когда
, когда ![]() так, что
так, что ![]() , то этот предел называют
определенным интегралом от функции
, то этот предел называют
определенным интегралом от функции ![]() на отрезке [a;b] и обозначают следующим
образом:
на отрезке [a;b] и обозначают следующим
образом: 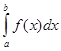 или
или 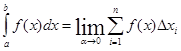 . В этом случае функция
. В этом случае функция ![]() называется интегрируемой на отрезке
[a;b] . Числа a и b называются
соответственно нижним и верхним пределами интегрирования,
называется интегрируемой на отрезке
[a;b] . Числа a и b называются
соответственно нижним и верхним пределами интегрирования, ![]() – подынтегральной функцией,
– подынтегральной функцией, ![]() – переменной интегрирования.
– переменной интегрирования.
Отметим, что непрерывность функции является достаточным условием ее интегрируемости.
Основные свойства определенного интеграла
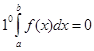 ;
; 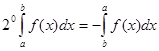 ;
;
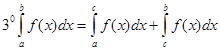 ;
где a, b, c любые числа.
;
где a, b, c любые числа.
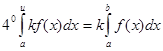 ;
;
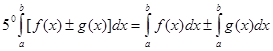 .
.
Формула Ньютона – Лейбница
Если функция ![]() непрерывна на
отрезке [a;b] и функция у = F(x) является некоторой ее
первообразной на этом отрезке, то имеет место формула Ньютона – Лейбница
непрерывна на
отрезке [a;b] и функция у = F(x) является некоторой ее
первообразной на этом отрезке, то имеет место формула Ньютона – Лейбница 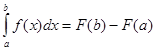 .
.
Вычисление определенных интегралов
Простым и удобным методом вычисления определенного
интеграла 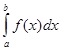 от непрерывной функции является
формула Ньютона-Лейбница:
от непрерывной функции является
формула Ньютона-Лейбница: 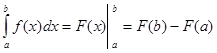 .
.
При вычислении определенных интегралов широко используется метод замены переменной и метод интегрирования по частям.
Интегрирование подстановкой
Пусть для вычисления интеграла 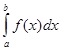 от непрерывной функции сделана
подстановка
от непрерывной функции сделана
подстановка ![]() =
=![]() (t)
(t)
Теорема. Если:
1) функция ![]() и её
производная
и её
производная ![]() непрерывны при
непрерывны при ![]() ;
;
2) множеством значений функции ![]() при
при
![]() является отрезок [a;b];
является отрезок [a;b];
3) ![]() и
и ![]() то
то 
Интегрирование по частям
Теорема. Если функции ![]()
![]() и
и ![]() имеют непрерывные производные на отрезке
[a;b], то имеет место формула
имеют непрерывные производные на отрезке
[a;b], то имеет место формула ![]() .
.
Пример. Вычислить ![]() .
.
Решение: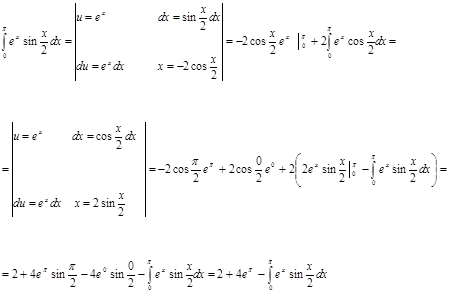
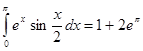
Ответ: 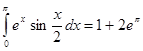
Неопределенный интеграл
Основные свойства неопределенного интеграла
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таблица основных интегралов.
![]() в частности,
в частности, ![]()
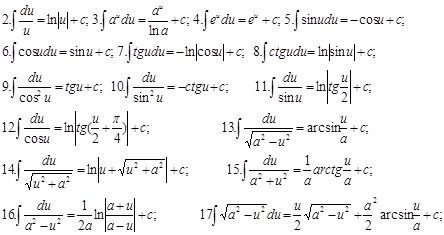
![]()
Основные методы интегрирования
Метод непосредственного интегрирования
Определение. Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интегрирования приводится к одному или нескольким табличным интегралом, называется непосредственном интегрированием.
Примеры:
1) ![]()
Метод интегрирования подстановкой
Метод подстановки (или замены переменной) заключается в
том, что заменяют ![]() на
на ![]() , где
, где ![]() -
непрерывно дифференцируемая функция, полагают
-
непрерывно дифференцируемая функция, полагают ![]() и
получают
и
получают ![]() .
.
13.3. Метод интегрирования по частям
![]()
Порядок проведения работы:
Используя теоретические сведения выполнить предложенное преподавателем задание
Содержание работы
№ 1. Вычислить определенный интегралы:
|
Вариант 1 |
Вариант 2 |
||
|
1. |
|
1. |
|
|
2. |
|
2. |
|
|
3. |
|
3. |
|
|
4. |
|
4. |
|
№2. Применяя метод непосредственного интегрирования, вычислить интегралы:
|
Вариант 1 |
Вариант 2 |
||
|
1. |
|
1. |
|
|
2. |
|
2. |
|
|
3. |
|
3. |
|
|
4. |
|
4. |
|
№3. Пользуясь методом подстановки вычислить интегралы:
Вариант 1 Вариант 2
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.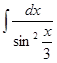 3.
3.![]()
4.![]() 4.
4.![]()
№ 4. С помощью метода интегрирования по частям вычислить интегралы:
Вариант 1 Вариант 2
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.![]() 3.
3. ![]()
4.![]() 4.
4. ![]()
8.Форма отчета: выполнение заданий в тетрадях для практических занятий.
9. Место проведения самоподготовки: читальный зал библиотеки.
Практическое занятие 4
1. Название темы Задача о наибольшем и наименьшем значениях
2. Учебная цель: Формирование умения решать задачи на нахождение наибольших и наименьших значений
3. Продолжительность занятия: 2 часа.
4.Материалы, оборудование, ТСО, программное обеспечение, оснащение, раздаточный материал ПК, проектор, сборник задач, карточки с алгоритмом решения задач
5. Литература, информационное обеспечение Элементы высшей математики Гончаренко В.М. и др.
6.Методические рекомендации по выполнению работы: изучите краткие теоретические и учебно-методические материалы по теме практического занятия. При выполнении работы соблюдайте последовательность действий.
7.Порядок выполнения работы:
Краткая теория
Пусть функция y = f (x) непрерывна на отрезке [a; b]. В этом случае, как известно, она принимает как наибольшее, так и наименьшее значения на этом отрезке. Во многих прикладных вопросах важно найти те точки отрезка [a; b], которым отвечают наибольшее и наименьшее значения функции.
При решении этой задачи возможны два случая:
1. либо наибольшее (наименьшее) значение функции достигается внутри отрезка, и тогда эти значения окажутся в числе экстремумов функции;
2. либо наибольшее (наименьшее) значение достигается на концах отрезка [a; b].
Итак, чтобы найти наибольшее и наименьшее значения непрерывной на отрезке функции y = f (x), достаточно:
1. Найти все критические точки, принадлежащие [a; b], и вычислить значения функции в этих точках.
2. Вычислить значения функции на концах отрезка [a; b], то есть найти f (a) и f (b).
3. Сравнить полученные результаты: наибольшее из найденных значений является наибольшим значением функции на отрезке [a; b]; аналогично, наименьшее из найденных значений является наименьшим значение функции на этом отрезке.
Замечание 1. При нахождении критических точек можно использовать соображения геометрического характера, изобразив схематически график функции.
Замечание 2. Отыскание наибольшего и наименьшего значений функции можно упростить, если воспользоваться следующими свойствами непрерывных функций:
1. если функция y = f (x) на отрезке [a; b] непрерывна и возрастает, то m = f (a) и M = f (b);
2. если функция y = f (x) на отрезке [a; b] непрерывна и убывает, то m = f (b) и M = f (a);
3. если функция y = f (x), непрерывная на отрезке [a; b], имеет на этом отрезке только одну точку максимума x0 (и ни одной точки минимума), то наибольшее значение на данном отрезке есть M = f (x0);
4. если функция y = f (x), непрерывная на отрезке [a; b], имеет на этом отрезке только одну точку минимума x0 (и ни одной точки максимума), то наименьшее значение на данном отрезке есть m = f (x0).
Алгоритм решения задач на нахождение наибольшего или наименьшего значения функции:
Если в задаче требуется найти максимальное или минимальное значение функции f(x) на отрезке [a; b], выполняем следующие действия:
1. Найти производную функции: f '(x).
2. Решить уравнение f''(x) = 0. Если корней нет, пропускаем третий шаг и переходим сразу к четвертому.
3. Из полученного набора корней вычеркнуть все, что лежит за пределами отрезка [a; b]. Оставшиеся числа обозначим x1, x2, ..., xn — их, как правило, будет немного.
4. Подставим концы отрезка [a; b] и точки x1, x2, ..., xn в исходную функцию. Получим набор чисел f(a), f(b), f(x1), f(x2), ..., f(xn), из которого выбираем наибольше или наименьшее значение — это и будет ответ.
Небольшое пояснение по поводу вычеркивания корней, когда они совпадают с концами отрезка. Их тоже можно вычеркнуть, поскольку на четвертом шаге концы отрезка все равно подставляются в функцию — даже если уравнение
f '(x) = 0 не имело решений.
Также следует внимательно читать условие задачи. Когда требуется найти значение функции (максимальное или минимальное), концы отрезка и точки x1, x2, ..., xn подставляются именно в функцию, а не в ее производную.
Задача 1. Найти наибольшее значение функции y = x3 + 3x2 − 9x – 7 на отрезке [−5; 0].
Решение. Для начала найдем производную: y' = (x3 + 3x2 − 9x − 7)’ = 3x2 + 6x − 9.
Затем решаем уравнение: y' = 0 ⇒ 3x2 + 6x − 9 = 0 ⇒ ... ⇒ x = −3; x = 1.
Вычеркиваем корень x = 1, потому что он не принадлежит отрезку [−5; 0].
Осталось вычислить значение функции
на концах отрезка и в точке x = −3:
y(−5) = (−5)3 + 4·(−5)2 − 9·(−5) − 7 = −12;
y(−3) = (−3)3 + 4·(−3)2 − 9·(−3) − 7 = 20;
y(0) = 03 + 4·02 − 9·0 − 7 = −7.
Очевидно, наибольшее значение равно 20 — оно достигается в точке x = −3.
Ответ: 20
Задача 2. Найти наибольшее и наименьшее значения функции
f (x) = 2x3 – 6x + 5 на отрезке .
Решение. 1. Находим критические точки, принадлежащие :
f (x) = 6x2 – 6 = 6(x2 – 1), 6(x2 – 1) = 0, x1 = –1, x2 = 1.
Вычислим значения функции в этих точках:
f (–1) = 2 (–1)3 – 6 (–1) + 5 = 9; f (1) = 2 13 – 6 1 + 5 = 1.
2. Вычислим значения функции на концах отрезка:
3. Таким образом, наибольшее значение данной функции на рассматриваемом отрезке есть f (–1) = 9, а наименьшее
Ответ: f (–1) = 9,
Задача 3 Найдите наименьшее значение функции на отрезке: у = на отрезке [1;14].
Решение. Заметим, что функция не определена в точке 0.
Берем производную дроби:
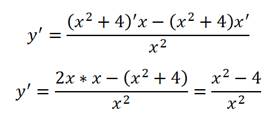
Приравниваем производную к нулю и отыскиваем корни:
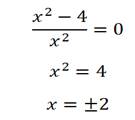
Один из корней нас не интересует, так как промежутку не принадлежит, а во второй точке производная меняет знак с отрицательного на положительный. То есть функция имеет минимум в данной точке. Определим ее минимальное значение:
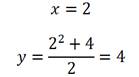 Ответ: 4.
Ответ: 4.
Задача 4. Найдите наибольшее значение функции ![]() на отрезке
на отрезке ![]() .
.
Решение. Найдём производную заданной функции:
![]()
Найдем нули производной:
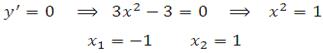
Указанному в условии интервалу принадлежит точка х = –1.
Вычисляем значения функции в точках –2, –1 и 0:
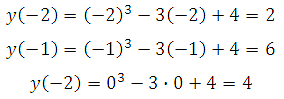
Наибольшее значение функции равно 6.
Ответ: 6
Задача 5. Найдите наибольшее значение функции у = х3 – 6х2 на отрезке
[–3;3].
Решение. Найдём производную заданной функции:
![]()
Найдем нули производной:
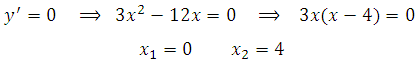
Указанному в услов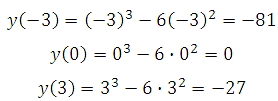 ии интервалу принадлежит точка х = 0.
ии интервалу принадлежит точка х = 0.
Вычисляем значения функции в точках –3, 0 и 3:
Наименьшее значение функции равно 0. Ответ: 0
Задача 6. Найдите наименьшее значение функции у = х3 – 2х2 + х +3 на отрезке [1;4].
Решение. Найдём производную заданной функции:
![]()
Найдем нули производной, решаем квадратное уравнение:
3х2 – 4х + 1 = 0
Получим корни: х1 = 1 х1 = 1/3.
Указанному в условии интервалу принадлежит только х = 1.
Найдём значения функции в точках 1 и 4:
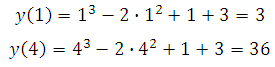
Получили, что наименьшее значение функции равно 3.
Ответ: 3
Критерии оценивания
Оценка «5» - все задачи решены верно.
Оценка «4» -все задачи решены верно, но допущены неточности или несущественные ошибки.
Оценка «3» - все задачи решены, но допущены существенные ошибки и неточности.
Оценка «2» - задачи не решены.
8.Форма отчета: выполнение заданий в тетрадях для практических занятий.
9. Место проведения самоподготовки: читальный зал библиотеки.
Практическое занятие 5
1. Название темы Вычисление двойного интеграла
2. Учебная цель: сформировать навык при решении примеров.
3. Продолжительность занятия: 2 часа.
4.Материалы, оборудование, ТСО, программное обеспечение, оснащение, раздаточный материал ПК, проектор, сборник задач, карточки с алгоритмом решения задач
5. Литература, информационное обеспечение Элементы высшей математики Гончаренко В.М. и др.
6.Методические рекомендации по выполнению работы: изучите краткие теоретические и учебно-методические материалы по теме практического занятия. При выполнении работы соблюдайте последовательность действий.
7.Порядок выполнения работы:
Краткая теория
Понятие двойного интеграла
Определение: Двойной интеграл представляет собой обобщение понятия определенного интеграла на случай функции двух переменных. В этом случае вместо отрезка интегрирования будет присутствовать какая-то плоская фигура.
Двойной интеграл в общем виде записывается следующим образом:
![]() ,
где
,
где ![]() – знак двойного интеграла;
– знак двойного интеграла;
D – область интегрирования (плоская фигура);
f(x;y) – подынтегральная функция двух переменных;
dx, dy – элементы площади интегрирования.
Пусть D – некоторая замкнутая ограниченная область, а f(x,y) – произвольная функция, определенная и ограниченная в этой области. Будем предполагать, что границы области D состоят из конечного числа кривых, заданных уравнениями вида y=f(x) или x=g(y), где f(x) и g(y) – непрерывные функции.
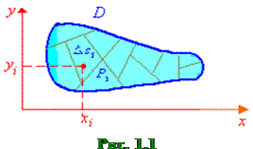
Свойства двойного интеграла
Правила вычисления двойного интеграла
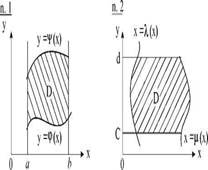
Для такой области интеграл вычисляется
следующим образом 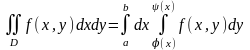
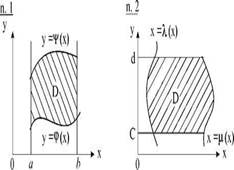
Для такой области интеграл вычисляется
следующим образом 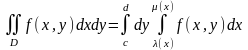
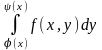 здесь х
считается постоянным числом.
здесь х
считается постоянным числом.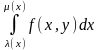 здесь у
считается постоянным числом.
здесь у
считается постоянным числом.Затем, вычисляется внешний интеграл также по формуле Ньютона-Лейбница.
Пример1. Вычислить двойной интеграл ![]() ,
где
,
где
![]()
Решение. 1. Строим область интегрирования D
2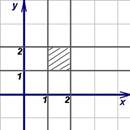 .
Находим границы области, то есть пределы интегрирования 1xy
.
Находим границы области, то есть пределы интегрирования 1xy
3. Выбираем вид области интегрирования ![]() .
.
Вычисляем внутренний (правый) интеграл, считая у - числом, которое
можно вынести за знак интеграла. Получаем 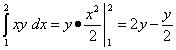 .
.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
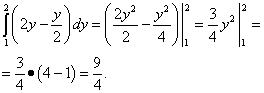
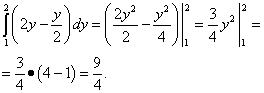
Результат и будет решением данного двойного интеграла.
Пример 2. Вычислить двойной интеграл ,
где .
Решение. 1. Строим область интегрирования D
2. Находим границы области, то есть пределы интегрирования 1xy
3. Выбираем вид области интегрирования
Вычисляем внутренний (правый) интеграл, считая х - число. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Ответить на контрольные вопросы:
Порядок и методика выполнения заданий:
1. Повторить теоретический материал по теме практического занятия.
2. Оформить решение задач в тетради.
Критерии оценивания:
Оценка «5» - все задачи уровня «С» решены верно.
Оценка «4» - все задачи уровня «В» решены верно или в решении задач уровня «С» допущены неточности, несущественные ошибки.
Оценка «3» - все задачи уровня «А» решены верно или в решении задач уровня «В» и уровня «С» допущены существенные ошибки и неточности.
Оценка «2» - задачи не решены или допущены существенные ошибки и неточности.
8.Форма отчета: выполнение заданий в тетрадях для практических занятий.
9. Место проведения самоподготовки: читальный зал библиотеки.
Практическое занятие 6
1. Название темы Решение задач на вычисление суммы ряда, на исследование сходимости числового ряда
2. Учебная цель: Познакомиться с признаками Коши и Даламбера,
на конкретных примерах научиться применять данные признаки для исследования ряда на сходимость.
3. Продолжительность занятия: 2 часа.
4.Материалы, оборудование, ТСО, программное обеспечение, оснащение, раздаточный материал ПК, проектор, сборник задач, карточки с алгоритмом решения задач
5. Литература, информационное обеспечение Элементы высшей математики Гончаренко В.М. и др.
6.Методические рекомендации по выполнению работы: изучите краткие теоретические и учебно-методические материалы по теме практического занятия. При выполнении работы соблюдайте последовательность действий.
7.Порядок выполнения работы:
Краткая теория
Признак Даламбера. (Жан Лерон Даламбер (1717 – 1783) – французский математик)
Если для
ряда ![]() с положительными членами
существует такое число q<1,
что для всех достаточно больших n
выполняется неравенство
с положительными членами
существует такое число q<1,
что для всех достаточно больших n
выполняется неравенство ![]() то ряд
то ряд ![]() сходится, если же для
всех достаточно больших n
выполняется условие
сходится, если же для
всех достаточно больших n
выполняется условие ![]() то
ряд
то
ряд ![]() расходится.
расходится.
Признак Коши (радикальный признак)
Если для
ряда ![]() с неотрицательными членами
существует такое число q<1,
что для всех достаточно больших n
выполняется неравенство
с неотрицательными членами
существует такое число q<1,
что для всех достаточно больших n
выполняется неравенство ![]() ,
,
то ряд ![]() сходится, если же для всех
достаточно больших n
выполняется неравенство
сходится, если же для всех
достаточно больших n
выполняется неравенство
![]() то
ряд
то
ряд ![]() расходится.
расходится.
Пример1:
Определить сходимость ряда 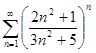 .
.
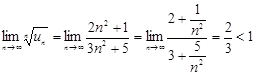 Вывод: ряд сходится.
Вывод: ряд сходится.
Пример2:
Исследовать на сходимость ряд 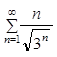 .
.
Решение. По признаку Даламбера ряд сходится, так как
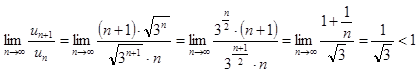 .
.
Задания для самостоятельной работы
|
1 вариант |
2 вариант |
3 вариант |
4 вариант |
5 вариант |
6 вариант |
|
1. Найти общий член числового ряда |
|||||
|
|
|
|
|
|
|
|
2. Исследовать ряд на сходимость |
|||||
|
|
|
|
|
|
|
8.Форма отчета: выполнение заданий в тетрадях для практических занятий.
9. Место проведения самоподготовки: читальный зал библиотеки.
Практическое занятие 7
1. Название темы Решение дифференциальных уравнений 2-го порядка
2. Учебная цель: На конкретных примерах научиться решать дифференциальные уравнения второго порядка
3. Продолжительность занятия: 2 часа.
4.Материалы, оборудование, ТСО, программное обеспечение, оснащение, раздаточный материал ПК, проектор, сборник задач, карточки с алгоритмом решения задач
5. Литература, информационное обеспечение Элементы высшей математики Гончаренко В.М. и др.
6.Методические рекомендации по выполнению работы: изучите краткие теоретические и учебно-методические материалы по теме практического занятия. При выполнении работы соблюдайте последовательность действий.
7.Порядок выполнения работы:
1. Повторить теоретический материал по теме практической работы.
2. Оформить решение в тетради.
Пример. Решить уравнение ![]()
Характеристическое
уравнение: ![]()
![]()
Общее решение: ![]()
Пример.
Решить уравнение ![]()
Характеристическое
уравнение: ![]()
![]()
![]() Общее
решение:
Общее
решение: ![]()
Задания для самостоятельной работы:
|
I вариант: |
I I вариант: |
I I I вариант: |
|
Решите уравнения 2го порядка |
||
|
а)
б)
|
а)
б)
|
а)
б)
|
Критерии оценивания
Оценка «5» - все задания вычислены верно.
Оценка «4» -все задания вычислены верно, но допущены неточности или несущественные ошибки.
Оценка «3» - все задания вычислены, но допущены существенные ошибки и неточности.
Оценка «2» - задания не вычислены.
8.Форма отчета: выполнение заданий в тетрадях для практических занятий.
9. Место проведения самоподготовки: читальный зал библиотеки.
Практическое занятие 8
1. Название темы Действия с матрицами
2. Учебная цель: Используя теоретический материал и образцы решения задач, решить примеры по теме «Действия с матрицами»
3. Продолжительность занятия: 2 часа.
4.Материалы, оборудование, ТСО, программное обеспечение, оснащение, раздаточный материал ПК, проектор, сборник задач, карточки с алгоритмом решения задач
5. Литература, информационное обеспечение Элементы высшей математики Гончаренко В.М. и др.
6.Методические рекомендации по выполнению работы: изучите краткие теоретические и учебно-методические материалы по теме практического занятия. При выполнении работы соблюдайте последовательность действий.
7.Порядок выполнения работы:
Краткие теоретические сведения:
Матрицей называется прямоугольная таблица чисел, состоящая из m строк и n столбцов, которую записывают в следующем виде:
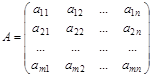 .
.
Для обозначения матрицы используют прописные латинские
буквы, для обозначения элементов матрицы – строчные латинские буквы с указанием
номера строки и столбца, на пересечении которых стоит данный элемент. Запись «
матрица B имеет размер mxn» означает, что речь идет о
матрице, состоящей из m строк и n столбцов. Например, матрица ![]() имеет размер 2x3.
Далее, bij - обозначение элемента, стоящего на пересечении i-й
строки и j-го столбца данной матрицы (в примере b23=5).
имеет размер 2x3.
Далее, bij - обозначение элемента, стоящего на пересечении i-й
строки и j-го столбца данной матрицы (в примере b23=5).
Матрица, у которой число строк совпадает с числом
столбцов, называется квадратной. Элементы a11 , a22 ,…,
ann квадратной матрицы A (размера nxn)
образуют главную диагональ. Квадратная матрица, у которой отличные от
нуля элементы могут стоять только на главной диагонали, называется диагональной.
Диагональная матрица, у которой все элементы (главной диагонали!) равны 1,
называется единичной. Наконец, квадратная матрица, у которой ниже (выше)
главной диагонали находятся только нули, называется верхней (нижней) треугольной
матрицей. Например, среди квадратных матриц размера 3x3 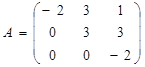 ,
, 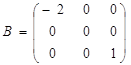 ,
,
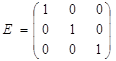 ,
, 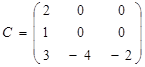 матрица
A является верхней треугольной, B – диагональной, C –
нижней треугольной, E – единичной.
матрица
A является верхней треугольной, B – диагональной, C –
нижней треугольной, E – единичной.
Матрицы A, B называются равными (A=B), если они имеют одинаковый размер, и их элементы, стоящие на одинаковых позициях, совпадают.
Арифметические действия с матрицами.
Чтобы умножить матрицу A на отличное от нуля вещественное число k, необходимо каждый элемент матрицы умножить на это число:
Чтобы найти сумму матриц A, B одной размерности, необходимо сложить элементы с одинаковыми индексами (стоящие на одинаковых местах):
Пример 1. Найти 2A-B, если 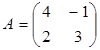 ,
, ![]() .
.
Решение. Сначала умножаем матрицу A на число «2», затем матрицу B на число «-1», и, наконец, находим сумму полученных матриц:
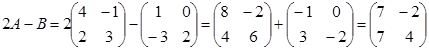
Имеем: 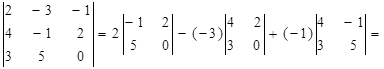 6
6
Произведение AB можно определить только для
матриц A размера mxn и B размера nxp,
при этом AB=C, матрица C имеет размер mxp, и ее
элемент cij находится как скалярное произведение i-й строки
матрицы A на j-й столбец матрицы B: ![]() (i=1,2,…,m; j=1,2,…,p).
Фактически необходимо каждую строку матрицы A (стоящей слева) умножить
скалярно на каждый столбец матрицы B (стоящей справа).
(i=1,2,…,m; j=1,2,…,p).
Фактически необходимо каждую строку матрицы A (стоящей слева) умножить
скалярно на каждый столбец матрицы B (стоящей справа).
Пример 2. Найти произведение матриц 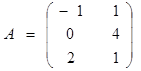 и
и 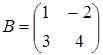 .
.
Решение. 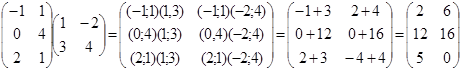 Матрицей,
транспонированной к матрице A размера mxn, называется
матрица AT размера nxm, строки которой являются
столбцами исходной матрицы.
Матрицей,
транспонированной к матрице A размера mxn, называется
матрица AT размера nxm, строки которой являются
столбцами исходной матрицы.
Например, если ![]() ,
то
,
то 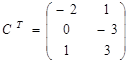 .
.
Пример 3. Найти 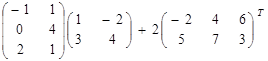 .
.
Решение. Воспользовавшись вычислениями, проведенными при решении примера, а также правилами умножения матрицы на число и сложения матриц, получим:
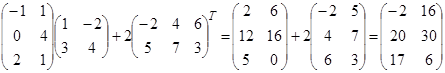 Матрицы A, B
называются эквивалентными, если одна получена из другой путем
элементарных преобразований.
Матрицы A, B
называются эквивалентными, если одна получена из другой путем
элементарных преобразований.
Рангом матрицы A в дальнейшем будем считать число строк эквивалентной ей ступенчатой матрицы, используя обозначение r(A). Так, в рассмотренном выше примере 3.4 r(A)=3, r(B)=2.
Вычисление определителей. Определитель матрицы A размера 2x2 (определитель 2-го порядка) – это число, которое можно найти по правилу:
![]()
(произведение элементов, стоящих на главной диагонали матрицы, минус произведение элементов, стоящих на побочной диагонали).
Определитель матрицы A размера 3x3 (определитель 3-го порядка) – число, вычисляемое по правилу «раскрытие определителя по первой строке»:
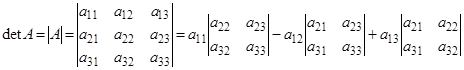 Порядок
проведения работы:
Порядок
проведения работы:
Используя теоретические сведения выполнить предложенный преподавателем вариант задания.
Примеры по теме:
Задание 1. Выполнить арифметические действия с матрицами:
1) ![]() ; 2)
; 2) 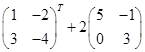 ;
;
3) 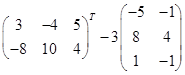 ; 4)
; 4) 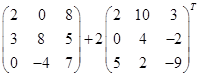 ;
;
5) ![]() ;
;
6)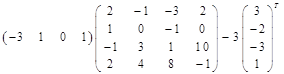 ;
;
7) 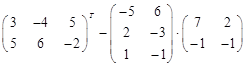
Задание 2. Доказать равенство (AB)C=A(BC) для матриц:
1) ![]() ,
, ![]() ,
, ![]() ;
;
2) 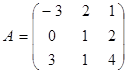 ,
, 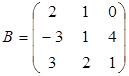 ,
, 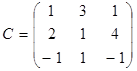 ;
;
3) 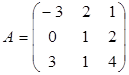 ,
, 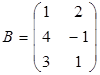 ,
, ![]() ;
;
Задание 3. Найти: 1) 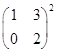 ; 2)
; 2) 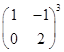 ; 3)
; 3) 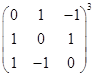 .
.
Задание 4. Вычислить определители:
|
1) |
3) |
|
|
4) |
6) |
Критерии оценивания
Оценка «5» - все задания вычислены верно.
Оценка «4» -все задания вычислены верно, но допущены неточности или несущественные ошибки.
Оценка «3» - все задания вычислены, но допущены существенные ошибки и неточности.
Оценка «2» - задания не вычислены.
8.Форма отчета: выполнение заданий в тетрадях для практических занятий.
9. Место проведения самоподготовки: читальный зал библиотеки.
Практическое занятие 9
1. Название темы Нахождение обратной матрицы
2. Учебная цель: Используя теоретический материал и образцы решения задач, решить примеры по теме «Действия с матрицами»
3. Продолжительность занятия: 2 часа.
4.Материалы, оборудование, ТСО, программное обеспечение, оснащение, раздаточный материал ПК, проектор, сборник задач, карточки с алгоритмом решения задач
5. Литература, информационное обеспечение Элементы высшей математики Гончаренко В.М. и др.
6.Методические рекомендации по выполнению работы: изучите краткие теоретические и учебно-методические материалы по теме практического занятия. При выполнении работы соблюдайте последовательность действий.
7.Порядок выполнения работы:
Краткие теоретические сведения:
Обратная матрица
Квадратная матрица называется вырожденной, если ее определитель равен нулю.
Невырожденной называется квадратная матрица, определитель которой не равен нулю.
Квадратная
матрица ![]() называется обратной к
невырожденной матрице
называется обратной к
невырожденной матрице ![]() если
если![]() , где
, где ![]() - это
единичная матрица соответствующего порядка.
- это
единичная матрица соответствующего порядка.
Свойства обратной матрицы
1.
![]()
2.
![]()
3.
![]()
4.
![]()
Правило:
Если
определитель квадратной матрицы А ![]() , то
обратная матрица существует и равна
, то
обратная матрица существует и равна
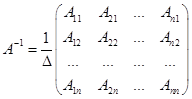
При
условии ![]() обратная
матрица находится по формуле
обратная
матрица находится по формуле
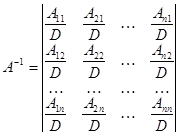
Для нахождения обратной матрицы используют следующую схему:
1. Находят определитель матрицы А;
2. Находят алгебраические дополнения Аij всех элементов матрицы А и записывают новую матрицу;
3. Меняют местами столбцы полученной матрицы (транспонирую матрицу);
4. Умножают
полученную матрицу на ![]()
Примеры
1)
Найти
обратную матрицу к матрице 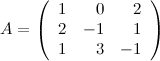
Решение:
Вычисляем определитель матрицы:
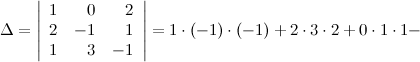
![]()
Так как определитель не равен нулю, то матрица имеет обратную.
Вычислим
алгебраические дополнения к элементам матрицы ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
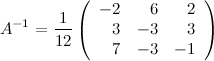
Критерии оценивания
Оценка «5» - все задания вычислены верно.
Оценка «4» -все задания вычислены верно, но допущены неточности или несущественные ошибки.
Оценка «3» - все задания вычислены, но допущены существенные ошибки и неточности.
Оценка «2» - задания не вычислены.
8.Форма отчета: выполнение заданий в тетрадях для практических занятий.
9. Место проведения самоподготовки: читальный зал библиотеки.
Практическое занятие 10
1. Название темы Решение систем линейных уравнений различными методами
2. Учебная цель: Используя теоретический материал и образцы решения задач, решить примеры по теме «Решение систем линейных алгебраических уравнений различными способами»
3. Продолжительность занятия: 2 часа.
4.Материалы, оборудование, ТСО, программное обеспечение, оснащение, раздаточный материал ПК, проектор, сборник задач, карточки с алгоритмом решения задач
5. Литература, информационное обеспечение Элементы высшей математики Гончаренко В.М. и др.
6.Методические рекомендации по выполнению работы: изучите краткие теоретические и учебно-методические материалы по теме практического занятия. При выполнении работы соблюдайте последовательность действий.
7.Порядок выполнения работы:
Краткие теоретические сведения
1.Пусть дана система линейных уравнений
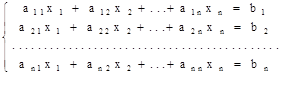 (1)
(1)
Коэффициенты a11,12,..., a1n, ... , an1 , b2 , ... , bn считаются заданными.
Вектор -строка íx1 , x2 , ... , xn ý - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D=çAê=ça ij ç, составленный из коэффициентов при неизвестных, называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи:
a) Если D¹, то
система (1) имеет единственное решение, которое может быть найдено по формулам
Крамера : x1=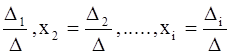 ,
где
,
где
определитель n-го порядка Di ( i=1,2,...,n) получается из определителя системы путем замены i-го столбца свободными членами b1 , b2 ,..., bn.
б) Если D= , то система (1) либо имеет бесконечное множество решений, либо несовместна ,т.е. решений нет.
2. Рекомендации по выполнению заданий
1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
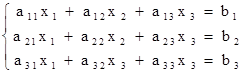 (2).
(2).
1. В данной системе составим определитель 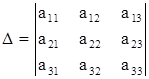 и вычислим.
и вычислим.
2. Составить и вычислить следующие определители:
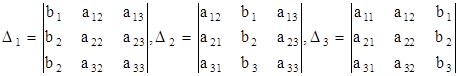 3. Воспользоваться
формулами Крамера.
3. Воспользоваться
формулами Крамера.
![]()
Практическое значение правила Крамера для решения системы n линейных уравнений с п неизвестными невелико, так как при его применении приходится вычислять п +1 определителей n-го порядка: D, Dx1, Dx2, …,Dxn. Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных.
Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных.
Дана система, содержащая m линейных уравнений с п неизвестными:
![]() а11х1
+ а12х2 + …+ а1nхn
= b1;
а11х1
+ а12х2 + …+ а1nхn
= b1;
а21х1 + а22х2 + …+ а2nхn = b2;
……………………………………
аm1х1 + аm2х2 + …+ аmnхn = bm
Метод Гаусса решения системы заключается в последовательном исключении переменных.
Алгоритм для решения системы линейных уравнений методом Гаусса
Выражаем первое неизвестное из первого уравнения и подставляем его в остальные уравнения.
Получаем новую систему, в которой число уравнений и неизвестных на 1 меньше.
С новой системой поступаем таким же образом и так продолжаем до тех пор, пока не останется одно линейное уравнение, которое легко решается.
Когда получено значение последнего неизвестного xn, подставляем его в уравнение, которое позволяет найти xn – 1 по xn.
По найденным xn – 1 и xn находим xn – 2 и таким образом находим последовательно все неизвестные.
Для систем нелинейных уравнений этот метод не всегда применим уже в силу того, что из уравнений системы совсем не обязательно можно будет выразить одну неизвестную через остальные.
Порядок выполнения работы:
Используя теоретические сведения выполнить предложенное преподавателем задание
Примеры по теме:
Решение систем линейных уравнений методом Крамера
Решить системы:
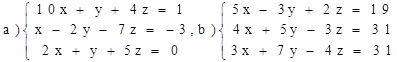
Примеры по теме:
Решение систем линейных уравнений методом Гаусса
Решить системы:
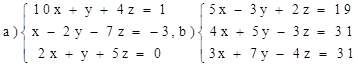
Критерии оценивания
Оценка «5» - все задания вычислены верно.
Оценка «4» -все задания вычислены верно, но допущены неточности или несущественные ошибки.
Оценка «3» - все задания вычислены, но допущены существенные ошибки и неточности.
Оценка «2» - задания не вычислены.
8.Форма отчета: выполнение заданий в тетрадях для практических занятий.
9. Место проведения самоподготовки: читальный зал библиотеки.
Практическое занятие 11
1. Название темы Прямоугольные координаты на плоскости
2. Учебная цель: формирование умения определять координаты точек в прямоугольной системе координат.
3. Продолжительность занятия: 2 часа.
4.Материалы, оборудование, ТСО, программное обеспечение, оснащение, раздаточный материал ПК, проектор, сборник задач, карточки с алгоритмом решения задач
5. Литература, информационное обеспечение Элементы высшей математики Гончаренко В.М. и др.
6.Методические рекомендации по выполнению работы: изучите краткие теоретические и учебно-методические материалы по теме практического занятия. При выполнении работы соблюдайте последовательность действий.
7.Порядок выполнения работы:
1. Повторить теоретический материал по теме практической работы.
2. Оформить решение заданий в тетради.
Краткая теория.
Ели на плоскости задана прямоугольная декартова система
координат xOy, то точку М этой плоскости, имеющую
координаты x и y, обозначают
М (x; y).
Расстояние d между точками М1(x1;y1) и М2(x2;y2) определяется по формуле:
|
|
(1) |
В частности, расстояние d точки М(x;y) от начала координат определяется по формуле:
|
|
(2) |
Координаты точки М(x;y), делящей в заданном отношении ë отрезок между двумя точками А(x1;y1) и В(x2;y2), определяется по формулам:
|
x=(x1+ëx2) /(1+ë) y=(y1+ëy2)/(1+ë) |
(3) |
В частности, при ë=1 получаем формулы для координат середины отрезка:
|
х=(х1+x2)/2 y=(y1+y2)/2 |
(4) |
ПРЯМАЯ НА ПЛОСКОСТИ
Общее уравнение прямой
Всякое уравнение первой степени, относительно х и у, т.е. уравнение вида:
|
Ах+Ву+С=0 |
(5) |
где А, В и С постоянные коэффициенты, причем А2+В2≠0, определяет на плоскости некоторую прямую.
Геометрическое место точек плоскости, координаты которых удовлетворяют уравнению Ах+Ву+С=0, называется прямой на плоскости.
Уравнение Ах+Ву+С=0 называется общим уравнением прямой.
Частные случаи:
1. С=0; А≠0, В≠0.
Прямая, определяемая уравнением Ах+Ву=0, проходит через начало координат.
2. А=0; В≠0, С≠0.
Прямая, определяемая уравнением Ву+С=0, параллельна оси Ох.
3. В=0, А≠0, С≠0.
Прямая, определяемая уравнением Ах+С=0, параллельна оси Oу.
4. В=С=0; А≠0.
Прямая, определяемая уравнением Ах=0, совпадает с осью Оу.
5. А=С=0; В≠0.
Прямая, определяемая уравнением Ву=0, совпадает с осью Ох.
Критерии оценивания
Оценка «5» - все задания вычислены верно.
Оценка «4» -все задания вычислены верно, но допущены неточности или несущественные ошибки.
Оценка «3» - все задания вычислены, но допущены существенные ошибки и неточности.
Оценка «2» - задания не вычислены.
8.Форма отчета: выполнение заданий в тетрадях для практических занятий.
9. Место проведения самоподготовки: читальный зал библиотеки.
Практическое занятие 12
1. Название темы Решение простейших задач аналитической геометрии на плоскости
2. Учебная цель: сформировать навык решения простейших задач аналитической геометрии на плоскости
3. Продолжительность занятия: 2 часа.
4.Материалы, оборудование, ТСО, программное обеспечение, оснащение, раздаточный материал ПК, проектор, сборник задач, карточки с алгоритмом решения задач
5. Литература, информационное обеспечение Элементы высшей математики Гончаренко В.М. и др.
6.Методические рекомендации по выполнению работы: изучите краткие теоретические и учебно-методические материалы по теме практического занятия. При выполнении работы соблюдайте последовательность действий.
7.Порядок выполнения работы:
1. Повторить теоретический материал по теме практической работе.
2. Оформить доказательство тождеств и упрощение выражений в тетради.
Теоретический материал
Аналитическая
геометрия – это раздел в геометрии, в котором
геометрические фигуры и их свойства исследуются средствами алгебры.
В
основе решения задач данного раздела геометрии лежит метод координат. Согласно
методу координат каждому геометрическому соотношению ставится в соответствие
некоторое уравнение, которое связывает координаты фигуры или тела.
Основателем
аналитической геометрии полноправно считается Декарт, который в 1637 году
серьезно взялся за развитие данного направления в математике. Среди ученых,
внесших свой вклад в развитие аналитической геометрии, можно выделить Ньютона,
Лейбница и др.
Все, что изучается в аналитической геометрии, можно разделить на два основных раздела:
· аналитическая геометрия на плоскости, изучающая такие элементы как преобразование координат, прямая, эллипс, окружность, парабола и гипербола;
· аналитическая геометрия в пространстве, изучающая плоскость, сферу, прямую.
При
решении задач по аналитической геометрии в первую очередь используются
различные действия над векторами, которые заданы в координатной форме.
Приведем примеры часто используемых формул:
·
расстояние
между двумя точками:
![]()
·
угол
между векторами:
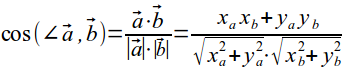
·
деление
отрезка в отношении λ:
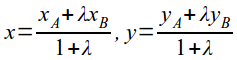
Понятие
«уравнение линии» это элемент дальнейшего развития метода координат. Через
любые две точки на плоскости можно провести прямую. Таким образом, если точка
на плоскости определяется двумя числами (т.е. координатами точки), то линия на
плоскости определяется уравнением, которое связывает координаты любой точки
линии.
Приведем примеры некоторых уравнений:
·
общее
уравнение прямой на плоскости:
![]()
·
Уравнение
окружности радиуса r с центром в точке (x0, y0):
![]()
· и многие другие.
Если
же мы имеем дело с пространством, то там все аналогично плоскости, за
исключением того, что координат используется не две, а три.
Приведем примеры уравнений и формул, используемых в пространственной аналитической геометрии:
·
уравнение
сферы:
![]()
·
расстояние
между двумя точками:
![]()
· и т.д.
Рассмотрим несколько задач из курса аналитической геометрии.
Пример
1. Составить уравнение линии, каждая точка которой
равноудалена от прямой
x = -1 и точки E(2;2).
Решение:
Этап 1. В условии
задачи точка E(2;2) определяется двумя координатами x =
2 и y = 2, следовательно, имеем «плоскую» задачу.
Этап 2. По условию задачи, можно выделить три различных фигуры – линия, точка, прямая.
Этап
3. Выполним схематический чертеж:
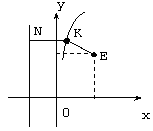
Этап 4.
1. Рассмотрим произвольную точку линии — K(x, y). Расстояние от точки K до прямой x = -1 есть длина перпендикуляра KN, который опущен из точки K на прямую x = -1. Далее определим координаты точки N. Абсцисса точки N равна -1, а ордината точки N равна ординате точки K, т.е. N(-1, y) — координаты точки.
2. По условию задачи
имеем ρ(K, N) = ρ(K, E). Тогда
для любой точки K(x, y), которая принадлежит
искомой линии, справедливо равенство:
![]()
или
![]()
3. Упростим
полученное уравнение:
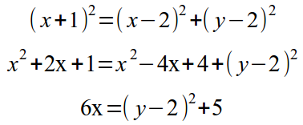
4. Искомое уравнение
линии:
![]()
Ответ: 6x = (y — 2)2 + 5.
Пример
2. Найти расстояние от точки M(1, 1, 1)
до плоскости α: 5x + y — z +
1 = 0.
Решение:
Этап 1. В условии
задачи точка M(1, 1, 1) определяется системой трех координат (x, y, z),
следовательно, имеем пространственную задачу.
Этап 2. По условию задачи, можно выделить две различных фигуры – точка и плоскость.
Этап
3. Выполним схематический чертеж:
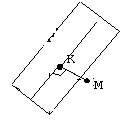
Этап 4.
1. Расстояние от точки M(1, 1, 1) до плоскости α есть длина перпендикуляра KN, опущенного из точки M на эту плоскость.
2. Расстояние от
точки до плоскости определяется по формуле:
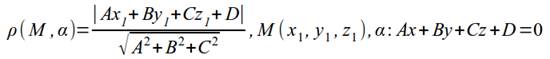
3. 3. Вычислим
искомое расстояние:
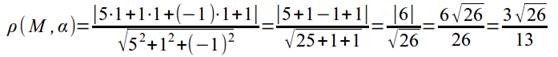
Ответ: ![]() .
.
Критерии оценивания
Оценка «5» - все задачи решены верно.
Оценка «4» -все задачи решены верно, но допущены неточности или несущественные ошибки.
Оценка «3» - все задачи решены, но допущены существенные ошибки и неточности.
Оценка «2» - задачи не решены.
8.Форма отчета: выполнение заданий в тетрадях для практических занятий.
9. Место проведения самоподготовки: читальный зал библиотеки.
.
Контрольная работа №1
1. Название темы Интеграл
2. Учебная цель: проверить усвоение изученного материала
3. Продолжительность занятия: 2 часа.
4.Материалы, оборудование, ТСО, программное обеспечение, оснащение, раздаточный материал ПК, проектор, сборник задач, карточки с алгоритмом решения задач
5. Литература, информационное обеспечение Элементы высшей математики Гончаренко В.М. и др.
6.Методические рекомендации по выполнению работы: изучите краткие теоретические и учебно-методические материалы по теме практического занятия. При выполнении работы соблюдайте последовательность действий.
7.Порядок выполнения работы:
Теоретические сведения
Первообразная функции. Неопределенный интеграл
Функция ![]() , определенная на
интервале
, определенная на
интервале ![]() ,
называется первообразной для функции
,
называется первообразной для функции ![]() , определенной на том же
интервале
, определенной на том же
интервале ![]() ,
если
,
если ![]()
Если ![]() — первообразная для
функции
— первообразная для
функции ![]() , то любая другая
первообразная
, то любая другая
первообразная ![]() для
функции
для
функции ![]() отличается от
отличается от ![]() на некоторое постоянное
слагаемое, т. е.
на некоторое постоянное
слагаемое, т. е. ![]() где
где
![]() .
.
Неопределенным интегралом
от
функции ![]() называется совокупность
всех первообразных для этой функции. Обозначается неопределенный интеграл:
называется совокупность
всех первообразных для этой функции. Обозначается неопределенный интеграл: ![]() где
где ![]()
Операция нахождений первообразной для данной функции называется интегрированием. Интегрирование является обратной операцией к дифференцированию:
![]()
Для проверки правильности выполненного интегрирования необходимо продифференцировать результат интегрирования и сравнить полученную функцию с подынтегральной.
Свойства неопределенного интеграла:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Таблица основных интегралов
1. ![]() 2.
2.
![]()
3. 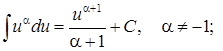
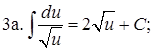
4. ![]() 5.
5.
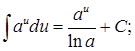
6. ![]() 7.
7.![]()
8. ![]() 9.
9.
![]()
10. ![]() 11.
11.
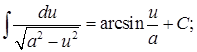
12. 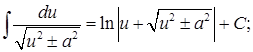 13.
13. ![]()
14. 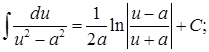 15.
15. 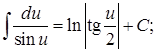
16. 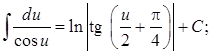 17.
17. ![]()
18. ![]()
Каждая из приведенных в таблице формул справедлива на промежутке, не содержащем точек разрыва подынтегральной функции. Вычисление интегралов с использованием таблицы и основных свойств называют непосредственным интегрированием.
Метод замены переменной
Теорема 1. Пусть ![]() монотонная, непрерывно
дифференцируемая функция, тогда
монотонная, непрерывно
дифференцируемая функция, тогда
![]() (1)
(1)
При этом, если ![]() то
то ![]() где
где ![]() —
функция, обратная
—
функция, обратная ![]() .
.
Формула (1) называется формулой замены переменной в неопределенном интеграле.
Алгоритм замены переменной:
1) Связать старую переменную
интегрирования ![]() с новой
переменной
с новой
переменной ![]() с помощью замены
с помощью замены ![]() .
.
2) Найти связь между дифференциалами ![]() .
.
3) Перейти под знаком интеграла к новой переменной.
4) Проинтегрировать и в полученной
первообразной вернуться к старой переменной, подставив ![]()
Пример1. Проинтегрировать подходящей заменой переменной.
![]()
![]()
![]()
Решение:
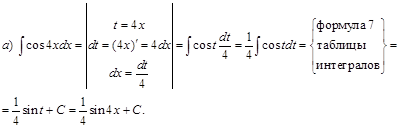
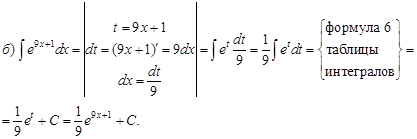
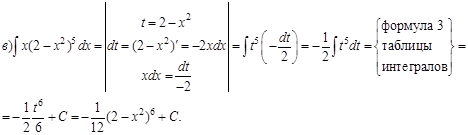
Интегрирование по
частям
Некоторые виды интегралов, вычисляемых по частям
Если производные функций ![]() и
и ![]() непрерывны,
то справедлива формула:
непрерывны,
то справедлива формула:
![]()
![]() (3)
(3)
называемая формулой интегрирования по частям.
В качестве ![]() обычно
выбирают функцию, которая упрощается при дифференцировании.
обычно
выбирают функцию, которая упрощается при дифференцировании.
Некоторые стандартные случаи функций,
интегрируемых по частям, указаны в таблице 1. Там же дается способ выбора
множителей ![]() и
и ![]() .
.
Таблица 1
|
Вид интеграла |
|
|
|
|
|
|
|
Вид интеграла |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
![]() — многочлен от
— многочлен от ![]() степени
степени ![]() , т. е.
, т. е. ![]() , где
, где ![]() .
.
Пример 2. Проинтегрировать по частям.
![]()
![]()
Решение.
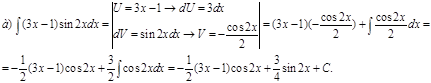
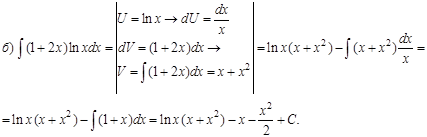
Задания для самостоятельной работы.
Задание 1. Проинтегрировать функции заменой переменной:
Вариант 1. ![]()
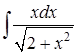
![]()
Вариант 2. ![]()
![]()
![]()
Вариант 3. ![]()
![]()
![]()
Задание 2. Найти интеграл интегрированием по частям:
Вариант 1. ![]()
![]()
Вариант 2. ![]()
![]()
Вариант3. ![]()
![]()
8.Форма отчета: выполнение заданий в тетрадях для практических занятий.
9. Место проведения самоподготовки: читальный зал библиотеки.
Контрольная работа № 2
1. Название темы Действия над векторами
2. Учебная цель: проверить усвоение материала по теме «Действия над векторами »
3. Продолжительность занятия: 2 часа.
4.Материалы, оборудование, ТСО, программное обеспечение, оснащение, раздаточный материал ПК, проектор, сборник задач, карточки с алгоритмом решения задач
5. Литература, информационное обеспечение Элементы высшей математики Гончаренко В.М. и др.
6.Методические рекомендации по выполнению работы: изучите краткие теоретические и учебно-методические материалы по теме практического занятия. При выполнении работы соблюдайте последовательность действий.
7. Порядок выполнения работы
Теоретические сведения
1 Вектором
называется отрезок, у которого указано, какой из концов является началом, а
какой – концом (направленный отрезок), обозначается ![]() ,
, ![]() , где
, где ![]() - начало вектора,
- начало вектора, ![]() - конец.
- конец.
2 Векторы называются коллинеарными, если они расположены на одной или параллельных прямых.
3 Векторы называются
ортогональными, если угол между ними ![]() .
.
4 Векторы можно
складывать ( по правилам треугольника и параллелограмма), можно умножать на
число: ![]()
![]()
![]() ;
; ![]() .
.
5 Необходимое и
достаточное условие коллинеарности векторов: 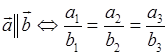
6 Модуль
вектора ![]() равен
равен ![]()
7 Если заданы начало ![]() и конец
и конец ![]() вектора
вектора ![]() , то его координаты и
длина находятся следующим образом:
, то его координаты и
длина находятся следующим образом:
![]() ;
; ![]() .
.
8 Скалярным произведением векторов называется число, равное произведению длин этих векторов на косинус угла между ними
![]()
![]()
9 Косинус угла между
векторами 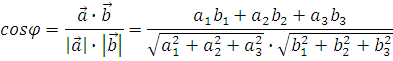
10 Необходимое и
достаточное условие ортогональности векторов: ![]() .
.
11 Проекция вектора на
направление: 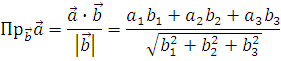
Задание
1
Найти линейную комбинацию векторов ![]()
2
Найти длины векторов ![]()
3
Найти косинусы углов между векторами ![]()
4
Найти ф![]()
5
Найти ![]()
6
Выяснить, коллинеарны ли векторы ![]() и
и ![]()
7
Выяснить, ортогональны ли векторы ![]() и
и ![]()
Исходные данные:
Задание 1
Решение:
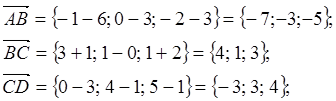
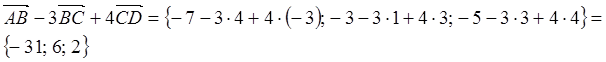
Задание 2
Решение:
![]()
![]()
![]()
Задание 3
Решение:
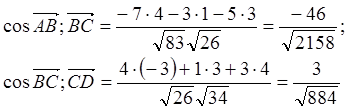
Задание 4
Решение:
Даны точки ![]() .
.
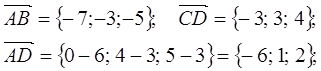
![]()
![]() Даны
точки
Даны
точки ![]()
Задание 5
Решение:
![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
![]() .
.
Задание 6
Решение:
![]() ,
, ![]()
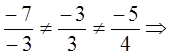 векторы не являются коллинеарными.
векторы не являются коллинеарными.
Задание 7
Решение:
![]() ,
, ![]()
![]() , следовательно, векторы не являются ортогональными.
, следовательно, векторы не являются ортогональными.
Задания к практической работе.
1 A (2; 3; -1); B (0; 1; 2); C (4; -1; -1); D (2; -3; 1)
2 A (3; -1; 1); B (1; 3; 2); C (1; -1; -1); D (4; 0; 3)
3 A (4; 1; 2); B (1; 0; 1); C (-1; 2; -1); D (3; 1; 0)
4 A (3; -2; 1); B (2; -1; 1); C (4; 0; 2); D (1; 1; -1)
5 A (-2; 2; 1); B (3; 0; 4); C (7; 1; 0); D (3; 0; 5)
6 A (1; -1; -1); B (2; 5; 7); C (-3; 1; -1); D (2; 2; 3)
7 A (-3; 1; 4); B (1; -2; -3); C (2; 2; 3); D (5; 3; 1)
8 A (2; -5; 1); B (4; 3; 5); C (-1; 0; 1); D (2; 1; 0)
9 A (-2; 2; 1); B (3; -1; 0); C (4; 4; 0); D (1; -1; 1)
10 A (4; 2; 5); B (0; 1; 3); C (-1; -1; 1); D (2; -2; 1)
11 A (1; 0; 1); B (7; 4; 3); C (3; -5; 1); D (-2; 2; 2)
12 A (5; 1; 0); B (-1; -1; -1); C (2; 4; 7); D (1; 0; 1)
13 A (10; 1; 1); B (-2; -1; 1); C (4; 3; 2); D (1; 0; -1)
14 A (2; -7; 4); B (2; -1; 3); C (1; 0; -1); D (2; 1; 3)
15 A (6; 3; 3); B (-1; 0; -2); C (3; 1; 1); D (0; 4; 5)
16 A (3; 2; 0); B (2; -1; 7); C (4; 0; 5); D (1; -2; -1)
17 A (4; -1; 2); B (1; 0; 3); C (-2; 1; 5); D (3; 8; -1)
18 A (1; 1; -3); B (-7; 5; 2); C (2; 1; 0); D (3; -3; 1)
19 A (5; 0; 1); B (2; -1; -1); C (-6; -1; 1); D (3; 1; 3)
20 A (3; 5; 1); B (7; -4; 3); C (2; 1; 1); D (0; -1; 3)
21 A (1; -2; 1); B (-1; 8; -3); C (3; 2; 1); D (5; 3; 1)
22 A (-3; -1; 1); B (2; -3; 0); C (1; 4; 5); D (2; 3; 4)
23 A (3; -1; 2); B (4; 0; 4); C (-1; 9; -1); D (3; -2; -2)
24 A (3; -2; 1); B (4; 2; 1); C (-1; -1; 1); D (3; 0; 1)
25 A (-2; 0; 1); B (4; -1; 3); C (-3; 2; 1); D (4; 1; 1)
26 A (2; -2; 1); B (2; 5; 7); C (1; 3; 5); D (7; 0; 3)
27 A (2; 3; 3); B (-2; 4; 1); C (3; 5; 2); D (3; 8; -1)
28 A (1; 1; -3); B (-3; 2; -1); C (4; 1; 2); D (7; -3; 0)
29 A (7; 6; 1); B (2; -1; -1); C (1; 0; 1); D (-2; 1; -1)
30 A (-7; 2; -1); B (2; 5; 1); C (2; 1; 1); D (0; 1; 3)
Критерии оценивания
Оценка «5» - все задания вычислены верно.
Оценка «4» -все задания вычислены верно, но допущены неточности или несущественные ошибки.
Оценка «3» - все задания вычислены, но допущены существенные ошибки и неточности.
Оценка «2» - задания не вычислены.
8.Форма отчета: выполнение заданий в тетрадях для практических занятий.
9. Место проведения самоподготовки: читальный зал библиотеки.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.