Методические рекомендации по использованию текстовых задач спортивной направленности в курсе математики

Государственное образовательное учреждение

среднего профессионального образования

Луганской Народной Республики

«Луганское высшее училище физической культуры»

Методические рекомендации

по использованию текстовых задач

спортивной направленности

в курсе математики  

2019 г.

Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи решайте их Д. Пойа.

В психологии, дидактике известны попытки дать определение задачи. Например, одно из них: “Задача – объект мыслительной деятельности, содержащий требование некоторого практического преобразования или ответа на теоретический вопрос посредством поиска условий, позволяющих раскрыть связи (отношения) между известными и неизвестными элементами” (Гурова Л.Л. Психологический анализ задач. – Воронеж, 1976..) 

В традиционном  школьном обучении математике текстовые задачи всегда занимали особое место. Они являются важным средством обучения математике. С их помощью учащиеся получают опыт работы с величинами, постигают взаимосвязи между ними, получают опыт применения математики к решению практических задач. Решение задач является наиболее эффективной формой развития математической деятельности.

При обучении математике задачи имеют образовательное, развивающее, воспитательное значение.

Они развивают логическое и алгоритмическое мышление учащихся, вырабатывают практические навыки применения математики. При обучении теоретическим знаниям задачи способствуют мотивации введения понятий, выявлению их существенных свойств, усвоению математической символики и терминологии, раскрывают взаимосвязи одного понятия с другими.

Воспитательное воздействие оказывает общий подход к решению задач: система задач, место, методы и формы ее решения, стиль общения учителя и учащихся, учащихся между собой при решении задач. Решение задач позволяет учащимся воспитывать в себе настойчивость, трудолюбие, активность, самостоятельность, формирует познавательный интерес, помогает вырабатывать и отстаивать свою точку зрения.

Развивающие функции задач заключаются в том, что в деятельности решения задач вырабатываются умения применять теоретические знания на практике, выделять общие способы решения, переносить их на новые задачи, развиваются логическое и творческое мышление, внимание, память, воображение.

Использование исторических задач и разнообразных старинных (арифметических) способов их решения не только обогащает опыт мыслительной деятельности учащихся, но и позволяет им осваивать важный культурно-исторический пласт истории человечества, связанный с поиском решения задач. Это важный внутренний (связанный с предметом), а не внешний (связанный с отметками, поощрениями и т.п.) стимул к поиску решений задач и изучению математики.

С изменением роли и места задач в обучении обновляются и видоизменяются и сами задачи. Раньше они формулировались с помощью слов “найти”, “построить”, “вычислить”, “доказать”, в современной школе чаще используются слова “обосновать”, “выбрать из различных способов решения наиболее рациональный”, “исследовать”, “спрогнозировать различные способы решения” и т.д.

Текстовые задачи подразделяются следующим образом:

·                     задачи на движение;

·                     задачи на работу;

·                     задачи на проценты;

·                     задачи на смеси, сплавы и концентрацию;

·                     задачи, в которых неизвестные – целые числа;

·                     задачи, для решения которых нужно находить наибольшее или наименьшее значение;

·                     задачи, решение которых требует рассмотрения нескольких вариантов;

·                     задачи, процесс решения которых приводит к системе уравнений, содержащей уравнений меньше, чем неизвестных;

·                     задачи, для решения которых необходимо использовать неравенства.

Учитывая специфику нашего учебного заведения, целесообразно акцентировать внимание на текстовых задачах спортивного содержания. Надо сказать, что в учебниках они встречаются в соответствующих разделах, однако в недостаточном количестве. Поэтому у педагога есть поле творческой деятельности в этом направлении. Предлагаю подборку задач спортивной направленности. Эти задачи учитель может использовать на различных этапах урока при изучении соответствующей темы в определённом классе или во время итогового повторения при подготовке к  ГИА или ЕГЭ:

 Задача 1

 Более 1000 лет назад были проведены первые Олимпийские игры. Их устраивали жители Греции. Празднования и состязания продолжались в течении 5 дней. Сколько дней потратили греки на состязания за 186 лет? 5х186=930(дней)

 Задача 2

 Согласно легенде, длину беговой дорожки определил знаменитый Геракл. Он отмерил 600 ступней в длину и получилась беговая дорожка длиной около 192 м. Какой длины получилась дорожка, когда он отмерил 216 таких ступней?.

Ответ : 69 м 12 см длина дорожки. 

Задача 3

 Бегун пробежал от дома до дачи за 4 ч, пробегая со скоростью 9 км/ч. С какой скоростью он должен бежать обратно, чтобы успеть за 3 ч?

Ответ: 12 км/ч. 

 Задача 4

В школе 180 человек занимаются гимнастикой. Спортивной гимнастикой занимаются две пятых учащихся, а остальные художественной. Сколько человек  занимаются художественной гимнастикой?

Ответ: 108 человек.

 Задача 5

 Высота футбольных ворот 2м40см, она в 2 раза больше высоты хоккейных ворот. Узнай высоту хоккейных ворот.

Ответ: 1м20см высота хоккейных ворот. 

Задача 6

Во сколько раз площадь мишени для стрельбы из положения лежа меньше мишени для ведения огня стоя, если в настоящее время размер (диаметр) мишеней биатлона составляет 45 мм для стрельбы из положения лежа и 117 мм для ведения огня стоя.

Ответ: 6,76

 Задача 7

Спортсмен пробежал дистанцию 5000 м за 7,5 мин. Какой результат покажет этот спортсмен на дистанции 1500 м, если будет бежать с той же скоростью.

 Ответ: 2,25 мин 

 Задача 8

 В список сборной команды  по фигурному катанию на сезон 2012/13 попало 120 фигуристов. 40% сборной составляют «взрослые участники», а остальные – юниоры и резервный состав, причем юниоров в 1,4 раза больше, чем запасных спортсменов. Сколько спортсменов каждой категории в сборной команде?

 Ответ: 48 «взрослых участников», 42 юниоров, 30 резервный состав 

Задача 9

 Длина санно-бобслейной трассы в Сочи составляет 1814 метров. Российская саночница за первую треть своего времени проезжает 45%, за вторую треть – 30% трассы. Сколько километров проезжает спортсменка за последнюю треть времени?

 Ответ: 453,5 метров 

Задача 10

 Трасса для скоростного спуска проходит по естественному рельефу склона и содержит в себе серии поворотов через направляющие ворота. Количество ворот для мужчин 62, что составляет 8 % от перепада высот в метрах. Найдите перепад высот на данной трассе.

 Ответ: 775 м 

Задача 11

 Найдите длину прыжка прыгуна с трамплина, если скорость спортсмена в безветренную погоду составляет 90 км/ч, скорость попутного ветра 3,5 м/с. Время полета спортсмена - 40 с.

Ответ: 1140 метров 

Задача 12

 Максимальная длина лыж для лыжного двоеборья может достигать 120% от роста спортсмена. Крепления должны быть установлены параллельно направлению движения и размещены таким образом, чтобы 57% от длины лыжи были ее передней частью. На каком расстоянии находятся крепления лыж, если лыжник имеет рост 1, 8 м.

Ответ: 1,23 м 

Задача 13

 Олимпийский фристайл включает могул и лыжную акробатику. Лыжная акробатика – серия различных сложных прыжков и сальто. Нарисуем на координатной плоскости элемент фристайла, для этого последовательно соединить точки отрезками.  1.(-2; -2)   2.(-1; -2)   3.( 4; 1)   4.( 5; 3)   5.( 4; 5)        6.( 2; 6)   7.( 0; 6)   8.(-2; 5)   9.(-3; 3)   10.(-2; 1)   11.( 3; -2)   12.( 6; -2) 

Задача 14

 В период Олимпийских игр на стадионе  олимпийского объекта Экстрим парк «Роза Хутор» в Сочи прошли соревнования по сноуборду. Протяженность трассы для параллельного гигантского слалома – 689 м. Определите, кто из спортсменов выиграет заезд и с каким преимуществом, если скорость одного сноубордиста 90 км/ч, а скорость второго составляет 0,8 скорости первого.

 Ответ: выиграет первый сноубордист с преимуществом 6,89 с 

Задача 15

 За 10 лет своего существования сборная России по хоккею на чемпионатах мира, на европейских хоккейных турнирах и олимпийских играх завоевала  24 медали разного достоинства. Из них серебряных медалей на одну меньше, чем золотых и на одну больше, чем бронзовых. Сколько медалей у сборной каждого достоинства? 

Задача 16 

Зимние Олимпийские игры 2014 -  международное спортивное мероприятие, которое проходило с 7 по 23 февраля 2014 года в российском городе Сочи. Расстояние от Москвы до Сочи 1648 км. Каким должен быть масштаб карты, чтобы это расстояние имело длину 8 см.

 Задача 17

  Футбольный мяч 5 размера, который используется во всех официальных соревнованиях, которые проводятся под эгидой ФИФА  во всём мире, имеет длину окружности 68см. Баскетбольный мяч 7 размера, который используется для мужских соревнований по баскетболу, имеет диаметр около 25 см. Найдите отношение объёмов воздуха, содержащегося в баскетбольном и футбольном мячах.  Определите длину окружности баскетбольного мяча.

Ответ: 1,6; 78,5 см

Задача 18

Основная часть легкоатлетического бегового барабана имеет форму цилиндра. Диаметр круга – 50см, высота цилиндра – 60см.  Найти объем цилиндра. Найти площадь поверхности цилиндра.

Ответ: 0,12 м ³ . 1,3 м²

Задача 19

Щиты для баскетбола изготавливаются из дерева или монолитного стекла толщиной в 3 см. Размеры - 1,8 на 1,1 метра. Размечены по центру прямоугольником со сторонами: по горизонтали - 59 см, по вертикали - 45 см.

Найдите отношение объёма стекла, которое потрачено на изготовление щита, и объёма центрального прямоугольного параллелепипеда;  отношение периметров прямоугольников;  отношение площадей прямоугольников.

Ответ: 7,5; 2,8; 7,5

Задача 20

 Стандартный размер баскетбольного кольца имеет диаметр 45 см.

Определите длину окружности баскетбольного кольца.

Ответ: 141,3 см

Схема этапов решения текстовых задач

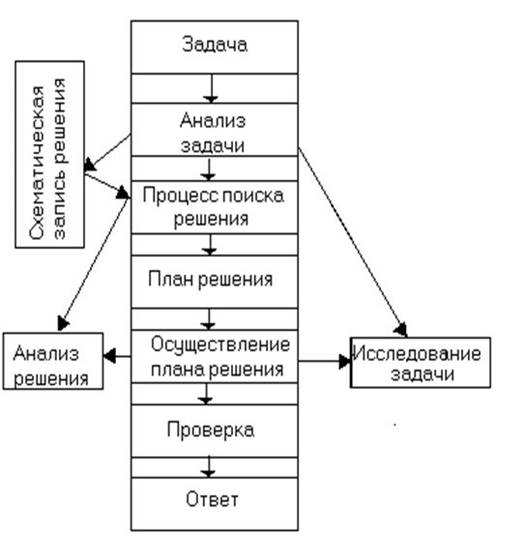
Решение текстовых задач развивает способность искать правильный путь в запутанных условиях. Хотя  изучение математики требует большого и упорного труда,  но оно приносит  много пользы в преодолении трудностей. Использование задач спортивного содержания обогащают опыт мыслительной деятельности учащихся, позволяют воспитывать логическую культуру, могут способствовать созданию благоприятного эмоционального фона обучения, развитию у школьников эстетического чувства применительно к решению задачи и изучению математики, вызывая интерес сначала к процессу поиска решения задачи, а потом и к изучаемому предмету.

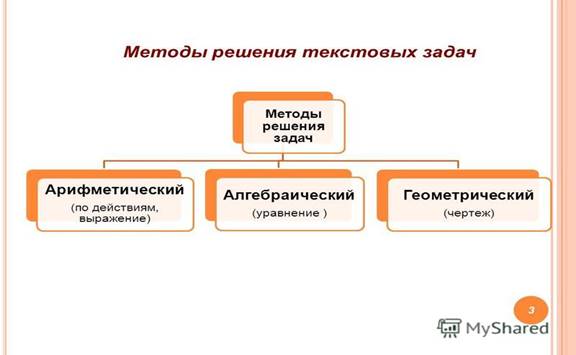
В практике используются разные способы решения задач. Необходимо выработать умения разделять задачи на составные части, использовать различные методы решения, применять приемы, помогающие понять задачу, составить план решения, выполнить его, проверить решение, уметь выполнять каждый из этапов решения. Необходимо учить выявлять связи и зависимости между величинами (данными и искомыми), формировать у учащихся аналитико- синтетическую деятельность. Работу по формированию умения решать текстовые задачи необходимо начинать с рассмотрения методов решения простых задач;  целесообразно рассмотрение решение одной и той же задачи разными методами; в конце обучения необходимо провести систематизацию и обобщение данной темы (рассмотреть классификации задач, как по методам решения, так и по содержанию);  полезно применять такие формы учебной работы как составление текстовых задач, составление взаимно-обратных задач самими учащимися. Творческая работа, направленная на составление задачи и ее решения, приводит к более осознанному пониманию зависимости между величинами, дает осознание, что числа берутся непроизвольно: некоторые задаются, а другие получаются на основе выбранных. Использование алгоритмов, таблиц, рисунков, схем, общих приемов дает возможность ликвидировать у большей части учащихся страх перед текстовой задачей, научить распознавать типы задач и правильно выбирать приемы решения. Табличная форма записи условия и требования текстовых задач -  эффектное средство обучения учащихся решению текстовых задач алгебраическим способом. Для сложных задач нужно использовать и другие, более «гибкие» модели поиска решения текстовых задач. При решении простых задач необходимо выявить и отработать общую схему решения. Это облегчит решение более сложных задач. Необходимо формировать у учащихся приемы самоконтроля при решении текстовых задач. Для формирования положительной мотивации, познавательного интереса у учащихся широко использовать внутрипредметные и межпредметные связи. Если руководствоваться данными методическими рекомендациями, то можно повысить эффективность обучения решению текстовых задач.