МИНИСТЕРСТВО ОБРАЗОВАНИЯ

И НАУКИ АЛТАЙСКОГО КРАЯ

КГБПОУ «АЛТАЙСКИЙ ТРАНСПОРТНЫЙ ТЕХНИКУМ» РЕСУРСНЫЙ ЦЕНТР ПО ТРАНСПОРТУ

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ  

по организации, планированию и подготовке

внеаудиторной самостоятельной работы  по учебной дисциплине «Математика»

Составитель:   Утева Л.П.

с.Первомайское

2022.

В учебно-методических рекомендациях представлены виды аудиторной и внеаудиторной работы. Представлены рекомендации по их реализации. 

Определены критерии оценивания для каждого вида самостоятельной работы. Представлена примерная тематика различных видов самостоятельной работы.

Учебно-методические рекомендации предлагаются для обучающихся и преподавателей. 

Содержание

Введение

1.  Цель и задачи учебной дисциплины

2.  Виды самостоятельной работы по темам

3.  Рекомендации по выполнению различных видов самостоятельной работы

      3.1 Рекомендации по подготовке, написанию, защите и оцениванию реферата как вида самостоятельной работы

          3.2.Рекомендации по подготовке и оцениванию презентации как вида самостоятельной работы

4.Критериями оценивания результатов самостоятельной работы студента

Литература

Приложения

Приложение А

Темы рефератов 

Приложение Б

Темы для создания презентаций

Введение

Эффективная подготовка компетентных работников и специалистов осуществляется благодаря сочетанию теоретического и практического компонентов, связующим звеном между которыми является самостоятельная работа. Самостоятельная работа направлена на систематизацию, закрепление и расширение теоретических знаний и формирование общих и профессиональных компетенций. Её реализация осуществляется на всех этапах обучения, поэтому она может быть как аудиторной так и внеаудиторной. 

Аудиторная самостоятельная работа предполагает выполнение заданий непосредственно во время занятий, а внеаудиторная самостоятельная работа предполагает выполнение заданий преподавателя студентами во внеаудиторное время, но без непосредственного участия преподавателя. 

Разнообразие видов аудиторной и внеаудиторной самостоятельной работы позволяет расширить спектр заданий процесса профессиональной подготовки. 

Аудиторная самостоятельная работа в колледже представлена такими видами как конспектирование учебного материала; работа с учебниками, пособиями, справочной литературой, материалами из Интернета; графическое представление учебного материала в форме технологических или инструктивных карт, графиков, схем. 

Внеаудиторная самостоятельная работа может быть представлена такими видами как работа с учебной и дополнительной литературой, предлагаемой преподавателем, подготовка реферата (доклада, презентации) по дисциплине, выполнение комплексного домашнего задания, подготовка эссе, решение отдельных задач, выполнение графических заданий, подготовка к лабораторнопрактическим работам, подготовка к проведению контрольных мероприятий. 

В учебно-методических рекомендациях раскрываются особенности организации, планирования и подготовки различных видов самостоятельной работы.

1. Цель и задачи учебной дисциплины

Внеаудиторная самостоятельная работа учащихся   – планируемая учебная, учебно-исследовательская,           научно-исследовательская,         проектная     работа, выполняемая за рамками  расписания учебных занятий  по заданию и при методическом руководстве преподавателя, но без его непосредственного участия и является обязательной для каждого студента.

Целью самостоятельной работы студентов является:

•      обеспечение профессиональной подготовки выпускника в соответствии с

ФГОС СПО;

•      формирование и развитие общих компетенций, определённых в ФГОС СПО;

•      формирование и развитие профессиональных компетенций, соответствующих основным видам профессиональной деятельности.  Задачами, реализуемые  в ходе проведения внеаудиторной самостоятельной работы студентов, в образовательной среде техникума являются:

•      систематизация, закрепление, углубление и расширение полученных теоретических знаний и практических умений студентов;

•      развитие познавательных способностей и активности студентов: творческой инициативы, самостоятельности, ответственности и организованности;

•      формирование самостоятельности мышления: способности к саморазвитию, самосовершенствованию и самореализации;

•      овладение практическими навыками применения информационнокоммуникационных технологий в профессиональной деятельности;

•      развитие исследовательских умений.

Самостоятельная работа над учебным материалом состоит из следующих элементов: 

•      Изучение материала по учебнику.

•      Выполнение еженедельных домашних заданий.

•      Выполнение внеаудиторной самостоятельной работы (ВСР).

При выполнении (ВСР)  студент может обращаться к преподавателю для получения консультации.

Контроль результатов самостоятельной работы  студентов осуществляется в время занятий и может проходить в письменной, устной или смешанной форме с предоставлением  продукта творческой деятельности. 

Выполнение ВСР способствует формированию общих компетенций:

ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

ОК 2. Организовывать собственную деятельность, исходя из цели и способов ее достижения, определенных руководителем.

ОК 3. Анализировать рабочую ситуацию, осуществлять текущий и итоговый контроль, оценку и коррекцию собственной деятельности, нести ответственность за результаты своей работы.

ОК 4. Осуществлять поиск информации, необходимой для эффективного выполнения профессиональных задач.

ОК 5. Использовать          информационно-коммуникационные технологии в профессиональной деятельности.

ОК 6. Работать в команде, эффективно общаться с коллегами, руководством, клиентами.

2. Виды самостоятельной работы по темам учебной дисциплины

«Математика»

План внеаудиторной самостоятельной работы:

№п/п	Наименование глав и тем	Количество часов	Вид работы
1 семестр
Раздел 1: Введение. - 2
1	Значение математической науки для решения задач, возникающих в теории и практике	2	Написание эссе
Раздел 2: Развитие понятия о числе. - 4
2	Действительные числа. Комплексные числа	4	Типовые расчёты
Раздел3: Корни, степени, логарифмы.  - 8
3	Решение иррациональных уравнений	4	Решение задач
4	Решение показательных и логарифмических уравнений и неравенств	4	Решение задач
Раздел 4: Прямые и плоскости в пространстве. - 6
5	Расстояние от точки до плоскости . Теорема о трех перпендикулярах	3	Решение задач
6	Взаимное расположение прямых и плоскостей в пространстве	3	Составление кроссворда на тему
Раздел 5: Комбинаторика. -2
7	Задачи комбинаторики	2	Решение задач
Раздел 6: Координаты и векторы. - 4
8	Действия над векторами в координатной  форме	4	Решение задач
Раздел7: Основы тригонометрии.  - 8
9	Тригонометрические формулы	4	Решение задач
10	Тригонометрические уравнения	4	Решение задач
Раздел 8: Функции, их свойства и графики. - 6
11	Построение графиков функции	6	Решение задач
Раздел 9: Многогранники и круглые тела. - 6
12	Выполнение моделей многогранников	6	Изготовление информационных моделей
Раздел 10: Тела  и поверхности вращения. - 2
13	Площадь поверхности и объемы фигур вращения	2	Решение задач
Раздел 11: Начала математического анализа. - 6
14	Применение производной к исследованию функции и построению графиков	6	Решение задач
Раздел 12: Интеграл и его применение. - 4
15	Вычисление площадей плоских фигур	4	Решение задач
Раздел 13: Измерения в геометрии. - 4
16	Геометрия Евклида	4	Сообщения, презентации
Раздел 14: Элементы теории вероятности и математической статистики. - 6
17 Элементы теории 6 Решение задач вероятностей и математической статистики
Раздел 16: Уравнения и неравенства. - 12
18	Решение алгебраических уравнений и неравенств с одной переменной	12
Раздел 17: Обобщающее повторение.
19	Домашняя контрольная работа	6(8)
	Итого часов	143(145)

Виды самостоятельной работы по темам:

•      решение заданий по образцу;

•      опережающие домашние задания;

•      выполнение заданий по алгоритму;

•      типовые расчеты;

•      решение экзаменационных вариантов, в том числе ЕГЭ;

•      составление алгоритмов для типовых заданий;

•      составление и решение самостоятельно составленных заданий;

•      выполнение расчетно-графических работ;

•      составление и заполнение таблиц для систематизации учебного материала;

•      составление теста и эталона к нему;

•      ответы на контрольные вопросы;

•      составление или решение математического кроссворда на математические понятия, определения и т.п.;

•      творческие работы (реферат, доклад);

•      разработка проекта, включающего элементы самостоятельного исследования и направленного на поиск новых методов решения поставленных задач (например, «Математика в моей профессии»).

Раздел 1: Введение

Самостоятельная работа №1 на тему: Значение математической науки для решения задач, возникающих в теории и практике

Цель: расширить кругозор учащихся, познакомить с широтой  и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;

Задание для учащихся.  Написать эссе на заданную тему «Значение математической науки для решения задач, возникающих в теории и практике»

Написание эссе- это вид внеаудиторной самостоятельной работы по написанию сочинения небольшого объёма и свободной композиции на частную тему, трактуемую субъективно и обычно не полно. Обучающийся должен раскрыть не  только суть проблемы, привести различные точки зрения, но и выразить собственные взгляды на неё. При раскрытии темы, необходимо проявить оригинальность подхода к решению проблемы, реалистичность и значимость предложенных идей, яркость , образность, художественную оригинальность изложения.

Этапы подготовки эссе:

1.  Подобрать и изучить источники по теме, содержащуюся в них информацию.

2.  Выбрать главное и второстепенное.

3.  Составить план эссе.

4.  Лаконично, но ёмко раскрыть содержание проблемы и свои подходы к её решению.

5.  Оформить эссе и сдать в установленный срок.

Контроль: Эссе может быть представлено на занятии в устной форме, либо сдано преподавателю в тетрадках для самостоятельных работ.

Интернет - ресурсы

1.Научно-популярный физико-математический журнал "Квант" (статьи по математике): http://kvant.mirror1.mccme.ru/rub/1.htm

2.Открытая математика. http://www.mathematics.ru/courses/index.htm

Раздел 2: Развитие понятия о числе Самостоятельная работа № 2 на тему: Действительные числа . Комплексные числа. Цель: способствовать развитию навыков самостоятельного применения знаний при алгебраических вычислениях.

Типовые расчёты.

Математика. Задачник: учеб.пособие для образ. уч.начального и сред.проф. образования/М.И. Башмаков.- М.: Академия,2014.

№ п\п	Название работы	Страница в задачнике	№ заданий
1	Действия с дробями	6	1.1:А; 1.2:А 1.3:А
2	Приближенные вычисления, погрешность	10	1.13
3	Комплексные числа.	12	1.17

Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок.

Раздел 3: Корни, степени, логарифмы 

Самостоятельная работа № 3 на тему: Решение иррациональных уравнений Цель: Закрепить навыки решения иррациональных уравнений.

Теоретический материал Формулы для повторения:

(𝑎 + 𝑏)² = 𝑎² + 2 ∙ 𝑎 ∙ 𝑏 + 𝑏²;

(𝑎 − 𝑏)² = 𝑎² − 2 ∙ 𝑎 ∙ 𝑏 + 𝑏²; Решение квадратных уравнений:

𝒂 ∙ 𝒙^𝟐 + 𝒃𝒙 + 𝒄 = 𝟎

𝑫 = 𝒃^𝟐 − 𝟒𝒂𝒄,

Если 𝑫 > 0, то 𝒙_{𝟏,𝟐        𝟐𝒂} Если 𝑫 = 𝟎, то 𝒙 = ^−𝒃

𝟐𝒂

Если 𝑫 < 0, то корней нет

Вариант  1

Решить уравнения

8.1 √х² − 4х  = √6 − 3х ; 

8.2 √х² + х − 3  = √1 − 2х ;

8.3 ;

8.4   =4 ;

8.5 При каких значениях х  функция у  принимает значение равное 2?

Вариант  2

Решить уравнения

1.      √х² − 10  = √−3х ;

2.      х      − 4х + 3         1 − ;

3.       ;

4.      =3 ;

5.      При каких значениях х  функция у  принимает значение равное 3?

Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок.

Самостоятельная работа № 4 на тему: Решение показательных и логарифмических уравнений и неравенств

Цель: Знать методы решения   показательных и логарифмических уравнений и неравенств, применять их при решении упражнений.

 Теоретический материал

Степени чисел от 0 до 10

n	0	1	2	3	4	5	6	7	8	9	10
𝟐𝒏	1	2	4	8	16	32	64	128	256	512	1024
𝟑𝒏	1	3	9	27	81	243	729	2187	6561	19683	59049
𝟒𝒏	1	4	16	64	256	1024	4096	16384	65536	262144
𝟓𝒏	1	5	25	125	625	3125	15625	78125	390625
𝟔𝒏	1	6	36	216	1296	7776	46656	279936
𝟕𝒏	1	7	49	343	2401	16807	117649
𝟖𝒏	1	8	64	512	4096	32768
𝟗𝒏	1	9	81	729	6561	59049
𝟏𝟎𝒏	1	10	100	1000	10000

Решение квадратных уравнений:

𝒂 ∙ 𝒙^𝟐 + 𝒃𝒙 + 𝒄 = 𝟎

𝑫 = 𝒃^𝟐 − 𝟒𝒂𝒄,

Если 𝑫 > 0, то 𝒙_{𝟏,𝟐  𝟐𝒂}

−𝒃

Если 𝑫 = 𝟎, то 𝒙 =

𝟐𝒂

Если 𝑫 < 0, то корней нет Формулы сокращенного умножения:

(𝒂 + 𝒃)^𝟐 = 𝒂^𝟐 + 𝟐𝒂𝒃 + 𝒃^𝟐

(𝒂 − 𝒃)^𝟐 = 𝒂^𝟐 − 𝟐𝒂𝒃 + 𝒃^𝟐

𝒂^𝟐 − 𝒃^𝟐 = (𝒂 − 𝒃) ∙ (𝒂 + 𝒃)

(𝒂 + 𝒃)^𝟑 = 𝒂^𝟑 + 𝟑𝒂^𝟐𝒃 + 𝟑𝒂𝒃^𝟐 + 𝒃^𝟑

Свойства степеней	Свойства корней n-ой степени
1.        𝒂𝒎 ∙ 𝒂𝒏 = 𝒂𝒎+𝒏 2.        𝒂𝒎𝒏 = 𝒂𝒎−𝒏 𝒂 3.        (𝒂𝒎)𝒏 = 𝒂𝒎∙𝒏 4.        𝒂𝒏 ∙ 𝒃𝒏 = (𝒂 ∙ 𝒃)𝒏 𝒎 5.        𝒂𝒏 = 𝒏√𝒂𝒎 6.        𝒂−𝒏 = 𝟏𝒏 𝒂 7.        𝒂𝟎 = 𝟏 𝒂 𝒏 𝒃 −𝒏 8.        ( )       = ( )                      𝒃                     𝒂 𝒎                    𝒏         𝒎 = 𝒂𝒏 9.        √𝒂	1. 2. 3. 4. 𝒏∙𝒌 5. 6. 𝒎            7. 𝒂𝒏 =	𝒃 𝒃   𝒎 𝒏∙𝒌            𝒏 𝒂𝒎 𝒂 𝒏            𝒎 √𝒂

(𝒂 − 𝒃)^𝟑 = 𝒂^𝟑 − 𝟑𝒂^𝟐𝒃 + 𝟑𝒂𝒃^𝟐 − 𝒃^𝟑

Показательное уравнение – это уравнение, в котором неизвестное содержится в показателе степени 

Решение показательных уравнений. Метод выноса за скобки

Образцы решения 1.          Решить уравнение: 

В левой части выносим за скобки степень с наименьшим показателем, то есть 3^х−2. В результате получим:

 

3х−2(3х+1−(х−2) − 2) = 25

3х−2(3х+1−х+2 − 2) = 25

3х−2 = 1 , Ответ: х = 2.

3х−2 = 30,    отсюда следует, что х = 2.

Уравнения, сводящиеся к квадратным (метод замены)

Образцы решения

                2.     Решить уравнение:    4^х + 2^х+1 − 24 = 0.

Решение: Заметив, что  4^х = (2²)^х = 2^2х = (2^х)²,     а       ^х Перепишем заданное уравнение в виде:

Вводим новую переменную: t , тогда уравнение примет вид: t² + 2t − 24 = 0

Решив квадратное уравнение, получим:      t₁ =4,    t₂ = −6.  Но так как    t = 2^x, то надо решить два уравнения:

                                                                                 2^х = 4           и          

Решим первое уравнение:

2^х = 2²    отсюда следует, что х = 2.

Рассмотрим второе уравнение. 

Второе уравнение не имеет решения, так как  2^х > 0 для любых значений х.

Ответ: 2.

Образцы решения логарифмических уравнений

                1.   Решить уравнение:

Решение: Используя формулу: , заменим сумму логарифмов произведением:  

х

х² − 4 − 2х + 1=0 х² − 2х − 3 = 0

х₁ = 3;    х₂ = −1. Проверка:

 

log₃ 5 = log₃ 5

х₂ = −1

log₃(−1 − 2) + log₃(−1 + 2) = log₃(2 ∙ (−1) − 1) - не существует.

Ответ: х= 3

2.         Решить уравнение: log²₄x + log₄ x − 2 = 0.  Используем метод замены.

log₄ x = t  ⟹  t² + t − 2 = 0

𝑡₁ = 1,               𝑡₂ = −2. Подставим в замену. log₄ x = 1 ⇒ x = 4¹ = 4,     log₄ x = −2 ⟹ x = 4⁻² =  = .

Ответ: x = 4;    х .

Образцы решения показательных неравенств

1.      Решить неравенство 2^х − 2^х−2 ≤ 3.

 Решение: 

Выносим за скобки степень с наименьшим показателем, т.е.  2^х−2.

Получим: 2^х−2(2² − 1) ≤ 3,

2^х ∙ 3 ≤ 3,

                                                                              2^х ≤ 1,         так как  2⁰ = 1 то

2х ≤ 20

Так как основание 2 > 1, то неравенство равносильно неравенству того же смысла х ≤ 0. Ответ: х 𝜖 (−∞; 0).

2.      Решить неравенство 7^2х − 8 ∙ 7^х + 7 > 0

Решение.

Заменим : 7^х = 𝑡, 𝑡 > 0;

Получим неравенство: 𝑡² − 8𝑡 + 7 > 0.  Трехчлен 𝑡² − 8𝑡 + 7 разложим на множители: (𝑡 − 7)(𝑡 − 1) > 0.

𝑡 < 7; 𝑡 > 1.

7^𝑥 < 7,     𝑎 = 7 > 1,   то    𝑥 < 1 7^𝑥 > 1,    7^𝑥 > 7⁰,     𝑎 = 7 > 1,     то   𝑥 > 0. Ответ: х 𝜖 (−∞; 1) ∪ (0; ∞).

Образцы решения логарифмических неравенств.

                1.   Решить неравенство:

№п/п	Вариант 1	Вариант 2
1	3х+2 − 3х = 72	2х − 2х−4 = 15
2	22х + 3 ∙ 2х − 10 = 0	2 ∙ 4х − 5 ∙ 2х + 2 = 0
3	𝑙𝑜𝑔32𝑥 − 2𝑙𝑜𝑔3𝑥 − 3 = 0	𝑙𝑜𝑔42𝑥 − 4 log4 𝑥 + 3 = 0
Показательные и логарифмические неравенства
1	2х + 2х+2 ≤ 20	1 3х+4                 1 3х+5                      ( )          + ( )         > 6                       5                5
2	log7(2 − х) ≤ log7(3х + 6)	log2,5(4х − 5) ≥ log2,5(3х − 6)
3	log(1 − 2х) > log(5х + 25)	log0,8(2х − 3) < log0,8(3х − 5)

Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок.

Раздел 4: Прямые и плоскости в пространстве

Самостоятельная работа № 5 на тему: Расстояние от точки до плоскости. Теорема о трех перпендикулярах

Цель: рассмотреть понятие- расстояния от точки до плоскости; изучить теорему о трёх перпендикулярах; рассмотреть типичные ситуации её применения на примерах решения задач.

Теоретический материал

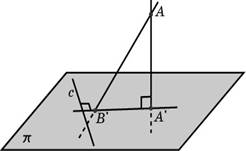Теорема: Прямая, проведенная в  плоскости через основание наклонной  перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной. 

Теорема (обратная): Прямая, проведенная в  плоскости через основание наклонной  перпендикулярно к ней, перпендикулярна и к ее

проекции.

Определение: Расстоянием от точки до плоскости в пространстве называется длина перпендикуляра, опущенного из данной точки на данную плоскость

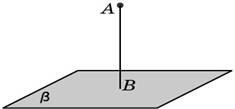
Вопросы для закрепления.

1.      Как найти расстояние от точки до плоскости?

2.      Может ли наклонная быть короче перпендикуляра, проведённого из той же точки к той же плоскости?

3.      Если наклонные, проведённые из одной точки к плоскости, равны, то, что можно сказать об их проекциях?

4.      Как формулируется обратное утверждение? Справедливо ли оно?

5.      Сформулируйте теорему о трёх перпендикулярах

6.      Как формулируется теорема, обратная теореме о трёх перпендикулярах?

7.      Если точка равноудалена от всех вершин многоугольника, то во что она проектируется?

8.      Если точка равноудалена от всех сторон многоугольника, то во что она проектируется?

9.      Что называется углом между прямой и плоскостью?

Решить самостоятельно.

Вариант 1

 

1.      Докажите, что если прямая, лежащая в плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и ортогональной проекции этой наклонной.

 

 

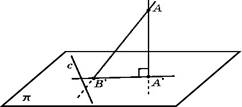
2.      Из точки к плоскости проведены две наклонные, одна из которых на 6 см длиннее второй. Проекция  наклонных равны 17 см и 7 см. Найдите наклонные.

 

 

3.      Диагонали квадрата АВСD пересекаются в точке О. SO – перпендикуляр к плоскости квадрата. SO см. 

1)      Докажите равенство углов, образованных прямыми SA, SB, SD с плоскостью квадрата.

2)      Найдите эти углы, если периметр АВСD равен 32 см.

 

   Вариант 2

1.      Докажите, что перпендикуляр, опущенный из точки на плоскость, короче всякой наклонной, проведенной из той же точки к той же плоскости. 

 

 

2.      Из точки к плоскости проведены две наклонные, равные 17 см и 15 см. Проекция одной из них на 4 см больше проекции другой. Найдите проекции наклонных.

 

3.      Диагонали квадрата АВСD пересекаются в точке О. SO – перпендикуляр к плоскости квадрата. SO= 4см. Точки K, L,  M,  N – середины сторон квадрата.

1)      Докажите равенство углов, образованных прямыми SK, SL, SM, SN с плоскостью квадрата.

2)      Найдите эти углы, если площадь  АВСD равен 64 см².

 

Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок.

 

       

 

Самостоятельная работа № 6 . Составление кроссвордов на тему: Взаимное расположение прямых и плоскостей в пространстве

Цель: развитие интереса к предмету, интуиции, логического мышления.

Кроссворд — игра, состоящая в разгадывании слов по определениям.

Правила составления кроссвордов 1. В общем случае определение должно состоять из одного предложения.

2.      Определения должны быть по во возможности краткими. Следует избегать перечислений, не злоупотреблять причастными и деепричастными оборотами, не перегружать текст прилагательными. Определение кроссворда - своего рода компромисс между краткостью и содержательностью.

3.      Запрещается использование в одной сетке двух и более одинаковых слов, даже с различными определениями.

4.      В вопросах следует избегать энциклопедических определений. В целом работа должна быть авторской, а не перепечаткой статей из словаря.

5.      Нежелательно начинать формулировку вопроса с цифры, глагола, деепричастия.

6.      Запрещается использование однокоренных слов в вопросах и ответах.

7.      В работе должна быть изюминка, то есть нечто, отличающее ее от миллионов других.

8.      Запрещается помещать слова без пересечений (встречается и такое).

9.      Не используются слова, пишущиеся через тире и имеющие уменьшительноласкательную окраску.

Образец оформления и составления кроссвордов:

По горизонтали:

1. Сторона прямоугольного треугольника.

4. Он есть у функции и последовательности.

8. Его штаны равны во все стороны.

10.  Полный круг вращения.

13.  Французский математик, специалисттеории вероятностей.

14.  Арифметическое действие.

16.  Гектар — ... площади.

17.  Часть матрицы.

18.  Свойство углов.

19.  Полупрямая.

22.  Нейтральный элемент относительно умножения.

23.  Группа повторяющихся цифр в бесконечной десятичной дроби.

24.  Наибольший общий ...По вертикали:

2.  Бублик как математический объект.

3.  Положение, нуждающееся в доказательстве.

4.  Поверхность, имеющая 2 измерения.

5.  Линейное алгебраическое уравнение.

6.  Тригонометрическая функция.

7.  Один из двух экстремумов.

9. Функция по своей сути.

11.  Часть прямой.

12.  Линия.

15. Геометрическая фигура, образованная двумя лучами.

17.  Полный квадрат первого двузначного числа.

18.  Для него необходимы натуральные числа.

20.  В теории графов: маршрут, все ребра которого различны.

21.  В теории графов: замкнутый маршрут, все ребра которого различны.

Ответы:

По горизонтали:  1-катет; 4-предел; 8-пифагор; 10-оборот; 13-пуассон; 14-умножение; 16-мера; 17-строка; 18-смежность; 19-луч; 22-единица; 23-период; 24-делитель;

По вертикали: 2-тор; 3-теорема; 4-плоскость; 5-лау; 8-синус; 7-максимум; 9-отображение; 11-отрезок; 12-кривая; 15-угол; 17-сто; 18-счёт; 20-цепь; 21-цикл.

Контроль: представить кроссворд в разгаданном виде на учебном занятии Раздел 5: Комбинаторика

Самостоятельная работа № 7  на тему: Задачи комбинаторики

Цель: закрепить навыки решения комбинаторных задач.

Теоретический материал.

Комбинаторика (комбинаторный анализ, комбинаторная математика) – раздел математики, посвящённый решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами_{m       n!}        Число размещений из п элементов по т определяется по формуле:  An ^ ₍n m_ )!

Произведение натуральных чисел от единицы до какого-либо данного натурального числа n, то есть  1•2•3•......•n , называется  «факториалом» (англ. factorial, от лат. factor – делающий, производящий) и обозначается  n! Термин ввёл Л. Арбогаст (1800), обозначение n! –К. Крамп (1808).

№1 Например, из 32 букв русского алфавита можно составить     _A32² _32 31 992* _ двухбуквенные комбинации, не содержащие повторений букв.

№2 Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один день из 4 различных предметов? Решение: Речь идёт о размещении из 8 элементов по 4. Имеем:   А⁴₈=8!/(8-4)!=8!/4!=8*7*6*5=1680

Ответ: расписание можно составить 1680 способами.

Для нахождения числа перестановок используют формулу    Pn = n!

№3 Сколькими способами могут быть расставлены 8 участниц забега на восьми беговых дорожках?

Решение: Число способов равно числу перестановок из 8 элементов. Р₈=8!=1*2*3*4*5*6*7*8=40320.

Ответ: существует 40320 способов расстановки участниц забега на 8 беговых дорожках.

Размещениями с повторениями, находится по формуле  A^m_n _n^m

№4 На пример, из 30 букв русского алфавита (исключая ь и ъ) можно составить 30² = 900 двухбуквенных серий (например, для денежных знаков)  и  30³ = 27 000  трехбуквенных серий.

Число этих перестановок вычисляется по формуле

Pⁿn1 , n2 , ... nk =   n!               , где п — общее количество элементов, входящих в перестановку, a n1!n2!...nk!

n1,  n2,, nk  — количество одинаковых элементов в первой, второй, ..., k-й группах.

№5 Определим число перестановок с повторениями, которое можно получить из букв, составляющих словоформу математика. Всего в перестановках участвует десять букв, т. е. n = 10; буква м повторяется два раза, поэтому если бы все остальные буквы были различными, то искомое число перестановок, было бы равно P2¹⁰= 10! / 2!. На самом деле, кроме двух одинаковых м в нашем слове имеются три а и два т. Поэтому общее число перестановок, полученных из букв, входящих в словоформу математика, равно

         P ^10[1]_,2,3 ~⁼   5 6 7 8 9                              10 151200     .

Группы комбинаций, различающиеся только элементами, называются сочетаниями из п элементов по т. Их число равно :   

                                                                                                   m             n!

^{Сn } m n m!(            )! №6 имеется пять гвоздик разного цвета. Требуется составить букет изтрёх гвоздик разного цвета.

Решение:С^[2][3][4]=5!/3!*(5-3)!=5!/3!*2!=4*5/1*2=20/2=10. Решите задачи:

                1.   Сколькими способами могут восемь человек стать в очередь к театральной кассе?

Раздел 6: Координаты и векторы. 

Самостоятельная работа № 8   на тему: Действие над векторами в координатной  форме

Цель: закрепить знания учащихся по теме в ходе решения задач.

Теоретический материал

Отложим вектор так, чтобы его начало совпало с началом координат. Тогда координаты его конца называются координатами вектора. Обозначим  𝑖⃗, 𝑗⃗,𝑘⃗⃗   векторы с координатами (1, 0, 0), (0, 1, 0), (0, 0, 1) соответственно. Их длины равны единице, а направления совпадают с направлениями соответствующих осей координат. Будем изображать эти векторы, отложенными от начала координат и называть их координатными векторами.

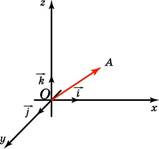
Теорема. Вектор   𝑎⃗ имеет координаты (x, y, z) тогда и только тогда,  когда он представим в виде 𝑎⃗ = 𝑥𝑖⃗+ 𝑦𝑗⃗+ 𝑧𝑘⃗⃗/

Вариант 1

№п/п	Название операции	Формулы
1	Найти сумму векторов	⃗𝒂⃗⃗{𝟏; −𝟐;𝟑},    ⃗𝒃⃗⃗{𝟒; 𝟎; −𝟏} ⃗𝒂⃗⃗ + ⃗𝒃⃗⃗{𝒙𝟏 + 𝒙𝟐 ; 𝒚𝟏 + 𝒚𝟐 ; 𝒛𝟏 + 𝒛𝟐 }
2	Найти разность векторов	⃗𝒂⃗⃗{𝟒; 𝟏; −𝟑},    ⃗𝒃⃗⃗{𝟎; −𝟓;𝟐} ⃗𝒂⃗⃗ − ⃗𝒃⃗⃗{𝒙𝟏 − 𝒙𝟐 ; 𝒚𝟏 − 𝒚𝟐 ; 𝒛𝟏 − 𝒛𝟐 }
3	Найти произведение вектора на число	⃗𝒂⃗⃗{−𝟏;𝟑; 𝟏},  𝜹 − число   𝜹 = −𝟑 𝜹⃗𝒂⃗⃗{𝜹 ∙ 𝒙; 𝜹𝒚 ; 𝜹𝒛}
4	Вычислить координаты середины отрезка	Точка A(𝟏; 𝟐; −𝟑)  Точка  B (-3;4;-1) Точка С- середина отрезка АВ. С(𝒙𝒄; 𝒚𝒄; 𝒛𝒄)                                        𝒙𝟏 + 𝒙𝟐                             𝒚𝟏 + 𝒚𝟐                             𝒙𝒄 =                    ,     𝒚𝒄 = ,                                               𝟐                                𝟐 𝒛𝟏 + 𝒛𝟐  𝒛𝒄 = 𝟐
5	Найти координаты вектора	Точка A(𝟓; 𝟎; −𝟑).  Точка  B (-1;4;-7).Находим координаты вектора ⃗АВ⃗⃗⃗⃗⃗. Из  координат конца вычислить координаты начала вектора ⃗АВ⃗⃗⃗⃗⃗ {𝒙𝟐 − 𝒙𝟏 ;𝒚𝟐 − 𝒚𝟏; 𝒛𝟐 − 𝒛𝟏}
6	Найти длину вектора	⃗ ⃗𝒂⃗⃗{𝟓; 𝟏; −𝟏}
		|⃗𝒂⃗⃗| = √𝒙𝟐 + 𝒚𝟐 + 𝒛𝟐
7	Вычислить скалярное произведение векторов	⃗𝒂⃗⃗{−𝟐;𝟑; 𝟕},    ⃗𝒃⃗⃗{−𝟗;𝟎; 𝟐} ⃗𝒂⃗⃗ ∙ ⃗𝒃⃗⃗ = 𝒙𝟏 ∙ 𝒙𝟐 + 𝒚𝟏 ∙ 𝒚𝟐 + 𝒛𝟏 ∙ 𝒛𝟐

Вариант 2

№п/ п	Название операции	Формулы
1	Найти сумму векторов	⃗𝒂⃗⃗{𝟐; −𝟑;𝟒},    ⃗𝒃⃗⃗{−𝟏;𝟐; 𝟎} ⃗𝒂⃗⃗ + ⃗𝒃⃗⃗{𝒙𝟏 + 𝒙𝟐 ; 𝒚𝟏 + 𝒚𝟐 ; 𝒛𝟏 + 𝒛𝟐 }
2	Найти разность векторов	⃗𝒂⃗⃗{𝟒; −𝟓;𝟕},    ⃗𝒃⃗⃗{𝟑; −𝟏;𝟐} ⃗𝒂⃗⃗ − ⃗𝒃⃗⃗{𝒙𝟏 − 𝒙𝟐 ; 𝒚𝟏 − 𝒚𝟐 ; 𝒛𝟏 − 𝒛𝟐 }
3	Найти пароизведение на число	⃗𝒂⃗⃗{−𝟐;𝟒; 𝟎},  𝜹 − число   𝜹 = −𝟒 𝜹⃗𝒂⃗⃗{𝜹 ∙ 𝒙; 𝜹𝒚 ; 𝜹𝒛}
4	Вычислить координаты середины отрезка	Точка A(−𝟑: 𝟏; 𝟐)  Точка  B (2;-3;1) Точка С- середина отрезка АВ. С(𝒙𝒄; 𝒚𝒄; 𝒛𝒄)                                         𝒙𝟏 + 𝒙𝟐                             𝒚𝟏 + 𝒚𝟐                              𝒙𝒄 =                    ,     𝒚𝒄 = ,                                               𝟐                                𝟐 𝒛𝟏 + 𝒛𝟐  𝒛𝒄 = 𝟐
5	Найти координаты вектора	Точка A(𝟔; −𝟑; 𝟒).  Точка  B (1;-4;7). Находим координаты вектора ⃗АВ⃗⃗⃗⃗⃗. Из  координат конца вычислить координаты начала вектора ⃗АВ⃗⃗⃗⃗⃗ {𝒙𝟐 − 𝒙𝟏 ;𝒚𝟐 − 𝒚𝟏; 𝒛𝟐 − 𝒛𝟏}
6	Найти длину вектора	⃗ ⃗𝒂⃗⃗{𝟕; 𝟐; −𝟏} |⃗𝒂⃗⃗| = √𝒙𝟐 + 𝒚𝟐 + 𝒛𝟐
7	Вычислить скалярное произведение векторов	⃗𝒂⃗⃗{−𝟑;𝟐; 𝟗},    ⃗𝒃⃗⃗{−𝟕;𝟎; 𝟑} ⃗𝒂⃗⃗ ∙ ⃗𝒃⃗⃗ = 𝒙𝟏 ∙ 𝒙𝟐 + 𝒚𝟏 ∙ 𝒚𝟐 + 𝒛𝟏 ∙ 𝒛𝟐

Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок.

Раздел 7:  Основы тригонометрии

Самостоятельная работа № 9 на тему: Тригонометрические формулы Цель: способствовать закреплению навыков преобразования тригонометрических выражений.

Основные формулы тригонометрии

𝑠𝑖𝑛²𝑥 + 𝑐𝑜𝑠²𝑥 = 1;

𝑠𝑖𝑛²𝑥 = 1 − 𝑐𝑜𝑠²𝑥;

𝑐𝑜𝑠²𝑥 = 1 − 𝑠𝑖𝑛²𝑥; 𝑡𝑔𝑥 = 𝑠𝑖𝑛𝑥  ; 𝑐𝑡𝑔𝑥 = ^{𝑐𝑜𝑠𝑥} ;  t𝑔𝑥 ∙ 𝑐𝑡𝑔𝑥 = 1;  𝑡𝑔𝑥 = ¹ ;  𝑐𝑡𝑔𝑥 = ¹ .

                       𝑐𝑜𝑠𝑥                                                  𝑠𝑖𝑛𝑥                                                                                                        𝑐𝑡𝑔𝑥                                                  𝑡𝑔𝑥

 Синус и косинус суммы и разности аргументов:

sin(𝛼 + 𝛽) = sin 𝛼 cos 𝛽 + sin 𝛽 + cos 𝛼 sin(𝛼 − 𝛽) = sin 𝛼 cos 𝛽 − sin 𝛽 + cos 𝛼 cos(𝛼 + 𝛽) = cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽 cos(𝛼 − 𝛽) = cos 𝛼 cos 𝛽 + sin 𝛼 sin 𝛽

𝑡𝑔𝛼 + 𝑡𝑔𝛽

𝑡𝑔

∙

Формулы двойного аргумента: sin 2𝛼 = 2 sin 𝛼 cos 𝛼

cos 2𝛼 = (cos 𝛼)² − (cos 𝛼)²

2 ∙ 𝑡𝑔𝛼

 𝑡𝑔

Формулы понижения степени:

² = 1 − cos 2𝛼

(sin 𝛼)

2

² = 1 + cos 2𝛼

(cos 𝛼)

2

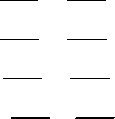
Преобразование сумм тригонометрических функций в произведение:

                                                                                                                      𝛼 + 𝛽       𝛼 − 𝛽

                                                                       sin 𝛼 + sin 𝛽 = 2 sin           cos

                                                                                                                           2               2

                                                                                                                      𝛼 − 𝛽       𝛼 + 𝛽

                                                                       sin 𝛼 − sin 𝛽 = 2 sin           cos

                                                                                                                           2               2

                                                                                                                       𝛼 + 𝛽       𝛼 − 𝛽

                                                                      cos 𝛼 + cos 𝛽 = 2 cos           cos

                                                                                                                            2               2

                                                                                                                         𝛼 + 𝛽       𝛼 − 𝛽

                                                                    cos 𝛼 − cos 𝛽 = −2 sin            sin

                                                                                                                               2              2

Вариант 1	Вариант 2
1.         Вычислить выражение, используя формулы синус и косинус суммы и разности аргументов:	1.         Вычислить выражение, используя формулы синус и косинус суммы и разности аргументов:
sin 1050	cos150
2.         Упростить выражение, используя формулы синус и косинус суммы и разности аргументов: 2.1.𝛼            1.2.       sin𝛼 sin 𝛽 + cos(𝛼 + 𝛽) 1.3.	2.                  Упростить выражение, используя формулы синус и косинус суммы и разности аргументов: 2.1.𝛼 2.2.   sin(𝛼 + 𝛽) − sin 𝛼 sin𝛽
3.                  Найдите значение выражения, используя формулы синус и косинус суммы и разности аргументов: 3.1.    cos 1070 cos 1070 + sin 1070 sin 170                                       𝜋         𝜋             𝜋        𝜋 3.2.    cos               cos          − sin      sin                                      12        4            12       4	3.                  Найдите значение выражения, используя формулы синус и косинус суммы и разности аргументов: 3.1.       cos 360 cos 240 − sin 360 sin 240                              5𝜋        3𝜋            5𝜋       3𝜋 3.2.       cos        cos          + sin      sin                               8           8              8          8
4.      Упростить выражение, используя формулы двойного аргумента: sin2𝛼 4.1.        = sin𝛼 cos 𝛼 4.2.       (cos150 + sin 150)2	4.      Упростить выражение, используя формулы двойного аргумента: 4.1.       (cos𝛼)2 − cos 2𝛼 4.2.       (cos 150)2 − (sin150)2
5.      Представить в виде произведения: 5.1.       sin 400 + sin160 5.2.       sin200 − sin 400 5.3.       cos 150 + cos 450 5.4.       cos460 − cos740	5.  Представить в виде произведения: 5.1.       sin 100 + sin500 5.2.       sin520 − sin 360 5.3.       cos200 + cos400 5.4.       cos750 − cos 150

Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок.

Самостоятельная работа № 10  на тему: Тригонометрические уравнения 

Цель: Знать методы решения тригонометрических уравнений и применять их при решении упражнений.

Теоретический материал

Формулы для повторения

arcsin(− a) = − arcsin a arccos (−a) = 𝜋 − arccos a arctg (−a) = − arctg a arcctg (−a) = 𝜋 − arcctg a

Общие формулы решения тригонометрических уравнений

х	I.        sin х = а,   |а| ≤ 1;  х = (−1)n arcsin a + πn,   n ϵ	II. cos x = а,    |а| ≤ 1  x = ± arccos a + 2πn,   n ϵ z
	II      tg x = a,   a – любое число T      x = arctg x + 𝜋𝑛, 𝑛𝜖𝑧	I       ctg x = a,   a – любое число           х= arcctgx + πn, nϵz

Частные решения  тригонометрических  уравнений

sin x=0  х=πn, nϵz	sin x=1      x=  + 2πn,    nϵz	sin x=-1 x= −  + 2πn, nϵz
cos x=0 x=  + πn, nϵz	cos x=1 x= 2πn, nϵz	cos x=-1 x=π + 2πn, nϵz

Значение тригонометрических функций

град	00	300	450	600	900
радиан	0	𝝅 𝟔	𝝅 𝟒	𝝅 𝟑	𝝅 𝟐
sin𝛼	0				1
cos 𝛼	1				0
tg 𝛼	0		1	√3	не существ
ctg 𝛼	Не существ	√3	1		0

Формулы для повторения:

𝑎𝑥² + 𝑏𝑥 + 𝑐 = 0,   𝐷 = 𝑏² − 4 ∙ 𝑎 ∙ 𝑐.

Если 𝐷 > 0, то корни квадратного уравнения находим по формуле:

−𝑏 ± √𝑏² − 4𝑎𝑐

х₁,2 =

2𝑎

Образцы решения тригонометрических уравнений второго порядка: Образец№1 Решить уравнение:

2sin²x − 5sinx + 2 = 0

Решение. Введем новую переменную: z = sin x.  Тогда уравнение примет вид: 2z² – 5z + 2 =0. Решая квадратное уравнение находим z1 = 2  и    z2 =  ¹ .

  2

Значит, либо sin x = 2,    либо sin x = . Первое уравнение не имеет корней, а из второго находим 

х = (−1)ⁿ arcsin  + πn,   nϵz

ⁿ π + πn, nϵz

x = (−1)

6 Образец №2 Решить уравнение:

cos²x − sin² x − cosx = 0

Решение:

Воспользуемся тем, что sin²x = 1 − cos²x

Тогда заданное уравнение можно записать в виде:

cos²x − (1 − cos²x) − cosx = 0

После преобразования получим:

2cos²x − cosx − 1 = 0

Введем новую переменную z = cos x. Тогда данное уравнение примет вид:

2z² –z -1 = 0.  Решая его, находим z₁ = 1, z₂ =−

Значит, либо cos x = 1, либо cos x = −

Решая первое уравнение cos x = 1, как частное, находим его решение

𝑥 = 2𝜋𝑛,    𝑛𝜖𝑧 . 

Решая второе уравнение, находим  решение:

x= ±arccos (− ) + 2πn, nϵz

x = ± (π − arccos  ) + 2πn,   nϵz

x = ±(π − ) + 2πn,   nϵz x = ±  + 2πn,    nϵz

Образец №3 Решить уравнение:

Решение:

С числом 2, содержащимся во правой части, поступим следующим образом. Известно, что sin²x + cos²x = 1 - это тождество верно для любого значения х.

Тогда 2(sin²x + cos²x) = 2sin²x + 2cos²x = 2.

Заменив в первом уравнении 2 на   2sin²x + 2cos²x , получим:   cosx + 5cos²x = 2sin²x + 2cos²x

cosx + 5

Обе части уравнения разделим на cos² x  почленно

sin²x

                                                                                

sinх

Так как  = tgх,  то полученное уравнение запишем в виде: cosх

  

Введя новую переменную t=tg x, получим квадратное уравнение:

        𝑡 +3=0, решая уравнение, получим: t

Итак,   

x= arctg n,    xn,  𝑛𝜖𝑍.

Решить самостоятельно

Вариант 1	Вариант 2
Решить уравнения: 1.       3sin2x – 5sinx – 2 = 0 2.       3cos2x + 10cosx + 3 = 0 3.       2sin2x + 3cosx = 0 4.       3tg2x + 2tgx – 1 = 0 5.       2sin2x − 5sinxcosx + 2cos2x = 0	Решить уравнения: 1.       6cos2x + cosx – 1 = 0 2.       2sin2x – 3sinx + 1 = 0 3.       5cos2x + 6sinx – 6 = 0 4.       2tg2x + 3tgx – 2 = 0 5.       3cos2x + 10sinxcosx + 3sin2x = 0

Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок.

Раздел 8: Функции, их свойства и графики.

Самостоятельная работа №11 на тему: Построение графиков функции Цель: способствовать формированию умения по графику функции определить ее свойства, а также строить графики функций.

Вариант 1

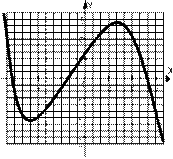
1. По графику функции 𝑦 = 𝑓(𝑥), изображенному на рисунке, определите промежуток убывания функции:

1.          (−∞; 5];   2. (−6; 4);     3.  [−6; 4]; 4. [4; ∞).

2.          По графику функции     𝑦 = 𝑓(𝑥), изображенному на рисунке, определить максимум и минимум функции.

3.          По графику функции     𝑦 = 𝑓(𝑥), изображенному на рисунке указать область определения и область значения функции.

4.          По графику функции     𝑦 = 𝑓(𝑥), изображенному на рисунке, указать промежутки, где 𝑓(𝑥) > 0 .

5.          Найти область определения функции 𝑦 .

1.    [4; ∞);  2.   (4; ∞);   3. (−∞; 4];    4. (−∞; 4)

6.          Найдите нули функции 𝑦 = 𝑥² + 2𝑥.

1.    {−1; −2};   2. {0}  ;  3.    {0; 2};   4.   {0; −2}.

7.          Постройте график функции: 𝑦 = (𝑥 − 2)² + 3

Вариант 2

1.      По графику функции 𝑦 = 𝑓(𝑥), изображенному на рисунке, определите промежуток возрастания функции.

1. (−∞; 4];   2. [−5; 4];   3. (−5; 4);   4. [4; ∞).

2.      По графику функции     𝑦 = 𝑓(𝑥), изображенному на рисунке, определить максимум и минимум функции.

3.      По графику функции     𝑦 = 𝑓(𝑥), изображенному на рисунке указать область определения и область значения функции.

4.      По графику функции     𝑦 = 𝑓(𝑥), изображенному на рисунке, указать промежутки, где 𝑓(𝑥) > 0 .

5

5.      Найти область определения функции  𝑦 = .

𝑥+4

1. (−∞; −4)⋃(−4; ∞);   2. (−4; ∞);   3.  [4; ∞);   4.  (−∞; −4]⋃[4; ∞).

6.  Найдите нули функции 𝑦 = 3𝑥 − 𝑥².

1. {−1; 3};   2. {0; −3}  ;  3.    {0};   4.   {0; 3}.

7.  Постройте график функции: 𝑦 = (𝑥 + 2)² + 1.

Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок.

Раздел 9: Многогранники и круглые тела

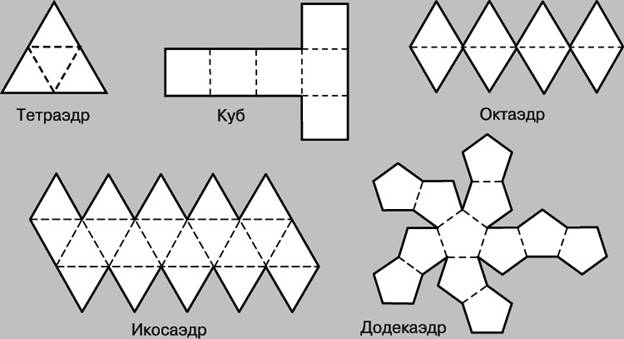
Самостоятельная работа № 12  на тему: Выполнение моделей многогранников Цель: Закрепить понятие правильных многогранников, при изготовлении моделей, используя развертки.     

Одним из способов изготовления правильных многогранников является способ с использованием, так называемых,  развёрток. 

Если модель поверхности многогранника изготовлена из гибкого нерастяжимого материала (бумаги, тонкого картона и т. п.), то эту модель можно разрезать по нескольким рёбрам и развернуть так, что она превратится в модель некоторого многоугольника. Этот многоугольник называют развёрткой поверхности многогранника. Для получения модели многогранника удобно сначала изготовить развёртку его поверхности.  При этом необходимыми инструментами являются клей и ножницы. Модели многогранников можно сделать, пользуясь одной разверткой, на которой будут расположены все грани. Однако в этом случае все грани будут одного цвета. 

Контроль: работу представить на учебном занятии в установленный срок.

Раздел 11: Тела  и поверхности вращения.

Самостоятельная работа №  13 на тему: Площади поверхности и объем фигур  вращения

Цель: Знать формулы для вычисления площадей поверхности фигур вращения и уметь применять их при решении задач.

Теоретический материал

№п/п	Наименование фигуры	Изображение	Формула площадей полной и боковой поверхности
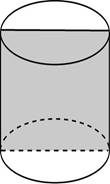
1	Цилиндр		𝑺б = 𝟐𝝅𝑹𝑯 𝑺п = 𝟐𝝅𝑹𝑯 + 𝟐𝝅𝑹𝟐 𝑺𝒐 = 𝝅𝑹𝟐 𝑽 = 𝝅𝑹𝟐 ∙ 𝑯
2	Конус		𝑺б = 𝝅𝑹𝒍 𝑺п = 𝝅𝑹𝒍 + 𝝅𝑹𝟐 𝑺𝒐 = 𝝅𝑹𝟐 𝑽𝝅𝑹𝟐 ∙ 𝑯 𝟑
3	Сфера, шар		𝑺п = 𝟒𝝅𝑹𝟐 𝟒 𝝅𝑹𝟑 𝑽 = 𝟑

Решить самостоятельно:

Вариант 1

1.      Радиус основания цилиндра равен 2 м,  высота - 3 м. Найдите площадь боковой поверхности и объем цилиндра.

2.      Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания.

3.      Площадь большого круга шара равна 3 см². Найдите площадь поверхности и объем шара.

4.      Прямоугольник вращается вокруг одной из сторон, равной 5см. Площадь боковой поверхности цилиндра, полученного при вращении, равна 100𝜋 см². Найдите площадь прямоугольника.

Вариант 2

1.      Осевое сечение цилиндра - квадрат. Площадь основания равна 1. Найдите площадь поверхности и объем цилиндра.

2.      Радиус основания конуса равен 3 м, высота - 4 м. Найдите площадь поверхности и объем конуса.

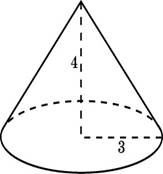
3.      Два конуса образованы вращением одного и того же прямоугольного треугольника вокруг его неравных катетов. Равны ли у этих конусов площади: а) боковых; б) полных поверхностей? в)объемы?

4.      Прямоугольник, одна из сторон которого равна  5см, вращается вокруг неизвестной стороны. Площадь боковой поверхности цилиндра, полученного при вращении, равна 60𝜋   см². Найдите площадь прямоугольника.

5.  

Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок.

Раздел 12:  Начала математического анализа

Самостоятельная работа № 14   на тему: Применение производной к исследованию функции

Цель:  Знать условия возрастания, убывания функции, точек максимума и минимума функции. Знать схему исследования функции и применять её при построении графика.

Признак возрастания функции: Если 𝑓^/(𝑥) > 0 в каждой точке некоторого промежутка, то на этом промежутке функция 𝑓(𝑥) возрастает.

Признак убывания  функции:    Если  𝑓^/(𝑥) < 0 в каждой точке некоторого промежутка, то на этом промежутке функция 𝑓(𝑥)убывает.

Признак максимума функции: Если функция   𝑓(𝑥)  непрерывна в точке х0,  а   𝑓^/(𝑥) > 0  на интервале  (𝑎; 𝑥₀)  и   𝑓^/(𝑥) < 0  на интервале (𝑥₀ ; 𝑎), то x0 является точкой максимума.

Упрощённая формулировка: Если в точке х0 производная меняет знак  с плюса на минус,  то х0 есть точка максимума.

Признак минимума функции: Если функция 𝑓(𝑥)   непрерывна в точке х0,  а 𝑓^/(𝑥) < 0  на интервале   (𝑎; 𝑥₀)  и   𝑓^/(𝑥) > 0  на интервале (𝑥₀ ; 𝑎), то x0 является точкой минимума

Упрощённая формулировка: Если в точке х0 производная меняет знак  с минуса на плюс,  то х0 есть точка максимума. Схема исследования функции.

•      Находим  область определения;

•      Вычисляем производную;

•      Находим стационарные точки

•      Определяем промежутки возрастания и убывания;

•      Находим точки максимума и минимума;  Вычисляем экстремум функции;  Данные заносят в таблицу.

•      На основании такого исследования строится график функции. Решить самостоятельно:

Вариант 1

I.                    Найти стационарные точки и промежутки возрастания и убывания

1.      𝑓(𝑥) = 2𝑥² − 1

2.      𝑓(𝑥) = −𝑥² + 2𝑥

II.                 Исследовать функцию и построить график

𝑓(𝑥) = 𝑥³ − 3𝑥² + 2

Вариант 2

I.                    Найти стационарные точки и промежутки возрастания и убывания

1.      𝑓(𝑥) = −𝑥² + 1

2.      𝑓(𝑥) = 𝑥² − 4𝑥

II.                 Исследовать функцию и построить график

𝑓(𝑥) = 𝑥³ + 3𝑥² − 1

Вариант 3

I.                    Найти стационарные точки и промежутки возрастания и убывания

1.      𝑓(𝑥) = −2𝑥² + 32

2.      𝑓(𝑥) = 𝑥² − 4𝑥

II.                 Исследовать функцию и построить график

𝑓(𝑥) = −𝑥³ + 6𝑥² + 2

Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок.

Раздел 13: Интеграл и его применение

Самостоятельная работа № 15  на тему: Вычисление площадей плоских фигур

Цель: закрепить знания, умения и навыки нахождения площади криволинейной трапеции с помощью интеграла; Теоретический материал

Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: 

F(x) + C. Записывают:  ∫ 𝑓(𝑥)𝑑𝑥 = 𝐹(𝑥) + 𝐶, где 𝐹(𝑥)- есть некоторая первообразная функции  𝑓(𝑥)  на этом промежутке, С – const. При этом знак  ∫ называется знаком интеграла, 𝑓(𝑥)  - подынтегральной функцией, 𝑓(𝑥)𝑑𝑥 - подынтегральным выражением, 𝑥 - переменная интегрирования, С- постоянная интегрирования.

Операция  нахождения неопределенного интеграла от данной функции называется интегрированием  данной функции. 

Интегрирование – операция, обратная операции дифференцирования.  У всякой непрерывной на данном интервале функции существует неопределенный интеграл.

Таблица неопределенных интегралов

∫ 𝑑𝑥 = 𝑥 + 𝐶	∫ 𝑠𝑖𝑛𝑥𝑑𝑥 = −𝑐𝑜𝑠𝑥 + 𝐶	𝑑𝑥         1            𝑥       ∫   2+𝑥2 = 𝑎 𝑎𝑟𝑐𝑡𝑔 𝑎 + 𝐶 𝑎
∫ 𝑥𝑛𝑑𝑥  𝐶	∫ 𝑐𝑜𝑠𝑥𝑑𝑥 = 𝑠𝑖𝑛𝑥 + 𝐶	∫ 𝑡𝑔𝑥𝑑𝑥 = −𝑙𝑛|𝑐𝑜𝑠𝑥| + 𝐶
𝑙𝑛|𝑥| + 𝐶		∫ 𝑐𝑡𝑔𝑥𝑑𝑥 = 𝑙𝑛|𝑥| + 𝐶
𝑎𝑥 ∫ 𝑎𝑥𝑑𝑥 =  + 𝐶 𝑙𝑛𝑎	𝑡𝑔𝑥 + 𝑐	𝑑𝑥                       𝑥 𝑎𝑟𝑐𝑠𝑖𝑛  + 𝐶          √𝑎2 − 𝑥2                                    𝑎
∫ ℓ𝑥𝑑𝑥 = ℓ𝑥 + 𝐶	𝑑𝑥 ∫     2 = 𝑎𝑟𝑐𝑡𝑔𝑥 + 𝐶 1 + 𝑥	𝑑𝑥           1        𝑥 − 𝑎 ∫  2 − 𝑎2 = 2𝑎 𝑙𝑛 |𝑥 + 𝑎| + 𝐶 𝑥

Свойства неопределенного интеграла:

∫ 𝑑𝐹(𝑥) = 𝐹(𝑥) + 𝐶;

∫ 𝑘𝑓(𝑥)𝑑𝑥 = 𝑘 ∫ 𝑓(𝑥)𝑑𝑥;

∫[𝑓(𝑥) ± 𝑔(𝑥)]𝑑𝑥 = ∫ 𝑓(𝑥)𝑑𝑥 ± ∫ 𝑔(𝑥)𝑑𝑥;

 𝐶;

𝑎

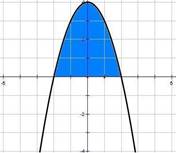
Определение: Фигура, ограниченная снизу отрезком [a, b] оси Ох ,сверху графиком непрерывной функции у= f(x), принимающей положительные значения , а с боков отрезками прямых х = а, х =b называется криволинейной трапецией.

                                                                                                       𝒃                                                       ^𝒃= 𝑭(𝒃) − 𝑭(𝒂).

𝑺 = ∫_𝒂 𝒇(𝒙)𝒅𝒙 = 𝑭(𝒙)| _𝒂

Образец решения:

Вычислить площадь криволинейной трапеции, ограниченной линиями

у = 4 - х² и у=0

Решение:

1.  у = 4 - х²- квадратичная функция, график – парабола, ветви направлены вниз, вершина (0;4) у = 0 - ось абсцисс.

2.  Найдём точки пересечения параболы с осью Х:               𝒙^𝟐 − 𝟒 = 𝟎;

𝒙^𝟐 = 𝟒,    𝒙 = 𝟐,     𝒙 = −𝟐.

3.  Найдём площадь криволинейной трапеции по формуле:

𝟐

                                                                                           𝒙𝟑           𝟐                          𝟐𝟑                                                    (−𝟐)𝟑

                                𝑺        ∫              𝟐                                                        |         = (𝟒 ∙ 𝟐 −         ) − (𝟒 ∙ (−𝟐) − ) =

                                                                                                     −𝟐                         𝟑                                        𝟑

−𝟐

                                                        = 𝟖 − 𝟖 + 𝟖 − 𝟖 = 𝟏𝟔 − 𝟏𝟔                      𝟏             𝟐         𝟐 )

                                                                                                                   = 𝟏𝟔 − 𝟓     = 𝟏𝟎     (ед.

                                                                     𝟑               𝟑                   𝟑                       𝟑             𝟑

Решить самостоятельно:

Вариант 1

                1.   Найти площадь фигуры, ограниченной линиями:

1.1 𝑓(𝑥) = 16 − 𝑥²,   𝑓(𝑥) = 0.

1.2.  𝑓(𝑥) = 1 + 𝑥²,    𝑦 = 2.

1.3.  𝑓(𝑥) = 5𝑐𝑜𝑠𝑥,    𝑓(𝑥) = 3𝑐𝑜𝑠𝑥.

Вариант 2

                1.   Найти площадь фигуры, ограниченной линиями:

1.1.  𝑓(𝑥) = 9 − 𝑥²,   𝑓(𝑥) = 0.

1.2.  𝑓(𝑥) = 3 + 𝑥²,    𝑦 = 4

1.3.  𝑓(𝑥) = 5𝑠𝑖𝑛𝑥,    𝑓(𝑥) = 3𝑠𝑖𝑛𝑥.

Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок.

Раздел 14: Измерения в геометрии

Самостоятельная работа № 16 на тему: Геометрия Евклида

Цель: расширить кругозор учащихся, познакомить с трудами великого математика Евклида.

Задание для учащихся. 

Написать сообщение на заданную тему.

Сообщение – это сокращенная запись информации, в которой должны быть отражены основные положения текста, сопровождающиеся аргументами, 1–2 самыми яркими и в то же время краткими примерами.

Сообщение составляется по нескольким источникам, связанным между собой одной темой. Вначале изучается тот источник, в котором данная тема изложена наиболее полно и на современном уровне научных и практических достижений. Записанное сообщение  дополняется материалом других источников.

Этапы подготовки сообщения:

1.  Прочитайте текст.

2.  Составьте его развернутый план.

3.  Подумайте, какие части можно сократить так, чтобы содержание было понятоправильно и, главное, не исчезло.

4.  Объедините близкие по смыслу части.

5.  В каждой части выделите главное и второстепенное, которое может быть сокращенопри конспектировании.

6.  При записи старайтесь сложные предложения заменить простыми.

Тематическое и смысловое единство сообщения  выражается в том, что все его компоненты связаны с темой первоисточника.

Сообщение  должно содержать информацию на 3-5 мин.  и сопровождаться презентацией, схемами, рисунками, таблицами и т.д.

Выполнить самостоятельно:

Написать сообщение на тему: (на выбор).

1.      Геометрия Евклида;

2.      Аксиоматика Евклида;

3.      Современная аксиоматика Евклида; 4.           Неевклидова геометрия;

                5.   От геометрии к логике.

Контроль: работу представить на занятии в установленный срок

Раздел 15: Элементы теории вероятностей и математической статистики

Самостоятельная работа № 17  на тему: Элементы теории вероятностей и математической статистики

Цель: закрепить навыки решения задач на вычисление вероятностей.

В теории вероятностей испытанием принято называть эксперимент, который (хотя бы теоретически) может быть произведён в одних и тех же условиях неограниченное число раз.

Результат или исход каждого испытания назовём событием. Каждое событие, которое может произойти, а может и не произойти, называется случайным событием. Мерой возможности появления события A при осуществлении комплекса условий  является вероятность P(А) этого события. Если результаты испытания можно представить в виде полной системы n равновозможных и попарно несовместимых событий и если случайное событие появляется только в m случаях, то вероятность события A равна  Р(A) = m/n, т. е. отношению количества случаев, благоприятствующих данному событию, к общему числу всех случаев.

Правило сложения вероятностей формулируется следующим образом. 

Вероятность объединения двух несовместных событий равна сумме вероятностей этих событий: 

Р(А+В) =Р(А)+ Р(В).

Таблица факториалов

1! =	1		6! =	720
2! =	2		7! =	5 040
3! =	6		8! =	40 320
4! =	24		9! =	362 880
5! =	120		10! =	3 628 800

Примеры решения задач.

№1 На полке 6 видеокассет. Найдите вероятность того, что все кассеты окажутся на свеем месте.

Решение : N=6!=720- число всех событий , N(А)=1- число благоприятствующих событий.

Р(А)=1/720 =0,0014. Ответ : 0,0014

№2 Слово апельсин написали на полоске картона и разрезали полоску на буквы. Девочка, играя, выложила их в ряд в случайном порядке. Найдите вероятность того, что это слово спаниель

Решение: : N=8!=40320 - число всех событий , N(А)=1- число благоприятствующих событий.

Р(А)=1/40320 =0,000025.

Ответ : 0,000025

№3. В лотерее 1000 билетов; из них на один билет падает выигрыш 500 руб., на 10 билетов - выигрыши по 100 руб., на 50 билетов - выигрыши по 20 руб., на 100 - билетов - выигрыши по 5 руб., остальные билеты невыигрышные. Некто покупает один билет. Найти вероятность выиграть не менее 20 руб. 

Решение. Рассмотрим события:

А - выиграть не менее 20 руб.,

А1 - выиграть 20 руб.,

А2 - выиграть 100 руб., А3 - выиграть 500 руб. 

Очевидно, А= А1 +А2+А3.

По правилу сложения вероятностей:

Р (А) = Р (А1) + Р (А2) + Р (А3) = 0,050 + 0,010 + 0,001 = 0,061 Решите задачи:

№1 Найдите вероятность того , что три последние цифры случайно выбранного телефонного номера- это цифры 2,3.1. в произвольном порядке.

№2 Для участие в телевикторине случайным образом выбирают 3 игрока из 8 претендентов. Какова вероятность того, что будут выбраны 1-й, 4-й, и 8-й игрок

№3 Производится бомбометание по трём складам боеприпасов, причём сбрасывается одна бомба. Вероятность попадания в первый склад 0,01; во второй 0,008; в третий 0,025. При попадании в один из складов взрываются все три. Найти вероятность того, что склады будут взорваны. 

№4

№5

Ответы(№2-0,018;№3-0,45;№4-0,545, 0,364, 0,091; №5-0, 559)

Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок.

Раздел 16: Уравнения и неравенства.

Самостоятельная работа № 18  на тему: Решение алгебраических уравнений и неравенств с одной переменной.

Цель: Знать методы решения линейных, квадратных уравнений и неравенств. Применять их при решении упражнений. 

Теоретический материал:

Простейшее линейное уравнение: 𝑎𝑥 + 𝑏 = 0.       

𝑏

𝑥 = −  , если 𝑎 ≠ 0;

𝑎

𝑥 ∈ (−∞; ∞), если 𝑎 = 0,    нет решения,если 𝑎 = 0, 𝑏 ≠ 0.

Приведенное квадратное уравнение: 𝑥² + 𝑝𝑥 + 𝑞 = 0        

Теорема  Виета:               𝑥₁ + 𝑥₂ = −𝑝,         𝑥₂ ∙ 𝑥₂ = 𝑞.

Решение квадратных уравнений:

𝑎 ∙ 𝑥² + 𝑏𝑥 + 𝑐 = 0

𝐷 = 𝑏² − 4𝑎𝑐,

Если 𝐷 > 0, то 𝑥1,2 = −𝑏2±𝑎√𝑑 Если 𝐷 = 0, то 𝑥 = ^−𝑏

2𝑎

Если 𝐷 < 0, то корней нет

Алгоритм решения квадратного уравнения	Решить квадратное уравнение
1.       Найдите коэффициенты квадратного уравнения 2.       Запишите формулу для нахождения дискриминанта квадратного уравнения 3.       Найдите дискриминант 4.       Запишите формулу для нахождения корней квадратного уравнения 5.       Найдите корни квадратного уравнения 6.       Запишите ответ	𝟐х𝟐 + 𝟓х − 𝟕 = 𝟎 a=     , b=    , c= D= D= х1,2= х1= х2= Ответ:

Решить самостоятельно уравнения:

№п/п	Вариант 1	Вариант 2	Вариант 3
1	𝑥2 = 3𝑥	𝑥2 + 3𝑥 = 0	3𝑥 − 𝑥2 = 0
2	2𝑥2 + 4 = 0	2𝑥2 − 4 = 0	3𝑥2 + 27 = 0
3	−3𝑥2 + 27 = 0	𝑥2  = 3 3	𝑥2 − 4𝑥 = 5
4	𝑥2 − 14𝑥 = −48	105 + 𝑥2 = 22𝑥	4𝑥 + 𝑥2 = −15
5	3𝑥 + 1 𝑥 − 1  = 1 +            𝑥 + 2                 𝑥 − 2	2𝑥 − 2      𝑥 + 3         − = 5            𝑥 + 3        3 − 𝑥	4                  4                 5 −                                                      = 9𝑥2 − 1         3х + 1          1 − 3х

Решение линейных и квадратных неравенств

Теоретический материал

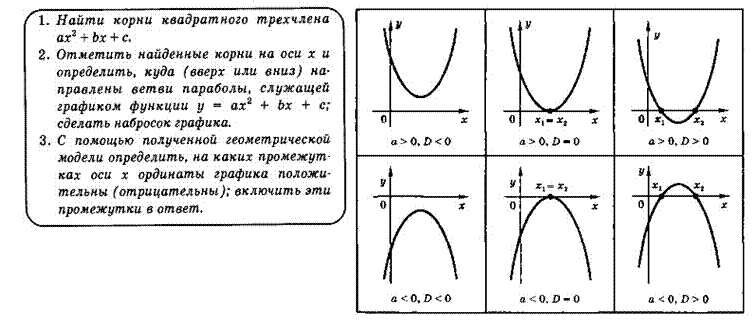
Алгоритм решения квадратного неравенства 𝒂𝒙^𝟐 + 𝒃𝒙 + 𝒄 > 0,   𝑎𝒙^𝟐 + 𝒃𝒙 + 𝒄 < 0

   Решить самостоятельно:

№п/п	Вариант 1	Вариант 2
1	𝟒х + 𝟐 < 0	−𝟖х − 𝟔 > 0
2	−𝟓х − 𝟏 ≤ 𝟎	𝟓х − 𝟔 ≤ −𝟐
3	−𝟏𝟎х + 𝟒 > −6	𝟓х + 𝟗 < −10
4	𝟔х − 𝟑 ≥ −𝟔 + 𝟖х	−𝟑х + 𝟐 < 4 + 3х
5	𝟒(𝟐 + х) ≤ 𝟏	𝟑(−𝟒 − х) ≤ 𝟗

Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок.

Раздел 17: Обобщающее повторение. Подготовка к экзамену

Самостоятельная работа № 19  на тему: Домашняя контрольная работа

Цель:  Контроль знаний учащихся

Выбор варианта (№1,4,7,10,13,16,19,22,25- ПЕРВЫЙ ВАРИАНТ)

(№2,5,8,11,14,17,20,23,26- ВТОРОЙ ВАРИАНТ)

(№3,6,9,12,15,18,21,24,27- ТРЕТИЙ ВАРИАНТ)

Вариант 1

1.      Решить уравнение: 2𝑠𝑖𝑛²𝑥 − 3𝑐𝑜𝑠𝑥 − 3 = 0

2.      Решить систему уравнений:   { ^{𝑥 − 𝑦 = 5} log₅(4𝑥 + 𝑦) = 2

3.      Найдите угловой коэффициент касательной. Проведенной к графику функции

4.      𝑓(𝑥) = 2𝑥³ − 𝑥 + 3 в точке с абсциссой  𝑥₀ = −1.

5.      Решить уравнение:   log(2𝑥 − 1) − log 16 = 5 6. Радиус основания цилиндра  равен 4 см, площадь боковой поверхности вдвое больше площади основания. Найти объем цилиндра. 7. Найдите область определения:     𝑦 = _𝑙𝑔 ^4−5𝑥.

𝑥−3

Вариант 2

1.      Решить уравнение: 2𝑠𝑖𝑛²𝑥 + 𝑐𝑜𝑠²𝑥 − 3𝑠𝑖𝑛𝑥 − 5 = 0

𝑥 − 𝑦 = 4

2.      Решить систему уравнений:   { log₄(3𝑥 + 𝑦) = 2

3.      Найдите угловой коэффициент касательной. Проведенной к графику функции

4.      𝑓(𝑥) = 4𝑥² + 7𝑥 + 1 в точке с абсциссой  𝑥₀ = −2.

5.      Решить уравнение:   log(3𝑥 + 2) − log = 2

6.      Найдите все первообразные функции:   𝑓(𝑥) = 𝑥⁷ − 𝑥⁹ − 𝑐𝑜𝑠5𝑥

7.      Радиус основания цилиндра  равен 3 см, площадь боковой поверхности  втрое больше площади основания. Найти объем цилиндра.

Вариант 3

1.      Решить уравнение: 𝑠𝑖𝑛²𝑥 + 2𝑐𝑜𝑠²𝑥 − 5𝑐𝑜𝑠𝑥 − 7 = 0

𝑥 + 𝑦 = 17

2.      Решить систему уравнений:   { log₃(3𝑥 + 𝑦) = 3

3.      Найдите угловой коэффициент касательной. Проведенной к графику функции

4.      𝑓(𝑥) = 4𝑥³ − 3𝑥 + 1 в точке с абсциссой  𝑥₀ = −2.

5.      Решить уравнение:   log₂(5 − 2𝑥) + log₂ 8 = 4

6.      Найдите все первообразные функции:   𝑓(𝑥) = 𝑥³ − 𝑥⁹ − 𝑐𝑜𝑠4𝑥

7.      Радиус основания цилиндра  равен 6 см, площадь боковой поверхности  в четыре раза больше  площади основания. Найти объем цилиндра.

Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок.

3.  РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ РАЗЛИЧНЫХ ВИДОВ

САМОСТОЯТЕЛЬНОЙ РАБОТЫ

3.1. Рекомендации по подготовке, написанию, защите и оцениванию реферата как вида самостоятельной работы

Реферат – (нем. Referat – докладываю) краткое изложение (перед аудиторией или в письменной форме) содержания книги, статьи, рассмотрения различных источников информации и т.д. Выбор темы реферата.

Предлагается преподавателем или выбирается самостоятельно обучаемым.

Поиск информации.

Если обучающемуся выдана только тема реферата, то поиски информации необходимо осуществлять в учебных и справочных источниках, энциклопедиях по основным (ключевым словам).   

Отбор материала.

Следует выбрать наиболее важный материал, который отображает основные теоретические сведения по тематике реферата. Можно использовать обобщающие таблицы, схемы, диаграммы, графики, рисунки, чертежи и другие иллюстративные материалы. 

Отобранный материал следует систематизировать, структурировать, построить в логической последовательности. Для этого необходимо составить план, который включает такие элементы как:

1.  Введение.

2.  Основная часть (не менее 2 пунктов реферата).

3.  Выводы.

4.  Приложения (в случае необходимости).

5.  Список использованной литературы.

Создание реферата.

Во введении должны быть раскрыты цель и основные задачи данной реферативной работы. 

В основной части должны быть последовательно раскрыты задачи реферата. При этом предлагается в первом пункте представить теоретические моменты по теме реферата. Во втором пункте практические моменты по теме реферата (последовательность осуществления действий, форма представления продукта деятельности, графики изменения деятельности).

В заключении необходимо продемонстрировать насколько решены поставленные задачи (во введении реферата).

В приложениях необходимо представить средства, которые позволяют визуализировать теоретические сведения (рисунки, графики, последовательность действий, фотографии). 

Пункт реферата список использованной литературы должен содержать информацию об источниках, которые использовались при написании реферата. 

Правила оформления и защиты реферата. Реферат должен иметь титульную страницу (см. рис. 1), содержание, изложение основного материала, выводы, приложения (при необходимости), список использованной литературы. 

Объем реферата составляет – 7-15 листов печатного текста, согласно следующих параметров: шрифт Times New Roman, 14 кегль, междустрочный интервал – 1,5 см; поля – 1,5 см; левое поле – 2 см.

Защита реферата представляет собой краткое, сжатое изложение самых основных положений, интересных и новых фактов, сделанных выводов. Для представления реферата необходимо подготовить сообщение, доклад продолжительностью до 5 минут. 

После представления реферата обучающиеся и преподаватель могут задавать вопросы, которые у них возникли. 

Оценивание реферата. Оценивается самостоятельная работа по подготовке и защите реферата в пределах 3-5 баллов. 

5 баллов – реферат содержит не только теоретические сведения, но и практическую информацию по особенностям выполнения действий, представления продукта деятельности; подготовленный по реферату доклад, раскрывает и теоретические и практические вопросы;

4 балла – реферат содержит и теоретические и практические сведения, однако в докладе представляются только теоретические(практические) сведения;

3 балла – реферат представлен теоретической и практической информацией, доклад по реферату не представлен.

2 балла – содержание реферата не соответствует его теме.

Темы рефератов по дисциплинам и список рекомендуемой литературы представлены в приложении А.

3.2 Рекомендации по подготовке и оцениванию презентации как вида самостоятельной работы

Одним из видов самостоятельной работы является подготовка презентаций по учебному заданию преподавателя. Презентация – это «..способ подачи информации, в котором присутствуют рисунки, фотографии, анимация и звук».

Презентация позволяет оценить качество выполненной работы. Созданию презентации предшествует работа с информацией, рисунками, схемами выполнения элементов профессиональной деятельности. Грамотно составленная презентация возможна при условии выполнения следующего алгоритма действий. 

1)     определение цели работы,  выбор основных понятий, необходимых для отражения в презентации;

2)     отбор рисунков, схем, картинок, роликов, которые предполагается использовать в презентации;

3)     выбор последовательности и способов представления материала – в виде таблицы, схемы или текста;

4)     выбор типов слайдов (программа PowerPoint):

–   темы слайда;

–   цветовой гаммы;

–   выбор эффектов и анимации, которую предполагается использовать

в презентации;

5)     проверка визуального восприятия презентации.

Рекомендации по созданию презентации:

–        подготовка всей информации отдельно на листе, с последующим переносом на слайды;

–        минимальное количество текстовой информации на слайде (5-7 слов), иначе ухудшается визуальное восприятие слайда;

–        количество слайдов от 10-20;

–        отражение в презентации темы, фамилии и инициалов ее создателя, плана презентации.

Оценивание презентации. Оценивается самостоятельная работа по подготовке и представлению презентации в пределах 3-5 баллов. 

5 баллов – четко определена структура презентации, на слайдах отсутствует лишняя информация, которая «перегружает» их, выбран рациональный способ представления информации и оформления слайдов, учтена психологические требования к оформлению презентаций; 

4 балла – четко определена структура презентации, однако на слайдах присутствует лишняя информация; выбран рациональный способ представления информации, учитывающий психологическое воздействие сочетания цвета фона, цвета текста, эффектов на обучаемых;

3 балла –отсутствует четкость в структуре презентации, презентация перегружена информацией, для которой не выбран способ ее представления, нарушены требования к оформлению презентаций;

2 балла – презентация не соответствует заявленной теме, выполнена с нарушением всех правил подготовки презентации. 

Предлагаемые темы для создания презентаций представлены в приложении

Б.

4.Критерии оценивания результатов самостоятельной работы студента

 

Критериями оценивания результатов самостоятельной работы студента являются:

-     уровень усвоения студентом учебного материала;

-     умение студента использовать теоретические знания при выполнении практических задач;

-     сформированность ключевых (общеучебных) компетенций;  обоснованность и четкость изложения материала;  уровень оформления работы. 

 

Оценивание индивидуальных образовательных достижений по результатам выполнения ВСР  производится в соответствии с универсальной шкалой (таблица). 

Процент результативности (правильных ответов)	Качественная оценка индивидуальных образовательных достижений
	балл (отметка)	вербальный аналог
90 ÷ 100	5	отлично
80 ÷ 89	4	хорошо
70 ÷ 79	3	удовлетворительно
менее 70	2	неудовлетворительно

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Литература: 1. Алгебра и начала анализа: учеб. Для 10-11 кл. общеобразоват. учреждений  / [Ш. А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.].-15-е изд. – М.: Просвещение, 2013. 

2.      Алгебра и начала математического анализа. 10-11 классы. В 2ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) /А.Г. Мордкович. – 10-е изд. Стер. – М.: Мнемозина, 2013.

3.      Алгебра и начала математического анализа. 10-11 классы. В 2ч. Ч.2. Задачник для учащихся общеобразовательных учреждений (базовый уровень) / [А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. – 10-е изд. Стер. – М.: Мнемозина, 2012.

4.      Математика. Задачник: учеб. пособие для образ. уч.начального и сред.проф. образования/М.И. Башмаков.- М.: Академия,2010.

5.      Математика. Учебник: учеб. пособие для образ. уч.начального и сред.проф. образования/М.И. Башмаков.- М.: Академия,2010.

6.      Севрюков П.Ф. Тригонометрические, показательные и логарифмические  уравнения и неравенства; учебное пособие /П.Ф. Севрюков, А.Н. Смоляков. – М.: Илекса; Народное образование; Ставрополь; Сервисмаш, 2011.

7.      Черкасов О.Ю., Якушев А.Г. Математика: интенсивный курс подготовки к экзамену. - М.: Рольф, 2005.

8.      Шабунин М.И. Математика для поступающих в вузы. Уравнения и системы уравнений. - М.: Аквариум, 2007.

9.      Шабунин М.И. Математика для поступающих в вузы. Неравенства и системы неравенств.- М.: Аквариум, 2007.

Интернет - ресурсы

1.      http://catalog.alledu.ru/predmet/math/

2.      Учебно-информационные комплексы по математике для средних школ: http://mschool.kubsu.ru/uik/index.htm  

3.      Сайт-справочник правил, формул и теорем по математике:        http://matemathik.narod.ru/  

4.      Мир Геометрии: http://geometr.info/

5.      Страна Математика: http://www.bymath.net/

6.      Научно-популярный физико-математический журнал "Квант" (статьи по математике): http://kvant.mirror1.mccme.ru/rub/1.htm 7. Графики функций" Небольшой сайт в помощь школьнику, изучающему графики функций: определения, примеры, задачник:

http://graphfunk.narod.ru/

8. Виртуальная школа юного математика http://math.ournet.md/indexr.html

       

       

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ АЛТАЙСКОГО КРАЯ КГБПОУ «АЛТАЙСКИЙ ТРАНСПОРТНЫЙ ТЕХНИКУМ» РЕСУРСНЫЙ ЦЕНТР ПО ТРАНСПОРТУ   РЕФЕРАТ на тему «                                                                              » по дисциплине «     »   Подготовил ________________  Проверил __________________       Оценка ____________________ _________________201__г.

Рис. 1. Образец оформления титульного листа реферата

Приложение А Тематика рефератов:

№	Темы
1	Функция и её свойства
2	Теория погрешностей
3	Теория поверхностей
4	Теорема о ранге матрицы
5	Спираль Архимеда. Логарифмическая, гиперболическая спираль
6	Софья Васильевна Ковалевская
7	Математика в моей профессии
8	Решение задачи Коши методом Рунге-Кутта
9	Рекуррентно заданные числовые последовательности
10	Расчет запаса жизненных сил. Время жизни после лечения
11	Применение кривых второго порядка в компьютерных системах
12	Применение двойного интеграла
13	Предикаты: определения и примеры
14	Почти возрастающая функция
15	Основы тригонометрических вычислений
16	Основы комбинаторики
17	Определение функции Ляпунова и реализация в Matlab
18	Метод Ньютона и его модификации
19	Математические модели технических систем
20	Максимумы, минимумы в геометрии
21	Лист Мёбиуса
22	Корреляционные зависимости в физическом эксперименте
23	История формирования понятия "алгоритм". Известнейшие алгоритмы в истории математики
24	Золотое сечение
25	Диофантовы уравнения
26	Двоичная система счисления
27	Волновое уравнение в математике
28	Виды поверхностей

 

29	Абсолютная и относительная погрешность
30	Эвклидова геометрия
31	Суммирование расходящихся рядов
32	Решение нелинейных уравнений методом итераций
33	Параметрические и непараметрические методы оценивания
34	Минимакс и многокритериальная оптимизация
35	Метод хорд
36	Интегральные характеристики векторных полей
37	Знаменитые задачи древности: удвоение куба
38	Жизнь и научная деятельность Андрея Николаевича Колмогорова
39	Дифференциальные операции второго порядка
40	Группы, кольца, поля
41	Аксиоматика Вейля
42	Эволюционная стратегия
43	Теория вероятности

 

44	Теоретические основы метода сеток. Построение конечно-разностной схемы. Погрешность аппроксимации, устойчивость. Основная теорема метода сеток
45	Случайные события в элементарной теории вероятностей
46	Различные методы решения планиметрических задач
47	Пчелиные соты
48	Онтологический статус основных понятий математической концепции Н. Бурбаки
49	Линейное программирование
50	Измерение геометрических величин

      

 

Приложение Б

Перечень тем для создания презентаций

1.     Непрерывные дроби

2.     Применение сложных процентов в экономических расчетах

3.     Параллельное проектирование

4.     Средние значения и их применение в статистике

5.     Векторное задание прямых и плоскостей в пространстве

6.     Сложение гармонических колебаний

7.     Графическое решение уравнений и неравенств

8.     Правильные и полуправильные многогранники

9.     Конические сечения и их применение в технике

10. Понятие дифференциала и его приложения

11. Схемы Бернулли повторных испытаний

12. Исследование уравнений и неравенств с параметром

 

      

 

58

---