Методические рекомендации по решению однородных уравнений  для учащихся 10 класса (повторение 8-9 класс)

Решение однородных уравнений

Определение. Если все члены уравнения (в левой и правой частях которого стоят многочлены от двух переменных или от двух видов переменных) имеют одинаковую суммарную степень, то уравнение называется однородным.

Однородное уравнение второй степени: ap²(x)+bp(x)q(x)+cq²(x)=0, где p(x),q(x) - выражения, зависящие от переменной x, с ненулевыми коэффициентами a, b и  c.  

Однородное уравнение третьей степени:  ap³(x)+bp²(x)q(x)+cp(x)q²(x)+dq³(x)=0, где          p(x),q(x) - выражения, зависящие от переменной x, с ненулевыми коэффициентами a, b,  c и d.  

            Как узнать однородное                           Примеры однородных уравнений

уравнение

 Рассмотрим однородное уравнение второй степени: ap²(x)+bp(x)q(x)+cq²(x)=0,

•    Приведём уравнение к виду, где правая часть равна нулю.

•    Внимательно просматриваем выражение в левой части уравнения и видим повторяющиеся фрагменты p(x) и q(x), содержащие переменную.

•    Эти фрагменты заменяем другими переменными: u = p(x), v = q(x), чтобы выражение представляло собой многочлен относительно u и

v.

•    Если этот многочлен является однородным относительно 2переменных, тогда и исходное выражение относительно p(x) и q(x) было однородным, а, значит, уравнение также является однородным

1)        2x⁴+3x²(x−2)=2(x−2)²

однородное уравнение относительно p(x) = x² и q(x) = (x-2)

2)        (x²−5)²−3(x²−5)(2x−5)+2(2 x−5)²=0

однородное уравнение относительно p(x) = (x²  -5) и q(x) = (2x-5)

Определите относительно каких выражений уравнения являются однородными:

3)        (x²−3 x−2)²−3(x²−3x−2)(x²−3)+2(x²−3)²=0 ;

4)        (x²−1)²+4(x⁴−1)+3(x²+1)²=0 ;

5)        2(x²+x+1)²−7(x−1)²=13(x³−1) ;

                   x−2 ²              x+2 ²               x²−4

6)        20( x+1 ) −5( x−1) +48( x₂−1)=0 ;

7)        x⁴+5 x²(x+1)=6(x+1)² ;

8)        3(x+2)²+2(x²−2 x+4)²=5(x³+8) ;

    ;

10*) sin²(x)−3sin(x)cos(x)+2cos²(x)=0 ;

11*) 5^2x−3⋅5^x⋅7^x+2⋅7^2x=0 .

 ap²(x)+bp(x)q(x)+cq²(x)=0,

Идея:  Решается однородное уравнение делением на наивысшую степень одной из переменных.

1) предполагаем, что  q(x) =0 , в этом случае корни уравнения совпадают с решениями системы p(x)=0; q(x)=0.

Решаем эту систему.

2.  Предполагаем, что       q(x)≠0    . Делим обе части уравнения на наивысшую степень данного выражения   q²(x) .

          p(x) ²             p(x)

a( ) +b +c=0, q(x) q(x)

3.  Замена:            p^(x)₌t q(x)

4.  Решаем уравнение с новой переменной. Выполняем обратную замену.

3) (x²−3 x−2)²−3(x²−3x−2)(x²−3)+2(x²−3)²=0

однородное уравнение относительно p(x) = (x²  -3x-2) и q(x) = (x²-3)         1) q(x) = (x²-3)=0                ⇒x²−3=0; ⇒x_∈∅

2

x −3 x−2=0.

решаем первое уравнение в системе:

также решаем второе уравнение:

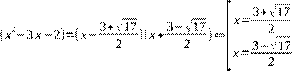
        2) q(x) = (x²-3) ≠ 0     

Разделим  почленно уравнение на наивысшую степень q(x):

(x²−3)² :

(x²−3 x−2)²                           3(x²−3 x−2)(x²−3) 2(x²−3)²

                            −                                       +                    =0⇔

          (x2−3)2                                   (x2−3)2                             (x2−3)2

        x²−3 x−2 ²               3(x²−3 x−2) 2=0

(     2 3 ) −           (x2−3)     + x −

(x²−3 x−2)

Замена:           (x₂−₃₎       =t

t²−3t+2=0⇔   (t−1)(t−2)=0⇔  [^t=1 t=2 Обратная замена:

(x²−3x−2)

              ²                              =1 [ ² 3x−2−x²+3=0 _⇔[    x⁼¹3           _⇔

            (x −3)                _⇔ x −

          2                                                2                                   2

          (x −3x−2)=2               x −3x−2−2x +6=0              x2₊3x₋4₌0

₂

(x −3)

1

                 x₌1                     x=

                      3         ⇔[ 3

(x+4)(x−1)=0 xx⁼₌⁻14 Ответ: −4; ;1

ap²(x)+bp(x)q(x)+cq²(x)=0,

Идея:  Решается однородное уравнение делением на наивысшую степень одной из переменных.

1) предполагаем, что  q(x) =0 , в этом случае корни уравнения совпадают с решениями системы p(x)=0; q(x)=0.

Решаем эту систему.

2.  Предполагаем, что       q(x)≠0    . Делим обе части уравнения на наивысшую степень данного выражения   q²(x) . p(x) ²                 p(x)

a( ) +b +c=0, q(x) q(x)

3.  Замена:            p^(x)₌t q(x)

4.  Решаем уравнение с новой переменной. Выполняем обратную замену.

4) (x²−1)²+4(x⁴−1)+3(x²+1)²=0

однородное уравнение относительно p(x) = (x²  -1) и q(x) = (x²+1)

1)  q(x) = (x²+1)=0                ⇒{x²₂+1=0; ⇒x_∈∅

x −1=0.

первое уравнение системы не имеет решений.

2)  q(x) = (x²+1) ≠ 0     

Разделим  почленно уравнение на наивысшую степень q(x):

(x²+1)² :

          (x²2−11)²+ 4(x²−1)(x²+1)+3(x²+1)²=0⇔                     ( x²−1 )²+ 4(x²−1) 3=0

+

      (x + )₂                     (x₂+1)₂                     (x₂+1)₂                                    x₂+1          (x₂+1)

Замена: (xx22−11))=t

( +

t²+4t+3=0⇔   (t+1)(t+3)=0⇔  [^t=−3 t=−1 Обратная замена:

(x²−1)

(x2+1)=−3⇔[ x2−1+x2+1=0 ⇔x=0

          2                                       2                           2

        (x −1)                     x −1=−3 x −3

          2              =−1

(x +1)

Ответ:     0

7)         x⁴+5 x²(x+1)=6(x+1)²

однородное уравнение относительно p(x) = x²   и q(x) = (x+1)

1)  q(x) = (x+1)=0                ⇒{ ^x4=0; ⇒x∈∅ x+1=0.

2)  q(x) = (x²-3) ≠ 0     

Разделим  почленно уравнение на наивысшую степень q(x): (x+1)² :

(x(x+²1)²)²+5(xx²(+x1+₎²1)+6₍(xx++11₎²)²=   xx+²1 ² (5x(+x1²)) 6=0

                                                              0⇔         (          ) +            +

(x²)

Замена:      =t

(x+1)

t²+5t−6=0⇔   (t+6)(t−1)=0⇔  [^t=−6 t=1 Обратная замена:

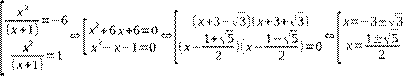
Ответ:     

Вопросы для контроля:

1.  Как распознать однородное уравнение?

2.  Какое свойство числового равенства применяется при решении однородного уравнения(деление уравнения)?

3.  Можно ли делить обе части однородного уравнения на выражение, содержащуюпеременную? Ответ поясните.

Задания для самостоятельного решения:

1)           2x⁴+3x²(x−2)=2(x−2)²

2)           (x²−5)²−3(x²−5)(2x−5)+2(2 x−5)²=0

3)           2(x²+x+1)²−7(x−1)²=13(x³−1) ;

                              2                                  2                       2

4)           20( xx−+12) −5( xx−+21) +48(xx2−−41)=0 ;

5)           3(x+2)²+2(x²−2 x+4)²=5(x³+8) ;

6)           4(x²−x+1)²+5(x+1)²=12(x³+1)

7)           x⁴+2 x²(x−1)=24(x−1)²

 ;

                         13

9)                                  2+ 2=−( 2       ) ;

              (5−x)       (x+5)            x −25

                      1                 2                  3

10)                              ₂             + ₂          − ₂          =0 ; x +2 x+1   x +4 x+4     x +3 x+2

Домашнее задание

1.  Решить однородные уравнения:

           x−2 2                         x+2 2                      x2−4                 3.                 34

           +              −           x −4

    Список литературы:

1.                  Мерзляк А.Г. Алгебра: 8 класс: учебник для учащихся общеобразовательныхорганизаций / А.Г. Мерзляк, В.П. Поляков. - 2-е изд., стереотип. - М.: Вентана-Граф, 2019. 384с. [глава 37]

2.                  Нелин Е.П. Алгебра. 7-11 классы. Определения, свойства, методы решения задач — втаблицах. Сер. Комплексная подготовка к ЕГЭ и ГИА (ОГЭ). - 4-е изд., испр. - М.: ИЛЕКСА, 2019 — 128 с.

3.                  Шарыгин И.Ф. Факультативный курс по математике: Решение задач: Учеб. Пособие для 10 кл. сред. шк. - М.: просвещение, 1989. - 252с. [§ 2 Уравнения и системы уравнений]

4.                  Подготовка к олимпиадам и ЕГЭ по математике и физике: И.В. Яковлев [Электронный ресурс]. - Режим доступа: https://mathus.ru/math/alguzap.pdf  [Дата обращения 30.06.2021]