Методические рекомендации по решению симметрических (возвратных) алгебраических уравнений для учащихся 10 класса
Методические рекомендации по решению симметрических (возвратных) уравнений для учащихся 10 класса (повторение 8-9 класс)
Решение симметрических и возвратных уравнений
Симметрические уравнения третьей и четвертой степени имеют следующий общий (канонический) вид:
ах3 + bх2 + bх + а = 0, а ≠ 0, (1) ах4 + bх3 + сх2 + bх + а = 0 , а≠ 0, (2)
В канонической записи симметрического уравнения его коэффициенты a, b и c симметричны относительно центрального слагаемого.
Возвратное уравнение четвертой степени имеет следующий общий (канонический) вид: ах4 + bх3 + сх2 + bkх + аk2 = 0 , а≠ 0, (3)
При k =1, имеем симметрическое уравнение четвертой степени.
Определите вид уравнения, для возвратных уравнений поределите значение коэффициента k.
1) 3 x3−2x2+2x−3=0 ;
2) 3 x4−2 x3+4 x2−4 x+12=0 ;
3) 2x4+3x3−4 x2−3 x+2=0 ;
4) x4+2 x3−12x2−4 x+4=0 ;
5) x4−5 x3+4 x2+5 x+1=0 ;
6) 9 x4+9 x3−4 x2−3 x+1=0 ;
7) 3 x4−2 x3+4 x2−4 x+12=0 ;
8) x4−8 x3+17 x2−8 x+1=0 ;
9) x4−5 x3+10x2−10 x+4=0 ;
10) 4(x3−x)=(x2+1)2 ;
11) x4−7 x3+12x2−21 x+9=0 ;
12) 6 x4+5 x3−38x2+5 x+6=0 ;
13) x4−2 x3−18 x2−6 x+9=0 ;
14) x4−3 x3−8 x2+12x+16=0 ;
15) x5+3 x4−x3+2 x2−24 x−32=0
обобщенное возвратное уравнение 5 степени, k = -2:
x5+3 x4−x3−x2(−2)−3 x(−2)3+(−2)5=0
Примеры решения симметрических и возвратных уравнений
Метод или идея решения Примеры решений симметрических уравнений
симметрическое уравнение 3-й степени
Идея: Симметрические уравнения третьей степени решаем методом разложения на множители.
1. Установить соответствие общему(каноническому виду) симметрического уравнения третьей степени.
2. Разложим многочлен в левой части уравнения на множители: a(x3+1)+bx(x+1)=a(x+1)(x2−x+1)+bx(x+1) (x+1)(ax2+(b−a)x+a)
Значит исходное уравнение равносильно следующему: (x+1)(ax2+(b−a)x+a)=0⇔
[ 2 x+1=0 . ax +(b−a) x+a=0
Решая совокупность уравнений, находим корни исходного уравнения.
Замечание: Симметрическое уравнение третьей (нечетной) степени всегда имеет корень x = -1.
Первое уравнение совокупности всегда х+1=0, а второе уравнение — возвратное уравнение четной степени.
1)
3
x3+4 x2+4 x+3=0
симметрическое уравнение 3-й степени.
Разложим многочлен f (x)=3 x3+4 x2+4 x+3 на множители:
3 x3+4 x2+4 x+3=3(x3+1)+4 x(x+1)=(x+1)(3 x2+x+3)
3 x3+4 x2+4 x+3=0⇔(x+1)(3 x2+x+3)=0⇔
[ x2 +1=0 ⇔x=−1
3 x +x+3=0
второе уравнение всовокупности не имеет корней.
Ответ: -1.
Перед рассмотрением метода решения симметрических и возвратных уравнений вспомните метод решения уравнения вида:
3(x2+x12)+(x+ 1x )−414 =0
(Методические рекомендации по применению метода замены переменной при решении алгебраических уравнений) .
Решаем уравнение методом замены переменной.
Замена: x+1x =t, x2+ x12=t2−2
Записать решение уравнения в тетрадь.
Ответ: {
;
;−2;−
}
|
Метод или идея решения |
Примеры решений возвратных уравнений |
|
ax4+bx3+сx2+bx+a=0, симметрическое уравнение 4-й степени (частный случай возвратного уравнения) ax4+bx3+сx2+bxk+ak2=0, Идея: уравнения 4-ой степени (четной степени) делим на х2 (на степень среднего члена) и группируем слагаемые с одинаковыми коээфициентами, далее решаем уравнение методом заены переменной. 1. Установить соответствие общему (каноническому виду) симметрического |
1) x4−5 x3+8 x2−5x+1=0 Решение: симметрическое уравнение 4-й степени. Средний член: 8·х2. Т.к. х = 0 не является корнем уравнения, то разделив уравнение на степень среднего члена х2, имеем уравнение равносильное данному: x2−5x+8−5+ x12=0 x Сгруппируем слагаемые, перепишем уравнение в виде: x2+ 12−5(x+1x)+8=0 x Замена: x+1=t , x2+ 12=t2−2 x x t2−5t+6=0⇔(t−2)(t−3)=0⇔[t=2 t=3 Обратная замена: |
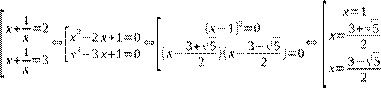уравнения
4-й степени (возвратного уравнения 4-ой степени).
2.
Замечаем, что х = 0 не является корнем уравнения. Разделим обе части уравнения
на (степень среднего члена) х2:
ax4+bx3+сx2+bx+a=0⇔ Ответ:
|
ax2+ a2+bx+bx +с=0⇔ x Сгруппируем слагаемые: a(x2+ 12−2)+b(x+1x )+с=0 x 1 3. Выполним замену x+ =t . x |
. |
2) 2x4+3x3−3 x2−3 x+2=0 Решение: возвратное уравнение 4-й степени, k= -1. Средний член: -3·х2. Т.к. х = 0 не является корнем уравнения, то разделив уравнение на степень среднего члена х2, имеем уравнение равносильное данному: 2x2+3x−3−3+ x22=0 x Сгруппируем слагаемые, перепишем уравнение в виде: |
в
результате замены получим квадратное уравнение относительно переменной t:
at2+bt+c−2a=0 . Замена: x
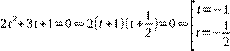
Обратная замена:
⇔
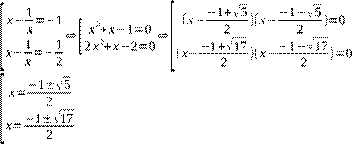Ответ:
Задания для самостоятельного решения:
1) 3 x3−2x2+2x−3=0 ;
2) 3 x4−2 x3+4 x2−4 x+12=0 ;
3) 2x4+3x3−4 x2−3 x+2=0 ;
4) x4+2 x3−12x2−4 x+4=0 ;
5) x4−5 x3+4 x2+5 x+1=0 ;
6) 9 x4+9 x3−4 x2−3 x+1=0 ;
7) 3 x4−2 x3+4 x2−4 x+12=0 ;
8) x4−8 x3+17 x2−8 x+1=0 ;
9) x4−5 x3+10x2−10 x+4=0 ;
10) 4(x3−x)=(x2+1)2 ;
11) x4−7 x3+12x2−21 x+9=0 ;
12) 6 x4+5 x3−38x2+5 x+6=0 ;
13) x4−2 x3−18 x2−6 x+9=0 ; 14) x4−3 x3−8 x2+12x+16=0 ;
15) x5+3 x4−x3+2 x2−24 x−32=0 .
Список литературы:
1. Мерзляк А.Г. Алгебра: 8 класс: учебник для учащихся общеобразовательныхорганизаций / А.Г. Мерзляк, В.П. Поляков. - 2-е изд., стереотип. - М.: Вентана-Граф, 2019. 384с. [глава 37]
2. Нелин Е.П. Алгебра. 7-11 классы. Определения, свойства, методы решения задач — втаблицах. Сер. Комплексная подготовка к ЕГЭ и ГИА (ОГЭ). - 4-е изд., испр. - М.: ИЛЕКСА, 2019 — 128 с.
3. Шарыгин И.Ф. Факультативный курс по математике: Решение задач: Учеб. Пособие для 10 кл. сред. шк. - М.: просвещение, 1989. - 252с. [§ 2 Уравнения и системы уравнений]
4. Подготовка к олимпиадам и ЕГЭ по математике и физике: И.В. Яковлев [Электронный ресурс]. - Режим доступа: https://mathus.ru/math/alguzap.pdf [Дата обращения 30.06.2021]
Методические рекомендации по решению симметрических (возвратных) уравнений для учащихся 10 класса (повторение 8-9 класс)
Примеры решения симметрических и возвратных уравнений
Ответ: { ; ; − 2 ; − }
Ответ: Задания для самостоятельного решения: 1) 3 x 3 − 2 x 2 + 2 x − 3 = 0 ; 2) 3 x 4…
© ООО «Знанио»
С вами с 2009 года.
