
Омский летно-технический колледж гражданской авиации имени А.В. Ляпидевского
- филиал федерального государственного бюджетного образовательного учреждения высшего образования
«Ульяновский институт гражданской авиации имени Главного маршала авиации Б.П. Бугаева»
(ОЛТК ГА – филиал ФГБОУ ВО УИ ГА)
 |
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ
по дисциплине
«Математика»
Специальности
25.02.01 Техническая эксплуатация летательных аппаратов и двигателей
25.02.04 Летная эксплуатация летательных аппаратов
Разработал:
Пищагина Е.С., преподаватель математики
Рассмотрено
на заседании ЦМК ЕНД
от «_____»__________20__г.
Протокол №_________
Омск - 2021
АННОТАЦИЯ
Методические рекомендации по выполнению практических работ по дисциплине «Математика», являющейся дисциплиной математического и общего естественнонаучного учебного цикла составлены в соответствии с требованиями Федерального государственного образовательного стандарта специальности и на основании программы учебной дисциплины ЕН.01, Математика (рассмотрена и утверждена на заседании ЦМК ЕНД «____» ___________20____г., протокол № ___)
Методические рекомендации по выполнению практических работ предназначены для курсантов 1 курса по специальностям:
25.02.01 Техническая эксплуатация летательных аппаратов и двигателей
25.02.04 Летная эксплуатация летательных аппаратов
Темы практических работ соответствует основным разделам программы, их выполнение обеспечивает более глубокое изучение материала, направлено на закрепление и систематизацию знаний, умений и формирование общих компетенций. Виды практических работ включают работу с понятийным аппаратом, вопросами по теме, подготовку к проверочным работам, решение задач, выполнение расчетно-графической работы.
Рецензент: ____________,
Пояснительная записка
Методические рекомендации по выполнению практических работ по естественно - научной дисциплине «Прикладная математика» предназначены для курсантов 1-го курса специальностей 25.02.01 Техническая эксплуатация летательных аппаратов и двигателей; 25.02.04 Летная эксплуатация летательных аппаратов
Объем практических работы курсантов определяется федеральным государственным образовательным стандартом среднего профессионального образования (ФГОС СПО).
Выполнение аудиторных практических работ является обязательным для каждого курсанта, их объём в часах определяется действующим рабочим учебным планом ОЛТК ГА филиала ФГБОУ ВО УИ ГА и составляет 36 часов.
Реализуемые цели выполнения практических работ:
- формирования общих и профессиональных компетенций
- систематизации и закрепления полученных теоретических знаний и практических умений студентов;
- углубления и расширения теоретических знаний;
- развития познавательных способностей и активности курсантов, самостоятельности, ответственности и организованности;
- формирования самостоятельности мышления, способностей к саморазвитию, самосовершенствованию и самореализации.
Выполнение практических работ представляет собой планируемую, организационно и методически направляемую преподавателем деятельность курсантов по освоению дисциплины «Прикладная математика».
Перед выполнением аудиторной практической работы курсант должен внимательно выслушать инструктаж преподавателя по выполнению задания, который включает определение цели задания, его содержание, ориентировочный объем работы, основные требования к результатам работы, критерии оценки. В процессе инструктажа преподаватель предупреждает курсантов о возможных типичных ошибках, встречающихся при выполнении задания.
Критериями оценки результатов аудиторной практической работы курсанта являются:
- уровень освоения курсантом учебного материала;
- умение курсанта использовать теоретические знания при выполнении практических задач;
- сформированность общеучебных умений;
- обоснованность и четкость изложения ответа;
- оформление материала в соответствии с требованиями.
Тематическое планирование практических работ
|
Тема 1.1 Матрицы, определители |
Практическая работа № 1. Операции с матрицами. Обратная матрица. |
2 |
|
Практическая работа № 2. Применение свойств определителей при их вычислении. |
2 |
|
|
Тема 1.2 Системы линейных уравнений |
Практическая работа № 3. Решение СЛАУ матричным методом. |
2 |
|
Практическая работа № 4. Решение СЛАУ методами Крамера и Гаусса. |
2 |
|
|
Тема 2.2 Действия над комплексными числами |
Практическая работа № 5. Выполнение алгебраических операций над комплексными числами в алгебраической форме. |
2 |
|
Практическая работа № 6. Выполнение алгебраических операций над комплексными числами в тригонометрической и показательной формах. |
2 |
|
|
Тема 3.2 Основные понятия теории пределов и непрерывности |
Практическая работа №7. Вычисление пределов, раскрытие неопределенностей (решение задач). |
2 |
|
Тема 4.1 Производная и дифференциал функции
|
Практическая работа №8. Вычисление производных и дифференциала функции |
2 |
|
Практическая работа №9. Вычисление производных и дифференциала сложных функций (решение задач). |
2 |
|
|
Тема 4.2 Неопределенный интеграл
|
Практическая работа № 10. Вычисление неопределенных интегралов непосредственным интегрированием (решение задач). |
2 |
|
Практическая работа № 11. Вычисление неопределенных интегралов методом подстановки и по частям (решение задач). |
2 |
|
|
Тема 4.3 Определенный интеграл |
Практическая работа № 12. Вычисление определенных интегралов непосредственным интегрированием (решение задач). |
2 |
|
Практическая работа № 13. Вычисление определенных интегралов методом подстановки и по частям (решение задач). |
2 |
|
|
Тема 4.4 Дифференциальные уравнения
|
Практическая работа № 14. Решение дифференциальных уравнений различного вида. |
2 |
|
Практическая работа № 15. Решение прикладных задач с помощью дифференциальных уравнений. |
2 |
|
|
Тема 5.1 Теория вероятностей |
Практическая работа № 16. Понятие о числе сочетаний (решение типовых задач). |
1 |
|
Тема 5.2 Случайная величина, ее функция распределения |
Практическая работа № 17. Произвольное, равномерное и биноминальное распределения. |
1 |
|
Тема 5.3 Математическое ожидание и дисперсия случайной величины |
Практическая работа № 18. Дисперсия случайной величины и ее свойства. |
1 |
|
Тема 5.4 Предмет и основные понятия математической статистики |
Практическая работа № 19. Построение вариационного ряда. |
1 |
|
Практическая работа № 20. Вычисление основных характеристик вариационного ряда. |
2 |
Требования к знаниям и умениям при выполнении практических работ
В результате выполнения практических работ, предусмотренных программой по данной специальности, курсант должен
знать:
- основные понятия и методы математического анализа, дискретной математики, теории вероятностей и математической статистики;
- основные численные методы решения прикладных задач.
уметь:
- определять производные сложных функций;
- исследовать функции с помощью производной;
- находить неопределенные интегралы;
- вычислять простейшие определенные интегралы;
- решать несложные задачи по теории вероятностей.
В каждой работе имеется теоретическая часть, включающая наиболее важные определения, теоремы и формулы.
В каждой работе разбирается один или несколько типовых примеров.
Задания, представленные в работах, соответствуют либо фронтальной, либо групповой, либо индивидуальной форме организации занятий.
По завершении работы курсанты должны ответить на контрольные вопросы, приведенные в методическом пособии.
Правила выполнения практических работ
1. курсант должен прийти на практическое занятие подготовленным к выполнению работы. Курсант, не подготовленный к работе, не может быть допущен к ее выполнению.
2. Каждый курсант после проведения работы должен представить отчет о проделанной работе с анализом полученных результатов и выводом по работе.
3. Отчет о проделанной работе следует выполнять в отдельной тетради. Содержание отчета указано ниже.
4. Расчет следует проводить с точностью до двух значащих цифр.
5. Если курсант не выполнил практическую работу или часть работы, то он может выполнить работу или оставшуюся часть во внеурочное время, согласованное с преподавателем.
6. Оценку по практической работе курсант получает, с учетом срока выполнения работы, если:
- расчеты выполнены правильно и полном объеме;
- студент может пояснить выполнение любого этапа работы;
- отчет выполнен в соответствии с требованиями к выполнению работы.
7. Зачет по практическим работам курсант получает при условии выполнения всех предусмотренных программой работ после сдачи отчетов по работам при удовлетворительных оценках за опросы и контрольные вопросы при выполнении практических заданий.
Содержание отчета
1. Название работы.
2. Цель работы.
3. Задание.
4. Формулы расчета.
5. Ответы на контрольные вопросы
Форма контроля и критерии оценки выполнения практических заданий.
Оценка «5» ставится, если: работа выполнена полностью; в логических рассуждениях и обосновании решения нет пробе лов и ошибок; в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Оценка «4» ставится, если: работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки); допущена одна существенная ошибка или два-три несущественных ошибки.
Оценка «3» ставится, если допущены более одной существенной ошибки или более двух-трех несущественных ошибок, но курсант владеет обязательными умениями по проверяемой теме; при этом правильно выполнено не менее половины работы.
Оценка «2» ставится, если: допущены существенные ошибки, показавшие, что курсант не владеет обязательными умениями по данной теме в полной мере.
Оценка «1» ставится, если: работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Практическая работа № 1
Операции с матрицами. Обратная матрица.
Цель: Формирование навыков выполнения операций над матрицами и вычисления определителей второго, третьего и четвертого порядков.
На выполнение практической работы отводится 1 час.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Операции над матрицами. Вычисление определителей
Прямоугольная матрица![]() размера
размера ![]() (
(![]() -матрица) имеет вид таблицы,
состоящей из
-матрица) имеет вид таблицы,
состоящей из ![]() строк и
строк и ![]() столбцов:
столбцов:
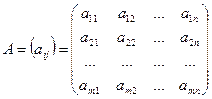 .
.
Элемент матрицы ![]() находится на пересечении
находится на пересечении ![]() -ой строки и
-ой строки и ![]() -го столбца,
-го столбца, ![]() ;
; ![]() .
.
У нулевой матрицы 0 все элементы равны нулю:
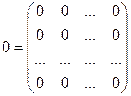 .
.
Матрица – столбец (![]() -матрица) состоит из одного
столбца:
-матрица) состоит из одного
столбца:
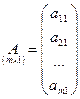 ,
,
а матрица – строка (![]() -матрица) из одной строки:
-матрица) из одной строки:
![]() .
.
Произведением двух матриц![]() и
и ![]() называется
матрица
называется
матрица ![]() , каждый элемент которой определяется
по правилу строка на столбец, то есть элемент стоки матрицы
, каждый элемент которой определяется
по правилу строка на столбец, то есть элемент стоки матрицы ![]() умножается на элемент столбца
матрицы
умножается на элемент столбца
матрицы ![]() стоящие на соответствующих местах.
стоящие на соответствующих местах.
Из определения произведения матриц
следует, что не любые две матрицы можно перемножать. Произведение ![]() имеет смысл только тогда, когда
число столбцов первой матрицы-сомножителя равно числу строк второй
матрицы-сомножителя, что символически записывается так:
имеет смысл только тогда, когда
число столбцов первой матрицы-сомножителя равно числу строк второй
матрицы-сомножителя, что символически записывается так:
![]() .
.
Транспонирование![]() -матрицы заключается в замене строк
столбцами, а столбцов – строками с теми же номерами:
-матрицы заключается в замене строк
столбцами, а столбцов – строками с теми же номерами:
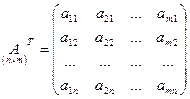 .
.
Матрица ![]() размера
размера
![]() называется суммой двух
называется суммой двух ![]() -матриц
-матриц ![]() и
и
![]() , если каждый элемент матрицы
, если каждый элемент матрицы ![]() равен сумме соответствующих
элементов матриц
равен сумме соответствующих
элементов матриц ![]() и
и ![]() :
:
![]() .
.
Определителем второго порядка называется число, определяемое равенством
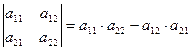 . (1)
. (1)
Числа ![]() называются
элементами определителя; при этом элементы
называются
элементами определителя; при этом элементы ![]() и
и
![]() образуют главную диагональ, а
элементы
образуют главную диагональ, а
элементы ![]() и
и ![]() -
побочную диагональ. Таким образом, определитель второго порядка равен
произведению элементов главной диагонали минус произведение элементов побочной
диагонали.
-
побочную диагональ. Таким образом, определитель второго порядка равен
произведению элементов главной диагонали минус произведение элементов побочной
диагонали.
Определителем третьего порядка называется число, определяемое равенством
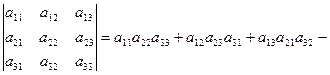 (2)
(2)
![]() .
.
Таким образом, каждый член определителя третьего порядка представляет собой произведение трех его элементов, взятых по одному из каждой строки и каждого столбца. Эти произведения берутся с определенными знаками: со знаком «плюс» – члена, состоящие из элементов главной диагонали и из элементов, расположенных в вершинах треугольников с основаниями, параллельными главной диагонали; со знаком «минус» – три члена, расположенные аналогичным образом относительно побочной диагонали.
Указанное правило, называется правилом треугольников.
Минором![]() элемента
элемента
![]() называется определитель
называется определитель ![]() , полученный из
, полученный из ![]() вычеркиванием
вычеркиванием ![]() -ой строки и
-ой строки и ![]() -го столбца.
-го столбца.
Алгебраическим дополнением ![]() элемента
элемента ![]() называется
его минор, умноженный на
называется
его минор, умноженный на ![]() :
:
![]() .
.
Определитель ![]() -го порядка равен сумме
произведений элементов какой – либо строки или столбца на их алгебраические
дополнения:
-го порядка равен сумме
произведений элементов какой – либо строки или столбца на их алгебраические
дополнения:
![]()
(разложение определителя по
элементам ![]() -ой строки) или
-ой строки) или
![]()
(разложение определителя по
элементам ![]() -го столбца).
-го столбца).
В частности, для определителя третьего порядка имеем
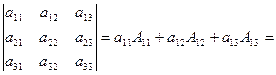
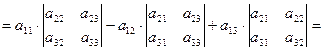
![]() ,
,
что совпадает с результатом, полученным по формуле (2).
Примеры
Задание 1: Найти сумму и разность
матриц 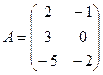 и
и 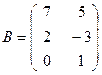 .
.
Решение: Здесь даны матрицы одного
размера ![]() , следовательно, существуют их
сумма и разность. Согласно определению алгебраической суммы матриц имеем
, следовательно, существуют их
сумма и разность. Согласно определению алгебраической суммы матриц имеем
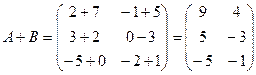 ,
,
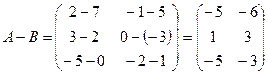 .
.
Задание 2: Вычислить определители: 1) ![]() ; 2)
; 2) 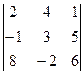 .
.
Решение: 1) По формуле (1) находим ![]() .
.
2) Разлагая данный определитель, например, по элементам первой строки, находим
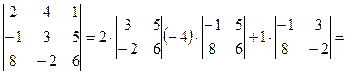
![]() .
.
Тот же результат получится, если воспользоваться формулой (2):
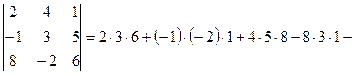
![]() .
.
Задания для самостоятельной работы
№1. Найдите сумму матриц 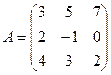 и
и 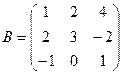 .
.
№2. Транспонируйте матрицу 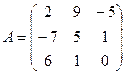 . Укажите размеры данной и
транспонированной матриц.
. Укажите размеры данной и
транспонированной матриц.
№3 Даны матрицы: ![]() ,
, ![]() .
Произведите указанные действия, а в случае, когда это невозможно, указать
причину:
.
Произведите указанные действия, а в случае, когда это невозможно, указать
причину:
1) ![]() ;
;
2) ![]() .
.
№4. Даны матрицы ![]() и
и 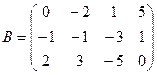 .
.
Найдите матрицу ![]() .
.
№5. Вычислите определители второго порядка:
а) ![]() ;
;
б) 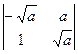 .
.
№6. Вычислите определители третьего порядка:
а) 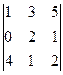 ;
;
б) 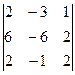 .
.
№7. Вычислите определитель
четвертого порядка 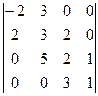 .
.
Вопросы для самоконтроля:
1. Что называется матрицей? Как установить размеры матрицы?
2. Назовите линейные операции над матрицами. Как они производятся?
3. Какие матрицы можно перемножать? Как это делается?
4. Что называется определителем? Как вычисляются определители второго и третьего порядков?
5.
Что называется
минором и алгебраическим дополнением для произвольного элемента ![]() определителя?
определителя?
Практическая работа № 2.
Применение свойств определителей при их вычислении. Вычисление обратных матриц.
Цель: Формирование навыков нахождения обратной матрицы.
На выполнение практической работы отводится 2 часа.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Нахождение обратной матрицы
Матрица, состоящая из ![]() строк и
строк и ![]() столбцов,
называется квадратной матрицей порядка
столбцов,
называется квадратной матрицей порядка ![]() :
:
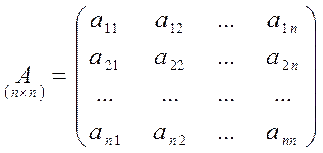 .
.
Элементы ![]() образуют
главную диагональ матрицы.
образуют
главную диагональ матрицы.
У единичной матрицы![]() порядка
порядка ![]() элементы
главной диагонали равны единицы, а остальные элементы равны нулю:
элементы
главной диагонали равны единицы, а остальные элементы равны нулю: 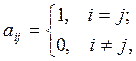 то есть
то есть
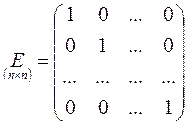 .
.
Для ![]() -
матриц справедливы равенства
-
матриц справедливы равенства ![]() .
.
Каждой ![]() -
матрице
-
матрице ![]() соответствует определитель
соответствует определитель ![]() -го порядка, который состоит из тех
же элементов, расположенных в том же порядке, что и в матрице:
-го порядка, который состоит из тех
же элементов, расположенных в том же порядке, что и в матрице:
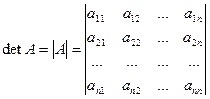 .
.
Произведение двух квадратных
матриц всегда определено; при этом определитель матрицы – произведения равен
произведению определителей матриц – сомножителей: ![]() .
.
Квадратная матрица называется
невырожденной, если ее определитель отличен от нуля ![]() ,
и вырожденной в противном случае
,
и вырожденной в противном случае ![]() .
.
Всякая невырожденная матрица ![]() порядка
порядка ![]() имеет
обратную матрицу того же
порядка
имеет
обратную матрицу того же
порядка ![]() , удовлетворяющую соотношениям
, удовлетворяющую соотношениям
![]() .
.
Обратная матрица имеет вид
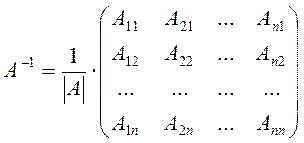 , (1)
, (1)
где ![]() -
алгебраическое дополнение элемента
-
алгебраическое дополнение элемента ![]() в определителе
в определителе ![]() матрицы
матрицы ![]() ,
то есть элементы обратной матрицы находятся по формулам
,
то есть элементы обратной матрицы находятся по формулам 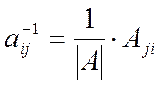 .
.
Свойства обратной матрицы
(здесь ![]() -
матрицы,
-
матрицы, ![]() - число)
- число)
![]() ;
;
![]() ;
;
![]() ;
;
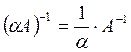 ;
;
![]() .
.
Пример
Задание: Для матрицы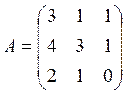 найти обратную матрицу и проверить,
что
найти обратную матрицу и проверить,
что ![]() .
.
Решение: Так как 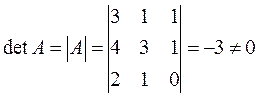 , то матрица
, то матрица ![]() имеет обратную матрицу, элементы
которой равны
имеет обратную матрицу, элементы
которой равны 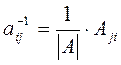 .
.
2) Вычислим алгебраические
дополнения ![]() элементов
элементов ![]() для
для
![]() :
:
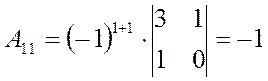 ;
; 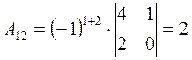 ;
;
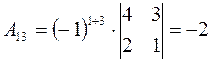 ;
; 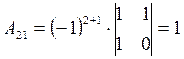 ;
;
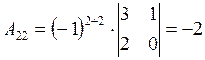 ;
; 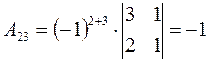 ;
;
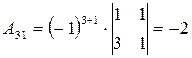 ;
; 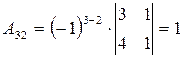 ;
;
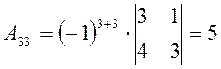 .
.
Теперь, используя формулу (1), находим обратную матрицу
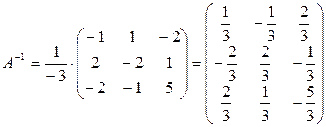 .
.
Далее вычислим произведение
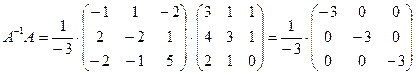 =
=
=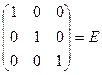 .
.
Аналогично находим
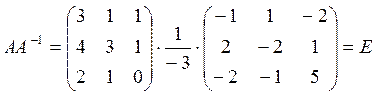 . Итак, обратная матрица вычислена
правильно.
. Итак, обратная матрица вычислена
правильно.
Задания для самостоятельной работы
№1. Для заданной матрицы 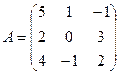 найти указанные элементы обратной
матрицы
найти указанные элементы обратной
матрицы ![]() :
:
1) ![]() ; 2)
; 2)
![]() ; 3)
; 3) ![]() ;
;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6)
![]() .
.
№2. Для матриц 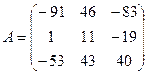 и
и 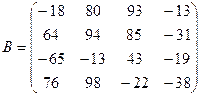 найдите
обратные матрицы,
найдите
обратные матрицы, ![]() и
и ![]() . Проверить, верно, ли они найдены.
. Проверить, верно, ли они найдены.
Вопросы для самоконтроля:
1. Какая матрица называется квадратной?
2. Какая матрица называется единичной, верхнетреугольной, нижнетреугольной, диагональной?
3. Дайте определение обратной матрицы. Всегда ли существует обратная матрица?
4. Как найти обратную матрицу?
Практическая работа № 3
Решение систем линейных уравнений матричным методом.
Цель: Формирование навыков решения СЛАУ матричным методом.
На выполнение практической работы отводится 2 часа.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Решение систем алгебраических уравнений матричным методом
Пример
Задание: Показать, что система имеет единственное решение и найти его
матричным методом.
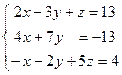
Решим данную систему матричным способом. Рассмотрим матрицы:
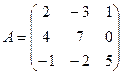 ;
; 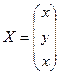 ;
;  ;
;
![]() - матрица коэффициентов при
неизвестных,
- матрица коэффициентов при
неизвестных,![]() - матрица – столбец неизвестных,
- матрица – столбец неизвестных,![]() - матрица – столбец свободных
членов.
- матрица – столбец свободных
членов.
Данную систему можно записать в виде:
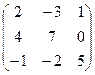
![]()
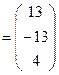 ;
;
При умножении матриц каждая строка
матрицы ![]() умножается на столбец матрицы
умножается на столбец матрицы ![]() и в результате получается
соответствующий элемент матрицы
и в результате получается
соответствующий элемент матрицы ![]() . Таким образом,
последняя матричная запись содержит все три уравнения данной системы линейных
алгебраических уравнений. Коротко ее можно записать так:
. Таким образом,
последняя матричная запись содержит все три уравнения данной системы линейных
алгебраических уравнений. Коротко ее можно записать так:
![]() (1)
(1)
Рассмотрим матрицу ![]() , обратную к матрице
, обратную к матрице ![]() . Это такая матрица, которая при умножении
на данную матрицу
. Это такая матрица, которая при умножении
на данную матрицу ![]() дает единичную матрицу
дает единичную матрицу ![]() :
: ![]() ,
где
,
где 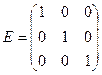 .
.
Умножая обе части матричного
равенства (2) на матрицу ![]() слева, получим:
слева, получим:
![]() ,
,
![]()
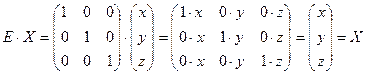 , и окончательно имеем:
, и окончательно имеем:
![]() (2)
(2)
Формула (2) используется для
нахождения решения системы линейных алгебраических уравнений. Предварительно
нужно вычислить обратную матрицу. Обратная матрица вычисляется по формуле: 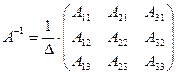 (3), где
(3), где ![]() - алгебраическое дополнение всех
элементов матрицы
- алгебраическое дополнение всех
элементов матрицы ![]() ,
,
![]() - главный определитель системы
- главный определитель системы ![]() .
.
В нашем примере ![]() .
.
Найдем теперь алгебраические
дополнения для всех элементов матрицы ![]() :
:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
Составим матрицу алгебраических дополнений:
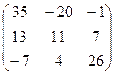 .
.
Транспонируем ее, то есть поменяем местами столбцы и строки с одинаковыми номерами:
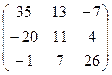 .
.
Обратную матрицу получим по
формуле (3), умножая каждый элемент последней матрицы на число, равное ![]() :
:
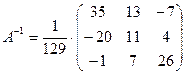 .
.
Решение системы линейных
алгебраических уравнений находим по формуле (2) умножением матрицы ![]() на матрицу свободных членов
на матрицу свободных членов ![]() :
:
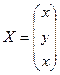 =
=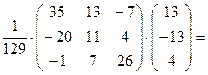
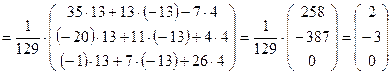 Отсюда следует, что
Отсюда следует, что ![]() ,
, ![]() ,
,
![]() .
.
Найденное решение ![]() было проверено выше, и совпадает с
результатом, полученным по правилу Крамера.
было проверено выше, и совпадает с
результатом, полученным по правилу Крамера.
Ответ: ![]() -
единственное решение системы.
-
единственное решение системы.
Задания для самостоятельной работы
Задание 1. По расширенной матрице выписать СЛАУ.
|
1) |
2) |
|
3) |
4) |
Задание 2. Решить системы уравнений матричным методом.
|
1) |
2) |
|
3) |
4) |
Задание 3. Решить СЛАУ (в случае неопределенной системы выписывать общее и два любых частных решения).
|
1) |
2) |
|
3) |
4) |
|
|
|
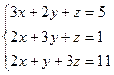 .
.
Вопросы для самоконтроля:
1. Что называется решение СЛАУ?
2. Какие случаи могут представиться при решении СЛАУ?
3. Какие СЛАУ называются совместными, несовместными?
4. При каком условии СЛАУ имеет единственное решение?
5. Что можно сказать о СЛАУ, если ее определитель равен нулю?
6. Как записать СЛАУ в матричном виде?
7. В чем состоит матричный метод решения СЛАУ?
Практическая работа № 4
Решение прикладных задач методом Крамера и методом Гаусса.
Цель: Формирование навыков решения СЛАУ методом Крамера, методом Гаусса
На выполнение практической работы отводится 2 часа.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Решение систем алгебраических уравнений по правилу Крамера
Теорема Крамера. Рассмотрим «квадратную» систему линейных уравнений (число неизвестных совпадает с числом уравнений) вида
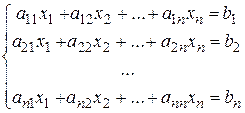 . (*)
. (*)
Если
определитель матрицы системы (*) отличен от нуля (![]() ), то данная система имеет
единственное решение, причем значения неизвестных находятся по формулам
), то данная система имеет
единственное решение, причем значения неизвестных находятся по формулам
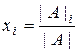 ,
i=1,2,…,n
,
i=1,2,…,n
где
![]() - определитель матрицы, полученной
из исходной матрицы системы путем замены i-го столбца на столбец свободных
членов.
- определитель матрицы, полученной
из исходной матрицы системы путем замены i-го столбца на столбец свободных
членов.
Пример
. Решить систему 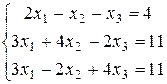 методом Крамера.
методом Крамера.
Решение. Выписываем A - матрицу системы и B - столбец свободных членов: 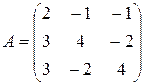 ,
, 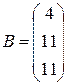 . Далее вычисляем определители:
. Далее вычисляем определители:
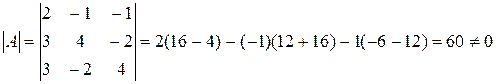 ;
;
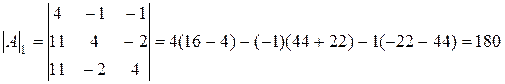 ;
;
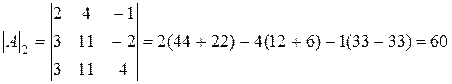 ;
;
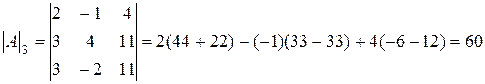 .
.
По теореме Крамера 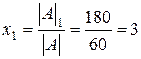 ;
; 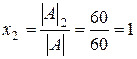 ;
;  . Для проверки результата подставим полученные значения
неизвестных в каждое уравнение системы:
. Для проверки результата подставим полученные значения
неизвестных в каждое уравнение системы: ![]() ,
, ![]() ,
, ![]() . Все уравнения обратились в тождества, значит, решение
найдено верно.
. Все уравнения обратились в тождества, значит, решение
найдено верно.
Пример
Задание: Показать, что система имеет единственное решение и найти его по правилу Крамера;
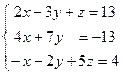
Решение: Данная система имеет
размер ![]() (три уравнения и три неизвестных).
Составим матрицу
(три уравнения и три неизвестных).
Составим матрицу ![]() из коэффициентов при
неизвестных:
из коэффициентов при
неизвестных:
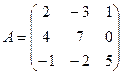 . Матрица
. Матрица ![]() квадратная
квадратная
![]() . Вычислим определитель матрицы
. Вычислим определитель матрицы ![]() , используя формулу его разложения
по элементам первой строки:
, используя формулу его разложения
по элементам первой строки:
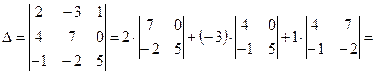
![]() .
.
Так как определитель системы ![]() , то данная система имеет
единственное решение. Это решение можно найти по правилу Крамера:
, то данная система имеет
единственное решение. Это решение можно найти по правилу Крамера: ![]() ;
; ![]() ;
;
![]() , где
, где ![]() -
главный определитель системы;
-
главный определитель системы; ![]() ,
, ![]() ,
, ![]() -
вспомогательные определители, которые получаются из главного путем замены
соответствующего столбца на столбец свободных членов, и вычисляются аналогично
определителю
-
вспомогательные определители, которые получаются из главного путем замены
соответствующего столбца на столбец свободных членов, и вычисляются аналогично
определителю ![]() .
.
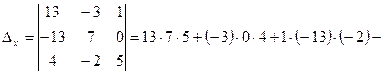
![]() ;
;
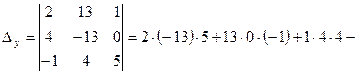
![]() ;
;
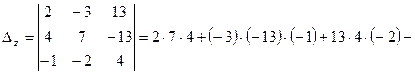
![]()
Отсюда по правилу Крамера имеем:
![]() ;
; ![]() ;
;
![]() .
.
Решение системы единственно, это
совокупность чисел ![]() .
.
Проверка: Подставим найденное решение во все уравнения исходной системы линейных алгебраических уравнений.
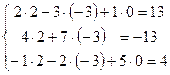
![]()
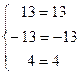
Так как все уравнения системы обратились в равенства, то решение найдено верно.
Ответ: ![]() .
.
Решение систем алгебраических уравнений методом Гаусса
Задачи, посвященные решению систем линейных алгебраических уравнений (СЛАУ) методом исключения неизвестных для случая, когда СЛАУ имеет бесконечное множество решений (совместная неопределенная СЛАУ). При решении системы предлагается использовать одну из равносильностей метода исключения неизвестных – метод Жордана – Гаусса или метода полного исключения.
В процессе решения система преобразуется в равносильные (эквивалентные) системы, то есть СЛАУ с тем же множеством решений.
К элементарным преобразованиям, сохраняющим равносильность СЛАУ, относятся следующие преобразования:
- смена мест уравнений СЛАУ;
- отбрасывание одного из двух одинаковых уравнений СЛАУ;
- умножение обеих частей какого-либо уравнения на число, отличное от нуля;
- замена одного из уравнений СЛАУ уравнением, полученным его почленным сложением с другим уравнением СЛАУ.
Сущность метода исключения состоит в том, что с помощью указанных элементарных преобразований, не нарушающих равносильности СЛАУ, выбранное неизвестное (ведущее) исключается из всех уравнений системы, кроме одного (ведущего уравнения). Метод осуществляется по шагам. На каждом шаге исключается только одно неизвестное. Шаги заканчиваются, когда ведущим побывают все уравнения системы (либо будет получено очевидное противоречие, говорящее об отсутствии решений СЛАУ).
Пример
Задание: Пользуясь методом исключения неизвестных найти общее решение системы линейных уравнений, а также два частных ее решения, одно из которых базисное:
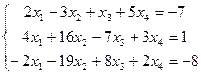
Решение: Система имеет размер ![]() (три уравнения, четыре
неизвестных). На каждом шаге выбираем одно ведущее уравнение и в нем одно
ведущее неизвестное. Ведущим каждое уравнение и каждое неизвестное могут быть
только один раз. На следующем шаге их за ведущие брать нельзя.
(три уравнения, четыре
неизвестных). На каждом шаге выбираем одно ведущее уравнение и в нем одно
ведущее неизвестное. Ведущим каждое уравнение и каждое неизвестное могут быть
только один раз. На следующем шаге их за ведущие брать нельзя.
Шаг первый. Выберем в качестве ведущего
уравнения первое, а в нем ведущее неизвестное ![]() ,
так как коэффициент при
,
так как коэффициент при ![]() равен единице,
что упрощает вычисления.
равен единице,
что упрощает вычисления.
Ведущее уравнение, то есть первое,
оставляем без изменения. Исключим ведущее неизвестное ![]() из
второго и третьего уравнений. Для этого нужно преобразовать эти уравнения к виду,
когда коэффициенты при
из
второго и третьего уравнений. Для этого нужно преобразовать эти уравнения к виду,
когда коэффициенты при ![]() в них станут равными
нулю.
в них станут равными
нулю.
Умножим обе части ведущего уравнения на число 7 и почленно сложим со вторым уравнением. Аналогично, умножим обе части ведущего уравнения на «-8» и почленно сложим с третьим уравнением. В итоге получим систему, равносильную исходной:
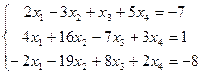
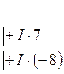
![]()
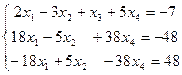
![]()
Теперь переменная ![]() содержится только в первом
уравнении. Заметим также, что два последних уравнения станут одинаковыми, если
в одном из них поменять знаки. Поэтому, отбросим одно из этих уравнений,
например, третье.
содержится только в первом
уравнении. Заметим также, что два последних уравнения станут одинаковыми, если
в одном из них поменять знаки. Поэтому, отбросим одно из этих уравнений,
например, третье.
Шаг второй. Выберем в качестве ведущего второе
(другое) уравнение. Так как в нем нет неизвестного с коэффициентом 1, то берем
любое неизвестное, с коэффициентом, отличным от нуля, и делим обе части нового
ведущего уравнения на этот коэффициент. Например, выберем во втором уравнении в
качестве ведущего неизвестное ![]() , с
коэффициентом «-5», и поделим обе части этого уравнения на «-5»:
, с
коэффициентом «-5», и поделим обе части этого уравнения на «-5»:
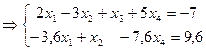
![]()
![]()
Чтобы исключить ![]() из первого уравнения, умножим обе
части ведущего (второго) уравнения на 3 и почленно сложим с первым. Ведущее
уравнение перепишем без изменения.
из первого уравнения, умножим обе
части ведущего (второго) уравнения на 3 и почленно сложим с первым. Ведущее
уравнение перепишем без изменения.
![]()
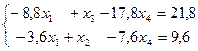
![]()
Ведущая переменная содержится теперь только во втором (ведущем) уравнении. Так как все уравнения уже были ведущими (каждое на своем шаге), то преобразования закончены.
Выразим из каждого уравнения то неизвестное, которое было в нем ведущим, и поэтому, не содержится в других уравнениях:
![]()
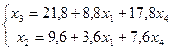 .
.
Получено общее решение данной
системы. Переменные ![]() и
и ![]() , которые мы выразили, называются
базисными. Остальные переменные
, которые мы выразили, называются
базисными. Остальные переменные ![]() и
и ![]() - называются свободными, они задаются
произвольно (свободно)
- называются свободными, они задаются
произвольно (свободно)
Общее решение СЛАУ представляет собой такую запись СЛАУ, когда часть ее переменных, называемых базисными, выражены через оставшиеся переменные, называемые свободными.
Частные решения СЛАУ могут быть получены из общего решения. Для этого задаем произвольно свободные переменные и вычисляем базисные по общему решению.
Например, пусть ![]() ;
; ![]() . Тогда
. Тогда
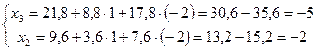 .
.
Таким образом, получено частное
решение системы: ![]() . Придавая свободным
переменным
. Придавая свободным
переменным ![]() и
и ![]() другие
значения, найдем, аналогичным образом, любое количество частных решений СЛАУ.
другие
значения, найдем, аналогичным образом, любое количество частных решений СЛАУ.
Базисное решение СЛАУ, это такое
частное решение, когда свободные переменные равны нулю, то есть ![]() ;
; ![]() ,
тогда
,
тогда 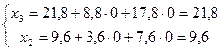 . Получено базисное решение
системы:
. Получено базисное решение
системы: ![]() .
.
Проверка: Проверим правильность нахождения двух частных решений, из которых базисное, подстановкой в исходную систему.
1) Проверяем решение ![]() :
:
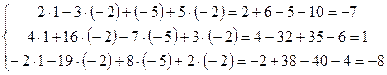 таким образом, все уравнения СЛАУ
выполняются.
таким образом, все уравнения СЛАУ
выполняются.
2) Проверим решение ![]() :
:
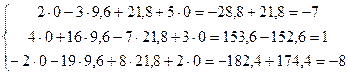 .
.
Решение удовлетворяет всем уравнениям исходной СЛАУ.
Ответ: 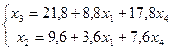 -
общее решение СЛАУ,
-
общее решение СЛАУ,
![]() - частное решение СЛАУ,
- частное решение СЛАУ,
![]() - базисное решение СЛАУ.
- базисное решение СЛАУ.
Задания для самостоятельной работы
Задание 1. Пользуясь методом исключения неизвестных, найти общее решение системы линейных уравнений, а также два частных ее решения, одно из которых базисное.
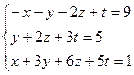 .
.
Задание 2. Решить системы уравнений методом Гаусса.
|
1) |
2) |
|
3) |
4) |
Задание 3. Решить СЛАУ (в случае неопределенной системы выписывать общее и два любых частных решения).
|
1) |
2) |
|
3) |
4) |
Задание 4. Решить системы уравнений методом Крамера.
|
1) |
2) |
|
3) |
4) |
Вопросы для самоконтроля:
1. Назовите элементарные преобразования, не нарушающие равносильности СЛАУ.
2. В чем состоит сущность метода Жордана – Гаусса для решения СЛАУ? Как осуществляется этот метод? Когда он применим?
3. Что называется общим решение СЛАУ?
4. Какие переменные называются базисными, а какие свободными?
5. Как найти частное решение СЛАУ? Сколько частных решений имеет СЛАУ?
6. Что называется базисным решением СЛАУ?
7. Сколько базисных решений имеет СЛАУ?
8. Дайте определение эквивалентных (равносильных) СЛАУ.
9. Напишите формулу Крамера. В каком случае они применимы?
Практическая работа № 5.
Выполнение алгебраических операций над комплексными числами
в алгебраической форме»
Цель: Формирование навыков выполнения действий над комплексными числами в алгебраической форме, решения квадратных уравнений с отрицательным дискриминантом.
На выполнение практической работы отводится 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы
2.Оформить задания в тетради для практических работ
Теоретический материал
Число вида ![]() , где a и b – действительные числа, i – так называемая мнимая единица. Число a называется действительной частью (Re z) комплексного числа z, число b называется мнимой частью (Im z) комплексного числа z.
, где a и b – действительные числа, i – так называемая мнимая единица. Число a называется действительной частью (Re z) комплексного числа z, число b называется мнимой частью (Im z) комплексного числа z.
Число ![]() называется сопряженным
комплексному числу z.
называется сопряженным
комплексному числу z.
Множество комплексных чисел принято обозначать «жирной» или
утолщенной буквой![]() .
Комплексная плоскость состоит из двух осей:
.
Комплексная плоскость состоит из двух осей:
![]() –
действительная ось
–
действительная ось
![]() –
мнимая ось
–
мнимая ось
Построим на комплексной плоскости
следующие комплексные числа:
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
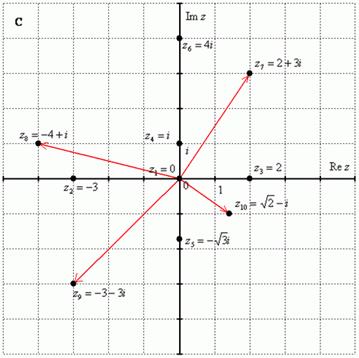
Модулем комплексного числа z называется расстояние от
начала координат до соответствующей точки комплексной плоскости. Попросту
говоря, модуль – это длина радиус-вектора, который на чертеже
обозначен красным цветом. Модуль комплексного числа z стандартно обозначают: ![]() . По теореме Пифагора легко
вывести формулу для нахождения модуля комплексного числа:
. По теореме Пифагора легко
вывести формулу для нахождения модуля комплексного числа: ![]()
Действия с комплексными числами
Пример №1. ![]()
![]()
Пример №2. ![]()
3. Умножение комплексных чисел. При умножении комплексных чисел
необходимо воспользоваться правилом умножения многочленов: чтобы умножить
многочлен на многочлен нужно каждый член одного многочлена умножить на каждый
член другого многочлена и помнить, что ![]()
Пример №3. 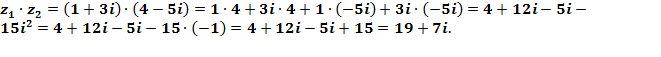
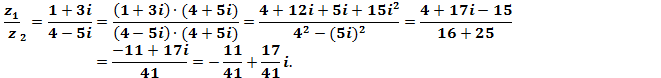
5.
Модуль
комплексного числа: ![]()
Пример №5.
![]() ;
; ![]()
6. Возведение мнимой единицы в степень.
Пример
№6. Возвести в степень комплексные
числа ![]() ,
, ![]() ,
, ![]()
Если мнимая единица
возводится в четную степень, то техника решения такова:
![]()
Если мнимая единица
возводится в нечетную степень, то «отщипываем» одно «и», получая четную
степень:
![]()
Если есть минус (или
любой действительный коэффициент), то его необходимо предварительно отделить:
![]()
Пример №7. ![]()
В комплексных числах извлечь корень – можно! А точнее, два корня:
![]()
Такие корни также называют сопряженными комплексными корнями.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
т.д.
и
т.д.
Во всех случаях получается два сопряженных комплексных корня.
Пример
8. Решить
квадратное уравнение ![]()
Вычислим дискриминант:
![]()
![]()
![]()
![]() –
сопряженные комплексные корни
–
сопряженные комплексные корни
Задания для самостоятельной работы
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
|
|
1. Изобразите на плоскости заданные комплексные числа: |
||||
|
Z1 = 4i Z2 = 3 + i Z3= - 4 +3i Z4= - 2 -5i |
Z1= -5i Z2= 4 + i Z3= -7 + 2i Z4= -3 – 6i |
Z1= -5i Z2= 4 + i Z3= -7 + 2i Z4= -3 – 6i |
Z1= -5i Z2= 4 + i Z3= -7 + 2i Z4= -3 – 6i |
|
|
2 . Вычислите модуль комплексного числа |
||||
|
Z = 3 + 4i |
Z = 8 + 6i |
Z = -1
+ |
|
|
|
3. Произведите сложение и вычитание комплексных чисел: |
||||
|
Z1 = (3 + 5i) , Z2 = (7 – 2i) |
Z1 = (3 – 2i), Z2 = (5 + 3i) |
Z1 = (4 + 2i), Z2 = (– 3 + 2i). |
Z1 = (– 2 + 3i), Z2 = (7 – 2i) |
|
|
4. Выполните действие над комплексными числами: |
||||
|
а) (2 + 3i)(5 – 7i), б) (3 + 2i)(3 – 2i), в) (3 + 5i)2, г) |
а) (3 + 2i)(1 + 3i), б) (7 – 6i)(7 + 6i), в) (2 – 7i)2, г) |
а) (– 2 + 3i)(3 + 5i), б) (4 + 3i)(4 – 3i), в) (4 + 2i)2, г) |
а) (6 + 4i)(5 + 2i), б) (2 – 5i)(2 + 5i), в) (3 – 2i)2, г) |
|
|
5. Решите уравнения: |
|
|
||
|
x2 – 4x + 13 = 0. |
2,5x2 + x + 1 = 0.. |
x2 + 3x + 4=0 |
4x2 – 20x + 26 = 0 |
|
Вопросы для самоконтроля:
1. Запишите алгебраическую форму комплексного числа.
2. Чему равно i2?
3. Сформулируйте правило сложения (вычитания) комплексных чисел.
4. Сформулируйте правило умножения комплексных чисел.
5. Сформулируйте правило деления комплексных чисел.
6. Сформулируйте правило возведения в степень комплексных чисел.
7. Запишите формулы степени мнимой единицы.
8. Какие числа называются сопряженными?
9. Сформулируйте свойство сопряженных чисел.
Практическая работа №6
Выполнение алгебраических операций над комплексными числами
в тригонометрической и показательной форме
Цель: Формирование навыков перевода комплексных чисел из одной формы в другую и выполнения действий над комплексными числами в тригонометрической и показательной формах.
На выполнение практической работы отводится 2 часа.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Для всякого комплексного числа z = a + ib справедливо равенство:
z=R(cosφ+ isinφ) называют тригонометрической формой комплексного числа,
z = ![]() – называют показательной формой комплексного
числа
– называют показательной формой комплексного
числа
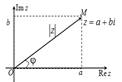 Здесь
Здесь ![]() - модуль комплексного числа -
расстояние от начала координат до соответствующей точки комплексной плоскости.
Попросту говоря, модуль
– это длина радиус-вектора.
- модуль комплексного числа -
расстояние от начала координат до соответствующей точки комплексной плоскости.
Попросту говоря, модуль
– это длина радиус-вектора.
Угол φ между положительной
полуосью действительной оси и радиус-вектором, проведенным из начала координат
к соответствующей точке, называется аргументом комплексного числа - ![]() .
.
Действия над комплексными числами в тригонометрической форме.
|
В тригонометрической форме z1 =R1(cosφ1 + isinφ1), z2 =R2(cosφ2 + isinφ2) |
В показательной форме Z1 = |
|
|
Умножение |
Z1 ∙ Z2 = R1∙R2(cos(φ1+φ2) + isin(φ1+φ2)). |
Z1·Z2=
|
|
Деление |
|
|
|
Возведение в степень |
zn =Rn(cos nφ + isin nφ) - формула Муавра |
|
|
Извлечение корня |
|
k = 0,1,2.....n-1 |
Примеры решения задач:
Пример.1
Представить
числа z1 = ![]() ,
, ![]() в тригонометрической
и показательной форме,
в тригонометрической
и показательной форме,
Решение
Получим
тригонометрическую и показательную форму z1 = ![]() ,
,
1)
Найдем модуль числа - ![]() , 2) Найдем аргумент
числа -
, 2) Найдем аргумент
числа - ![]() ,
,
3) запишем к.ч. в тригонометрической и показательной форме:
z1
= ![]() .
.
![]() ,
,
1)
![]() - модуль числа,
- модуль числа,
2)
![]() - аргумент числа
- аргумент числа
3) запишем к.ч. в тригонометрической и показательной форме:
![]() .
.
Пример.2
Вычислить
в тригонометрической форме: 1) z1∙z2; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]()
Произведение:
z1∙z2
= ![]()
![]() .
.
Частное:
![]() =
=
![]() .
.
Возведение в степень:
![]()
![]() .
.
Извлечение из под знака корня:
![]() .
.
При k=0: ![]() ;
;
При k=1:
![]() .
.
Задания для самостоятельной работы
1. Изобразить комплексные числа на комплексной плоскости.
2. Определить длину и аргумент каждого комплексного числа.
3. Представить данные комплексные числа в тригонометрической и показательной форме.
4. Вычислить в тригонометрической и показательной формах:
1) z1∙z2; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]()
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
|
Z1= 2- 2i; Z2=
|
Z1=
|
Z1=
|
Z1=
|
Вопросы для самоконтроля:
1. Запишите тригонометрическую форму комплексного числа.
2. Запишите показательную форму комплексного числа.
3. Сформулируйте правило перевода комплексных чисел из алгебраической формы в тригонометрическую и показательную формы.
4. Сформулируйте правило умножения комплексных чисел в тригонометрической и показательной формах.
5. Сформулируйте правило деления комплексных чисел в тригонометрической и показательной формах.
6. Сформулируйте правило возведения в степень комплексных чисел в тригонометрической и показательной формах.
7. Сформулируйте правило извлечения корня из комплексных чисел в тригонометрической и показательной формах.
Практическая работа №7.
Вычисление пределов, раскрытие неопределенностей (решение задач).
Цель: Формирование навыков вычисления пределов с помощью замечательных пределов, раскрытия неопределенностей.
На выполнение практической работы отводится 2 часа.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Вычисление пределов с помощью замечательных пределов, раскрытие неопределенностей
Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() ,
стремящемся к
,
стремящемся к ![]() , если для любого числа
, если для любого числа ![]() найдется такое число
найдется такое число ![]() , что при всех
, что при всех ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() , будет выполнено неравенство
, будет выполнено неравенство ![]() .
.
Вычисление
предела функции ![]() следует начинать с
подстановки предельного значения аргумента
следует начинать с
подстановки предельного значения аргумента ![]() ,
(
,
(![]() - число или один из символов
- число или один из символов ![]() ,
, ![]() ,
,
![]() ) в выражение, определяющее эту
функцию. При этом приходится сталкиваться с двумя существенно различными типами
примеров.
) в выражение, определяющее эту
функцию. При этом приходится сталкиваться с двумя существенно различными типами
примеров.
I. Если основная элементарная функция определена в
предельной точке ![]() , то
, то ![]() .
.
Имеют место основные теоремы, на которых основано вычисление пределов элементарных функций.
Если ![]() - постоянная величина, то
- постоянная величина, то ![]() .
.
Если ![]() - постоянная величина, то
- постоянная величина, то ![]() .
.
Если
существуют конечные пределы ![]() и
и ![]() , то:
, то:
![]() ;
;
![]() ;
;
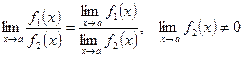 .
.
II. Функция ![]() в
предельной точке
в
предельной точке ![]() не определена. Тогда
вычисление предела требует в каждом случае индивидуального подхода. В одних
случаях (наиболее простых) вопрос сводится к применению теорем о свойствах
бесконечно малых и бесконечно больших функций и связи между ними.
не определена. Тогда
вычисление предела требует в каждом случае индивидуального подхода. В одних
случаях (наиболее простых) вопрос сводится к применению теорем о свойствах
бесконечно малых и бесконечно больших функций и связи между ними.
Более
сложными случаями нахождения предела являются такие, когда подстановка предельного
значения аргумента в выражение для ![]() приводит к
одной из неопределенностей:
приводит к
одной из неопределенностей:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
Тогда вычисление предела заключается в раскрытии полученных неопределенностей.
Здесь могут оказаться полезными:
первый
замечательный предел![]() , (
, (![]() - радианная мера угла);
- радианная мера угла);
второй
замечательный предел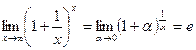 .
.
Кроме того, при раскрытии неопределенностей используют следующие приемы:
сокращение
дроби на критический множитель ![]() при
при ![]() ;
;
избавление от иррациональности в числителе или знаменателе дроби;
разложение
многочленов на линейные или квадратичные множители при ![]() ,
,
![]() .
.
Пример
Вычислить пределы:
Задание
1: 1) ![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4) ![]() .
.
Решение: 1) ![]() ,
, ![]() при
при
![]() , (на ноль делить нельзя). Таким
образом,
, (на ноль делить нельзя). Таким
образом, ![]() есть величина бесконечно малая, а
обратная ей величина
есть величина бесконечно малая, а
обратная ей величина ![]() - бесконечно большая.
Поэтому при
- бесконечно большая.
Поэтому при ![]() произведение
произведение ![]() есть величина бесконечно большая,
то есть
есть величина бесконечно большая,
то есть ![]() .
.
2) ![]()
![]()
![]() =
=
=![]() .
.
3) ![]() ; умножим числитель и знаменатель
на сопряженный знаменателю множитель
; умножим числитель и знаменатель
на сопряженный знаменателю множитель ![]() .
.
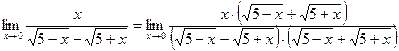 =
=
= ![]() .
.
4) ![]() ; вынесем
; вынесем ![]() за
скобки, получим
за
скобки, получим ![]() (при
(при ![]()
![]() ,
,
![]() ,
, ![]() -
бесконечно малые величины и их пределы равны нулю).
-
бесконечно малые величины и их пределы равны нулю).
Задание
2: 1) 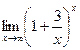 ; 2)
; 2)
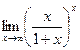 .
.
Решение: 1) 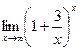 ; выполним преобразования и
воспользуемся вторым замечательным пределом.
; выполним преобразования и
воспользуемся вторым замечательным пределом.
 .
.
2) 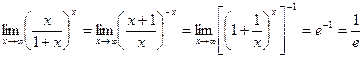 .
.
Задания для самостоятельной работы
Вычислить пределы:
1) ![]() ; 2)
; 2)
![]() ; 3)
; 3) ![]() ;
;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ;
;
7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) 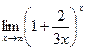 ;
;
10) ![]() ; 11)
; 11) ![]() ; 12)
; 12) 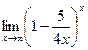 ;
;
13) ![]() ; 14)
; 14) ![]() ; 15)
; 15) ![]() ;
;
16) ![]() .
.
Вопросы для самоконтроля:
1. Что называется пределом функции?
2. Каким образом определяется число ![]() ?
?
3. Сформулируйте основные теоремы вычисления пределов.
4. Запишите формулы соответствующие первому и второму замечательным пределам.
5. Какие приемы используются при раскрытии неопределенностей?
Практическая работа № 8.
Вычисление производных и дифференциала функции (решение задач)
Цель: Формирование навыков вычисления производных функций по определению
производной
На выполнение практической работы отводится 2 часа.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Вычисление производных функций по определению производной
Производной
функции ![]() в точке
в точке ![]() (производной
первого порядка) называется предел отношения приращения функции
(производной
первого порядка) называется предел отношения приращения функции ![]() к приращению аргумента
к приращению аргумента ![]() , когда последнее стремится к нулю:
, когда последнее стремится к нулю:
![]() .
.
Если этот
предел конечен, то функция ![]() называется
дифференцируемой в точке
называется
дифференцируемой в точке ![]() ; в противном
случае (то есть если он не существует или равен бесконечности) – недифференцируемой.
В том случае, когда предел есть бесконечность, говорят, что функция
; в противном
случае (то есть если он не существует или равен бесконечности) – недифференцируемой.
В том случае, когда предел есть бесконечность, говорят, что функция ![]() имеет в точке бесконечную
производную.
имеет в точке бесконечную
производную.
Дифференциалом![]() функции
функции ![]() (дифференциалом
первого порядка) называется главная часть ее приращения, пропорциональная
приращению
(дифференциалом
первого порядка) называется главная часть ее приращения, пропорциональная
приращению ![]() независимой переменной
независимой переменной ![]() .
.
Дифференциал
![]() независимой
переменной
независимой
переменной ![]() равен
ее приращению
равен
ее приращению ![]() :
:
![]() .
.
Дифференциал
любой дифференцируемой функции ![]() равен
произведению ее производной на дифференциал независимой переменной:
равен
произведению ее производной на дифференциал независимой переменной:
![]() . (1)
. (1)
Соотношение
(1) остается в силе и тогда, когда ![]() есть функция
другого аргумента – в этом заключается инвариантность формы первого
дифференциала.
есть функция
другого аргумента – в этом заключается инвариантность формы первого
дифференциала.
Из
соотношения (1) получаем ![]() , то есть
производная первого порядка функции
, то есть
производная первого порядка функции ![]() равна отношению
первого дифференциала функции к дифференциалу ее аргумента.
равна отношению
первого дифференциала функции к дифференциалу ее аргумента.
Пример
Задание: Пользуясь определением
производной, найти производную и дифференциал функции ![]() .
Вычислить
.
Вычислить ![]() .
.
Решение: Найдем приращение
функции ![]() , соответствующее данному приращению
, соответствующее данному приращению
![]() аргумента
аргумента ![]() :
:
![]() .
.
Тогда
![]()
и
![]()
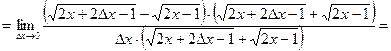
![]() .
.
По формуле (1) находим дифференциал функции:
![]() .
.
Подставляя
в выражение для ![]() значение
значение ![]() , получим
, получим
![]() .
.
Задания для самостоятельной работы
1. Найдите производные и дифференциалы от указанных функций, пользуясь непосредственно определением производной:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ;
;
7) ![]() ; 8)
; 8) ![]() ; 9)
; 9)
![]() .
.
2.
Дана функция ![]() . Найти
. Найти ![]() .
.
3.
Дана функция ![]() . Найти
. Найти ![]() .
.
4.
Дана функция ![]() . Найти
. Найти ![]() ,
а затем вычислить
,
а затем вычислить ![]() ,
, ![]() .
.
5.
Дана функция ![]() . Найти
. Найти ![]() ,
, ![]() .
.
6.
Дана функция ![]() . Найти
. Найти ![]() ,
, ![]() .
.
7.
Дана функция ![]() . Показать, что
. Показать, что ![]() .
.
8.
Показать, что
функция ![]() не дифференцируема в точке
не дифференцируема в точке ![]() .
.
?
Вопросы для самоконтроля:
1. Дайте определение производной первого порядка.
2. Какая функция называется дифференцируемой? Какая функция называется не дифференцируемой Что называется дифференциалом первого порядка?
3. Сформулируйте определение дифференциала функции.
4. В чем заключается инвариантность формы первого дифференциала.
5. Сформулируйте общее правило нахождения производной функции.
Практическая работа № 9.
Вычисление производных и дифференциала сложных функций (решение задач)
Цель: Формирование навыков вычисления производных сложных функций
На выполнение практической работы отводится 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы
2.Оформить задания в тетради для практических работ
Теоретический материал
Вычисление производных сложных функций
Пусть ![]() и
и
![]() - дифференцируемые функции. Тогда
сложная функция
- дифференцируемые функции. Тогда
сложная функция ![]() есть также дифференцируемая
функция, причем
есть также дифференцируемая
функция, причем
![]() , или
, или ![]() (1)
(1)
Это правило распространяется на цепочку из любого количества дифференцируемых функций: производная сложной функции равна произведению производных функций, ее составляющих.
Пример
Задание: Найдите производные функций: 1) ![]() ;
;
2) ![]() .
.
Решение: 1) Предположим, что ![]() , где
, где ![]() .
Тогда по формуле (1) найдем
.
Тогда по формуле (1) найдем
![]() .
.
2)
Предполагая, что ![]() ,
, ![]() ,
,
![]() , получим
, получим
![]() .
.
Задания для самостоятельной работы
Вычислить производные заданных функций:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3)
![]() ;
;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ;
;
7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() ;
;
10) ![]() ; 11)
; 11) ![]() ; 12)
; 12) ![]() .
.
Вопросы для самоконтроля:
1. Дайте определение производной функции.
2. Перечислите правила нахождения производной функции.
3. Какие функции называются дифференцируемыми?
4. Какая функция называется сложной?
5. Как найти производную сложной функции?
Практическая работа № 10.
Вычисление неопределенных интегралов непосредственным интегрированием (решение задач)
Цель: Закрепление и систематизация знания по данной теме; отработка навыков вычисления неопределённого интеграла методом непосредственное интегрировани.
На выполнение практической работы отводится 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы
2.Оформить задания в тетради для практических работ
Теоретический материал
Операция интегрирования сводится к
нахождению функции F-
первообразной, производная которой равна данной функции, т.е. ![]() .
.
При этом если функция y=F(x) является первообразной для функции y=f(x) на промежутке (a, b) или Х, то и любая функция y=F(x) +C является первообразной для функции y=f(x) на этом промежутке.
Действительно: (F(x)+C)` = F`(x)+C` = f(x), т.к. С` =0, где С- const.
Если функция f(x) имеет на промежутке (a, b) или Х хотя бы одну первообразную, то ее называют интегрируемой на этом промежутке.
Совокупность всех первообразных функции – есть неопределенный интеграл.
![]() ,
,
где:
|
|
знак интеграла |
|
|
F(x) - |
подынтегральная функция, |
|
|
F(x)dx - |
подынтегральное выражение, |
|
|
Х – |
переменная интегрирования, |
|
|
С – |
постоянная интегрирования. |
Геометрический смысл неопределенного интеграла: совокупность графиков всех первообразных подынтегральной функции.
Таблица основных интегралов
|
1.
2.
3.
4.
5.
6. |
7.
8.
9.
10.
11.
12. |
13.
14.
15.
16.
|
Свойства неопределенного интеграла.
1. Интеграл от суммы функций равен сумме интегралов слагаемых.
![]()
2.
Постоянный
множитель можно выносить за знак интеграла. ![]() .
.
3.
Если ![]() , то
, то ![]() .
.
Методы интегрирования:
ü непосредственное интегрирование- интегрирование на основании формул интегрирования и свойств неопределенного интегрирования.
ü замена переменных (метод
подстановки)- интегрирование через вспомогательную переменную т.е в подынтегральную
функцию f(x)dx
можно ввести вместо х вспомогательную переменную Z, связанную с х некоторой зависимостью x=f(z), тогда ![]() при этом, если
интеграл
при этом, если
интеграл ![]() принадлежит табличным или сводится
к ним легче, чем исходный, то преобразования достигли цели.
принадлежит табличным или сводится
к ним легче, чем исходный, то преобразования достигли цели.
ü по частям.- метод сводится к
сведению данного интеграла ![]() к интегралу
к интегралу ![]() с помощью формулы
с помощью формулы ![]() , что дает возможность получить
более легкий для вычисления интеграл
, что дает возможность получить
более легкий для вычисления интеграл ![]() .
.
Пример 1
Вычислите неопределенный интеграл:
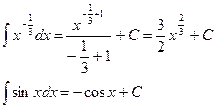
Пример 2
Вычислите неопределенный интеграл с использованием его свойств:
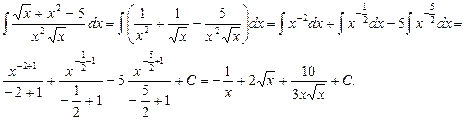
![]()
Задания для самостоятельной работы
Вычислите интегралы:

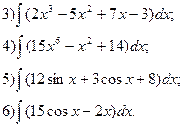
Вопросы для самоконтроля:
1) Какое действие называется интегрированием?
2) Какая функция называется интегрируемой?
3) Какая функция называется первообразной для функции f(x)?
4) Чем отличаются друг от друга различные первообразные функции для данной функции f(x)?
5) Дайте определение неопределённого интеграла.
6) Как проверить результат интегрирования?
7) Каков геометрический смысл неопределенного интеграла?
8) Какими свойствами обладают неопределённые интегралы?
9) Перечислите методы интегрирования.
Практическая работа № 11.
Вычисление неопределенных интегралов методом подстановки
и по частям (решение задач)
Цель: Формирование навыков нахождения неопределенных интегралов методами замены переменной и по частям.
На выполнение практической работы отводится 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы
2.Оформить задания в тетради для практических работ
Теоретический материал
Интегрирование заменой переменной в неопределенном интеграле
Проинтегрировать функцию ![]() - значит найти ее неопределенный
интеграл. Непосредственное интегрирование основано на прямом использовании
основных свойств неопределенного интеграла и таблицы простейших интегралов.
- значит найти ее неопределенный
интеграл. Непосредственное интегрирование основано на прямом использовании
основных свойств неопределенного интеграла и таблицы простейших интегралов.
В основе интегрирования способом
подстановки (или замены переменной) лежит свойство инвариантности формул
интегрирования, которое заключается в следующем: если ![]() , то
, то ![]() ,
где
,
где ![]() - произвольная дифференцируемая
функция от
- произвольная дифференцируемая
функция от ![]() .
.
Замена переменной в неопределенном интеграле производится с помощью подстановок следующих двух типов:
![]() - где
- где ![]() -
новая переменная, а
-
новая переменная, а ![]() - непрерывно
дифференцируемая функция. В этом случае формула замены переменной такова:
- непрерывно
дифференцируемая функция. В этом случае формула замены переменной такова:
![]() (1)
(1)
Функцию ![]() стараются
выбирать таким образом, чтобы правая часть формулы (1) приобрела более удобный
для интегрирования вид;
стараются
выбирать таким образом, чтобы правая часть формулы (1) приобрела более удобный
для интегрирования вид;
![]() , где
, где ![]() -
новая переменная. В этом случае формула замены переменной имеет вид
-
новая переменная. В этом случае формула замены переменной имеет вид
![]() (2)
(2)
Интегрирование по частям в неопределенном интеграле
Интегрированием по частям называется нахождение интеграла по формуле
![]() (3)
(3)
где ![]() и
и
![]() - непрерывно дифференцируемые
функции от
- непрерывно дифференцируемые
функции от ![]() . С помощью формулы (3) отыскание
интеграла
. С помощью формулы (3) отыскание
интеграла ![]() сводится к нахождению другого интеграла
сводится к нахождению другого интеграла
![]() , ее применение целесообразно в тех
случаях, когда последний интеграл либо проще исходного, либо ему подобен.
, ее применение целесообразно в тех
случаях, когда последний интеграл либо проще исходного, либо ему подобен.
При этом в качестве ![]() берется функция, которая при
дифференцировании упрощается, а в качестве
берется функция, которая при
дифференцировании упрощается, а в качестве ![]() -
та часть подынтегрального выражения, интеграл от которой известен или может
быть найден.
-
та часть подынтегрального выражения, интеграл от которой известен или может
быть найден.
Так, при нахождении интегралов вида
![]()
за ![]() следует
принять многочлен
следует
принять многочлен ![]() , а за
, а за ![]() - соответственно выражения
- соответственно выражения ![]() ,
, ![]() ;
при отыскании интегралов вида
;
при отыскании интегралов вида
![]()
за ![]() принимаются соответственно функции
принимаются соответственно функции ![]() ,
, ![]() ,
, ![]() , а за
, а за ![]() - выражение
- выражение ![]() .
.
Примеры
Найти интегралы: 1) ![]() ; 2)
; 2)
![]() .
.
Решение: 1) Данный интеграл окажется
табличным, если под знаком дифференциала будет находиться аргумент ![]() подынтегральной функции
подынтегральной функции ![]() . Так как
. Так как ![]() ,
то
,
то ![]() . Следовательно, подстановка
. Следовательно, подстановка ![]() приводит рассматриваемый интеграл
к табличному:
приводит рассматриваемый интеграл
к табличному: ![]() . Возвращаясь к старой
переменной
. Возвращаясь к старой
переменной ![]() , окончательно получим
, окончательно получим ![]() .
.
2) Предполагая ![]() ,
, ![]() , найдем
, найдем ![]() ,
, ![]() .
Следовательно,
.
Следовательно,
![]() .
.
Задания для самостоятельной работы
1. Найти интегралы методом непосредственного интегрирования:
1) ![]() ; 2)
; 2)
![]() ;
;
3) ![]() ; 4)
; 4) ![]() ;
;
5) ![]() ; 6)
; 6) ![]() ;
;
7) ![]() ; 8)
; 8)
![]() ;
;
9) ![]()
2. Найти интегралы способом подстановки:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3)
![]() ;
;
4) ![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ; 7)
; 7)
![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() .
.
3. Найдите интегралы при помощи интегрирования по частям:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3)
![]() ; 4)
; 4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() .
.
Вопросы для самоконтроля:
1. Что называется первообразной? Перечислите свойства первообразной функции.
2. Что называется неопределенным интегралом?
3. Какие свойства неопределенного интеграла вы знаете?
4. Перечислите основные формулы интегрирования.
5. Какие методы интегрирования вы знаете? В чем заключается их сущность?
Практическая работа № 12
Вычисление определенных интегралов непосредственным интегрированием
(решение задач)
Цель: Формирование навыков вычисления определенного интеграла при помощи формулы Ньютона – Лейбница. Формирование навыков вычисления площадей фигур с помощью определенных интегралов.
На выполнение практической работы отводится 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы
2.Оформить задания в тетради для практических работ
Теоретический материал
Вычисление определенных интегралов
1. Определенный интеграл
Пусть функция f(x) определена на отрезке [a; b]. Разобьем этот отрезок на n частей точками a< x0< x1< x2 <....< xn=b, выберем на каждом элементарном отрезке xk – 1 £ x £ xk произвольную точку xk и обозначим через D xk длину каждого такого отрезка.
Интегральной суммой для функции f(x) на отрезке [a; b] называется сумма вида:
n
S f(xk) Dxk = f(x1)D x1 + f(x2)D x2 +...+ f(xn)D xn
k=1
Определение. Определенным интегралом от функции f(x) на отрезке [a; b] называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
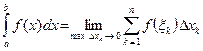
Для вычисления определенного интеграла от функции f(x) служит формула Ньютона-Лейбница:
|
|
т. е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
2. Основные свойства определенного интеграла
10. Постоянный множитель можно выносить за знак интеграла, т. е. если а = const, то
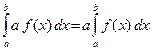
20. Определенный интеграл от алгебраической суммы двух непрерывных функций равен алгебраической сумме их интегралов, т. е.
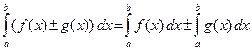
30. Если a < c < b, то
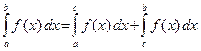
40. Если функция f(x) неотрицательна на отрезке [a; b], где a < b, то
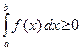
50. Если f(x) ³ g(x) для всех x Î [a; b], где a < b, то
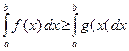
3. Методы вычисления определенного интеграла
Чтобы вычислить определенный интеграл 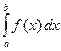 , нужно:
, нужно:
1) найти какую-нибудь первообразную F(x) для функции f(x) (найти неопределенный интеграл от функции f(x), в котором можно принять С = 0);
2) в полученном выражении подставить вместо x сначала верхний предел a, а затем нижний предел b, и из результата первой подстановки вычесть результат второй.
Пример 1.
Вычислить ![]()
Решение.
По формуле Ньютона-Лейбница получаем:  =
=
![]() =
=![]() 19, 5
19, 5
Пример 2.
Вычислить ![]()
Решение.
По формуле Ньютона-Лейбница:![]() =
= ![]()
Пример 3. Найти ![]()
Решение. ![]() =
= ![]()
Примеры
Вычислить следующие определенные интегралы:
1) ![]() ; 2)
; 2)
![]() ; 3)
; 3) ![]() .
.
Решение:1) 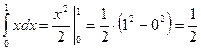 ;
;
2) ![]() ;
;
3)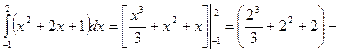
![]()
![]() .
.
Вычисление площадей фигур с помощью определенных интегралов
Определенный интеграл широко применяется при вычислениях различных геометрических фигур и физических величин.
![]() Найдем площадь
Найдем площадь ![]() криволинейной
трапеции, ограниченной кривой
криволинейной
трапеции, ограниченной кривой ![]() , осью
, осью ![]() и двумя прямыми
и двумя прямыми ![]() и
и ![]() , где
, где ![]() ,
, ![]() (рис.
1).
(рис.
1).
Так как
дифференциал переменной площади ![]() есть площадь
прямоугольника с основанием
есть площадь
прямоугольника с основанием ![]() и высотой
и высотой ![]() , то есть
, то есть ![]() ,
то, интегрируя это равенство в пределах от
,
то, интегрируя это равенство в пределах от ![]() до
до
![]() , получим
, получим 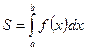 .
.
![]() Если
криволинейная трапеция прилегает к оси
Если
криволинейная трапеция прилегает к оси ![]() так, что
так, что ![]() ,
, ![]() (рис. 2), то дифференциал переменной
площади
(рис. 2), то дифференциал переменной
площади ![]() равен
равен ![]() ,
откуда
,
откуда 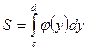 .
.
![]() В том случае,
когда криволинейная трапеция, ограниченная кривой
В том случае,
когда криволинейная трапеция, ограниченная кривой ![]() ,
осью
,
осью ![]() и прямыми
и прямыми ![]() и
и
![]() , лежит под осью
, лежит под осью ![]() (рис.3), площадь находится по формуле
(рис.3), площадь находится по формуле
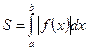 .
.
Если
фигура, ограниченная кривой x![]() , осью
, осью ![]() и прямыми
и прямыми ![]() и
и
![]() , расположена по обе стороны от оси
, расположена по обе стороны от оси
![]() (рис. 4), то
(рис. 4), то 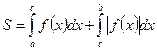 .
.
![]()
![]()
Пусть
фигура ![]() ограничена двумя пересекающимися
кривыми
ограничена двумя пересекающимися
кривыми ![]() и
и ![]() ,
и прямыми
,
и прямыми ![]() и
и ![]() ,
где
,
где ![]() и
и ![]() (рис.
5). Тогда ее площадь находится по формуле
(рис.
5). Тогда ее площадь находится по формуле 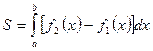 .
.
Примеры
Задание: Вычислить площади фигур, ограниченных указанными линиями:
![]() 1)
1) ![]() ,
, ![]() ,
, ![]() и
и
![]() ;
;
Решение: 1) Строим прямую ![]() по двум точкам
по двум точкам ![]() и
и ![]() .
.
Выразим ![]() через
через ![]() ,
получим
,
получим ![]() . Найдем площадь полученной фигуры:
. Найдем площадь полученной фигуры:

Ответ: ![]()
![]() 2)
2) ![]() ,
, ![]() ,
, ![]() и
и
![]() .
.
![]() - квадратичная функция;
- квадратичная функция; ![]() ; график – парабола, ветви
направлены вверх. Найдем координаты вершины параболы:
; график – парабола, ветви
направлены вверх. Найдем координаты вершины параболы: ![]() , отсюда следует, что
, отсюда следует, что ![]() . Таким образом, вершина параболы
имеет координаты:
. Таким образом, вершина параболы
имеет координаты: ![]() . Найдем площадь полученной
фигуры:
. Найдем площадь полученной
фигуры:
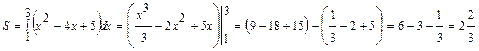 .
.
Ответ: ![]()
Задания для самостоятельной работы
1.
Найти площадь
фигуры, ограниченной прямыми ![]() ,
, ![]() ,
, ![]() и
осью абсцисс.
и
осью абсцисс.
2.
Найти площадь
фигуры, заключенной между осями координат и прямыми ![]() и
и
![]() .
.
3.
Найти площадь
фигуры, ограниченной ветвью гиперболы ![]() и
прямыми
и
прямыми ![]() ,
, ![]() .
.
4.
Найти площадь
фигуры, ограниченной параболой ![]() , осями
координат и прямой
, осями
координат и прямой ![]() .
.
5.
Найти площадь
фигуры, заключенной между прямыми ![]() ,
, ![]() ,
, ![]() и
и
![]() .
.
6.
Найти площадь
фигуры, заключенной между параболами ![]() и
и ![]() .
.
7.
Вычислить
площадь фигуры, заключенной между кривыми ![]() и
и
![]() .
.
8. Вычислить определенные интегралы:
a)
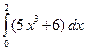
b)
![]()
c)
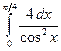
d)
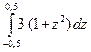
e)
![]()
f)
![]()
g)
![]()
h)
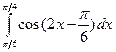
i)
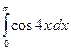
j)
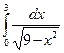
k)
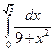
Вопросы для самоконтроля:
Практическая работа № 13
Вычисление определенных интегралов методом подстановки и по частям
(решение задач)
Цель: Формирование навыков вычисления определенного интеграла методом подстановки и по частям
На выполнение практической работы отводится 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы
2.Оформить задания в тетради для практических работ
Теоретический материал
Метод замены переменной (метод подстановки)
При вычислении определенного интеграла методом подстановки новая переменная вводится подобно случаю неопределенного интеграла. Однако в отличие от неопределенного интеграл а, где в полученном результате мы снова возвращались к прежнему переменному, здесь этого делать не надо.
Пример. Вычислить ![]()
Решение. Введем новую переменную
интегрирования с помощью подстановки ![]() .
Дифференцируя, имеем:
.
Дифференцируя, имеем:
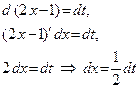
Находим новые пределы интегрирования. Для этого подставим в
соотношение ![]() значения x = 1 и x = 2, соответственно получим:
значения x = 1 и x = 2, соответственно получим: ![]()
![]()
![]()
Следовательно,
![]() =
= ![]()
Интегрирование по частям
Если функции u(x) и v(x)
и их производные u¢(x) и v¢(x) непрерывны в промежутке ![]() ,
то формула интегрирования по частям для определенного интеграла имеет вид:
,
то формула интегрирования по частям для определенного интеграла имеет вид:
|
|
Пример. Вычислить 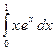
Решение. Положим ![]() , Тогда
, Тогда ![]() ,
,
![]()
Следовательно,
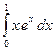 =
= 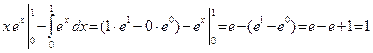
Задания для самостоятельной работы
|
1) |
6) |
11) |
|
2) |
7) |
12) |
|
3) |
8) |
13) |
|
4) |
9) |
14) |
|
55) |
10) |
15) |
Вопросы для самоконтроля:
1. Дайте определение определенного интеграла.
2. Чему равен определенный интеграл с равными пределами интегрирования?
3. Чему равен определенный интеграл от алгебраической суммы функций?
4. Что происходит при перестановки пределов интегрирования местами?
5. Напишите формулу Ньютона-Лейбница.
6. Сформулируйте порядок вычисления определенного интеграла.
7. Как вычислить определенный интеграл методом подстановки?
8. В чем заключается геометрический смысл определенного интеграла?
9. Напишите формулу для определения площади плоской фигуры.
Практическая работа № 14
Решение дифференциальных уравнений различного вида
Цель: Формирование навыков решения дифференциальных уравнений первого порядка с разделяющимися переменными; однородных дифференциальных уравнений первого порядка и линейных дифференциальных уравнений первого порядка
На выполнение практической работы отводится 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы
2.Оформить задания в тетради для практических работ
Теоретический материал
Решение дифференциальных уравнений первого порядка с разделяющимися переменными; однородных дифференциальных уравнений первого порядка и линейных дифференциальных уравнений первого порядка
Дифференциальным уравнением называется уравнение,
связывающее между собой независимую переменную ![]() ,
искомую функцию
,
искомую функцию ![]() и ее производные или
дифференциалы.
и ее производные или
дифференциалы.
Символически дифференциальное уравнение записывается так:
![]() ,
,
![]() ,
, ![]() .
.
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.
Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.
Решением (или интегралом) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.
Общим решением (или общим интегралом) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.
Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определенных начальных значениях аргумента и функции.
Дифференциальным уравнением первого порядка называется уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
![]() .
.
Для решения этого уравнения нужно сначала разделить переменные:
![]() ,
,
а затем проинтегрировать обе части полученного равенства:
![]() .
.
Уравнение вида ![]() , где
, где ![]() и
и ![]() -
функции от
-
функции от ![]() , называется линейным
дифференциальным уравнением первого порядка. В частности
, называется линейным
дифференциальным уравнением первого порядка. В частности ![]() и
и ![]() могут
быть постоянными величинами.
могут
быть постоянными величинами.
Это уравнение приводится к уравнению с разделяющимися
переменными с помощью подстановки ![]() , где
, где ![]() и
и ![]() -
новые функции от
-
новые функции от ![]() .
.
Примеры
Задание 1: Найдите общее решение уравнения ![]() .
.
Решение: Разделив переменные, имеем ![]() . Интегрируем обе части полученного
уравнения:
. Интегрируем обе части полученного
уравнения:
![]() ;
; ![]() .
.
Так как произвольная постоянная ![]() может
принимать любые числовые значения, то для удобства дальнейших преобразований
вместо
может
принимать любые числовые значения, то для удобства дальнейших преобразований
вместо ![]() мы написали
мы написали ![]() . Потенцируя последнее равенство,
получим
. Потенцируя последнее равенство,
получим ![]() .
.
Это и есть общее решение данного уравнения.
Задание 2: Найти частное решение уравнения ![]() , удовлетворяющее начальным
условиям
, удовлетворяющее начальным
условиям ![]() при
при ![]() .
.
Решение: Разделив переменные, имеем ![]() . Проинтегрируем обе части полученного
уравнения:
. Проинтегрируем обе части полученного
уравнения:
![]() ;
; ![]() ,
,
или
![]() ,
, ![]() .
.
Это общее решение данного уравнения. Для нахождения значения
произвольной постоянной ![]() подставим
значения
подставим
значения ![]() и
и ![]() в
выражение для общего решения:
в
выражение для общего решения: ![]() , или
, или ![]() , откуда
, откуда ![]() .
.
Следовательно, искомое частное решение, удовлетворяющее
указанным начальным условиям, имеет вид ![]() .
.
Задание 3: Найдите общее решение уравнения ![]() .
.
Решение: Это линейное уравнение: здесь ![]() ,
, ![]() .
Положим
.
Положим ![]() и продифференцируем это равенство
по
и продифференцируем это равенство
по ![]() :
:
![]() .
.
Подставив теперь выражения для ![]() и
и
![]() в данное уравнение, получим
в данное уравнение, получим
![]() ,
,
или
![]() . (*)
. (*)
Так как одну из вспомогательных функций ![]() или
или ![]() можно
выбрать произвольно, то в качестве
можно
выбрать произвольно, то в качестве ![]() возьмем одно из
частных решений уравнения
возьмем одно из
частных решений уравнения ![]() . Разделив в
этом уравнении переменные и проинтегрируя, имеем
. Разделив в
этом уравнении переменные и проинтегрируя, имеем ![]() ,
,
![]() ;
; ![]() ,
,
![]() (произвольную постоянную
(произвольную постоянную ![]() принимаем равной нулю, так как
находим одно из частных решений).
принимаем равной нулю, так как
находим одно из частных решений).
Подставим теперь выражение для ![]() в
уравнение (*);
тогда получим уравнение
в
уравнение (*);
тогда получим уравнение ![]() , или
, или ![]() .
.
Отсюда находим ![]() ;
; ![]() .
.
Зная ![]() и
и ![]() , теперь получим общее решение
данного уравнения:
, теперь получим общее решение
данного уравнения:
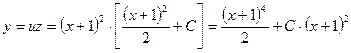 .
.
Задания для самостоятельной работы
1. Найдите общее решение уравнений:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3)
![]() ;
;
4) ![]() ; 5)
; 5) ![]() ;
;
6) ![]() ; 7)
; 7) ![]() ;
;
8) ![]() .
.
2. Найдите частные решения уравнений, удовлетворяющие указанным начальным условиям:
1) ![]() ;
; ![]() при
при ![]() ;
;
2) ![]() ;
; ![]() при
при ![]() ;
;
3) ![]() ;
; ![]() при
при
![]() ;
;
4) ![]() ;
; ![]() при
при
![]() ;
;
5) ![]() ;
; ![]() при
при
![]() ;
;
6) ![]() ;
; ![]() при
при ![]() ;
;
7) ![]() ;
; ![]() при
при ![]() .
.
3. Найдите общие решения уравнения:
1) ![]() ; 2)
; 2)
![]() ;
;
3) ![]() ; 4)
; 4) ![]() ;
;
5) ![]() ; 6)
; 6) ![]() .
.
Вопросы для самоконтроля:
1. Какое уравнение называется дифференциальным?
2. Что называется решением дифференциального уравнения?
3. Какое решение дифференциального уравнения называется общим?
4. Какое решение дифференциального уравнения называется частным?
5. Какие дифференциальные уравнения называются уравнениями первого порядка?
6. Какие дифференциальные уравнения называются уравнениями с разделяющимися переменными?
Практическая работа № 15
Решение прикладных задач с помощью дифференциальных уравнений
Цель: Формирование навыков решения прикладных задач с помощью дифференциальных уравнений
На выполнение практической работы отводится 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы
2.Оформить задания в тетради для практических работ
Теоретический материал
Понятие о дифференциальных уравнениях. Дифференциальные уравнения используются при изучении явлений и процессов в физике, химии, биологии, медицине, фармации, астрофизике, кибернетике, социологии и других областях знаний. Сформулировав задачу на языке дифференциальных уравнений, специалист любой отрасли знаний получает в руки готовый аппарат для численного решения задачи, изучения качественных особенностей этого решения. Многие вопросы естествознания и техники сводятся к нахождению неизвестной функции у = f(x), если известно уравнение, содержащее х, у и производные разных порядков функции f(x): f¢(x), f¢¢(x), …, f(n)(x) или дифференциалы функции df, d2f, …, dnf. Такие уравнения называются дифференциальными.
Рассмотрим задачу, приводящую к дифференциальному уравнению: установить закон изменения скорости u свободно падающего тела массой т без учета силы сопротивления воздуха.
Согласно второму закону Ньютона,
![]()
где mg – сила тяжести.
Полученное уравнение является дифференциальным, так как в него входит производная du/dt искомой функции u. Решить дифференциальное уравнение – значит найти такую функцию u = f(t) , которая тождественно удовлетворяет этому уравнению. Легко проверить, что уравнению удовлетворяет функция вида u = gt + C, где С – любое число. Указав начальные условия, можно найти одну функцию, удовлетворяющую уравнению. Так, если при t = 0 u = u0, то получим функцию u = u0 + gt.
Существует много задач из различных областей знаний, решение которых сводится к составлению и решению дифференциальных уравнений.
Основные определения теории обыкновенных дифференциальных уравнений. Дифференциальным называют уравнение, связывающее аргумент х, искомую функцию у = f(x), ее производные f¢(x), f¢¢(x), …, f(п)(x) или дифференциалы df, d2f, …, dпf.
Дифференциальное уравнение в общем виде можно записать так:
F(x, f(x), f¢(x), f¢¢(x), …, f(п)(x)) = 0
или
F(x, y, y¢, y¢¢, …, y(n)) = 0.
Если искомая функция y = f(x) есть функция одного аргумента, то дифференциальное уравнение называют обыкновенным.
Если функция u = f(x, y,
z, …, t) зависит от двух и большего числа аргументов, то
уравнение будет содержать частные производные ![]() и
т.д. Такое уравнение носит название дифференциального уравнения в частных
производных. Мы будем рассматривать только обыкновенные дифференциальные
уравнения.
и
т.д. Такое уравнение носит название дифференциального уравнения в частных
производных. Мы будем рассматривать только обыкновенные дифференциальные
уравнения.
Порядком дифференциального уравнения называется порядок наивысшей производной или дифференциала, входящих в уравнение.
Например, у¢ = 2ху2 + 5 – уравнение первого порядка, а у¢¢ + у =0 – второго.
Общим решением дифференциального уравнения порядка r называется функция y = f(x,C1, C2, …, Cr) от х с произвольными постоянными C1, C2, …, Cr,обращающая это уравнение в тождество.
Общее решение, записанное в неявном виде Ф(x, у,C1, …, Cr) = 0, называется общим интегралом.
Так, решением дифференциального уравнения у¢¢ + у =0 является функция у = С1 sin x + C2 cos x, где C1 и C2 – произвольные постоянные. При подстановке функции у = С1 sin x + C2 cos x в уравнение у¢¢ + у =0 оно превращается в тождество. Действительно,
у¢х = C1 cos x – С2 sin x; у¢¢хх = - С1 sin x - C2 cos x;
- С1 sin x - C2 cos x + С1 sin x + C2 cos x =0.
При любом наборе конкретных постоянных получаются частные решения. На практике частное решение получают из общего не прямым заданием значений произвольных постоянных, а с учетом тех условий, которым должно удовлетворять искомое частное решение. Задание таких условий называется заданием начальных условий и записывается кратко так:
f(x0) = y0; f¢(x0) = y¢0;…; f(r-1)(x0) = y0(r-1).
Задача нахождения частного решения, удовлетворяющего начальным условиям, называется задачей Коши.
Составление и решение дифференциальных уравнений на примерах прикладных задач.
Общие замечания. Дифференциальные уравнения занимают важное место в решении задач физико-химического, фармацевтического и медико-биологического содержания. Пользуясь ими, мы устанавливаем связь между переменными величинами, характеризующими данный процесс или явление.
Решение любой задачи с помощью математического анализа можно разбить на три этапа:
1) перевод условий задачи на язык математики;
2) решение задачи;
3) оценка результатов.
Первая часть работы обычно заключается в составлении дифференциального уравнения и является наиболее трудной, так как общих методов составления дифференциальных уравнений нет и навыки в этой области могут быть приобретены лишь в результате изучения конкретных примеров.
Закон охлаждения тела. Согласно закону Ньютона, скорость охлаждения тела пропорциональна разности между температурами тела и окружающей среды. Пусть тело нагрето до температуры То, температуру окружающей среды будем считать постоянной и равной Тс, Тс < То. В момент времени t температура тела равна Т. Скорость изменения температуры dT/dt пропорциональна разности Т – Тс, то есть
dT/dt = - r(Т – Тс).
Минус означает, что с возрастанием времени t температура Т тела уменьшается. Производная убывающей функции отрицательна, а скорость по смыслу – положительная величина. Коэффициент пропорциональности r зависит от физических свойств тела, так и от его геометрической формы.
Разделим переменные в уравнении и проинтегрируем его:
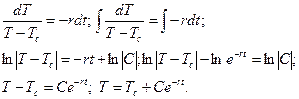
Подставив начальные условия t=0, Т=То, найдем значение С и подставим в последнее уравнение:
Т0=Тс+Се-r0; С=Т0-Тс;
Т=Тс+(Т0-Тс)е-rt.
Это закон охлаждения тела с течением времени.
Задача о скорости размножения бактерий. Скорость размножения бактерий пропорциональна их количеству. В начальный момент имелось 100 бактерий, в течение трех часов их число удвоилось. Найти зависимость количества бактерий от времени.
Решение. Пусть N – количество бактерий в момент времени t. Тогда согласно условию
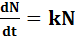
где k - коэффициент пропорциональности.
Уравнение представляет собой уравнение с разделяющимися переменными и его
решение имеет вид: ![]()
Из начального условия известно, что N (0) = 100 . Следовательно,
![]()
![]() и
и ![]() . C
= 100 и
. C
= 100 и ![]()
Из дополнительного условия N (3) = 200. Тогда
![]() ,
, ![]() ,
, 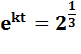
Таким образом, для искомой функции получаем:
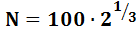
Задача об увеличении количества фермента. В культуре пивных дрожжей быстрота прироста действующего фермента пропорциональна его начальному количеству x. Первоначальное количество фермента а в течение часа удвоилось. Найти зависимость x(t).
Решение. По условию задачи дифференциальное уравнение процесса имеет вид
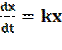
где k – коэффициент пропорциональности.
Общее решение уравнения (уравнение с разделяющимися переменными) имеет вид:
![]()
Постоянную С найдем из начального условия x(0)= a : ![]()
Тогда ![]()
Известно также,
что x(1) = 2a. Значит ![]() , отсюда
, отсюда ![]() = 2 и окончательно имеем
= 2 и окончательно имеем
![]()
Задания для самостоятельной работы
Составив дифференциальные уравнения, решите задачи:
3. Тело движется прямолинейно с ускорением а = 5 см/с2. Начальная скорость тела vo = 2 м/с. Вывести закон движения этого тела и вычислить путь, который оно пройдет за первые 10 мин движения.
4. Найти зависимость потенциальной энергии сжатой пружины от величины деформации.
Указание. Потенциальная энергия сжатой пружины равна работе силы F = Rx на пути от 0 до х.
5. Скорость охлаждения тела пропорциональна разности температур тела и окружающей среды. До какой температуры охладится тело за 30 мин, если за 10 мин оно охладилось от 100 до 60° С? Температура окружающей среды 20° С.
6. Уменьшение интенсивности света при прохождении через поглощающее вещество пропорционально интенсивности падающего света и толщине поглощающего слоя. Найти закон убывания интенсивности света, если известно, что при прохождении слоя l = 0,5 м интенсивность света убывает в два раза.
7. Найти закон убывания лекарственного препарата в организме человека, если через 1 ч после введения 10 мг препарата масса его уменьшилась вдвое. Какое количество препарата останется в организме через 2 ч?
8. Составить дифференциальное уравнение, описывающее движение математического маятника, считая, что углы отклонения маятника малы.
Практическая работа № 16.
Понятие о числе сочетаний (решение типовых задач).
Цель: Формирование навыков решения задач по определению вероятностей
На выполнение практической работы отводится 1 час.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
1.Основные понятия и определения
Теоремы о сложении вероятностей
![]() Если события A и В несовместны, то вероятность суммы событий
равна сумме вероятностей этих событий
Если события A и В несовместны, то вероятность суммы событий
равна сумме вероятностей этих событий
![]() Если события A и В совместны и зависимы, то вероятность суммы событий определяется
по формуле:
Если события A и В совместны и зависимы, то вероятность суммы событий определяется
по формуле:
![]() Если события A и В совместны,
но независимы, то
вероятность суммы событий определяется по формуле:
Если события A и В совместны,
но независимы, то
вероятность суммы событий определяется по формуле:
2.Решение задач
Задача № 1. Спортсмен стреляет по мишени, разделенной на три сектора. Вероятность попадания в первый сектор равна 0,5, во второй – 0,3. Какова вероятность попадания либо в первый, либо во второй сектор?
![]() Решение.
Решение.
![]() Так как события А и В несовместны,
то
Так как события А и В несовместны,
то
Задача № 2.. Два стрелка стреляют по мишени с вероятностью 0,7 и 0,8, соответственно. Найти вероятность того, что хотя бы один из них попадает в цель.
![]() Решение
Решение
![]() Так как события совместны и
независимы, то
Так как события совместны и
независимы, то
Задача № 3. Симметричная монета подброшена три раза. Какова вероятность того, что цифра выпадет два раза?
Решение
событие А1 - «при первом подбрасывании выпадает цифра»;
событие А2 - «при втором подбрасывании выпадает цифра»;
событие А3 - «при третьем подбрасывании выпадает цифра»
Событие А - «при трех подбрасываниях цифра выпадает два раза»
![]()
![]()
![]()
![]() Поскольку события
Поскольку события
и
являются независимыми, то
![]()
События А1, А2 и А3 - независимы, поэтому
![]()
![]()
Задача № 4 Три стрелка попадают в мишень соответственно с вероятностями 0,8; 0,7 и 0,6. Найти вероятность того, что при одном выстреле хотя бы один из них попадет в мишень.
Решение
А – «первый стрелок попадает в мишень»
В – «второй стрелок попадает в мишень»
С – «третий стрелок попадает в мишень»
Тогда событие:
![]() – «хотя бы один из стрелков попадает в цель».
– «хотя бы один из стрелков попадает в цель».
![]() Событие, противоположное событию D:
Событие, противоположное событию D:
Теперь, вероятность р события D:
![]()
![]()
![]()
![]() где
где
![]()
Задания для самостоятельной работы
Задание 1. По данным задачи №4 ответить на следующие вопросы:
а) Какова вероятность того, что в мишень попадет только один стрелок?
б) Какова вероятность того, что в мишень попадут два стрелка?
в) Какова вероятность того, что в мишень попадут три стрелка?
г) Какова вероятность того, что в мишень не попадет ни один стрелок?
Задание 2. Используя классическое определение вероятности события, решить следующие задачи:
1. В коробке 4 красных, 5 зеленых, 8 желтых, 7 белых и 1 черный шар. Найти вероятность вытащить: красный шар; синий шар; белый шар; цветной шар; или зеленый или белый шар; не красный шар; шар одного из цветов светофора.
2. В семье – двое детей. Какова вероятность, что старший ребенок – девочка, если известно, что в семье есть дети обоего пола?
3. Мастер, имея 10 деталей, из которых 4 – нестандартных, проверяет детали одну за другой, пока ему не попадется стандартная. Какова вероятность, что он проверит ровно две детали?
4. В одном ящике 3 белых и 7 черных шаров, в другом ящике – 6 белых и 8 черных шара. Найти вероятность того, что хотя бы из одного ящика будет вынут белый шар, если из каждого ящика вынуто по одному шару.
5. Издательство отправило газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,9, во второе - 0,7, в третье - 0,85. Найти вероятность следующих событий:
а) только одно отделение получит газеты вовремя;
б) хотя бы одно отделение получит газеты с опозданием.
6. В первой урне находятся 12 белых и 4 черных шаров, а во второй 5 белых и 10 черных шаров. Из каждой урны вынули по шару. Какова вероятность того, что оба шара окажутся черными? Какова вероятность, что оба шара окажутся белыми?
7. В партии из 25 деталей находятся 8 бракованных. Вынимают из партии наудачу две детали. Определить, какова вероятность того, что обе детали окажутся бракованными.
8. Подброшены две игральные кости. Найти вероятность события A того, что выпадет хотя бы одна шестерка.
9. Найти вероятность, что при бросании игральной кости выпадет число, большее 4.
10. Найти вероятность, что при бросании игральной кости выпадет число, не меньшее 2 и не большее 5.
Задание 3. Используя формулы полной вероятности и Байеса, решить следующие задачи:
1. Имеются 2 одинаковые урны. В первой урне находятся 7 белых и 3 черных шаров, во второй – 6 белых и 4 черных. Наугад выбираются урна и из нее извлекается один шар. Выбранный шар оказался черным. Какова вероятность, что этот шар из 2 урны?
2. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру =0,5, ко второму =0,6. Вероятность того, что годная деталь будет признана стандартной первым контролером =0,94, а вторым =0,92. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.
3. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартная равна 0,9, а второго – 0,8. Найти вероятность того, что взятая наудачу деталь – стандартная.
4. Имеются 3 одинаковые урны. В первой урне находятся 6 синих и 4 черных шаров, во второй – только синие и в третьей – только черные. Наугад выбираются урна и из нее извлекается один шар. Какова вероятность, что этот шар синий?
5. Имеются 2 одинаковые урны. В первой урне находятся 7 белых и 3 черных шаров, во второй – 6 белых и 4 черных. Наугад выбираются урна и из нее извлекается один шар. Выбранный шар оказался черным. Какова вероятность, что этот шар из 1 урны?
Задание 4. Используя формулу Бернулли, решить следующие задачи:
1. Вероятность того, что расход электроэнергии на продолжении одних суток не превысит установленной нормы равна 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
2. Найти вероятность осуществления от одного до трех разговоров по телефону при наблюдении шести независимых вызовов, если вероятность того, что разговор состоится, равна 0,6.
3. Прибор состоит из пяти элементов, включенных в цепь параллельно и работающих независимо друг от друга. Вероятность безотказной работы каждого элемента за время Т равна 0,5. Для безаварийной работы прибора достаточно, чтобы хотя бы один элемент был исправен. Какова вероятность того, что за время Т прибор будет работать безотказно?
4. Вероятность выигрыша по одному лотерейному билету =0,3. Какова вероятность того, что из семи приобретенных билетов три билета окажутся выигрышными?
5. Магазин получил 40 деталей. Вероятность наличия нестандартной детали в партии равна 0,04. Найти наиболее вероятное число нестандартных деталей в этой партии.
6. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найдя вероятности возможного числа появления бракованных деталей среди 5 отобранных, найти наивероятнейшее число появления бракованных деталей из 5 отобранных, указав его вероятность.
7. Сколько раз необходимо подбросить игральную кость, чтобы наивероятнейшее выпадение тройки было равно 10?
8. Для данного участника игры вероятность набросить кольцо на колышек =0,3. Какова вероятность того, что при шести бросках 3 кольца окажутся на колышке?
9. На самолете имеются 4 одинаковых двигателя. Вероятность нормальной работы каждого двигателя в полете равна р. Найти вероятность того, что в полете могут возникнуть неполадки в одном двигателе.
10. Вероятность отказа каждого прибора при испытании равна 0,4. Что вероятнее ожидать: отказ двух приборов при испытании четырех или отказ трех приборов при испытании шести, если приборы испытываются независимо друг от друга?
11. Вероятность того, что на некотором предприятии расход электроэнергии не превысит суточной нормы равна 0,8. Какова вероятность того, что в течение пяти рабочих дней из семи перерасхода электроэнергии не будет?
Вопросы для самоконтроля:
1. Дайте классическое определение вероятности.
2. Какое событие называется достоверным, какое – невозможным и какое – случайным?
3. В каком диапазоне изменяется вероятность случайного события?
4. Что такое диаграмма Эйлера-Венна применительно к теории вероятности?
5. Записать формулы для вероятности суммы и произведения случайных событий.
Практическая работа № 17.
Произвольное, равномерное и биноминальное распределение
Цель: научиться применять формулу Бернулли для составления закона распределения случайной величины, изображать закон графически, находить вероятности конкретных значений случайной величины.
На выполнение практической работы отводится 1 час.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
1. Формула Бернулли
Пусть производится конечное число одинаковых испытаний, в результате каждого из которых может произойти или не произойти некоторое событие А. Будем считать, что вероятность события А в каждом испытании одна и та же Р(А) = р и не зависит от того, произойдет или нет событие А в других испытаниях. Такие испытания называются независимыми. Найдем вероятность того, что среди n независимых испытаний событие А произойдет ровно m раз. Искомую вероятность обозначим Pn(m) и для ее нахождения используем формулу Бернулли:
Pn(m) = n!/(m!· (n – m)!) · pm · (1 – p)n – m.
Пример 1
Вероятность попадания в цель при одном выстреле составляет p=0,8. Найти вероятность четырех попаданий при шести выстрелах.
Решение
Здесь n = 6, m = 4, p = 0,8. По формуле Бернулли находим
P6(4) = 6! / (4! · (6 – 4)!) · 0,84 · (1 – 0,8)6 – 4 = 0,246.
2. Закон распределения случайной величины
Случайной величиной называется переменная величина, которая может принимать те или иные значения в зависимости от случая. Случайные величины обозначаются прописными буквами латинского алфавита: X, Y, Z и т. д., а их значения – соответствующими строчными буквами: x, y, z и т. д.Случайные величины делятся на дискретные (или прерывные) и непрерывные.
Случайная величина называется дискретной, если множество ее значений конечно или счетно, т. е. множество ее значений представляет собой конечную последовательность x1, x2,…, xn или бесконечную последовательность x1, x2,…, xn,…
Функция, связывающая значения случайной величины с соответствующими им вероятностями, называется законом распределения дискретной случайной величины. Его удобно задавать в виде следующей таблицы:
|
|
|
|
|
|
Значения |
xi |
1 |
2 |
3 |
n |
|
Вероятности |
pi |
1 |
2 |
3 |
n |
Таблица 1. Закон распределения случайной величины
События X = xi (i = 1, 2, 3, …, n) являются несовместными и единственно возможными, т. е. они образуют полную систему событий. Поэтому сумма их вероятностей равна единице:
p1 + p2 + p3 + … + pn = 1.
Пример 2
Разыгрываются две вещи стоимостью по 5 тыс. руб. и одна вещь стоимостью 30 тыс. руб. Составить закон распределения выигрыша для человека, купившего один билет из 50.
Решение
Искомая случайная величина Х представляет собой выигрыш и может принимать три значения: 0, 5 и 30 тыс. руб. Первому результату благоприятствует 47 случаев, второму результату – два случая и третьему – один случай. Найдем их вероятности:
P(x1) = 47/50 = 0,94;
P(x2) = 2/50 = 0,04;
P(x3) = 1/50 = 0,02.
Закон распределения случайной величины имеет вид
|
Значения |
xi |
0 |
5 |
30 |
n |
|
Вероятности |
pi |
0,94 |
0,04 |
0,02 |
n |
|
|
|
В качестве проверки найдем
P(x1) + P(x2) + P(x3) = 0,94 + 0,04 + 0,02 = 1.
3. Биномиальное распределение
Пусть производится определенное число n независимых испытаний, причем в каждом из них с одной и той же вероятностью может наступить некоторое событие А. Рассмотрим случайную величину Х, представляющую собой число наступлений события А в n испытаниях. Закон ее распределения имеет вид
|
Значения |
xi |
0 |
1 |
2 |
… |
n |
|
Вероятности |
pi |
Pn(0) |
Pn(1) |
Pn(2) |
… |
Pn(n) |
где Pn(m) вычисляются по формуле Бернулли. Закон распределения случайной величины Х, который характеризуется такой таблицей, называется биномиальным распределением.
Задания для самостоятельной работы
Задача № 1
По мишени стреляют 15 раз, причем вероятность попадания при одном выстреле равна 0,3. Выполнить следующие задания:
1) Составить закон распределения случайной величины Х – число попаданий в цель.
2) Изобразить графически закон распределения.
3) Найти наименее вероятное число попаданий.
4) Найти наиболее вероятное число попаданий.
5) Определить вероятность того, что число попаданий
а) m≥4; б) m<5; в) не менее 10; г) более 6; д) от 6 до 12
Задача № 2
По мишени стреляют 14 раз, причем вероятность попадания при одном выстреле равна 0,6. Выполнить следующие задания:
1) Составить закон распределения случайной величины Х – число попаданий в цель.
2) Изобразить графически закон распределения.
3) Найти наименее вероятное число попаданий.
4) Найти наиболее вероятное число попаданий.
5) Определить вероятность того, что число попаданий
а) m>9; б) m≤11; в) менее 8; г) не более 6; д) более 10, но менее 13
Задача № 3
По мишени стреляют 12 раз, причем вероятность попадания при одном выстреле равна 0,4. Выполнить следующие задания:
1) Составить закон распределения случайной величины Х – число попаданий в цель.
2) Изобразить графически закон распределения.
3) Найти наименее вероятное число попаданий.
4) Найти наиболее вероятное число попаданий.
5) Определить вероятность того, что число попаданий
а) m>9; б) m≤8; в) менее 5; г) не более 10; д) более 3, но не более 10
Вопросы для самоконтроля:
1. Какая величина называется случайной?
2. Какая случайная величина называется дискретной?
3. Опишите схему Бернулли. Какие элементарные события повторяются в этих испытаниях?
4. Запишите формулу Бернулли.
5. Что называется законом распределения случайной величины?
6 Какой закон распределения называется биномиальным?
Практическая работа № 18
Дисперсия случайной величины и ее свойства
Цель: Освоение методов построения закона распределения случайной величины
На выполнение практической работы отводится 1 час.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
1.Основные понятия и определения
Если для случайной величины X известны все значения x1, x2, x3,…xn , которые она может принимать, и все вероятности p1, p2, …,pn, с которыми эти значения принимаются, то говорят, что задан закон распределения случайной величины.
Закон распределения обычно записывают в виде таблицы:
|
x1 |
x2 |
x3 |
… |
xn |
|
p1 |
p2, |
p3 |
… |
pn |
Нетрудно заметить, что, поскольку события
А1 – « случайная величина X принимает значение x1»;
А2 - « случайная величина X принимает значение x2»;
…………………………………………………
Аn - « случайная величина X принимает значение xn»
несовместны, то их сумма является достоверным событием, то
есть, сумма всех вероятностей 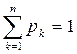 .
.
2. Примеры
Пример №1. Пусть случайная величина X – число очков, выпавших при подбрасывании игральной кости. Найти закон распределения.
Решение. Случайная величина X принимает значения x1=1, x2=2, …, x6=6 ,с вероятностями p1= p2=… p6=1/6.Поэтому закон распределения задается таблицей
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
Пример №2. Симметричная монета подбрасывается два раза. Случайная величина X – число появлений герба. Найти закон распределения.
Решение: Случайная величина X принимает значения 0, 1 и 2.
Полная группа событий может быть представлена следующим образом:
Г Г Г Ц Ц Г Ц Ц
Т.е., полную группу событий составляют четыре элементарных исхода. Из них два элементарных исхода благоприятствуют событию, когда число появлений герба равно одному, один элементарный исход благоприятствуют событию, когда число появлений герба равно нулю и один элементарный исход благоприятствуют событию, когда число появлений герба равно двум.
Поэтому, согласно формуле классической вероятности, ![]()
![]() и
и
![]()
Таким образом, закон распределения имеет вид:
|
X |
0 |
1 |
2 |
|
P |
1/4 |
2/4 |
1/4 |
Задания для самостоятельной работы
1. Дискретная случайная величина X имеет закон распределения:
|
X |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
P |
0,1 |
0,2 |
0,4 |
P4 |
0,1 |
Найти вероятность P4.
2. Дискретная случайная величина X имеет закон распределения:
|
X |
3 |
4 |
5 |
6 |
7 |
|
P |
p1 |
0,15 |
р3 |
0,25 |
0,35 |
Найти вероятности p1 и p3, если известно, что p3 в четыре раза больше p1.
3. Подбрасываются два игральных кубика. Подсчитывается число очков, выпавших на обеих верхних гранях. Найти закон распределения дискретной случайной величины X – суммы выпавших очков на двух игральных кубиках.
4. В урне 7 шаров, из которых 4 синих, а остальные красные. Из урны извлекаются 3 шара. Найти закон распределения дискретной случайной величины X – число синих шаров в выборке.
Вопросы для самоконтроля:
1. Дайте определение закона распределения случайной величины.
2. Чему равна сумма всех вероятностей, указанных в законе распределения?
3. Какая случайная величина называется дискретной, а какая - непрерывной?
Практическая работа № 19.
Построение вариационного ряда.
Цель: Освоение методов определения математического ожидания, дисперсии и среднего квадратичного отклонения случайной величины, заданной законом распределения
На выполнение практической работы отводится 1 час.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Нахождение математического ожидания, дисперсии и среднего квадратичного отклонения случайной величины, заданной законом распределения
1. Основные понятия и определения.
Пусть дан закон распределения дискретной случайной величины X
|
x1 |
x2 |
x3 |
… |
xn |
|
p1 |
p2, |
p3 |
… |
pn |
Математическим ожиданием дискретной случайной величины X называется сумма произведений ее значений на их соответствующие вероятности.
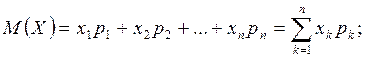
при этом 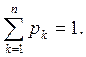
Для математического ожидания используются и другие символы: EX, a, mx
Математическое ожидание дискретной случайной величины приближенно равно среднему арифметическому всех ее возможных значений.
Свойства математического ожидания дискретной случайной величины.
1.Значения математического ожидания дискретной случайной величины X заключено между ее наибольшим и наименьшим значениями:
![]()
2.Математическое ожидание постоянной величины равно этой постоянной:
![]()
3.Постоянный множитель можно вынести за знак математического ожидания:
![]()
4. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
![]()
5. Математическое ожидание разности двух случайных величин равно разности их математических ожиданий:
![]()
6. Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий:
![]()
Пример. Найти математическое ожидание дискретной случайной величины, закон распределения которой задан таблицей
|
X |
3 |
4 |
5 |
6 |
7 |
|
Р |
0.1 |
0,2 |
0, 4 |
0,2 |
0,1 |
![]()
Разность X – M (X) называется отклонением случайной величины X от ее математического ожидания.
Дисперсией, или рассеянием, случайной величины X называется математическое ожидание квадрата ее отклонения:
![]()
Дисперсию можно вычислять по формуле:
![]()
Средним квадратичным отклонением случайной величины X называется корень квадратный из ее дисперсии:
![]()
2. Пример
Закон распределения случайной дискретной величины X задан таблицей
|
X |
-2 |
-1 |
0 |
1 |
2 |
|
P |
0.1 |
0,2 |
0, 4 |
0,2 |
0,1 |
Вычислить дисперсию случайной дискретной величины X
Решение
![]()
Закон распределения случайной
дискретной величины ![]()
|
|
(- 2- 0)2 |
(-1-0)2 |
(0 - 0)2 |
(1 - 0)2 |
(2 - 0)2 |
|
P |
0,1 |
0,2 |
0,4 |
0,2 |
0,1 |
Дисперсия случайной величины X :
![]()
Задания для самостоятельной работы
1. Известны математические ожидания двух случайных величин X и Y: M(X) = 3; M(Y) = 5
Найти математические ожидания суммы и разности этих величин.
2. Найти математическое ожидание случайной величины Y = 8X + 5 , если известно, M(X) = 2
Вопросы для самоконтроля:
1.Что такое математическое ожидание случайной величины?
2. Перечислить свойства математического ожидания.
Практическая работа № 20.
Построение вариационного ряда. Вычисление основных характеристик.
Цель: Овладение способами построения рядов распределения и методами расчета числовых характеристик
На выполнение практической работы отводится 2 часа.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Задача. Имеются данные о числе рабочих дней без простоя для пятидесяти буровых бригад одного из районов страны:
|
261 |
272 |
268 |
264 |
259 |
262 |
258 |
254 |
261 |
270 |
264 |
261 |
265 |
|
269 |
270 |
263 |
260 |
260 |
259 |
260 |
258 |
265 |
259 |
265 |
261 |
258 |
|
259 |
259 |
258 |
262 |
264 |
258 |
259 |
263 |
266 |
259 |
261 |
266 |
262 |
|
259 |
262 |
261 |
266 |
262 |
259 |
262 |
261 |
259 |
262 |
262 |
260 |
269 |
|
261 |
260 |
258 |
263 |
257 |
260 |
259 |
264 |
261 |
260 |
264 |
261 |
265 |
|
261 |
260 |
263 |
260 |
260 |
259 |
260 |
258 |
265 |
259 |
265 |
261 |
258 |
|
256 |
259 |
258 |
262 |
264 |
258 |
259 |
263 |
266 |
259 |
261 |
268 |
262 |
|
258 |
262 |
261 |
266 |
262 |
259 |
262 |
261 |
259 |
262 |
262 |
261 |
266 |
|
250 |
262 |
262 |
265 |
268 |
259 |
260 |
265 |
259 |
255 |
260 |
256 |
254 |
|
259 |
262 |
261 |
266 |
262 |
259 |
262 |
261 |
259 |
262 |
262 |
260 |
269 |
|
261 |
260 |
258 |
263 |
257 |
260 |
259 |
264 |
261 |
260 |
264 |
261 |
265 |
|
261 |
260 |
263 |
260 |
260 |
259 |
260 |
258 |
265 |
259 |
265 |
261 |
258 |
|
256 |
248 |
254 |
252 |
264 |
258 |
258 |
253 |
266 |
259 |
261 |
268 |
262 |
|
259 |
262 |
261 |
266 |
262 |
259 |
262 |
261 |
262 |
262 |
262 |
261 |
266 |
Обозначим через Х число рабочих дней без простоя для пятидесяти буровых бригад одного из районов страны.
1.1. По данным выборки строим интервальный вариационный ряд.
а) Поскольку, как легко выяснить, xmax = 272, xmin = 248, то размах варьирования признака Х равен
R = xmax –xmin = 272 – 248 = 24.
б) Определяя число k интервалов (число столбцов в
таблице) вариационного ряда, положим ![]() .
.
в) Длина h каждого частичного интервала равна
![]() .
.
Так как исходные данные мало
отличаются друг от друга и содержат целые числа, то величину h округляем до целого: ![]() .
.
г) Подсчитываем число вариант,
попадающих в каждый интервал, по данным выборки. Значение ![]() , попадающее на границу интервала,
относим к левому концу. За начало
, попадающее на границу интервала,
относим к левому концу. За начало ![]() первого
интервала берем величину
первого
интервала берем величину
![]() .
.
Конец ![]() последнего
интервала находим по формуле
последнего
интервала находим по формуле
![]() .
.
Сформированный интервальный вариационный ряд записываем в виде
|
Варианты-интервалы |
246- 249 |
249- 252 |
252- 255 |
255- 258 |
258- 261 |
261- 264 |
264- 267 |
267- 270 |
270- 273 |
|
Частоты, ni |
1 |
2 |
5 |
21 |
77 |
45 |
21 |
9 |
1 |
Контроль: ![]() ,
и объем выборки
,
и объем выборки ![]() .
.
1.2. Записываем дискретный вариационный ряд (табл. 2). В
качестве вариант ![]() берем середины
интервалов интервального вариационного ряда.
берем середины
интервалов интервального вариационного ряда.
|
варианты, |
247,5 |
250,5 |
253,5 |
256,5 |
259,5 |
262,5 |
265,5 |
268,5 |
271,5 |
|
частоты, ni |
1 |
2 |
5 |
21 |
77 |
45 |
21 |
9 |
1 |
1.3. Изображаем интервальный и дискретный вариационные ряды графически, построив гистограмму и полигон частот в одной системе координат (рис. 1).
2. Строим график накопленных частот — кумуляту (рис. 2). Предварительно составляем расчетную табл. 3.
|
Варианты, |
247,5 |
250,5 |
253,5 |
256,5 |
259,5 |
262,5 |
265,5 |
268,5 |
271,5 |
|
относительные частоты, wi = ni / n |
0,0055 |
0,0110 |
0,0275 |
0,1154 |
0,4231 |
0,2473 |
0,1154 |
0,0495 |
0,0055 |
|
Накопительные относительные частоты, Wi = Wi – 1 + wi |
0,0055 |
0,0165 |
0,0440 |
0,1593 |
0,5824 |
0,8297 |
0,9451 |
0,9945 |
1 |
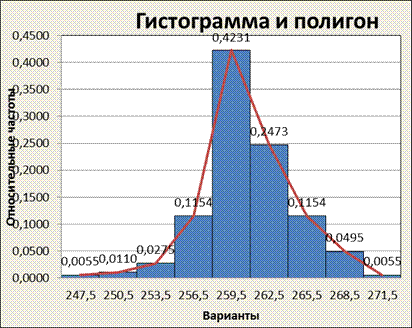
Рис. 1 Гистограмма и полигон
3. Находим эмпирическую функцию распределения. Воспользуемся формулой (1):
Fв (x)![]() .
.
Если х £ 247,5, то Fв (x) = 0 — по свойству эмпирической функции распределения.
Если 247,5< х £ 250,5, то Fв (x)![]() .
.
Если 250,5< х £ 253,5, то Fв (x)![]() .
.
Если 253,5< х £ 256,5, то Fв (x)![]() .
.
Если 256,5< х £ 259,5, то Fв (x)![]() .
.
Если 259,5< х £ 262,5, то Fв (x)![]() .
.
Если 262,5< х £ 265,5, то Fв (x)![]() .
.
Если 265,5< х £ 268,5, то Fв (x)![]() .
.
Если 268,5< х £ 271,5, то Fв (x)![]() .
.
Если ![]() ,
то Fв (x) = 1 — по свойству эмпирической функции
распределения.
,
то Fв (x) = 1 — по свойству эмпирической функции
распределения.
Записываем полученную эмпирическую функцию в виде:
Fв (x)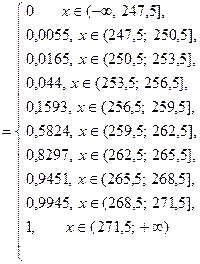
График функции Fв (x) представлен на рис.3.
Соединив середины вертикальных
частей ступенчатой кусочно-постоянной кривой, являющейся графиком функции Fв (x), получаем плавную кривую (на рис. 3 это штриховая
линия). Абсциссами точек этой кривой служат значения чисел рабочих дней без
простоя для пятидесяти буровых бригад одного из районов страны, а ординатами —
значения эмпирической функции распределения, характеризующей оценку вероятности
события X £ ![]() , т.е. вероятности попадания
возможных значений чисел рабочих дней без простоя для пятидесяти буровых бригад
на промежуток
, т.е. вероятности попадания
возможных значений чисел рабочих дней без простоя для пятидесяти буровых бригад
на промежуток ![]() .
.
Для нахождения числовых характеристик признака Х — чисел рабочих дней без простоя для пятидесяти буровых бригад (несмещенных оценок для
![]() ,
,
![]()
а также ![]() ,
,
![]() ,
, ![]() ,
,
![]() ) воспользуемся табл. 2.
) воспользуемся табл. 2.
4.1. Так как варианта ![]() в
табл. 2 встречается с наибольшей частотой
в
табл. 2 встречается с наибольшей частотой ![]() ,
то
,
то ![]() , т.е. это значение чисел рабочих
дней без простоя для пятидесяти буровых бригад, встречающееся в данной выборке
с наибольшей частотой.
, т.е. это значение чисел рабочих
дней без простоя для пятидесяти буровых бригад, встречающееся в данной выборке
с наибольшей частотой.
Находим ![]() .
Так как табл. 2 содержит нечетное число столбцов, то
.
Так как табл. 2 содержит нечетное число столбцов, то ![]() .
Это значение чисел рабочих дней без простоя для пятидесяти буровых бригад,
которое делит данные выборки признака Х на равные части.
.
Это значение чисел рабочих дней без простоя для пятидесяти буровых бригад,
которое делит данные выборки признака Х на равные части.
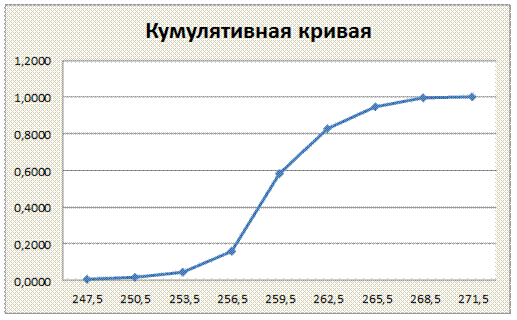
Рис. 2 Кумулятивная кривая
4.2. Для нахождения остальных статистик, характеризующих обводненность нефти, воспользуемся методом произведений. Введем, согласно (9), условные варианты
![]() ;
;
![]() ,
, ![]() .
.
Составим расчетную табл. 4.
|
|
|
|
|
|
|
|
Контрольный столбец |
|
247,5 |
1 |
-4 |
-4 |
16 |
-64 |
256 |
9 |
|
250,5 |
2 |
-3 |
-6 |
18 |
-54 |
162 |
8 |
|
253,5 |
5 |
-2 |
-10 |
20 |
-40 |
80 |
5 |
|
256,5 |
21 |
-1 |
-21 |
21 |
-21 |
21 |
0 |
|
259,5 |
77 |
0 |
0 |
0 |
0 |
0 |
77 |
|
262,5 |
45 |
1 |
45 |
45 |
45 |
45 |
180 |
Контроль вычислений проводим по формуле:
![]() ,
,
![]()
![]() .
.
Следовательно, вычисления проведены верно.
![]()
Рис. 3 Кумулята и эмпирическая функция распределения
|
265,5 |
21 |
2 |
42 |
84 |
168 |
336 |
189 |
|
268,5 |
9 |
3 |
27 |
81 |
243 |
729 |
144 |
|
271,5 |
1 |
4 |
4 |
16 |
64 |
256 |
25 |
|
|
182 |
0 |
77 |
301 |
341 |
1885 |
637 |
4.3. Пользуясь результатами последней строки табл. 10, находим условные начальные моменты (11) — (14):
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
4.4. Находим выборочную среднюю (15):
![]() ,
,
которая характеризует среднее число рабочих дней без простоя для пятидесяти буровых бригад, составляющую 261рабочий день.
4.5. Находим выборочную дисперсию (16):
![]()
4.6. Вычисляем выборочное среднее квадратичное отклонение (17):
![]() .
.
4.7. Величина ![]() характеризует
степень рассеяния значений числа рабочих дней без простоя для пятидесяти
буровых бригад относительно среднего числа рабочих дней. Для определения
колеблемости значений числа рабочих дней без простоя для пятидесяти буровых
бригад в процентном отношении вычисляем коэффициент вариации (22):
характеризует
степень рассеяния значений числа рабочих дней без простоя для пятидесяти
буровых бригад относительно среднего числа рабочих дней. Для определения
колеблемости значений числа рабочих дней без простоя для пятидесяти буровых
бригад в процентном отношении вычисляем коэффициент вариации (22):
![]() .
.
Величина коэффициента вариации мала (составляет 1%), что означает тесную сгруппированность значений обводненности нефти около центра рассеяния, т.е. около средней обводненности нефти.
4.8. Для предварительной оценки отклонения значений числа рабочих дней без простоя от нормального распределения вычисляем асимметрию и эксцесс. Сначала находим центральные моменты третьего и четвертого порядков (20), (21):
![]() .
.
![]()
![]() .
.
4.9. Тогда в соответствии с (18), (19), находим:
![]() ,
,
![]() .
.
Резюме. Значения ![]() и
и ![]() мало
отличаются от нуля. Поэтому можно предположить близость данной выборки,
характеризующей число рабочих дней без простоя, к нормальному распределению.
Эта гипотеза будет проверяться в лабораторной работе № 2.
мало
отличаются от нуля. Поэтому можно предположить близость данной выборки,
характеризующей число рабочих дней без простоя, к нормальному распределению.
Эта гипотеза будет проверяться в лабораторной работе № 2.
5. Произведем оценку генеральной средней ![]() и генерального
среднеквадратического отклонения s = S
по выборочным статистикам
и генерального
среднеквадратического отклонения s = S
по выборочным статистикам ![]() и
и ![]() , используя теорию доверительных
интервалов для нормального распределения. Доверительный интервал для истинного
значения обводненности нефти с надежностью
, используя теорию доверительных
интервалов для нормального распределения. Доверительный интервал для истинного
значения обводненности нефти с надежностью ![]() находим,
согласно (23):
находим,
согласно (23):
![]() .
.
Согласно приложению 3, при ![]() и
и ![]() находим
находим
![]() . Записываем доверительный
интервал:
. Записываем доверительный
интервал:
![]() ,
или
,
или ![]() .
.
Таким образом, среднее число
рабочих дней без простоя (в количестве дней) по данным выборки должна
находиться в промежутке ![]() .
.
Запишем доверительный интервал для
генерального среднеквадратического отклонения ![]() .
При заданных
.
При заданных ![]() и
и ![]() по
таблице приложения 4 находим
по
таблице приложения 4 находим ![]() . Так как
. Так как ![]() , то доверительный интервал
записываем в виде (24):
, то доверительный интервал
записываем в виде (24):
![]() ,
,
или
![]() ,
,
или
![]() ;
;
следовательно, отклонения истинных
значений число рабочих дней без простоя не должны выходить за пределы
промежутка ![]() .
.
Задания для самостоятельной работы
1. Закон распределения случайной дискретной величины X задан таблицей
|
X |
1 |
2 |
3 |
4 |
5 |
|
P |
0.05 |
0,15 |
0, 3 |
0,4 |
0,1 |
Вычислить дисперсию случайной дискретной величины X
2. Закон распределения случайной дискретной величины X задан таблицей
|
X |
-0,1 |
0 |
0,1 |
0,4 |
|
P |
0.3 |
0,15 |
0, 3 |
0,25 |
Вычислить ![]()
![]()
![]() случайной дискретной величины X
случайной дискретной величины X
Вопросы для самоконтроля:
1. Что такое дисперсия случайной величины?
2. Что такое среднее квадратичное отклонение случайной величины?
Библиографический список
Основные источники:
1. Григорьев В.П., Дубинский Ю.А. «Элементы высшей математики. Учебник для среднего профессионального образования». – М.: Академия, 2008.
2. Гмурман В.Е. «Теория вероятностей и математическая статистика». - М., Высшая школа, 2006.
3. Гмурман В.Е. «Руководство к решению задач по теории вероятностей и математическая статистика». - М., Высшая школа, 2006.
4. Дадаян А.А. «Математика. Учебник для среднего профессионального образования». – М.: Форум – Инфра – М, 2003.
5. Дадаян А.А. «Сборник задач по математике. Учебное пособие для среднего профессионального образования». – М.: Форум – Инфра – М, 2003.
6. Кудрявцев В.А., Демидович Б. П. «Краткий курс высшей математики» - М.: Наука, 2005.
7. Гончаренко, В.М. Элементы высшей математики : учебник / Гончаренко В.М., Липагина Л.В., Рылов А.А. - Москва: КноРус, 2020. — 363 с. — ISBN 978-5-406-01472-1. — URL: https://book.ru/book/935921— Текст: электронный.
8. Гулиян, Б.Ш. Элементы высшей математики : учебное пособие / Гулиян Б.Ш., Гулиян Г.Б. — Москва : КноРус, 2021. — 436 с. — ISBN 978-5-406-06303-3. — URL: https://book.ru/book/939826 — Текст: электронный.
9. Бахтина, Е.В. Комплект контрольно-измерительных материалов составлен для текущего контроля по дисциплине «Математика : монография / Бахтина Е.В., Корякина М.Л., Киселева И.И., Шулятьева Н.Н. — Москва : Русайнс, 2019. — 77 с. — ISBN 978-5-4365-3744-3. — URL: https://book.ru/book/934593). — Текст : электронный.
Дополнительные источники:
1. Богомолов Н.В. «Практическое занятие по математике». – М.: Высшая школа, 2000.
2. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов. – М.: Наука, 1989.
3. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: «ДИС», 1999.
4. Зубков А.М., Севастьянов Б.А., Чистяков В.П. Сборник задач по теории вероятностей. – М.: Наука, 1989.
5. Калинина В.Н., Панкин В.Ф. «Математическая статистика. Учебник для среднего профессионального образования». – М.: Высшая школа, 1998.
6. Фомин Г.П. Математические методы и модели в коммерческой деятельности. – М.: Финансы и статистика, 2005.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.