

Министерство образования и науки Самарской области
государственное автономное профессиональное образовательное учреждение
Самарской области
«ТОЛЬЯТТИНСКИЙ МАШИНОСТРОИТЕЛЬНЫЙ КОЛЛЕДЖ»
МЕТОДИЧЕСКИЕ указания
для обучающихся по выполнению
самостоятельной работы
по дисциплине ЕН.01 Элементы высшей математики
специальности 09.02.07 Информационные системы и программирование
Тольятти, 2018
|
ОДОБРЕНО |
|
методической комиссией ЕН и ОД протокол от 21 мая 2018 № 10 |
|
Председатель МК ________________/Г.И. Рожнова/ |
Составитель:
Рожнова Г.И. преподаватель ГАПОУ СО «ТМК».
Методические указания предназначены для самостоятельной работы обучающихся специальности 09.02.07 Информационные системы и программирование, при изучении ЕН.01 Элементы высшей математики.
Методические указания призваны помочь обучающимся самостоятельно освоить некоторые теоретические положения и практические вопросы по ЕН.01 Элементы высшей математики.
Содержание
|
1. |
Введение ………………………………………………………………… |
4 |
|
2. |
Карта самостоятельной работы………………………………………… |
5 |
|
3. |
Задания для самостоятельной работы………………………………… |
6 |
|
4. |
Список рекомендуемой литературы …………………………………... |
13 |
Введение
Уважаемый студент!
Данные методические указания разработаны Вам в помощь для выполнения внеаудиторной самостоятельной работы.
Приступая к выполнению внеаудиторной самостоятельной работы, Вы должны внимательно ознакомиться с требованиями к уровню Вашей подготовки в соответствии с федеральным государственным образовательным стандартом среднего профессионального образования.
В результате освоения дисциплины, Вы должны:
уметь:
- выполнять операции над матрицами и решать системы линейных уравнений - выбирать оптимальный численный метод для решения поставленной задачи;
- решать задачи, используя уравнения прямых и кривых второго порядка на плоскости;
- применять методы дифференциального и интегрального исчисления;
- решать дифференциальные уравнения;
- пользоваться понятиями теории комплексных чисел.
знать:
- основы математического анализа, линейной алгебры и аналитической геометрии;
- основы дифференциального и интегрального исчисления;
- основы теории комплексных чисел.
Процесс выполнения внеаудиторной самостоятельной работы способствует формированию общих компетенций (ОК):
ОК 1. Выбирать способы решения задач профессиональной деятельности, применительно к различным контекстам.
ОК 5. Осуществлять устную и письменную коммуникацию на государственном языке с учетом особенностей социального и культурного контекста.
Перед выполнением внеаудиторной самостоятельной работы преподаватель проводит инструктаж (консультацию) с определением цели задания, его содержания, сроков выполнения, основных требований к результатам работы, критериев оценки, форм контроля и перечня литературы.
Все задания внеаудиторной самостоятельной работы Вы должны выполнять в соответствии с инструкцией.
Отчет о выполнении внеаудиторной самостоятельной работы Вы должны выполнить по приведенному алгоритму.
Внимание! Если в процессе выполнения внеаудиторной самостоятельной работы у Вас возникают вопросы, разрешить которые самостоятельно не удается, необходимо обратиться к преподавателю для получения разъяснений или указаний в дни проведения дополнительных занятий.
Время проведения дополнительных занятий можно узнать у преподавателя или посмотреть на двери его кабинета.
Желаем Вам успехов!!!
КАРТА САМОСТОЯТЕЛЬНОЙ РАБОТЫ
|
Наименование разделов и тем |
Час |
Содержание самостоятельной работы |
Форма контроля |
|
1 |
2 |
3 |
|
|
Раздел 4 Интегральное исчисление функции одной действительной переменной
|
1 |
|
|
|
Тема 4.1 Интегральное исчисление функции одной действительной переменной |
1 |
Самостоятельная работа №1: Решить примеры по теме: «Определенные интегралы» |
Проверка примеров |
|
Раздел 7 Теория рядов
|
1 |
|
|
|
Тема 7.1 Теория рядов |
1 |
Самостоятельная работа №2: Решить примеры по теме: «Теория рядов» |
Проверка примеров |
|
Всего |
2 |
|
|
ЗАДАНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Раздел 4 Интегральное исчисление функции одной действительной переменной
Тема 4.1 Интегральное исчисление функции одной действительной переменной
Самостоятельная работа №1
Задание:
Решить примеры по теме: «Определенные интегралы»
Основной теоретический материал:
Функция, ![]() интегрируемая на промежутке
интегрируемая на промежутке ![]() , если при любых разбиениях
, если при любых разбиениях ![]() промежутка
промежутка ![]() ,
таких, что
,
таких, что ![]() при произвольном выборе точек
при произвольном выборе точек ![]() (где
(где ![]() ),
сумма
),
сумма ![]() при
при ![]() стремится
к пределу
стремится
к пределу ![]() .
.
Предел ![]() называют определенным
интегралом от функции
называют определенным
интегралом от функции ![]() на промежутке
на промежутке ![]() и обозначают
и обозначают 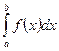 , то есть
, то есть 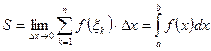 .
.
Число ![]() называется нижним пределом
интеграла,
называется нижним пределом
интеграла, ![]() - верхним. Промежуток
- верхним. Промежуток ![]() называется промежутком
интегрирования,
называется промежутком
интегрирования, ![]() - переменной
интегрирования.
- переменной
интегрирования.
Для
вычисления определенного интеграла от функции ![]() в
том случае, когда можно найти соответствующий неопределенный интеграл
в
том случае, когда можно найти соответствующий неопределенный интеграл ![]() , служит формула Ньютона – Лейбница:
, служит формула Ньютона – Лейбница:
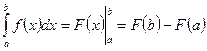 . То есть определенный интеграл
равен разности значений первообразной при верхнем и нижнем пределах
интегрирования.
. То есть определенный интеграл
равен разности значений первообразной при верхнем и нижнем пределах
интегрирования.
Задание
Вычислить определенные интегралы:
1)
![]() ;
;
2)
2) ![]() ;
;
3)
3) ![]() ;
;
4) ![]() ;
;
5) 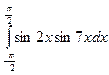
6) ![]() ;
;
7)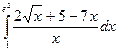 ;
;
8) 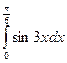 ;
;
9) 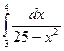 ;
;
10) 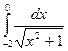 ;
;
11) ![]() ;
;
12) 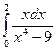 ;
;
13) 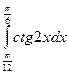 ;
;
14) 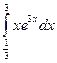 ;
;
Порядок выполнения самостоятельной работы и/или инструкции по выполнению самостоятельной работы
- изучить теоретический материал;
- рассмотреть примеры;
- выполнить задания.
Примеры:
Вычислить следующие определенные интегралы:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
Решение:1) 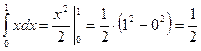 ;
;
2) ![]() ;
;
3)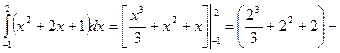
![]()
![]() .
.
Форма контроля самостоятельной работы:
Выполненная работа представляется преподавателю в тетради для самостоятельной работе на следующий урок.
Раздел 7 Теория рядов
Тема 7.1 Теория рядов
Самостоятельная работа №2
Задание:
Решить примеры по теме: «Теория рядов»
Основной теоретический материал:
Числовым рядом называется сумма вида
![]() , (1)
, (1)
где числа ![]() ,
,
![]() ,
, ![]() ,
…,
,
…, ![]() , …, называемые членами ряда,
образуют бесконечную последовательность; член
, …, называемые членами ряда,
образуют бесконечную последовательность; член ![]() называется
общим членом ряда.
называется
общим членом ряда.
Суммы
![]() ,
,
![]() ,
,
![]() ,
,
………………
![]() ,
,
составленные из первых членов рядя (1), называются частичными суммами этого ряда.
Каждому ряду
можно сопоставить последовательность частичных сумм ![]() ,
,
![]() ,
, ![]() ,
…,
,
…, ![]() …. Если при бесконечном возрастании
номера
…. Если при бесконечном возрастании
номера ![]() частичная сумма ряда
частичная сумма ряда ![]() стремится к пределу
стремится к пределу ![]() , то ряд называется сходящимся, а
число
, то ряд называется сходящимся, а
число ![]() - суммой сходящегося ряда, то есть
- суммой сходящегося ряда, то есть
![]() или
или ![]() .
Эта запись равносильна записи
.
Эта запись равносильна записи ![]() .
.
Если частичная
сумма ![]() ряда (1) при неограниченном
возрастании
ряда (1) при неограниченном
возрастании ![]() не имеет конечного предела (в
частности, стремится к
не имеет конечного предела (в
частности, стремится к ![]() или к
или к ![]() ), то такой ряд называется расходящимся.
), то такой ряд называется расходящимся.
Если ряд
сходится, то значение ![]() при достаточно большом
при достаточно большом ![]() является приближенным выражением
суммы ряда
является приближенным выражением
суммы ряда ![]() .
.
Разность ![]() называется остатком ряда.
Если ряд сходится, то его остаток стремится к нулю, то есть
называется остатком ряда.
Если ряд сходится, то его остаток стремится к нулю, то есть ![]() , и наоборот, если остаток
стремится к нулю, то ряд сходится.
, и наоборот, если остаток
стремится к нулю, то ряд сходится.
Для знакоположительных числовых рядов имеет место признак сравнении, при помощи которого можно установить сходимость или расходимость.
Признак сравнения. Если члены положительного ряда
![]() , (2)
, (2)
начиная с некоторого номера, не превосходят соответствующих членов ряда
![]() , (3)
, (3)
то из сходимости ряда (3) следует сходимости ряда (2), а из расходимости ряда (2) следует расходимость ряда (3).
При
исследовании рядов на сходимость и расходимость по этому признаку часто используются
геометрическая прогрессия![]()
![]() , которая сходится при
, которая сходится при ![]() и расходится при
и расходится при ![]() , и гармонический ряд
, и гармонический ряд![]() , являющийся расходящимся рядом.
, являющийся расходящимся рядом.
Числовой ряд
![]() (1)
(1)
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
Числовой ряд (1) называется знакочередующимся, если любые два стоящие рядом члена имеют противоположные знаки. Этот ряд является частным случаем знакопеременного ряда.
Признак
сходимости Лейбница для знакочередующихся рядов. Если члены знакочередующегося
ряда (1) монотонно убывают по абсолютной величине и общий член ![]() стремиться к нулю при
стремиться к нулю при ![]() , то ряд (1) сходится.
, то ряд (1) сходится.
Этот признак служит достаточным признаком сходимости знакочередующихся рядов.
Знакопеременный ряд (1) называется абсолютно сходящимся, если сходится ряд
![]() , (2)
, (2)
составленный из абсолютных величин его членов, то есть всякий абсолютно сходящийся ряд является сходящимся.
Если знакопеременный ряд (1) сходится, а составленный из абсолютных величин его членов ряд (2) расходится, то данный ряд (1) называется условно (неабсолютно) сходящимся. Заметим, что из расходимость ряда (2) в общем случае не следует расходимость ряда (1).
Для установления абсолютной сходимости знакопеременного (и знакочередующегося) ряда используются те же признаки, что и для сходимости ряда с положительными членами.
Для решения вопроса об абсолютной или условной сходимости знакочередующегося ряда необходимо рассмотреть ряд, составленный из абсолютных величин членов знакочередующегося ряда.
Если при исследовании этого ряда с помощью одного из признаков сходимости (признака Даламбера, признака сравнения рядов) ряд окажется сходящимся, то данный знакочередующийся ряд сходится абсолютно; если же ряд окажется расходящимся, то знакочередующийся ряд сходится условно.
Вариант 1:
Задание
1. Найдите первые пять членов ряда по его заданному общему члену:
1) ![]() ;
;
2) ![]() .
.
2. Найти формулу общего члена ряда по его данным первым членам:
1) ![]() ;
;
2) ![]() ;
;
3. Вычислите сумму членов ряда:
![]() ;
;
4. Пользуясь признаком сравнения, исследовать на сходимость следующие ряды:
![]() ;
;
5. Используя признак Лейбница, исследуйте сходимость знакочередующегося ряда:
![]() ;
;
6. Исследовать на сходимость (абсолютную или условную) знакочередующиеся ряды:
![]() ;
;
Вариант 2:
Задание
1. Найдите первые пять членов ряда по его заданному общему члену:
1) ![]() ;
;
2) ![]() ;
;
2. Найти формулу общего члена ряда по его данным первым членам:
1) ![]() ;
;
2) ![]() ;
;
3. Вычислите сумму членов ряда:
![]() ;
;
4. Пользуясь признаком сравнения, исследовать на сходимость следующие ряды:
![]() .
.
5. Используя признак Лейбница, исследуйте сходимость знакочередующегося ряда:
![]() ;
;
6. Исследовать на сходимость (абсолютную или условную) знакочередующиеся ряды:
![]() ;
;
Порядок выполнения самостоятельной работы и/или инструкции по выполнению самостоятельной работы
- изучить теоретический материал;
- рассмотреть примеры;
- выполнить задания.
Пример 1:
Найти сумму членов ряда:
1) ![]() ;
;
2) ![]() .
.
Решение: 1) Находим частичные суммы членов ряда:
![]() ;
; ![]() ;
; ![]() ;
;
![]() ; ….
; ….
Запишем
последовательность частичных сумм: ![]() ,
, ![]() ,
, ![]() ,
,
![]() , …,
, …, ![]() ,
… . Общий член этой последовательности есть
,
… . Общий член этой последовательности есть 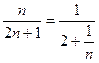 .
Следовательно,
.
Следовательно, 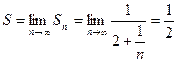 . Последовательность
частичных сумм имеет предел, равный
. Последовательность
частичных сумм имеет предел, равный ![]() . Итак, рая
сходится и его сумма равна
. Итак, рая
сходится и его сумма равна ![]() .
.
2) Это
бесконечно убывающая геометрическая прогрессия, в которой ![]() ,
, ![]() .
Используя формулу
.
Используя формулу ![]() , получим
, получим 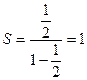 . Значит, ряд сходится и его сумма
равна 1.
. Значит, ряд сходится и его сумма
равна 1.
Пример 2.
С помощью признака сравнения исследовать на сходимость ряды:
1) ![]() ;
;
2) ![]() .
.
Решение: 1) Сравним данный ряд с рядом
![]() .
. ![]()
Ряд ![]() сходится, так как его член
образует бесконечно убывающую геометрическую прогрессию со знаменателем
сходится, так как его член
образует бесконечно убывающую геометрическую прогрессию со знаменателем ![]() . При это каждый член
. При это каждый член ![]() исследуемого ряда меньше
соответствующего члена
исследуемого ряда меньше
соответствующего члена ![]() ряда
ряда ![]() . Поэтому, согласно признака
сравнения, данный ряд сходится.
. Поэтому, согласно признака
сравнения, данный ряд сходится.
2) Сравним данный ряд с гармоническим рядом
![]() .
. ![]()
Каждый член ![]() исследуемого ряда, начиная со
второго, больше соответствующего члена
исследуемого ряда, начиная со
второго, больше соответствующего члена![]() ряда
ряда
![]() . Так как гармонический ряд
расходится, то, согласно признаку сравнения, расходится и данный ряд.
. Так как гармонический ряд
расходится, то, согласно признаку сравнения, расходится и данный ряд.
Пример 3.
Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() .
.
Решение: 1) Члены данного ряда по абсолютной величине
монотонно убывают: ![]() и
и ![]() . Следовательно, согласно признаку
Лейбницу, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно.
. Следовательно, согласно признаку
Лейбницу, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно.
Ряд ![]() , составленный из абсолютных
величин членов данного ряда, который, как, известно, расходится. Поэтому данный
ряд сходится условно.
, составленный из абсолютных
величин членов данного ряда, который, как, известно, расходится. Поэтому данный
ряд сходится условно.
2) Члены данного
ряда по абсолютной величине монотонно убывают ![]() ,
но
,
но 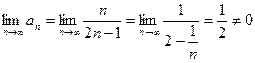 . Ряд расходится, так как признак
Лейбница не выполняется.
. Ряд расходится, так как признак
Лейбница не выполняется.
3) Используя
признак Лейбница, получим ![]() ;
; ![]() , то есть ряд сходится.
, то есть ряд сходится.
Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:
![]() . Это геометрический ряд вида
. Это геометрический ряд вида ![]()
![]() , который сходится. Поэтому данный
ряд сходится абсолютно.
, который сходится. Поэтому данный
ряд сходится абсолютно.
4) Используя
признак Лейбница, имеем ![]() ;
; ![]() , то есть ряд сходится.
, то есть ряд сходится.
Рассмотрим ряд, составленный из абсолютных величин членов данного рада:
![]() , или
, или 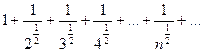 .
Это обобщенный гармонический ряд, который расходится, так как
.
Это обобщенный гармонический ряд, который расходится, так как ![]() . Следовательно, данный ряд
сходится условно.
. Следовательно, данный ряд
сходится условно.
Форма контроля самостоятельной работы:
Выполненная работа представляется преподавателю в тетради для самостоятельной работе на следующий урок.
Список рекомендуемой литературы
1.Численные методы и программирование: Учебное пособие / В.Д. Колдаев; Под ред. Л.Г. Гагариной. - М.: ИД ФОРУМ: НИЦ Инфра-М, 2016. - 336 с…
2. Гателюк, О. В. Численные методы : учеб. пособие для СПО / О. В. Гателюк, Ш. К. Исмаилов, Н. В. Манюкова. — М. : Издательство Юрайт, 2018. — 140 с. — (Серия : Профессиональное образование)
3.Бахвалов Н.С., Лапин А.В., Чижонков Е.В. «Численные методы в задачах и упражнениях»/ Под ред. В.А.Садовничего – М.:Высш.шк.,2016
4. Вержбицкий В.М. «Численные методы. Математический анализ и обыкновенные дифференциальные уравнения» - М.: Высшая школа, 2017
5. Волков Е.А. «Численные методы» - СПб.: Издательство «Лань», 2015
6. Исаков В.Н. «Элементы численных методов» - М.: Издательский центр «Академия», 2016.
7. Бахвалов Н.С., Лапин А.В., Чижонков Е.В.; Под ред. Садовничий В.А Численные методы в задачах и упражнениях: Учебное пособие /., - 4-е изд., (эл.) - М.:БИНОМ. Лаб. знаний, 2015. - 243 с.: ISBN 978-5-9963-2980-9 - Режим доступа: http://znanium.com/
8. А.В. Гулин, О.С. Мажорова, В.А. Морозова Введение в численные методы в задачах и упражнениях : учеб. пособие /. — М. : ИНФРА-М, 2017. — 368 с. — (Высшее образование: Бакалавриат). - Режим доступа: http://znanium.com/
9. Калиткин Н.Н., Численные методы: Учебное пособие / - 2-е изд., исправленное. - СПб:БХВ-Петербург, 2015. - 587 с. ISBN 978-5-9775-2575-6 - Режим доступа: http://znanium.com/catalog/product/94450
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.