МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ОП.02. ТЕХНИЧЕСКАЯ МЕХАНИКА ДЛЯ ОБУЧАЮЩИХСЯ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ, СПЕЦИАЛЬНОСТИ 08.02.01 СТРОИТЕЛЬСТВО И ЭКСПЛУАТАЦИЯ ЗДАНИЙ И СООРУЖЕНИЙ

Бахчисарайский колледж строительства, архитектуры и дизайна

                  (филиал) ФГАОУ ВО «КФУ им. В.И. Вернадского»

 

Утверждаю Директор Бахчисарайского колледжа строительства, архитектуры и дизайна (филиал) ФГАОУ ВО «КФУ им. В.И. Вернадского» _____________ Г.П. Пехарь

 

 

методическИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ по ОП.02. ТехническАЯ механикА

для обучающихся заочноЙ ФОРМЫ ОБУЧЕНИЯ,  специальности

08.02.01 Строительство и эксплуатация зданий и сооружений

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Бахчисарай  2023

                                                                                                  

 

Рассмотрено и одобрено на заседании методического совета, протокол № ___ от «___» ______ 2023 г.

Введено в действие приказом директора от «___» ________ 2023 г. № ____

Составитель:

Мухамедова Л.М., преподаватель профессиональных дисциплин высшей квалификационной категории. Методические указания и контрольные задания по дисциплине ОП.02. Техническая механика для обучающихся заочной формы обучения среднего профессионального образования специальности 08.02.01 Строительство и эксплуатация зданий и сооружений. – Бахчисарай: БКСАиД, 2023. – 38 стр.

 

Аннотация

к методическим указаниям и контрольным заданиям по дисциплине ОП.02. Техническая механика для обучающихся заочной формы обучения среднего профессионального образования специальности 08.02.01 Строительство и эксплуатация зданий и сооружений.

 

         Методические указания составлены в соответствии с  рабочей программой дисциплины ОП.02. Техническая механика и  могут быть использованы обучающимися заочного отделения специальности 08.02.01 Строительство и эксплуатация зданий и сооружений. В настоящее пособие включены краткие сведения из теории, задания к домашним контрольным работам №1 и №2, методические указания и подробно решенные характерные примеры решения задач,  вопросы для самопроверки и перечень учебной литературы.

 

 

Рассмотрены и утверждены на заседании цикловой методической комиссии № 3 «Дисциплин профессиональной подготовки 08.02.01 Строительство и эксплуатация зданий и сооружений.

«___» __________ 2023 г.   Протокол № ___

 

 

 

Председатель ЦМК _______________ Е.А. Базарная

 

СОДЕРЖАНИЕ

                                                                                                                                 Стр.

1. Введение………………………………………………………………..4

2. Домашняя контрольная работа № 1. Варианты заданий и методические указания к решению задач……………………………………………......6

    Задача № 1.1.…………………………………………………………  6

    Методические указания к решению задачи № 1.1…………………...7

    Примеры  1 и 2  решения задачи № 1.1…………………………………...8

    Задача № 1.2.…………………………………………………………..11

    Методические указания к решению задачи № 1.2………………….13

    Примеры 3 и 4 решения задачи № 1.2……………………………………...14

    Задача № 1.3…………………………………………………………...17

    Методические указания к решению задачи № 1.3………………….20

    Пример 5  решения задачи № 1.3…………………………………………...21

    Задача № 1.4…………………………………………………………...23

    Методические указания к решению задачи № 1.4………………….25

    Пример 6 решения задачи № 1.4……………………………………………26

    Задача № 1.5…………………………………………………………...28

    Методические указания к решению задачи № 1.5……………….....31

    Пример 7 решения задачи № 1.5…………………………………………...32

    Задача № 1.6…………………………………………………………..35

    Методические указания к решению задачи № 1.6…………………38

    Пример 8  решения задачи № 1.6………………………………………….38

3. Домашняя контрольная  работа № 2. Варианты заданий и методические указания к решению задач……………………………………………...40

   Задача № 2.1…………………………………………………………..40

   Методические указания к решению задачи № 2.1…………………43

   Пример 9  решения задачи № 2.1………………………………………….44

   Задача № 2.2………………………………………………………… 47

   Методические указания к решению задачи № 2.2…………………50

   Пример 10 решения задачи № 2.2………………………………………..51

   Задача № 2.3……………………………………………………………55

   Методические указания к решению задачи № 2.3…………………...58

   Пример11  решения задачи № 2.3……………………………………………59

4. Вопросы для самопроверки ………………………………………………… .63

5. Список  литературы …………………………..................................................67

 1.Введение

Техническая механика является одной из важнейших общепрофессиональных дисциплин, изучаемых в средних профессиональных учебных заведениях. Одним из важнейших видов самостоятельной работы обучающихся при изучении этой дисциплины является выполнение домашних контрольных работ, которые служат для закрепления и углубления знаний  и развития  навыков в решении различных практических задач.

Дисциплина ОП.02. Техническая механика включает в себя три раздела: теоретическую механику, сопротивление материалов и статику сооружений. Цель изучения дисциплины – дать будущим техникам-строителям основные сведения о равновесии материальных тел, о методах расчета элементов конструкций на прочность, жесткость и устойчивость и методах статического расчета.  Весь материал программы разделен на две домашние контрольные работы: ДКР №1- теоретическая механика и сопротивление материалов (выполняется по втором семестре) и ДКР № 2- статика сооружений (выполняется в 3 семестре учебного года). В зависимости от варианта обучающийся должен решить 6 задач в первой контрольной работе и три задачи во второй контрольной работе. Номер варианта соответствует порядковому номеру обучающегося в групповом журнале учебных занятий или  определяется по двум последним цифрам шифра обучающегося. При выполнении контрольных работ необходимо соблюдать следующие требования:

 1.Каждую контрольную работу выполнять строго в соответствии с вариантом в отдельной тетради в клетку. Все задания выполнять четко и аккуратно. Для пометок и замечаний преподавателя соблюдать достаточный интервал между строчками и оставлять на листах поля шириной примерно 20 мм. Каждую задачу начинать с новой страницы. В конце контрольной работы оставлять чистый лист для рецензии. В противном случае контрольные работы  не зачитываются и возвращаются для переделки в соответствии с данным требованием.

2.На титульном листе тетради указывать фамилию, имя, отчество, номер шифра, наименование дисциплины, номер контрольной работы,  дату отправления, почтовый адрес обучающегося; на последнем листе выполненной контрольной работы привести перечень использованной литературы.

3.Каждую задачу начинать с новой страницы, тексты условий задач переписывать обязательно. Задачи должны быть выполнены аккуратно, сопровождаться расчетными схемами и  краткими объяснениями производимых операций, ссылками на соответствующие законы и формулы и ссылками на теоремы, законы, правила.

4.Решения задач пояснять аккуратно выполненными схемами (эскизами), с указаниями, что дано, что определяется, что рассматривается и т.д.

5.Проверять правильность ответа, решив задачу иным способом и сравнить полученные результаты. Сделать соответствующие выводы.

6.Задачи рекомендуется  решать в общем виде, а затем, подставляя числовые значения величин, вычислять результат. Перед чистовым оформлением следует тщательно проверить все действия, правильность подстановки величин, соблюдение размерности определяемых величин.

            Выполненную контрольную работу необходимо своевременно выслать на проверку в колледж. После получения зачтенной контрольной работы, внимательно изучить рецензию и все замечания преподавателя, обратить внимание на допущенные ошибки. Не зачтенная работа выполняется заново или переделывается частично, в той же тетради, по указанию преподавателя.

           Для допуска к дифференцированному зачету  обучающемуся необходимо выполнить все, предусмотренные учебным планом,  контрольные работы, сделать все необходимые исправления, указанные преподавателем в рецензиях и защитить упомянутые работы, т.е в процессе опроса по ним показать хорошую осведомленность и самостоятельность выполнения. Все контрольные работы обязательно подлежат защите в установленном порядке.

2. Домашняя контрольная работа № 1. ( Раздел 1.Теоретическая механика и раздел 2. Сопротивление материалов).

Варианты заданий и методические указания к решению задач.

Задача № 1.1. Определить величину и направление реакций связи R_АВ, R_ВС,  в равновесной механической системе, под действием заданной силы F, изображенной на схеме  к задаче №1. Исходные данные приведены в таблице 1, искомые силы представлены знаком вопроса (?), схемы вариантов на рис.1.

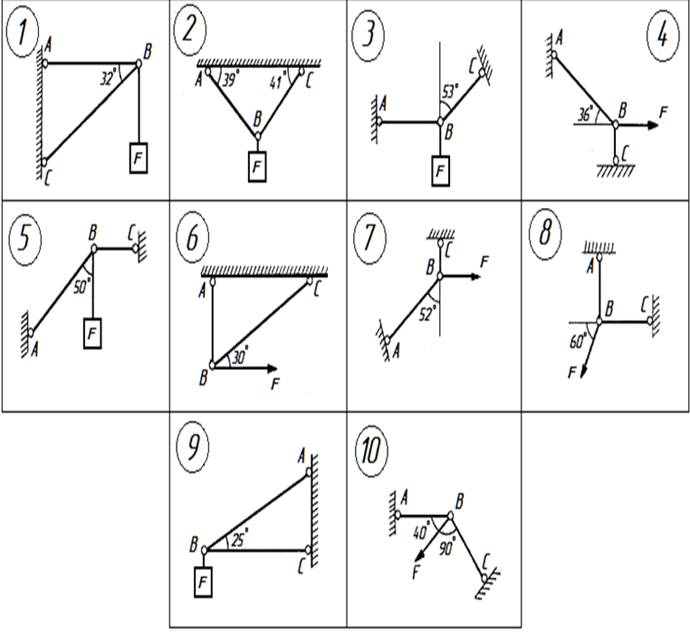                                Рис. 1.  Схемы вариантов к задаче № 1.1.             

                                                                                                        Таблица 1.

                                                                                                          

Номер схемы на рис. 1										Силы, кН
1	2	3	4	5	6	7	8	9	10	F	RАВ	RСВ
Варианты  заданий
01	02	03	04	05	06	07	08	09	10	0,5	?	?
11	12	13	14	15	16	17	17	19	20	0,6	?	?
21	22	23	24	25	26	27	28	29	30	0,7	?	?
30	31	32	33	34	35	36	37	38	39	0,8	?	?

          Методические указания к решению задачи № 1.1.

          К решению задачи следует приступать после изучения тем: «Основные понятия и аксиомы статики»; «Геометрическое и аналитическое условия равновесия плоской системы сходящихся сил»; раздел 1. Теоретическая механика; приведенных ниже указаний и разбора примеров решения задач статики на условия равновесия плоской системы сходящихся сил. В задаче рассматривается материальная точка, находящаяся в равновесии под действием плоской системы сходящихся сил. Аналитический метод решения задачи сводится к решению системы уравнений равновесия:     ΣFx  = 0;     ΣFу  = 0;

(сумма проекций всех сил системы на каждую из координатных осей при равновесии всегда равна нулю). Можно упростить решение задач путем рационального выбора направления координатных осей, т. е. выбирать оси так, чтобы одна из осей (Х или Y) совпадала с направлением какой-нибудь неизвестной силы. Составить уравнения равновесия, т.е. спроектировать все действующие силы на координатные оси и сумму проекций сил на каждую из осей приравнять к нулю, решить составленные уравнения относительно неизвестных величин, аналитическим методом, затем следует  проверить правильность решения с помощью графического или геометрического метода.

При решении задач на равновесие плоской системы сходящихся сил рекомендуется придерживаться следующей последовательности:

1. Освободить  от связей тело или (материальную точку), указать на схеме действующие заданные силы  и реакции связей. При этом на схеме векторы всех действующих на тело  активных и реактивных сил должны исходить из одной точки (сходящаяся система  сил).

2. Составить уравнения равновесия и определить неизвестные силы. Для этого векторы действующих на тело активных и реактивных сил спроектировать на выбранные координатные оси, и сумму проекций всех сил на каждую ось приравнять к нулю, решить составленные уравнения равновесия для каждой из координатных осей, относительно неизвестных сил.

3. После решения задачи аналитическим методом решить задачу графическим или геометрическим способом, сравнить полученные результаты, сделать выводы.

Подробное решение задачи № 1.1 рассмотрим  на примерах 1 и  2.

Примеры решения задачи № 1.1.

Пример 1. Определить величину и направление реакций связи F_АВ, F_ВС,  в равновесной механической системе, под действием заданной силы F = 2,04 кН.                                          Решение 1. Механизм состоит из стержней АВ, СВ, соединенных шарниром В, который вертикальной тягой связан с грузом  F.  Поскольку тяга груза F, стержни АВ и СВ связаны одним телом – шарниром В, то освобождаем от связей шарнир В, представив его в виде материальной точки, к которой приложены внешние силы (сила тяжести груза) и реактивные силы (реакции стержней). 2. Упрощаем схему, мысленно отбросив тягу и стержни. 3. Из материальной точки (шарнир В) направляем активную силу F вниз, реакцию стержня СВ – горизонтально влево, от шарнира В, предположив что все стержни растянуты, а реакцию стержня АВ – под углом 20˚ к горизонту (как на схеме) влево вверх от шарнира В. Направление реакций можно выбрать произвольно, при этом если в результате решения задачи модуль определяемой силы получится  отрицательным (со знаком «-»), значит, изначально направление было выбрано неверно, и вектор силы нужно будет изменить на противоположный.

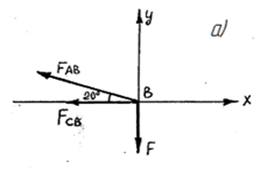
Точку В перемещаем в начало осей координат, ось Х совмещаем с вектором F_СB, ось Y направляем перпендикулярно  оси Х.Составляем уравнения равновесия:

ΣFx  = 0;     -F_АВ cos 20⁰ - F_СВ = 0;   

ΣFу  = 0;    F_АВ sin 20⁰  - F = 0.         Решаем составленные  уравнения:

F_АВ = F / sin20⁰ = 2,04 / 0,342 =6 kH.

F_СВ = - F_АВ cos20⁰  =- 6*0,9396= - 5,64 kH. Поскольку сила F_СВ в результате решения уравнения получилась отрицательной, значит направление ее вектора на схеме выбрано неверно, т. е. этот вектор должен быть направлен в противоположную сторону.

3. Для проверки правильности решения задачи используем графический метод. В произвольно выбранном масштабе (например  1 см. = 1 кН.) строим замкнутый силовой треугольник и, используя масштаб, определяем неизвестные силы. При построении силового треугольника сначала откладываем известную силу F(с учетом направления и масштаба), а затем к концам вектора этой силы пристраиваем вектора искомых сил, проведенных параллельно стержням АВ и ВС. Полученный силовой треугольник должен замкнуться, поскольку система является уравновешенной. Следует отметить, что векторный треугольник показывает действительное, направление искомых усилий.

  

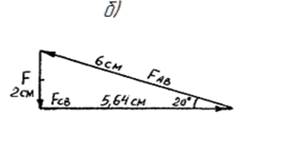
После решения задачи графическим способом, сравниваем результаты с ответами, полученными при решении задачи аналитическим методом.

 Задачу можно решить и геометрическим способом, для этого необходимо рассмотреть полученный прямоугольный силовой треугольник, в котором известен катет  F = 2,045 кН., и угол ά=20⁰,необходимо определить  катет  F_СВ и  гипотенузу F_АВ.   Ответ: F_АВ  =  6 kH.         F_ВС =- 5,64 kH

Пример 2. Вычислить натяжение  Т троса АВ и усилие R стрелы АС мачтового крана, несущего груз весом G=2 kH.

Решение. Рассмотрим равновесие стрелы АС. В точке А к ней приложена активная сила G (сила тяжести груза). Мысленно освободимся от связей и заменим их реакциями, Реакция троса АВ направлена от точки А к В; реакция опоры С направлена вдоль стрелы АС.  Рассмотрим условие равновесия узла  А, в котором  пересекаются все три силы. В точке А выберем начало координат и проведем координатные оси .Ось Х горизонтально, ось У перпендикулярно оси Х, вверх. Составим уравнения равновесия:

 

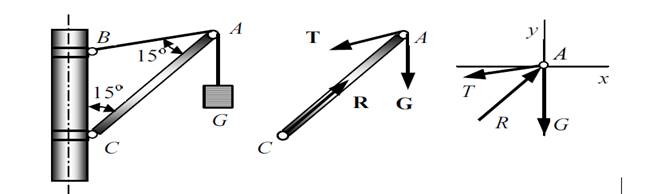
ΣFx  = 0;    - Tsin30⁰ +Rsin15⁰=0.

ΣFу  = 0;     Rcos15⁰ –Tcos 30⁰ – G =0. Решаем совметно два уравнения:

Из первого уравнения R = T* sin30⁰ / sin15⁰; подставим во второе уравнение:

T* sin30⁰ *сos 15⁰ / sin15⁰ -  T*cos 30⁰ – G=0.    T = G /( sin30⁰ сos 15⁰ / sin15⁰ - cos 30⁰); T=2 /(0,5*0,9659 /0,2588 – 0,866)=2 kH.

R = T* sin30⁰ / sin15⁰=2*0,5 /0,2588 = 3,86 kH.  Отbет: R  = 3,86 kH; T  = 2 kH.

 

Задача № 1.2.

Определить реакции опор двухопорной балки АВ нагруженной силой F, равномерно распределенной нагрузкой q и парой сил с моментом М.

Исходные данные для решения задачи по каждому варианту приведены в таблице 2 и на схемах рисунка 2.                                                                                                                                                        

                                                                                                             Таблица 2.

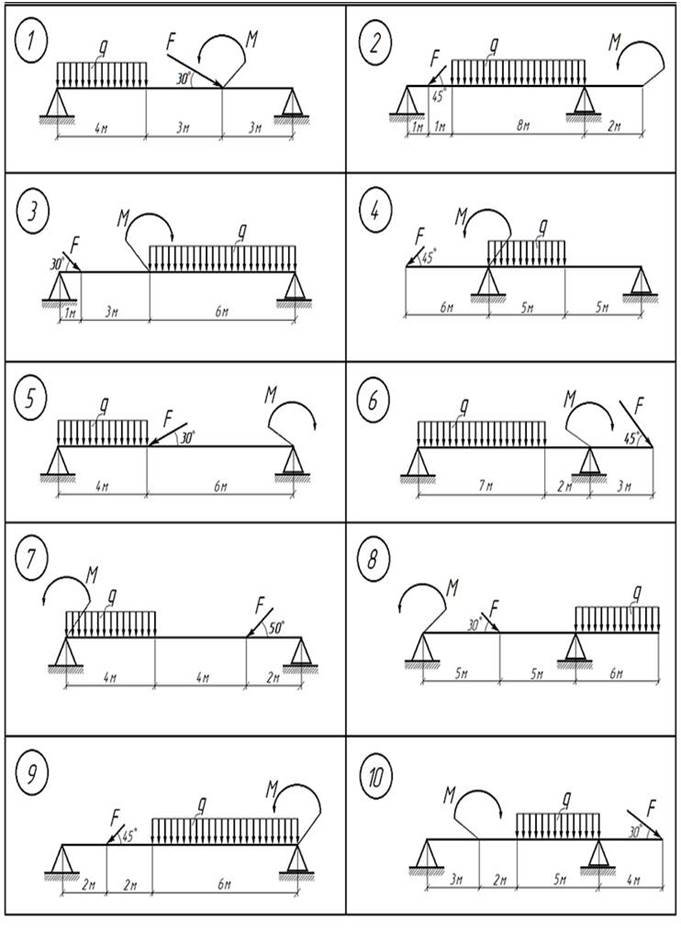
                                     Рис.   2.   Схемы вариантов  к задаче № 1.2.

Методические указания к решению задачи №  1.2.

К решению  задач следует приступать после изучения тем: «Пара сил и момент силы относительно точки», «Система сил, произвольно расположенных в плоскости. Условия равновесия произвольной плоской системы сил». Раздел 1. Теоретическая механика. При решении задач рекомендуется придерживаться следующей последовательности:

1. Обозначить шарнирно-неподвижную опору балки через точку А, а шарнирно-подвижную опору балки через точку В. Освободить балку АВ от связей, действия опор  А и В  заменить их реакциями R_A и У_B, направление которых выбирать произвольно (в случае ошибочно выбранного направления реактивной силы ее модуль при решении задачи получится отрицательным, следовательно нужно будет изменить направление вектора на противоположное). Реакцию неподвижной опоры А разложить на горизонтальную и вертикальную составляющие У_A  и  Х_A, реакция подвижной опоры В может быть только вертикальной и направленной перпендикулярно вверх, обозначим ее через  У_В.

3. Силу F  разложить на горизонтальную F_х и вертикальную F_у составляющие.

4. Равномерно распределенную нагрузку q заменить сосредоточенной нагрузкой Q. В соответствии с условием  равновесия произвольно расположенных на плоскости сил, сумма проекций всех сил на координатные оси равна нулю, и сумма моментов всех сил относительно любой точки плоскости тоже равна нулю.

Поскольку в задаче две неизвестные силы (реакции опор), для ее решения использовать уравнение моментов сил, при этом за точки, относительно которых будут рассматриваться моменты сил, принять  поочередно опоры А и В, исключив тем самым одну из неизвестных реакций из уравнения равновесия (сила, линия действия которой проходит через точку, не образует момент относительно этой точки, т. е. момент в данном случае равен нулю).

Подробное решение задачи № 1.2 рассмотрим  на примерах 3 и  4.

Пример 3. Определить реакции опор двухопорной балки АВ нагруженной  сосредоточенной силой F = 16 кН, равномерно распределенной нагрузкой интенсивностью q = 1,2 кН/м, угол α =30⁰, а = 3 м.,b=7 м.,L=12 м., сила тяжести балки G=5 kH.                                                                                                                                                          

Решение:  Действие опор на балку заменяем реакциями  Х_A,  У_A    У_В . Распределенную нагрузку  ее равнодействующей Q = q (L-b)=1,2*(12-7)=6 kH, приложенной в середине отрезка DB. Составим уравнения равновесия:

 ∑M_A (F_i )=0;  (F sin α)* a + GL/2 +Q* (b+(L-b) /2) – Y_B*L=0;

                        16*0,5*3 +5*12/2 +6*(7+(12-7) /2) -  Y_B*12 =0.

                        Y_B*12=24+30 +57;    Y_B = 9,25 kH.

 

 ∑M_B (F_i )=0;  - (F sin α)* (L-a)+ Y_A*L - GL/2 - Q* (L-b) /2) =0;

                       -16*0,5*9 + Y_A*12 -5*12 /2 – 6*2,5=0

                         Y_A*12 =72+30+15;     Y_A = 9,75 kH.

 

 ∑F_Xi=0;          X_A  - F*cos α = 0;      X_A  =16*0,866 =13,86 kH.

 

                         R_A ² = Y_A² + X_A² ;      R_A  =16,95kH.

Проверка решения:

∑F_У i=0;      Y_A - F sin α –G - Q+ Y_B =0;  9,75-8 -5 -6 +9,25=19 – 19=0.Опорные реакции найдены верно.

Ответ: R_A  =16,95kH; ;    Y_B = 9,25 kH.

Пример 4. Определить реакции шарнирных опор А и В балки, находящейся под действием сосредоточенной силы F = 60 Н, равномерно распределенной нагрузки с интенсивностью q = 15 Н/м и пары сил с моментом М = 40 Н·м; расстояние a = 1 м.

 

Решение. Вычертим заданную схему балки, согласно варианта, придерживаясь определенного масштаба. Заменим равномерно распределенную нагрузку эквивалентной сосредоточенной , равной по модулю Q = q·2a = 30 Н и приложенной в средней точке нагруженного участка. Реакция связи в опоре А-

_A неизвестна по величине и направлению, поэтому разложим её на две неизвестные по величине составляющие X_A, Y_A, направленные по координатным осям. Опора в точке В не препятствует её перемещению вдоль наклонной плоскости и, следовательно, реакцию _B следует направить перпендикулярно наклонной плоскости. Таким образом, в задаче имеется три неизвестных скалярных величины: X_A, Y_A, R_B.

 

 

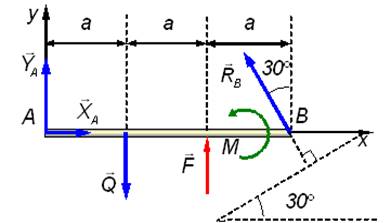
Составим уравнения равновесия для полученной эквивалентной силовой схемы.

,

,

.

Напомним, что алгебраические моменты сил берутся со знаком плюс, если они направлены против хода часовой стрелки. При вычислении момента реакции _B относительно точки А выделена её вертикальная составляющая, равная R_B cos 30° и имеющая плечо 3a, а горизонтальная составляющая имеет нулевой момент относительно точки А.

Из третьего уравнения находим:

R_B = (Q - 2F – M /a)/(3cos 30°) -50,0 Н.

Подставив в первое и второе, получим:

Х_A=((Q - 2F – M /a) /(3cos 30°))sin30°-25,0 Н,

Y_A = (2Q - F + M/a) /3 13,3 Н.

Отbет: Полученные отрицательные значения R_B и X_A означают, что сила _B и составляющая реакции X_A противоположны показанным на схеме направлениям этих векторов. Величину полной реакции на опоре А, определим по формуле

 R_A = (X_A² + Y_A²) 28,3 Н. Направление вектора R_A определим по следующей формуле:

Соsα = X_A / R_A =25,0 / 28,3 =0,8834.    Вектор R_A составляет с осью Х угол α = 28⁰.

 

Задача 1.3. Для заданного составного поперечного сечения  определить положение центра тяжести сечения, состоящего из простых геометрических фигур. Исходные данные для решения задачи по каждому варианту приведены на схемах рисунка 3.

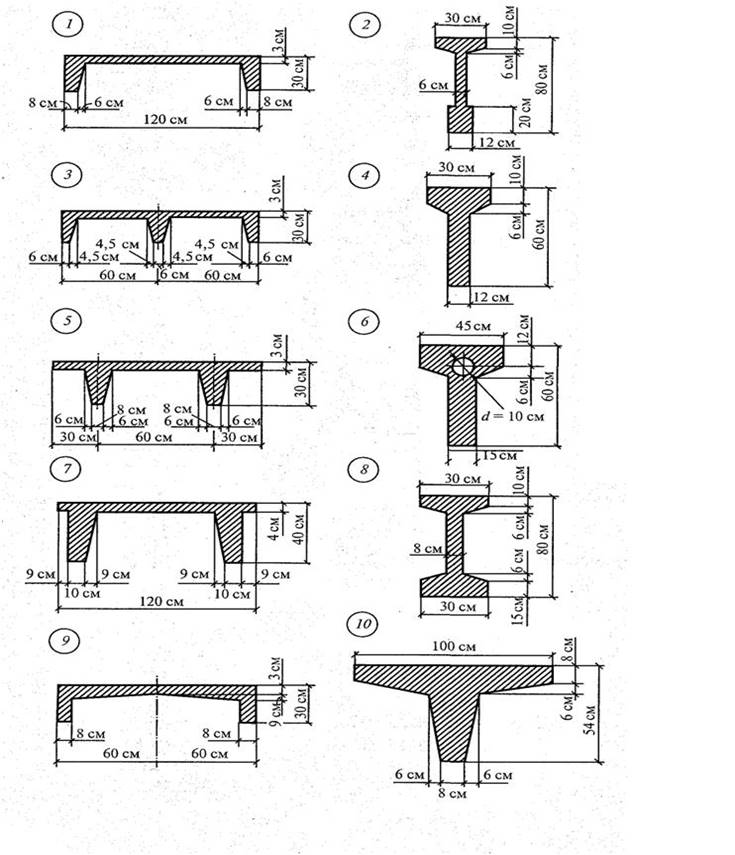
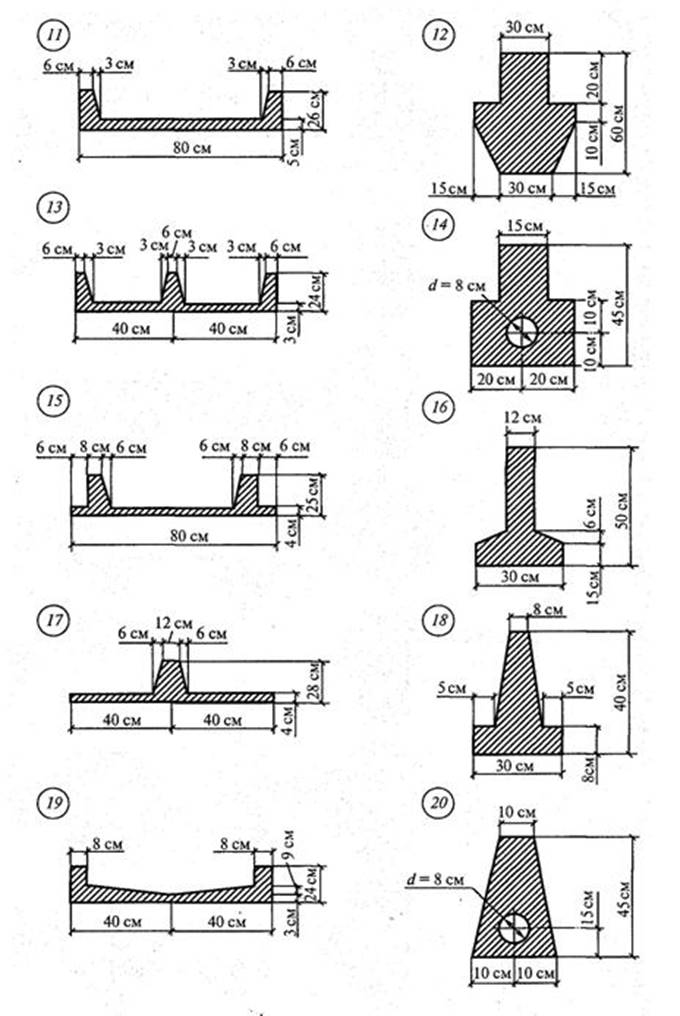
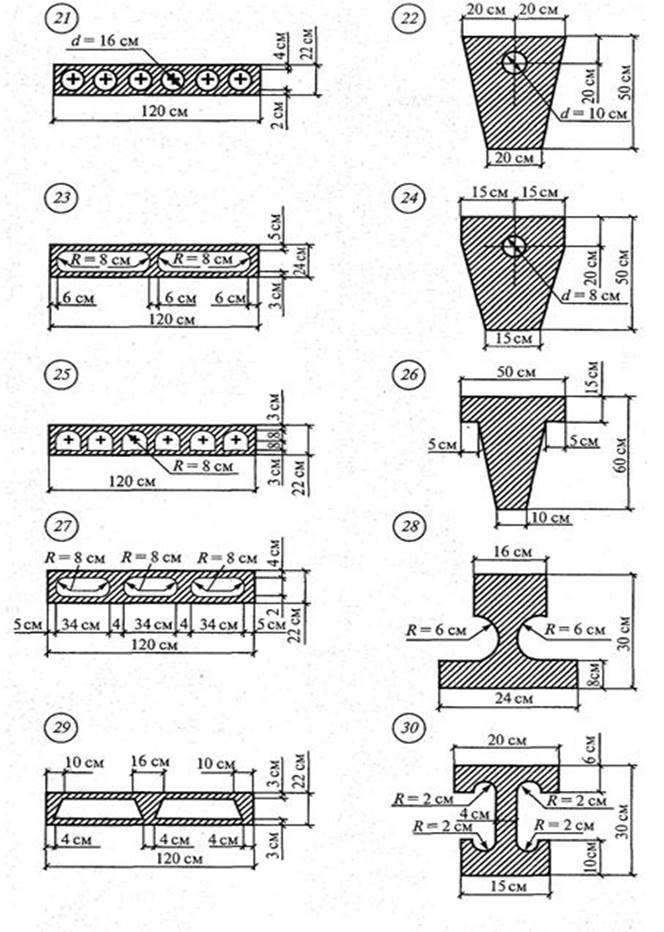
                                   Рис. 3.   Схемы вариантов  к задаче  № 1.3.

Методические указания к решению задачи №  1.3.

К решению  задачи следует приступать после изучения темы: «Центр тяжести». Раздел 1. Теоретическая механика.Центры тяжести простейших геометрических фигур указаны на схемах точками;

Основные методы расчета: метод симметрии, метод разделения на простые части, метод отрицательных  площадей.  При решении задачи рекомендуется придерживаться следующего порядка определения  положения  центра  тяжести составного сечения.

1. Разбить сечение на простые геометрические фигуры (прямоугольник, квадрат, треугольник, круг и т.д.)

2. Указать на схеме центры тяжести каждой фигуры  и обозначить их через  С₁, С₂  С_{3 ,} С₄ … С_n.

3. Выбрать систему координатных осей. В задачах  все сечения имеют одну ось симметрии, поэтому рекомендуется одну из координатных осей совмещать с ней. Вторую ось координат направляют перпендикулярно к первой так, чтобы она пересекала центры тяжести одной или большого числа фигур. При этом начало координат может совпадать с центром тяжести одной из фигур или не совпадать с ним. Вторую ось можно направить так, чтобы она прошла через нижнюю (крайнюю) точку сечения. В первом случае вычисления окажутся более простыми.

4. Выписать необходимые формулы для определения координат центра тяжести всего сечения:

                         Х_с = ∑ Аi * хi / А;

        

                        Y_c = ∑ Аi * уi / А,

где А_і – площадь сечения элементарной геометрической фигуры;

х_і; у_і – координаты центров тяжестей элементарных геометрических фигур;

А – площадь всего сечения.

5.Определить площадь каждой фигуры и обозначить через  А₁, А₂ … А_n

6. Определить координаты  центров тяжести каждой фигуры и обозначить через  х₁, х₂ … х_n, и y₁, y₂ … y_n , относительно выбранных осей координат. Количество слагаемых в числителе и знаменателе формул зависит от числа фигур, из которых состоит сечение. Полученные величины подставляют в формулу и находят X_c или Y_c . Следует помнить, что, если координатная ось х совмещена с осью симметрии, то координата Y_c = 0, а если ось у совмещена с осью симметрии, то X_c = 0.

6. Указать положение центра тяжести на схеме, придерживаясь определенного масштаба, и показать расстояние от центра тяжести до координатных осей.

7. Выполнить проверку правильности решения, для чего можно изменить положение координатных осей (или одной оси) и найти координаты центра тяжести относительно новых осей. Положение центра тяжести не зависит от того, как выбрана система координатных осей.

Рассмотрим подробное решение задачи № 1.3 на примере  5.

Пример 5. Определить координаты центра тяжести плоского сечения, составленного из простых геометрических фигур. Данные для своего варианта взять на схеме вариантов (рисунок 3).

Решение: Вычертим заданную схему, согласно своего варианта, придерживаясь определенного масштаба. Проведем координатные оси ОХ и ОУ.

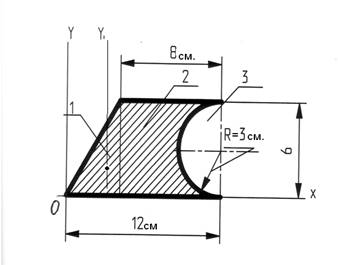
 Разбиваем заданное сечение на три простые геометрические фигуры:

1 – треугольник; площадь треугольника А₁ =(40*60) / 2 =1200 мм². =12 см².

2 – прямоугольник; площадь прямоугольника А₂ = 80 * 60 =4800 мм². = 48 см².

3 – полукруг, площадь полукруга А₃ =/2 =3,14*30² / 2=1413 мм² =14,13см² Определим площадь всего сечения А =А₁ +А₂ +А₃ =12 +48 – 14,13=45,87см².

Определяем координаты центров тяжестей каждой элементарной фигуры:

Центр тяжести фигуры 1: х₁ = 40*2/3= 26,7 мм.=2,67 см.

                                               у₁ =60*1/3 =20 мм. =2 см.

Центр тяжести фигуры 2: х₂ = 40 +80/2= 80 мм.=8 см.

                                               у₁ =60/2 =30 мм. =3 см.

Центр тяжести фигуры 3: х₃ = 120 – 4*30/ 3*3,14= 107,3 мм.=10,73 см.

                                               У₃ =R =30 мм. =3 см.

Определим координаты центра тяжести всего составного сечения:

Х_с = ∑ Аi * Хi / А =(12*2,67+48*8- 14,13*10,73) / 45,87 = 5,76 см.

Y_c = ∑ Аi * Уi / А =(12*2+48*3-14,13*3) / 45,87 = 2,74 см.

Выполним проверку правильности решения, для этого изменим положение координатных осей: ось У перенесем в центр тяжести первой фигуры в положение   У₁ и определим абсциссы центров тяжести элементарных сечений  относительно положения новых осей.

Центр тяжести фигуры 1: х₁ = 0 см.

Центр тяжести фигуры 2: х₂ = 4*1/3 + 4= 5,33 см.

Центр тяжести фигуры 3: х₃ = 1,33+8 – 4*3/ 3*3,14=8,057 см. Подставим найденные значения в формулу:

Хс1 = ∑ Аi * Хi / А = (48*5,33 – 14,13*8,057) /45,87 =3,09 см.

Хс  -  Хс1 = 5,76- 3,09 =2,67 см. Это и есть расстояние между осями У иУ₁ . Таким образом центр тяжести всего сечения находится в той же точке, что и в первом случае.

Ответ: Координаты центра тяжести составного сечения определены верно

Х_С =5,76 см.    Y_С = 2,74 см.

Задача 1.4. Для заданного стального бруса построить эпюры продольных сил и нормальных напряжений,  а также определить перемещение Δl свободного конца бруса. Проверить прочность бруса, если [σ]_р =160 МПа, Е_стали =2*10⁵ МПа.

Схемы на рис.4. варианты  заданий  к задаче в таблице 4.

                                                                                                                       Таблица 4.

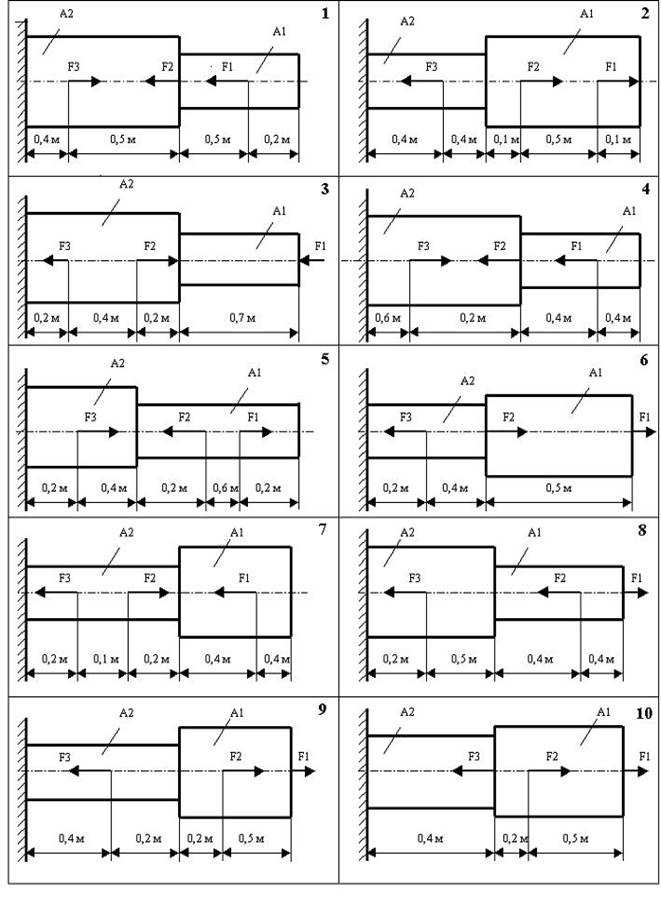
                                  Рис.   4.    Схемы вариантов  к задаче  № 1.4.

 

Методические указания к решению задачи №  1.4.

К решению задачи можно приступить только после изучения темы «Растяжение и сжатие. Продольная деформация. Закон Гука. Нормальные и касательные напряжения», раздел 2.  Сопротивление материалов. К ступенчатому брусу АВСД приложены сосредоточенные силы F₁ ,F₂ ,F₃. Необходимо построить эпюры внутренних продольных сил и нормальных напряжений при растяжении бруса. Определить перемещение Δl свободного конца бруса. Для определения внутренних силовых факторов применить метод сечений (РОЗУ). Выполнить сечения последовательно на характерных участках Мысленно отбросить левую отсеченную часть, действие отброшенной части заменить внутренней продольной силой N, направленной от сечения  и рассмотреть равновесие оставшейся правой  части, составить уравнение равновесия для оставшейся части бруса и определить значение продольной силы в соответствующих сечениях:

Сечение 1-1   ∑Fу_i =0; 

Сечение 2-2:  ∑Fу_i =0; 

Сечение 3-3:  ∑Fу_i =0; 

Сечение 4-4:  ∑Fу_i =0;

Построить эпюру продольных сил по длине бруса.

Далее  определить нормальные напряжения в этих же сечениях по формулам:

σ₁ =   N₁ /А₁

σ₂  = N₂ /А₂

σ₃  = N₃ /А₂

σ₄ = N₄ /А₄

Построить эпюру нормальных напряжений  σ.

Определить перемещение свободного конца бруса по закону Гука:

Δl = 1/E* ( N₁l₁ / А₁ + N₂l₂  / А₁ +N₃l₃ / А₂ + N₄l₄ / А₂ ).

Для проверки прочности бруса по нормальным напряжениям определить расчетное нормальное напряжение и сравнить с заданным допускаемым напряжением. σ _max = N _max / A < [σ]_р

Сделать соответствующие выводы и записать ответ к задаче.

Подробное решение задачи № 1.4 рассмотрим на примере 6.

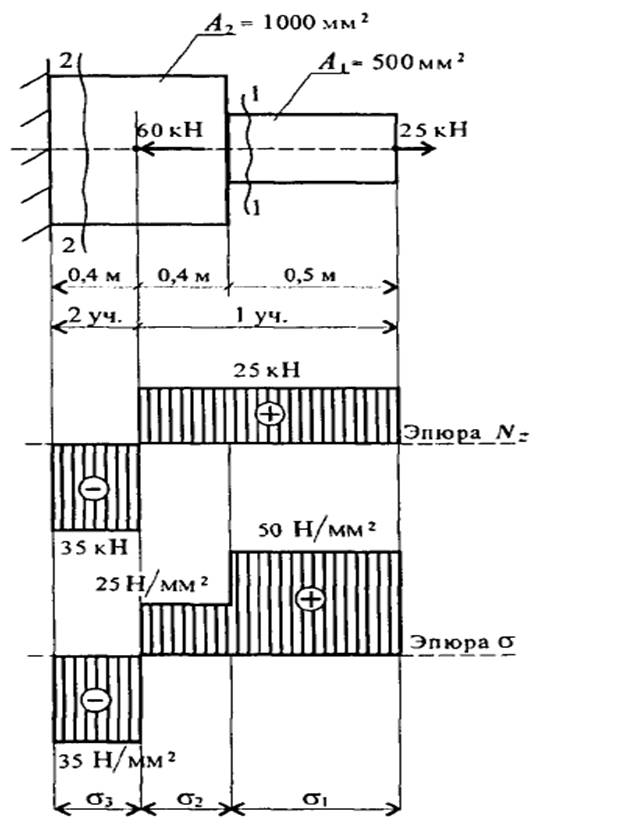
Пример 6. Для заданного стального бруса построить эпюры продольных сил и нормальных напряжений,  а также определить перемещение Δl свободного конца бруса. Е_стали =2*10⁵ МПа.

Решение: Брус защемлен, в заделке возникает неизвестная опорная реакция, поэтому расчет целесообразно начинать со свободного конца (справа). Для определения внутренних силовых факторов применяем метод сечений (РОЗУ). 1.Мысленно отбрасываем левую часть и рассматриваем равновесие оставшейся правой части, составляем уравнение равновесия для оставшейся части бруса и определяем значение продольной силы в соответствующих сечениях:

 Сечение 1-1:   ∑Fу_i =0; - N₁+F₁=0; N₁ = F₁=25 Кн.(участок 1-1 растянут)

 Сечение 2-2:   ∑Fу_i =0; - N₂ +F₁ – F₂=0; N₂ = F₁- F₂=- 35 Кн.( 2-2 сжат)

 Строим эпюру продольных сил N(кН).

2.Определяем нормальные напряжения в сечениях (три участка напряжения):

σ₁ =   N₁ /А₁ =25*10³ / 500 = 50 Н/мм²

σ₂  = N₁ /А₂ =  25*10³ / 1000 = 25 Н/мм²

σ₃ = N₂ /А₂ =-35* 10³ / 1000 =- 35 Н/мм²

Строим эпюру нормальных напряжений σ(Н/мм²).

3. Определяем перемещение свободного конца бруса по закону Гука; удлинения участков(материал сталь Е=2*10⁵МПа)

Δl₁ = σ₁l₁/E=(50*0,5*10³)/2*10⁵=0,125 мм.

Δl₂ = σ₂l₂/E=(25*0,4*10³)/ 2*10⁵=0,05 мм.

Δl₃ = σ₃l₃/E=(-35*0,4*10³)/ 2*10⁵=-0,07 мм.

4.Суммарное удлинение бруса (перемещение свободного конца)

 Δl =  Δl₁+  Δl₂+ Δl₃ =0,125+0,05-0,07=0,105 мм.                     

 Ответ: брус под действием заданной  нагрузки удлинится на 0,105 мм.

 

 

 

Задача 1.5. Для заданной  балки, круглого поперечного сечения, построить эпюры внутренних силовых факторов Q и M; проверить прочность балки, если допускаемое нормальное напряжение по материалу [σ]=180 МПа, диаметр поперечного сечения балки d = 0,20 м. Схемы вариантов на рис. 5.

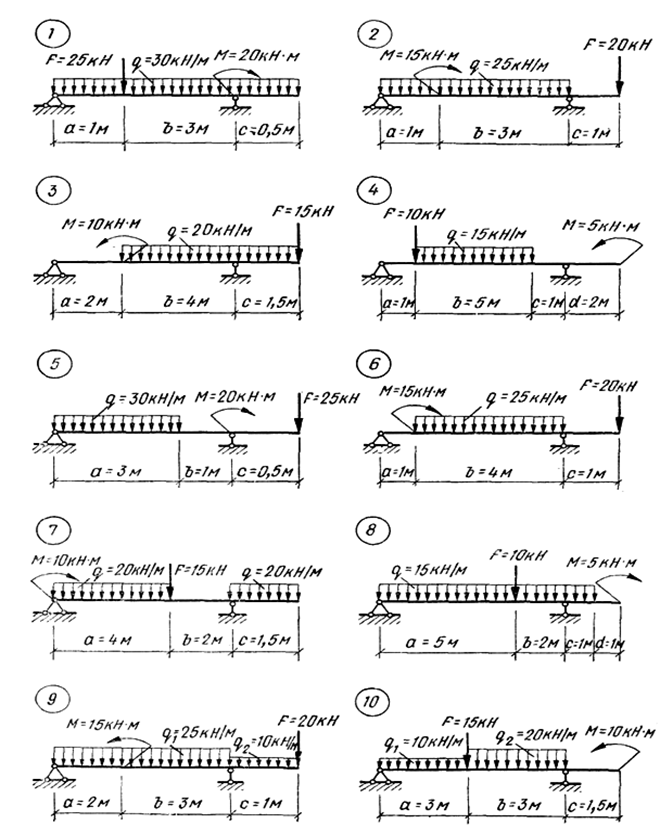
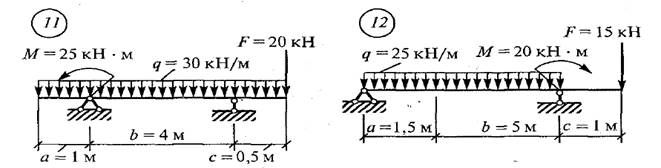
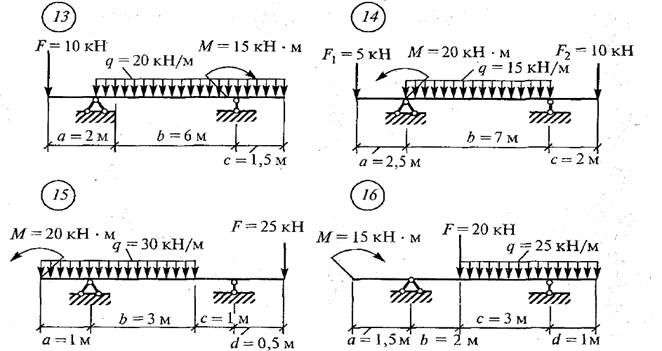
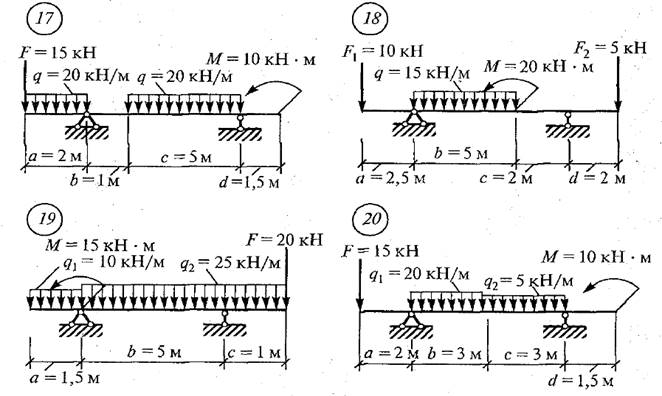
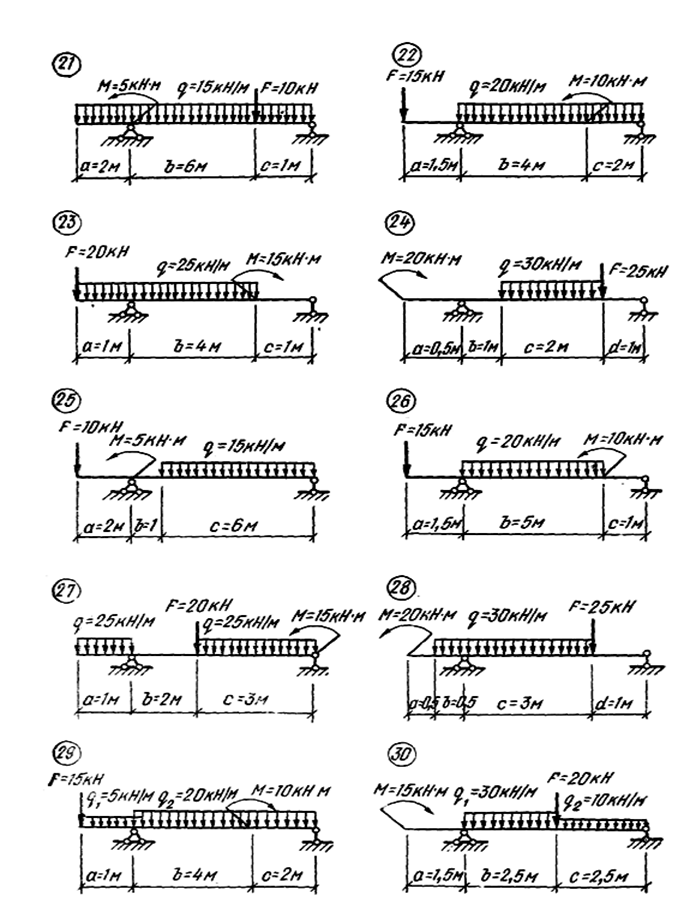
                                 Рис. 5.  Схемы вариантов  к задаче  № 1.5.

                       

Методические указания к решению задачи №  1.5.

К решению задачи можно приступить только после изучения темы «Изгиб прямого бруса», раздел 2. Сопротивление материалов.

Решение задачи состоит из следующего алгоритма: 1.Определяем опорные реакции балки АВ. Мысленно освобождаемся от опор и заменяем их действие на балку реакциями, которые обозначим Vа и Vв. После определения опорных реакций выполняем проверку. 2.Обозначаем характерные сечения балки, обозначив заглавными буквами точки, которые являются концевыми сечениями балки, опоры, точки приложения сосредоточенных сил и моментов пар сил, начало и конец равномерно-распределенной нагрузки. 3.Определяем значения поперечных сил в характерных сечениях. Поперечная сила в сечении равна сумме проекций всех сил, расположенных слева от рассматриваемого сечения на ось, перпендикулярную оси балки. В точках приложения сосредоточенных сил необходимо определять два значения поперечной силы: чуть левее рассматриваемой точки и чуть правее ее.  4.Строим эпюру поперечных сил Q_х. Для этого найденные значения поперечных сил в характерных сечениях откладываем в некотором масштабе от нулевой линии, строго под схемой заданной балки и соединяем прямыми линиями. 5.Определяем значения изгибающих моментов в характерных сечениях. Изгибающий момент в сечении равен сумме моментов всех сил, расположенных только слева от сечения. В точках приложения моментов, необходимо определять два значения изгибающего момента, чуть левее рассматриваемой точки и чуть правее ее. В точках приложения сосредоточенных сил определяется одно значение изгибающего момента, строго соблюдаем правило знаков.  Полученные значения откладываем в некотором масштабе  от нулевой линии, строго под схемой балки. Соединяем эти значения прямыми линиями, если на участке нет равномерно-распределенной нагрузки, если на участке балки приложена равномерно-распределенная нагрузка, то на этом участке значения изгибающих моментов соединяются по параболе, которая имеет выпуклость в сторону действия нагрузки.  Проверка заключается в том, что суммы моментов всех левых и всех правых сил, взятые отдельно, в любой точке балки должны быть равны между собой. 6.Для проверки прочности балки по нормальным напряжениям определяем расчетное нормальное напряжение и сравниваем с заданным допускаемым нормальным напряжением по материалу.

σ _max = М _max / W_x < [σ]_.

Подробное решение задачи № 1.5 рассмотрим на примере 7.

 

Пример 7. Для заданной  балки, круглого поперечного сечения, построить эпюры внутренних силовых факторов Q и M; проверить прочность балки, если [σ]=160 МПа (допускаемое нормальное напряжение по материалу),диаметр сечения балки d = 0,25 м.

Дано: F = 15 Кн., q = 20 Кн/м., М =25 Кнм; d = 0,25 м.

 [σ] =160 МПа (допускаемое нормальное напряжение по материалу)

Решение:

1. Определяем опорные реакции балки АВ. Балка имеет одну шарнирно-неподвижную и вторую шарнирно-подвижную опору. Мысленно освобождаемся от опор и заменяем их действие на балку реакциями, которые обозначим Vа и Vв. 

Для полученной плоской системы сил составляем уравнения равновесия:

∑m_А(F_i) =0; - F(a+b) + q(b+c)((b+c)/ 2 –b)) – V_b(c+d) -M = 0;   

Vв = (-30+240-25) / 7 = 26,4 Кн.

∑m_В(F_i) =0;   F(a+b+c+d) – q(b+c)((b+c)/ 2 +d)) +Vа(c+d)-M = 0

Vа=(135+600+25) / 7 = 108,6 kH.

Выполним проверку:

∑Fу_i =0; Vа + Vв + F₃ – F – q(b+c) = 108,6 +26,4 -15- 120 =0

Опорные реакции определены верно. 135-135=0.

2. Обозначаем характерные сечения балки:  С, Д, A, Е, В, K и  

определим значения поперечных сил в характерных сечениях :

Q_с^прав = - F=- 15 kH.; Q_D= Q_С^прав=-15 kH.

Q_А^лев = -F -qb=-15 -20 =-35 kH.

Q_А^прав= Q_А^лев + Vа  =  -35+ 108,6 = 73,6 kH.

Q_Е = -F –q(b+c)+ Vа =- 15-120+108,6 = 26,4kH.

Q_В^лев =  Q_E = -26,4 kH.

Q_В^прав = Q_В^лев + Vв  = -26,4 + 26,4 =0.     Q_K = 0.

 По найденным величинам усилий строим эпюру поперечных сил Q_х.

Эпюра Q_х.на участке АЕ пересекает нулевую линию, определим положение точки пересечения из подобия треугольников HRL и HNS;

X₀ / 5=73,6 / 100;   X₀ =73,6.5/100 = 3,68 м.

3. Определяем изгибающие моменты в характерных сечениях:

М_С  = 0;

М_D = - Fa  =- 15 kH.м

М_A =- F(a+b)-(qb)(b/2)= -30-10 =- 40 kH.м

М_E = =- F(a+b+c) -q(b+c)(b+c)/ 2) +V_A* c= =-105-360+543 =78 kH.м

М_X0 =-F(a+b+xo)-q(b+xo)(b+xo)/ 2 V_A*xo =-85,2-219,024+399,65=95,4 kHм.

M_B ==- F(a+b+c+d) -q(b+c)((b+c)/ 2+d)) +V_A*(c+d)=-15*9-20*6*5+108,6*7=     -135-600+760,2=25,2kHм.

М_К ^лев.=- F(a+b+c+d+е) -q(b+c)((b+c)/ 2+d+е)) +V_A*(c+d+е)+ V_В*(е)=-15*10,5-20*6*6,5+108,6*8,5+26,4*1,5=-157,5-780+923+39,5=25 кНм.

М_К ^прав. = М_К ^лев. –М = 25 -25=0.

По найденным изгибающим моментам в  сечениях строим эпюру  М_х/

4. Проверим прочность балки по нормальным допускаемым напряжениям:

σ_расч. = М_max / W_x  <[σ]

 

Определим момент сопротивления заданного круглого сечения балки:

W_x = d³/ 32 =3,14*0,25³/32=0,00153 м³

 σ_расч. = М_max / W_x  = 95,4*10³/ 0,00153 =62352941 Па =62,353 МПа.

 

Вывод: прочность балки круглого поперечного сечения обеспечена, т.к. выполняется условие прочности по нормальным напряжениям, т.е. выполняется неравенство        σ_расч < [σ] ;          62,353 МПа < 160 МПа.

                                                           

                                

 

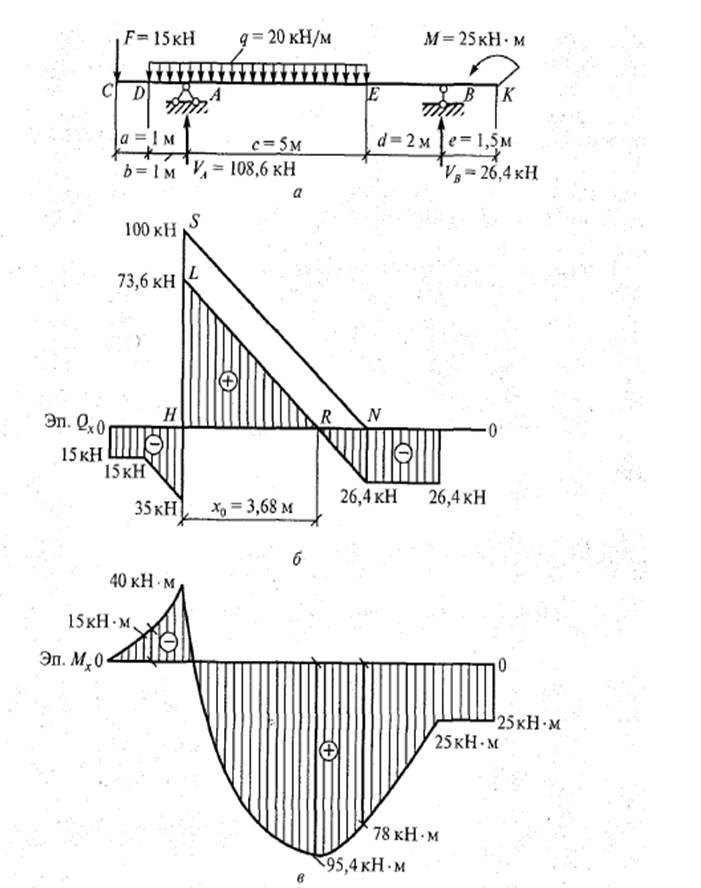
Задача 1.6. Определить  допускаемое значение  сжимающей силы для центрально сжатой стойки. Материал стойки сталь с расчетным сопротивлением R=240 МПа. Дано сечение стойки и его длина, μ (коэффициент приведения длины, зависит от от способа закрепления концов стойки).  Схемы вариантов на рис. 6.

  

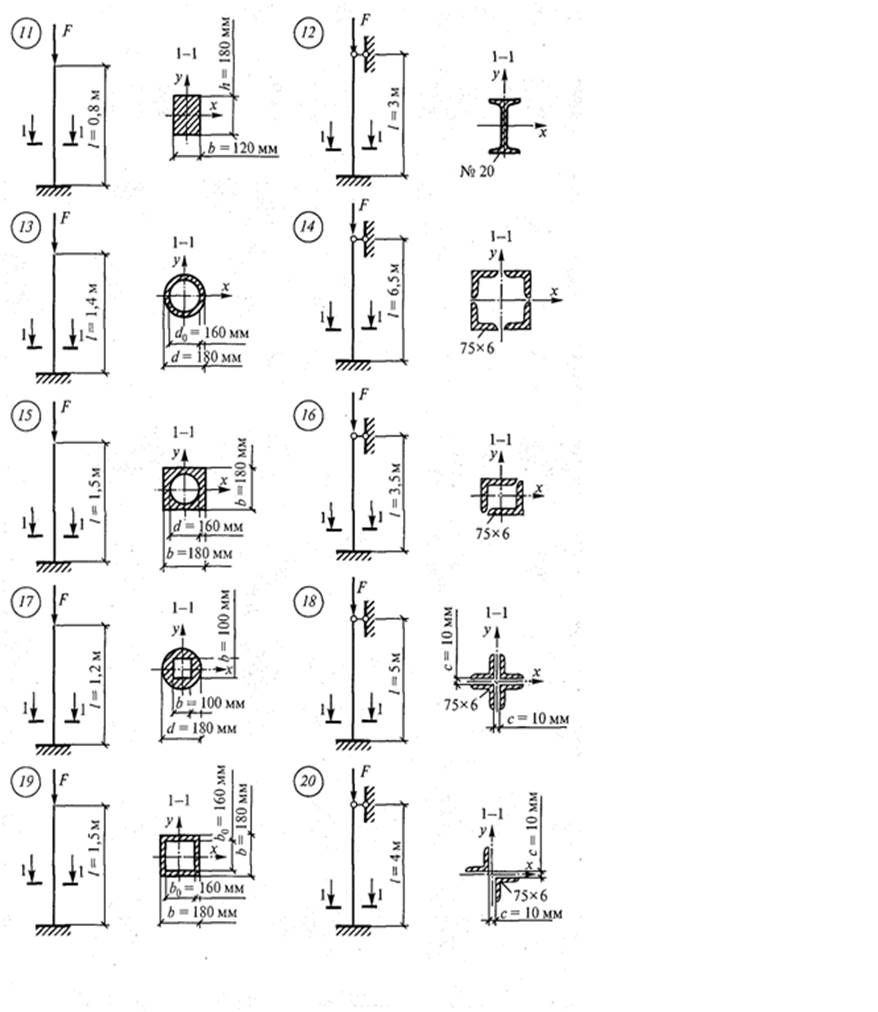
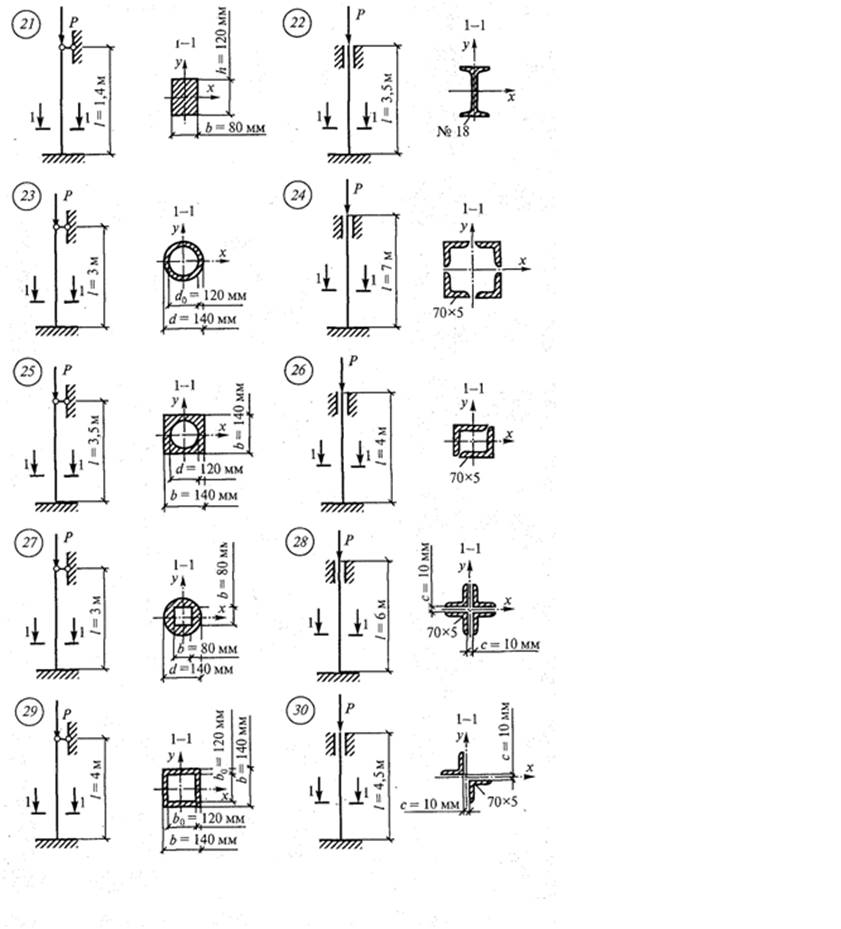                        Рис.   6.   Схемы вариантов  к задаче  № 1.6.

Методические указания к решению задачи № 1.6.

К решению задачи можно приступить только после изучения темы «Устойчивость центрально-сжатых стержней», раздел 2. Сопротивление материалов, а также  разобрать понятие об устойчивых и неустойчивых формах равновесия центрально-сжатых стержней; понятие продольного изгиба и критической силы, гибкость стержня. На практике очень часто приходится решать задачу об устойчивости сжатых стержней. Для определения допустимого значения центрально-сжимающей силы, при которой стержень или колонна сохранит устойчивую форму равновесия решаем задачу по следующему алгоритму: 1.Определяем площадь поперечного сечения стойки. Размеры сечения или тип и номер профиля проката, по которым из таблиц сортамента прокатной стали определяем площадь сечения. 2.Определяем расчетную (эффективную) длину стержня по формуле  ℓ_рас. = μ*ℓ, где ℓ- заданная геометрическая длина стержня, μ - коэффициент приведения длины, который зависит от способа закрепления концов стержня. 3.Определяем моменты инерции  сечения I_x и I_у, относительно главных центральных осей инерции сечения. Моменты инерции простых геометрических фигур относительно собственных осей определяем  по соответствующим формулам, а  моменты инерции профилей проката приведены в таблицах сортамента прокатной стали. 4.Определяем радиусы инерции сечения относительно осей х  и  у по формулам i_х=(I_x /А)^1/2  и  i_у =(I_у /А)^1/2. Принимаем наименьший из них, обозначив через  i_min.  Далее определяем гибкость стержня по формуле  λ = ℓ_рас / i _min. По значению гибкости из таблиц определяем коэффициент продольного изгиба  ψ_. Определяем величину допускаемого значения сжимающей силы по формуле N = R ψ А. Подробное решение задачи № 1.6.на пример 8.

Пример 8. Определить значение допускаемой  сжимающей силы для центрально сжатой стойки. Материал стойки сталь с расчетным сопротивлением R=290 МПа. Дано: ℓ=2,5 м., d₀ = 140 мм.=14 см. = 0,14м.;   d = 160 мм.=16 см.=0,16 м., μ=1 (коэффициент приведения длины, зависит от способа

 закрепления концов стойки)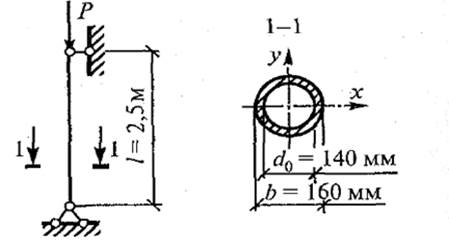

Решение:

1.Определяем площадь поперечного сечения стойки:

А =   = 3,14*( 8² – 7² ) = 3,14* (64 – 49)= 47,1 см²

2.Определяем расчетную длину стойки:

 ℓ_рас. = μ ℓ = 1 * 2,5 м =  2,5 м. = 250 см.

3.Определяем моменты инерции сечения относительно главных центральных осей сечения, причем моменты инерции   I_x = I_y , так как сечение имеет две оси симметрии:

I_{x =}=(  d⁴- d⁴⁾/64 =3,14*(65536 – 38416) / 64 =1330,58 см⁴

4.Определяем радиус инерции сечения:

     i_х  =  i_у =√ I_x /А =√1330,58/ 47,1  = 5,315 см.

5.Определяем наибольшую гибкость стержня:

             λ = ℓ_рас / i_х  = 250/ 5,315 =47,037

6.По найденному значению гибкости определяем коэффициент продольного изгиба, при этом используем интерполяцию:

при   λ=40  (ψ=0,894), при       λ=50  (ψ=0,852)

   ψ= о,894 – (0,894-0,852/10)*(47,037-40) = 0,864 (при λ =47,037)

7.Определяем величину допускаемого значения сжимающей силы:

 N = R ψ А =290*0,864*47,1* 10^-4 =1,18013 Мн.=1180,13 Кн.

 Ответ: величина допускаемого значения центрально сжимающей силы равна 1180,13 Кн.

3. Домашняя контрольная работа № 2. (Раздел 3. Статика соотружений ).

Варианты заданий и методические указания к решению задач.

Задача № 2.1. Для заданной статически определимой, многопролетной, шарнирной балки построить эпюры поперечных сил Q_X , эпюры изгибающих моментов М_Х, указать опасное сечение балки и величину максимального изгибающего момента.Схемы вариантов на рис.№ 8, данные в таблице 2.1

 

  

  

 

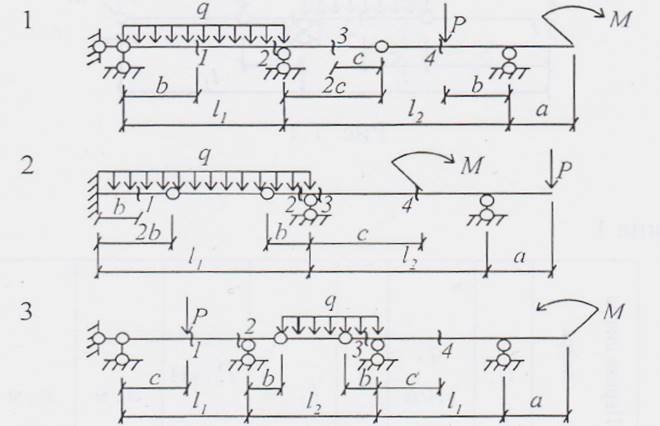
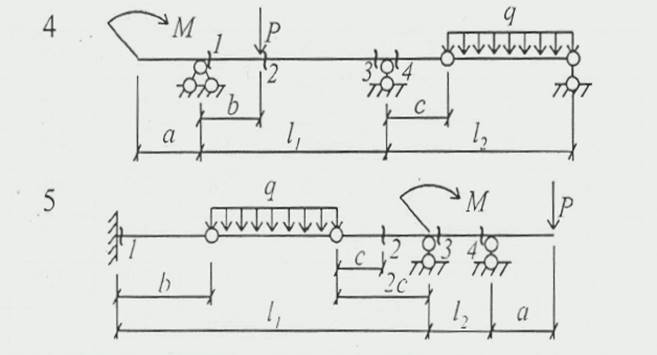
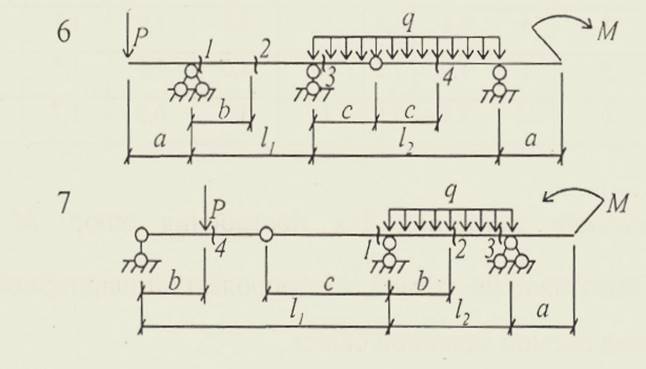
                            Рис. 8.   Схемы вариантов  к задаче  № 2.1.

                                                                                              Таблица 2.1

№ варианта и    №   схемы			L1   (м)	q (kH/м)	b (м)	L2 (м)	P (kH)	a (м)	c (м)	M (kHм)
1	1		10	1,2	1,0	8	3,0	1,0	1,0	2,0
2	2		14	2,0	0,8	7	2,5	1,2	2,2	2,2
3	3		8	1,8	1,0	9	6,0	2,0	1,4	2,7
4	4		12	3,0	1,4	6	2,8	2,2	1,6	2,4
5	5		9	1,5	1,6	11	7,0	1,3	1,8	2,5
6	6		11	2,5	2,1	10	3,3	2,1	2,0	1,1
7	7		7	1,4	1,2	12	5,0	1,4	1,1	2,6
8	8		6	0,8	1,8	15	8,0	1,0	1,3	3,0
9	9		5	1,0	1,5	14	4,0	1,5	1,5	2,8
10	0		13	2,2	2,0	16	3,2	0,8	1,7	1,5
11	0		10	1,2	1,0	8	3,0	1,0	1,0	2,0
12	1		14	2,0	0,8	7	2,5	1,2	2,2	2,2
13	2		8	1,8	1,0	9	6,0	2,0	1,4	2,7
14	3		12	3,0	1,4	6	2,8	2,2	1,6	2,4
15	4		9	1,5	1,6	11	7,0	1,3	1,8	2,5
16		5	11	2,5	2,1	10	3,3	2,1	2,0	1,1
17		6	7	1,4	1,2	12	5,0	1,4	1,1	2,6
18		7	6	0,8	1,8	15	8,0	1,0	1,3	3,0
19		8	5	1,0	1,5	14	4,0	1,5	1,5	2,8
20		9	13	2,2	2,0	16	3,2	0,8	1,7	1,5
21		0	10	1,2	1,0	8	3,0	1,0	1,0	2,0
22		8	14	2,0	0,8	7	2,5	1,2	2,2	2,2
23		7	8	1,8	1,0	9	6,0	2,0	1,4	2,7
24		6	12	3,0	1,4	6	2,8	2,2	1,6	2,4
25		5	9	1,5	1,6	11	7,0	1,3	1,8	2,5

 

Методические указания к решению задачи № 2.1.

К решению задачи можно приступить только после изучения темы «Многопролетные статически определимые (шарнирные) балки». Изучить преимущества и недостатки шарнирно-консольных балок; правила размещения шарниров в пролетах,  раздел 3. Статика сооружений.

Шарнирно-консольной балкой является многопролетная балка, которая состоит из нескольких простых балок, соединенных между собой шарнирами. Такие балки называют иногда разрезными многопролетными балками. В них шарнир как бы перерезает цельный брус, позволяя поворачиваться одному сечению относительно другого, но исключая при этом возможность перемещения одной простой балки относительно другой. Расчет шарнирно-консольных балок практически не отличается от расчета простых балок, так как шарнирная балка представляет собой систему простых балок. Чтобы установить, как взаимодействуют между собой простые балки, из которых составлена шарнирная балка, сначала строят так называемую этажную схему. После построения этажной схемы определяют опорные реакции и внутренние усилия Мх и Qx для каждой простой балки начиная с той, которая не несет нагрузок от других смежных балок. Это, как правило, верхняя балка в этажной схеме. Затем опорные реакции рассчитанной балки прикладывают к консольному участку нижележащей балки, считая их внешней нагрузкой для этой балки, и т.д. И, наконец, объединяя построенные эпюры простых балок, получают эпюры заданной шарнирно-консольной балки. Для проверки выполненных расчетов используют следующее правило: сумма моментов всех сил, приложенных слева или справа от любого шарнира, должна быть равна нулю.  При вычислениях используются те же правила знаков, что и в сопротивлении материалов. При построении эпюр изгибающих моментов эпюра моментов строится на оси бруса, и ордината момента откладывается в сторону выпуклости упругой линии, т.е., как говорят, эпюра моментов строится на растянутом волокне. Во всех случаях поперечная сила для прямого бруса равна сумме проекций на плоскость сечения всех внешних сил, лежащих по одну сторону от сечения.  Подробное решение задачи № 2.1. рассмотрим на примере 9.

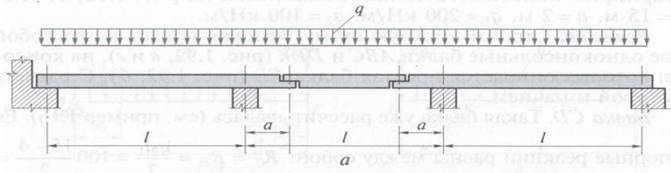
Пример 9.Построить эпюры Qx и Му для трехпролетной шарнирно-консольной балки, если L= 15 м, a = 2 м, q₁ = 200 к Н /м , q₂= 100 к Н / м. L₁ = 15 – 2 a =15 -4 = 11м.

Решение. Строим этажную схему, которая представляет собой две одноконсольные балки АВС и DEK, на консоли которых опирается простая балка CD, c  расчета

которой и начнем.

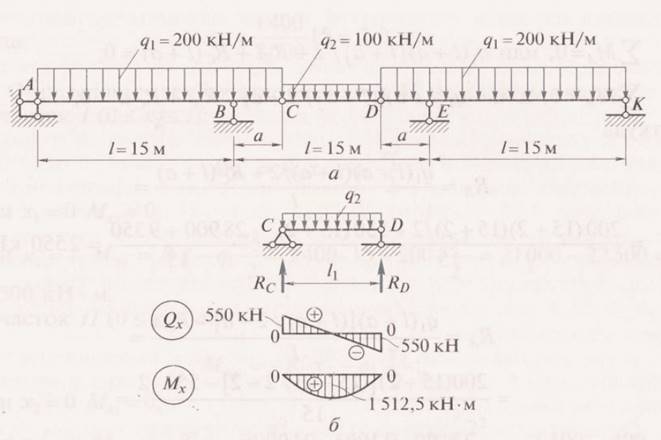
Балка CD.  Ее опорные реакции равны между собой: RC = RD = q_2*L/2 = 100 (15-4)/2 =

= 550 к Н. Эпюры Qx и Мх изображены строго под балкой. Максимальные значения

Q max = R_C = 550 кН; M max =q_2* L₁²/ 8 = 100* 11²/ 8 = 1512,5 kHм.

Балка ABC. Эта балка несет собственную распределенную нагрузку q₁ и нагрузку R¹_С  балки CD, которая равна R_С и направлена вниз, т. е. R'_С= 550  кН. Такую балку следует рассчитывать обычным способом.

1. Определяем опорные реакции, составляя уравнения равновесия:

       ∑ М_А =0; q_1* ( L+ a)² / 2 – R_B* L+. R'_С ( L + a)=0.

 

       ∑ М_B =0;  - q_1* ( L+ a)*( ( L+ a ) / 2 – a ) +R_A* L+. R'_С * a=0.

      

       R_B = (q_1* ( L+ a)² / 2 +. R'_С (L + a)) / L = (200*(15+2)²/2 + 550*(15+2))/ 15 = 2550 kH.

 

R_A = (q_1* ( L+ a)*( ( L+ a) /2 – a) - R'_С * a) / L=( 200*(15+2)*((15+2)/2 – 2) – 550*2=1400 kH.

 Выполним проверку правильности опорных реакций балки  АВС:

∑У_i = 0;   - q_1* ( L+ a) + R_A + R_B - R'_С = -200*17 +1400+ 2550 – 550= -3950 + 3950 = 0.

Опорные реакции балки определены верно.

 

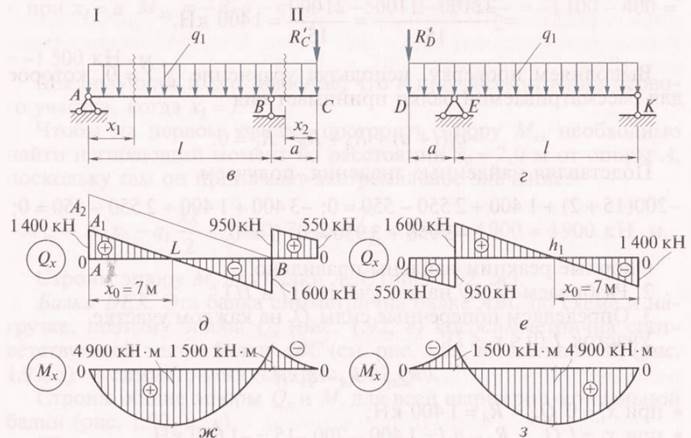
      2. Вычислим значения поперечных сил в характерных сечениях  балки АВС:

Q_a^прав = R_А = 1400  кН.

Q_В^лев = R_А – q₁*L  = 1400 – 200*15 = - 1600 кН ;  Q_B^прав = Q_B^лев + R_B = 950  кН.

  Q_C^лев = R_А – q₁*(L+a) + R_B = 1400 – 200*17 + 2550 = 550  kH;

Q_C^прав = Q_C^лев + R¹_C  = 550 - 550 = 0. Строим эпюру Q для балки АВС. Из подобия треугольников А LА₁  и АВА₂ отределим  х_0.

Х₀ / 15 = 1499 / 300;  Х₀ =7 м.

 3. Вычислим значения изгибающих моментов в характерных сечениях балки

М_A =0;  М_Х0 = R_A *7 – q_1* 49 / 2 = 4900 кНм

М_B = R_A *15 – q_1* 15² / 2 = 1400 * 15 – 200*225 / 2 = 1500  кНм

М_C = R_A *17 – q_1* 17² / 2 +  R_B* 2) = 1400*17 – 200*289 / 2 + 2550 = 28900 – 28900=0.

      Строим эпюры изгибающих моментов и поперечных сил для балки  АВС.

    3. Балка DEK. Эта балка симметрична балке ABC по схеме и нагрузке, поэтому        эпюра Qx кососимметрична соответствующей эпюре балки ABC ,а эпюра Мх  — симметрична эпюре изгибающих моментов балки АВС. Строим эпюры изгибающих моментов и поперечных сил под балкой  DEK .

    4. Строим общие эпюры Qx и Мх для всей многопролетной  шарнирной балки .

Шарнирно-консольные балки обладают одним очень важным свойством: изменяя места установки их шарниров, можно регулировать величину изгибающих моментов на промежуточных опорах и в пролетах.

  5. Величина максимального изгибающего момента  Мmax = 4900 kHм.

Опасными сечениями являются точки отстоящие на расстоянии 7 метров от опоры А вправо и на расстоянии 7 метров от опоры К влево.

 

Задача № 2.2. Для заданной простейшей одноконтурной рамы построить эпюры поперечных сил, изгибающих моментов и продольных сил. Проверить правильность их построения. Данные к задаче  № 2.2. на рис 9.

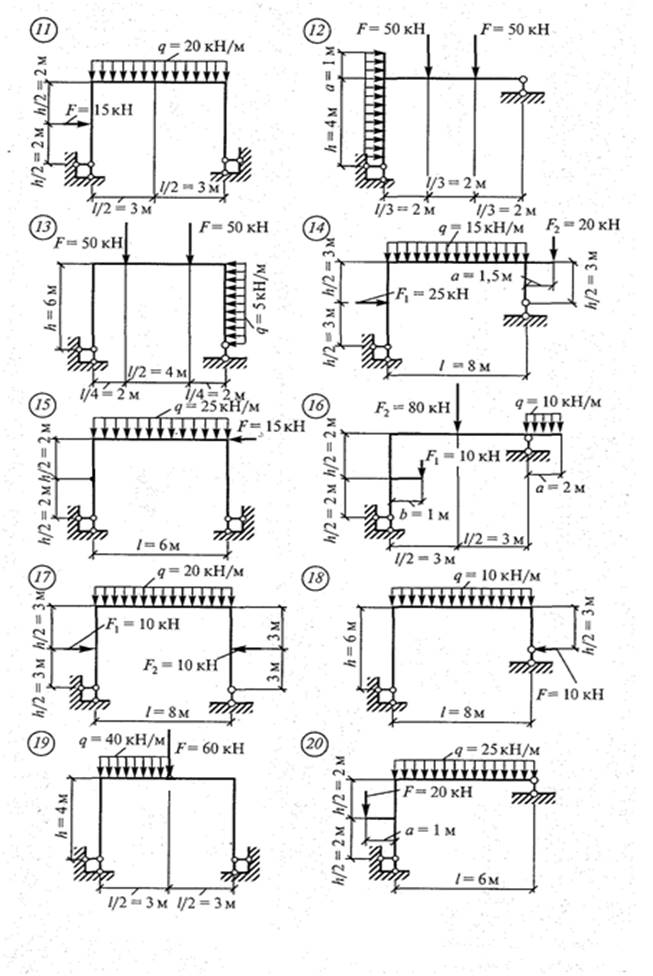
                            Рис. 9.   Схемы вариантов  к задаче  № 2.2.

 

Методические указания к решению задачи № 2.2.

Рамой называется геометрически неизменяемая стержневая система, стержни которой жёстко связаны между собой во всех или нескольких узлах. Горизонтальные  элементы рамы называются ригелями, а вертикальные– стойками. Расстояние между центрами опор соседних стоек называется пролётом рамы. Геометрические схемы рам могут быть однопролётными, многопролётными, одноэтажными и многоэтажными. Аналитический расчёт рамы заключается в определении трёх внутренних силовых факторов от внешних нагрузок – в построении эпюр изгибающих моментов, поперечных и продольных сил. Эпюры Q, М, и N строятся на геометрической схеме рамы, по осям стоек и ригелей. Штриховка эпюр выполняется перпендикулярно оси соответствующего стержня. При вычислении внутренних усилий в сечениях элементов рамы, наблюдатель расположен внутри рамы и обращен к рассматриваемому сечению.  Поперечную силу определяем как алгебраическую сумму проекций всех внешних сил, расположенных по одну сторону от сечения, на ось перпендикулярную  продольной оси рассматриваемого элемента. Ординаты эпюры Q откладываются вверх по оси ригеля и влево от оси стойки с указанием знака. Ординаты эпюры N откладываются симметрично по обе стороны от оси рассматриваемого стержня с обязательным указанием знака. На эпюре М знаки не ставят, а ординаты изгибающих моментов откладывают со стороны растянутых волокон. Ординаты на эпюрах Q и N снабжают знаками по следующим правилам: поперечная сила считается положительной, если внешняя нагрузка при рассмотрении левой отсеченной части рамы стремится сдвинуть эту часть в направлении от наблюдателя или при рассмотрении правой части – приблизить ее  к наблюдателю. Если же внешняя нагрузка стремится приблизить левую часть рамы к наблюдателю или правую отодвинуть от него, то поперечную силу считаем отрицательной. Изгибающий момент в любом сечении рамы численно равен алгебраической сумме моментов всех внешних сил, расположенных по одну сторону от рассматриваемого сечения, относительно точки сечения. Если  внешняя сила стремится повернуть левую часть рамы по часовой стрелке или правую ее часть против вращения часовой стрелки, то изгибающий момент положительный, если наблюдателю вращение представляется в противоположном направлении, то изгибающий момент отрицательный; продольная сила считается положительной при растяжении стержня и отрицательной при её сжатии. Для выполнения расчётов принимаем положительные значения изгибающих моментов и поперечных сил при следующих направлениях:

                                           М_х                                 М_х                       

                                            

                                           Q_y                                     Q_y

Порядок выполнения работы

1. Строим расчётную схему рамы, на которой изображаем все активные и реактивные силы. 2. Определяем  опорные реакции рамы и выполняем проверку правильности  определенных опорных реакций. 3. Переходим к определению значений внутренних силовых факторов Q, М, и N. Для этого  мысленно разрезаем раму в пределах каждого силового участка сечением на две части. Отбрасываем одну из частей и её влияние заменяем Q, М, N. Для оставшейся части рамы составляем, по три уравнения статического равновесия от всех сил, приложенных к этой части. Вычисляем значения поперечных сил в стойках и ригеле, строим эпюру Q_. Далее вычисляем значения изгибающих моментов и продольных сил, по определенным значениям изгибающих моментов и продольных сил в характерных сечениях, строим эпюры М и N.

Проверяем правильность построения эпюр, исходя из условия равновесия всех узлов рамы. Подробное решение задачи № 2.2. рассмотрим на примере 10.

Пример 10. Для заданной рамы, построить эпюры поперечных сил, изгибающих моментов и продольных сил. Равномерно распределенная нагрузка задана в Кн/м., сосредоточенные силы в кН., размеры сторон рамы в метрах. После построения эпюр,  выполнить проверку.

 

Решение:1.Определение опорных реакций рамы. Определим реакцию опоры Н:

∑М_А = 0. – V_H*L + P₂ (L –a) + q₂L²/2 +P₁a + q₁ h²/2 = 0.

V_H = ( P₂ (L –a) + q₂L²/2 +P₁a + q₁ h²/2) / L = 10,17 kH.

                  

 Реакцию V_А определим из уравнения:

 ∑М_Н = 0.  V_А*L - P₂ a - q₂L²/2 – P₁ (L- a )  + q₁ h²/2 = 0. Откуда

V_А =( P₂ a + q₂L²/2 +  P₁(L- a ) - q₁ h²/2) / L= 4, 83 кН.

Реакцию Н_А определим из уравнения: ∑Х_i = 0; - Н_А + q₁h = 0.  Н_А = q₁h =0,5*8 = 4 kH. Для проверки правильности определения вертикальных опорных реакций, спроектируем все внешние силы, приложенные к раме на ось ОУ:

 ∑У_i = 0;  V_А – P₁ -  q₂L – P₂ +  V_Н = 4,83 – 1,5 – 12 – 1,5 + 10,17 = 0. Все реакции определены верно, т. к. выполняется равенство ∑У_i = 0; 

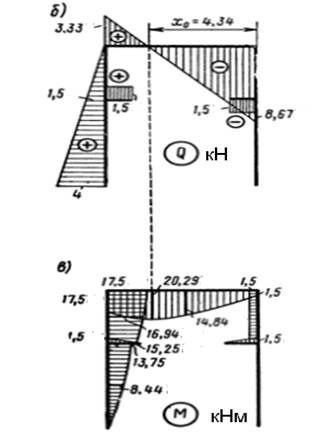
2. Построение эпюры поперечных сил. Стойка АD.

Поперечная сила Q_X = H_A – q₁x = 4 – 0,5x; при х = 0;  Q_А = 4 кН. При х = 8 м.,

Q_D = 4 – 0,5*8 = 0;  Q_B = 4 – 0,5*5 =1,5 kH.

Ригель DE: Q_D = V_А - P₁ = 4,83 – 1,5 = 3,33 kH. Q_E = Q_D – q₂L = 3,33 – 12 = 8,67 kH.

При определении поперечной силы учтены силы, приложенные к левой отсеченной части рамы, поэтому сила Р₂ не сходит в уравнение Q_D.

Стойка EH: Поперечная сила в любом сечении этой стойки равна нулю, так как, внешние силы, приложенные к правой нижней отсеченной части рамы перпендикулярны поперечному сечению Q_EН = 0.

Элементы  ВС и GF.  Q_BC = 1,5 kH.   имеет постоянное значение.

Q_GF = - 1,5 kH. По полученным данным строим эпюру поперечных сил Q_X .

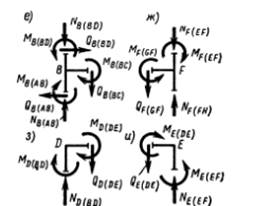
3.Построение эпюры изгибающих моментов.

Стойка AD. Эта стойка имеет два участка АВ и ВD. Проведем в пределах участка АВ сечение на расстоянии х от точки А и рассмотрим нижнюю отсеченную часть, изгибающий момент в данном сечении  М_Х = Н_А*х – q₁* x² / 2= 4x – 0,25x².

При  х = 0    М_Х =0;  при х = 2,5 м.  М_Х = 8,44 кНм.;   при х = 5 м.  М_В^лев. = 13,75 кНм.

Изгибающий момент в сечении участка ВD, на расстоянии х от точки А будет равен:

М_Х = Н_А*х – q₁* x² / 2 +Р*a = 4x – 0,5x²/2 +1,5*1,0 = 4x – 0,25 x² +1,5. На этом участке х может принимать значения от 5 до 8 метров,  при х = 5 м.  М_В^прав. = 15,25 кНм.;

При х =6,5 м. М_Х = 16,94 кНм.;   при х = 8 м. М_D = 17,5 кНм.;

Ригель DЕ. Проведем сечение на расстоянии х₁ от точки Е и рассмотрим правую отсеченную часть рамы, так как к ней приложено меньше сил, чем к левой части. Запишем уравнение изгибающих моментов в этом сечении:

М_Х1 = V_H *x₁ – P₂ (x₁ – 1) – q₂* x₁²/ 2 = 10,17x₁ – 1,5 (x₁ – 1) – x₁². Определим расстояние х₀, до сечения, в котором Q =0. Для этого выразим поперечную силу через х₀ и приравняем ее нулю: Q_x0 = - V_Н  + P₂ + q₂х₀ = 0; откуда х₀ = (V_Н  + P₂) / q₂ =(10,17 – 1,5) / 2 = 4, 34 м.

Подставим числовые значения х₁ в уравнение изгибающих моментов:

При  х₁ = 0;     М_Е = 10,17*0 – 1,5*(0 – 1) – 0² = 1,5 кНм.

При х₁ = 2 м;  М_х1 = 10,17*2 – 1,5*(2 – 1) – 2² = 14,84  кНм.

При х₁ = х₀ = 4,34;  М_мах = 10,17*4,34 – 1,5*(4,34 – 1) – 4,34² = 20,29  кНм.

При х₁ =6 м.;    М_D = 10,17*6 – 1,5*(6 – 1) – 6² = 17,5  кНм.

Стойка ЕН. Изгибающий момент в любом сечении участка  FH равен нулю, так как реакция V_H , приложенная к правой нижней отсеченной части направлена вдоль стержня.

Во всех сечениях стержня  _ЕF изгибающий момент вызывает сила P₂ :

М_EF = P₂* a = 1,5*1,0 = 1,5  кНм.

Элемент ВС : идем от свободного конца элемента: М_В = - Р₁* a= - 1,5 *1,0 =1,5 кНм

М_С = 0

Элемент GF. Аналогично изгибающие моменты в характерных точках этого элемента будут равны: М_G =0;   M_F = - P₂* a = - 1,5*1,0 = - 1,5  кНм.

По найденным значениям изгибающих моментов, откладываем ординаты со стороны растянутых волокон элементов рамы, строим эпюру М.

4.Построение эпюры продольных сил. Стойка АD. Рассматриваем левую отсеченную часть. Участок АВ  N_AB = - V_A = - 4,83 kH.

Участок  ВD той же стойки  N_BD = - V_A + P₁ = - 4,83 +1,5 = - 3, 33 kH.

Ригель DЕ. Все силы приложенные к этой части рамы перпендикулярны его продольной оси, в связи с этим N_DE = 0.

Стойка ЕН. Участок ЕF, правой стойки. Рассматриваем правую отсеченную часть рамы, действующие силы Р₂  и реакция V_Н, следовательно N _EF = Р₂ - V_Н = - 8,67 kH. Продольная сила на участке FН равна N _FН =  - V_Н = - 10,17 kH. По найденным значениям строим эпюру продольных сил N.

5.Проверка правильности построения эпюр  Q, M, N. Для этого необходимо мысленно вырезать из рамы узлы В, F, D , Е. и проверить их равновесие. После вырезания узла, действие отброшенных частей рамы заменим сосредоточенными силами, изгибающими моментами и продольными силами, взятыми из эпюр Q, M, N. Для примера рассмотрим равновесие узла D: ∑Х_i = 0; все силы действующие на узел перпендикулярны к оси х. 

 ∑У_i =  N _{B( ВD)} – Q _D(DЕ) =3,33 – 3,33 = 0;

∑М_D = М _D(BD) – M _D(DE) = 17,5 – 17,5 = 0. И так далее с каждым узлом.

Задача № 2.3. Для плоской фермы, с заданными размерами и нагрузкой, определить усилия во всех стержнях, графическим способом, путем построения диаграммы усилий Максвелла-Кремоны. Проверку выполнить

способом Риттера (способ моментных точек) или способом вырезания узлов.

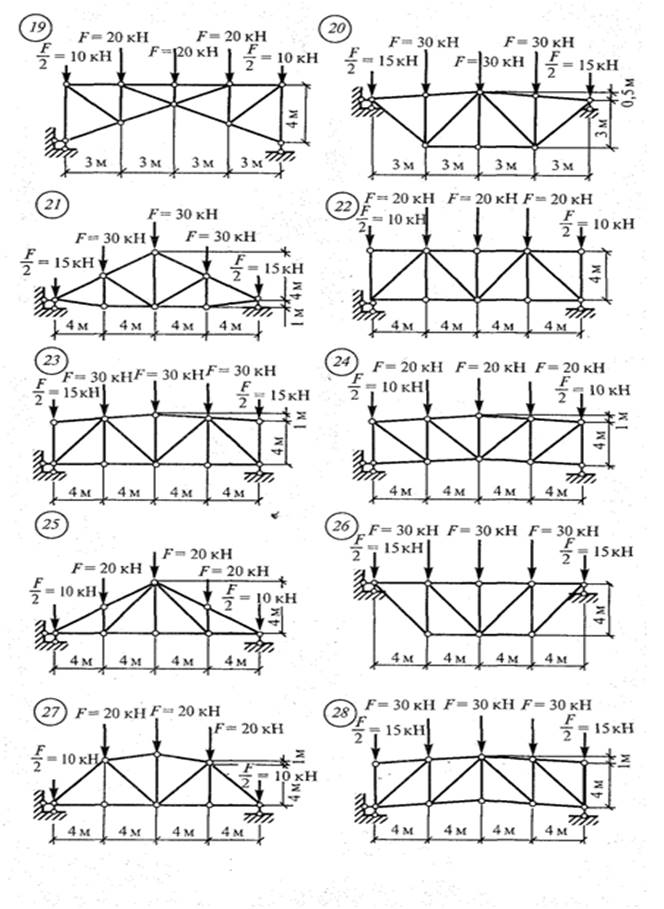                        Рис. 10.           Схемы вариантов к задаче 2.3.

 

Методические указания к решению задачи № 2.3.

          К решению задачи можно приступить только после изучения темы «Расчет плоских ферм», раздел 3.Статика сооружений, а также  разобрать классификацию методов расчета. Расчет ферм состоит в определении продольных сил в их стержнях. При узловой передаче внешней нагрузки, в качестве расчетной схемы принимается шарнирная ферма. При этом в сечениях возникают только продольные силы, вызывающие центральное растяжение или сжатие. Определение усилий можно выполнять аналитическим и графическим способами. Разновидностью аналитического  метода является способ вырезания узлов и способ сечений. Способ вырезания узлов состоит в  последовательном проведении разрезов, из которых каждый отсекает от фермы по одному узлу. Порядок расчета: определить опорные реакции; вырезать узел, в котором сходятся не более двух стержней; в местах сечений приложить внутренние продольные силы, направляя их от сечений; для вырезанного узла составить уравнения равновесия в виде суммы проекций на любые две непараллельные оси и определить неизвестные усилия. Далее отсекают следующий узел с двумя неизвестными усилиями и определяют их также, уравнения равновесия для последнего  вырезанного узла служат для проверки расчетов. К графическому методу относят способ построения диаграммы Максвелла-Кремоны и определения значения усилий,  измеренных в построенной диаграмме, с учетом принятого масштаба сил. Способ сечений (метод Риттера) применяется в том случае, когда можно разделить ферму на две части, причем в этом сечении неизвестных сил не должно быть более трех. Порядок расчета: определить опорные реакции; рассечь ферму на две части таким образом, чтобы в сечении было не более трех стержней с неизвестными усилиями; отбросить одну из частей, а ее действие на другую заменить усилиями в перерезанных стержнях; для оставшейся части фермы составить уравнения равновесия так, чтобы каждое из них содержало одно неизвестное усилие. Для этого сумму моментов составляют относительно точки пересечения двух неизвестных сил. Из уравнений равновесия определить неизвестные усилия. Подробное решение задачи № 2.3 рассмотрим на примере 11.

Пример 11. Для плоской фермы, с заданными размерами и нагрузкой, определить усилия во всех стержнях, графическим способом, путем построения диаграммы усилий Максвелла-Кремоны. Проверку выполнить способом Риттера (способ моментных точек) или способом вырезания узлов. Дано: d=3 м; h=3,6 м; h₁ = 8/9 h =3,2 м; h₂ =5/9 h=2 м; P₁ =P₇ =1 kH;  P₂ =P₃ =P₄ =P₅ =P₆ =2 kH.

Решение: а) Определение опорных реакций. Ввиду симметрии фермы и действующей нагрузки, реакции в опорах равны между собой.

 V_A = V_B = ∑P / 2 =12 /2 = 6 kH.

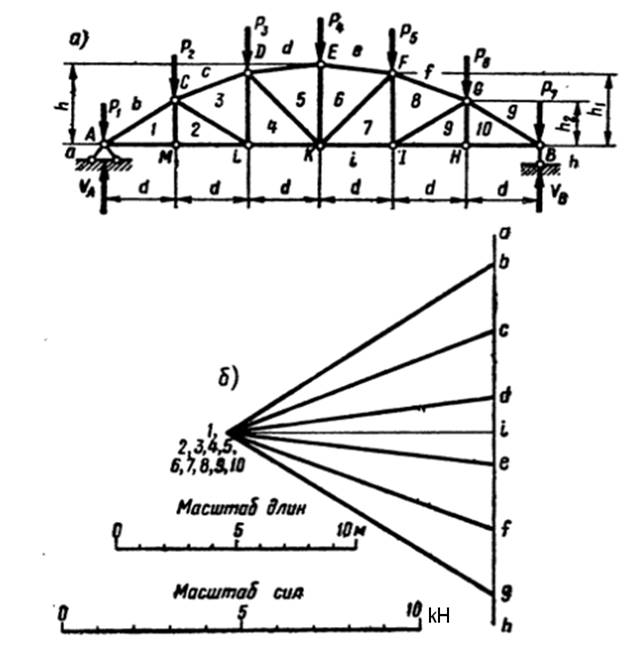
Обозначим поля на схеме фермы. Внешнее поле, ограниченное реакцией V_A и силой Р₁ , обозначим буквой а. Далее в порядке, при обходе контура фермы по часовой стрелке, все остальные внешние поля фермы обозначим также буквами b, c, d, e, f, g, h, i. Внутренние  поля фермы нумеруем по порядку цифрами 1, 2, 3…10.

б). Построение диаграммы усилий. В принятом масштабе сил, из заданных и реактивных сил, строим замкнутый силовой многоугольник a- b- c- d- e- f- g- h- i- a.

Затем мысленно вырезаем узел А, в котором сходятся два стержня, определим в них усилия. Для этого из точки b диаграммы проведем прямую, параллельную стержню b – 1, a из точки i – прямую параллельную стержню 1 – i, до взаимного пересечения, в результате на диаграмме получим точку 1. При обходе узла А по часовой стрелке стержни читаются  b – 1 и 1 - i, то усилие b – 1 на диаграмме направлено от точки b к точке 1, а усилие 1 – i, от точки 1 к точке i. Перенесем, мысленно, эти направления на соответствующие стержни и увидим, что усилие  

b – 1 направлено к узлу А, а усилие 1 – i от узла А.Таким образом, первое из них является сжимающим, второе растягивающим. Далее рассмотрим узел М, в котором сходятся три стержня, но в одном из них, а именно в  i – 1, усилие уже известно. Остается найти усилия в стержнях 1 – 2  и 2 – i. Проводим на диаграмме из точки 1 прямую, параллельную стержню  1 – 2, а из точки i – прямую, параллельную стержню 2 – i. На их пересечении получаем точку 2. Эта точка совпала с точкой 1, а это означает, что усилие 1 – 2 равно нулю, а усилие в стержне 2 – i равно усилию в стержне  i – 1 ( на диаграмме эти усилия совпадают) и тоже направлено от узла М, т.е. является растягивающим. Далее рассмотрим узел С, в котором сходятся четыре стержня, а неизвестными являются усилия в двух стержнях с – 3 и 3 – 2. Рассуждая аналогично, строим полную диаграмму усилий, последовательно рассматривая узлы L, D, E, K и т.д. Значения усилий, измеренных в построенной диаграмме, с учетом принятого масштаба сил сведены в таблицу:

Наименование стержней фермы	b – 1; g – 10	c – 3; f - 8	d – 5; e - 6	1 – i; 2 – i; 4 – i; 7 – i; 9 – i; 10 - i	1 – 2; 2 - 3; 3 - 4; 4 – 5; 5 – 6; 6 – 7; 7 – 8; 8 – 9; 9 – 10.
Усилия в стержнях фермы в(kH))	- 9, 0	- 8,07	- 7,56	7,5	0,00

Графический способ определения усилий в стержнях фермы, путем построения диаграммы усилий разработали Максвелл Джеймс Клерк - английский физик (автор теории взаимных фигур) и Кремона Луижи итальянский геометр, который в 1872 году развил теорию взаимных фигур, предложенную Максвеллом, применительно к теории расчета ферм графическим способом.

Способ Риттера. (Риттер Георг Август Дитрих, немецкий физик в 1863 г. предложил для расчета ферм использовать способ сечений, который в дальнейшем был усовершенствован русском ученым Ф.С.Ясинским), или  способом  моментных точек,по которому выполним проверку усилий в стержнях третьей панели фермы, которая имеет три стержня DE, DK  и  LK, оси которых не пересекаются в одной точке. Для определения усилий в этих стержнях проведем сечение 1 – 1, пересекающее все три стержня и разделяющее ферму на две части. Мысленно отбросим правую часть фермы, изобразим  на схеме оставшуюся левую часть и рассмотрим ее равновесие. Указанные на схеме усилия в рассеченных стержнях S_DE, S_LK  и S_DK, заменяют действие отброшенной правой части на левую часть.

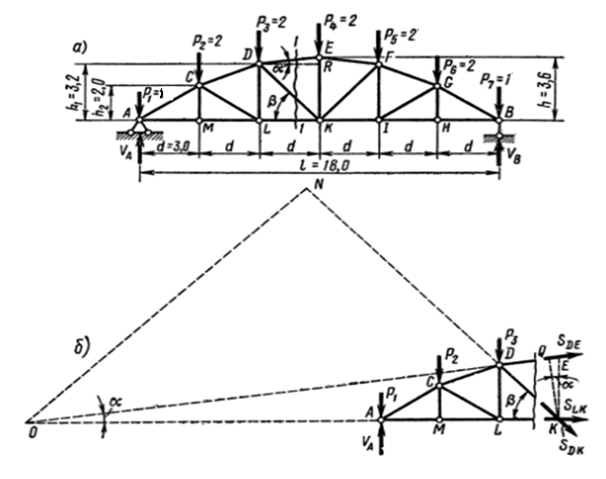
Рассмотрим левую часть сечения 1-1. Стержень DE, моментной точкой для этого стержня является точка К, точка пересечения осей двух других рассеченных стержней DK и LK. Составим относительно этой точки уравнение моментов всех сил, приложенных к левой части фермы:  ∑М_К = (V_A – P₁)*3d – P₂ *2d – P₃ *d + S_DE * KQ = 0; откуда  S_DE = ( - (V_A – P₁)*3d + P₂ *2d + P₃ *d)) / KQ .

Плечо KQ определим из прямоугольного треугольника QЕК (рис.б).

KQ = ЕК*cos α = h* cos α =3,57 м. После подстановки определим значение

 S_DE = - 7,56 Кн.(стержень сжат, на диаграмме этот стержень обозначен как  d – 5).

Проверим значение усилия в стержне DK. Продолжим до взаимного пересечения линии действия усилий S_DE  и  S_{LK .} Полученная точка О, служит моментной точкой стержня  DK. Составим уравнение моментов всех сил, действующих на левую часть, относительно точки О:   ∑М_О = S_DК * ОN + P₃*OL+ P₂*OM +( P₁ - V_A)* OA = 0.

Плечо  ОN определяем из прямоугольного треугольника  ОNК.   ОN= ОК*sinβ.

 ОК=EK / tg α =3,6 / 0,1333 = 27 м.;   tg β =DL / LK =h₁ /d =3,2 / 3 =1,067; угол β=46^о51^/

Sin β =0,7284. Подставим найденные значения, определим ОN=27*0,7284=19,67 м.

Подставим в уравнение моментов относительно точки О и определим S_DК.

S_DК = ( - P₃*OL- P₂*OM - ( P₁ - V_A)* OA) / ОN =(-2*24 – 2*21- (1 – 6)*18) /19,67 = 0.

Таким образом стержень DК ( на диаграмме усилий обозначен  5-4) является нулевым.

Проверяем значение усилия в стержне LK. Моментной точкой этого стержня является точка D. Составим относительно этой точки уравнение моментов всех сил, приложенных к отсеченной части фермы и найдем искомое усилие S_LК.

∑М_D = (V_A – P₁)*2d– P₂ *d –  S_LK * h₁ =0;  S_LK =( (V_A – P₁)*2d– P₂ *d) / h₁;

S_LK =((6 – 1)*2*3 – 2*3) / 3,2 = 7,5 kH. Cтержень LK растянут.Усилие S_LK на диаграмме усилий обозначен  4 – i .Таким образом, сравнивая значения усилий в стержнях третьей панели, найденные способом Риттера и значения тех же усилий, полученные графическим способом, видим, что они совершенно одинаковые..

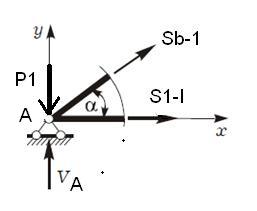
Проверим  значения усилий в стержнях АС и АМ, способом вырезания узлов. Мысленно вырежем узел А и рассмотрим его равновесие. Приложим к стержням продольные силы, предполагая, что стержни растянуты, неизвестные усилия обозначим через S_b-1 и  S_1-i. Начало системы координат поместим в точке А и составим уравнения суммы проекций всех сил, приложенных к узлу А на координатные оси, тогда:

∑ У_i  = S_B-1 * sin α +V_A – P₁ = 0;    ∑ X_i  = S_b-₁ *cos α +S_1-I =0, отсюда из первого уравнения    S_b-1 =( - V_A +P₁) / sin α = - 5 / 0,5555 = - 9,0 kH.

sin α =СМ /АС =2 /3,6 =0,5555;      cos α =АМ / АС =3 /3,6055 =0,8320

Подставим во второе уравнение  S_1-I =- S_b-1*cos α = 9 * 0,83206 = 7,5 kH.; сравнивая значения усилий в стержнях найденные способом вырезания узлов и значения тех же усилий, полученные графическим способом, видим, что они одинаковые.

.

Далее необходимо рассмотреть равновесие узла М, за тем равновесие узла С и т.д. Правильность определения усилий можно проконтролировать равновесием вырезанного узла В. Способом вырезания узлов может быть произведен расчет любой статически определимой фермы. Однако для сложных ферм он приводит к большому числу уравнений и применяется, главным образом как вспомогательный

 

4. Вопросы для самопроверки

Раздел 1. Теоретическая механика.

Часть 1. Статика.

1. Основные  и аксиомы статики (абсолютно твердое тело, материальная точка, сила как вектор, единицы измерения силы).

2. Система сил. Эквивалентные системы сил. Равнодействующая системы сил, уравновешивающая сила. Силы внешние и внутренние.

3. Связи и реакции связей. Принцип освобождаемости от связей.

4. Основные виды балочных опор и их реакции

5. Плоская система сходящихся сил. Силовой многоугольник.

6. Геометрическое условие равновесия плоской системы сходящихся сил.

7. Проекция силы на ось, правило знаков. Проекция силы на две взаимно-

перпендикулярные оси.

8. Аналитическое условие равновесия плоской системы сходящихся сил.

9. Пара сил. Вращательное действие пары сил на тело. Момент пары сил. Основные свойства пар сил.

10. Момент силы относительно точки, знак момента.

11. Приведение силы к заданному центру. Метод Луи Пуансо.

12. Приведение плоской системы сил к заданному центру. Главный вектор и главный момент произвольной плоской системы сил.

13. Теорема Вариньона о моменте равнодействующей произвольной плоской системы сил. Равновесие плоской системы сил.

14. Уравнения равновесия произвольной плоской системы сил (три формы).

15. Аналитическое определение опорных реакций балочных систем

Часть 2. Элементы кинематики.

16. Дайте определение абсолютному и относительному движению. Что такое  траектория точки?

17. Перечислите и охарактеризуйте способы задания движения точки.

18. Что такое скорость точки? Какими единицами (в системе СИ) она измеряется и какими параметрами характеризуется? Что такое средняя и истинная скорость точки?

19. Ускорение точки. Какими единицами (в системе СИ) оно измеряется и какими параметрами характеризуется?

20. Нормальное и касательное ускорения. Сформулируйте теорему о нормальном и касательном ускорении.

21. Перечислите и охарактеризуйте виды движения точки в зависимости от величины ее касательного и нормального ускорения.

22. Поступательное, вращательное, плоскопараллельное и сложное движения твердого тела.

Часть 3. Элементы  динамики.

23. Перечислите основные законы динамики и поясните их смысл.

24. Сформулируйте принцип независимости действия сил и поясните его смысл. Две основные задачи динамики.

25. Сила трения и сила инерции.

26. Сформулируйте и поясните сущность метода кинетостатики для решения задач динамики (принцип Д`Аламбера).

Раздел 2. Сопротивление материалов.

27. Перечислите основные задачи науки о сопротивлении материалов. Что такое прочность, жесткость, устойчивость?

28. Перечислите основные гипотезы и допущения, принимаемых в расчетах сопротивления материалов и поясните суть.

29. Перечислите основные виды нагрузок и деформаций, возникающих в процессе работы машин и сооружений.

30. В чём заключается метод сечений, используемый при решении задач сопротивления материалов?

31. Какие силовые факторы могут возникать в поперечном сечении бруса и какие виды деформаций они вызывают? Что такое эпюра?

32. Что такое напряжение и в каких единицах оно измеряется?

33. Сформулируйте закон Гука при растяжении и сжатии и поясните его смысл. Что такое модуль продольной упругости и  коэффициент Пуассона?

34. Сформулируйте условие прочности материалов и конструкций при  растяжении и сжатии, представьте его в виде расчетной формулы. Что такое коэффициент запаса прочности?

35. Механические испытания материалов. Диаграмма растяжения пластичных и хрупких материалов, их механические характеристики.

36. Определение главных центральных моментов инерции составных сечений, имеющих ось симметрии.

37. Главные оси инерции и главные центральные моменты инерции.

38. Осевые моменты инерции простейших сечений: прямоугольник, квадрат, треугольник, круг, кольцо.

39. Зависимость между осевыми моментами инерции относительно параллельных осей, одна из которых центральная.

40. Моменты инерции: осевые, полярные и центробежные.

41. Понятие о геометрических характеристиках плоских поперечных сечений бруса и их связь с различными видами деформаций.

42. Осевые моменты сопротивления сечений.

43. Сформулируйте условие прочности материалов и конструкций при сдвиге, представьте его в виде расчетной формулы. Что такое срез (скалывание)?

44. Сформулируйте закон Гука при сдвиге и объясните его сущность. Что такое модуль упругости сдвига (модуль упругости второго рода)?

45. Что такое статический момент площади плоской фигуры? Какими единицами системы СИ он измеряется?

46. Какие деформации и напряжения в сечениях бруса возникают при кручении?

47. Сформулируйте условие прочности бруса при кручении. Приведите расчетную формулу на прочность при кручении и поясните ее сущность.

48. Что такое чистый изгиб, прямой изгиб, косой изгиб? Какие напряжения возникают в поперечном сечении бруса при чистом изгибе?

49. Сформулируйте условие прочности балки (бруса) при изгибе. Приведите расчетную формулу и поясните ее сущность.

50. Нормальные напряжения при чистом изгибе. Формула для определения  нормальных напряжений в поперечном сечении бруса.

51. Что такое продольный изгиб? Приведите формулу Эйлера для определения величины критической силы при продольном изгибе и поясните ее сущность.

52. Расчёт центрально-сжатых стержней на устойчивость с использованием коэффициента продольного изгиба.

Раздел 3. Статика сооружений.

53. Основные понятия и нагрузки в статике сооружений.

54. Кинематический анализ конструкций.

55. Статически определимые и статически не определимые системы.

      56. По какой формуле определяется  степень свободы плоской системы.  

57. Эпюра поперечных сил в статически определимой шарнирной балке строится     по этажной схеме. С какой балки необходимо начинать расчет.

58. В точке приложения внешней сосредоточенной силы как выглядит  эпюра поперечных сил.

59. Когда в эпюре изгибающих моментов в сечении возникают скачки.

60. Балочные фермы. Какие фермы называются балочными.

61. Какие допущения используют при расчете ферм.

62. Какие деформации возникают в стержнях фермы при узловой   нагрузке.

63. Перечислите методы определения усилий в статически определимой ферме? 

64. Как определить растягивающей или сжимающей является  продольная сила?

65.Как составляются  уравнения статического равновесия системы сил?

66.Трёхшарнирные конструкции. Трехшарнирные арки.

67. Определение усилий в сечениях трехшарнирной арки.

68.Трёхшарнирные рамы. Что называется рамой.

69.Элементы рамы и типы рам. Ригель. Стойка рамы.

70.Как определить реакции в опорах рамы.

71. Правила знаков при построении эпюр изгибающих моментов, поперечных и продольных сил.

72.На чём основана проверка правильности построения эпюр М, Q и N.

73.Как определить правильность построения эпюр М, Q и N?

74.Расчет статически неопределимых рам.

75.Расчет неразрезной балки по уравнению трех моментов.

 

                                       5. Список  литературы.

1.Зиомковский В.М., Троицкий И.В.; под научной редакцией Вешкурцева В.И. Техническая механика. Учебное пособие для СПО. Москва: «Издательство Юрайт», 2020. Екатеринбург издательство Уральского университета.

2.Асадуллина Е.Ю. Техническая механика. Сопротивление материалов. Учебник и практикум для СПО. Москва: «Издательство Юрайт», 2020.

3.Асадуллина Е.Ю. Сопротивление материалов. Практикум. Учебное пособие для СПО, 2-е издание исправ. и допол. Москва: «Издательство Юрайт», 2020 – 158 с. 4.Кривошапко С.Н. Сопротивление материалов. Учебник и практикум для СПО,2-е издание перераб. и дополн. Москва: «Издательство Юрайт», 2021  (Профессиональное образование). — ISBN 978-5-534-03862-0. — Текст : электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/471425 /р 17-39.

5.Кривошапко С.Н., Копнов В.А. Сопротивление материалов. Практикум. Учебное пособие для СПО. 4-е изд., испр. и доп. Москва: «Издательство Юрайт», 2020 -353 с. (Профессиональное образование). — ISBN 978-5-9916-8043-1. — Текст: электронный // ЭБС Юрайт [сайт]. — URL https://urait.ru/bcode/452271

6.Олофинская В.П. Техническая механика. Курс лекций с вариантами практических и тестовых заданий  для обучающихся СПО, М., 2016 ;

7. Сетков В.И. Сборник задач по технической механике: Учебное пособие для сред.  Проф. Образования: – М., Издательский центр Академия 2003;

8.Эрдеди А.А., Эрдеди Н.А. Техническая механика – М.: ОИЦ «Академия», 2016;

9.Эрдеди А.А., Эрдеди Н.А. Теоретическая механика. Сопротивление материалов. – М.: ОИЦ «Академия», 2013.

10. Вереина Л.И., Краснов М.М. «Техническая механика». М: ОИЦ «Академия», 2014 г., 353 с. – Серия: Профессиональное образование.

11. Аркуша А.И. Техническая механика. Теоретическая механика и сопротивление материалов. М: Либроком, 2015 г., 354 с. - Серия: среднее профессиональное образование.

12. Вереина Л.И. Техническая механика. Учебник для студентов учреждений среднего профессионального образования, 10-е издание, М: Академия, 2015г., 224с.- Серия: профессиональное образование.

 

 

 

 

Скачано с www.znanio.ru