МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ ПРАКТИЧЕСКИХ РАБОТ по дисциплине ЕН.01 МАТЕМАТИКА Математического и общего естественнонаучного цикла для специальности 31.02.03 Лабораторная диагностика

Министерство образования и науки Пермского края

государственное бюджетное профессиональное образовательное учреждение

 «Пермский базовый медицинский колледж»

 

 

 

 

 

 

 

 

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ ПРАКТИЧЕСКИХ РАБОТ

по дисциплине

ЕН.01 Математика

Математического и общего естественнонаучного цикла

для специальности 

31.02.03 Лабораторная диагностика

базовая подготовка, форма обучения очная

 

 

 

 

                      

 

 

 

 

 

 

 

 

 

 

Пермь, 2019

.«Рассмотрено» на заседании ЦМК «Общепрофессиональных  и естественнонаучных дисциплин»  протокол №1 от «30» августа 2019 г	«Утверждаю» Директор ГБПОУ «ПБМК» _________________/Е.А.Колесова/ «2» сентября 2019 г МП

 

 

 

Методические указания по выполнению и оформлению практических работ разработаны на основе Федерального государственного образовательного стандарта среднего профессионального образования по специальности 31.02.03. Лабораторная диагностика базовой подготовки, рабочей программы по учебной дисциплине ЕН.01.Математика.

 

 

 

 

 

Разработчик:  Кандакова О.В., преподаватель первой квалификационной категории ГБПОУ «ПБМК»

 

СОДЕРЖАНИЕ

         1.        Введение …………………………………………….........................4

         2.        Ход выполнения практической работы……………………………5

         3.        Перечень практических работ……………………………………...6

         4.        Практическая работа №1……………………………………………7

         5.        Практическая работа №2……………………………………………10

         6.        Практическая работа №3……………………………………………12

         7.        Практическая работа №4……………………………………………19

         8.        Практическая работа №5……………………………………………20

         9.        Практическая работа №6……………………………………………22

      10.      Практическая работа №7……………………………………………27

      11.      Рекомендуемая литература………………………………………… 28

 

 

ВВЕДЕНИЕ

 Методические указания предназначены для проведения практических работ по дисциплине ЕН.01. Математика.

Практические  занятия  являются  связующим  звеном  между  теорией  и  практикой. Они необходимы для закрепления теоретических знаний, полученных на уроках теоретического обучения, а так же для получения практических знаний.

 Цель разработки: оказание помощи обучающимся в выполнении практических работ.

Содержание практических работ позволяет освоить:

-       практические приемы вычисления пределов;

-       практические приемы вычисления с помощью методов дифференциального и интегрального исчисления;

-       виды и методы решения простейших дифференциальных уравнений;

-       приложение определенного интеграла к решению прикладных задач;

-       основные понятия и методы теории вероятностей и математической статистики;

-       основные математические методы решения прикладных задач в области профессиональной деятельности.

В методических указаниях к выполнению практических работ содержится инструкция с четким алгоритмом хода работы.

 

 

ХОД ВЫПОЛНЕНИЯ ПРАКТИЧЕСКОЙ РАБОТЫ

 

   Практические работы необходимо выполнять в специальных тетрадях с указанием номера, темы, целей работы.

 

Ход работы:

1.     Повторить теоретический материал (основные понятия, определения, формулы). Устный опрос.

2.     В тетрадях для практических работ выполнить самостоятельную работу или решить номера, которые указаны в работе.

3.      Сдать преподавателю тетради для практических работ.

 

Критерии оценивания практических работ

 

       Оценка «5» ставится, если верно и рационально решено 90%-100% предлагаемых заданий, допустим 1 недочет, неискажающий сути решения.

       Оценка «4» ставится при  безошибочном решении 80% предлагаемых заданий.

       Оценка «3» ставится, если выполнено 70% предлагаемых заданий, допустим 1 недочет.

       Оценка «2» - решено мене 70% предлагаемых заданий.

 

 

ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ РАБОТ

 

№ работы	Тема
1	Вычисление пределов (2ч)
2	Вычисление производных и дифференциалов функций (2ч)
3	Приложение определенного интеграла к решению прикладных задач (2ч)
4	Решение задач теории вероятности (2ч)
5	Решение задач математической статистики (2ч)
6	Применение математических методов в профессиональной деятельности (4ч)
7	Итоговое занятие (2ч)

Практическая работа №1

«Вычисление пределов»

Цель работы:

На конкретных примерах научиться вычислять пределы различными способами.

Содержание работы:

1.                 Вопросы для самоконтроля:

–       Что такое предел функции в точке?

–       Какая функция называется непрерывной?

–       Какие свойства пределов функций используются при вычислении пределов?

–       Какие приемы используют при раскрытии неопределенностей типа; ?

–       Что такое I (II) замечательный предел?

2.     Выписать примеры (1-6):

Типы неопределенностей и методы их раскрытия

Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем. Рассмотрим некоторые приемы раскрытия неопределенностей.

I. Неопределенность вида

Пример 1. Вычислить предел  

Решение: При подстановке вместо переменной х числа 5 видим, что получается неопределенность вида .  Для ее раскрытия нужно разложить знаменатель на множители:  х² -25 = (х-5)*(х+5),  получили общий множитель (х-5),  на который можно сократить дробь. Задан­ный предел примет вид: . Подставив х=5, получим результат: ===

Пример 2. Вычислить предел  

Решение: При подстановке вместо переменной х числа 3  видим, что получается неопределенность вида . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель х-3. В результате получим новый предел, знаменатель ко­торого при подстановке вместо переменной х числа 3 не равен нулю. Этот предел легко вы­числяется по теоремам. Таким образом, неопределенность будет раскрыта.

            

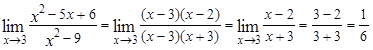
Пример 3. Вычислить предел  

Решение: При подстановке вместо переменной х числа 0 видим, что получается неопределенность вида . Для ее раскрытия воспользуемся первым замечательным пределом  и его следствием  . После чего предел легко вычисляется по теоремам. Таким образом, неопределенность будет раскрыта.

II. Неопределенность вида

Пример 4. Вычислить предел  

Решение: При подстановке вместо переменной  х бесконечности () видим, что получается неопределенность вида .  Для ее раскрытия нужно числитель и знаменатель разделить на наивысшую степень, в данном случае на х. Получим:

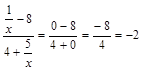 ==, т.к. величины являются бесконечно малыми и их пределы равны 0.

III. Неопределенность вида

Пример 5. Вычислить предел

Решение: При подстановке вместо переменной  х бесконечности () видим, что получается неопределенность вида  Для ее раскрытия воспользуемся вторым замечательным пределом  или . После чего предел легко вычисляется по теоремам. Таким образом, неопределенность будет раскрыта.

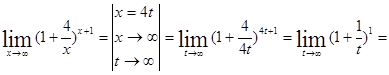
Пример 6. Вычислить предел

Решение: При подстановке вместо переменной  х бесконечности () видим, что получается неопределенность вида  Для ее раскрытия воспользуемся вторым замечательным пределом  или . После чего предел легко вычисляется по теоремам. Таким образом, неопределенность будет раскрыта.

 ===

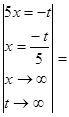
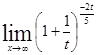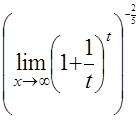3.                 Задания:

 Используя свойства пределов, вычислите пределы функций:

–       решить задачи из Омельченко В. П. , Демидова А. А. «Математика: Компьютерные технологии в медицине»   на стр.39-40 №1.7(нечетные); №1.8 (нечетные); №1.9(нечетные)

–       решить контрольную работу №1 по теме «Пределы и их свойства».

4.         Задания на дом:

–       подготовить сообщение по теме «Математика в медицине»;

–       решить задачи из Омельченко В. П. , Демидова А. А. «Математика: Компьютерные технологии в медицине»   на стр.39-40 №1.7(четные); №1.8 (четные); №1.9(четные);

–       выучить правила дифференцирования функции и научиться пользоваться таблицей производных (лекции).

 

 

Практическая работа №2

«Вычисление производных и дифференциалов функций»

Цель работы:

Проверить умения нахождения производной и дифференциалов функций.

Содержание работы:

1.       Вопросы для самоконтроля:

–   Что такое производная функции в точке?

–   Какая операция называется дифференцированием функции?

–   В чем заключается физический и геометрический смысл производной?

–   Каковы основные правила дифференцирования функций?

–   Для чего используется правило Лопиталя?

2.     Таблица производных основных элементарных функций:

 

1. 2. 3.    4. 5. 6. 7. 8. 9. 10. 11.

12.  13. 14. 15. 16. 17. 18. 19. 20.

 

3.     Задания:

Используя правила дифференцирования и производные основных элементарных функций, определите производные следующих функций:

1. у = х³ – 3х                                     7.

2.                              8.

3.                                       9.

4.                                    10.

5. .                                       11.

6.                                     12.

Используя правило Лопиталя, вычислите пределы функций:

13.                    14.             15.

Решить контрольную работу №2 по теме «Дифференциальное исчисление».

4.       Задания на дом:

–       составить кроссворд по теме «Дифференциальное исчисление»;

–       решить задачи из Омельченко В. П. , Демидова А. А. «Математика: Компьютерные технологии в медицине»   на стр.53-54 №2.1(четные); №2.2(1,2,4); на стр.56-57 №2.3 (четные);

–       выучить основные методы интегрирования функции и научиться пользоваться таблицей неопределенных интегралов (лекции).

 

 

 

 

 

Практическая работа №3

«Приложение определенного интеграла к решению прикладных задач»

Цель работы:

–       познакомить с понятием криволинейной трапеции;

–       на конкретных примерах научиться находить площадь криволинейной трапеции;

–       на конкретных примерах научиться находить объем фигуры вращения.

Содержание работы:

1.                   Вопросы для самоконтроля:

–   Понятие криволинейной трапеции;

–   Понятие определенного интеграла и его свойства;

–   Формула Ньютона-Лейбница;

–   Формулы для вычисления площади криволинейной трапеции;

–   Формулы для вычисления объема фигуры вращения.

Таблица интегралов

 

1. 2. 3. 4. 5. 6.

7. 8. 9. 10.  11. 12.

13. 14. 15. 16.

 

Методы интегрирования

1. Непосредственное интегрирование

Этот способ интегрирования предполагает такое преобразование подынтегральной функции, которое позволило бы использовать для решения табличные интегралы.

Пример 1. Вычислите

Решение: Для вычисления интеграла сначала воспользуемся 2 и 3 свойствами неопре­деленного интеграла, а затем применим 1 и 4 табличные интегралы:

 Пример 2. Вычислите

 Решение: Для вычисления интеграла сначала каждый член числителя почленно разделим на знаменатель, затем  воспользуемся 2 и 3 свойствами неопре­деленного интеграла и применим 1 и 3 табличные интегралы:

 

 

2. Метод замены переменной (метод подстановки)

Он является одним из наиболее эффективных и распространенных приемов интегри­рования, позволяющих во многих случаях упростить вычисление интеграла. Суть этого ме­тода состоит в том, что путем введения новой переменной интегрирования заданный инте­грал сводится к новому интегралу, который легко вычисляется непосредственным интегри­рованием.

Пример 3. Вычислите

Решение: Введем новую переменную t = 3x-4, тогда  , откуда . Подставим новую переменную в интеграл (вместо выражения 3х-4 подставим t, вместо подставим ).                  

 

Далее нужно вернуться к первоначальной переменной. Для этого сделаем обратную замену (вместо t подставим выражение 3х-4), получим окончательный ответ.

 

3.Интегрирование по частям.

Используем формулу интегрирования по частям:

Пример 4. Вычислить интеграл

 Решение: Используем формулу интегрирования по частям  . Пусть . Тогда

       

 Следовательно,

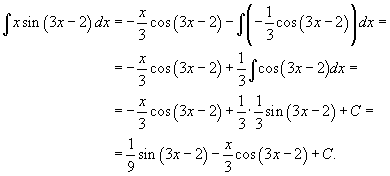
2.     Выписать примеры (1-2):

Площадь криволинейной трапеции, ограниченной непрерывной кривой у=f(х), двумя прямыми х=а и х=b и осью абсцисс, вычисляется с помощью определенного интеграла по формулам:

 

 

Пример 1. Вычислить площадь фигуры, ограниченной линиями , осями координат и прямой   х=2.

Решение: Построим данные линии

 

Найдем точки пересечения графика функции с осью Ох: ,  ,   

 

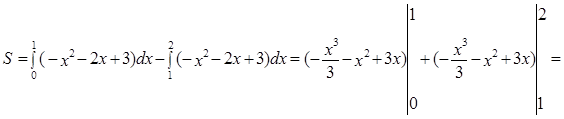
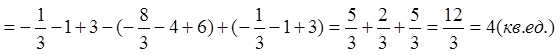
Пример2. Найти объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями:

Решение: Построим криволинейную трапецию, вращением которой получается тело вращения  

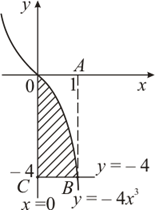
Чтобы получить объем тела вращения из объема  тела, полученного вращением фигуры ОАВС, вычтем объем  тела, полученного вращением фигуры ОАВ. Тогда искомый объем . По формуле (12) найдем  и :       (ед. объема);

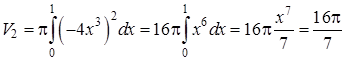 (ед. объема);

(ед. объема).

3.     Задания:

Используя формулу Ньютона-Лейбница, площади криволинейной трапеции,  объема фигуры вращения и методы интегрирования для определенного интеграла:

–   решить задачи из Омельченко В. П. , Демидова А. А. «Математика: Компьютерные технологии в медицине»   на стр.78 №3.5(нечетные); №3.7 (нечетные);

Вычислить определенный интеграл:

1)                    2)                3)

4)                    5)                       6)

7)          8)                           9)                                         10) 1)        12)

13)               14)                              15)                                                        16)                      17)                            18)

19)                         20)                                21)                                                           22)             23)                          24)

Решить контрольную работу №3 по теме «Интегральное исчисление».

4.       Задания на дом:

–   решить задачи из Омельченко В. П. , Демидова А. А. «Математика: Компьютерные технологии в медицине»  на стр.78 №3.5(четные); №3.7 (четные);

–   подготовить сообщение по теме «Решение геометрических, физических и прикладных задач интегральным способом»;

–   выучить основные понятия и формулы комбинаторики, классическую формулу нахождения вероятности, теоремы сложения и умножения вероятностей.

Практическая работа №4

«Решение задач теории вероятности»

Цель работы:

На конкретных примерах сформировать умение решать задачи на нахождение вероятностей.

Содержание работы:

1.                 Вопросы для самоконтроля:

–       Случайные события, их виды;

–       Вероятность случайного события, способы ее получения;

–       Комбинаторика. Применение элементов комбинаторики к вычислению вероятности;

–       Действия над случайными событиями, вычисление вероятностей результатов действий;

–       Случайные величины, их виды. Закон распределения случайной величины;

–       Ряд и функция распределения дискретной случайной величины;

–       Математическое ожидание дискретной случайной величины;

–       Дисперсия дискретной случайной величины.

2.                 Выписать примеры (1-6):

Классическое определение вероятности

Раздел математики, изучающий закономерности случайных событий, называется теорией вероятностей.

Вероятностью Р(А) события А в испытании с равновозможными элементарными исходами называют отношение числа исходов m,  благоприятствующих событию А, к числу n всех исходов испытания.

Пример 1. В партии из 30 миксеров 2 бракованных. Найти вероятность купить исправный миксер.

Решение:

Пример 2.  Из 34 экзаменационных билетов, пронумерованных с помощью чисел от 1 до 34, наудачу извлекается один. Какова вероятность, что номер вытянутого билета есть число, кратное трем.

Решение: Найдем количество чисел от 1 до 34, кратных трем. Это числа 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33. Всего таких чисел 11. Таким образом, искомая вероятность

Пример 3.  Вероятность поражения одной мишени – 0,7, а другой – 0,8. Какова вероятность, что будет поражена хотя бы одна мишень, если по ним стреляют независимо друг от друга.

Решение: Т.к. события совместны, то

Пример 4.  В двух коробках лежат ручки разного цвета. В первой коробке – 4 красных и 6 черных, во второй – 3 красных, 5 синих и 2 черных. Из обеих коробок вынимают по одной ручки. Найти вероятность, что обе ручки красные.

Решение: Найдем вероятности «вытащить красную ручку из каждой коробки» n₁=10, m₁=4, p₁=0,4, n₂=10, m₂=3, p₂=0,3

Тогда вероятность того, что обе ручки красные: 

Пример5. Случайная величина Х задана таблицей распределения вероятностей. Найти М(Х), D(Х), σ(Х).

хi	2	5	8	9
рi	0,1	0,4	0,3	0,2

Решение:

 

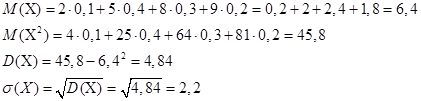
Пример6.  Найти математическое ожидание и дисперсию числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 100 билетов, а вероятность выигрыша на каждый билет равна 0,05.

Решение:

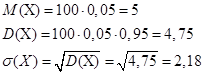
3.                 Задания:

–   решить задачи из Омельченко В. П. , Демидова А. А. «Математика: Компьютерные технологии в медицине»   на стр.96-97 №5.1; №5.3 (нечетные); на стр.110-111 №5.4(нечетные); №5.5(нечетные); на стр.129-131 №5.6; 5.7; 5.9.

–   решить контрольную работу №4 по теме «Основные понятия теории вероятности».

4.                 Задания на дом:

–   решить задачи из Омельченко В. П. , Демидова А. А. «Математика: Компьютерные технологии в медицине на стр.96-97 №5.1; №5.3 (четные); на стр.110-111 №5.4(четные); №5.5(четные); на стр.129-131 №5.8; 5.10.

–   подготовить сообщение на тему «Теория вероятности в медицине».

 

 

 

 

 

Практическая работа №5

«Решение задач математической статистики»

Цель работы:

На конкретных примерах сформировать умение решать задачи математической статистики.

Содержание работы:

1.                 Вопросы для самоконтроля:

–       Понятие вариационного ряда;

–       Этапы медико-статистического исследования;

–       Формулы медико-демографических показателей;

–       Понятие демографии;

–       Перепись населения, обработка информации.            

2.      Выписать примеры (1-2):

Гистограммой называется график, по оси абсцисс которого отложены границы классов, а по оси ординат – их частота.

Графические изображения, использующиеся для более наглядного изображения статистических данных, называют диаграммами. Наиболее часто используются следующие виды диаграмм: линейные, столбиковые и круговые.

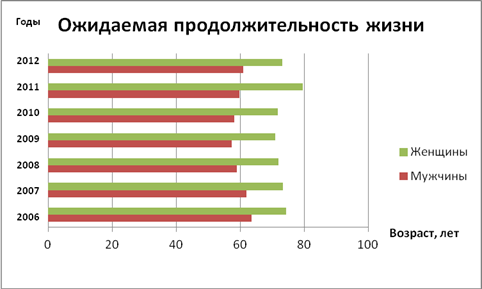
Пример1.Представить в виде линейной диаграммы ожидаемую продолжительность жизни в России с 2006 по 2012 год. Данные приведены в таблице.

Годы	2006	2007	2008	2009	2010	2011	2012
Мужчины	63,5	62,0	58,9	57,4	58,2	59,7	61,0
Женщины	74,3	73,3	71,9	71,0	71,7	79,5	73,1

Решение:

 

 

Столбиковая диаграмма отображает значения анализируемых величин в виде прямоугольных столбиков, высота которых пропорциональна их значению.

Круговые диаграммы позволяют наглядно изобразить исследуемые величины, выраженные в процентных соотношениях или в относительных значениях.

Пример2.Представить в виде круговой диаграммы данные о больных, поступивших в травматологическое отделение. Данные приведены в таблице.

Характер повреждения	Количество больных	%
1.     Изолированные травмы	22	44
2.     Множественные травмы	14	28
3.     Сочетанные травмы	6	12
4.     Прочие	8	16
Итого	50	100

Решение: Исходя из процентных соотношений, находят углы секторов, соответствующие характерам повреждений:

1)    44% * 3,6 = 158,4

2)    28% * 3,6

3)    12% * 3,6 43,2

4)    16% * 3,6 57,6

 

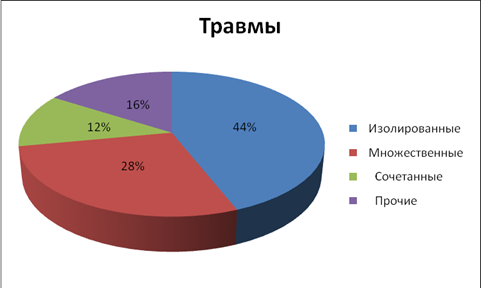
Демография - наука о народонаселении.

Демографическая статистика изучает численность, состав, плотность расселения, механическое (миграция) и естественное движение населения и их влияние на состояние здоровья и здравоохранение.

Демографическая статистика подразделяется на статику и динамику населения.

Статистика населения – раздел медицинской демографии, изучающие численный состав населения, структуру населения по полу, возрасту, уровню образования, национальности, семейному положению и т.д.

 Основной медико-демографический показатель статистики – численность населения.

Динамика населения – изучает естественное, механическое и социальное движения населения.

Рождаемость населения является важнейшим показателем воспроизводства населения.

Общий показатель рождаемости =

Для оценки воспроизводства населения страны важную роль играет показатель смертности.

Смертность населения – процесс естественного сокращения численности людей за счет случаев смерти.

Общий показатель смертности =

Разница между общими показателями рождаемости и смертности населения за год отражает процесс воспроизводства населения. Этот показатель называется естественный прирост населения.

Основные научно-организационные методы,

применяемые при переписи населения.

–       периодичность;

–       всеобщность;

–       единая программа сбора и обработки данных;

–       одномоментность;

–       сбор сведений методом опроса;

–       поименность при сборе информации;

–       строгое соблюдение тайны переписи.

3.      Задания:

–   решить задачи из Омельченко В. П. , Демидова А. А. «Математика: Компьютерные технологии в медицине»   на стр.146-148; №6.1; №6.3 ; №6.5; на стр. 168-169;  №6.12; №6.15; №6.16; №6.17.

–   решить контрольную работу №5 по теме «Математическая статистика»

4.                 Задания на дом:

–   решить задачи из Омельченко В. П. , Демидова А. А. «Математика: Компьютерные технологии в медицине на стр.146-148; №6.2; №6.4; №6.6; на стр.168-169; №6.13; №6.18; №6.19; №6.20.

–   подготовить сообщение на тему «Статистика в медицине»

 

 

 

 

 

 

 

Практическая работа №6

«Применение математических методов в профессиональной деятельности»

Цель работы:

На конкретных примерах сформировать умение решать задачи на применение математических методов в профессиональной деятельности.

Содержание работы:

1.  Вопросы для самоконтроля:

–       Что такое процент?

–       Какие три типа задач применяются для решения задач на проценты?

–       Что такое пропорция?

–       Сформулировать основное свойство пропорции.

–       Написать формулу для вычисления процентной концентрации раствора.

–       Написать формулу для расчета прибавки роста и массы детей;

–       Написать формулу для расчета питания детей;

–       Оценка пропорциональности развития ребенка, используя антропометрические индексы.

2.   Выписать примеры (1-6):

Формула сложных процентов

 

 

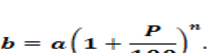
Масса раствора состоит из массы вещества и массы воды, т.е.

 

Концентрация раствора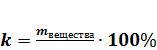 

Для дезинфекции чаще всего используются растворы хлорамина:

0,5% - для обработки рук;

1% - для уборки палат;

2% - для дезинфекции термометров;

3% - для текущей уборки в процедурном кабинете; для дезинфекции клизменных наконечников;

5% - для дезинфекции плевательницы туберкулезных больных. Хлорную известь используют для уборки коридоров, санузлов.

Маточный раствор - это 10% раствор хлорной извести.

Разведение антибиотиков

Стандартное разведение:

1        г (пенициллина) соответствует 1000 000 ЕД и 5 мл (новокаина). Флаконы могут быть по 1 000 000 ЕД;   500 000 ЕД ; 250 000 ЕД.

Расчёт массы тела

 - масса при рождении

 – масса долженствующая

 - масса фактическая

Определение массы тела до 6 месяцев

 =  + 800,

                n – число месяцев,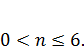 

Определение массы тела после от 6-ти месяцев до 1 года

= + 4800+400(n – 6)

                n - число месяцев, ;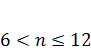

Определение массы тела ребёнка  от 1 года до 10 лет

  Массу тела ребёнка до 10 лет в кг можно вычислить по формуле:

                        = 10+2n,

где 10кг - средний вес ребёнка в 1 год,

2кг - ежегодная прибавка веса,

n - возраст ребёнка.

Массу тела ребёнка после 10 лет в кг можно вычислить по формуле

  = 30+4(n -10), где 30 - средний вес ребёнка в 10 лет, 4 - ежегодная прибавка веса, n - возраст ребёнка.

Определение степени гипотрофии

I     степень - дефицит массы 10 - 20%

II       степень - дефицит массы 20 – 30%

III        степень - дефицит массы > 30%

РАСЧЁТ:

   -  100%

                                  -  х%

                    х% = ():

Степень гипотрофии = 100% - х%

Расчёт длины тела

Длина тела ребёнка до года увеличивается ежемесячно

в 1 квартале на 3см,

во 2-м  - на 2,5см,

в 3-м  - на 1,5см, 

в 4-м - на 1 см.

Рост ребёнка после года можно вычислить по формуле: 75+6n,  где 75см - средний рост ребёнка в 1 год, 6см - среднегодовая прибавка, n - возраст ребёнка.

Расчет питания. Формула Шкарина

Vсут=800  50n

Если n - число недель, недостающее до 8-ми недель, тогда формула берется со знаком минус.

Если  n - число месяцев больше 2-х, формула берется со знаком плюс.

V_раз = ,  N - число кормлений в сутки.

 

Пример1. Торговая фирма покупает товар по оптовой цене 2300 рублей и продает его в розницу с надбавкой в 6%. Какова розничная цена?

Решение: По условию, розничная цена составляет 106% сотых от 2300 рублей. 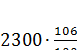  = 2438 (руб.)

Пример2. Какой должен быть первоначальный капитал, чтобы при начислении по 15% в месяц, получить через полгода миллион рублей?

Решение: Подставим в формулу сложных процентов р = 15, n = 6,

 b = 1000000 и найдем а:

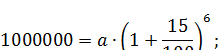
a  432 328 (руб.)

Пример 3. Сколько необходимо вещества и воды для приготовления 1л  2% раствора?

Решение: Количество раствора 1 л (1000г). Известно, что раствор 2%, значит, количество вещества составляет 2% от количества раствора:

Количество воды есть разность между количеством раствора и количеством вещества:

Ответ: Для приготовления 1 л 2% раствора необходимо 980г воды и 20г вещества.

Пример4. К 2 кг шестидесятипроцентного раствора серной кислоты добавили восьмидесятипроцентной - 4кг кислоты. Какова концентрация нового раствора?

Решение:1. Пусть х кг-количество серной кислоты в 60%растворе. Составим пропорцию:  2 кг - 100%

х кг -  60%

Найдем х.     (кг).

2.            Пусть у кг - количество серной кислоты в 80% растворе.

Составим пропорцию:

1кг - 100%

у кг -  80%

Найдем у. 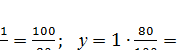  0,8(кг)

3.          Найдем: а) массу нового раствора

    2 кг + 1 кг = 3 кг.

б) количество серной кислоты в новом растворе

     х + у = 1,2 кг +0,8 кг = 2 кг.

4.        Пусть к% - концентрация нового раствора. Составим пропорцию:

3кг- 100%

2 кг -  к%

Найдем концентрацию к: 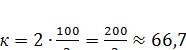(%) Ответ:  66,7%

Пример 5. Во флаконе 500000ЕД пенициллина. Пациенту врач назначил ввести 100000ЕД пенициллина 4 раза в сутки. Какое количество растворителя необходимо ввести во флакон для разведения, и сколько миллилитров раствора надо набрать в шприц?

Решение: 1. Определим количество растворителя. Для этого составим пропорцию и найдем х.

1мл   -  200 000 ЕД

 хмл   -  500 000  ЕД

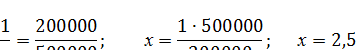
2,5 мл растворителя введем во флакон.

2. Определим количество раствора лекарственного вещество, которое необходимо набрать в шприц.

1мл  -  200 000 ЕД

хмл - 100 000 ЕД

 

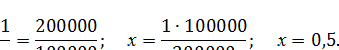
 0,5 мл раствора наберем в шприц для введения пациенту

Ответ: 2,5 мл растворителя; 0,5 мл раствора.

Пример 6.  Ребенок родился с весом тела 3 кг. В 3 месяца вес ребёнка составляет 4 кг. Определите дефицит массы тела ребёнка.

Решение: Долженствующая масса тела ребёнка в 4 месяца равна 5,4кг. Разность  составляет 1,4кг.

5,4 - 100%

1,4 – х%                     

Ответ: дефицит 2 степени.

Пример 7. Определить рост 7-ми месячного ребенка.

Решение:  Р = 75 – 41 – 21,5 = 68 см.

Пример 8. Ребенку три месяца. При кормлении он высасывает 80мл молока.

Оценить: достаточно ли молока ребенку, или нет.

Решение: V_сут = 800+503 = 800+150 = 950(мл)

В сутки 6 кормлений.     V_p =  =160(мл)     Ответ: не достаточно.

3.      Задания:

–   решить задачи из Омельченко В. П. , Демидова А. А. «Математика: Компьютерные технологии в медицине»   на стр.190-191; №7.1; №7.3 ; №7.5; №7.7; №7.9; №7.11; №7.13; №7.15;.№7.17.

–   решить контрольную работу №6 по теме «Применение математических методов в профессиональной деятельности».

4.   Задания на дом:

–   решить задачи из Омельченко В. П. , Демидова А. А. «Математика: Компьютерные технологии в медицине »   на стр.190-191; №7.2; №7.4; №7.6; №7.8; №7.10; №7.12; №7.14; №7.16.

–   подготовиться к зачету.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Практическая работа №7

«Итоговое занятие»

Цель работы:

На конкретных примерах сформировать умение решать задачи математической статистики.

Содержание работы:

1.  Вопросы для самоконтроля:

–       Числовые множества (действительные, целые, рациональные, иррациональные, натуральные), обозначение множеств, примеры.

–       Первый замечательный предел. Какую неопределённость помогает раскрыть?

–       Второй замечательный предел. Какую неопределённость помогает раскрыть?

–       Что такое приращение аргумента? Что такое приращение функции? Формулы.

–       Касательная. Уравнение касательной.

–       Правило Лопиталя. Где оно применяется?

–       Асимптота. Определение, формулы (горизонтальная, вертикальная, наклонная асимптота).

–       Определение первообразной, определение неопределённого интеграла.

–       Способы интегрирования.

–       Интегрирование по частям (формула).

–       Формула Ньютона-Лейбница. Где она применяется?

–       Формула для нахождения площади криволинейной трапеции.

–       Формула для вычисления объёма тела вращения.

–       Обыкновенное дифференциальное уравнение I порядка (определение).

–       Что такое задача Коши?

–       Определение математического ожидания (формула).

–       Определение дисперсии (формула).

–        Что такое антропометрические индексы? Где они применяются?

2.  Написать тест по теории: в тесте 10 вопросов. Выбрать один правильный ответ.

3.  Написать тест по практике: в тесте 7вопросов. Решить и выбрать один правильный ответ.

 

 

 

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Основные источники

1.           Пехлецкий И.Д. Математика. Учебник.  Москва:  ACADEMA, 2016г.

2.           Омельченко В. П. , Демидова А. А. Математика: Компьютерные технологии в медицине.   Ростов - на Дону: Феникс, 2018 г.

 

Дополнительная литература:

 

1.           Елисеева Н.Н., Юзбяшев М.М. Общая теория статистики. М.Р. и С., 2008г.

2.           Матвеева Н.М. Курс математики для техникумов. Москва: Наука, 2008г.

3.           Нахимсон Л.М. Элементы интегрального исчисления. Москва: Высшая школа, 2009г.

 

 

 

 

Скачано с www.znanio.ru