МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ - Тема: Применение численных методов для решения дифференциальных уравнений.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

               Применение численных методов для решения дифференциальных уравнений.

Цель работы:

-  применить теоретический материал по данной теме через решение упражнений;

-          применить умения приближенно находить решение обыкновенного дифференциального уравнения первого порядка методом Эйлера, методом Рунге-Кутта.

Оборудование:

1. Рабочая тетрадь в клетку.

2. Раздаточный материал: инструкционные карты-20шт.

3. Калькулятор простой.

Задание:

Задание 1.

Решить задачу Коши для дифференциального уравнения y’=f(x,y) на отрезке [a;b] при заданном начальном условии y(a)=y₀   и шаге интегрирования h методом Эйлера:

а) с применением «ручных» вычислений с шагом 2h.

б) с помощью программы для компьютера с шагом h.

в) Свести результаты вычислений в одну таблицу и сопоставить точность полученных значений функции. Пользуясь таблицей, сделать ручную прикидку графика интегральной кривой на бумаге.

Задание 2

Решить задачу Коши для дифференциального уравнения y’=f(x,y) на отрезке [a;b] при заданном начальном условии y(a)=y₀  методом Рунге-Кутта с помощью программы для компьютера с шагом h и с шагом h/2.

На основе результатов двойного счета сделать вывод о точности полученного решения.

Задание 3

Найти точное решение задачи Коши.

Порядок выполнения:

1.      Внимательно прочитать тему и цель практической работы.

2.      Изучить учебный материал по теме.

3.      Ответить на вопросы.

4.      Выполнить задания.

5.      Подготовить отчет.

Пояснения к работе (учебный материал):

Численные методы решения дифференциальных уравнений.

Постановка задач

Простейшим обыкновенным дифференциальным уравнением является уравнение первого порядка, разрешенное относительно производной:

y’=f(x,y)  (1)

Эта задача известна, как задача Коши: найти решение уравнения (5.1) в виде функции y(x), удовлетворяющей начальному условию

y(x_{0) =} y_0.  (2)

Геометрически это означает, что требуется найти интегральную кривую y=y(x), проходящую через заданную точку М₀ (x₀,y₀), при выполнении равенства (5.1).

Существует несколько классов дифференциальных уравнений 1-го порядка, для которых решение может быть найдено аналитически. Но даже для таких уравнений решение не всегда удается довести до вида y=y(x). Многие же дифференциальные уравнения, к которым приводят математические модели реальных процессов, не могут быть решены аналитически. По этой причине разработаны многочисленные методы приближенного решения дифференциальных уравнений.

Эти методы подразделяются на 3 основные группы:

1)     аналитические методы, применения которых дает приближенное решение дифференциальных уравнений в виде формулы;

2)     графические методы, дающие приближенное решение в виде графика;

3)     численные методы, когда искомая функция получается в виде таблицы.  

Метод Эйлера

В основе метода ломанных Эйлера лежит идея графического построения решения дифференциального уравнения. Однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.

Пусть дано уравнение (1)  с начальным условием (2), т.е. поставлена раздача Коши.

Вначале найдем простейшим способом приближенное значение решения в некоторой точке , где h – достаточно малый шаг.

Заметим, что уравнение (5.1) совместно с начальным условием (5.2) задают направление касательной к искомой интегральной кривой в точке М(x,y). Двигаясь вдоль этой касательной, получим приближенное значение решения в точке х:

        (3)

Аналогично, найдем приближенное значение решения в точке , и т.д.

Продолжая эту идею, построим систему равностоящих точек , i=0,..,n.

Получение таблицы значений искомой функции y(x) по методу Эйлера заключается в циклическом применении пары формул:

     (4)

Геометрическая иллюстрация метода Эйлера:

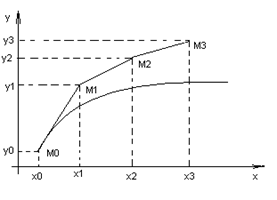
Рис 1 Построение ломаной Эйлера

Вместо кривой в реальности получается совокупность прямых – ломаная Эйлера.

Методы численного интегрирования дифференциальных уравнений, в которых решение получается от одного узла к другому, называются  пошаговыми.

Метод Эйлера – простейший пошаговый метод.

Отметим, что оценка погрешности метода при таком элементарном рассмотрении невозможна даже на первом шаге. Кроме того, особенностью любого пошагового метода является то, что, начиная со второго шага, исходное значение y в формуле (4) само является приближенным, т.е. погрешность на каждом шаге систематически возрастает.

Наиболее используемым методом оценки точности, как метода Эйлера, так и других пошаговых методов приближенного численного интегрирования обыкновенных дифференциальных уравнений является способ двойного прохождения заданного отрезка с шагом h и с шагом h/2. Совпадение соответствующих десятичных знаков  в полученных двумя способами результатах дает основание считать их верными.

Пример: Решить методом Эйлера дифференциальное уравнение c начальным условием y(0) = 1,3 на отрезке [0;1] применив h=0,2.

Решение: Имеем .

Составим таблицу значений функции f(x,y)  с шагом h и h/2.

При составлении таблицы проводились следующие вычисления:

Если h=0,2:

1)      х₀=0, у₀=1,3 из начального условия;

2)       х₁=0,1,

3)      х₂=0,2,

И т.д.

Аналогичные вычисления проводились и для h=0,1.

Таким образом, приближенное решение уравнения получаем в виде таблицы. Построим ломаную Эйлера для h=0,2 и h=0,1 в одной системе координат.

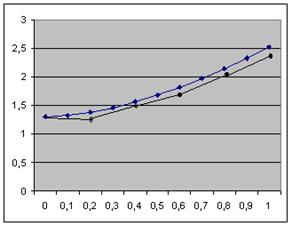
Метод Рунге-Кутта

Если к методу Эйлера подойти другим путем, не используя геометрических построений, то необходимо рассматривать производные функции f(x,y) и раскладывать эту функцию в степенной ряд. Но нахождение производных не является стандартной задачей, применяемой при решении математических задач систем программирования.

Альтернативный путь открывает метод Рунге-Кутта, названный по имени его создателей.

Основная идея метода Рунге-Кутта такова: вместо использования в формулах частных производных функции f(x,y) использовать лишь саму эту функцию, но на каждом шаге вычислять ее  значение в нескольких точках.

На практике соблюдается некоторый компромисс между высоким порядком формул и их громоздкостью с одной стороны, и объемом вычислений по ним для достижения заданной точности, с другой. Запишем самую распространяемую формулу Рунге-Кутта четвертого порядка: 

,        (5)

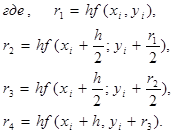                 (6)

Общий недостаток методов Рунге-Кутта – отсутствие простых способов оценки погрешности метода. Погрешность на одном шаге оценить сравнительно не трудно, гораздо труднее оценить накопление погрешностей на протяжении многих шагов. Широко используемый на практике для этих методов способ контроля точности – двойной счет: вычисляем решение дифференциального уравнение с шагом h и h/2 , а потом сравниваем полученные результаты.

Пример: Решить дифференциальное уравнение  на отрезке  с начальным условием у(0)=1 и шагом h=0.05.

Решение: Сначала решим это уравнение аналитически:

- уравнение с разделяющимися переменными.

,

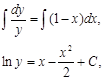
Применим начальное условие , получим:

Таким образом, частное решение данного уравнения, удовлетворяющее заданному начальному условию:

.

Пользуясь этой формулой, можно получить таблицу «точного» решение уравнения.

Найдем приближенное решение дифференциальное уравнение по методу Рунге-Кутта. Проведем последовательные вычисления по формулам (5), (6):

Имеем: f(x,y)=y(1-x), =0, =1, h=0.05. Тогда

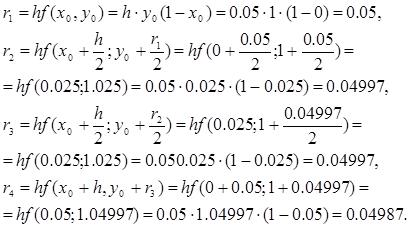
Подставим найденные значения в формулу (5):

Поскольку вычисления достаточно громоздки и трудоемки, то численные решения заданного уравнения можно найти с помощью программы на компьютере.

Для сравнения результатов построим таблицу, в которой укажем численные решения, полученные по методу Эйлера, методу Рунге-Кутта и «точное решение».

Из таблицы видно, что результаты, получения по методу Рунге-Кутта практически совпадают с «точным» решением уравнения, в отличие от соответствующих значений, полученных по методу Эйлера.

Вопросы для закрепления теоретического материала к практическому занятию:

1.      Что является решением дифференциального уравнения?

2.      На какие группы подразделяются приближенные методы решения дифференциальных уравнений?

3.      В какой форме получается приближенное решение дифференциального уравнения по методу Эйлера?

4.      В чем основная идея метода Рунге-Кутта?

5.      В чем отличие одношаговых методов Эйлера и Рунге-Кутта?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

- Численные методы и программирование: Учебное пособие / В.Д. Колдаев; Под ред. Л.Г. Гагариной. - М.: ИД ФОРУМ: НИЦ Инфра-М, 2016. - 336 с…

- Гателюк, О. В. Численные методы : учеб. пособие для СПО / О. В. Гателюк, Ш. К. Исмаилов, Н. В. Манюкова. — М. : Издательство Юрайт, 2018. — 140 с. — (Серия : Профессиональное образование)

- Бахвалов Н.С., Лапин А.В., Чижонков Е.В. «Численные методы в задачах и упражнениях»/ Под ред. В.А.Садовничего – М.:Высш.шк.,2016

-  Вержбицкий В.М. «Численные методы. Математический анализ и обыкновенные дифференциальные уравнения» - М.: Высшая школа, 2017

- Волков Е.А. «Численные методы» - СПб.: Издательство «Лань», 2015

- Исаков В.Н. «Элементы численных методов» - М.: Издательский центр «Академия», 2016.

- Бахвалов Н.С., Лапин А.В., Чижонков Е.В.; Под ред. Садовничий В.А Численные методы в задачах и упражнениях: Учебное пособие /., - 4-е изд., (эл.) - М.:БИНОМ. Лаб. знаний, 2015. - 243 с.: ISBN 978-5-9963-2980-9 - Режим доступа: http://znanium.com/

- А.В. Гулин, О.С. Мажорова, В.А. Морозова Введение в численные методы в задачах и упражнениях : учеб. пособие /. — М. : ИНФРА-М, 2017. — 368 с. — (Высшее образование: Бакалавриат). - Режим доступа: http://znanium.com/

- Калиткин Н.Н., Численные методы: Учебное пособие / - 2-е изд., исправленное. - СПб:БХВ-Петербург, 2015. - 587 с. ISBN 978-5-9775-2575-6 - Режим доступа: http://znanium.com/catalog/product/94450.

Скачано с www.znanio.ru