МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ - Тема: Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций.

Цель работы:

-          применить умения отделять корни алгебраических уравнений;

-          применить умения решать алгебраические уравнений приближенными методами (метод половинного деления, метод хорд, метод касательных);

Оборудование:

1. Рабочая тетрадь в клетку.

2. Раздаточный материал: инструкционные карты-20шт.

3. Калькулятор простой.

Задание:

Вариант 1

1. Методом половинного деления с точностью 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения

1.      Методом итераций решить уравнение с точностью до 0,001

Вариант 2

1. Методом половинного деления с точностью 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения

2. Методом итераций решить с точностью до 0,001 уравнение.

Порядок выполнения:

1.      Внимательно прочитать тему и цель практической работы.

2.      Изучить учебный материал по теме.

3.      Ответить на вопросы.

4.      Выполнить задания.

5.      Подготовить отчет.

Пояснения к работе (учебный материал):

Число  из области определения функции  называется корнем уравнения , если .

Процесс нахождения корней уравнения распадается на несколько этапов:

1)      определяются границы интервала, в котором находятся все корни уравнения ;

2)      устанавливаются возможно малые промежутки, в каждом из которых содержатся ровно один корень.

3)      каждый из корней вычисляется с заданной точностью.

К сожалению, определение в общем виде границ интервала, в котором находятся все корни уравнения , можно дать только для алгебраического уравнения в каноническом виде, т.е. для уравнения вида:

                                                                              (1)

В дальнейшем будем находить действительные корни алгебраических уравнений.

Теорема 1 (основная теорема алгебры).

Уравнения вида (1) имеет ровно n корней, действительных или комплексных, если корень кратности k считать за k корней.

Числоназывается корнем кратности k уравнения (1), если при  обращается в нуль сама функция  и ее производные до (k-1)-го порядка включительно, т.е.

Корень кратности  называется простым.

Теорема 2.

1) Число действительных корней уравнения (1) четной степени с действительными коэффициентами всегда четно (в том числе и может равняться нулю).

Если кроме этого , то уравнение четной степени имеет, по крайней мере, два действительных корня разного знака.

2) Уравнение (1) нечетной степени имеет по крайней мере один действительный корень того же знака, что и «».

Теорема 3 (теорема Декарта).

Число положительных корней уравнения (1) равно или на четное число меньше числа перемен знака в ряду коэффициентов  уравнения. Так как при замене «х» на «-у» корни уравнения (1) меняют знаки, то с помощью этой теоремы можно оценить и число  отрицательных корней.

Примеры.

1. В уравнении нечетной степени  коэффициенты  и 

Кроме этого, число перемен знаков равно 1.

Следовательно, по теоремам 2 и 3, оно имеет один действительный положительный корень.

2. В уравнении нечетной степени коэффициенты и  Следовательно по теореме 2, оно имеет по крайней мере один действительный отрицательный корень.

Число перемен знаков в данном уравнении равно двум, следовательно, по теореме 3, оно имеет либо два, либо 0 положительных действительных корней.

Оценим число действительных отрицательных корней. Для этого заменим «х» на     «-у». Получим уравнение, или, или . Число перемен знаков в этом уравнении равно 1, следовательно, исходное уравнение имеет один действительный отрицательный корень.

3. В уравнении четной степени коэффициенты  и . Следовательно, по теореме 2, оно имеет два действительных корня разного знака.

4. В уравнении четной степени  коэффициенты  и . Следовательно, по теореме 2, оно имеет по крайней мере два действительных корня разного знака.

            Число перемен знаков в данном уравнении равно 1, следовательно, по теореме 3, оно имеет один положительный действительный корень.

Оценим число действительных отрицательных корней. Для этого  заменим «х» на    «-у». Получим уравнение или . Число перемен знаков в этом уравнении равно 1, следовательно, исходное уравнение имеет один  действительный корень.

Дадим теперь формулировку теоремы, позволяющей достаточно грубо определять  границы интервала, в котором находятся все действительные корни уравнения (1).

Теорема 4.

1) Если, где 0; , где , и , то .

2) Все положительные действительные корни уравнения находятся в промежутке , а все  отрицательные действительные корни уравнения (1) находятся в промежутке .

Теорема 5.

Если непрерывная и дифференцируемая функции , определяющая алгебраическое уравнение , на концах отрезка  принимает значения разных знаков, т.е. , и ее первая производная сохраняет знак внутри этого отрезка, но на  находится ровно один действительный корень данного уравнения.

Замечание. Для алгебраических уравнений (1), степень которых больше трех, трудно аналитически находить интервалы знакопостоянства функции . Поэтому для нахождения возможно малых промежутков, содержащих ровно один действительный корень можно на практике использовать следующие способы:

1)     средствами машинной графики функция  представляется на дисплее и приближенно определяются возможно малые промежутки, содержащие ровно один корень (т.е. промежутки содержащие одну точку пересечения графика функции  с осью Ох);

2)     если график функции  построить трудно, то формируют простые функции  и , такие, что уравнение преобразуется в виде  =. Затем строятся графики функций у= и y= и приближенно определяются промежутки, содержащие  абсциссы точек пересечения этих графиков.

Так, например, уравнение  можно преобразовать к виду  и затем построить графики функции  и .

Начиная третий этап, дадим формулировку теоремы, позволяющей оценивать погрешность приближенного решения.

Теорема 6.

Если  точный, а  - приближенный, корни уравнения (1), принадлежащие одному и тому же промежутку, то справедливая оценка: , где m – наименьшее значение модуля производной функции  на промежутке .

Пример 1.

Графически решить уравнение x ln(x)=1.

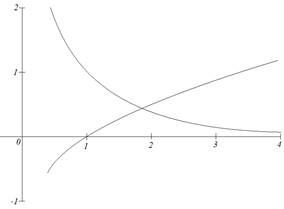Решение. Запишем исходное уравнение в виде: , т.е.  и . Таким образом, корни данного уравнения могут быть найдены как абсциссы точек пересечения кривых  и .

Теперь построим графики функций и определим интервал изоляции корня.

Пример 2.

Аналитически отделить корни данного алгебраического уравнения, используя теорему Штурма:

Решение.

,

Построим таблицу для подсчета смены знаков:

Из таблицы подсчета смены знаков видно, что есть один корень данного уравнения, и он находится на .

Метод половинного деления.

Поставим задачу: методом половинного деления найти приближенное значение положительного действительного корня  алгебраического уравнения  с точностью до .

Решение.

1) Предположим, что удалось найти достаточно малый промежуток , содержащий ровно один действительный корень  алгебраического уравнения . Тогда, согласно теореме 5, непрерывная и дифференцируемая функция  принимает на его концах значения разных знаков, т.е. .

2) Разделим промежуток  точкой  на два одинаковых:  и .

Если , то корень  содержится в промежутке .

Если же , то корень  содержится в промежутке .

Предположим, для определенности, что корень находится в промежутке .

3) Рассмотрим абсолютное значение разности . Если , то процесс нахождения приближенного значения следует закончить и в качестве  взять величину .

Если же , то следует разделить промежуток  точкой  на два одинаковых:  и  и повторить действия, указанные в пп. 2 и 3, до достижения заданной точности .

Метод итераций.

Если данное уравнение приведено к виду где  всюду на отрезке , на котором исходное уравнение имеет единственный корень, то исходя из некоторого начального значения  принадлежащего отрезку  можно построить такую последовательность:

  …,

Пределом этой последовательности является единственный корень уравнения  на отрезке  Погрешность приближенного значения  корня  найденного методом итераций, оценивается неравенством

Для нахождения приближенного значения корня с погрешностью, не превышающей , достаточно определить  так, чтобы выполнялось неравенство

При выполнении практической работы рассмотрите следующие примеры:

Пример 1.

Методом половинного деления уточнить корень уравнения , лежащий на отрезке .

Решение. .

1этап:  

            значит корня на отрезке  нет.

             значит корень находится на .

2 этап:  

              значит корня на отрезке  нет.

              значит корень находится на .

Дальше процесс продолжается аналогичным образом.

И т.д.

Можно принять

Пример 2.

Отделить корни уравнения аналитически и уточнить один из них методом итерации  с точностью до 0,001.         

 x-2x+7x+3=0.

Решение:

Полагаем f(x)= x-2x+7x+3=0. Составим таблицу знаков функции для определения интервала, в котором лежат корни уравнения:

Т.е. корни уравнения находятся в интервалах [-1;0].

Уточним этот корень методом итерации. Для этого приведём функцию к виду  x= φ(x), где | φ(x)|<1.

1.      Находим f’(x)=3x- 4x+7.

2.      f’(-1)=3+4+7=14       f’(0)=0-0+7=7.

3.      Q =max| f’(x)|= max(14 и 7)=14.

4.      Определяем k=10. (берем меньшее ближайшее удобное число к 14)

5.      φ(x)= х - ; φ(x)= х - + - -  = х -0,1х+0,2х-0,7х-0,3

6.      φ(x)= -0,1х+0,2х-0,3х-0,3.

7.      Пусть х=0, тогда х= φ(x). Все вычисления располагаем в таблице:

Вычисляем до тех пор, пока |x-x|≤0,001.

F(0)= -0,3;

f(-0,3)= 0,0027+0,018-0,09-0,3= -0,3693;

f(-0,3693)= 0,0050+0,0273-0,1107-0,3= -0,3784;

f(-0,3784)= 0,0054+0,0286-0,1135-0,3= -0,3795;

f(-0,3795)= 0,0055+0,0288-0,1139-0,3= -0,3796;

|x-x|= |-0,3796-(-0,3795)|=0,001.

Ответ: х ≈ -0,3796.

Вопросы для закрепления теоретического материала к практическому занятию:

1.      Что называется корнем уравнения?

2.      В чем суть решения уравнений методом половинного деления?

3.      В чем суть решения уравнений методом итераций?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

- Численные методы и программирование: Учебное пособие / В.Д. Колдаев; Под ред. Л.Г. Гагариной. - М.: ИД ФОРУМ: НИЦ Инфра-М, 2016. - 336 с…

- Гателюк, О. В. Численные методы : учеб. пособие для СПО / О. В. Гателюк, Ш. К. Исмаилов, Н. В. Манюкова. — М. : Издательство Юрайт, 2018. — 140 с. — (Серия : Профессиональное образование)

- Бахвалов Н.С., Лапин А.В., Чижонков Е.В. «Численные методы в задачах и упражнениях»/ Под ред. В.А.Садовничего – М.:Высш.шк.,2016

-  Вержбицкий В.М. «Численные методы. Математический анализ и обыкновенные дифференциальные уравнения» - М.: Высшая школа, 2017

- Волков Е.А. «Численные методы» - СПб.: Издательство «Лань», 2015

- Исаков В.Н. «Элементы численных методов» - М.: Издательский центр «Академия», 2016.

- Бахвалов Н.С., Лапин А.В., Чижонков Е.В.; Под ред. Садовничий В.А Численные методы в задачах и упражнениях: Учебное пособие /., - 4-е изд., (эл.) - М.:БИНОМ. Лаб. знаний, 2015. - 243 с.: ISBN 978-5-9963-2980-9 - Режим доступа: http://znanium.com/

- А.В. Гулин, О.С. Мажорова, В.А. Морозова Введение в численные методы в задачах и упражнениях : учеб. пособие /. — М. : ИНФРА-М, 2017. — 368 с. — (Высшее образование: Бакалавриат). - Режим доступа: http://znanium.com/

- Калиткин Н.Н., Численные методы: Учебное пособие / - 2-е изд., исправленное. - СПб:БХВ-Петербург, 2015. - 587 с. ISBN 978-5-9775-2575-6 - Режим доступа: http://znanium.com/catalog/product/94450.

Скачано с www.znanio.ru