
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ В СПО
Разработал преподаватель: Игнатьева Елена Сергеевна
Тема:
Вычисление интегралов методами численного интегрирования.
Цель работы:
- применить теоретический материал по данной теме через решение упражнений;
- применить умения приближенно вычислять интегралы при помощи формул Ньютона-Котеса (формула прямоугольников, формула трапеций, формула парабол (Симпсона)).
Оборудование:
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
Задание:
Вариант 1 Вариант 2
1.
Вычислите интеграл от заданной функции ![]() на
отрезке
на
отрезке ![]() при делении отрезка на 10 равных
частей тремя способами по формулам: прямоугольников, трапеций, Симпсона.
при делении отрезка на 10 равных
частей тремя способами по формулам: прямоугольников, трапеций, Симпсона.
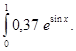
![]()
2.Вычислите
интеграл от заданной функции ![]() на заданном
отрезке способом Гаусса.
на заданном
отрезке способом Гаусса.
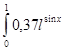
![]()
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Формулы прямоугольников
Формулы прямоугольников имеют вид
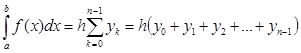 (1)
(1)
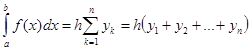 (2)
(2)
![]() (3)
(3)
Формула (1) называется формулой левых прямоугольников (рис. 1 а), а формула (2) – формулой правых прямоугольников (рис. 1 б).
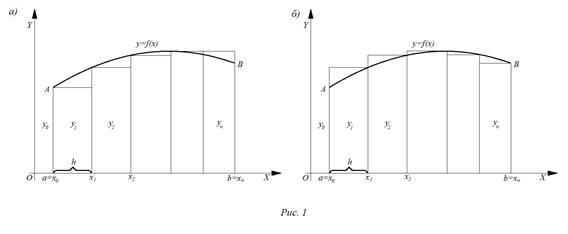
Абсолютная погрешность метода прямоугольников определяется неравенством
![]() (4)
(4)
где
![]() .
.
Формула трапеций.
Формула трапеций имеет вид
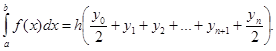 (5)
(5)
где ![]()
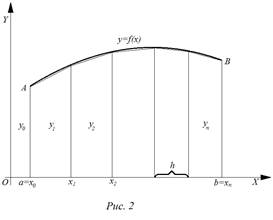
Правая
часть этой формулы выражает площадь фигуры, состоящей из трапеций, высота
каждой из которых равна h (рис 2). Если ![]() - остаточный член приближённой
формулы (5), то
- остаточный член приближённой
формулы (5), то
![]() (6)
(6)
где ![]()
Формула парабол
Формула парабол (или формула Симпсона) имеет вид
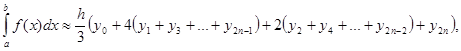 (7)
(7)
![]()
![]() (8)
(8)
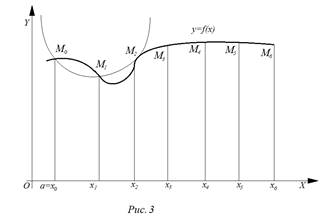
Правая
часть формулы (7) выражает площадь фигуры, составленной из параболических
трапеций ![]() и т.д. (рис. 3). Дуга
и т.д. (рис. 3). Дуга ![]() графика подынтегральной функции
здесь заменена дугой параболы, проходящей через точки
графика подынтегральной функции
здесь заменена дугой параболы, проходящей через точки ![]() .
Аналогичная замена произведена и для остальных дуг.
.
Аналогичная замена произведена и для остальных дуг.
Для остаточного члена формулы (7) выполняется неравенство.
![]() (9)
(9)
где
![]()
При переходе от формулы трапеции к
формуле Симпсона точность вычисления интеграла (при фиксированном значении n) возрастает столь
значительно, потому что возрастает порядок аппроксимации подынтегральной
функции ![]() интерполяционным многочленом:
линейная аппроксимация сменяется на параболическую. При этом метод трапеции
приводит, естественно, к точному значению интеграла, если
интерполяционным многочленом:
линейная аппроксимация сменяется на параболическую. При этом метод трапеции
приводит, естественно, к точному значению интеграла, если ![]() линейна на каждом из отрезков
линейна на каждом из отрезков ![]() , а метод Симпсона - если
, а метод Симпсона - если ![]() квадратична на каждом их этих
отрезков. Выбора узлов
квадратична на каждом их этих
отрезков. Выбора узлов ![]() на исходном отрезке с
точки зрения теории произволен (на практике предпочитают использовать
равностоящие узлы).
на исходном отрезке с
точки зрения теории произволен (на практике предпочитают использовать
равностоящие узлы).
Существует, однако, иной связанный с именем Гаусса, подход к построению квадратурных формул, в котором центральное место играет выбор узлов для интерполирования подынтегральной функции. Ознакомится с этим подходом в его простейшей реализации.
Традиционно при получении квадратурных
формул Гаусса в исходном интеграле выполняется замена переменной, переводящая
интеграл по отрезку ![]() в интеграл по отрезку
в интеграл по отрезку ![]() :
:
![]() , или
, или ![]() (10)
(10)
Тогда
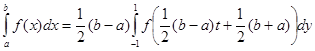 (11)
(11)
и
можно далее, не теряя общности, развивать метод Гаусса применительно к
интегралу вида ![]() .
.
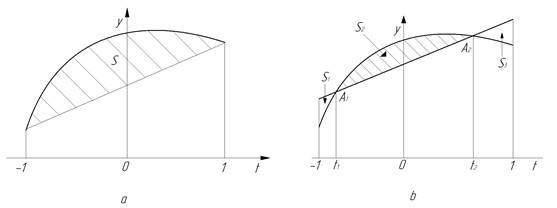
Для разъяснения существа метода Гаусса
обратимся к рис. Будем использовать простейшую (т.е. линейную) интерполяцию
подынтегральной функции. Если в качестве узлов взять концы отрезка ![]() (так делалось при получении
формулы трапеций), то различие в площадях криволинейной трапеции, ограниченной
сверху прямой.
(так делалось при получении
формулы трапеций), то различие в площадях криволинейной трапеции, ограниченной
сверху прямой.
Проведенной через концы указанной кривой![]() , и «обычной» трапеции,
ограниченной сверху прямой, проведённой через концы указанной кривой,
фиксировано видом функции
, и «обычной» трапеции,
ограниченной сверху прямой, проведённой через концы указанной кривой,
фиксировано видом функции ![]() (рис.а). Однако
если сделать узлы интерполяции «подвижными» (рис.б), то можно выбрать их таким
образом, чтобы разносить между площадями криволинейной и «обычной» трапеций
была значительно меньше. Чем в случае а. Более того, можно сделать это площади
равными. Т.е. аппроксимировать интеграл точно, но в уравнения для определения
(рис.а). Однако
если сделать узлы интерполяции «подвижными» (рис.б), то можно выбрать их таким
образом, чтобы разносить между площадями криволинейной и «обычной» трапеций
была значительно меньше. Чем в случае а. Более того, можно сделать это площади
равными. Т.е. аппроксимировать интеграл точно, но в уравнения для определения ![]() и
и ![]() войдёт
точное значение интеграла, т.е. практической пользы такой прием не принесёт.
войдёт
точное значение интеграла, т.е. практической пользы такой прием не принесёт.
Вместо этого сформулируем задачу следующим
образом: выбрать значения ![]() и
и ![]() так, чтобы площадь трапеции,
ограниченной сверху прямой, проходящей через точки
так, чтобы площадь трапеции,
ограниченной сверху прямой, проходящей через точки ![]() и
и
![]() , была равна интегралу от любого
многочлена некоторой (наивысшей возможной) степени. Поскольку положение точек
, была равна интегралу от любого
многочлена некоторой (наивысшей возможной) степени. Поскольку положение точек ![]() и
и ![]() определяют
четыре координаты, то этот многочлен может определяться максимум четырьмя
коэффициентами, т.е. являются многочленом 3-й степени
определяют
четыре координаты, то этот многочлен может определяться максимум четырьмя
коэффициентами, т.е. являются многочленом 3-й степени
![]() (12)
(12)
Легко установить, что уравнение прямой,
проходящей через точки ![]() и
и ![]() , имеет вид
, имеет вид
![]() (13)
(13)
где
![]()
таким образом. Возникает следующая
техническая задача: выбрать ![]() и
и ![]() так, чтобы равенство
так, чтобы равенство
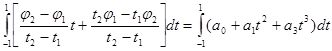 (14)
(14)
имело
место при любых значениях ![]()
Для её решения вычислим интегралы в (5):
![]()
Подставим в этом равенство ![]() и
и ![]()
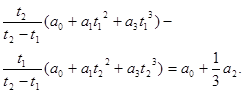
Перегруппируем слагаемые в левой части равенства
![]()
Для того чтобы последнее равенство
выполнялось при любых значениях ![]() необходимо и
достаточно, чтобы
необходимо и
достаточно, чтобы
![]()
![]()
Отсюда следует одно из двух решений:
![]()
![]()
![]()
![]()
Отличающийся
лишь нумерацией значений ![]() и
и ![]() .
.
И так, если взять узлами линейной интерполяции числа
![]()
![]() (15)
(15)
то
интеграл, вычисленный по формуле 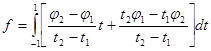 ,точно
совпадает с интегралом от любого многочлена 3-й степени. Вычислив интеграл по
указанной формуле с учётом (6), получим
,точно
совпадает с интегралом от любого многочлена 3-й степени. Вычислив интеграл по
указанной формуле с учётом (6), получим ![]() .
.
Формула
![]() (16)
(16)
применима
к любой (интегрируемой) функции ![]() и называется квадратной
формулой Гаусса. Разумеется, для функции, не являются многочленом не старше
3-й степени, эта формула даёт лишь приближенное значение интеграла. Но
интуитивно ясно, что это значение ближе к истинному, нежели то, которое даёт
формула трапеций, также исходящая из интегрирования вспомогательной линейной
функции вместо исходной.
и называется квадратной
формулой Гаусса. Разумеется, для функции, не являются многочленом не старше
3-й степени, эта формула даёт лишь приближенное значение интеграла. Но
интуитивно ясно, что это значение ближе к истинному, нежели то, которое даёт
формула трапеций, также исходящая из интегрирования вспомогательной линейной
функции вместо исходной.
Воспользовавшись формулой (11), можно для удобства использования записать формулу Гаусса применительно к исходному виду интеграла:
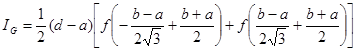 . (17)
. (17)
Формулу доя оценки погрешности вычисления интеграла по методу Гаусса приведём без вывода:
![]() ;
; ![]() . (18)
. (18)
Разумеется, для повышения точности
вычисления интеграла по методу гаусса отрезок![]() можно
так же, как это делалось в методах трапеции и Симпсона, разделить на несколько
можно
так же, как это делалось в методах трапеции и Симпсона, разделить на несколько ![]() частей и применять формулу (6) к
каждому из них. Получим (при делении отрезка на равные части) практически
используемые формулы для вычисления интеграла и оценки погрешности:
частей и применять формулу (6) к
каждому из них. Получим (при делении отрезка на равные части) практически
используемые формулы для вычисления интеграла и оценки погрешности:
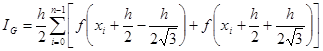 (19)
(19)
![]() (20)
(20)
При практическом использовании формулы Гаусса (19) справедливы те же соображения. Которые привели к полуэмпирической оценке точности результата при двоичном счете.
Отметим, что формула (17) – лишь одна из семейства формул, называемых формулами гаусса для вычисления интегралов. Опираясь на изложенную ранее идею, можно строить квадратные формулы, точные для любого алгебраического многочлена любой нечестной степени.
При выполнении практической работы рассмотрите следующие примеры:
Пример 1.
По формулам
прямоугольников, приняв ![]() , вычислить
, вычислить ![]() .
.
В данном случае ![]() . С помощью формул (3) находим
. С помощью формул (3) находим ![]()
![]()
![]()
По формулам (1) и (2) получаем
![]()
![]()
![]()
Пример 2.
На
сколько частей следует разбить промежуток интегрирования, чтобы с точностью 0,1
вычислить ![]()
Абсолютная
погрешность при вычислении определённого интеграла по методу прямоугольников
определяется формулой (4). Если ставится задача, чтобы ![]() ,
т.е.
,
т.е. ![]() , то
, то ![]() .
В данном случае
.
В данном случае ![]() . Так как
. Так как ![]() ,
, ![]() .
.
![]() , то
, то ![]() .
Поскольку n – целое число,
можно принять
.
Поскольку n – целое число,
можно принять ![]() (для удобства вычислений
можно взять
(для удобства вычислений
можно взять ![]() , так как
, так как ![]() ).
).
Пример 3.
Вычислить
приближённо интеграл ![]() по формуле трапеций,
приняв
по формуле трапеций,
приняв ![]() .
.
В
данном случае по расчетной формуле ![]() , где
, где ![]() , получаем
, получаем ![]() . Так как
. Так как ![]() ,
то
,
то ![]() . Находим значение
. Находим значение![]()
![]()
![]()
![]()
По формуле (5) получаем
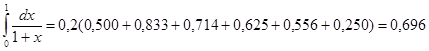
Пример 4.
На
сколько частей нужно разбить промежуток интегрирования, чтобы по формуле
трапеций вычислить интеграл ![]() с точностью
с точностью ![]()
Для
определения числа n отрезков, на которые нужно разбить
промежуток интегрирования, воспользуемся формулой (6). Неравенство ![]() будет выполнено, если
будет выполнено, если ![]() , откуда
, откуда ![]() . Поскольку
. Поскольку ![]() , то
, то ![]() .
Аналогично находим
.
Аналогично находим ![]() .
.
Пример 5.
По
формуле парабол вычислить 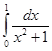 , приняв
, приняв ![]() .
.
По
первой из формул (8) находим ![]() . Составляем
таблицу значений
. Составляем
таблицу значений ![]() (табл. 1). В последней
строке этой таблицы стоят числа, равные суммам чисел, находящихся в
соответствующих столбцах.
(табл. 1). В последней
строке этой таблицы стоят числа, равные суммам чисел, находящихся в
соответствующих столбцах.
Таблица 1.
|
|
|
|
|
|
|
|
0 |
0 |
1,00000 |
1,0 |
|
|
|
1 |
0,125 |
1,01563 |
|
|
|
|
2 |
0,250 |
1,06250 |
|
|
|
|
3 |
0,375 |
1,14063 |
|
|
|
|
4 |
0,500 |
1,25000 |
|
|
|
|
5 |
0,625 |
1,39063 |
|
|
|
|
6 |
0,750 |
1,56250 |
|
|
|
|
7 |
0,875 |
1,76563 |
|
|
|
|
8 |
1,000 |
2,00000 |
0,5 |
|
|
|
|
|
|
1,5 |
3,14678 |
2,38118 |
По формуле (7) получаем:
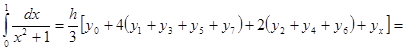
![]()
Пример 6:
Вычислим
интеграл 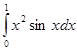 по формуле Гаусса (8) при том же
числе отрезков разбиения (n=10).
по формуле Гаусса (8) при том же
числе отрезков разбиения (n=10).
Составим таблицу значений функции в точках, выходящих в формулу (8) (табл.1).
Таким
образом, согласно (8) ![]() .
.
Сравнивая формулы погрешностей методов Гаусса и Симпсона, видим, что они практически тождественны за
|
|
|
|
|
|
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0 |
0,02113249
0,12113249
0,22113249
0,32113249
0,42113249
0,52113249
0,62113249
0,72113249
0,82113249
0,92113249 |
0,078868
0,178868
0,278868
0,378868
0,478868
0,578868
0,678868
0,0778868
0,878868
0,978868 |
0,00000944 0,00049005
0,00177304 0,00569215
0,01072537 0,02140672
0,03255086 0,05309115
0,07250071 0,10566206
0,13520907 0,18331848
0,22452206 0,28918023
0,34334373 0,42614496
0,49350196 0,59476723
0,67563779 0,79516236
|
|
|
|
|
|
Исключением числового коэффициента, благодаря которому оценка погрешности метода Гаусса благоприятнее в 24 раза.
Вопросы для закрепления теоретического материала к практическому занятию:
1. Запишите формулы прямоугольников для вычислений определённых интегралов.
2. Запишите формулу трапеции для вычисления определённых интегралов.
3. Запишите формулу парабол для вычисления определенных интегралов.
4. На какой основной идее основывается построение квадратных формул Гаусса?
5. Каким способом можно повысить точность вычисления интеграла по методу Гаусса?
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
- Численные методы и программирование: Учебное пособие / В.Д. Колдаев; Под ред. Л.Г. Гагариной. - М.: ИД ФОРУМ: НИЦ Инфра-М, 2016. - 336 с…
- Гателюк, О. В. Численные методы : учеб. пособие для СПО / О. В. Гателюк, Ш. К. Исмаилов, Н. В. Манюкова. — М. : Издательство Юрайт, 2018. — 140 с. — (Серия : Профессиональное образование)
- Бахвалов Н.С., Лапин А.В., Чижонков Е.В. «Численные методы в задачах и упражнениях»/ Под ред. В.А.Садовничего – М.:Высш.шк.,2016
- Вержбицкий В.М. «Численные методы. Математический анализ и обыкновенные дифференциальные уравнения» - М.: Высшая школа, 2017
- Волков Е.А. «Численные методы» - СПб.: Издательство «Лань», 2015
- Исаков В.Н. «Элементы численных методов» - М.: Издательский центр «Академия», 2016.
- Бахвалов Н.С., Лапин А.В., Чижонков Е.В.; Под ред. Садовничий В.А Численные методы в задачах и упражнениях: Учебное пособие /., - 4-е изд., (эл.) - М.:БИНОМ. Лаб. знаний, 2015. - 243 с.: ISBN 978-5-9963-2980-9 - Режим доступа: http://znanium.com/
- А.В. Гулин, О.С. Мажорова, В.А. Морозова Введение в численные методы в задачах и упражнениях : учеб. пособие /. — М. : ИНФРА-М, 2017. — 368 с. — (Высшее образование: Бакалавриат). - Режим доступа: http://znanium.com/
- Калиткин Н.Н., Численные методы: Учебное пособие / - 2-е изд., исправленное. - СПб:БХВ-Петербург, 2015. - 587 с. ISBN 978-5-9775-2575-6 - Режим доступа: http://znanium.com/catalog/product/94450.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.