МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ - Тема: Вычисление погрешностей результатов арифметических действий над приближёнными числами.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Вычисление погрешностей результатов арифметических действий над приближёнными числами.

Цель работы:

-          применить умения вычислять погрешности результатов арифметических действий;

-          применить умения определять количество верных цифр в числе, вычислять относительные и абсолютные погрешности.

Оборудование:

1. Рабочая тетрадь в клетку.

2. Раздаточный материал: инструкционные карты-20шт.

3. Калькулятор простой.

Задание:

Вариант 1

1.      Определить, какое равенство точнее.

а)  или

б)  или

2. Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры

а) в узком смысле 0,2387;

б) в широком смысле 42,884.

Вариант 2

2.      Определить, какое равенство точнее.

а)  или

б)  или

2. Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры

а) в узком смысле 3,751;

б) в широком смысле 0,537.

Порядок выполнения:

1.      Внимательно прочитать тему и цель практической работы.

2.      Изучить учебный материал по теме.

3.      Ответить на вопросы.

4.      Выполнить задания.

5.      Подготовить отчет.

Пояснения к работе (учебный материал):

Приближенным числом a называется число, незначительно отличающееся от точного числа А и заменяющее последнее в вычислениях.

Значащими цифрами приближенного числа называются все цифры его записи, начиная с первой ненулевой слева.

Примеры:

1)      У числа 5142,39 все цифры значащие.

2)      У числа 0,0046 только две значащих цифры: 4 и 6.

3)      У числа 0,004600 четыре значащих цифры: 4, 6 и два последних нуля.

Абсолютная величина разности между точным числом А и его приближенным значением а называется абсолютной погрешностью приближенного числа а ().

.

Пример.

Точное значение числа А часто бывает неизвестно, значит неизвестна абсолютная погрешность числа а, поэтому пользуются понятием границы абсолютной погрешности.

Граница абсолютной погрешности, то есть число заведомо превышающее абсолютную погрешность или в крайнем случае равное ей, называется предельной абсолютной погрешностью .

Значение точного числа А всегда заключено в следующих границах .

Цифра приближенного числа называется верной в широком смысле, если абсолютная (предельная абсолютная) погрешность этого числа не превосходит единицы десятичного разряда, соответствующего этой цифре, в противном случае сомнительной в широком смысле.

Пусть. Определим верные и сомнительные в широком смысле цифры приближенного числа 7,158. Заметим, что . Т.к., то цифра 7 верная в широком смысле. Т.к. , то цифра 1 верная в широком смысле. Т.к. , то цифра 5 верная в широком смысле. Т.к. , то цифра 8 сомнительная в широком смысле.

Цифра приближенного числа называется верной в узком смысле, если абсолютная (предельная абсолютная) погрешность этого числа не превосходит половины единицы десятичного разряда, соответствующего этой цифре, в противном случае сомнительной в узком смысле.

Определим верные и сомнительные в узком смысле цифры приближенного числа 7,158 из предыдущего примера. Т.к. , то цифра 7 верная в узком смысле. Т.к. , то цифра 1 верная в узком смысле. Т.к. , то цифра 5 сомнительная в узком смысле. Очевидно, что цифра 8 также сомнительная в узком смысле.

Относительной погрешностью приближенного числа а называется отношение абсолютной погрешности  к модулю точного числа А.

,

.

            Число  , заведомо превышающее относительную погрешность или в крайнем случае равное ей, называется предельной относительной погрешностью .

.

При выполнении практической работы рассмотрите следующие примеры:

Пример 1.

Определить, какое равенство точнее  или .

Решение.

Находим значения данных выражений с большим числом десятичных знаков:

            Затем вычисляем предельные абсолютные погрешности, округляя их с избытком:

            Предельные относительные погрешности составляют

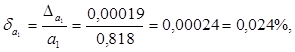
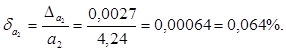
Так как , то первое равенство  является более точным.

Ответ: .

Пример 2.

            Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры

а) в узком смысле 0,4357;

б) в широком смысле 12,384.

Решение.

а) Так как все четыре цифры числа  верны в узком смысле, то предельная абсолютная погрешность вычисляется по формуле

а относительная погрешность

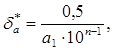
где - количество верных значащих цифр

      - старший десятичный разряд числа

      - цифра числа, причем

Значит,

б) Так как все пять цифр числа  верны в широком смысле, то абсолютная погрешность вычисляется по формуле

а относительная погрешность

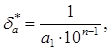
где - количество верных значащих цифр

      - старший десятичный разряд числа

      - цифра числа, причем

Следовательно,

Ответ:

а)

б)

Вопросы для закрепления теоретического материала к практическому занятию:

1. Что такое абсолютная и относительная погрешности?

2. Что такое предельная абсолютная и предельная относительная погрешности?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

- Численные методы и программирование: Учебное пособие / В.Д. Колдаев; Под ред. Л.Г. Гагариной. - М.: ИД ФОРУМ: НИЦ Инфра-М, 2016. - 336 с…

- Гателюк, О. В. Численные методы : учеб. пособие для СПО / О. В. Гателюк, Ш. К. Исмаилов, Н. В. Манюкова. — М. : Издательство Юрайт, 2018. — 140 с. — (Серия : Профессиональное образование)

- Бахвалов Н.С., Лапин А.В., Чижонков Е.В. «Численные методы в задачах и упражнениях»/ Под ред. В.А.Садовничего – М.:Высш.шк.,2016

-  Вержбицкий В.М. «Численные методы. Математический анализ и обыкновенные дифференциальные уравнения» - М.: Высшая школа, 2017

- Волков Е.А. «Численные методы» - СПб.: Издательство «Лань», 2015

- Исаков В.Н. «Элементы численных методов» - М.: Издательский центр «Академия», 2016.

- Бахвалов Н.С., Лапин А.В., Чижонков Е.В.; Под ред. Садовничий В.А Численные методы в задачах и упражнениях: Учебное пособие /., - 4-е изд., (эл.) - М.:БИНОМ. Лаб. знаний, 2015. - 243 с.: ISBN 978-5-9963-2980-9 - Режим доступа: http://znanium.com/

- А.В. Гулин, О.С. Мажорова, В.А. Морозова Введение в численные методы в задачах и упражнениях : учеб. пособие /. — М. : ИНФРА-М, 2017. — 368 с. — (Высшее образование: Бакалавриат). - Режим доступа: http://znanium.com/

- Калиткин Н.Н., Численные методы: Учебное пособие / - 2-е изд., исправленное. - СПб:БХВ-Петербург, 2015. - 587 с. ISBN 978-5-9775-2575-6 - Режим доступа: http://znanium.com/catalog/product/94450.

Скачано с www.znanio.ru