МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ = Тема: Решение показательных, логарифмических уравнений и неравенств.

Тема практической работы №32:

Решение показательных, логарифмических уравнений и неравенств.

Цель работы: 

- применить умения по владению стандартными приемами решения показательных, логарифмических  уравнений и неравенств.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

I Вариант                                                                         II Вариант

1.  Решить показательные уравнения:

а);                                                                        а)

б);                                                                     б)

в)                                                                         в)

2.   Решить логарифмические уравнения:

 а)                                                                   а)

 б)                                                            б)

3.   Решить графически уравнение:

4.Решить показательные неравенства:

а);                                                                                     а)

 б);                                                                      б)

в)                                                                                 в)

5.Решить логарифмические неравенства:

а)                                                                              а)

б)                                                                        б)

6.Решить графически неравенство: 

 а)  >  x - 2;                                                                                 а)  ≤  x - 2;

б)                                                                                  б)

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

Показательными уравнениями называются уравнения, в которых неизвестное содержится в показателе степени.

1)  Простейшие уравнения, т.е. такие, левую и правую части которых можно привести к одному основанию решаются так:

2)   Уравнения вида решаются вынесением за скобки степени с наименьшим показателем.

3)   Уравнения, вида  решаются с помощью подстановки  а^х  = у , сводится к квадратному.

4)   При решения уравнения вида обе части уравнения необходимо разделить на , т.к. ≠  0

.

Уравнения, содержащие неизвестное под знаком логарифма, называются логарифмическими.

Такие уравнения решаются с помощью определения логарифма, теорем о логарифмах и утверждения, что если положительные числа равны, то и равны их логарифмы при данном основании и обратно, если логарифмы чисел равны, то равны и соответствующие им числа. Во всех случаях полученные решения необходимо проверить подстановкой их в данное уравнение и исключить посторонний корень. Часто используется формула перехода от одного основания  к другому

 Решение показательных неравенств сводится к решению простейших неравенств вида 

или

Если   а > 1  и , то  х > b

Если   0 < a < 1 и   ,  то  x  <  b.

При решении простейших логарифмических неравенств типа необходимо использовать следующее правило:

   Если а > 1,  то знак неравенства не меняется, т.е. х > b

   Если  0 < а < 1, то знак неравенства меняется на противоположный, т.е.  х < b.

При решении логарифмических неравенств необходимо проверить, входит ли полученное решение в область определения неравенства.

При выполнении практической работы рассмотрите следующие примеры:

Пример 1:

Решить уравнение: 5^{2x + 1} – 26 · 5^x + 5 = 0

5^x = y,
5y² – 26y + 5 = 0,
D = 676 – 4·25 = 576,
y₁ = 5,     y₂ =
5^x = 5
x = 1,
5^x =
x = – 1

Ответ: x = 1 и x = –1

Пример 2:

Решить уравнение:

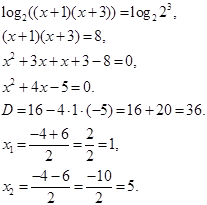
Проверка:

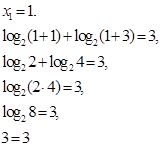
Ответ:3.

Пример 3:

Решить уравнение:

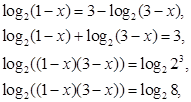
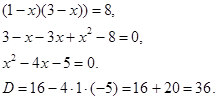
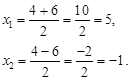
Проверка:

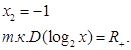                 Ответ: нет корней.

Пример 4:

Решить уравнение:

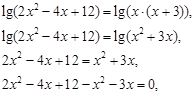
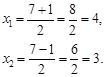
Проверка.

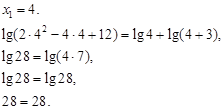
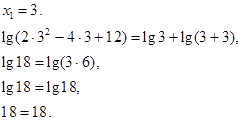
Пример 5:

Решить уравнение:

Проверка.

Ответ: нет корней.

Пример 6:

Решить неравенство   

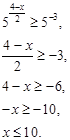
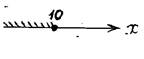
Ответ: 

Пример 7:

Решить неравенство         

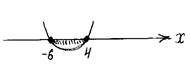
но по условию  у > 0 ,   поэтому получаем   0  ≤  8 ^х ≤ 4

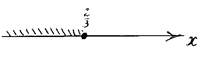
Ответ:   

Пример 8:

Решите неравенство

Логарифмическая функция  - возрастает, т.к.  и , поэтому:

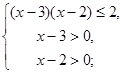
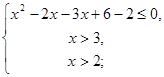
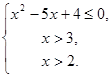
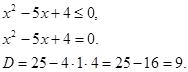
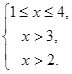
Ответ:

Пример 9:

Решите неравенство

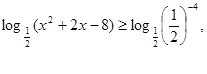
Логарифмическая функция  - убывает, т.к.  и , поэтому:

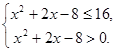
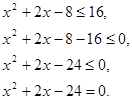
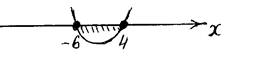
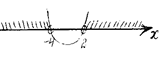
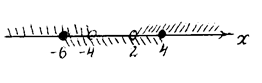
Ответ: .

Вопросы для закрепления теоретического материала к практическому занятию:

1.    Какие уравнения называются показательными?

2.    Какие неравенства называются показательными?

3.    Какие уравнения называются логарифмическими?

4.    Какие неравенства называются логарифмическими?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.