МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Решение задач по теме: «Признаки и свойства параллельных и перпендикулярных плоскостей».

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Решение задач по теме: «Признаки и свойства параллельных и перпендикулярных плоскостей».

Цель работы: 

- применить  умения и навыки применения изученных теоретических фактов в ходе решения задач

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

Вариант 1

№ 1. АВСDA₁В₁С₁D₁ – куб. Точки Е и F – середины ребер АА₁ и СС₁ соответственно. Определите число сторон сечения плоскостью, которая определяется точками В, Е и F.

№ 2. MCDN – ромб, длина стороны которого 4 см; MNKP – параллелограмм. Найдите периметр четырехугольника CDKP, если NK = 8 см и СМР = 60⁰.

№ 3. В треугольной пирамиде МАВС все ребра равны 6 см. Найдите периметр сечения, проведенного параллельно стороне ВС и проходящего через точки А и К, где К – середина ВМ.

№ 4. АВСDA₁В₁С₁D₁ – куб. К – середина АD, М – середина СD. В каком отношении, считая от точки А, делит ребро АА₁ плоскость, проходящая через точки В₁, К и М?

№ 5. КО – перпендикуляр к плоскости α, КМ и КР – наклонные к плоскости α, ОМ и ОР – проекции наклонных, причем сумма их длин равна 15 см. Найдите расстояние от точки К до плоскости α, если КМ = 15 см и КР =  см.

№ 6. Треугольник АВС – прямоугольный, С = 90⁰ , АС = 8 см, ВС = 6 см. Отрезок СD – перпендикуляр к плоскости АВС. Найдите СD, если расстояние от точки D  до стороны АВ равно 5 см.

Вариант 2

№ 1. АВСDA₁В₁С₁D₁ – куб, Е – середина СС₁. Определите число сторон сечения плоскостью, которая проходит через точки А, В₁ и Е.

№ 2. CDЕК – ромб, сторона которого равна 8 см; СКMN – параллелограмм. Найдите периметр четырехугольника DЕМN, если KМ = 6 см и DСN = 60⁰.

№ 3. В треугольной пирамиде SMEF все ребра равны 4 см. Найдите периметр сечения, проведенного параллельно ребру MF и проходящего через точки E и P, где P – середина SF.

№ 4. АВСDA₁В₁С₁D₁ – куб, точка Е – середина СD, F делит ребро  АD в отношении 1 : 3, считая от точки D. В каком отношении делит ребро АА₁ (считая от точки А) плоскость, проходящая через точки В₁, Е и F?

№ 5. ВО – перпендикуляр к плоскости α, ВА и ВС – наклонные, ОА и ОС – их проекции на плоскость α, причем сумма их длин равна 24 см. Найдите расстояние от точки В до плоскости α, если АВ = см и ВС = 12 см.

№ 6. Треугольник АВС – прямоугольный, А = 60⁰, С = 90⁰ . СН – высота треугольника АВС, причем СН = 8 см. Отрезок ВК перпендикуляр к плоскости треугольника АВС. Найдите отрезок ВК, если расстояние от точки К  до стороны АС равно 20 см.

Порядок выполнения:

1.    Внимательно прочитать тему и цель практической работы.

1.        Изучить учебный материал по теме.

2.        Ответить на вопросы.

3.        Выполнить задания.

4.        Подготовить отчет.

Пояснения к работе (учебный материал):

Параллельные плоскости – плоскости, не имеющие общих точек.

Признаки параллельности плоскостей:

1.      Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

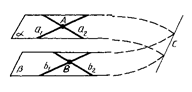
2.      Если две плоскости перпендикулярны одной и той же прямой, то эти плоскости параллельны.

Свойства параллельных плоскостей:

1.      Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны.

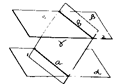
2.      Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.

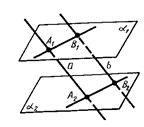
Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен девяноста градусам.                                                                                                   Пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым

Если плоскости   перпендикулярны, то можно также сказать, что плоскость  перпендикулярна к плоскости  или плоскость перпендикулярна к плоскости . Поэтому перпендикулярные плоскости часто называют взаимно перпендикулярными.

В качестве примера перпендикулярных плоскостей можно привести плоскости стены и пола в комнате.

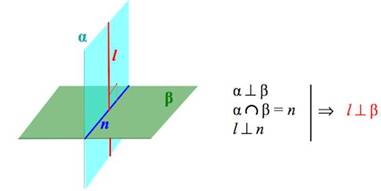
Признак перпендикулярности двух плоскостей

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то заданные плоскости перпендикулярны.

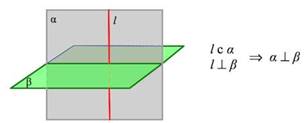
Свойство перпендикулярных плоскостей

Если прямая лежит в одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна второй плоскости. 

При выполнении практической работы рассмотрите следующие примеры:

Пример 1:                                                                                       Дано: ABCD квадрат; AM - прямая; АМ ⊥ (ABCD); АС ∩ BD = О (рис. 1).

Доказать: a) BD ⊥ (АМО); б) МО ⊥ BD.

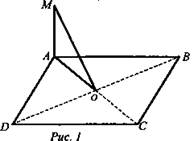
Доказательство:

1) Так как МА ⊥ (ABCD), то МА ⊥ BD (по определению прямой, перпендикулярной плоскости). BD ⊥ AC (по свойству диагоналей квадрата). МА ⊂ (МАО) и АС ⊂ (МАО), МА ∩ АС = А. Следовательно, BD ⊥  (MAO) (по признаку перпендикулярности прямой и плоскости).

2) Так как BD ⊥ (МАО), то BD ⊥ МО, МО ⊂ (МАО) (по определению прямой, перпендикулярной плоскости).

Пример2:

Дано: АВ - отрезок; α; АВ ⊥ α; О - середина АВ, О ∈ α; ХА = ХВ. (рис. 2).

Доказать: X ∈ α.

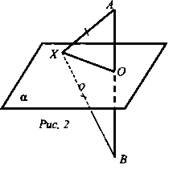
Доказательство:

1) Если X ∈ АВ, то Х = О, и поэтому X ∈ а.

2) Если X ∉ АВ, то ХО - медиана ΔАХВ. ΔАХВ - равнобедренный (по определению), значит, ХО - высота (по свойству медианы равнобедренного треугольника), то есть ХО ⊥ АВ. Таким образом, О ∈ ХО, О ∈ АВ и ХО ⊥ АВ, следовательно, ХО ⊂ а (по задаче № 134) и X ∈ а.

Пример 3:

Параллельные плоскости  и пересекают сторону АВ угла ВАС, соответственно, в точках А₁ и А₂, а сторону АС этого угла, соответственно, в точках В₁ и В₂ (Рис. 1)

Найдите:

а) АА₂ и АВ₂, если А₁А₂=2А₁А=12 см,  АВ₁=5 см., 

б) А₂В₂ и АА₂, если А₁В₁=18 см, АА₁=24 см,

Рис. 1.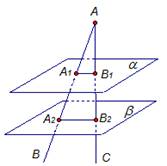

Решение:

а) Пусть А₁А = k, тогда по условию длина А₁А₂=2k =12 см., следовательно, k =6 см. Тогда отрезок АА₂=3k=3∙6=18, т.е. АА₂=18 см.

Две параллельные плоскости и рассечены плоскостью угла ВАС. Из первого свойства следует, что прямые А₁В₁ и А₂В₂ параллельны. Значит, треугольники АА₂В₂ и АА₁В₁ подобны по двум углам (угол ВАС общий, углы АА₁В₁ и АА₂В₂ равны). Из подобия имеем:

 Ответ: АА₂ = 18 см, АВ₂ = 15 см.

б) Пусть А₁А₂ = k, тогда длина отрезка, А по условию. Длина отрезка АА₂ состоит из длин двух отрезков: АА₂=АА₁+ А₁А₂, т.е. получаем уравнение относительно к:

Значит, см.

Из подобия треугольников АА₂В₂ и АА₁В₁ следует, что

см

Ответ: А₂В₂ = 54 см, АА₂ = 72 см.

Вопросы для закрепления теоретического материала к практическому занятию:

1. Какие плоскости называются параллельными?

2. Назовите признаки параллельности плоскостей?

3. Какие плоскости в пространстве называются перпендикулярными?

4. Сформулируйте признак перпендикулярности плоскостей.

5. Приведите примеры перпендикулярных плоскостей.

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.