МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Использование свойств и графиков функций для решения уравнений и неравенств

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Использование свойств и графиков функций для решения уравнений и неравенств

Цель работы: 

- применить умения по владению стандартными приемами решения уравнений и систем.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

Если графики функций пересекаются в одной точке, то уравнение имеет один корень, если в двух, то два решения.

Если графики не пересекаются, то уравнение не имеет корней.

Первый способ графического решения квадратного уравнения заключается в построении параболы y=ax² + bx + c и нахождении корней уравнения ax²+bx+c=0 как абсцисс точек пересечения параболы с осью Оx.

Если парабола пересекает ось Оx в двух точках, то соответствующее уравнение имеет два действительных корня;

если парабола касается оси Оx, то уравнение имеет два равных действительных корня;

наконец, если парабола не пересекает Ось Оx, то уравнение не имеет действительных корней.

Второй способ  графического решения квадратного уравнения заключается в том, что уравнение в виде

При выполнении практической работы рассмотрите следующие примеры:

Пример 1.

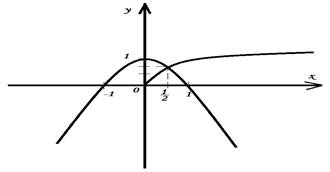Выяснить с помощью графиков, сколько корней имеет уравнение / Найти приближённое значение этих корней.

Решение: Построим на одном рисунке , используя свойства этих функций.

Графики пересекаются в одной точке (≈0,5; ≈0,75)

Ответ: x≈0.5.

Пример 2.

 Решите неравенство

Решение. Неравенство удобно решить графически.

Построим на одном чертеже графики функций , используя свойства функций.

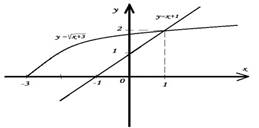
Ответ:  -3  ≤  x  <  1

Пример 3.

Решить неравенство 

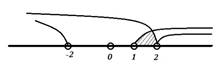
Решение. Неравенство показательное, т.к. , то данное неравенство равносильно неравенству , область определения которого − промежуток   x ≤ 2. При x ≤ 0 оно не имеет решений, т.к. , итак, решения неравенства содержится в промежутке 0  <  x  ≤  2. Возводя неравенство  с обеими положительными частями в квадрат, получаем 2 − x < x², x² + x − 2 > 0  => x < -2 или x > 1.

Пример 4. 

 Решите графически 

Парабола и окружность пересекаются в точках: (-3;4); (0; -5) и (3; 4).

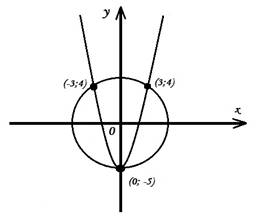
Ответ: (-3;4); (0; -5); (3; 4).

Пример 5.

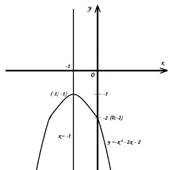
Решить неравенство −x² − 2x −2 < 0.

Рассмотрим функцию  y =−x² − 2x −2

Ветви параболы направлены вниз, т.к. a=−1<0.  Имеем D=b²−4ac=

= (−2)² − 4(−1)∙(−2) = − 4 < 0 => функция не имеет корней. Находим координаты вершины параболы: ,

. Уравнение оси симметрии есть x=−1.

С осью Oy парабола пересекается в точке (0; −2).

Для всех значениях аргумента функции   принимает отрицательные значения => . Если бы мы решали неравенство , то оно не имело бы решений, т.к.  не может принимать положительные значения.

Вопросы для закрепления теоретического материала к практическому занятию:

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

Башмаков М.И. Математика: Учебник. — М., 2016