МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Нахождение наибольшего, наименьшего значения функции. Экстремумы функции.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Нахождение наибольшего, наименьшего значения функции. Экстремумы функции.

Цель работы: 

- применить умения по владению представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

Достаточное условие экстремума. Пусть функция y=f(x) непрерывна на промежутке x и имеет внутри промежутка стационарную или критическую точку x=x₀.

Тогда:

а) если у этой точки существует такая окрестность, в которой выполняется неравенство f '(x)<0. при x<x₀, а при x>x₀ - неравенство f '(x)>0, то x=x₀ - точка минимума;

            б)если у этой точки существует такая окрестность, в которой при x<x₀ выполняется неравенство f '(x)>0, а при x>x₀ - неравенство f '(x)<0, то x=x₀ - точка максимума;

            в) если у этой точки существует такая окрестность, что в ней и слева, и справа от точки x₀ знаки производной одинаковы, то в точке x₀ экстремумов нет.

Алгоритм исследования непрерывной функции y=f(x) на монотонность и экстремумы:

1) Найти производную f '(x)
2) Найти стационарные и критические точки.
3) Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
4) Опираясь на теорему, сделать выводы о монотонности и  точках экстремума.

При выполнении практической работы рассмотрите следующие примеры:

Пример 1:

Исследовать функцию на экстремумы.

Решение. Функция непрерывна, кроме точки x=0.
 1)Найдем производную:

2)x=2  и  x=-2 - стационарные точки. При x=0, производная не существует, это точка разрыва.

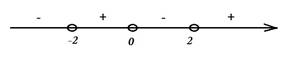3)

4) x=-2 - точка минимума, у_min=8
x=2 - точка максимума, y_min=8.

            Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции y=f(x) на отрезке [а;b]

            1)Найти производную f '(x).

            2)Найти стационарные и критические точки функции, лежащие внутри отрезка [a;b].

            3)Вычислить значение функции y=f(x) в точках, отображаемых на втором шаге и в точках a и b, выбрать среди этих значений наименьшее (y_наим) и наибольшее (это будет y_наиб).

Пример 2. Найти наименьшее и наибольшее значение функции

y=x³-3x²-45x+1 на отрезке [0;6].
Решение. Воспользуемся алгоритмом

 y'=3x²-6x-45                                                 

3x²-6x-45=0

x²-2x-15=0

x₁=-3,      x₂=5

Составим таблицу:

y _наим=-174, y_наиб=1
Пусть функция y=f(x) непрерывна на промежутке х и имеет внутри него единственную стационарную или критическую точку х=х₀
Тогда:
а) если х=х₀ точка максимума, то y_наиб=f(x₀)
б) если x=x₀ точка минимума, то y_наим=f(x₀).

Пример 3. Найти наибольшее значение функции  на луче [0; +∞).

Решение . . Производная всюду существует, значит, критических точек у функции нет. y’=0, 1-x²=0, x=1 или x=-1.

Заданному лучу  При x >1, y’>0, а при x >1, y’<0.

Значит, x = 1 – точка максимума .

x=1 – единственная стационарная точка функции на заданном промежутке, причём точка максимума.

Вопросы для закрепления теоретического материала к практическому занятию:

1.      Какая точка называется точкой максимума?

2.      Какая точка называется точкой минимума?

3.      Перечислите правила дифференцирования.

4.      Назовите алгоритм нахождения наибольшего и наименьшего значения функции на отрезке.

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.