Поделиться
Практическая работа по математике №22.docx
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО
Разработал преподаватель: Игнатьева Елена Сергеевна
Тема:
Преобразование суммы тригонометрических функций в произведение, преобразование произведения тригонометрических функций в сумму
Цель работы:
- применить умения в упрощении тригонометрических выражений, применяя основные формулы тригонометрии для вычисления значений.
Оборудование:
1. Рабочая тетрадь в клетку
2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.
3. Калькулятор простой.
4. Ручка.
Задание:
Вариант 1.
1. Вычислить, используя формулы приведения, сложения:
б) 
2. Известно, что 
Найдите
.
3. Упростить выражения:
а) 
б) 
4. Доказать тождество: 
5. Найдите значение x (в радианах), если х находится в первой четверти и
6. Вычислите без помощи таблиц:
Вариант 2.
1. Вычислить, используя формулы приведения, сложения:
б) 
2. Известно, что 
Найдите
.
3. Упростить выражения:
а) 
б) 
4. Доказать тождество: 
.
5. Найдите значение 
(в радианах), если х
находится в первой четверти и
6. Вычислите без помощи таблиц:
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Определение. Тригонометрия (от греч. trígōnon — треугольники metréo — измеряю), раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии.
Тригонометрические тождества — математические выражения для тригонометрических функций, которые выполняются при всех значениях аргумента.
Основные формулы тригонометрии
Перевод градусной меры угла в радианную и обратно.
Пусть α — градусная мера угла, β — радианная, тогда справедливы формулы:
|
|
|
Формулы зависимости между функциями одного и того же аргумента.
|
1. |
|
4. |
|
|
2. |
|
5. |
|
|
3. |
|
6. |
|
Формулы сложения.
|
|
|
|
|
|
Формулы двойных и половинных углов.
|
1. |
|
5. |
|
|
2. |
|
6. |
|
|
3. |
|
7. |
|
|
4. |
|
8. |
|
Формулы преобразования суммы в произведение:
|
|
|
|
|
|
|
|
|
|
|
|
Формулы преобразования произведения в сумму:
|
|
|
|
|
|
Формулы приведения:
|
|
|
|
|
|
|
|
|
|
|
|
sin φ |
- sin α |
cos α |
cos α |
sin α |
- sin α |
- cos α |
- cos α |
- sin α |
sin α |
|
cos φ |
cos α |
sin α |
- sin α |
- cos α |
- cos α |
- sin α |
sin α |
cos α |
cos α |
|
tg φ |
- tg α |
ctg α |
- ctg α |
- tg α |
tg α |
ctg α |
- ctg α |
- tg α |
tg α |
|
ctg φ |
- ctg α |
tg α |
- tg α |
- ctg α |
ctg α |
tg α |
- tg α |
- ctg α |
ctg α |
При выполнении практической работы рассмотрите следующие примеры:
Пример 1:
Упростить выражение: 
.
Так как числитель заданной дроби имеет достаточно простой вид, начнем с
упрощения знаменателя. Для этого применим представление 
Приведем полученную разность дробей
к общему знаменателю: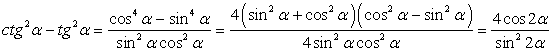 
Следовательно:
Пример 2:
Найти значение следующих тригонометрических выражений: sin 2α, cos 2α, tg 2α, если
Решение: Выпишем формулы для вычисления искомых функций:
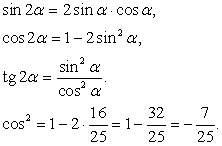
Далее найдем значение искомых функций:
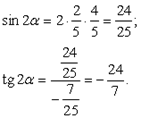
Пример 3:
Доказать тождество:
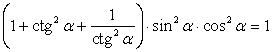
Решение:
=1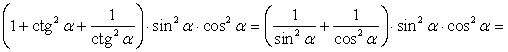
Тождество доказано.
Пример 4:
Вычислить sin10º sin30º sin50º sin70º Используем формулу преобразования произведения тригонометрических функций в сумму: sin10º sin50º = 1/2 (cos40º - cos60º ) = 1/2 cos 40º - 1/4. Подставим в первоначальное произведение это выражение и учтем, что sin30º = 1/2, получаем:
Вопросы для закрепления теоретического материала к практическому занятию:
1.Что такое тригонометрия?
2.Перечислите формулы зависимости между функциями одного и того же аргумента.
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.
2. Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.
3. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
4. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
5. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
6. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
7. Башмаков М.И. Математика: Учебник. — М., 2016.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
