
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО
Разработал преподаватель: Игнатьева Елена Сергеевна
Тема:
Преобразования графика функции. Гармонические колебания. Прикладные задачи.
Цель работы:
- применить умения по выполнению преобразований графиков функций.
Оборудование:
1. Рабочая тетрадь в клетку
2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.
3. Калькулятор простой.
4. Ручка.
Задание:
I Вариант II Вариант
1. Построить графики функций.
а) ![]() а)
а)
![]()
б) ![]() б)
б)
![]()
в)![]() в)
в) ![]()
г) ![]() г)
г)
![]()
2. Найти все корни уравнения, принадлежащие отрезку [0; 3π] :
![]()
![]()
3.Найти все решения неравенства, принадлежащие отрезку [0; 3π] :
![]()
![]()
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Простейшие преобразования графиков - это параллельный перенос, сжатие (растяжение) и различные виды симметрии.
|
№ |
Функция |
Преобразование |
Графики |
|
1 |
|
Сначала строим график функции |
|
|
2 |
|
Сначала строим график функции |
|
|
3 |
|
Сначала строим график функции |
|
|
4 |
|
Сначала строим график функции "−" − → "+" − ← |
|
|
5 |
|
Сначала строим график функции |
|
|
6, 7
|
|
Сначала строим график функции
|
|
|
8 |
|
Сначала строим график функции |
|
|
9 |
|
Сначала строим график функции |
|
|
10 |
|
|
|
Построение графиков тригонометрических функций с помощью тригонометрических преобразований.
Это случай когда АРГУМЕНТ функции умножен на число, больше единицы.
Правило:
чтобы построить график функции ![]() , где
, где ![]() , нужно график функции
, нужно график функции ![]() сжать к оси
сжать к оси![]() в
в ![]() раз.
раз.
Правило:
чтобы построить график функции ![]() , где
, где ![]() , нужно график функции
, нужно график функции![]() растянуть от оси
растянуть от оси ![]() в
в ![]() раз.
раз.
Это
противоположное действие, теперь баян не сжимается, а растягивается.
Случай имеет место, когда АРГУМЕНТ функции умножается на число ![]()
Операции сжатия/растяжения графиков, разумеется, выполнимы не только для тригонометрических функций.
При выполнении практической работы рассмотрите следующие примеры:
Пример 1:
Построить график функции ![]() .
.
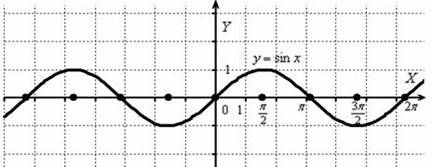
Сначала изобразим график синуса,
его период равен ![]() :
:
К слову, чертить графики тригонометрических функций вручную – занятие
кропотливое, поскольку ![]() и т.д., то есть
на стандартной клетчатой бумаге аккуратным нужно быть вплоть до миллиметра,
даже до полумиллиметра. Впрочем, многие с этим уже столкнулись.
и т.д., то есть
на стандартной клетчатой бумаге аккуратным нужно быть вплоть до миллиметра,
даже до полумиллиметра. Впрочем, многие с этим уже столкнулись.
Теперь поиграем на бесконечно
длинном баяне. Мысленно возьмём синусоиду в руки и сожмём её к оси
![]() в
2 раза:
в
2 раза:
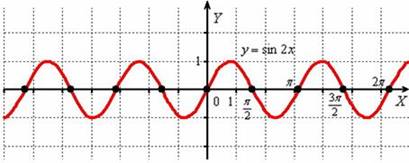
То есть, график функции ![]() получается путём
сжатия графика
получается путём
сжатия графика ![]() к оси ординат в два
раза. Логично, что период итоговой функции тоже уполовинился:
к оси ординат в два
раза. Логично, что период итоговой функции тоже уполовинился: ![]() .
.
В целях самоконтроля можно взять
2-3 значения «икс» и устно либо на черновике выполнить подстановку:
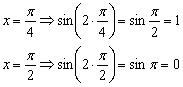
Смотрим на чертёж, и видим, что это действительно так.
Пример 2:
Построить график функции ![]()
«Чёрная гармошка» ![]() сжимается к оси
сжимается к оси ![]() в 3 раза:
в 3 раза:
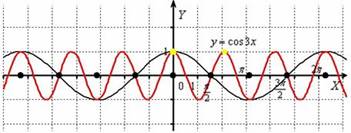
Итоговый график ![]() проведён красным цветом.
проведён красным цветом.
Исходный период ![]() косинуса закономерно
уменьшается в три раза:
косинуса закономерно
уменьшается в три раза: ![]() (отграничен
жёлтыми точками).
(отграничен
жёлтыми точками).
Пример 3:
Построить график функции ![]()
Берём в руки нашу «бесконечную
гармошку»:
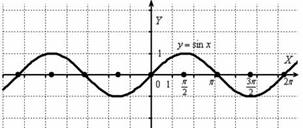
И растягиваем её от оси ![]() в 2 раза:
в 2 раза:
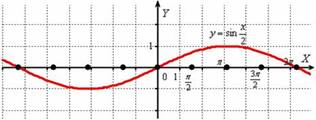
То есть, график функции ![]() получается путём растяжения
графика
получается путём растяжения
графика![]() от оси ординат в
два раза. Период итоговой функции увеличивается в 2 раза:
от оси ординат в
два раза. Период итоговой функции увеличивается в 2 раза: ![]() , он толком даже не вместился на
данный чертёж.
, он толком даже не вместился на
данный чертёж.
Вопросы для закрепления теоретического материала к практическому занятию:
1. Какие простейшие преобразования графиков вы знаете?
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.
2. Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.
3. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
4. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
5. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
6. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
7. Башмаков М.И. Математика: Учебник. — М., 2016.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.