МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Приближенные вычисления и решения прикладных задач.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Приближенные вычисления и решения прикладных задач.

Цель работы: 

- применить умения по владению методами доказательств и алгоритмов решения, умение их применять, проводить  доказательные рассуждения в ходе  решения  задач.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

Вариант 1.

№1

№2

В начальный момент времени было 8 бактерий. Через 2 часа после помещения бактерий в питательную среду, их число возросло до 100. Через сколько времени с момента размещения в питательную среду следует ожидать появления 500 бактерий?

№3

Вариант 2.

№1

№2

№3

Для обогрева помещения, температура в котором равна Т_п = 20⁰С, через радиатор отопления, пропускают горячую воду температурой  Т_в = 100⁰С. Расход проходящей через трубу воды m = 0,2 кг/с. Проходя по трубе расстояние x (м), вода охлаждается до температуры Т⁰С, при чём

где с = 4200Дж/кг*С — теплоемкость воды

 = 42 Вт/м ^{* 0}С— коэффициент теплообмена

a = 1,4 — постоянная.

До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 28 м?

 Порядок выполнения:

1.    Внимательно прочитать тему и цель практической работы.

2.    Изучить учебный материал по теме.

3.    Ответить на вопросы.

4.    Выполнить задания.

5.    Подготовить отчет.

Пояснения к работе (учебный материал):

Свойства логарифмов:

1° - основное логарифмическое тождество.

2°

3°

Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.

4° - логарифм произведения.

Логарифм произведения равен сумме логарифмов сомножителей.

5° - логарифм частного.

Логарифм частного (дроби) равен разности логарифмов сомножителей.

6° - логарифм степени.

Логарифм степени равен произведению показателя степени на логарифм ее основания.

7°

8°

9° - переход к новому основанию.

При выполнении практической работы рассмотрите следующие примеры:

Пример 1:

Ёмкость высоковольтного конденсатора в телевизоре C = 5∙10^-6Ф. Параллельно с конденсатором подключен резистор с сопротивлением R = 2∙10 Ом. Во время работы телевизора напряжение на конденсаторе U₀ = 25 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за  время,   определяемое  выражением:

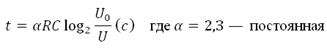
Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 46 с.   

Нам необходимо найти наибольшее возможное U на конденсаторе, при условии, что прошло не менее  46 секунд, то есть t ≥ 46.

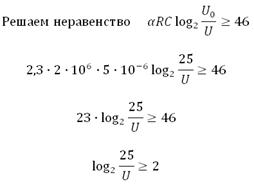
Двойку представим в виде логарифма с основанием 2:

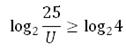
Знаки логарифмов мы можем снять, так как основания логарифмов в обеих частях равны. Знак неравенства не изменяется, так как основание логарифма больше единицы. Таким образом, далее будем неравенство:

Напряжение величина положительная, знак неравенства не меняется (при умножении частей неравенства на отрицательное число знак изменяется на противоположный):

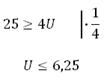
Наибольшее возможное напряжение на конденсаторе 6,25 кВ.

Ответ: 6,25

Пример 2:

Находящийся в воде водолазный колокол, содержащий υ = 6 моля  воздуха при давлении p₁ = 2,5 атмосферы, медленно опускают на дно водоема. При этом происходит изотермическое сжатие воздуха. Работа, совершаемая водой при сжатии воздуха, определяется выражением:

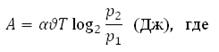
α = 5,75— постоянная — постоянная

Т = 300К — температура воздуха

p₁ (атм) — начальное давление 

p₂ (атм) — конечное давление воздуха в колоколе.

До какого наибольшего давления p₂ можно сжать воздух в колоколе, если при сжатии воздуха совершается работа не более чем 10350 Дж? Ответ приведите в атмосферах.          

Сказано, что «совершается работа не более, чем 10350 Дж», то есть максимальная работа, которая совершается при сжатии воздуха это 10350 Дж. Наибольшее давление будет достигнуто именно при максимальной работе, поэтому подставив все известные величины в выражение,  решим уравнение и найдём  p₂:

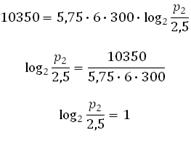
Используем понятие основного логарифмического тождества:

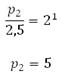
При заданных условиях воздух можно сжать до 5 атмосфер.

Ответ: 5

Пример 3:

Водолазный колокол, содержащий в начальный момент времени υ = 4 моля воздуха объемом V₁ = 15л, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного объёма V₂. Работа, совершаемая водой при сжатии воздуха, определяется выражением:

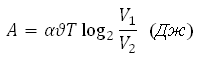
где α = 9,15— постоянная

Т = 300К— температура воздуха.

Какой объём V₂ (в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 10980 Дж.

В данной задаче необходимо найти V₂, подставив все известные значения в формулу:

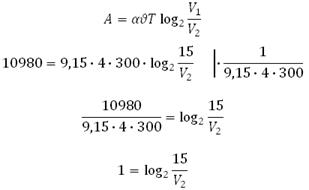
В отличие от уже решённых задач, так можно использовать определение основного логарифмического тождества:

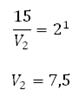
Воздух станет занимать 7,5 литра.

Ответ: 7,5

Пример 4:

Для обогрева помещения, температура в котором равна Т_п = 20⁰С, через радиатор отопления, пропускают горячую воду температурой  Т_в = 100⁰С. Расход проходящей через трубу воды m = 0,2 кг/с. Проходя по трубе расстояние x (м), вода охлаждается до температуры Т⁰С, при чём

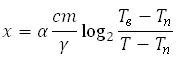
где с = 4200Дж/кг∙С — теплоемкость воды

γ = 42 Вт/м∙⁰С— коэффициент теплообмена

α = 1,4 — постоянная.

До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 28 м?

В данном случае необходимо решить уравнение:

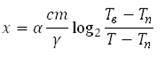
Найдём Т,  подставив  все  известные значения:

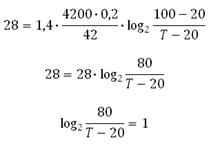
Единицу представим в виде логарифма с основанием 1:

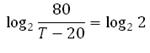
Так как основания логарифмов равны, то равны их подлогарифмические выражения:

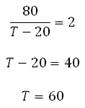
Вода охладится до температуры 60 градусов Цельсия.

Ответ: 60

Вопросы для закрепления теоретического материала к практическому занятию:

1.    Перечислите свойства логарифма?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.

Скачано с www.znanio.ru