МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Применение интеграла к вычислению физических величин и площадей.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Применение интеграла к вычислению физических величин и площадей.

Цель работы: 

- применить умения по владению представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

Дадим математическое описание той модели, которая была построена для функции y= f(x), непрерывной на отрезке [a;b].

1)        разбивают отрезок [a;b] на n равных частей.

2)        составляем сумму S_n = f(x₀)∆x₀ + f(x₁)∆x₁ + ...+ f(x_n-1)∆x_n-1.

3)        вычисляем    

Этот предел называют определённым интегралом от функции y= f(x) на отрезке [a;b] и обозначают так :

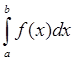
числа a и b  называют пределами интегрирования (соответственно нижним и верхним).

При выполнении практической работы рассмотрите следующие примеры:

Пример 1. Вычислить площадь фигуры, ограниченной полуволной синусоиды y=sin x и осью абсцисс.

Решение:

Можно взять полуволну синусоиды от точки x=0 до точки x= при следующих условиях: a=0, x=, f(x)=sin x.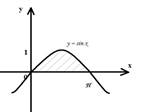

Пример 2. Вычислить площадь фигуры, ограниченной линиями y = x, y = 5-x, x=1, x=2.

Решение: Фигура, площадь которой надо найти, изображена на рисунке.

Воспользовавшись формулой Ньютона - Лейбница, получим

Ответ: S = 2.

Пример 3. Сила тока вычисляется по формуле  J . Определите количество электричества, протекшее через поперечное сечение проводника за 10 секунд, считая время от начала опыта.

Решение:  Q 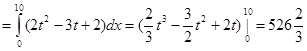k

Пример 4. Тяжелая цепь длиною L = 200м поднимается, навиваясь на ворот. Определить работу силы веса при поднятии цепи, пренебрегая размерами ворота, если погонный метр цепи весит 50 кг.

Решение. Пусть к некоторому моменту времени на ворот навернулся отрезок цепи длиной L-x. Весит эта часть (L-x)∙50кг. Элементарная работа силы веса на перемещение dx будет равна  A=-(L-x)∙50dx.

(«−» так как сила веса направлена на противоположно перемещению) Полную работу найдём как интеграл от элементарной работы

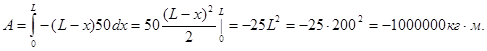
Вопросы для закрепления теоретического материала к практическому занятию:

1.        Какой интеграл называется определённым?

2.        Перечислите свойства определённого интеграла.

3.        Алгоритм вычисления площадей заштрихованных фигур.

4.        Какой интеграл называется неопределённым?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.