МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Применение свойств параллельного проектирования для построений и вычисление площади ортогональной проекции многоугольника

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Применение свойств параллельного проектирования для построений и вычисление площади   ортогональной проекции многоугольника

Цель работы: 

- применить  умения и навыки решения задач на вычисление площади   ортогональной проекции многоугольника.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

Вариант 1.

Задача 1                                                                                                                                                            Стороны основания прямого параллелепипеда равны 4 и 5, угол между ними равен 30°. Найти площадь сечения параллелепипеда плоскостью, пересекающей все его боковые рёбра и образующей с плоскостью основания угол в 45°

Задача 2.

Стороны основания треугольной пирамиды равны 6см, 10см и 14см. Каждый двугранный угол при её основании равен 30°. Найти площадь боковой поверхности.

Задача 3.

В правильной усечённой четырёхугольной пирамиде стороны нижнего и

верхнего оснований равны соответственно a и b (a> b). Найти площадь полной поверхности усечённой пирамиды, если её боковые  грани наклонены к плоскости основания под углом a.

Задача 4.                                                                                                                                Основанием пирамиды является прямоугольный треугольник, катеты которого равны 3 и 4. Каждая боковая грань пирамиды наклонена к плоскости основания под углом в 60°. Найти площадь полной поверхности пирамиды.

Вариант 2.

Задача 1.                                                                                                                                                            В правильной четырёхугольной призме сторона основания равна 4см. Через диагональ основания под углом 45°к плоскости основания проведена плоскость, пересекающая боковое ребро. Найти площадь сечения.

Задача 2.                                                                                                                                                     Боковые грани пирамиды, в основании которой лежит ромб, наклонены к плоскости основания под углом 30°. Диагонали ромба равны 10 см и 24 см. Найти площадь боковой поверхности пирамиды.

Задача 3                                                                                                                                                              В правильной четырёхугольной призме через диагональ основания под углом 30°к плоскости основания проведена плоскость, пересекающая боковое ребро. Найти диагональ основания, если площадь сечения равна 38см2

Задача 4.

Основанием пирамиды является ромб с диагоналями 6 и 8. Высота пирамиды равна

1. Найти площадь полной поверхности этой пирамиды, если все двугранные углы при её основании равны.

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

1.        Ответить на вопросы.

2.        Выполнить задания.

3.        Подготовить отчет.

Пояснения к работе (учебный материал):

Параллельное проектирование, при котором проектирующие прямые перпендикулярны к плоскости проекций, называется ортогональным.

Ортогональной проекцией  фигуры на данную плоскость называют множество точек

пересечений с этой плоскостью перпендикулярных к ней прямых, проходящих через все

точки этой фигуры

Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекций.

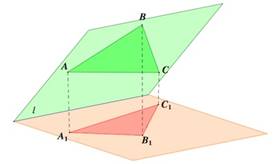
При выполнении практической работы рассмотрите следующие примеры:

Задача.

Ребро куба равно 2 см. Через диагональ основания под углом к плоскости основания проведена плоскость, пересекающая боковое ребро. Найти площадь сечения.

Решение:

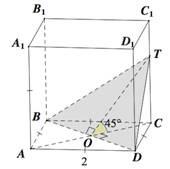
Пусть плоскость сечения проведена через диагональ ВД и пересекает боковое ребро СС₁

в точке Т. =  ВСД– проекция треугольника ВТД на плоскость основания, — угол между плоскостями ВСД

где треугольник, ВТД

 =  =2

Ответ: 2

Вопросы для закрепления теоретического материала к практическому занятию:

1. Что называют ортогональной проекцией  фигуры?

2. Чему равна площадь ортогональной проекции многоугольника на плоскость?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.