МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Радианный метод измерения углов вращения и связь с градусной мерой

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Радианный метод измерения углов вращения и связь с градусной мерой

Цель работы: 

- применить  умения установления связи радианного метода измерения углов вращения с градусной мерой.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

Вариант 1.

1. Выразите в радианах углы, равные 225°, 45°, 60°, 90°, 180°, 320°, 140°.

2.      Переведите из градусной меры в радианную: 120°; 220°; 300°;  765°;

3.      Выразите в градусах: 2,5p;  4p; 1,25p; 7p;

4. Окружность разделена на шесть равных частей. Выразить в градусах и радианах сумму:  2-х дуг; 7 дуг; 4-х дуг.
5. Угол А трапеции ABCD (AD || BC) на 70° меньше угла В и на 10° больше угла D. Найдите радианную меру каждого из углов трапеции.

Вариант 2.

1. Выразите в радианах углы, равные 240°, 45°, 60°, 18°, 330°, 30°, 120°.
2. Переведите из градусной меры в радианную: 210°;  150°;  315°;  675°.

3.      Выразите в градусах: 1,5p;  3p; 0,25p;  p;     

4.      Окружность разделена на двенадцать равных частей. Выразить в градусах и радианах сумму:  2-х дуг; 7 дуг; 4-х дуг.

5.      Угол А трапеции ABCD (AD || BC) на 60° меньше угла В и на 200° больше угла D. Найдите радианную меру каждого из углов трапеции.

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

Углы, получающиеся при непрерывном вращении, удобно измерять не в градусах, а с помощью таких чисел, которые отражали бы сам процесс построения угла, т.е. вращение.
Для описания непрерывного вращения градусная мера угла поворота становится неудобной – с ней трудно связывать другие характеристики движения, например, скорость или соединять вращательное движение с иными движениями. Поэтому вводят другую меру угла поворота, так называемую радианную меру.

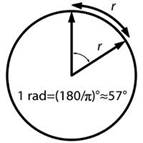
Углом в 1 радиан называется центральный угол, который опирается на дугу, равную радиусу:      

.

 Соотношение между радианной и  градусной мерой измерения угла выражается равенством:

ß°∏=180°x,

где ß° - градусная мера измерения угла, x- радианная мера. Например, чтобы определить, сколько градусов содержит угол ∏/10 радиан, нужно в равенство вместо х подставить ∏/10. Получим:

ß°∏=180°∏/10  (1)

ß°=18°. Чтобы определить, сколько радиан содержит угол 60°, надо в равенство (1) вместо ß° поставить 60°:

60°∏=180°х

x=∏/3.

При выполнении заданий рассмотрите таблицу и формулы:

Таблица соответствия между радианной и градусной мерой измерения углов выглядит так:

Угол в радианах        Угол в градусах

      0                              0

     ∏/6                         30°

     ∏/4                          45°

     ∏/3                          60°

     ∏/2                          90

       ∏                         180°

     2∏                         360°

∏/180                           1°

Вопросы для закрепления теоретического материала к практическому занятию:

1.      Чему равен один радиан?

2.      Как перевести градусную меру угла в радианную?

3.      Как перевести радианную меру угла в градусную?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.