МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Решение иррациональных уравнений.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Решение иррациональных уравнений.

Цель работы: 

- применить умения по владению стандартными приемами решения иррациональных уравнений.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

Определение. Уравнение с одной переменной  называют иррациональным, если хотя бы одна из функций  или  содержит переменную под знаком радикала.

При решении иррациональных уравнений необходимо установить область допустимых значений переменных, исходя из условия, что все радикалы, входящие в уравнение, должны быть арифметическими.

1. Метод пристального взгляда

Этот метод основан на следующем теоретическом положении: “Если функция возрастает в области определения и число  входит в множество значений, то уравнение  имеет единственное решение.”

Для реализации метода, основанного на этом утверждении требуется:

а) Выделить функцию, которая фигурирует в уравнении.

b) Записать область определения данной функции.

c) Доказать ее монотонность в области определения.

d) Угадать корень уравнения.

t) Обосновать, что других корней нет.

f) Записать ответ.

2. Метод возведения обеих частей уравнений в одну и ту же степень.

Теорема.

Если возвести обе части уравнения  (1) в натуральную степень , то уравнение  (2) является следствием уравнения (1).

Доказательство. Если выполняется числовое равенство , то по свойствам степени выполняется равенство , т.е. каждый корень уравнения (1) является и корнем уравнения (2), это значит, что уравнение (2) является следствием уравнения (1).

Если , то справедливо и обратная теорема. В этом случае уравнения (1) и (2) равносильны.

Если , равенство  справедливо, если выполняется хотя бы одно из равенств и . Значит уравнения (1) и (2) в этом случае не равносильны. Поэтому, если в ходе решения иррационального уравнения  приходилось возводить обе его части в степень с четным показателем, то могли появиться посторонние корни. Чтобы отделить их, проверки можно избежать, введя дополнительное требование . В этом случае уравнение  равносильно системе 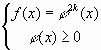. В системе отсутствует требование , обеспечивающее существование корня степени , т.к. оно было бы излишним в связи с равенством .

3. Решение уравнений с использованием замены переменной.

Введение вспомогательной переменной в ряде случаев приводит к упрощению уравнения. Чаще всего в качестве новой переменной используют входящий в уравнение радикал. При этом уравнение становится рациональным относительно новой переменной.

4. Метод разложения на множители выражений, входящих в уравнение.

Теорема.

Уравнение , определенное на всей числовой оси, равносильно совокупности уравнений 

5. Метод выделения полных квадратов при решении иррациональных уравнений.

При решении некоторых иррациональных уравнений полезна формула 

6. Метод оценки.

Этот способ применим в том случае, когда подкоренные выражения представляют собой квадратный трехчлен, не раскладывающийся на линейные множители. Поэтому целесообразно оценить левую и правую части уравнения.

7. Иррациональные уравнения, содержащие степени выше второй.

Если уравнение имеет вид то его можно решить , возводя обе части этого уравнения в степень . Полученное уравнение  при нечетном равносильно данному уравнению, а при четном является нго следствием, аналогично рассмотренному выше случаю при

При выполнении практической работы рассмотрите следующие примеры:

Пример 1:

Решение:

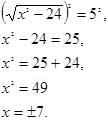
Проверка:

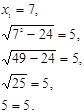
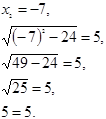
Ответ:

Пример 2:

Решение:

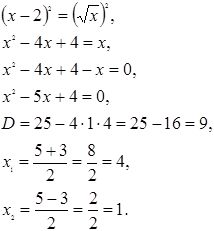
Проверка:

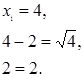
- не является корнем,

Ответ: 4.

Пример 3:

.

Решение:

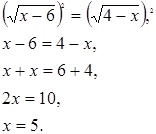
Проверка:

х = 5 – не является корнем, т.к. левая часть уравнения не определена при x=5.

Ответ: нет корней.

Вопросы для закрепления теоретического материала к практическому занятию:

1.Какое уравнение называется иррациональным?

2.Какие методы решения иррациональных уравнений вы знаете? В чем их суть?

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.