МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Решение простейших тригонометрических уравнений и неравенств.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Решение простейших тригонометрических уравнений и неравенств.

Цель работы: 

- применить умения по владению стандартными приемами решения тригонометрических уравнений и неравенств.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:                 

I Вариант                                                                           II Вариант

1.Решить уравнения:      

2.Найти нули функции:

3. Решить уравнение  и найти                                                       

4. Решить неравенства:

а)                                                            а)

б)                                               б)

в)                                                           в)

5. Найти значение x при которых график функции

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

1. Из определения косинуса следует, что . Поэтому, если  а  >1, то уравнение cosx=a не имеет решения. Например, уравнение cosx=-1,5 не имеет корней.

Если cosx=0,  .

Если cosx=-1, то х = π+2πn, n Є z.

Если cosx=1 , то x=2πn, n Є z.

Если cosx=a, где ,то x= arccos a + 2πn, n Є z.

2.Из определения синуса следует, что

sin α Є [ -1; 1] . Поэтому уравнение

sin x = 3 не имеет корней.

Если sin x = 0 , то x = πn, n Є z.

Если sin x = 1 , то.

Если sin x = -1 ,то

sin x = a ,  1

x = (1)^k arcsin a +πk , k Є z

3. Из определения тангенса следует , что  tg x может принимать любое действительное  значение. Поэтому уравнение  tg x = a имеет корни при любом значении a.

x = arctg a + πn , n Є z

tg x = 0 , x = πn , n Є z

tg x = 1 , x =  + πn , n Є z

tg x = -1 , x = -  +πn , n Є z

4. Из определения котангенса следует, что ctgx может принимать любое значение. Поэтому уравнение ctgx = a имеет корни при любом значении а.

x = arcctg a + πn, n Є z.

5. Решения простейших тригонометрических неравенств выполняем с помощью единичной окружности.

При выполнении практической работы рассмотрите следующие примеры:

Пример 1:

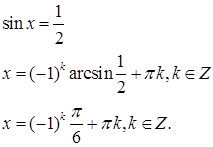
Пример 2:

Ответ:

Пример 3:

 –наименьший положительный корень

Ответ:

Пример 4:

Найти нули функции  

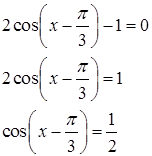
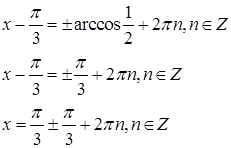
Ответ:

Пример 5:

 –наименьший положительный корень

Ответ:

Пример 6:

2cosx ≥ 1;

cosx ≥

x Є , n Є z

Пример 7:

 2cosx <;

cosx <

x Є

в) sinx >

x Є

г) tgx ≥ 1

x Є

Вопросы для закрепления теоретического материала к практическому занятию:

1. Сформулируйте определение косинуса.

Запишите общую формулу решения уравнения cosx = a.

2. Сформулируйте определение синуса.

Запишите общую формулу решения уравнения sinx = a.

3. Запишите формулу решения уравнения tgx = a.

4. Перечислите алгоритм решения простейшего тригонометрического уравнения.

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.