Поделиться
Практическая работа по математике №33.docx
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО
Разработал преподаватель: Игнатьева Елена Сергеевна
Тема:
Решение тригонометрических уравнений и неравенств.
Цель работы:
- применить умения по владению стандартными приемами решения тригонометрических уравнений и неравенств.
Оборудование:
1. Рабочая тетрадь в клетку
2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.
3. Калькулятор простой.
4. Ручка.
Задание:
I Вариант II Вариант
1. Решите уравнения:
1) 
1)
2) 
2)
3) 
;
3) 
4) 
4)
5)
5) 
2. Решить неравенства:
1) 
; 1)
2) 
; 2)
3) 
; 3)
4) 
4)
5) 
5)
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К их числу относятся простейшие тригонометрические уравнения, т. е. уравнения вида:
sin x = a, cos x = a, tg x = а, где а — действительное число.
1) если |a| < 1, то решения уравнения cos x =а имеют вид
х = ±arccos a + 2πп; 
2) если |a| < 1, то решения уравнения sin x = а имеют вид
х =
(-1)n arcsin a + πп, 
;
3) если |а| > 1, то уравнения cos x = a, sin x = а не имеют решений;
4) решения уравнения tg x = а для любого значения а имеют вид
х = arctg a + πп;
5) частные случаи:
sin x = 0, х = πп; 
sin x = 1, х = 
+ 2πn; 
sin x = -1, х = - 
+ 2πn; 
cos x = 0, х = 
+ πn; 
cos x = 1, х = 2πn; 
cos x = - 1, х = π + 2πn. 
Для решения тригонометрических уравнений чаще всего используются два метода: метод сведения тригонометрического уравнения к алгебраическому и разложение на множители.
Метод введения новой переменной применяется при решении тригонометрических уравнений в тех случаях, когда путем замены тригонометрического выражения на новую переменную уравнение удаётся свести к алгебраическому.
При решении уравнений методом разложения на множители кроме общепринятых способов разложения на множители, таких как вынесение за скобки общего множителя, способ группировки, применение формул сокращённого умножения и т.п., при решении тригонометрических уравнений также используются формулы преобразования суммы тригонометрических функций в произведение и другие. В результате удаётся привести исходное выражение к виду, удобному для разложения на множители.
Решение тригонометрических уравнений методом понижения степени.
Если в формуле 
заменить
на 
, получим
Таким образом, 
, значит,
Если в формуле 
заменить
на
, получим
Таким образом, 
значит,
Полученные две формулы называют формулами понижения степени.
К формулам понижения степени относятся и формулы:
При решении уравнений методом понижения степени, необходимо знать формулы преобразования сумм тригонометрических функций в произведение.
Решение однородных тригонометрических уравнений.
Уравнения вида
, 
и т.д. являются однородными относительно sin x и cos x. Сумма показателей степеней в каждом слагаемом при sin x и cos x у таких уравнений одинакова, и она, называется степенью
уравнения. Метод решения уравнений такого вида состоит в делении левой и
правой частей на cosn x ≠ 0 и получении целого уравнения n-ой степени относительно tg x.
Отметим, что полученное уравнение равносильно исходному, т.к. cosn x ≠ 0 ограничение не приводит к потере корней. Действительно, если предположить, что cos x = 0, то из исходного уравнения следует, что и sin x = 0. что противоречит основному тригонометрическому тождеству.
Уравнение вида 
{z≠0) не является однородным, но его можно свести к
однородному, представив правую часть в виде z = z (sin x + cos2 x). Однако при его решении возможна потеря корней в
результате деления нa cos2 x.
Практические советы.
При решении уравнений общими методами необходимо знать формулы:
1) sin2x + cos2 x = l ;
2)tg x = 
;
3) ctg x =
;
4) ctg x = 
;
5) l+tg2x =
;
6) l+ctg2x = 
;
7) 1 + cos 2x = 2 cos2 x;
8) 1- cos 2x = 2 sin2 x;
9) tg 2x= 
;
10) sin 2x=
;
11) cos 2x=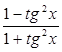 
;
12) sin 2x = 2 sin x cos x;
13) cos 2x = cos2 x - sin2 x, или cos 2x = 2cos2 x - 1, или cos 2x= 1 - 2 sin2 x;
14) Формулы приведения;
Неравенства, содержащие переменную под знаком тригонометрической функции, называются тригонометрическими.
При решении тригонометрических неравенств используют единичную окружность.
При выполнении практической работы рассмотрите следующие примеры:
Пример 1:
2 sin2x - 7cos x - 5 = 0.
Решение.
2(1 - cos2 x) - 7cos x - 5 = 0,
2 cos2 x + 7cos x + 3 = 0,
cos x = y,
2у2 + 7у + 3 = 0,
y1 = -3, y2= - 
.
1) cos x= -3< -1, х — не имеет решения;
2) cos x = - 
, х = ± 
π + 2πk, kÎΖ.
Ответ: х = ± 
π + 2 πk, kÎZ.
Пример 2:
cos 2x + 3 sin x = 2.
Решение.
1 - 2 sin2x + 3 sin x = 2,
2 sin2x - 3 sin x + 1 =0,
sin x = y,
2y2 - 3y + l= 0,
y1 = 
, y2
= l.
1) sin x = 
, x =
(-l)n 
+ πn , nÎZ;
2)
sin x = l, х = 
+2 πk, kÎZ.
Ответ: x = (- 1)n
+ πn, 
+ 2 πk, n,kÎZ.
Пример 3:
2 cos23x + sin 3x – 1 = 0.
Решение.
2(1— sin2 3х) + sin 3х - 1 = 0,
2 sin2 3х - sin 3х - 1 = 0,
sin 3x = y,
2у2 – y -1 = 0,
y1 = 1, y2 = - 
1) sin 3х = 1,
3х =
+ 2 π k, kÎZ;
х =
+ 2
π k, kÎZ;
х =
+ 
π k, kÎZ;
2) sin 3x= - 
,
х = (-1)n+l 
+
n, nÎΖ.
Ответ: х =
+ 
π k, kÎZ; , x = (- 1)"+1
+
n, nÎZ.
Пример 4:
Решите уравнение методом понижения степени.
Решение.
,
,
,
1) 
, или 2)
, 
,
.
Ответ: 
; 
.
Пример 5:
Решить
неравенство cos x > 
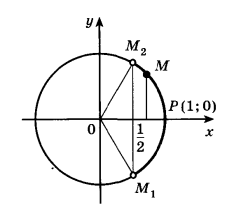
По определению cos x – это
абсцисса точки единичной окружности. Абсциссу, равную , имеют две точки единичной окружности
М1 и М2 . Абсциссу, большую имеют все точки М дуги единичной
окружности, лежащие правее прямой М1М2 . Таким образом,
решениями неравенства cos x > являются
все числа х из промежутка 
.
Все решения данного неравенства –
множество интервалов 
Ответ: 
Пример 6:
Решить
неравенство 
.
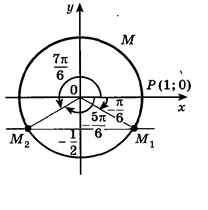
Ординату, не меньшую 
, имеют все точки дуги 
единичной окружности. Поэтому
решениями неравенства 
являются числа 
, принадлежащие промежутку 
. Все решения данного неравенства –
множество отрезков 
Отметим, что все точки
окружности, лежащие ниже прямой 
имеют ординату,
меньшую 
. Поэтому все числа 
являются решениями неравенства 
. Все решения этого неравенства –
интервалы 
Вопросы для закрепления теоретического материала к практическому занятию:
1. Какие уравнения называются тригонометрическими?
2. Какие методы решения тригонометрических уравнений вы знаете?
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.
2. Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.
3. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
4. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
5. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
6. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
7. Башмаков М.И. Математика: Учебник. — М., 2016.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
